- Учителю
- Производная и ее применение
Производная и ее применение
Открытый урок по теме "Производная и ее применение"
Разработала : преподаватель математики Жукова Е.А.
Урок обобщающего повторения (90 мин.)
Цели:
1. Повторить, систематизировать и закрепить знания по изучаемой теме.
2. Воспитывать такие качества личности как самостоятельность, внимательность, способствовать развитию творческих способностей путем составления самостоятельной работы.
3. Побуждать учащихся к самоконтролю, взаимоконтролю, самоанализу своей деятельности.
Оборудование: экран, проектор, магнитная доска, набор плакатов.
У учащихся на рабочем месте: оценочные листы, карточки с заданиями, карточки с вопросами по теории, копировальная бумага.
Вся работа на этом занятии сопровождается индивидуальным оценочным листом.
Оценочный лист учащегося.
Фамилия________________________________________________
Имя____________________________________________________
Урок
Этапы
Задания
Кол-во баллов
I
I
II
III
IV
Теоретическая разминка
Устная работа
Упражнения на нахождении производной
Решение задач на применении производной
II
IV
V
Решение задач на применении производной (продолжение)
Самостоятельная работа
Итоговое количество баллов
Оценка
Во всех этапах урока за каждый правильный ответ ученик зарабатывает по 1 баллу.
Критерии оценок:
"5" -с 43 до 47 баллов;
"4" - с38 до 42 баллов;
"3" - с 22 до 37 баллов;
"2" -меньше 22 баллов.
За самостоятельную работу выставляется отдельная оценка.
Предварительное домашнее задание: повторить вопросы и задачи на повторение, которые заданы в конце главы II. "Производная и ее применения" на стр. 166-168.
Ход урока
Вводная беседа (1 мин.)
Сегодня на уроке мы повторим, обобщим, приведем в систему изученные формулы, определения и правила вычисления производных и их применения.
I этап. Теоретическая разминка (25 мин.)
Начало урока посвящается повторению узловых вопросов темы.
Три человека выходят к доске. Класс задает им три вопроса из подготовленных по всему повторяемому материалу.
Вызванные отвечают по очереди. Затем выходят следующая тройка и продолжают отвечать на следующие вопросы, задаваемые учащимися и так продолжают до тех пор, пока не ответят на все вопросы. За каждый правильный ответ ученик проставляет по 1 баллу в свой оценочный лист.
После того как ученик ответил на заданный вопрос на магнитной доске вывешивается плакат с текстом данного определения или правила.
Вопросы теории:
-
Сформулируйте определение производной функции в точке.
-
В чем состоит геометрический смысл производной?
-
В чем состоит физический смысл производной?
-
Показать правила дифференцирования.
-
Показать формулы дифференцирования.
-
Написать уравнения касательной.
-
Исследование на экстремум.
-
Какие точки называются критическими?
-
В чем состоит необходимое условие экстремума?
-
В чем состоит достаточный признак существования экстремума?
-
Сформулируйте т. Вейерштрасса о наименьшем и наибольшем значениях функции на отрезке.
-
Дать алгоритм отыскания наибольшего и наименьшего значений функции y=f(x), непрерывной на отрезке [a;b].
-
Дать схему применения метода поиска наибольших и наименьших значений функции к решению прикладных задач.
-
Дать схему исследования и построения графика функции.
Плакаты.
1 плакат. Определение. Производной функции в точке Х0 называется число, к которому стремится разностное отношение f'(X0) = ![]() =
=![]() при
при ![]() Х, стремящемся к нулю.
Х, стремящемся к нулю.
2 плакат. Определение. Производная с геометрической точки зрения это угловой коэффициент касательной k = tg![]() =
= ![]() = f'(x0).
= f'(x0).
3 плакат. Определение. Производная с физической точки зрения - это мгновенная скорость V(t)= x'(t).
4 плакат. Правила дифференцирования:
(u + v)'= u'+v'
(u v)'= u'v + uv'
(![]() )'=
)'=![]()
(Cu)'= Сu', где с-const.
5 плакат. Формулы дифференцирования
С'=0 5. (cos x)'=-Sin x
(xn)'=nxn-1 6. (t g x)'=![]()
(![]() '=
'=![]()
![]() 7. (ctg x)'= -
7. (ctg x)'= -![]()
(sin x)'=cos x 8. h(x)=g(f(x))
h'(x)=g'(f(x))![]() f'(x).
f'(x).
6 плакат. Уравнение касательной Y=f(x0)+f'(x0)(x-x0)
7 плакат. Определение. Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции.
8 плакат. Необходимое условие экстремума.
Если точка х0 является точкой экстремума функции f и в этой точке существует производная f', то она равна нулю:
f'(x)=0
9 плакат. Достаточный признак существования экстремума.
Признак максимума. Если функция f непрерывна в точке х0, a f'(x)![]() 0 на интервале (а; х0) и f'(x)
0 на интервале (а; х0) и f'(x)![]() 0 на интервале (хо; в), то точка хо является точкой максимума функции f. (Если в точке хо производная меняет знак с плюса на минус, то хо есть точка максимума функции f).
0 на интервале (хо; в), то точка хо является точкой максимума функции f. (Если в точке хо производная меняет знак с плюса на минус, то хо есть точка максимума функции f).
Признак минимума функции. Если функция f непрерывна в точке хо, а f'(x)<0 на интервале
(а; хо) и f'(x)>0 на интервале (х0; в), то точка х0 является точкой минимума функции f. (Если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка минимума функции f).
10 плакат. Теорема Вейерштрасса о наименьшем и наибольшем значениях функции на отрезке.
Т. Вейерштрасса утверждает, что непрерывная на отрезке [ a; b] функция f принимает на этом отрезке наибольшее и наименьшее значения, т.е. существуют точки отрезка [a; b], в которых f принимает наибольшее и наименьшее на [a; b] значения.
11 плакат. Алгоритм отыскания наибольшего и наименьшего значений функции у= f(x), непрерывной на отрезке [a; b].
Найти f'(x).
Найти критические точки, т.е. где f'(x)=0 и f'(x) не существует, и отобрать из них те, что лежат внутри отрезка [a; b].
Вычислить значения функции y=f(x) в критических точках и на концах отрезка, и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции y=f(x) на отрезке [a;b], которые обозначают так: max[a;b] y(x) и m in[a;b]y(x).
12 плакат. Схема применения метода поиска наибольших и наименьших значений функции к решению прикладных задач.
Задача "переводится" на язык функций. Для этого выбирают удобный параметр х, через который интересующую нас величину выражают как функцию f(x);
Средствами анализа ищется наибольшее или наименьшее значение этой функции на некотором промежутке;
Выясняется, какой практический смысл (в терминах первоначальной задачи) имеет полученный (на языке функций) результат.
13 плакат. Алгоритм исследования функции и построения графика.
- Находят ее область определения;
- выясняют, является ли функция f четной или нечетной, является ли периодической;
- находят точки пересечения графика с осями координат;
- находят промежутки знакопостоянства;
- промежутки возрастания и убывания;
- точки экстремума и значения f в этих точках;
- исследуют поведение функции в окрестности " особых" точек и при больших по модулю х;
- на основании такого исследования строится график функции.
Итак, мы повторили все узловые вопросы по изученной теме. А теперь поупражняемся на применении этих правил.
II этап. Устная работа. (4 мин.)
Задания отразить диапроектором на экран, после ответов учащихся демонстрировать ответы на экран. Учащиеся заработанное количество баллов выставляют в оценочные листы.
g(x)= 2x-3 b) g(x)=3x4-7x3+2x2+![]() в) g(x)=
в) g(x)=![]() +1
+1
г) f(x)=(x-3)4 д) f(x)=(3-4x)3 e) f(x)= cos5x
Ответы: a) 2; b) 12x3-21x2+4x; в) -![]() ; г) 4(x-3)3; д) -12(3-4 x)2; е) -5sin5x.
; г) 4(x-3)3; д) -12(3-4 x)2; е) -5sin5x.
III этап. Выполнение упражнений на нахождение производной.(10 мин.)
Отразить задания диапроектором на экран. Как закончат, обмениваются тетрадями. Учитель включает проектор, демонстрирует ответы на экране. Происходит быстрая проверка и комментарий заданий. Учащиеся заработанное количество баллов выставляют в оценочные листы.
Задание. Найти значение производной при заданном значении аргумента.
f(x)=4x3+6x+3; x0=1
f(x)=x2- 4![]() ; x0=4
; x0=4
f(x)= ![]() ; x0=0
; x0=0
f(x)=x sinx; x0=![]()
f(x)=sin2x; x0=![]()
f(x)= 2x+cos2x; x0 = ![]()
Ответы: 1. 18; 2. 7; 3. 1; 4. 1; 5. -2; 6. 1.
Оценка - 6 баллов (по 1 баллу за каждый верно выполненный пример).
IV этап. Решение задач на применении производной. (Работа на доске) (20 мин.)
У всех имеются карточки с условиями задач. Учащиеся по вызову выходят к доске, показывают решение, а в это время все остальные выполняют эту работу в тетрадях, после проверяют и сверяют правильность выполнения, заработанное количество баллов выставляют в оценочные листы.
Содержание карточки.
Задачи о касательной.
-
Определить угол, который составляет с осью ох касательная к графику функции у=2х2 в точках с абсциссами х0=
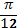 и х0=1.
и х0=1. -
Найти точки, в которых касательные к кривой у=х3+х-2 параллельны прямой у=4х-1.
-
Найти координаты точки, в которой касательная к параболе у=х2-х-12 образует с осью ох угол 45
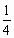 .
.
Задачи о скорости.
-
Закон прямолинейного движения материальной точки задан зависимостью S(t)=5t3-8t+2, где s и t измеряются соответственно в метрах и секундах. Найти скорость и ускорение в момент времени t=2с.
Исследование на экстремум.
-
Найти точки экстремума функции у = х3- 3 х2 + 18
6. Найти наименьшее и наибольшее значение функции у=2х3 + 3х2 - 12х на отрезке [-4;2].
7. Исследовать функцию у=3х - ![]() х3 и построить ее график.
х3 и построить ее график.
Ответы:
-
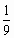 = 45
= 45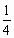
![]() =artg4.
=artg4.
-
(-1; -4), (1; 0)
-
А(1; -12)
-
52 м/с; 60 м/с2
-
х = 0 - точка максимума, уmax = y(0) = 18
X = 2 - точка минимума, ymin = y(2) = 14
-
унаим. = -32 при х = -4
Унаим. = 20 при х = - 2.
-
У = 3х -
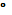 х3
х3
D(y)=R
f(-x)= -(3x - ![]() x3) = - f(x), следовательно, функция нечетная и ее график симметричен относительно начала координат.
x3) = - f(x), следовательно, функция нечетная и ее график симметричен относительно начала координат.
Ось Оу график пересекает в точке (0;0)
Ось Ох график пересекает при х1 = - 3![]() ; x2 = 0; x3 = 3
; x2 = 0; x3 = 3![]()
f'(x) = 3 - ![]() x2 ; D(f') = R, f'(x) = 0 при х1 = - 3; х2 = 3.
x2 ; D(f') = R, f'(x) = 0 при х1 = - 3; х2 = 3.
Х
(- ![]() ; -3)
; -3)
- 3
(- 3; 3)
3
(3; ![]() )
)
f'(x)
-
0
+
0
-
f(x)
![]()
- 6
![]()
6
![]()
V этап. Самостоятельная работа (28 мин.)
В конце проводиться самостоятельная работа (под копированную бумагу) в двух вариантах. Листок на котором лежала "копирка" учащиеся подписывают и сдают учителю, а по записям в тетрадях учащиеся осуществляют самопроверку по готовым решениям на экране, получают разъяснения по возникающим при этом вопросам. Учитель после проверки листков выставляет оценки за самостоятельную работу.
-
Исследуйте функцию y=6x5-10x3 [y=5x3 -3x2 ] на монотонность и экстремумы и постройте ее график.
-
Найдите наибольшее и наименьшее значения функции f(x)=sin 2x-2x на отрезке [ -
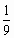 ;
;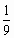 ].
].
[ 2. Найдите точки экстремума функции у = х + ![]() ].
].
-
Составьте уравнения касательной к графику функции f(x)=x2-x3, проходящей через точку графика с абсциссой x0=-1.
[3 составьте уравнения касательных к графику функции y=2x-x2 в точках графика ординатой y0= -3 ].
Ответы:
1. Функция ![]() на (-
на (-![]() ;-1]
;-1] ![]() [1;
[1;![]() ),
), ![]() на [-1;1];
на [-1;1];
Х=- 1- точка максимума, х=1- точка минимума;
4-максимум; -4-минимум функции.
График изображен на рис.1.
2. Наименьшее значение равно -![]() ;
;
наибольшее значение равно ![]() .
.
3. Y=-5x-3
[1. Функция ![]() на (-
на (-![]() ;-1]
;-1]![]() [1;
[1;![]() ) и
) и ![]() на [-1;1];
на [-1;1];
Х=-1-точка минимума; Х=1-точка максимума;
-2-минимум; 2-максимум функции
График изображен на рис. 2.
2. х=0,75 (точка максимума)
3. y=4х+1 и y=-4х+9]
Подведение итогов (2 мин.).
Учитель проводит фронтальный обзор основных этапов урока, оценивает работу учащихся, выставляет оценки за I часть и за самостоятельную работу, ориентирует учащихся в домашнем задании.
Тем, кто допустил ошибок, дается решать дома самостоятельную работу другого варианта, а остальным дается задание на составление самостоятельной работы на данную тему.