Сценарий учебного занятия по математике в технологии задачная форма организации учебной деятельности в 8 классе по теме: «Решение дробно-рациональных уравнений».

Сценарий учебного занятия по математике в технологии задачная форма организации учебной деятельности в 8 классе по теме:

«Решение дробно-рациональных уравнений».

1.Учащиеся знают:

1. что такое уравнение;

2. способы решения линейных и квадратных уравнений;

3. пропорция, основное свойство пропорции;

4. понятие равносильности уравнений;

5. область определения уравнения (т.е. область допустимых значений переменной в уравнении)

6. дробное рациональное выражение; когда дробь равна 0.

Учащиеся умеют:

1. решать целые уравнения, используя основное свойство пропорции, умножая обе части уравнения на наименьший общий знаменатель;

2. находить область определения алгебраической дроби, сокращать и приводить к новому знаменателю;

3. умеют выполнять действия с алгебраическими дробями.

2. Основной способ, по отношению к которому разворачивается учебная ситуация, это составление алгоритма решения дробно-рационального уравнения.

1) привести его к целому уравнению, умножив левую и правую части на общий знаменатель;

2)решить получившееся целое уравнение;

3)исключить из множества корней целого уравнения те корни , при которых левая или правая части уравнения не имеют смысла, т.е. обращают в нуль общий знаменатель дробей.

3. Ученики должны научиться находить посторонние корни, т.е. для каждого корня уравнения сделать проверку.

4. Учебная задача: составление алгоритма решения дробно-рационального уравнения.

5. Предметное содержание, которое будет осваиваться учениками на уроке - это решение дробно-рационального уравнения.

6.На данном уроке осваивается деятельностное (метапредметное) содержание: анализ, сравнение, обобщение, рефлексия.

7. Решить уравнения (самостоятельная работа учащихся и последующая демонстрация своего решения у доски)

_4.

_{8.Возможные варианты выполнения заданий:}

1 уравнение: (возможные варианты решения)

9х = 18∙5

9х = 90

х = 90:9

х = 10

Ответ: 10.

2 уравнение: (возможные варианты решения)

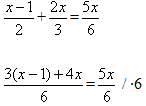
3х-3+4х = 5х

7х-5х = 3

2х = 3

х = 3:2

х = 1,5

Ответ: 1,5.

3 уравнение: (возможные варианты решения)

(х-2)(х-4) = (х+2)(х+3)

х²-4х-2х+8 = х²+3х+2х+6

х²-6х-х²-5х = 6-8

-11х = -2

х = -2:(-11)

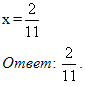
4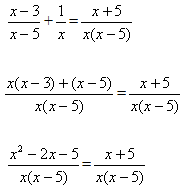 уравнение: (возможные варианты решения)

9. Выполняя данное задание, учащиеся или ошибочно решают данное уравнение, или, дойдя в решении до определенного момента, получают «явный сбой» (т.е. у учащихся не хватает средств для решения данного уравнения). Здесь происходит выход на постановку учебной задачи.

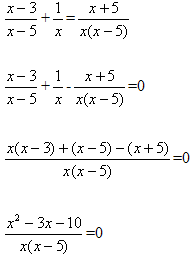
х²-3х-10=0 , D=49 , х₁=5 , х₂=-2.

Если х=5, то х(х-5)=0, значит 5- посторонний корень.

Если х=-2, то х(х-5)≠0.

10. Организация рефлексии:

1. Объясните, почему так получилось?

2. Почему в одном случае три корня, в другом - два?

3.Что делали при решении 1 уравнения?

4.Как делали?

3. Какие же числа являются корнями данного уравнения?

5. Как выяснить является ли число корнем уравнения?

11. Организация выхода к поиску нового способа возникает в ходе решения учащимися 4-го уравнения, когда получается два корня.

1. Почему в 4 уравнении, внешне похоже на 3 уравнение, появились посторонние корни?

2. Что делать?

_{2. Необходима проверка корней или нет?}

_{Учащиеся проверяют каждый этап решения на равносильность.}

_{Устанавливают, после преобразований они перешли к уравнению-следствию (т.е. перешли к неравносильному уравнению)}

_{Необходима проверка корней!}

_{12. В группах по 4 человека идет обсуждение выдвинутых версий.}

_{Версии:1.НОЗ;}

_{2. Обе части уравнения умножить на ОЗ;}

_{3.Решить целое уравнение;}

_{4. Для каждого корня уравнения №4 сделать проверку;}

_{5.Записать ответ.}

_{13. Способ2:}

_{Учитель организует рефлексию по фиксации способа2.}

_{1)в чем заключалась основная трудность при решении уравнения?}

_{2)как вы смогли её преодолеть?}

_{3) учитель предлагает учащимся выделить основные этапы решения уравнений данного вида и зафиксировать эти этапы в виде алгоритма.}

Учащиеся выделяют основные этапы решения уравнений данного вида.

И в итоге фиксируем алгоритм:

1) привести его к целому уравнению, умножив левую и правую части на общий знаменатель;

2)решить получившееся целое уравнение;

3)исключить из множества корней целого уравнения те корни, при которых левая или правая части уравнения не имеют смысла, т.е. обращают в нуль общий знаменатель дробей.

4) Записать ответ.

14. Домашнее задание:

Изучить п.34. Выполнить №769(а),775(а),№775(г) по желанию.

Рефлексия:

1.Ребята, что для каждого из вас сегодня было важно?

2. Какое открытие ты для себя сделал?

Всем спасибо, урок окончен.