АрхимедClassical Greek philosophy

Көне пәлсапа

Archimedes Thoughtful by Fetti (1620)

Аты:

Archimedes of Syracuse (Юнанша: Άρχιμήδης)

Тууы:

c. 287 BC (Syracuse, Sicily, Magna Graecia)

Өлімі:

c. 212 BC (Syracuse)

Ағымы/салты:

Euclid of Alexandria

Natural philosophy

Басты мүдделері:

математика, физика, механика,астрономия

Архимед (көне грекше: Αρχιμήδης, б.з.б. 287-212) Ежелгі Грекияның ұлы ғалымы, математигі, механигі. Ол Сицилия аралындағы Сиракуз қаласында, туып сонда өмір сүрген. Архимед астроном Фидийдің баласы деген жорамал бар. Архимед сол замандағы ірі мәдениет орталығы - Мысырды аралап, александриялық ғалымдардан, солардың ішінде Конон мен Эратосфеннен білім алған. Оның математикалық еңбектері өз заманынан озық болған, бұл еңбектері дифференциалдық және интегралдық есептеу ашылғанда (17 ғасыр) дұрыс бағаланған. Архимедтің көптеген математикалық еңбектерінің ішінен қисық сызықтардың ұзындықтарын, әр түрлі фигуралар мен денелердің көлемін және беттердің ауданын есептеу ерекше орын алды.^[1]

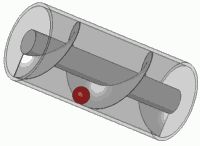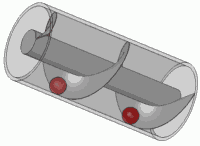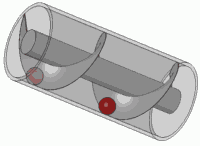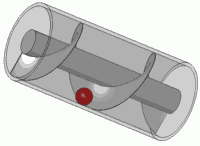
Денелерді Архимед винтімен көтеру

Архимед рычаг заңын, суда өлшеу арқылы қорытпаның құрамын анықтау тәсілін тапқан, өз атымен аталған гидростатика заңын (Архимед заңы) ашқан, жер суаратын механизмдерді, жүк көтеретін рычаг жүйелері мен блоктарды, тас ататын қамал бұзатын соғыс қондырғыларын, т.б. ойлап шығарған. Рычагтың математикалық заңын тапқанда, Архимед "Тіреу нүктесін берсеңдер, Жерді де төңкеріп тастаймын" деп айтқан екен. Архимед шығармаларының көпшілігі сақталмаған, ал оның "Эратосфенге жолдаған" хаты 1906 жылы ғана табылған. 9-11 ғасырларда Архимедтің еңбектері араб тіліне, ал 13 ғасырда олар араб тілінен латын тіліне аударылып, Батыс Еуропа елдеріне тарай бастаған. 1823 жылы Архимедтің "Шар мен цилиндр" және "Дөңгелекті өлшеу және леммалар" атты екі кітабы орыс тіліне аударылған.

Об Архимеде - великом математике и механике - известно больше, чем о других ученых древности. Прежде всего достоверен год его смерти - год падения Сиракуз, когда ученый погиб от руки римского солдата. Впрочем, историки древности Полибий, Ливии, Плутарх мало рассказывали о его математических заслугах, от них до наших времен дошли сведения о чудесных изобретениях ученого, сделанных во время службы у царя Гие-рона II. Известна история о золотом венце царя. Чистоту его состава Архимед проверил при помощи найденного им закона выталкивающей силы, и его возгласе «Эврика!», т.е. «Нашел!». Другая легенда рассказывает, что Архимед соорудил систему блоков, с помощью которой один человек смог спустить на воду огромный корабль «Сирахоеия», Крылатыми стали произнесенные тогда слова Архимеда: «Дайте мне точку опоры, и я поверну Землю».

Инженерный гений Архимеда с особой силой проявился при осаде Сиракуз, богатого торгового города на острове Сицилия.

Воины римского консула Марцелла были надолго задержаны у стен города невиданными машинами: мощные катапульты прицельно стреляли каменными глыбами, в бойницах были установлены метательные машины, выбрасывающие грады ядер, береговые краны поворачивались за пределы стен и забрасывали корабли противника каменными и свинцовыми глыбами, крючья подхватывали корабли и бросали их вниз с большой высоты, системы вогнутых зеркал (в некоторых рассказах -щитов) поджигали корабли. В «Истории Марцелла» Плутарх описывает ужас, царивший в рядах римских воинов: «Как только они замечали, что из-за крепостной стены показывается веревка или бревно, они обращались в бегство с криком, что вот Архимед еще выдумал новую машину на их погибель».

Огромен вклад Архимеда и в развитие математики. Спираль Архимеда (см. Спирали), описываемая точкой, двигающейся по вращающемуся кругу, стояла особняком среди многочисленных кривых, известных его современникам. Следующая кинематически определенная кривая-циклоида-появилась только в XVII в. Архимед научился находить касательную к своей спирали (а его предшественники умели проводить касательные только к коническим сечениям), нашел площадь ее витка, а также площадь эллипса, поверхности конуса и шара, объемы шара и сферического сегмента. Особенно он гордился открытым им соотношением объема шара и описанного вокруг него цилиндра, которое равно 2:3 (см. Вписанные и описанные фигуры). Архимед много занимался и проблемой квадратуры круга (см. Знаменитые задачи древности). Ученый вычислил отношение длины окружности к диаметру (число П) и нашел, что оно заключено между 3 10/71 и 3 1/7.

Созданный им метод вычисления длины окружности и площади фигуры был существенным шагом к созданию дифференциального и интегрального исчислений, появившихся лишь 2000 лет спустя.

Архимед нашел также сумму бесконечной геометрической прогрессии со знаменателем 1/4. В математике это был первый пример бесконечного ряда.

Большую роль в развитии математики сыграло его сочинение «Псаммит»-«О числе песчинок», в котором он показывает, как с помощью существовавшей системы счисления можно выражать сколь угодно большие числа. В качестве повода для своих рассуждений он использует задачу о подсчете количества песчинок внутри видимой Вселенной. Тем самым было опровергнуто существовавшее тогда мнение о наличии таинственных «самых больших чисел».

Карл Фридрих Гаусс

Гаусс, Карл Фридрих

(1777-1855)

Карл Фридрих Гаусс (нем. Johann Carl Friedrich Gauß; 30 сәуір 1777,Брауншвейг - 23 ақпан 1855, Гёттинген) - ұлы неміс математигі, астрономы және физигі, Санкт-Петербург ғылым академиясының құрметті мүшесі (1824).18 ғасырдың соңында Германиада бір сабақта мұғалім оқушыларына "1 - ден 100 ге дейінгі натурал сандардың қосындысын табуды" тапсырыпты. Оқушылардың біреуі: ізделген қосынды 5050-ге тең деп жауап беріпті. бұл оқушы кейіннен аты әлемге әйгілі болған Математиктер королі Карл Фридрих Гаусс екен.

Еңбектері:Геттинген университетінде оқыған (1795 - 98).

• 1807 жылдан Геттинген универститетінің профессоры және Геттинген астрономиялық обсерваториясының директоры болды.

Оның еңбектері алгебраның, сандар теориясының, дифференциалдық геометрияның, тартылыс теориясының, электр және магнит құбылыстарының классикалық теориясының,геодезияның, теориялық астрономияның дамуына орасан зор ықпал етті. Кез келген алгебралық теңдеудің кем дегенде бір түбірі болатындығы жөніндегі алгебраның негізгі теоремасын дәлелдеген (1799). Гаусс сондай-ақ,астрономия, ықтималдық теориясы, шексіз қатарлар теориясы, потенциалдар теориясы, т.б. салалар бойынша да іргелі еңбектер жазған, жоғары геоздезияның математикасы негізін қалаған. Ол өлшеу кезінде жіберілетін қателіктерді есептей отырып, ең кіші квадраттар тәсілін және 3 рет бақылау нәтижесінде планеталардың эллипстік орбитасын есептеу тәсілін ұсынған.1830 - 40 ж. неміс физигі В. Вебермен біріге отырып теориялық физикадан елеулі табысқа жетті. Сөйтіп электр магниттік бірліктердің абсолют жүйесін (қ. Бірліктердің СГС жүйесі) құрды.

1833 ж. Германиядағы тұңғыш электр магниттік телеграфты құрастырды. Ол Н.И. Лобачевскийдің еңбектерінде дамытылған Евклидтік емес геометриялардың идеяларына ерекше мән берді. (1+100)+(2+99)+......+(49+52)+(50+51)=(100+1)∗50=5050{\displaystyle ~(1+100)+(2+99)+......+(49+52)+(50+51)=(100+1)*50=5050}

Салу есептері

Салу есептерді ежелгі математиктер еңбектері арасынан елеулі орын алған. Өйткені, бұл кезеңде барлық математикалық деректер сызба көмегімен геометриялық тілде негізделген. Сызғыш пен циркульді пайдаланып көпбұрыштарды, оның ішінде дұрыс көпбұрыштарды салу мәселесі немістің ұлы математигі Карл Гауссқа дейін өз шешімін таппай келді. Бұл мәселені тек 1801 жылы ғана К. Гаусс алгебралық жолмен толық шешті. Оның дәлелдемесі бойынша дұрыс n-бұрышты циркульді және сызғышты пайдаланып салу үшін n=2m. P1·…·P k, m€Z, m≥0, P1, …, P k2²+1, ал 7 мұндай түрде жазылмайды, яғни жетібұрышты циркулді және сызғышты пайдаланып салуға болмайды.

Карл Фридрих Гаусс

(Математические вычисления заменили Гауссу обычные детские игры. Он делил единицу на все простые числа р из первой тысячи подряд, подмечая, что десятичные знаки рано или поздно начинают повторяться. Рассмотрев большое количество примеров, Гаусс доказал, что число цифр в периоде не превосходит р - 1 и всегда является делителем р - 1. Он интересовался случаями, когда период в точности равен р - 1, и это постепенно привело его к первому открытию.Ученый доказал, что правильный n-угольник, где n -число простое, может быть построен циркулем и линейкой в том, и только в том, случае, когда п имеет вид 22 + 1. Например, если k = О, 1, 2, 3, то правильные трех-, пяти-, семнадцати- и 257-угольники можно построить циркулем и линейкой, а семиугольник -нельзя. Еще древние математики (в их числе Архимед) умели строить циркулем и линейкой правильные n-угольники при п = 3, 4, 5, 6 и вообще при п = 2"; 2"*3; 2"*5; 2**15, и только такие. Ученые безуспешно пытались построить правильный семиугольник, девятиугольник. А Гаусс дал полное решение проблемы, над которой трудились ученые в течение 2 тыс. лет.

С этого момента девятнадцатилетний Гаусс окончательно решил заниматься математикой (до этого он не мог сделать выбор между математикой и филологией). И всего через 9 дней в его дневнике появляется запись о втором открытии. Гаусс доказал так называемый квадратичный закон взаимности-один из основных в теории чисел. Этот закон открыл еще Л. Эйлер, но доказать его не смог.С именем К.Ф. Гаусса связаны многие замечательные страницы в истории математики. Он дал доказательство основной теоремы алгебры (всякое алгебраическое уравнение с действительными коэффициентами имеет корень). Гаусс создал теорию поверхностей. До него были изучены геометрии только на двух поверхностях: на плоскости (планиметрия Евклида) и на сфере (сферическая геометрия). Гаусс нашел способ построения геометрии на любой поверхности, определил, какие линии играют на поверхности роль прямых, как мерить расстояния между точками на поверхности и т.д. Теория Гаусса получила название внутренней геометрии. Он не опубликовал своих работ по неевклидовой геометрии и теории эллиптических функций. Эти результаты были открыты заново его младшими современниками: русским математиком Н.И. Лобачевским и венгерским математиком Я. Больяй-в первом случае и норвежским математиком Г. X. Абелем и немецким математиком К. Г. Якоби - во втором.Гаусс занимался также астрономией, электромагнетизмом. Ему удалось вычислить орбиту малой планеты (астероида) Цереры. Решение этой сложной задачи принесло ученому известность, и он был приглашен заведовать кафедрой математики и астрономии, с которой была связана должность директора Гет-тингенской обсерватории. Этот пост Гаусс не покидал до конца жизни. Результаты своих исследований по астрономии Гаусс объединил в фундаментальном труде «Теория движения небесных тел».

Леонард Эйлер

(1707-1783)

Леонард Эйлер, нем. Leonhard Euler. 4.1707, Базель, Швейцария - 7(18).9.1783, Санкт-Петербург, Ресей) - швейцариялық математик, механик жәнефизик. Базель университетін бітірген. 1727 жылдан Санкт-Петербургакадемиясында қызмет істеді. Ол - Санкт-Петербург және Берлинакадемияларынан басқа Париж академиясының, Лондон корольдық қоғамының,Санкт-Петербург академиясының , т.б. көптеген ірі ғыл. қоғамдардыңмүшесі болды. Эйлердің негізгі еңбектері сол кездегі математика мен механиканың барлық саласына, серпімділік теориясына, математикалық физикаға, оптикаға, музыка теориясына, машиналар теориясына, баллистикаға, теңіз ғылымына, т.б. арналған. Оның ғылыми еңбектерінің жинағы ауқымды 60-80 том көлемінде деп болжанады.Эйлер "Аналитикалық түрде баяндалған механика не қозғалыс туралы ғылым" (2 томдық, 1736), "Анализге кіріспе" (2 томдық, 1748), "Дифференциалдық есептеу" (1755), "Универсал арифметика" (2 томдық, 1768 - 1769) және 6 тілде 30 шақты рет басылып шыққан "Интегралдық есептеу" (3 томдық, 1768 - 1770; 4 томдық, 1794), т.б. осы сияқты бірқатар классик.монографияларында өзінің және басқа ғалымдардың зерттеулерінің нәтижелерін жүйеге келтірді. Ол "Механика" атты монографиясында жаңа математикалық анализдің көмегі арқылы нүктединамикасын тұңғыш рет кең көлемде баяндады, ал "Қатты денелер қозғалысы теориясында" қатты дененіңкинематикасы мен динамикасының теориясын жетілдірді және қатты дененің қозғалмайтын нүкте маңынан айналу теңдеуін (гироскоптар теориясының бастамасы болған) тапты. Аспан механикасы бойынша да үлкен жаңалықтар ашты. 1757 - 1771 жылдары жарық көрген мемуарлары тұтас орта механикасы жөнінен жүргізілген зерттеулерге қосылған елеулі үлесі болды. Эйлер вариациялық есептеу мен дифференциалдық теңдеулер теориясының негізін жасады, дифференциалдық және интегралдық есептеулерді жалпылап, одан әрі дамытты. Ол - 886 мақала менмемуардың авторы.

Леонард Эйлер

Эйлер, крупнейший математик XVIII в., родился в Швейцарии. В 1727 г. по приглашению Петербургской академии наук он приехал в Россию. В Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков, астрономов, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.

Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома. Среди его работ-первые учебники по дифференциальному и интегральному исчислению.

В теории чисел Эйлер продолжил деятельность французского математика П. Ферма и доказал ряд утверждений: малую теорему Ферма, великую теорему Ферма для показателей 3 и 4 (см. Ферма великая теорема), Он сформулировал проблемы, которые определили горизонты теории чисел на десятилетия.

Эйлер предложил применить в теории чисел средства математического анализа и сделал первые шаги по этому пути. Он понимал, что, двигаясь дальше, можно оценить число простых чисел, не превосходящих п, и наметил утверждение, которое затем докажут в XIX в. математики П. Л. Чебышев и Ж. Адамар.Эйлер много работает в области математического анализа. Здесь он постоянно пользуется комплексными числами. Его имя носит формула е" = cosx + isinx, устанавливающая связь тригонометрических и показательной функций, возникающую при использовании комплексных чисел.Ученый впервые разработал общее учение о логарифмической функции, согласно которому все комплексные числа, кроме нуля, имеют логарифмы, причем каждому числу соответствует бесчисленное множество значений логарифма.В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку-топологию.

Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В - Р + Г = 2.

Даже основные результаты научной деятельности Эйлера трудно перечислить. Здесь и геометрия кривых и поверхностей, и первое изложение вариационного исчисления с многочисленными новыми конкретными результатами. У него были труды по гидравлике, кораблестроению, артиллерии, геометрической оптике и даже по теории музыки. Он впервые дает аналитическое изложение механики вместо геометрического изложения Ньютона, строит механику твердого тела, а не только материальной точки или твердой пластины.

Одно из самых замечательных достижений Эйлера связано с астрономией и небесной механикой. Он построил точную теорию движения Луны с учетом притяжения не только Земли, но и Солнца. Это пример решения очень трудной задачи.

Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него наиболее громоздкие вычисления.

Для многих поколений математиков Эйлер был учителем. По его математическим руководствам, книгам по механике и физике училось несколько поколений. Основное содержание этих книг вошло и в современные учебники.

Пифагор

( 570-500 гг. до н.э.)

Самостық Пифагор (еж.-грек. Πυθαγόρας ὁ Σάμιος, лат. Pythagoras; 570-490 жж. б.з.д) - ежелгі грек философы және математигі. «Философия» (пәлсапа) сөзін алғаш рет қолданған Антика дәуірінің атақты философы және математигі Пифагор болған.

Пифагордың өмірбаяны

Пифагоршылардың күннің шығуын күтіп алуы, суретті Fyodor Bronnikov сызған (1827-1902)

Ұлы ғалым Пифагор б.з.д. 570 жылы Самос аралында туған. Пифагордың әкесі Мнесарх зергер болған. Пифагордың анасының аты белгісіз. Көптеген жазбалар бойынша туған бала өте әдемі болған және өсе келе өзінің ерекше қабілетімен көзге түскен.

Жас Пифагордың ұстаздарынан Гермодамант пен Ферекид Сиросскийді атауға болады(алайда Пифагордың алғашқы ұстаздары Гермодамант пен Ферекид екені нақты емес). Жас Пифагор күні бойы Гермодаманттың жанында жүріп, Гомердің жақсы әуендерді тыңдап өскен.

Гомердің әуендерін Пифагор жадында мәңгі сақтады. Пифагорды ойшыл деп мойындағаннан кейін жас талант әр күнін оқушылардың арасында Гомердің әуенімен бастаған. Ферекид Италия мектебінің негізін қалаған философ болған. Осылай, Гермодамант Пифагорды музыкаға, Ферекид ғылымға үйреткен. Ферекид Пифагорға табиғат сенің алғашқы да басты ұстазың деген. Жас Пифагорға өз қиялын іске асыру үшін Самостар болды, сондықтан ол Милетке сапар шегіп, онда басқа ғалым - Фалесті кездестірді. Фалес оған білім алу үшін Египетке бар деп кеңес берді. Пифагор оның кеңесін жөн көрді.

Күн батып бара жатқан мезгілдегі көлеңкеңнің ұзарғанына қарап өзіңді ұлы адаммын деп ойлап қалма. (Пифагор)

Пифагор б.з.д. 548 жылы үй - жай және тамақ табылатын Навкратис жеріне келді. Фараонның түсіндірме хатына қарамастан білгірлер Пифагорға өз құпияларын ашуға асықпай, оған қиын сынақтар қойды. Пифагор білімге деген құштарлығының арқасында сынақтардан оңай өтті. Ол кездегі Египет геометриясы жаратылыстану бағытындағы ғылым болғандықтан египеттік білгірлер оған көп нәрсені үйрете алмады. Білгірлер берген білімді меңгерген Пифагор өз Отанына Элладаға қашып кетті. Біраз жол жүрген Пифагорды үйіне қарай бет алып бара жатқан Вавилон билеушісі Камбиз тұтқынға алады.

ІІІ ғ. Пифагор бедерленген монета Пифагордың Вавилондағы өмірі аса қиын болған жоқ. Вавилон математикасы Египеттікіне қарағанда аса дамыған болатын және Пифагордың үйренетіні де көп еді. Бірақ б.з.д. 530 жылдары Кир Орта Азиядағы тайпаларға қарсы жорыққа шығады. Қаладағы бұл жағдайды пайдаланып Пифагор Отанына қашып кетеді. Бұл кезде Самос аралығындағы билік Поликрат патшаның қолында еді. әрине Пифагор жартылай құл ретінде өмір сүруді ұнатпады,сондықтан ол Самостың жанындағы үңгірге кетіп қалады. Бірнеше айдан соң Пифагор Кротонға көшіп келеді. Кротонда Пифагор өздерін пифагорлықтар деп атаған адамдардан діни одақ құрады. Ол әрі діни бірлестік,саяси клуб және ғылыми одақ болған. Пифагордың кейбір әдеттері үлгі алуға лайықты.... 20 жыл өтті. Одақтың атағы бар әлемге тарады. Бір күні Пифагорға бай,бірақ жексұрын Килон одаққа бірігу үшін келеді. Пифагор Килонның бетін қайтарады. Килон Пифагордың үйінің өртенгенін пайдаланып,оған қарсы шығады. өрт кезінде пифагорлықтар өз өмірлерін қиып,ұстаздарын құтқарып алады. Қатты қайғырған Пифагор өз - өзіне қол жұмсайды.

Пифагор философиясы

Пифагор музыканы үйретуде, «Афина мектебі», Рафаэль сызған.

Пифагордың философиялық идеялары Орфей дінінің ықпалына ұшыраған, қою мистикалық сипатқа ие. Ол грек философиясында санға айырықша назар аудару дәстүрін қалыптастырды, бүкіл ғарышты, зат атаулыны сан арқылы тануға, тіпті санның бойынан киелі мағыналар оқуға тырысты.^[1]

Бұл туралы ежелгі грек ойшылы Аристотель былай деп жазды:

"Пифагоршылдар тұңыш рет математикалық біліммен айналысушылар болды. Олар математикалық қағидалар барлық заттың ортақ қағидасы деп танып, ең жоғары ғылым ретінде барынша тереңдеуге тырысты." («Метафизика 1-5»

Пифагор математика арқылы музыкалық ырғақты зерттеп, содан күні бүгінге дейін кең қолданылатын "гармония" ұғымын туғызды. Бүкіл ғарыш, бүкіл адам болмысы, адамның ішкі жан әлемі түгелдей гаромниялық үндестікке, ғажайып үйлесімге ие. Дүниенің нағыз қуанышы сол үндестікті оқу, үйлесімділікті сезіну. Ол тіпті аспандағы жұлдыздар гармониялы нүктелерге орналасқан, олардың қозғалысынан туған тоғыспалы үн "ғарыш күйі" болып ойналады деп есептеді. ^[2]

Ғарышты түсіндіруде, Пифагор Милет мектебінің дәстүрін өзінің Сан туралы идеяларымен ұштастырды. Ол көптеген шекті әлемдер өмір сүреді, жер шары шар пішінде, бірақ жер ғаламның орталығы емес деп есептеді. Оның бұл идеяларын қазіргі танылған шындықтарға негізінен жат келмейді деп бағалауға болады.

Пифагордың сан туралы зерттеулері кейінгі идеализмнің, жалпылық туралы теориялардың қалыптасуына ықпал етті. Ол танымды идеяда танылатын және сезімде танылатын деп екіге ажыратты. Идеяда танылатыны кемел, мәңгілік, мәнді даналық. Ал, сезімде танылатыны уақыттық, шекті, кемелсіз білімдер. Бұл пікірді кейін Платон ары қарай дамытып өзінің негізгі философиялық идеясы етіп жүйеледі.^[3]

Оның «Алтын нақылдар» деген жинағында мынадай пікірлер де айтылған: "Құдайлардан да ежелгі нәрселер бар, ол үміт пен үрей"; "Құдайлар адамды жаратқанына өкінді ме? Жоқ, қайта адам Құдайларды жаратқанына өкінді;" "Аз сөйле, одан да аз жаз"...^[4]

Пифагор сандары - натурал сандар үштігі, бұл сандар үшбұрыш қабырғаларының ұзындығына пропорционал (немесе тең) болса, онда үшбұрыш тікбұрышты болып табылады. Бұл үшін Пифагордың кері теоремасы бойынша ол сандардың х2+у2=z2 түріндегі диофант теңдеуін қанағаттандыруы жеткілікті (мыс., х=3, у=4, z=5). Өзара жай Пифагор сандарының кез-келген үштігі мына формулалар арқылы анықталады: х=m2-n2, у=2mn, z=m2+n2, мұндағы m және n - бүтін сандар (m>n>0).^[5]

Пифагор теогремасы

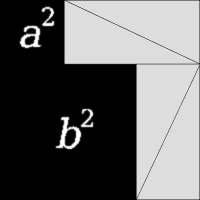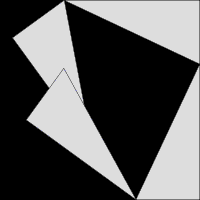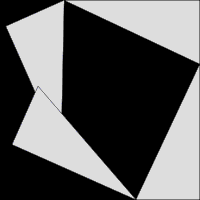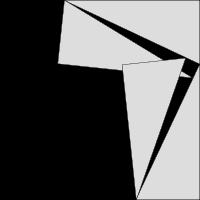Пифагор теогремасы - тік бұрышты үшбұрыштың қабырғаларының арасындағы байланысты тұжырымдайтын геометрия теоремасы. Пифагор теогремасы Пифагорға дейін де белгілі болған, бірақ оны жалпы түрде дәлелдеген Пифагор. Алғашында теорема тік бұрышты үшбұрыштың гипотенузасы мен катеттеріне салынған квадраттар аудандарының қатынасын тұжырымдаған: гипотенузаға тұрғызылған квадрат ауданы катеттерге тұрғызылған квадраттар аудандарының қосындысына тең. Пифагор теогремасы қысқаша былай тұжырымдалады: тік бұрышты үшбұрыштың гипотенузасының квадраты катеттері квадраттарының қосындысына тең. Пифагор теогремасына төмендегідей кері теорема да дұрыс: егер үшбұрыштың бір қабырғасы ұзындығының квадраты қалған екі қабырғасы ұзындықтарының квадратына тең болса, онда ол үшбұрыш тік бұрышты болады

Теореманың тарихы

Теоременың тарихы ежелгі Қытайдан бастау алады. Ондағы негізгі назар аудартатын математикалық кітап Чу - пей. Бұл шығармада қабырғалары 3,4,5 - ке тең пифагор үшбұрышы туралы айтылады.

Егер тік бұрышты құрайтын 3 - ке тең қабырға мен 4 - ке тең биіктіктің ұштарын қоссақ пайда болған түзу 5 - ке тең болады..

Кантор (ұлы неміс математика тарихын зерттеуші) бұл кітапта үнді Бхаскар геометриясындағы сызбанұсқаға ұқсас сурет бар, деп есептеген.

Бұл теңдік египтіктерге б .з.д. 2300 жылы Аменемхета I патшаның кезінде белгілі болған (Берлин музейіндегі 6619 - жазбалар бойынша).

Кантордың ойынша гарпедонаптар немесе «арқан тартушылар» тік бұрышты қабырғалары 3,4,5 - ке тең тікбұрышты үшбұрыштар арқылы тұрғызған. Олардың құрылу әдісін оңай көрсетуге болады. Ұзындығы 12 метрге тең арқанды алып,бір ұшынан 3 метр,екінші ұшынан 4 метр арақашықтықты өлшеп белгілейміз. Тік бұрыш 3 - ке және 4 - ке тең қабырғалар арасында болады. Қабырғалардың ұштарының арақашықтығы 5 - ке тең болады.

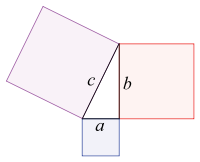
Тік бұрышты үшбұрыштың гипотенузасына салынған квадраттың ауданы катеттеріне салынған квадраттардың аудандарының қосындысына тең...

Бұл Пифагор теоремасы деп аталатын ежелден белгілі геометриялық теорема. Гректің ұлы математигі , әрі философы Пифагор Самосский осыдан 2,5 мың жыл бұрын өмір сүрген. Пифагор Шығыс елдеріне, Египетке және Вавилонға көп саяхат жасаған.Оңтүстік Италияның грек колонияларының бірінде ежелгі Грецияның ғылыми және саяси өмірінде үлкен роль атқарған белгілі «Пифагор мектебінің» негізін салған. Бұл белгілі геометриялық теореманың дәлелдеуін Пифагор практикада қолдана білген.

Бірақ, бұл теореманы Пифагорға дейін 1500 жыл бұрын ежелгі египеттіктер қабырғалары 3,4 және 5 тең болатын үшбұрыш тікбұрышты болатынын білген және бұл қасиетті жер учаскелерін, құрылыс тұрғызу үшін қолданған. Сонымен қатар мың жылдықтар бұрын Египеттегі, Вавилондағы, Қытайдағы үлкен храмдар салу үшін де қолданған. Пифагордан 600 жыл бұрын қытайдың математика-астрономиялық «Чжоу-би» шығармасында тікбұрышты үшбұрышқа қатысты басқа да теоремалар арасында Пифагор теоремасы да бар. Бұдан да ертерек теорема үндістерге де белгілі болған.

Теореманың қарапайым дәлелдеуі

Тік бұрышты үшбұрыштың гипотенузасына салынған квадрат катеттеріне салынған квадраттардың қосындысымен тең шамалы. Теореманың қарапайым дәлелдеуі тең бүйірлі үшбұрыш жағдайында қарастырылады. Теореманың өзі де осыдан басталған.

Теореманың дұрыстығына көз жеткізу үшін тең бүйірлі тікбұрышты үшбұрыштар мозаикасына қарау жеткілікті. Мысалы, ΔABC үшін : АС гипотенузасына салынған квадрат 4 үшбұрыштан құралған, ал катеттерге салынған квадраттардың әрқайсысы екі үшбұрыштан тұрады. Теорема дәлелденді.

Теореманы алгебралық әдіспен дәлелдеу

Т - катеттері а, b және гипотенузасы с болатын тікбұрышты үшбұрыш болсын. с2=а2+b2 екенін дәлелдеу керек.

Қабырғалары а+b -ға тең Q квадратын саламыз. Q квадратының қабырғаларынан А, В, С, D нүктелерін, пайда болған АВ, ВС, CD, DA кесінділері катеттері а және b -ға тең Т1, Т2, Т3, Т4 тікбұрышты үшбұрыштар құратындай етіп саламыз. ABCD тіктөртбұрышын Р деп белгілейміз. Енді Р қабырғалары с-ға тең квадрат екенін көрсетуіміз қажет.Барлық Т1, Т2, Т3, Т4 тік бұрышты үшбұрыштары Т тік бұрышты үшбұрышына тең (екі катеті бойынша). Сондықтан олардың гипотенузалары Т тікбұрышты үшбұрышының гипотенузасына, яғни с кесіндісіне тең. Енді бұл төртбұрыштың бұрыштары тік екенін дәлелдейміз.және - Т үшбұрышының сүйір бұрыштары. Онда + = 90° екендігі белгілі. Р төртбұрышының А төбесіндегі бұрышы , бұрыштарымен қоса жазыңқы бұрышты құрайды. Сондықтан + + =180°. + = 90° болғандықтан =90°. Р төртбұрышының басқа бұрыштарының да тік екендігі дәл осылай дәлелденеді. Осыдан, Р төртбұрышы қабырғасы с болатын квадрат екендігі шығады.

Қабырғасы а+b -ға тең Q квадраты қабырғасы с-ға тең Р квадраты мен Т үшбұрышына тең төрт үшбұрыштан тұрады. Сондықтан олардың аудандары үшін S(Q)=S(P)+4S(T)орындалады.

S(Q)=(a+b)2;

S(P)=c2 және

S(T)=½a*b өрнектерін S(Q)=S(P)+4S(T) теңдігіне қою арқылы (a + b)2 = c2 + 4*½a*b теңдігін аламыз. (

(a+b)2=a2+b2+2*a*b болғандықтан (a+b)2=c 2+4*½a*b теңдігін мына түрде жазуға болады: a2+b2+2*a*b=c2 +2*a*b.

a2+b2+2*a*b=c2+2*a*b теңдігінен с2=а2+b2 тең екендігі шығады.

Қабырғасы а+b -ға тең Q квадраты қабырғасы с-ға тең Р квадраты мен Т үшбұрышына тең төрт үшбұрыштан тұрады. Сондықтан олардың аудандары үшін S(Q)=S(P)+4S(T)орындалады.

S(Q)=(a+b)2;

S(P)=c2 және

S(T)=½a*b өрнектерін S(Q)=S(P)+4S(T) теңдігіне қою арқылы (a + b)2 = c2 + 4*½a*b теңдігін аламыз. (

(a+b)2=a2+b2+2*a*b болғандықтан (a+b)2=c 2+4*½a*b теңдігін мына түрде жазуға болады: a2+b2+2*a*b=c2 +2*a*b.

a2+b2+2*a*b=c2+2*a*b теңдігінен с2=а2+b2 тең екендігі шығады.

Фигуралардың тең шамалылығын пайдала отырып дәлелдеу

Берілген тікбұрышты үшбұрыштың гипотенузасына салынған квадрат катеттерге салынған квадраттар құрастырылған фигуралардан тұратынын дәлелдеуді қарастыруға болады. 2 суретте екі тең квадраттар бейнеленген. Әрбір квадраттың қабырғаларының ұзындығы а + b-ға тең. Квадраттардың әрбіреуі квадраттар мен тікбұрышты үшбұрыштардан тұратын бөліктерге бөлінген.Егер квадрат ауданынан катеттері а және b-ға тең тік бұрышты үшбұрыштың 4 еселенген ауданын алып тастасақ, онда тең шамалы аудандар қалады, яғни c2 = a2 + b2 . Бұл дәлелдеуді ұсынған ежелгі үндістер дәлелдеуді жазбаған, тек сызбаны «қара!» деген сөзбен түсіндірген.

Пифагор

Письменных документов о Пифагоре Самосском не осталось, а по более поздним свидетельствам трудно восстановить подлинную картину его жизни и достижений. Известно, что Пифагор покинул свой родной остров Самос в Эгейском море у берегов Малой Азии в знак протеста против тирании правителя и уже в зрелом возрасте (по преданию в 40 лет) появился в греческом городе Кротоне на юге Италии. Пифагор и его последователи - пифагорейцы - образовали тайный союз, игравший немалую роль в жизни греческих колоний в Италии. Пифагорейцы узнавали друг друга по звездчатому пятиугольнику-пентаграмме.

На учение Пифагора большое влияние оказала философия и религия Востока. Он много путешествовал по странам Востока: был в Египте и в Вавилоне. Там Пифагор познакомился и с восточной математикой. Математика стала частью его учения, и важнейшей частью.

Пифагорейцы верили, что в числовых закономерностях спрятана тайна мира. Мир чисел жил для пифагорейца особой жизнью, числа имели свой особый жизненный смысл. Числа, равные сумме своих делителей, воспринимались как совершенные (6, 28, 496, 8128); дружественными называли пары чисел, из которых каждое равнялось сумме делителей другого (например, 220 и 284). Пифагор впервые разделил числа на четные и нечетные, простые и составные, ввел понятие фигурного числа. В его школе были подробно рассмотрены пифагоровы тройки натуральных чисел, у которых квадрат одного равнялся сумме квадратов двух других (см. Ферма великая теорема). Пифагору приписывается высказывание: «Все есть число». К числам (а он имел в виду лишь натуральные числа) он хотел свести весь мир, и математику в частности. Но в самой школе Пифагора было сделано открытие, нарушавшее эту гармонию. Было доказано, что у 2 не является рациональным числом, т.е. не выражается через натуральные числа.

Естественно, что геометрия у Пифагора была подчинена арифметике, это ярко проявилось в теореме, носящей его имя и ставшей в дальнейшем основой применения численных методов в геометрии. (Позже Евклид вновь вывел на первое место геометрию, подчинив ей алгебру.) По-видимому, пифагорейцы знали правильные тела: тетраэдр, куб и додекаэдр.

Пифагору приписывают систематическое введение доказательств в геометрию, создание планиметрии прямолинейных фигур, учения о подобии.

С именем Пифагора связывают учение об арифметических, геометрических и гармонических пропорциях, средних.Следует заметить, что Пифагор считал Землю шаром, движущимся вокруг Солнца. Когда в XVI в. церковь начала ожесточенно преследовать учение Коперника, это учение упорно именовалось пифагорейским.

Рене Декарт

Рене Декарт

(1596-1650)

Қайтыс болған күні:

11 ақпан 1650

Қайтыс болған жері:

Стокгольм, Швеция патшалығы

Азаматтығы:

Франция

Ұлты:

Француз

Негізгі пікірі:

"Ойлағандықтан бармын" (Cogito ergo sum); методтуралы; Шегіне жеткізе күдіктену; Декарт координата жүйесі, Декарт дуализмі, Құдай барлығына онтологиялықсипаттама және дәлел беру; Еуропалық жаңа философияның негізгі мәселелері.

Қотаңбасы:

Рене Декарт(фр. René Descartes [ʁəˈne deˈkaʁt], лат. Renatus Cartesius; (1596-1650жж.) - француз ғалымы, философ, математик,физик және физиолог. Ол қазіргі заман математикасының дамуына зор үлес қосып, Геометриялық координаттар жүйесін формулаға айналдыруы арқылы "аналитикалық геометрияның атасы" деп аталды. Ол дуализмдік (қоснегізді) идеалистік философия жүйесін жасап, әйгілі "Ойлағандықтан бармын" (ойлау болмысты анықтайтын бірегей негіз) нақылын тұжырымдады. Ол анық, толық ақиқатқа жету үшін "бәрінен күдіктену" әдіснамасын жасап, қазіргі заманғы батысфилософиясының рационализм бағытының көшбасшысы болды.

Декарт және Абай

Декарттың ғылыми және философиялық ойлары еуропа құрлығымен шектелмей, басқа халықтардың ағартушылық қозғалысына да пайдалы ықпал етті. Мысалы, қазақтың ұлы ойшылы Абай Құнанбайұлы Декарттың еңбегімен жете танысып, оның жан мен тән,индукция мен дедукция, Тәңірінің ақиқаттығы, ғылым адам игілігіне қызмет етуі тиіс" деген секілді көптеген тұжырымдарын қостады және ол туралы «Қара сөздерінде» өз көзқарасын Шығыс философиясыменбайланыстыра отырып пайымдады. Мұхтар Әуезов абайтанусаласындағы барлық еңбектерінде Декарттың Абайдыңфилософиялық көзқарастарына әсерін ерекше атап өтеді. Ол «Абай (Ибраһим) Құнанбайұлы (1845- 1904)» атты (1959) монографиясындаАбайдың да «терең ойдың телміріп соңына ермей», адам жаратылысы туралы дуалистік жолда болғанына, жаңа идеалистік санадағы Декартқа кебірек жақындағанына талдау жасайды (20 томдық шығармалар жинағы, 1985, 20-том, 166-бет).^[1][2]

Ғұмырбаяны

1596 жылы 31 наурызда Рене Декарт францияның Туреньдегі Эндр-Луарада (Лаэ, қазір "Декарт" деп аталады,) дәрежесі төменірек ақсүйек отбасында дүниеге келіпті. Әкесі Joachim сол Лаэдегі Бретань парламентінің мүшесі болып сайлаған екен. 1 жасында Декарттың шешесі өкпе туберкулезі ауыруынан қайтыс болады. Бала Декартқа шешесінің ауруы жұғып кеткендіктен, денесі әлжуаз, көп ауыратын бала болып өсіпті. Шешесі қайтыс болған соң әкесі басқа қыстаққа кетіп, сонда қайта үйленіпті. Декартты нағашы әжесі бағып өсірген екен. Ол әкесін сирек көріпті, бірақ әкесі оған экономикалық жағынан қамсыздандырып, жақсы тәрбие алуына заттық мүмкіндік жасап беріпті. Бұл оның тұрмыстық істерге назарын аудармай, өз арманына талпынуына мүмкіндік берген көрінеді.

1606, не 1607 жылы Декарт Ла-Флештегі иезуиттік қоғамның Королдік колледжіне түсіп білім алған. Онда олматематика, физика қатарлы пәндерді үйренген. Тіпті сонда әйгілі ғалым Галилео Галилейдің жұмыстарымен де танысқан көрінеді. 1616 жылы желтоқсанда аталған оқу орынын тамамдап, әкесінің қалауы бойынша адвокат болу үшінПуатье университетіне заң мамандығын үйренеді. Университеттен кейін ол жұмыс таңдауда екіойлы болып, "Дүние деген ұлы кітаптың даналығын" оқу үшін еуропаны аралап көруге бел байлайды.

Декарт былай деген болатын:

"Мен университетке мол білім алып, көкейімдегі сұрақтарыма жауап табамын, түрлі мәселелерді шешім ететін қабілетті игеремін деп түскен болатынмын. Университет бітіргенде байқасам, өзімнің дұрыс ойлай алмайтын, жаттанды сөз сөйлейтін, неге сенерін білмеген, білімі таяз топасқа айналыппын. Енді мен нағыз білімді дүние-өмірдің ұлы кітабынан алуға тиіспін."

1618 жылы Рене Декарт әскери қызмет өтеу үшін Нидерландтың Нассаудағы Морис қосынына тіркеледі. Бірақ Нидерланд және Испания ортасында соғыс тоқтату келісімі жасалғандықтан, ол осы бос уақытында математикалық білімін жетілдірумен болады.

Декарт өмір сүрген мезгілде латын тілі оқымыстылар тілі болды, ғылым мен философия латын тілінде жазылғаны белгілі. Сол дәстүр бойынша Декарт өз кітабына латынша атымен Renatus Cartesius деп қол қойған екен. Сондықтан кейде оның атындағы координата Картезий координатасы деп те аталады.

Оның математика мен физиканы біріктіру ойы осы Нидерландта әскери қызмет өтеп жүргенде пайда болады. 1618 жылы 10 қарашада жолдағы жарнама тақтайшасынан Фландрии тіліндегі мәселе есепті көріп қатты таңырқап, бір кісіге аталған есепті латыншаға аудартып алады. Оған көмектескен кісі одан 8 жас үлкен Isaac Beeckman деген кісі екен. Ол да математика мен физикаға ерекше қабілетті болып, біртіндеп Декарттың ұстазына айналады. 4 айдан кейін Декарт оған "Сіз мені бейғамдық ұйқысынан ояттыңыз ..." деп хат жазады және осы аралықта математикадан ашқан 4 жаңалығын жеткізеді. Оның әскери өмірі осылайша физика, алгебра, геометрия, логика, медицина қатарлы салаларда үйрену және ізденіс жасаумен өтеді.

1621 жылы Декарт әскерден қайтады.

1622 жылы 26 жастағы Рене Декарт әкесінен қалған мұраны түгел сатып жіберіп, сол қаражатқа еуропаны 4 жыл бойы аралаумен болады және 2 жыл Италияда болып, соңында Парижге оралады.

Ол кезде Францияда шіркеудің ықпалы күшті болып, діни мәселелерді еркін талқылауға жол қойылмайтын. Сондықтан 1628 жылы Нидерландқа қайта орапған Декарт сонда 20 жыл тұрады. Осы аралықта ол өзінің көптеген философиялық және ғылыми еңбектерін жазады. «Әдіс жөніндегі пікірлер», «Метафизикалық толғаныстар» （«Бірінші философиялық толғаныс» деп те аталады）, «Философия ережелері» қатарлы әйгілі туындыларын осы мезгілде жазып, еуропаның сол замандағы ең ықпалды философына айналады.

1649 жылы Декарт Швеция ханшайымы Кристинаның ұсынысыменСтокгольмде ханшайымның жеке ұстазы болады. Бірақ осынау "аю, мұз және жартасы бар өңірде" өкпе қабыну ауыруына шалдыққан ұлы ойшыл, 1650 жылы 11 ақпанда 54 жасында дүниеден озады.

1663 жылы оның кітаптары Рим мен Парижде бірдей тиым салынған кітаптар қатарына енеді. Тек бір ғасырға жуық уақыт өткенде, 1740 жылы ғана Парижде бұл шектеу күшін жояды. Өйткені сол кезде францияға Исаак Ньютонның ғаламдық жүйе туралы ілімі кең тарап, Декарттың идеялары мен ғылыми жетістіктері балама ретінде қолдау таба бастайды.

Шығармалары

Декарттың ең негізгі философиялық еңбектері: «Әдіс жөніндегі пікірлер»,（Discours de la méthode） «Метафизикалық толғаныстар» （«Бірінші философиялық толғаныс» деп те аталады, Méditations métaphysiques）, «Философия ережелері»（les Principes de la philosophie）қатарлылар.

Философиядағы үлесі

Декарт өмірге келген үй (Турендегі Гаага)

Декарт батыстың қазіргі замандық философиялық-ғылыми ойлауының негізін қалаушы тұлға ретінде толық философиялық жүйе жасады. Ол философиядадуализм (қоснегіз) мен рационализм (зердешілдік) бағытын дамытты.

Декарттың пікірінше адам баласы математикалық логикалық әдіс арқылы --- яғни зерделі түрде философиялық ой жүгіртуге тиіс. Адам ақылды нәрсе және барлық нәрсені ақылмен түсіндіруге болады. Зерде сезім мүшелеріне қарағанда сенімді куәлік етеді, сенімді білм береді. Мысалы, Түс көрген кезімізде біз шын өмірде жүргендей сезінеміз. Бірақ зерделеу арқылы түстік шын өмір емес екенін тұжырымдап шығамыз деді. Ол логика, геометрия, алгебра арқылы төрт ережені ұсынды:

1. Еш нәрсені де ақыл-зердемен танудан бұрын шын деп есептеме, тек күдіктен толық арылғанда барып ақиқат айқындалады. Күдік ақиқатқа жетуде міндетті түрде басып өтетін жол талабы.

2. Күрделі мәселені оны құраған ұсақ мәселелерге бөліп, жеке жеке шешу арқылы шешуге болады.

3. Ой қарапайымнан күрделіге дамиды. Ойлау қарапайымнан бастап күрделіге ауысуы керек.

4. Әрқашан өз ізденісімізді түбегейлі қайта қарап, ізденіс желімізден адасып қалмай, әлдебір қажетті мазмұнды жоғалтып алмағанымызды, әлдебір қателікке ұрынып қалмағанымызды тексеріп тұруға тиіспіз.

Декарт бұл әдісті философиялық ойлауда қолданып қана қоймай, геометрияда тіке қолданып, аналитикалық геометрияның негізін қалады.

Декарт философиялық әдіснама арқылы рационалді философияның мынадай мәселелерін қарастырды:

1. Дүниені танудағы ақыл-ойдың рөлі;

2. Субстанция, оның атрибутары мен модустары;

3. Философиядағы материализм мен идеализм бағыттарын келісімге келтіру, дуализмӘ;

4. Танымның ғылыми әдісі және «туа біткен» идеялар теориясы.

Болмыс[өңдеу]

Болмыс мәселесін зерттеу барысында Декарт болмыс мәнін сипаттайтын базалық, негіз болатын ұғымды табуға талпынды. Өз ізденістері нәтижесінде Декарт субстанция ұғымнын тұжырымдады.

Субстанция - өз тіршілігі үшін өзінен басқаны қажетсінбейтінің бәрі. Ондай қасетке (өз тіршілігі үшін басқаны қажетсінбеу) тек субстанция ғана ие және ондай субстанция Құдай ғана бола алады. Құдай мәңгі, құдіретті, жойылмайды және барлық нәрсенің себебі мен өзегі. Құдай өзі Субстанция, өзі Жаратушы болғандықтан субстанциялардан құралған дүниені жаратты. Құдай жаратқан субстанциялар да (жеке заттар, идеялар) субстанциялық басты қасиетке ие - тіршілік ету үшін өзінен басқаны қажет етпейді. Алайда бір-біріне қатысты алғанда өзіне-өзі жетімді (жеткілікті) болғанмен Құдайға қатысты алғанда олардың бәрі екінші және оған тәуелді (өйткені оларды жасаған Құдай). Жаратылған субстанцияларды Декарт екі текке жіктейді:

1. материалды (заттар),

2. рухани (идеялар).

Сонымен қоса олардың әрқайсысының тек өздеріне ғана тиесілі қасиеттері (атрибуттарды) болатының атап көрсетеді: дәйектілік - материалды заттардікі, ойлау - рухани идеялардікі. Осылайша, барлық материалды субстанциялардың бәріне тән қасиет дәйектілік (ұзындығына, еніне, биіктігіне, тереңдігіне қарай) және олар сансыз көп рет (шексіздікке дейін) бөліне береді. Рухани субстанцияларға ойлау қасиеті тән және олар, кірісінше, бөлінбейді. Материалды және рухани субстанциялардың басты қасиеттерінен (атрибуттарынан) тарайтын басқа да қасиеттері модустар деп аталады. Мысалы, дәйектіліктің модустары - форма, қозғалыс, кеңістіктегі жағдай, т.б.; ойлаудың модустары - сезімдер, тілектер, түйсіктер, т.б.

Адам

Адам, Декарт пікірінше, екі - материалды (тәндік-дәйекті) және рухани (ойлаушы) субстанциялардан құралған. Адам - өзі бойына екі бірдей субстанцияны (әрі материалды, әрі рухани) қатар біріктіретін тіршілік иесі, сондықтан ол табиғаттан жоғары көтеріле алады. Адам өз бойында екі субстанцияны қатар біріктіретіндіктен келіп дуализм (екіұдайлық, қосарлылық) идеясы туындайды.

Р.Декарт «философияның негізгі сұрағын» да дуализм тұрғысынан шешеді:

«Не бірінші: материя ма, әлде, с ана ма? Таласы мағынасыз. Материя мен сана тек адам бойында бірігетіндіктен, адам табиғаты дуалистік болғандықтан (өз бойында екі - материалды және рухани - субстанцияны біріктіретіндіктен), материя да, сана да бірінші бола алмайды - олар әрқашан болған және тұтас болмыстың екі түрлі көрінісі». Физикада, математикада, т.б. түрлі ғылым салаларында қолданылатын ғылыми әдіс таным процесінде қолданылмайды, дейді Декарт. Ғылыми әдісті таным процесінде белсенді қолдану арқылы таным процесін әлдеқайда алға жыджытуға, танымды өндірістен өнеркәсіп өндірісіне айналдыруға болады. Ондай ғылыми әдіс ретінде Декарт дедукцияны ұсынады. Декарттың философиялық, гносеологиялық әдісінің мағынасы - таным процесінде тек абсолютті, деректі, шын сүйену және ақыл арқылы логикалық тәсілдер арқылы жаңа, ақиқат білім алу. Декарт пікірі бойынша, дедукция әдісін пайдалану арқылы ғана танымның барлық салаларында шын білімге қол жеткізуге болады.

Дедукция[өңдеу]

"Метод туралы"

Рационалистік - дедуктивті әдісті қолданумен қатар Декарт мынадай зерттеу тәсілдерін ұсынады:

1. Зерттеу барысында бастапқы қағидалар ретінде тек ақиқат, шын, ақылмен және логикамен дәлелденген, ешбір күдік туғызбайтын білімдерді ғана пайдалану;

2. Күрделі мәселені қарапайым бөлшектерге, бөліп қарастыру;

3. Белгілі және дәлелденген сұрақтардан белгісіз, дәлелденбеген сұрақтарға жүйелі түрде өту;

4. Зерттеудің жүйелілігін, логикалық тізбегін қатаң сақтап, сол тізбектегі бірде-бір зерттеу бөлшегін тысқары қалдырмау.

Тума идея[өңдеу]

Декарт координатасы, х және у осін табуға пайдаланылады.

Декарт тума идеялар теориясын ұсынады: таным және дедукция арқылы алынатын білімдермен қатар, ешбір дәлелді қажет етпейтін ерекше, туа біткен идеялар болады. Ол ақиқаттар (аксиомалар) о бастан айқын және шын, олар Құдай ақылы мен адам ақылында әрдайым болған және болатын, ұрпақтан-ұрпаққа беріліп отыратын білімдер.

Ол білімдер екі түрде:

1. Ұғымдар;

2. Пікірлер

түрінде беріледі.

Туа біткен ұғымдарға жататындар: «Құдай» (бар); «сан» (бар); «ерік»; «тән»; «жан»; «құрылым», т.б.

Туа біткен пікірлер: «бүтін өз бөлшектерінен үлкен»; «жоқтан ештеңе пайда болмайды»; «бір мезгілде болу және болмау мүмкін емес», т.б. Декарт практикалық танымды жақтады. Декарт бойынша таным мақсаттары мынадай болуы тиіс:

1. адамның қоршаған дүние туралы білімдерін кеңейту және тереңдету;

2. ол білімдерді адам мүддесі үшін табиғатты барынша пайдалануға қолдану;

3. адамды жетілдіруге және

4. түпкі мақсат - адамның табиғатқа үстемдігіне пайдалану.

Діни сенімі[өңдеу]

Декарттың діни сенімі туралы талас-тартыс қазірге дейін жалғасуда. Ол өзін адал католик мүриті деп есептеп, өз толғаныстары христиандық сенімді қорғау үшін деп жазады. Бірақ заманда Декарт қоғам жағынан пантеист, атеист деп айыпталған. Онымен бір дәуірде жасаған әйгілі ғалым, философ Блез Паскаль былай деп жазады: "Мен Декартты кешіре алмаймын. Ол өз философиясының барлық саласында Құдайдан жалтарумен болды. Ол Құдай Тағала түртпесе дүние қозғалмайтын болған соң Құдай туралы айтқаны болмаса, басқа мәселеде ол Құдайды дүние өзгерісіне қатыстырмады."^[3][4]

Декарттың ғұмырбаянын жазған StephenGaukroger былай дейді: "Ол католик ретінде терең діни сенімі болды, соны қайтыс болғанға дейін берік ұстанды. Ол ақиқатқа бар қажыр-қайратымен құштарлана ұмтылды."^[5]

Декарт қайтыс болған соң Швеция ханшайымы Кристина католикті қабылдап тақтан бас тартты, -- Швеция заңдары бойынша патша міндетті түрде протестант болуға міндетті болатын. Кристина ханышайым араласқан бірден бір католик Декарт болатын және Декарт оған отбасы оқытушысы болған еді.^[6]

Қызық жағдайлар

Декарт қайтыс болғаннан кейін көп уақыттан кейін оның қабірі тоналған екен. Бас сүйегі қолдан қолға өтіп, кезекте Париждегі Palais de Chaillot сарайындағы адамзат мұражайында （Musée de l'Homme） сақталуда.

Декарт тірі кезінде немістердің розенкреузер ордені (Rosenkreuzer) қоғамына қатысым жоқ деген болатын. Бірақ кейінгі көптеген деректер Декарттың Розенкреузермен өте байланысы бар екені анықталды. Оның мойындамауышіркеуден қорыққандықтан болуы мүмкін.

Декарт өзінің Геометрия және алгебра Интеграциясы туралы зерттеулерін Бекман деген ғалыммен бөлісіп: "егер сіз менің зерттеулерім мен ойларымды қолдансаңыз, оны өзіңіздікі деп тани беріңіз" деп ағынан жарылған көрінеді. Бұл Декарттың кішпейліділікпен айта салғаны болса керек. Бірақ, Бекман деген кісі Декарттың бұл зерттеулерін шындап өзінікі етіп меншіктей бастағанда Декарт қатты ашуланыпты, оны "топас және ғылыми сауаты жоқ" деп айыптаған көрінеді.

Ғылыми эксперт-бағалау (peer-review - маманның бағалауы) түзімі Декарттан басталған екен. Ол "Бірінші философиялық толғаныстар" жарияланудан бұрын қолжазбаны сол заманның әйгілі философтарына, теологтарына оқып баға беруіне жіберіп беріпті. Олардан алты тойтарыс тапсырып алған соң, бұл тойтарыстарға өз жауабын жазып, аталған кітапта соның бәрін түгел қамтып жариялапты. Сөйтіп бұл тарихтағы философтар мен теологиятеологтардыңэкспертінен өткен, өз заманындағы ғұламалар тіке бағалаған ұлы шығарма болды.

Рене Декарт

(1596-1650)

Декарт далеко не сразу нашел свое место в жизни. Дворянин по происхождению, окончив коллеж в Ла-Флеше, он с головой окунается в светскую жизнь Парижа, затем бросает все ради занятий наукой.

Декарт неторопливо продумывает контуры своего будущего учения -аналитического метода познания мира. Он накапливает жизненный опыт, несколько лет проводит в путешествиях. Декарт стремился и в философии и в любой другой науке найти математические законы, свести каждый вопрос или каждую задачу к математической. Он хотел создать такой универсальный математический метод, который позволил бы всякому овладевшему им решить любую задачу. В 1637 г. в Лейдене выходит 4 тома его «Философских опытов». Последний том назывался «Геометрия».

Декарт отводил математике особое место в своей системе, он считал ее принципы установления истины образцом для других наук.

Главное достижение Декарта-построение аналитической геометрии (термин предложил И. Ньютон, см. Геометрия), в которой геометрические задачи переводились на язык алгебры при помощи метода координат. Нужно отметить, что у Декарта в точном виде еще не было того, что сегодня называется декартовой системой координат. Декарт начал с того, что перевел на алгебраический язык задачи на построение циркулем и линейкой (см. Геометрические построения), затем обнаружил, что любимые древними конические сечения-это то же самое, что кривые второго порядка, т.е. с алгебраической точки зрения следующий по сложности за прямыми (кривыми первого порядка) класс кривых. При переходе на алгебраический язык многие трудные геометрические задачи становятся почти тривиальными.

Немалой заслугой Декарта было введение удобных обозначений, сохранившихся до наших дней: латинских букв х, у, z-для неизвестных; а, Ь, с-для коэффициентов, х2, у5, а7 -для степеней. Он сформулировал основную теорему алгебры: «число корней алгебраического уравнения равно его степени», доказательство которой было получено лишь в конце XVIII в. К.Ф. Гауссом.

Интересы Декарта не ограничиваются математикой, а включают механику, оптику, биологию. В 1649 г. Декарт после долгих колебаний переезжает в Швецию. Это решение оказалось для его здоровья роковым. Через полгода Декарт умер от пневмонии.

Карл Фридрих Гаусс[өңдеу]

Уикипедия - ашық энциклопедиясынан алынған мәлімет

Гаусс, Карл Фридрих

Карл Фридрих Гаусс (нем. Johann Carl Friedrich Gauß; 30 сәуір 1777,Брауншвейг - 23 ақпан 1855, Гёттинген) - ұлы неміс математигі, астрономы және физигі, Санкт-Петербург ғылым академиясының құрметті мүшесі (1824).

18 ғасырдың соңында Германиада бір сабақта мұғалім оқушыларына "1 - ден 100 ге дейінгі натурал сандардың қосындысын табуды" тапсырыпты. Оқушылардың біреуі: ізделген қосынды 5050-ге тең деп жауап беріпті. бұл оқушы кейіннен аты әлемге әйгілі болған Математиктер королі Карл Фридрих Гаусс екен.

Еңбектері[өңдеу]

• Геттинген университетінде оқыған (1795 - 98).

• 1807 жылдан Геттинген универститетінің профессоры және Геттинген астрономиялық обсерваториясының директоры болды.

Оның еңбектері алгебраның, сандар теориясының, дифференциалдық геометрияның, тартылыс теориясының, электр және магнит құбылыстарының классикалық теориясының,геодезияның, теориялық астрономияның дамуына орасан зор ықпал етті. Кез келген алгебралық теңдеудің кем дегенде бір түбірі болатындығы жөніндегі алгебраның негізгі теоремасын дәлелдеген (1799). Гаусс сондай-ақ,астрономия, ықтималдық теориясы, шексіз қатарлар теориясы, потенциалдар теориясы, т.б. салалар бойынша да іргелі еңбектер жазған, жоғары геоздезияның математикасы негізін қалаған. Ол өлшеу кезінде жіберілетін қателіктерді есептей отырып, ең кіші квадраттар тәсілін және 3 рет бақылау нәтижесінде планеталардың эллипстік орбитасын есептеу тәсілін ұсынған.

• 1830 - 40 ж. неміс физигі В. Вебермен біріге отырып теориялық физикадан елеулі табысқа жетті. Сөйтіп электр магниттік бірліктердің абсолют жүйесін (қ. Бірліктердің СГС жүйесі) құрды.

• 1833 ж. Германиядағы тұңғыш электр магниттік телеграфты құрастырды. Ол Н.И. Лобачевскийдің еңбектерінде дамытылған Евклидтік емес геометриялардың идеяларына ерекше мән берді.

(1+100)+(2+99)+......+(49+52)+(50+51)=(100+1)∗50=5050{\displaystyle ~(1+100)+(2+99)+......+(49+52)+(50+51)=(100+1)*50=5050}Салу есептері

Салу есептерді ежелгі математиктер еңбектері арасынан елеулі орын алған. Өйткені, бұл кезеңде барлық математикалық деректер сызба көмегімен геометриялық тілде негізделген. Сызғыш пен циркульді пайдаланып көпбұрыштарды, оның ішінде дұрыс көпбұрыштарды салу мәселесі немістің ұлы математигі Карл Гауссқа дейін өз шешімін таппай келді. Бұл мәселені тек 1801 жылы ғана К. Гаусс алгебралық жолмен толық шешті. Оның дәлелдемесі бойынша дұрыс n-бұрышты циркульді және сызғышты пайдаланып салу үшін n=2m. P1·…·P k, m€Z, m≥0, P1, …, P k2²+1, ал 7 мұндай түрде жазылмайды, яғни жетібұрышты циркулді және сызғышты пайдаланып салуға болмайды.^[1]

Евклид[өңдеу]

Уикипедия - ашық энциклопедиясынан алынған мәліметEuclid

Euclid in Raphael's School of Athens

туған

fl. 300 BC

Қайтыс болды

unknown

Тұратын жері

Alexandria, Egypt

Зерттеу салалары

Mathematics

Еңбегі үшін әйгілі

Euclidean geometry

Euclid's Elements

Евклид (көне грекше: Εὐκλείδης,Б.д.д. 325 - 265ж) ежелгі дәуірдегі грек математикгі.

Оксфорд университетіндегі тарих музейіндегі ескерткіш

Ол математикадан жазылған теориялық алғашқы трактаттың авторы, Александрия қарамағындағы мектептің тұңғыш математигі. Оның өмірі жайлы деректер жоқтың қасы. Евклидтің басты еңбегі - «Негіздер». Онда планиметрияның, стреометрияның кейбір мәселелері талданған. Сөйтіп, ол өзінен бқрынғы грек математикасының одан әрі дамуының ірге тасын қалаған. Евклидтің «Негіздерден» басқа «Фигураны бөлу туралы», «Канустың қималары» деп аталатын еңбектері бар. Ол астраномиядан,музыкадан, т.б. салалардан да еңбектер жазған. Евклидтің бізге жеткен шығармалары мына басылымда жинақталған: «Eudidis Opera Menge». Онда грекше түр нұсқасы, латыннан аудармасы және кейінгі авторлардың түсініктемелері берілген. Евклид «Негіздерінің» математиканы дамытуда әсері орасан зор болады. Бұл еңбектен тәлім алмаған ірім-ұсақты математик жоқ деуге болады. «Негіздер»орыс тілінде тұңғыш рет 1739 жылы аударылып басталып шықты, ал ең кейінгі жаңартылған аудармасы 1948-1950 жылдары жарық көрді. Математиканы сүйетін әрбір талапкердің ғылымының классикалық бұл еңбегімен танысып аса пайдалы болар еді.

Исаак Ньютон

Уикипедия - ашық энциклопедиясынан алынған мәліметИсаак Ньютон

туған

қаңтардың 4 (373 жас)

Вулсторптағы Колстерворт

Линкольншир, Англия

Қайтыс болды

1727 ж. наурыздың 31(84 жаста)

Кенсингтон, Лондон, Англия

Тұратын жері

Англия

Ұлты

ағылшын

Салалары

физика, математика,астрономия,

табиғи философия, алхимия,

теология

Институттары

Кембридж университеті

Корольдік қоғам

Alma mater

Тринити колледж (Кембридж)

Academic advisors

Исаак Барроу

Бенжамин Пуллейн

Notable students

Роджер Коутс

Уиллиам Уистон

Джон Уиккинс

Хамфри Ньютон

Еңбегі үшін танылған

Ньютон механикасы

Бүкіләлемдік тартылыс заңы

санақ

оптика

Influenced

Николас Фатио де Дюлльер

Джон Кайл

Religious stance

Англиканизм

Signature

Исаак Ньютон, ағылш. Sir Isaac Newton ( 4 қаңтар 1643 жыл - 31 наурыз 1727) - ағылшын физигі, математигі, астрономы, табиғифилософы, алхимигі және теологы, Корольдік қоғамның мүшесі . Оның1687 жылы жарық көрген Табиғи философияның математикалық бастамалары (латынша: «Philosophiæ Naturalis Principia Mathematica») деген кітабы ғылым тарихындағы ең ықпалды шығарма болып саналады. Осы еңбегінде Ньютон бүкіләлемдік тартылыс заңын жәнеқозғалыс заңдарын тұжырымдап, содан кейінгі үш ғасырда үстемдік еткен және қазіргі заманғы инженерлік ғылымның негізі болып табылатын классикалық механиканың негізін қалады. Ньютон өзінің тартылыс заңы мен Кеплердің ғаламшарлар қозғалысының заңдарының арасындағы сәйкестікті дәлелдеп, жер бетіндегі заттардың қозғалысы мен аспан денелерінің қозғалысы бірдей заңдарға бағынатынын көрсетті. Осылайша ол гелиоцентризм туралы соңғы күмәнды сейілтіп, ғылыми революцияның басын бастап берді.

Механикада Ньютон импульстың және бұрыштық импульстың сақталу заңын алға тартты. Оптикаға қосқан үлесі: ол рефлекторлы телескопжасап шығарып, үшбұрышты призманың жарықты көзге көрінетін жеті түске бөлетінін ашты. Ол Ньютонның суу заңын тұжырымдап,дыбыстың жылдамдығын зерттеді.

Математикада Ньютон Готтфрид Лейбницпен қатар дифференциалдық және интегралдық санақты ойлап шығарды. Сонымен қатар ол биномдық теореманы көрсетіп, функцияның нөлін шамалауға қолданылатын Ньютон әдісін тапты. Дәрежелік қатарлардызерттеуге де үлес қосты.

Ньютонның дінге деген қызығушылығы да зор болды, оның діни еңбектері көлемі жағынан ғылымға қосқан үлесінен үлкен.

Денелердің Орталық күш әсерінен қозғалу траекториясы конустық қима болатынын, оған себеп барлық планеталар мен кометалардың Күнге, ал планета серіктерінің өз планеталарына ара қашықтықтың квадратына кері пропорционал күшпен тартылуы екенін дәлелдеп, бүкіләлемдік тартылыс заңын тұжырымдады. Физикада Ньютон қызған денелердің суыну заңын, ақ жарықтың монохромат сәулелерге жіктелуін, сфералық мөлдір денелердің түйіскен нүктесінің айналасында интерференц. сақиналардың пайда болатынын, т.б. ашты. Ол - термометрді ойлап шығарған алғашқы ғалымдардың бірі.^[1]Астрономияны телескоптық бақылау мен математикаға сүйенетін жаңа ғылыми сатыға көтерді. Өзі жасаған екі айналы телескоп арқылы (1668) аспан құбылыстарын тікелей бақылады. Аспан денелерінің қозғалыс теориясын жасап, аспан механикасының негізін салды.^[2]Ньютонның астрономиялық еңбектері механика мен физикадағы табыстарына ұштасып жатады. Математикада дифференциалды және интегралдық есептеулерді (Г.Лейбницке тәуелсіз) ойлап тапты, шамалардың ең үлкен және ең кіші мәндерін табу, қисық сызыққа жанама жүргізу, қисық сызықтың ұзындығын, жазықтықтағы тұйық сызықтың қоршайтын ауданын табу, функцияларды қатарларға жіктеу, т.б. жаңалықтар ашты. Бұлар математикалық анализдің негізі болып табылады. Ньютонның ғыл. шығармаларының жинағы 5 том болып 1779 - 85 жылы Лондонда латын тілінде басылған.^[3]

2005 жылы өткізілген сауалнамаға сұралғандардың көпшілігі Ньютонның ғылым тарихына жасаған ықпалы Альберт Эйнштейндікінен әлдеқайда күшті болған деп ойлайтындарын айтқан.^[4]

Мазмұны

[жасыру]

• 1Кембридждағы өмірбаяны

• 2Шығармашылығы

• 3Тағы қараңыз

• 4Дереккөздер

• 5Сыртқы сілтемелер</</p>

Кембридждағы өмірбаяны

• 1664 жылы Кембридж университетінің бөлімшесі Тринити колледжін бітірді

• 1665 жылы бакалавр дәрежесін алды

• 1669 жылы Кембридж университетінің профессор және физика-математика кафедрасының меңгерушісі болды

• 1672 жылы 1 қаңтарда Лондон Корольдік қоғамының мүшесі болып сайланды (1703 жылдан өмірінің соңына дейін президенті болды)

Шығармашылығы

• 1687 жылы "Табиғат философиясының математикалық негіздері"

• 1704 жылы "Оптика"

• 1672 жылы ″Жарық пен түстің жаңа теориялары"

• 1684 жылы ″Дененің орбитадағы қозғалысы″

• 1707 жылы "Әмбебап арифметика"

• 1728 жылы " Әлем жүйесі "