Учителю
Урок геометрии 7-8 классы в малокомплектной школе

Урок геометрии 7-8 классы в малокомплектной школе

Автор публикации: Павлюченко В.И.

Дата публикации: 22.05.2015

Краткое описание: Предмет: геометрияКласс: 7Тема:Медианы ,биссектрисы и высоты треугольникаТип урока: урок изучения нового материала.Продолжительность урока: 45 минутЦель урока: раскрыть математический смысл понятий «медиана», «биссектриса», «высота».Задачи:· Образовательные: вы

предварительный просмотр материала

КГУ «Владыкинская основная школа»

Разработка урока геометрии

в малокомплектной школе

Тема:

«Медианы ,биссектрисы и высоты треугольника» - 7 класс,

«Замечательные точки треугольника» - 8 класс

Работу подготовила:

Павлюченко Валентина Ивановна

учитель математики

2 категории высшего уровня

Урок геометрии в 7 и 8 классе

малокомплектной школы

Тема:

«Медианы ,биссектрисы и высоты треугольника» - 7 класс,

«Замечательные точки треугольника» - 8 класс

Автор работы: Павлюченко Валентина Ивановна,

учитель математики,

Владыкинской основной школы

Федоровского района

Костанайской области

Категория: Вторая

Предмет: геометрия

Класс: 7

Тема: Медианы ,биссектрисы и высоты треугольника

Тип урока: урок изучения нового материала.

Продолжительность урока: 45 минут

Цель урока: раскрыть математический смысл понятий «медиана», «биссектриса», «высота».

Задачи:

Образовательные: вывести понятие биссектрисы, высоты, медианы треугольника, перпендикуляра к прямой, сформулировать и доказать теорему о единственности перпендикуляра к прямой, рассмотреть замечательные свойства треугольника. ввести межпредметные связи (физика, география, биология, история, литература).

Развивающая: сознательное восприятие учебного материала.
Воспитательная: воспитывать познавательную активность, культуру общения.
Методы: репродуктивный, частично-поисковый.
Формы: фронтальная, групповая, парная, индивидуальная.
Оборудование: тексты учебника, транспортир, треугольник, опорный конспект, плакат с заданиями, линейка.

Рисунок 1.
Модели треугольников, изготовленные из плотного цветного картона, с закреплёнными в вершинах цветными тесёмками (для каждого ученика и учителя).
Чертёж прямоугольного треугольника с изображением 3-х его высот, которые пересекаются в вершине прямого угла.
Магнитофон, кассета с записью песни "Когда я стану кошкой" (Музыка Фадеева М., слова Секачёвой И.) для проведения физминутки.
Весёлые рисунки геометрических зверят: биссектриса - крыса, медиана - обезьяна, высота похожа на кота.
На каждой парте 3 треугольника из цветного картона с изображением на них высот, медиан, биссектрис (аппликация).
Физическая карта Америки.

Предмет: геометрия

Класс: 8

Тема: «Замечательные точки треугольника»

Тип урока: урок изучение нового материала

Продолжительность урока: 45 минут

Цель и задачи урока.

Обучающая цель урока:

раскрыть понятие - замечательные точки и линии треугольника;
рассмотреть замечательные точки и линии треугольника;
коррекция знаний учащихся через изучение умений правильно выполнять задания;
показать практическое применение этих знаний при решении задач.

Развивающие и воспитывающие задачи урока:

создать условия для самоконтроля и контроля знаний учащихся;
способствовать развитию аналитико-синтетического мышления; смысловой памяти; произвольного внимания и речи обучающихся.
формированию у школьников личностной позиции в определении результата своей деятельности и других учащихся.
расширять кругозор обучающихся, познакомить с фрагментами истории, геометрии;
воспитывать познавательную активность, культуру общения, , сотрудничество.

Оборудование и учебные материалы: модели треугольников, изготовленные из плотного цветного картона; тесты, чертежные инструменты, раздаточный материал, карточки с заданиями.

Методы обучения: наглядно-иллюстративный, демонстрационный, самоконтроль.

Формы работы на уроке: индивидуальная, групповая, фронтальная.

План урока:

I. Орг. момент. (2 мин)
II. Проверка и актуализация знаний. (4 мин)
III. Теоретическая часть. (7 мин)

IV.Первичное закрепление (7 мин)

V. Физминутка (2 мин)
VI. Практическая часть ( 10 мин)

VII. Закрепление (9 мин)

VIII Д/з (2 мин)
IX.Итог урока. Рефлексия (2 мин)

Конспект урока.

7 класс

8 класс

Деятельность учителя

Деятельность ученика

Деятельность учителя

Деятельность ученика

1.Организационный момент

Вступительное слово учителя:

-Человеческая доброта - самое удивительное явление в мире. Попробуйте с помощью улыбки передать своё настроение. Я вижу настроение у вас хорошее, деловое, итак за работу.

Взаимное приветствие учащихся и учителя; проверка отсутствующих.

1.Организационный момент

Вступительное слово учителя:

Взаимное приветствие учащихся и учителя; проверка отсутствующих.

2. Мотивация к учебной деятельности.

- Какую геометрическую фигуру вы видите на весёлом рисунке?

(Треугольник).

А что называется треугольником?

(Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).

Сколько у него элементов? (6)

Назовите элементы треугольника. (Три стороны и три угла).

Кто из вас не слышал о загадочном Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты?

(Он находится в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида).

А ведь знакомый всем нам треугольник также таит в себе немало интересного и загадочного.

Зовётся он треугольник,
И с ним хлопот не оберётся школьник!

Отвечают на вопросы.

2. Проверка домашнего задания. (фронтально)

Сегодня нам предстоит не только изучить очень интересную тему, но и повторить приобретенные на прошлых уроках знания.

-какая фигура называется треугольником?

-из чего состоит треугольник?

-виды треугольников?

-что называется: биссектрисой ,медианой, высотой? Все эти знания вам пригодятся при выполнении тестовых заданий

Предлагаю выполнить тестовые задания

(тестовые задания в приложении)

Если вы уже закончили выполнение теста, отложите ручки. Хорошо, прошу вас обратить внимание на доску. Здесь представлены таблицы с кодами ответов и критерии оценок. Поменяйтесь тетрадями с соседом по парте и по представленным таблицам оцените работу друг друга. Оценивается тест по таблице правильных ответов.

Ответы:

КРИТЕРИИ ОЦЕНКИ:

Количество правильных ответов

Оценка

4 правильных ответа

5 правильных ответа

6 правильных ответа

таблицы представлены на доске.

Выпол

няют

тест

Учащиеся проверяют работу друг друга и подсчитывают

количество правильных ответов

Определение темы урока и целей учащимися.

Молодцы! Так какова же тема нашего сегодняшнего урока?

Тема сегодняшнего урока: "Медиана, биссектриса и высота треугольника".

Преодолеть хлопоты - трудности, связанные с новыми понятиями - медиана, биссектриса и высота треугольника - нам сегодня помогут три мои ассистента: Антон ,Владик и Динара (одноклассники, подготовленные учителем заранее)

Учащиеся определяют тему и цель урока

Слушают сообщение.

3. Объяснение нового материала.

1. Медиана.

Начертите треугольник АВС и найдите середину стороны ВС - точку М.

Что называется серединой отрезка? (Серединой отрезка называется точка отрезка, которая делит его пополам, то есть на два равных отрезка).

Запись на доске: АМ=МС. Рис. 2.

Соедините точку М с вершиной В. Отре-зок ВМ называется медианой треугольника.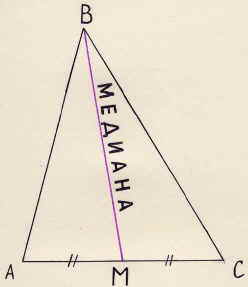

Определение. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Сколько вершин у треугольника? (3).

Сколько у него сторон? (3).

Сколько медиан можно провести в треугольнике?(3).

"Проведите" три медианы на моделях треугольников. (Ассистентки контролируют правильность выполнения задания, помогают в случае необходимости).

Какое свойство медиан вы заметили?

В любом треугольнике все медианы пересекаются в одной точке.

Эта точка называется центром тяжести треугольника. [1].

№ 114 (стр. 37) [4] - у доски.

Докажите, что в равных треугольниках медианы, проведённые к равным сторонам, равны. Рис. 3.

Дано: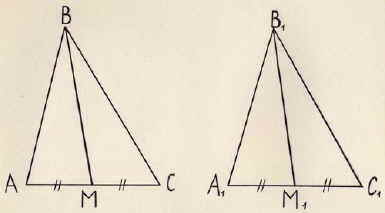

АВС, А₁В₁С_1,
АС=А₁С₁,
АМ=МС,
А₁М₁=М₁С₁.

Доказать:

ВМ=В₁М_1.

Доказательство:

(Самостоятельно)

2. Высота.

Запись на доске: ВН АС, Н АС. Рис. 4.

С помощью чертёжного угольника из вершины В треугольника АВС проведём перпендикуляр ВН к прямой АС. Он называется высотой треугольника.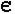

Определение. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противолежащую сторону.

Сколько высот имеет треугольник? (3).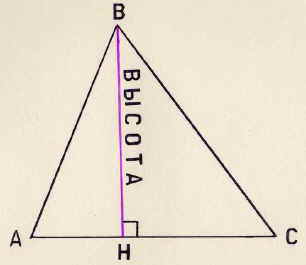

3. Биссектриса.

Вспомните определение биссектрисы угла.

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.Запись на доске: АВК = СВК,

К АС. Рис. 10.

Постройте биссектрису ВК угла В с по-мощью транспортира. Она пересечёт отрезок АС в точке К. Отрезок ВК называется биссектрисой угла В треугольника АВС.

Определение. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину угла треугольника с точкой противоположной стороны треугольника.

Покажите все три биссектрисы на вашей модели треугольника.

(Контроль со стороны учителя и ассистенток).

Сформулируйте свойство биссектрис треугольника.

В любом треугольнике биссектрисы пересекаются в одной точке.

Отвечают на вопросы

Выполняют задание

3.Знакомство с новой темой:

Центр тяжести треугольника, его ортоцентр и точка пересечения биссектрис треугольника называются (особыми) замечательными точками треугольника.

Замечательные точки есть у треугольника.
Точка первая - она
Чувством гордости полна:
Медианы в ней пересекаются,
Центром тяжести та точка называется.
Ортоцентр - вторая точка,
Архимед её открыл,
Все высоты в ней встречаются,
Удивив учёный мир.
Третья точка - тоже важная
Биссектрисы всех углов,
Бросив вызов свой отважный,
В ней "сошлись", не тратя слов.
Эйлер точки все заметил,
Свойства новые открыл, -
Так на радость школьникам
Возникла новая ветвь математики -
Геометрия треугольника..

Теорему о точке пересечения высот треугольника провожу с комментированием по заранее заготовленному чертежу, а детальное доказательство предлагаю учащимся провести самостоятельно или с помощью учебника.

4.Закрепление изученного материала.

1.№ 103

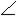
Решение

1) АВО = 180° - АВN = 180° - СВN = CВО, то есть ВО - биссектриса АВС, аналогично СО - биссектриса АСВ.

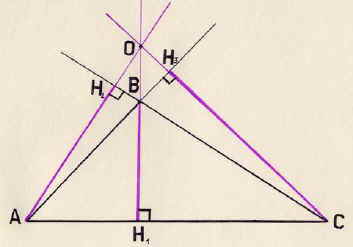
2) По теореме о биссектрисе угла точка О равноудалена от сторон АВ, ВС, АС. Таким образом, ОН1 = ОН2 = ОН3, где ОН1 АВ, ОН2 ВС, ОН3 АС.

2. Получили, что АВ, ВС, АС - касательные к окружности с центром в точке О и радиусом, равным ОН1.

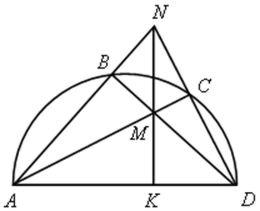
2. Решить устно:

Дуга АD - полуокружность.

Доказать MN АD.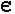

3. Решить № 104 самостоятельно с взаимопроверкой

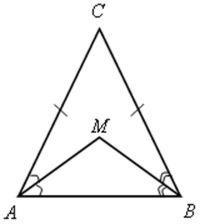
№ 104.

Решение

1) По свойству углов при основании равнобедренного треугольника САВ = СВА.

Тогда МАС = МАВ = САВ = СВА =МВС = МВА.

2) МАВ - равнобедренный, АМ = ВМ и точка М лежит на серединном перпендикуляре к АВ.

3) Так как АС = СВ, то точка С также лежит на серединном перпендикуляре к АВ. Таким образом, СМ АВ.

Работают по учебникам: самостоятельно проводят доказательство и делают вывод.

Решают у доски с объяснением.

Устная работа.

Выполняют задание самостоятельно с взаимопроверкой

4. Первичное усвоение знаний.

"Постройте" все три высоты на модели вашего треугольника. (ассистенты проверяют). Обладают ли высоты аналогичным свойством, что и медианы? (Да).

У некоторых из вас модели прямоугольных треугольников. Где пересеклись их высоты? (В вершине прямого угла).Учащимся показывается ответ на рисунке (плакат на доске).

№ 103 (стр. 36) [4] - у доски.

Начертите треугольник АВС, у которого угол В - тупой. С помощью чертёжного угольника проведите его высоты.

Решение.

ВН₁ АС, АН₂ ВС, СН₃ АВ. Рис. 6.

Вывод. Высоты или их продолжения пересекаются в одной точке.Эта точка называется ортоцентром. [1]

Выполнение работы на листах.

5.Физминутка: «Веселая разминка»

(Её проводит Динара в образе кошки под запись песни "Когда я стану кошкой").Для физминутки она не зря выбрала образ кошки. Он поможет нам в запоминании нового понятия - высота.

Динара (первая ассистентка).

Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом. [2] Рис.

(Стихи иллюстрируются весёлым рисунком).

Конечно, геометрия - наука серьёзная, и учить её надо серьёзно и вдумчиво. Но и забавные стихи и весёлые "геометрические" зверята помогают учению.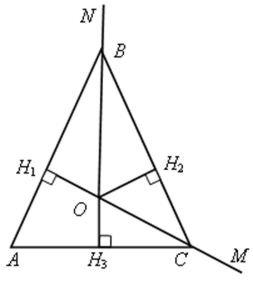

Владик (второй ассистент).

Медиана-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас. [2] Рис.

Антон (третий ассистент).

Биссектриса - это крыса,
Которая бегает по углам
И делит угол пополам. Рис.

(Строки сопровождаются показом рисунков).

6. Исследовательская работа

Работа в парах.

На каждой парте лежат три треугольника, разносторонние, разных цветов. На одном из них изображены три медианы, на другом - высоты, на третьем - биссектрисы.

Найдите треугольник с изображением высот. ( Фиолетовые и красные).
Найдите треугольник, на котором изображены медианы. (Синие, жёлтые и оранжевые).
Найдите треугольник с изображением биссектрис. (Зелёные, чёрные).

Работают в парах,

выполняют задание.

6. Решение задач с объяснением.

№ 107.

Решение

1) Построим серединный перпендикуляр m к отрезку АВ.

2) Точка М - точка пересечения m c а.

3) М - искомая.

Задача имеет решение в случае, если прямая АВ не перпендикулярна к данной прямой а.

Решение задач у доски.

7. Закрепление знаний.

Самостоятельная практическая работа .

1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.

а) Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

б) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом единственный.

2. Верны ли следующие утверждения? (В случае "нет" напишите верный ответ).

а) В любом треугольнике можно провести три медианы. (Да).

б) Точка пересечения высот любого треугольника лежит внутри треугольника. (Не всегда).
в) Все биссектрисы треугольника пересекаются в одной точке. (Да).

7. Закрепление знаний.

Тест с выбором ответа. Ответив на эти вопросы ,вы поймете ,как вы поняли новую тему.

Может ли точка пересечения биссектрис треугольника находиться в не этого треугольника?
Ответ: да, нет.
Может ли точка пересечения медиан находиться вне этого треугольника?
Ответ: да, нет.
Может ли точка пересечения высот находиться вне этого треугольника?
Ответ: да, нет.
Где находится точка пересечения серединных перпендикуляров к сторонам:
- прямоугольного треугольника ……(ответ: в средине гипотенузы)
- остроугольного треугольника ……..(ответ: внутри треугольника)
- тупоугольного треугольника …….. (ответ: вне треугольника).

Самостоятельная работа с учебником.

8. Домашнее задание -Стр. 33- 34, № 101, 102, 106.

Запись в дневник

8.Домашнее задание - §7, №111,№114

Запись в дневник

9.Итог урока. Рефлексия.

- Что нового я узнал сегодня на уроке?

- Что было интересным для меня?

- Я смог решить задачу самостоятельно…

- Я справлюсь с домашним заданием…

Отвечают на вопросы рефлексии

9.Итог урока. Рефлексия.

- Что нового я узнал сегодня на уроке?

- Что было интересным для меня?

- Я смог решить задачу самостоятельно…

- Я справлюсь с домашним заданием…

Отвечают на вопросы рефлексии

Приложение.

Самостоятельная практическая работа 7 класс.

1. Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.

б) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом единственный.

2. Верны ли следующие утверждения? (В случае "нет" напишите верный ответ).

а) В любом треугольнике можно провести три медианы. (Да).

Тест с выбором ответа.

Может ли точка пересечения биссектрис треугольника находиться в не этого треугольника?
Ответ: да, нет.
Может ли точка пересечения медиан находиться вне этого треугольника?
Ответ: да, нет.
Может ли точка пересечения высот находиться вне этого треугольника?
Ответ: да, нет.
Где находится точка пересечения серединных перпендикуляров к сторонам:
- прямоугольного треугольника ……(ответ: в средине гипотенузы)
- остроугольного треугольника ……..(ответ: внутри треугольника)
- тупоугольного треугольника …….. (ответ: вне треугольника).

⇧

⇩