Карточки для подготовки к ОГЭ 9 класс Задание 10

Карточки для подготовки к ОГЭ 9 класс

Задание 10

Составила: учитель математики

Шмакова Татьяна Валерьевна

2016 год

Задание 10 № 311503. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.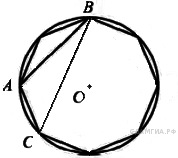

Решение.

Построим OA и OC радиусы. Центральный угол AOC равен 360°:8 = 45°. Угол ABC - вписанный и опирается на ту же дугу, поэтому он равен 45°:2 = 22,5°. Ответ: 22,5.

Задание 10 № 339483. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.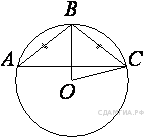

Решение.

Сумма углов треугольника равна 180°. Треугольник - равнобедренный, следовательно, Угол - вписанный, поэтому он равен половине дуги, на которую опирается. Угол - центральный, поэтому он равен величине дуги, на которую опирается. Углы и опираются на одну и ту же дугу, следовательно, Ответ: 3.

Задание 10 № 341116. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 66°. Найдите величину угла BOC. Ответ дайте в градусах.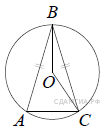

Решение.

Сумма углов треугольника равна 180°. Треугольник - равнобедренный, следовательно, Угол - вписанный, поэтому он равен половине дуги, на которую опирается. Угол - центральный, поэтому он равен величине дуги, на которую опирается. Углы и опираются на одну и ту же дугу, следовательно, Ответ: 114.

Задание 10 № 339828. Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.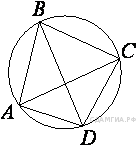

Решение.

Угол ABC - вписанный, опирается на дугу ADC, поэтому величина дуги ADC равна 2 · 70° = 140°. Угол CAD - вписанный, опирается на дугу CD, поэтому величина дуги CD равна 2 · 49° = 98°. Угол ABD - вписанный, опирается на дугу AD, поэтому ∠ABD = ∪AD/2 = (∪ADC − ∪CD)/2 = (140° − 98°)/2 = 21°. Ответ: 21.

Задание 10 № 341707. Найдите площадь квадрата, описанного вокруг окружности радиуса 7.

Решение.

Пусть и соответственно радиус и диаметр окружности, - сторона квадрата. Сторона квадрата равна диаметру вписанной окружности. Найдём площадь квадрата: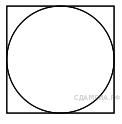

Ответ: 196.

Задание 10 № 316346. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Решение. Воспользуемся теоремой косинусов:

Здесь и - боковые стороны равнобедренного треугольника, - основание.

Диаметр описанной окружности вычислим по формуле: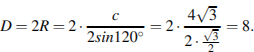

Задание 10 № 311410. Радиус OB окружности с центром в точке O пересекает хордуAC в точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1 см, а радиус окружности равен 5 см.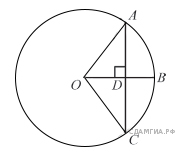

Решение.

Найдем отрезок DO: DO = OB − BD = 5 − 1 = 4. Так как OB перпендикулярен AC, треугольник AOD - прямоугольный. По теореме Пифагора имеем: . Треугольник AOC - равнобедренный так какAO = OC = r, тогда AD = DC. Таким образом, AC = AD·2 = 6. Ответ: 6.

Задание 10 № 311488. Найдите величину (в градусах) вписанного угла α, опирающегося на хорду AB, равную радиусу окружности.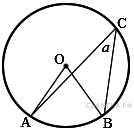

Решение.

Проведем радиусы OA и OB. Так как по условию задачи хорда AB равна радиусу, то треугольник AOB - равносторонний, следовательно, все его углы равны 60°. Угол AOB - центральный и равен 60° Угол ACB - вписанный и опирается на ту же дугу, что и угол AOB. Таким образом, Ответ: 30.

Задание 10 № 311681. К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 12 см, AO = 13 см.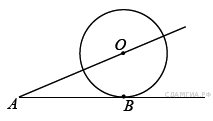

Решение.

Соединим отрезком точки O и B; полученный отрезок - радиус, проведённый в точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника AOB: по теореме Пифагора равен 5 см. Ответ: 5.

Задание 10 № 311912.

В треугольнике ABC угол C равен 90°, AC = 30 , BC = Найдите радиус окружности, описанной около этого треугольника.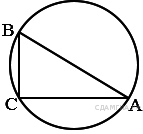

Решение.

Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы. По теореме Пифагора имеем: Ответ: 17,5.

Задание 10 № 324868. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:4:11. Найдите радиус окружности, если меньшая из сторон равна 14.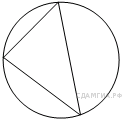

Решение.

Пусть первая дуга имеет градусную меру тогда вторая дуга имеет градусную меру а третья - Три дуги в сумме составляют окружность, поэтому получаем:

Поэтому меньшая дуга окружности равна Угол треугольника, опирающийся на эту дугу является вписанным, поэтому он равен половине дуги: Меньший угол треугольника лежит против меньшей стороны. Найдём радиус описанной окружности:

Ответ: 14.

Тренажер

Задание 10 № 311503. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Задание 10 № 316346. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Задание 10 № 339483. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.

Задание 10 № 339828. Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.

Задание 10 № 341707. Найдите площадь квадрата, описанного вокруг окружности радиуса 7.

Задание 10 № 311503. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.

Задание 10 № 316346. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.

Задание 10 № 339483. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB = BC и ∠ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.

Задание 10 № 339828. Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.

Задание 10 № 341707. Найдите площадь квадрата, описанного вокруг окружности радиуса 7.

Используемая литература:

1) Геометрия. Учебник для 7 класса общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев. Научный редактор - академик А.Н. Тихонова. - 22-е изд. - М.: Просвещение, 2013.

2). Сборник для подготовки ОГЭ. И.В. Ященко, С.А.Шестаков, А.В. Семенов.

3) Сайт: www fipi..ru

4) Сайт:alexlarin.net/ для подготовки ОГЭ

5) Сайт: открытый банк заданий для подготовки ОГЭ по математике.