- Учителю
- Разложение разности квадратов на множители
Разложение разности квадратов на множители
Конспект урока по алгебре в 7-м классе
"Разложение разности квадратов на множители"
дата
Цели урока:
-
Развитие опыта применения формулы, умения работать в группах, учиться слушать других, учиться вместе.
-
На основании формулы учащиеся должны научиться делать следующие преобразования:
-
раскладывать на множители;
-
сокращенно умножать сумму двух выражений на их разность;
-
решать уравнения;
-
доказывать тождества;
-
применять формулу для вычислений.
Мотив:
Зная данную формулу, мы сможем делать все эти преобразования, а в дальнейшем и сокращать дроби.
Тип урока: урок-исследование.
Вид урока: комбинированный.
</ Ход урока
Устные упражнения помогут нам в дальнейшей работе.
1 учащийся у доски: замените пропуски одночленами, чтобы выполнялось равенство
-
( __ - 15a)( __ + __ ) = 4c2 - __
-
81a2 - __ = ( __ + __ )( __ - 11с)
-
0,49x6 - __ = ( __ - 10k2)( __ + __ )
1. Прочитайте выражения:
-
a2 - b2;
-
(a - b)2;
-
y+5;
-
(m - n)(m + n).
2. Представьте выражение в виде квадрата одночлена:
-
4p2;
-
0,16n2;
-
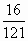 a2;
a2;
-
a2b2.
3. Решить уравнение:
(x + 4)(x - 1) = 0
Ответ: x = -4; x = 1
4. Вычислить: ![]()
5. Заполните таблицу, выбрав буквы, соответственно верным и неверным равенствам, назовите ошибку (можно совещаться).
(3a2)2 = 27a4
(9a - 7b)(7b + 9a) = 81a2 - 49b2
(0,1xy3)2 = 0,01x2y6
(a - b)(a + b) = a2 - b2 +2ab
(a - b)2 = a2 + b2 - 2ab
(m + n)(n - m) = m2 - n2
На доске (a - b)(a + b) = a2 - b2
Историческая справка: это две взаимно обратные операции. Чем отличаются скобки? Знаком! Такие выражения называются сопряженными.
Еще в глубокой древности было подмечено, что некоторые многочлены можно умножать короче, быстрее, чем остальные, итак появились формулы сокращенного умножения, некоторые правила сокращенного умножения были известны около 4 тыс. лет тому назад. Их знали вавилоняне и другие некоторые народы древности. Сегодня нам предстоит сыграть роль "исследователей", для того чтобы "открыть", где может данная формула применяться.
Задание выполняется в группах
1 группа: повторим, как применяется формула сокращенного умножения (выполняем у доски сложные задания).
Задание: выполните умножение
-
(4x2 - 2y3)(4x2 + 2y3) = (4x2)2 - (2y3)2 = 16x4 - 4y6
-
(10m + 8n5)( 10m - 8n5) = (10m)2 - (8n5)2 = 100m2 - 64n10
2 группа: повторим, как применяется формула, если надо разложить на множители (выполняем задание у доски).
Задание: разложите на множители
-
(225x2 - 64y4) = (15x - 8y2)( 15x + 8y2)
-
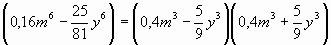
Остальные листочки разбирают по группам, каждая группа выполняет задание на месте, потом рассматривают решение на доске. Узнаем, где еще применяется данная формула.
3 группа:
Задание: вычислить
-
872 - 132
-
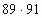
4 группа:
Задание: решить уравнение
-
x2 - 49 = 0
-
25y2 - 16 = 0
5 группа:
Задание: докажите тождество
(x + y)(x - y) + (y - a)(y + a) = (x - a)(x + a)
6 группа:
Задание: упростите выражение
-
(3b - 1)(3b + 1) - (b - 5)(b + 5)
-
(7m - 10n)(7m + 10n) - 100n2
Решение уравнения (с комментарием) у доски:
8x(1 + 2x) - (4x + 3)(4x - 3) = 2x
8x + 16x2 - 16x2 + 9 =2x
8x - 2x = 9
6x = 9
x=![]()
x = ![]()
Ответ: x = 1,5
Подведение итогов:
Каждая группа рассказа о своем применении формулы (a - b)(a + b) = a2 - b2 .
Какие же результаты мы получили? Она применяется для:
-
сокращенного умножения;
-
разложения на множители;
-
решения уравнений;
-
упрощения выражений;
-
вычислений.
Учились учиться вместе, работая в группах, увидели, что успех команды зависит от вклада каждого ученика.
Домашнее задание: №859,863,867
1 группа: повторим, как применяется формула сокращенного умножения (выполняем у доски сложные задания).
Задание: выполните умножение
-
(4x2 - 2y3)(4x2 + 2y3) = (4x2)2 - (2y3)2 = 16x4 - 4y6
-
(10m + 8n5)( 10m - 8n5) = (10m)2 - (8n5)2 = 100m2 - 64n10
2 группа: повторим, как применяется формула, если надо разложить на множители (выполняем задание у доски).
Задание: разложите на множители
-
(225x2 - 64y4) = (15x - 8y2)( 15x + 8y2)
-
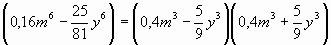
Остальные листочки разбирают по группам, каждая группа выполняет задание на месте, потом рассматривают решение на доске. Узнаем, где еще применяется данная формула.
3 группа:
Задание: вычислить
-
872 - 132
-
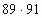
4 группа:
Задание: решить уравнение
-
x2 - 49 = 0
-
25y2 - 16 = 0
5 группа:
Задание: докажите тождество
(x + y)(x - y) + (y - a)(y + a) = (x - a)(x + a)
6 группа:
Задание: упростите выражение
-
(3b - 1)(3b + 1) - (b - 5)(b + 5)
-
(7m - 10n)(7m + 10n) - 100n2
Решение уравнения (с комментарием) у доски:
8x(1 + 2x) - (4x + 3)(4x - 3) = 2x
8x + 16x2 - 16x2 + 9 =2x
8x - 2x = 9
6x = 9
x=![]()
x = ![]()
Ответ: x = 1,5