Учителю
Конспект урока для 11 класса «Решение логарифмических уравнений»

Конспект урока для 11 класса «Решение логарифмических уравнений»

Автор публикации: Советникова Н.Н.

Дата публикации: 30.01.2014

Краткое описание: "Описание материала:Урок по математике в 11 классе с использованием сингапурской методики материал можно использовать при закрепление темы логарифмических уравнений. обучающих и кооперации .Используется коллективная работа обучающих.Обучающие в процессе урока должны"

предварительный просмотр материала

МБОО «Старо - Матакская

средняя общеобразовательная школа»

Алькеевского муниципального района РТ

Учителя математики

Советниковой Н. Н.

Тема урока: «Решение логарифмических уравнений»

Тип урока: урок обобщения, систематизация знаний.

Цели:

Образовательные:

Обобщение знаний, умений и навыков по теме «Решение логарифмических уравнений». выработать у обучающихся умения решать основные виды логарифмических уравнений
Предоставить каждому обучающему возможность проверить свои знания и повысить их уровень.
Активизировать работу класса через разные формы работы.

Развивающие:

Развивать навыки самоконтроля.

Воспитательные:

воспитание трудолюбия, аккуратности, математической культуры, самостоятельности, интереса к предмету.

ЗАДАЧИ:

повторить понятия, связанные с функцией;
проверить и откорректировать умения решать виды логарифмических уравнений;
закрепить навыки решение логарифмических уравнений;
развитие логического мышления, памяти, внимания; умение классифицировать объекты
применить свои знания в творческих заданиях.

Формы организации учебной деятельности: коллективная, групповая, индивидуальная,.

Техническое обеспечение урока: компьютер, мультимедийный проектор с экраном, доска.

Обучающиеся сидят в группах по четыре человека

Ход урока.

1.Организационный момент: Здравствуйте ребята

Слайд1

Обучающая структура Таймд-раунд - робин «в которой каждый ученик проговаривает ответ в команде по кругу в течение определенного количества времени»

1.Какие уравнения называются логарифмическими.

2 . И какие способы их решения вы знаете.

Слайд 2

Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим примером логарифмического уравнения служит уравнение log_a х = b (где а > 0, а 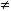1).

Решение уравнений на основании определения логарифма, например, уравнение log_a х = б (а > 0, а 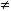1, б>0 ) имеет решение х = а^b.
Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их:
если log_a f(х) = log_a g(х), то f(х) = g(х), f(х)>0, g(х)>0, а > 0, а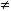 1.
Метод введение новой переменной.
Метод логарифмирования обеих частей уравнения.
Метод приведения логарифмов к одному и тому же основанию.
Функционально - графический метод.

Обучающая структура КОНЭРС «в которой ученики распределяются по разным углам в зависимости от выбранного ими варианта ответа»

log₂ x=2 ; log _x 64=3 ; log₂ (x-3)=3; log₆² х +log ₆ х -2 = 0; log₃ (x² +2x-1)= log₃ (3x+1)

log₂ ( 3x-1)= log₂ (7x+1) 3 log₆² х +4log ₆ х -7 = 0

log₃ х = 11-х log_0,1 х = 3х+1

подчеркнутые уравнения решить у доски.

Обозначение углов:

Решение уравнений на основании определения логарифма, например, уравнение log_a х = б (а > 0, а 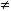1, б>0 ) имеет решение х = а^b.
Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их:
если log_a f(х) = log_a g(х), то f(х) = g(х), f(х)>0, g(х)>0, а > 0, а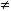 1.
Метод введение новой переменной. .
Функционально - графический метод.

СИМАЛТИНИУС РАЙУНД ТЭЙБЛ -обучающая структура, в которой 4 ученика в команде одновременно выполняют письменную работу на отдельных листочках и по окончанию передают друг другу по кругу. Каждый решает под своим номером (ученик под номером1 решит 4 уравнение в 4 карточках под номером 1.

1 log₂ x=2

2 log₆² х +log ₆ х -2 = 0

Log₀_,2² х +log _0,2 х -6 = 0

Log_0,₄ (х+2)+ log_0,₄ (x+3) = log_0,3 (1-х)

log₃ (х-2)+ log₃ (x+2) = log₃ (2x-1)

2 log₄ (-x² +5x+7)= log₄ (10x-7)

log₃ (x² +2x-1)= log₃ (3x+1)

log _x 64=3

log₆² х +3log ₆ х +2= 0

Log₃ (x-2)=2

log₂ (x-3)=3

Log₂ (x² +x-1)= log₂ (-x+7)

log₂ ( 3x-1)= log₂ (7x+1)

log₁₁ (х+4)+ log₁₁ (x-7) = log₁₁ (7-х)

Log_0,3 (х+3)+ log_0,3 (x-3) = log_0,3 (2x-1)

3 log₆² х +4log ₆ х -7 = 0

Физкультминутка 3 мин МИКС-ФРИЗ-ГРКП обучающая структура, в которой ученики смешиваются под музыку, замирают, когда музыка прекращается, и объединяются в группы , количество участников в которых зависит от ответа на какой -либо вопрос.

- Ребята встаньте пожалуйста, задвиньте стулья , спасибо. И так, я включаю музыку, вы передвигаетесь, музыка останавливается, я задаю вопрос. Вы должны сформировать группу с таким же количеством человек, которое является ответом на вопрос.

1) log₂ 8= Поблагодарите друг друга.

2) log₃ 9 Поблагодарите друг друга.

3) log₂ 32 Поблагодарите друг друга.

4) log₄ 64 Поблагодарите друг друга.

СИНГЛ РАУНД РОБИН -обучающая структура ,в которой учащиеся проговаривают ответы на данный вопрос по кругу один раз

«Проверь себя». Слайд-4

1)
2. log₅ (121 - x²), (121 - x²)  0, x  - 11, x  11.
3)
4)
5) lg x² = 2lg x.

Это задание позволит учителю проверить внимание учащихся, их знания

Ответы: 1(.-3 -отрицательное число), 2. ((121 - x²) >0 ; -11< х <11), 3. (log₃5 ),

4. ( 5⁴ ) , 5. (модуль ).

ФИНК_РАЙТ_РАУНД РОБИН- «подумай -запиши -обсуди в команде» Во время выполнения данный структуры обучающие обдумывают решение уравнения ,записывают свои решения и по очереди объясняют свои решения.

Слайд №5

. lg³x + 5lg²x -12lgx =2lgx

ОДЗ: х>0

lg³x + 5lg²x -14gx =0

(lg²x+5lgx-12)lgx=0

x=1 a²- 5a - 14 = 0
Ответ: х=1; х=10⁷; х=