Урок-игра «Научно-исследовательские лаборатории» по теме: «Сложение смешанных чисел» (5 класс)

Петрушенко Светлана Дмитриевна, учитель математики,

средняя общеобразовательная школа №9

город Екибастуз, Павлодарская область

электронный адрес: PSD510@mail.ru

Урок-игра «Научно-исследовательские лаборатории»

Тема: «Сложение смешанных чисел» 5 классЦели урока:

образовательные: формирование учебно-познавательной компетенции через организацию исследовательской деятельности учащихся; формирование знаний способа сложения смешанных чисел, навыка его применения при решении задач, установление связи со сложением обыкновенных дробей.

развивающие: развитие у учащихся навыков сравнения, обобщения, анализа; создание условий для развития у учащихся умений выделять проблемы, их формулировать, предлагать пути решения.

воспитательные: содействовать развитию у школьников навыков коммуникации, повышать самооценку и уверенность в себе, проводить рефлексию собственной деятельности.

Тип урока: изучения нового материала.

Оборудование: раздаточный материал (цветные карточки с заданиями), плакаты с названиями этапов, картинка совы, ватманы, маркеры, оценочные листы.

Методы: наглядный, частично-поисковый, практический.

I. Вводно-мотивационный этап.

Задача: стимулировать положительную мотивацию учебной деятельности учащихся.Проверка готовности к уроку.

Приветствие. Вступительное слово: Представьте себе, что сегодня наш класс - научно-исследовательский институт. А вы, ученики-сотрудники этого института. А, именно, сотруд-ники различных лабораторий по проблемам математики. Вас всех пригласили принять участие в заседании ученого совета этого НИИ, чтобы обсудить с вами тему: «Обыкновенные дроби». В процессе деятельности вам предстоит поработать в различных лабораториях. У каждого из вас на столе оценочный лист, где вы будите фиксировать свои достижения, и в конце работы оцените свою деятельность.

Учащиеся настраиваются на позитивную деятельность. Обеспечивается мотивация учения школьников.

Оценочный лист________________________________

теоретиков

Лаборатория

алгоритмов

Лаборатория

исследова-

ний

Лаборатория

раскрытия

тайн

Лаборатория

эксперимен-тальная

Актив-ность

Всего баллов

Оценка

II. Этап актуализации знаний.

Задача: понимание учащимися практической и личностной значимости изучаемого материала.

Устная работа:

Выясните в какие группы можно обьеди-нить дроби из данного ряда.

Итак, мы получили пропуск в лаборатории.

1.Лаборатория теоретиков.

Предлагаю вам принять участие в её работе. В ней много правил, которые мы изучили ранее. У каждого из вас имеется карточка-домино. Она содержит вопрос и ответ. Первым начинает тот, у кого карточка содержит слова «Финиш» и «Старт». Он задаёт стартовый вопрос и он же даёт финиш-ный ответ. Каждому необходимо внимательно следить за ходом игры, чтобы не пропустить ответ. Ответив, ученик задаёт свой вопрос и т. д..За игру в домино в оценочный лист вы себе поставите 1 балл, если верно ответите , и 0 баллов, если пропустите свой ответ. Тот, кто дал верный ответ в устной работе добавляет себе ещё один балл.

Учащиеся дают ответы фронтально.

Отвечают поочередно, соблюдая условия игры.

Осуществляют самооценку.

«Математическое домино» ФИНИШ: ОТВЕТ: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

СТАРТ: ВОПРОС: Какое действие выполняет черта в обыкновенной дроби?

ОТВЕТ: Деление.

ВОПРОС: Что называется числителем дроби?

­­­­­­­­­­ОТВЕТ: Число над чертой дроби.

ВОПРОС: Что называется знаменателем дроби?

ОТВЕТ: Число под чертой дроби.

ВОПРОС: Какая дробь называется правильной?

ОТВЕТ: Дробь, у которой числитель меньше знаменателя.

ВОПРОС: Какое число называется смешанным?

ОТВЕТ: Число, состоящее из целой части и дробной части.

ВОПРОС: Что называется сокращением дроби?

ОТВЕТ: Деление и числителя, и знаменателя дроби на их общий делитель, отличный от единицы.

ВОПРОС: Какие дроби называются единичными дробями?

ОТВЕТ: Дроби с числителем, равным единице.

ВОПРОС: Какая дробь называется неправильной?

ОТВЕТ: Дробь, у которой числитель равен или больше знаменателя.

ВОПРОС: Что называется наименьшим общим знаменателем данных несократимых дробей?

ОТВЕТ: Наименьшее общее кратное знаменателей этих дробей.

ВОПРОС: Какая из дробей с одинаковыми знаменателями больше?

ОТВЕТ: Та, у которой числитель больше.

ВОПРОС: Как сложить дроби с одинаковым знаменателем?

ОТВЕТ: Числители складывают, а знаменатель оставляют тот же.

ВОПРОС: Какую дробь называют несократимой дробь?

ОТВЕТ: Дробь, числитель и знаменатель которой взаимно простые числа.

ВОПРОС: Какая из дробей с одинаковыми числителями больше, какая меньше?

ОТВЕТ: Больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше.

ВОПРОС: Как формулируется основное свойство дроби ?

2. Лаборатория алгоритмов.

Задача: повторение способов сложения обыкновенных дробей; создание проблемной ситуации, постановка цели урока.I-вариант _{Ответы:}

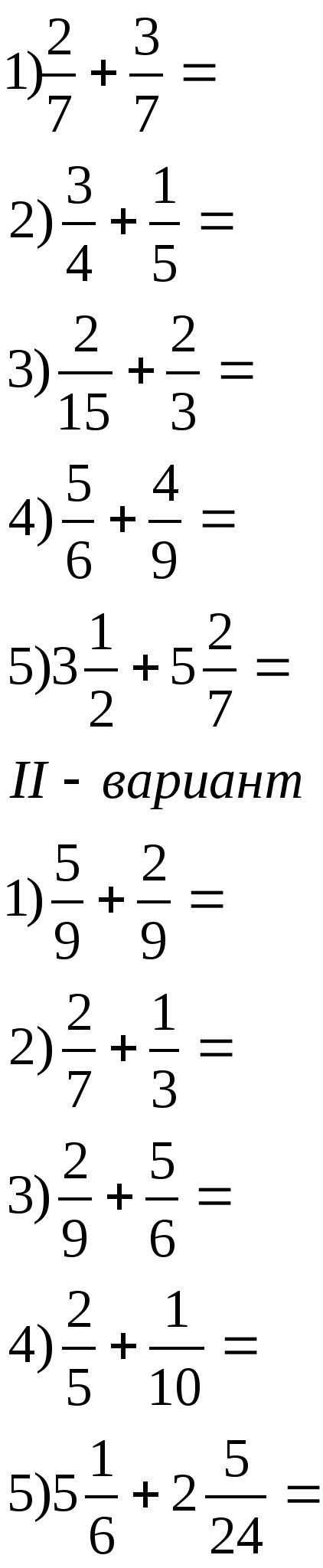
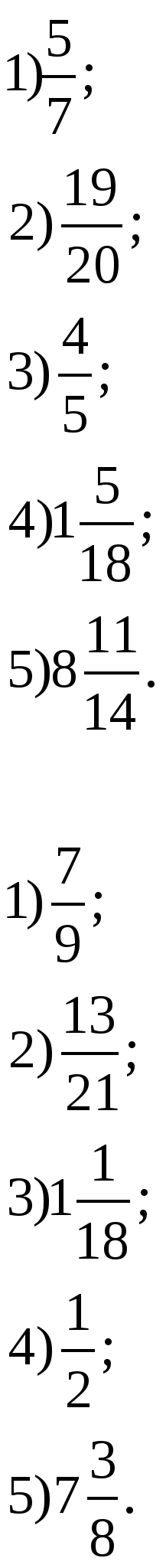
Выполняют задание индивидуально на карточке.

- Согните карточки по чёрной линии и сравните свои ответы с ответами на карточке.

- Ко всем ли примерам нашёлся ответ?

-Что вызвало затруднения?

- Итак, мы столкнулись с проблемой.

- Постарайтесь её сформулировать и найти пути решения. - Ваша цель совпала с моей (открыть доску). Откройте тетради, запишите число, классная работа и тему урока «Сложение смешан ных чисел». - Чтобы найти пути решения проблемы, перейдём в следующую лабораторию. Но прежде, в оценочный лист выставьте по 1 баллу за каждый верно решённый пример. Итак, переходим в лабораторию исследований.

Осуществляют самоконтроль. Пример 5 вызвал затруднения. Учащиеся формулируют проблему: сложение смешанных чисел.Озвучивают цели урока. Учитель записывает тему урока на доске, а ученики в тетрадях.

III. Организация восприятия и осмысления.

Задача: организация и направление к цели исследовательской деятельности учащихся.

3. Лаборатория исследований.

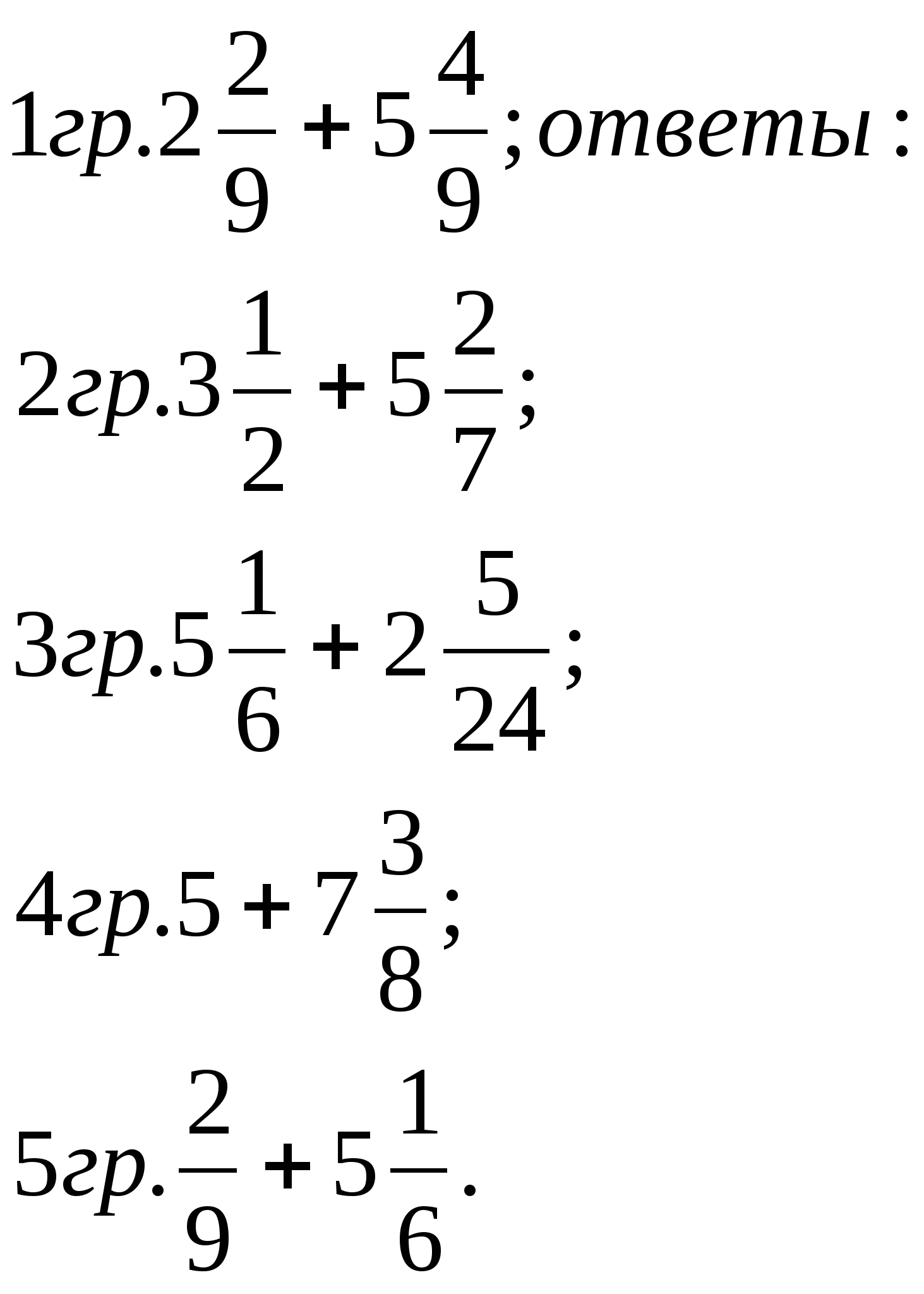
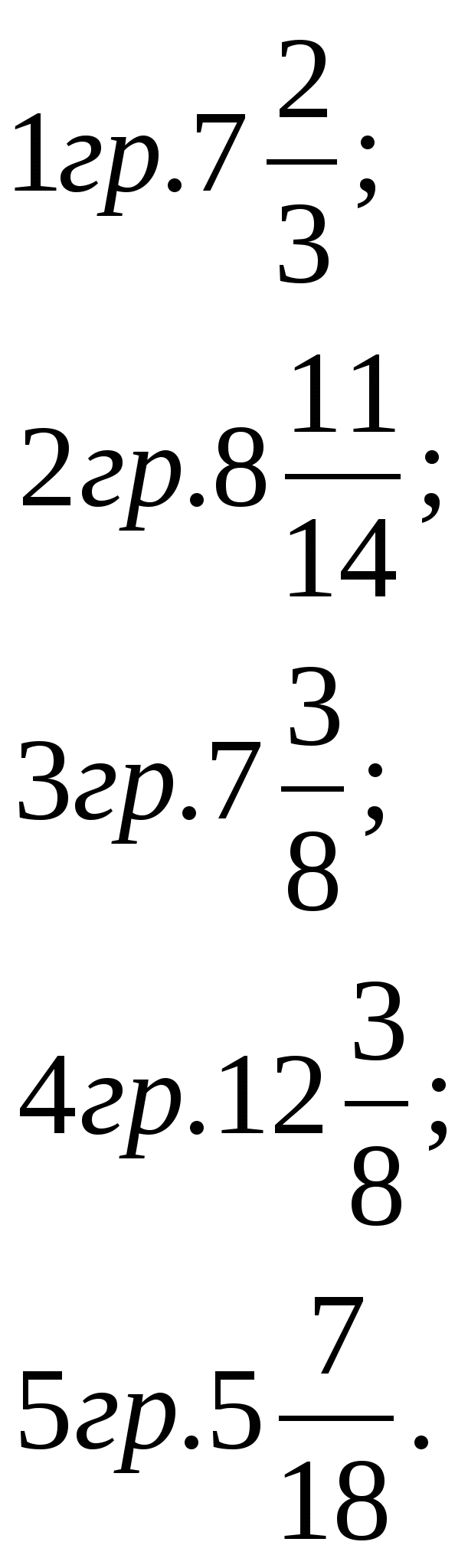
-Предлагаю сформулировать ваши гипотезы.

-Вы услышали выводы каждой исследовательской группы. Давайте вспомним как вы рассуждали и выработаем алгоритм сложения смешанных чисел.

Вернемся к примеру 5 и решим его.

Форма работы-групповая.

Учащиеся приступают к выполнению заданий. Решение записывают маркерами на ватмане и составляют алгоритм.

1гр. Сложение смешанных чисел с одинаковыми знаменателями.

2,3 гр. Сложение смешанных чисел с разными знаменателями.

4гр. Сложение натурального и смешанного чисел.

5гр.Сложение правильной дроби и смешанного числа.

Вывешивают на доску ватманы. Один ученик от группы озвучивает версию алгоритма. Устанавливают связь с правилами сложения обыкновенных дробей.

-Чтобы проверить наши предположения обратимся к учебнику. Откройте страницы 134-135.

-Совпадают ли наши выводы с правилами в учебнике?

-Какие вы, молодцы!

А, теперь пришло время отдохнуть.

Пройдём в комнату отдыха.

Физкультминутка.

Потрудились - отдохнём,

Встанем ,глубоко вздохнём.

Руки в стороны, вперёд,

Влево, вправо поворот.

Три наклона, прямо встать.

Руки вниз и вверх поднять.

Руки плавно опустили,

Всем улыбки подарили.

-Вспомните , одной из целей было показать применение алгоритма в различных ситуациях.

-Следующая «Лаборатория тайн».

Работа в группах.

Работа с учебником. Анализирут, сравнивают, сопоставляют результаты исследовательской работы.

Выполняют физические упражнения.

IV. Первичная проверка понимания.

Задача: Установить правильность и осознанность изученного материала.

4.«Лаборатория раскрытия тайн». Задание на розовой карточке.

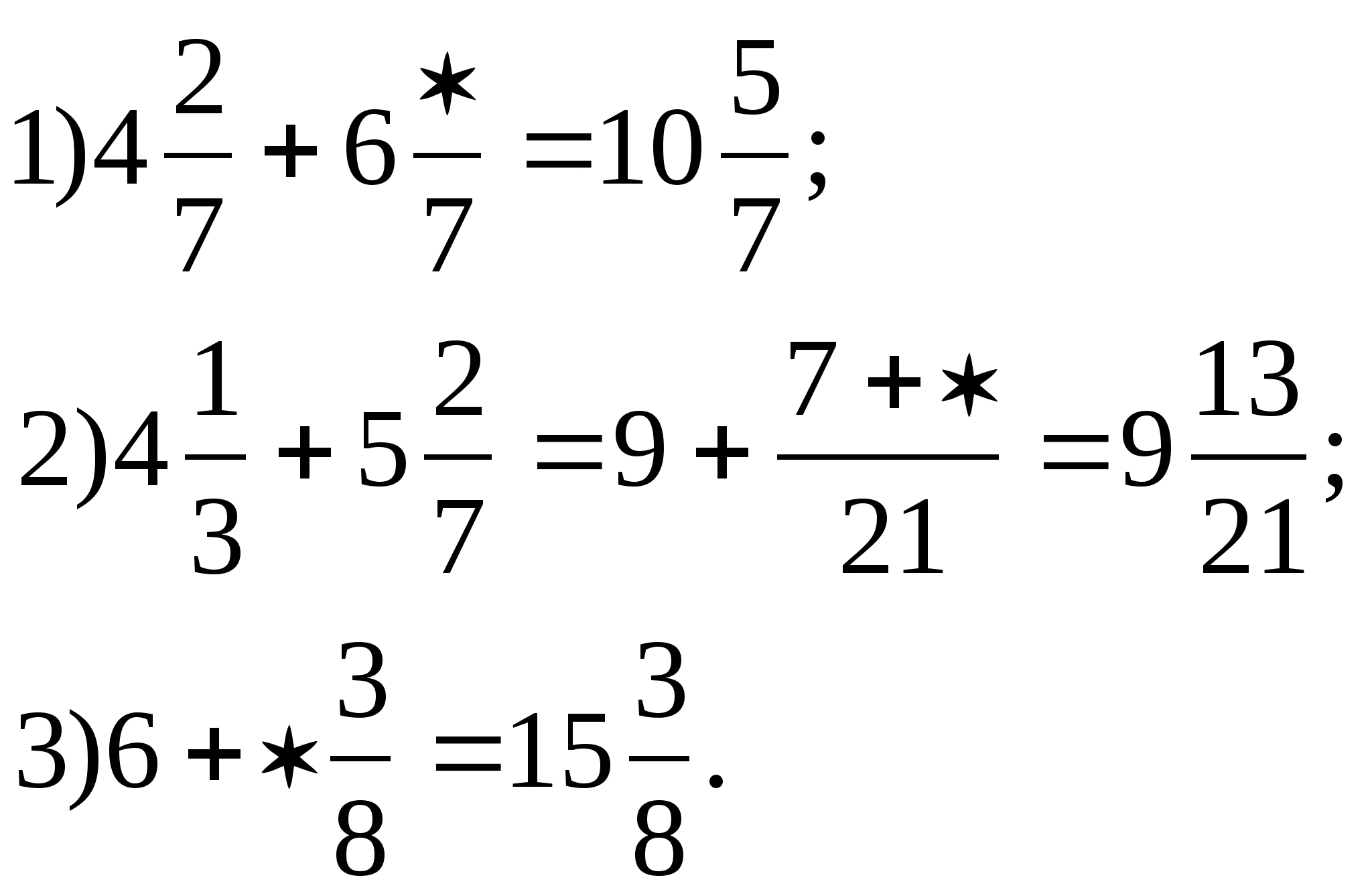Ответы: 1) 3; 2) 6; 3) 9.

-Ответы озвучьте.

Проставьте баллы в оценочный лист.

За каждый правильно решённый пример проставьте по 1 баллу в оценочный лист.

Работа в малых группах (по 4 ученика).

Сопоставляют результаты.

V.Организация первичного закрепления.

Задача: Организация собственной деятельности учащихся в форме, позволяющей проконтролировать её ход и получаемые результаты.

5.«Лаборатория экспериментальная»

-Предлагаю вам самостоятельную работу в двух вариантах на голубых карточках.

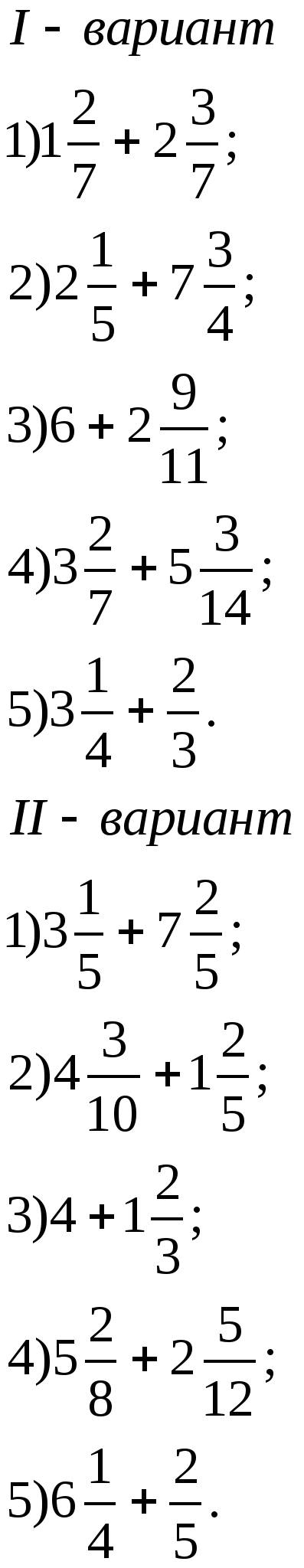
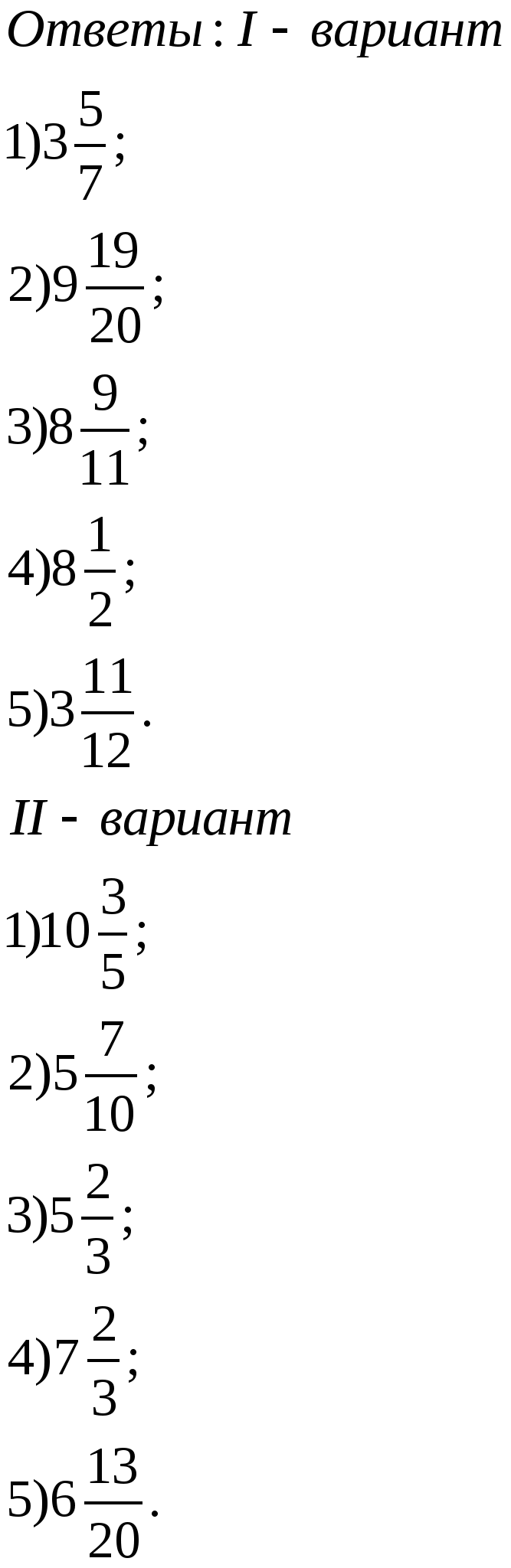
-Обменяйтесь тетрадями. Проведём взаимопроверку. На обратной стороне карточки верные ответы.

За каждый правильно решённый пример проставьте по 1 баллу в оценочный лист.

Самостоятельно применяют полученные знания.

Обмениваются тетрадями в парах, осуществляют взаимоконтроль и оценивают друг друга в таблице ответов.

VI. Анализ. Подведение итогов.

Задача: умение учащихся анализировать свою деятельность, осуществлять самооценку.

-Что мы делали , чтобы её достичь?

-Значит, ребята, мы цели своей достигли.

-За активность на уроке добавьте от 1 до 3б.

-А теперь подведём итоги нашей научной работы. Подсчитайте количество набранных баллов.

-У кого от 14-18б.-«5»,

от 11-13б.-«4»,

от 9-10б.-«3».

-Выставьте оценки в оценочный лист.

-Поднимите руки у кого «5», «4», «3».

Анализируют что делали в каждой из лабораторий.

Осуществляют самооценку:

подсчитывают количество набранных баллов, выставляют оценки.

VII. Постановка домашнего задания.

Задача: сообщить учащимся домашнее задание, дать краткий инструктаж по его выполнению.

Найти в тексте параграфа пример автора (пример 2), который мы не рассматривали. Выясните в чём его особенность и запишите в тетрадь.

Записывают домашнее задание в дневник.

VIII. Рефлексия.

Задача: провести рефлексию по поводу своего психо-эмоционального состояния.цвет которой соответствует вашему настроению.

-Если мы так будем работать и дальше, можем стать магистрами наук, символ которых - учёная сова.

-Урок окончен. Всем спасибо!

Выражают своё отношение к уроку .

Получают в подарок символ совы.

Используемая литература:

1. Математика. Учебник для 5 класса общеобразовательной школы.К.Алдамуратова, Е.Байшоланов. - Алматы: Атамура, 2010 г.

2. Математика. Дидактические материалы для 5 класса общеобразовательной школы. К.Алдамуратова, О.Кособокова,Р.Базаканова - Алматы: Атамура, 2010 г.

3. Математика. Методическое руководство для 5 класса общеобразовательной школы. К.Алдамуратова, Е.Байшоланов - Алматы: Атамура, 2010 г.

4. Математика. Сборник контрольных работ. К.Алдамуратова, Ж.Кобдикова. - Алматы: Атамура, 2006 г.