Контрольные работы в 10- 11 классе

Контрольные работы по алгебре и началам анализа в 10 классе

Входной срез.

Вариант 1.

1. Решите систему уравнений

2. Решите неравенство

3. Представьте выражение в виде степени с основанием a.

4. Постройте график функции Укажите, при каких значениях x функция принимает положительные значения.

5. Упростите выражение

Вариант 2.

1. Решите систему уравнений

2. Решите неравенство

3. Представьте выражение в виде степени с основанием y.

4. Постройте график функции Укажите, при каких значениях x функция принимает отрицательные значения.

5. Упростите выражение

Вводная контрольная работа по алгебре

Вариант 1

Часть 1

1. Найдите область определения функции

1)х ≥ 5; 2) х ≥ -5; 3) х ≥ 0; 4) х ≤ 5.

2. Разложите квадратный трёхчлен 5х² - 6х + 1 на множители

1) 5(х - 1)(5х - 1); 2) (х - 1)(5х - 1); 3) (х - 1)(х - 0,2); 4) (5х - 1)(х - 0,2).

3. Найдите координаты вершины параболы, заданной формулой у = 2х² - 8х + 6

1) (2; -2); 2) (-2; 30); 3) (2; 18); 4) (4; 6).

4. Решите неравенство 3х² - 4х - 7 < 0

1) 2) (-∞; +∞); 3) ; 4) .

5. Ордината вершины параболы у = -(х + 6)² + 5 равна

1) -5; 2) 5; 3) -6; 4) 6.

6. Решением системы является пара чисел

1) (-5; -3); 2) (1; 3) и (-2; 0); 3) (1; -3); 4) (2; 0).

7. Найдите разность арифметической прогрессии 5; 8; 11…

1) -3; 2) 3; 3) 13; 4) 1,6.

8. Шестой член арифметической прогрессии 1; -2; -5… равен

1) -14; 2) 12; 3) -15; 4) 16.

9. Знаменатель геометрической прогрессии 4; 12; 36… равен

1) 48; 2) 3; 3) -8; 4) 8.

10. Пятый член геометрической прогрессии 2; -6; 18… равен

1) -54; 2) 162; 3) -162; 4) 16.

11. Найдите значение разности

1) -63; 2) 3; 3) -135; 4) -3.

Часть 2

1. Решите уравнение х⁴ - 13х² + 36 = 0

2. Решите неравенство 3х² + 2х - 1 ≥ 0

3. Решите систему

4. Сумма трёх чисел, составляющих арифметическую прогрессию, равна 12, а произведение первого и второго - 8. Найдите эти числа.

Вариант 2

Часть 1

1. Найдите область определения функции

1)х ≥ 4; 2) х ≥ -4; 3) х ≥ 0; 4) х ≤ 4.

2. Разложите квадратный трёхчлен 2х² + 5х - 3 на множители

1) 2(х - 3)(х - 0,5); 2) 2(х - 3)(х + 0,5); 3) (х + 3)(х - 0,5); 4) (х + 3)(2х - 1).

3. Найдите координаты вершины параболы, заданной формулой у = 3х² - 6х + 2

1) (2; 2); 2) (-1; 11); 3) (1; -1); 4) (4; 6).

4. Решите неравенство 4х² - 3х - 1 < 0

1) 2) (-∞; +∞); 3) ; 4) .

5. Ордината вершины параболы у = -(х - 5)² + 6 равна

1) -5; 2) 5; 3) -6; 4) 6.

6. Решением системы является пара чисел

1) (-5; -8); 2) (2; -1) и (-1; -4); 3) (2; 1); 4) (-2; 1).

7. Найдите разность арифметической прогрессии 6; 10; 14…

1) -4; 2) 4; 3) 16; 4) 0,6.

8. Шестой член арифметической прогрессии 2; -3; -8… равен

1) -23; 2) 12; 3) -18; 4) 16.

9. Знаменатель геометрической прогрессии 2; 6; 18… равен

1) 48; 2) 3; 3) -8; 4) 8.

10. Пятый член геометрической прогрессии -2; -6; -18… равен

1) -54; 2) 162; 3) -162; 4) 16.

11. Найдите значение разности

1) 561; 2) 3; 3) 1; 4) -3.

Часть 2

1. Решите уравнение х⁴ - 65х² + 64 = 0

2. Решите неравенство 3х² - 5х - 2 ≤ 0

3. Решите систему

4. Сумма трёх чисел, составляющих арифметическую прогрессию, равна произведению первого и второго чисел и равна 15. Найдите эти числа.

Контрольная работа № 1

по теме«Действительные числа»

Вариант 1

1. Вычислить: 1) ; 2) .

2. Известно, что 12^х = 3. Найти 12^{2х - 1} .

3. Выполнить действия (а>0, b> 0): 1) ; 2) - .

4. Сравнить числа: 1) ; 2) .

5. Записать бесконечную периодическую десятичную дробь 0,2(7) в виде обыкновенной.

6. Упростить

Вариант 2

1. Вычислить1) ; 2) .

2. Известно, что 8^х = 5. Найти 8 ^{- х + 2} .

3. Выполнить действия (а>0, b> 0): 1) ; 2) - .

4. Сравнить числа: 1) ; 2) .

5. Записать бесконечную периодическую десятичную дробь 0,3(1) в виде обыкновенной.

6. Упростить

Контрольная работа № 2

по теме «Степенная функция»

Вариант 1

1. Найти область определения функции .

2. Изобразить эскиз графика функции у = х ^{- 5}.

1. Выяснить, на каких промежутках функция убывает

2. Сравнить числа: а) ; б) (3,2)^{- 5} и .

3. Решить уравнение: 1) 2) ; 3)

4)

4. Найти функцию, обратную к функции у = (х - 8) ^{- 1},указать её область определения и множество значений.

5. Решить неравенство

Вариант 2

1. Найти область определения функции у = .

2. Изобразить эскиз графика функции у = х ^{- 6}.

1. Выяснить, на каких промежутках функция возрастает.

2. Сравнить числа: а) ; б) (4,2)^{- 6} и .

3. Решить уравнение: 1) 2) ; 3)

4)

4. Найти функцию, обратную к функции у = 2(х + 6) ^{- 1},указать её область определения и множество значений

5. Решить неравенство

Контрольная работа № 3

по теме «Показательная функция»

Вариант 1

1. Решить уравнение: 1) 2) 4^х + 2^х - 20 = 0.

2. Решить неравенство

3. Решить систему уравнений

4. Решить неравенство: 1) 2)

5. Решить уравнение 7^{х + 1} + 3∙7^х = 2^{х + 5}+ 3 ∙ 2^х.

Вариант 2

1. Решить уравнение:1) 2) 9^х - 7 ∙ 3^х - 18 = 0.

2. Решить неравенство

3. Решить систему уравнений

4. Решить неравенство: 1) 2)

5. Решить уравнение3^{х + 3} + 3^х = 5∙2^{х + 4} - 17 ∙ 2^х.

Контрольная работа № 4

по теме «Логарифмическая функция»

Вариант 1

1. Вычислить: 1) 16; 2) ; 3)

2. В одной системе координат схематически построить графики функций y=, y=.

3. Сравнить числа и .

4. Решить уравнение(2x - 1) = 2.

5. Решить неравенство

6. Решить уравнение x = 3.

7. Решить уравнениеx +

8. Решить неравенство

Вариант 2

1. Вычислить:1) ; 2) ; 3)

2. В одной системе координат схематически построить графики функций y = , y = .

3. Сравнить числа и .

4. Решить уравнение(2x+ 3) = 3.

5. Решить неравенство

6. Решить уравнениеx = 2.

7. Решить уравнениеx +

8. Решить неравенство

Контрольная работа № 5

по теме «Основные тригонометрические формулы»

Вариант 1

1. Вычислить: 1) ; 2) .

2. Вычислить , если

3. Упростить выражение: 1) ; 2) .

4. Решить уравнение.

5. Доказать тождество.

Вариант 2

1. Вычислить 1) ; 2) .

2. Вычислить, если

3. Упростить выражение 1) ; 2)

4. Решить уравнение.

5. Доказать тождество.

Контрольная работа № 6

по теме «Тригонометрические уравнения»

Вариант 1

1. Решить уравнение: 1) 2)

2. Найти решение уравнения на отрезке [0; З].

3. Решить уравнение 1) 3

2) 6 sin ²x - sin x = 1; 3) 4 sin x + 5 cos x = 4; 4) sin⁴x + cos⁴x = cos²2x + 0,25.

Вариант 2

1. Решить уравнение: 1) 2)

2. Найти решение уравнения на отрезке [0; 4].

3. Решить уравнение 1)

2) 10 cos²x + 3 cos x = 1; 3) 5 sin x + cos x = 5; 4) sin⁴x + cos⁴x = sin²2x - 0,5.

Итоговая контрольная работа № 7

Вариант 1

1. Решите неравенство х²(2х + 1)(х - 3) 0.

2. Решите уравнение:

а) б) 4^х - 3∙ 4^{х - 2} = 52; в)

3. Сколько корней имеет уравнение 2cos²x - sin (x - ) + tgxtg(x + ) = 0 на промежутке (0; 2)? Укажите их.

4. Найдите целые решения системы неравенств:

Вариант 2

1. Решите неравенство

2. Решите уравнение:

а) б) 5^х - 7∙ 5^{х - 2} = 90; в)

3. Сколько корней имеет уравнение sin²x + cos²2x + cos²( ) cosxtgx = 1 на промежутке (0; 2)? Укажите их.

4. Найдите целые решения системы неравенств:

Контрольные работы по алгебре и началам анализа в 11 классе

Контрольная работа № 1

по теме «Тригонометрические функции»

Вариант 1

1. Найдите область определения и множество значений функции у = 2 cosx.

2. Выясните, является ли функция у = sinx - tgx четной или нечетной.

3. Изобразите схематически график функции у = sinx+ 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = 3sinx∙cosx + 1.

5. Постройте график функции у = 0,5 cosx - 2. При каких значениях х функция возрастает? Убывает?

Вариант 2

1. Найдите область определения и множество значений функции у = 0,5 cosx.

2. Выясните, является ли функция у = cosx-x² четной или нечетной.

3. Изобразите схематически график функции у = cosx- 1 на отрезке .

4. Найдите наибольшее и наименьшее значения функции у = + 1.

5. Постройте график функции у = 2sinx+ 1. При каких значениях х функция возрастает? Убывает?

Контрольная работа № 2

по теме «Производная и ее геометрический смысл»

Вариант 1

1. Найдите производную функции: а) 3х² - б) в) г)

2. Найдите значение производной функции f(x) = в точке х₀ = 8.

3. Запишите уравнение касательной к графику функции f(x) = sinx - 3x + 2 в точке х₀ = 0.

4. Найдите значения х, при которых значения производной функции f(x)= положительны.

5. Найдите точки графика функции f(x)= х³ - 3х², в которых касательная к нему параллельна оси абсцисс.

6. Найдите производную функции f(x) = .

Вариант 2

1. Найдите производную функции: а) 2х³ - б) в) г)

2. Найдите значение производной функции f(x) = в точке х₀ = .

3. Запишите уравнение касательной к графику функции f(x) = 4x - sinx + 1 в точке х₀ = 0.

4. Найдите значения х, при которых значения производной функции f(x)= отрицательны.

5. Найдите точки графика функции f(x)= х³ + 3х², в которых касательная к нему параллельна оси абсцисс.

6. Найдите производную функции f(x) = cos.

Контрольная работа № 3

по теме «Применение производной к исследованию функций»

Вариант 1

1. Найдите стационарные точки функции f(x) = х³- 2х² +х +3.

2. Найдите экстремумы функции: а) f(x) =х³ - 2х² + х + 3; б) f(x) =.

3. Найдите интервалы возрастания и убывания функции f(x) = х³- 2х² +х +3.

4. Постройте график функции f(x) = х³- 2х² +х +3 на отрезке .

5. Найдите наибольшее и наименьшее значения функции f(x) = х³- 2х² +х +3 на отрезке .

6. Среди прямоугольников, сумма длин трех сторон которых равна 20, найдите прямоугольник наибольшей площади.

Вариант 2

1. Найдите стационарные точки функции f(x) = х³- х² - х +2.

2. Найдите экстремумы функции: а) f(x) =х³- х² - х +2; б) f(x) =.

3. Найдите интервалы возрастания и убывания функции f(x) = х³- х² - х +2.

4. Постройте график функции f(x) = х³- х² - х +2 на отрезке .

5. Найдите наибольшее и наименьшее значения функции f(x) = х³- х² - х +2 на отрезке .

6. Найдите ромб с наибольшей площадью, если известно, что сумма длин его диагоналей равна 10.

Контрольная работа № 4

по теме «Интеграл»

Вариант 1

1. Докажите, что функция F(x) = 3х + sinx - e^2xявляется первообразной функции f (x) = 3 + cosx - 2e^2x на всей числовой оси.

2. Найдите первообразную F функции f (x) = 2, график которой проходит через точку А(0; ).

3. Вычислите площадь фигуры, изображенной на рисунке.

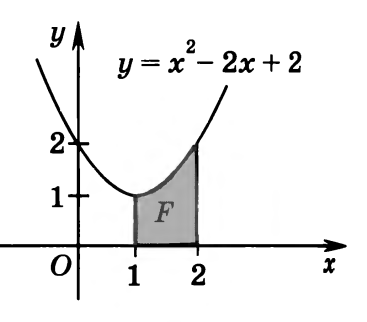
4. Вычислить интеграл: а) dx; б) .

5. Найдите площадь фигуры, ограниченной прямой у = 1 - 2х и графиком функции у = х² - 5х - 3.

Вариант 2

1. Докажите, что функция F(x) = х + cosx+e^3xявляется первообразной функции f (x) = 1- sinx+3e^3x на всей числовой оси.

2. Найдите первообразную F функции f (x) = - 3, график которой проходит через точку А(0; ).

3. Вычислите площадь фигуры, изображенной на рисунке.

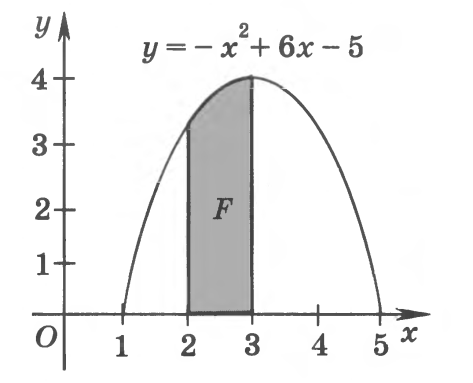
4. Вычислить интеграл: а) dx; б) .

5. Найдите площадь фигуры, ограниченной прямой у = 3 - 2х и графиком функции у = х²+3х - 3.

Тест

для проверки обязательных результатов обучения

за курс алгебры и начал анализа

1. Вычислить .

а) 8; б) ±8; в) 4; г) ±4.

2. Вычислить ∙

а) 8; б) ±8; в) 16; г) ±64.

3. Вычислить

а) ; б) ; в) ; г) ±1

4. Найти , если а 0.

а) а²⁰; б) а⁶; в) ± а²⁰; г) ±а⁶.

5. Упростить , если а0.

a) б); в) -; г) .

6. Вынести множитель из-под знака корня:

а) 2; б) 3; в) 18; г) 5

7. Извлечь корень:

а); б)2 - ; в) 1 - ; г) 1 - .

8. Найти значение выражения 5⁰ + .

а) ; б) ; в) ; г) - 3

9. Найти значение выражения .

а) ; б) ; в) ; г) 25

10. Представить выражение гдеав виде степени.

а); б); в) а⁹; г) а²⁰.

11. Выполнить деление: :.

а) 1; б) 2; в) 4²; г) .

12. Возвести в степень: .

а) ; б) ; в); г)

12. Сравнить числа (0,35) и (0,35)³.

а) (0,35)< (0,35)³; б) (0,35)= (0,35)³; в) (0,35)>(0,35)³

12. Упростить выражение

а) ; б); в) а + b; г) а-b.

12. Решить уравнение = х.

а) х = -3; б) х₁ = -3, х₂ = 3; в) х =; г) нет корней.

12. Решить уравнение 2^х = -4.

а) х = -2; б) х = - 0,5; в) х = 2; г) нет корней.

12. Решить неравенство> 25.

а) х<-2; б) х>-2; в) х<2; г) х = 2.

12. Указать уравнение, корнем которого является логарифм числа 5 по основанию 3.

а) 5^х = 3; б) х⁵ = 3; в) 3^х = 5; г) х³ = 5.

12. Найти log_0,5 8.

а) 3; б) -3; в) 4; г) -4.

12. Вычислить .

а) 7; б) 8; в) 12; г) 256.

12. Упростить разность log₆72-log₆2.

a)log₆70; б) в) 2; г) 6.

12. Найти lga³, если lgа = m.

а); б) 3 + m; в) 3т; г) т³.

12. Выразить log₅ e через натуральный логарифм.

а) ; б) ; в) ; г)

12. Решить уравнение log₅x = -2.

а) х = -2; б) х = 0,1; в) х = 0,04; г) нет корней.

12. Решить неравенство log₀,₃x>l.

а) х>1; б) х> 0,3; в) х<0,3; г) 0<х<0,3.

12. Найти радианную меру угла 240°.

а) ; б) ; в) ; г)

27. Найти значение выражения

a) ; б) ; ; в ;; г) ;

28. Найти sinа, если cosa=b

а) ; б) ; в) ; г) -

29. Найти tga, если ctga= 0,4

а) ; б) ; в) ; г) -

30. Найти sin2а, если sina=, cosa = - .

а) - ; б) ; в) ; г) -

31. Найтиcos 2a, еслиsina = - , cosa = -

а)1; б) ; в) ; г)

32. Записать cos 580° с помощью наименьшего положительного угла.

а) sin50°; б) -sin50°; в) -cos40°;г)cos40°.

33. Упростить выражение

a) cosa sin a-tga; 6) cos²a + tga;в) cos²a-ctga; r) - sin²a + ctga

34. Указать выражение, которое не имеет смысла.

а) arccos; б) arcsin 1; в) arctg 15; г) arccos/

35. Решить уравнение cosx = -l (в ответахkZ)

a)x = + k; б)x = + 2k; в)x=+2k; г) х = -+2k

36. Решить уравнение sinx = 0 (в ответахkZ)

a)x = + k; б)x = + 2k; в)x=k; г) х =2k

37. Найти arcsin

a) ; б) ; в) - ; г) -.

38. Найти arccos

a) ; б) ; в) - ; г) -.

39. Найти производную функции , где х>0

а); б); в); г)x⁵.

40. Найти производную функции 3cosx + 5

a) 3sinx; б) -3sinx; в) 2cosx + 4; г) -3sinx + 5

41. Найти производную функции xlog₂x

а) 1 + ; б) ; в) x + ; г) x + .

42. Найти точку (точки) экстремума функции у = 2х³-3х².

а) ; б) x₁ = 0, х₂=; в) x₁₌ 0, х₂=1; г) y₁ = 0, у₂ = - 1

43. Найти промежуток убывания функции у = -х² + 4х- 3.

а) [2; + ∞); б) (-∞; 2]; в) [1; + ∞); г) (-∞; 1]

44. Найти все первообразные функции у = х⁶.

а) 6х⁵ + С; б) ; в) г)

45. Найти первообразную функции f(x) = sinx, если F

a) cosx + 2 + б) -cosx + 2 +в) cosx+l; г) -cosx+l

Литература

1. алгебра и начала анализа 10-11, тематические тесты: учеб.пособие./В.К.Шарапова. - Ростов н/Д.: Феникс, 2007.

2. Контрольно-измерительные материалы. Алгебра и начала анализа: 10 класс / сост. А.Н. Рурукин. - М.: ВАКО, 2011

3.Примерные программы по математике . Сборник нормативных документов. Математика / сост. Э.Д. Днепров, А.Г. Аркадьев. М.: Дрофа, 2009

4. Дидактические материалы по алгебре и началам анализа для 10 и 11 класса /Б.И. Ивлев, С.И.Саакян, С.И.Шварцбург. М.: Просвещение ,2005

5.Контрольные и проверочные работы по алгебре. 10 11 кл.: Методическое пособие / Звавич Л.И., Шляпочник Л.Я. М.: Дрофа, 1997

6.Алгебра и начала анализа. Тесты. 10 11 классы: учебно-метод. Пособие. М.: Дрофа, 2010

</ 7.Алгебра и начала анализа: сборник задач для подготовки и проведения итоговой аттестации за курс средней школы / И.Р. Высоцкий, Л.И. Звавич, Б.П. Пигарев и др.; под ред. С.А. Шестакова. М.: Внешсигма-М, 2008

1