Урок по теме 'Преобразование выражений, содержащих квадратный корень'

Открытый урок в 8 классе по алгебре

Тема «Преобразование выражений, содержащих арифметический квадратный корень»

Цель: обобщить и систематизировать знания по теме «Применение свойств арифметического квадратного корня»

Задачи: 1. дидактические: формировать умения применять эти свойства

2. воспитательные: способствовать развитию навыка самостоятельного применения знаний при преобразовании выражений, содержащих квадратные корни

3. развивающие: развивать познавательную активность, логическое мышление, творческую способность учащихся, прививать интерес к предмету.

Каждому ученику выдан опросный лист, в который они заносят набранное количество балов за выполненные задания и даются комментарии по оценкам.

ФИ

Тест « »

теория

Дом раб

устно

проверка

Планета преобразований

итог

1а

1б

1в

1. Чтобы обобщить и систематизировать знания по нашей теме, необходимо вспомнить теоретический материал. Ученикам даны конверты, в которых находятся определения, свойства арифметических квадратных корней, алгоритмы выполнения для заданий, но они разрезаны на части, надо данные части собрать в одно целое, чтобы получились правильные формулировки и их поместить на магнитную доску (формулировки даны на группу из 3- 4 человек)

Квадратным корнем из неотрицательного числа а называют такое неотрицательное число, квадрат которого равен а.

1) 0 2)( )²=а

Квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней из этих чисел.

= , а≥0, b≥0

Если a≥0, b>0, то квадратный корень из частного равен частному корней=

Если а≥0 и n- натуральное число, то =аⁿ

Чтобы освободиться от иррациональности в знаменателе используют два приёма

1. если знаменатель имеет вид , то числитель и знаменатель следует умножить на

2 если знаменатель имеет вид, то числитель и знаменатель надо умножить соответственно на

Чтобы внести множитель под знак квадратного корня, надо его возвести в квадрат, внести под корень

и выполнить соответствующие действия под корнем, а чтобы вынести множитель из под знака

корня, надо выражение разложить на произведение корней и по мере возможности извлечь их

2. Проверка домашней работы. В порядке возрастания номеров соединить отрезками последовательно точки, рядом с которыми написаны как верные, так и неверные результаты. Должен получиться рисунок

7,3

2

P⁵q^6,

-2

2

P⁵q^6,5

P⁵q⁶

3. Историческая справка

Начиная с 13 века итальянские и др европейские математики обозначали корень латинским словом RADIX (корень) или сокращённо Rx, в 15 веке писали R²12 вместо

, некоторые немецкие учёные в 15 веке обозначали квадратный корень V, в 16 веке- V0, в круге писали цифру 2. В 1626 г нидерландский математик Ширар ввёл обозначение корня , это обозначение вытеснили Rx, однако долго писалиVa+b, лишь в 1637г Р Декарт ввёл современное обозначение корня. Этот знак вошёл во всеобщее употребление в начале 18 века. Он был введён практически необходимостью, зная площадь квадрата людям в 16 веке уже надо было сосчитать сторону квадрата, для этого и ввели квадратные корни.

4. Устный счёт

Найти правильные ответы, заменить их соответствующими буквами, получить в результате слово.

11

30

12

36

6

20

1,6

200

к

л

п

к

и

р

а

и

а

а

д

е

с

РАДИКАЛ

5. Конкурс «Если бы я был учителем». Оцени работу воображаемого ученика по фамилии Рассуждалкин. Критерии оценки расписаны.

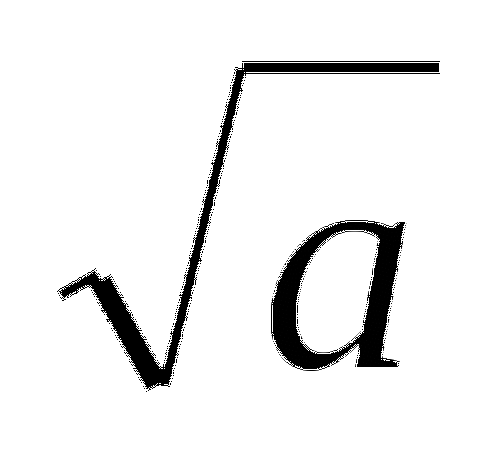
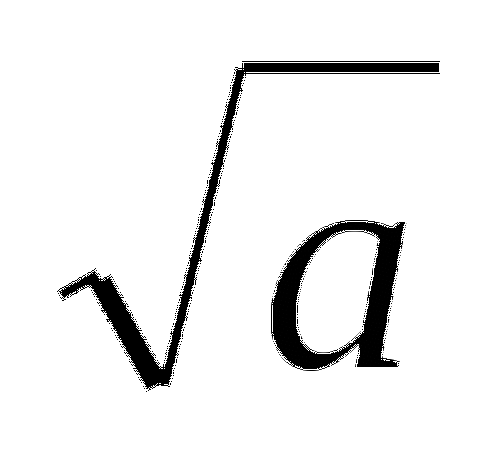
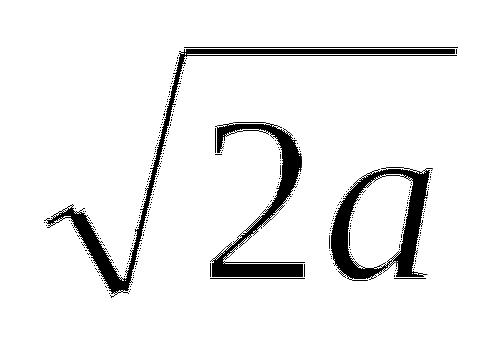
Критерии оценок: за 1 ошибку - «4»

За 2-3 ошибки - «3»

Больше трёх ошибок - «2»

Нет ошибок - «5»

6. Посетим планету «Преобразований»

Каждый учащийся хотя бы один раз должен выйти к доске. Чем больше заданий сделано за определённое время, тем больше балов (задания из учебника)

7. Итог. Выполнить тест на компьютере (в конструкторе тестов).

1. Найдите значение выражения

1) 1 2) 2 3) 7 4) 14

2. Упростите выражение + -

1) - 2) 3) 3 4) 0

3. Вынесите множитель из-под знака корня

1) -2в 2) 2в 3) -2в 4) 2в

4. Внесите множитель под знак корня

1) 2) 3) 4)

5. Расположите числа в порядке возрастания ; 2; 3

1) ; 3; 2. 2) 2; ; 3. 3) 3; ; 2. 4) 3; 2;

6. Освободите дробь от знака корня в знаменателе

1) 2) 3) 2 4)

8. Домашнее задание. Итог урока. Оценки за урок, согласно набранным балам в опросном листе.

Учащиеся сочиняли синквейн

Корень.

Арифметический, квадратный.

Умей им пользоваться.

Под знаком квадратного корня должно стоять неотрицательное число.