- Учителю
- Проект урока алгебры по теме «Сложные проценты» по модульной технологии в 9 классе
Проект урока алгебры по теме «Сложные проценты» по модульной технологии в 9 классе
Учитель МАОУ «СОШ №16»
г.Перми Юрченко Л.Т.
Проект урока алгебры по теме «Сложные проценты»
по модульной технологии в 9 классе
Модуль №4 Решение задач на «сложные проценты»
Научимся решать задачи по формуле расчета сложных процентов
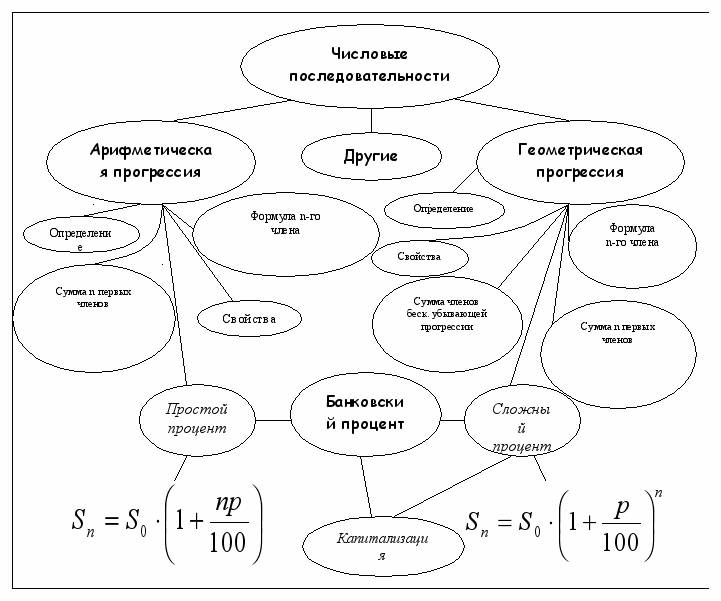
1.Определи место сложных процентов в теме «Последовательности»
Входной тест
1. Запишите 29% в виде обыкновенной дроби.
А. 29/100 Б.. 29/10 В. 29
2. Запишите 27% в виде десятичной дроби.
А. 0,27. Б. 0,73. В. 0,027.
3. Найдите 25% от 48.
А. 12. Б. 1,2. В. 120.
4. В школьном саду 40 фруктовых деревьев. 30% этих деревьев яблони. Сколько яблонь в саду?
А. 120. Б. 12. В. 28.
5. В кассе кинотеатра было 500 билетов. 70% всех билетов продали. Сколько билетов осталось не продано?
А. 35. Б. 350. В. 150.
6. В первый день на ярмарке продали 30% привезенных для продажи саженцев, а во второй день еще 45% . Сколько процентов саженцев осталось продать?
А. 40%. Б. 25%. В. 15%.
7. Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Сколько денег будет на этом счете через год?
А. 960 р. Б. 820 р. В. 160 р.
8. Школьники посадили 50 деревьев: дубы, акации и липы. Дубы составили 35% всех деревьев, акации 25%. Сколько лип посадили школьники?
А. 2. Б. 20. В. 200.
Проверь себя
1. а
2. а
3. а
4. б
5. в
6. б
7. а
8. б
Прочитай текст и ответь на вопросы.
Вопросы
1.Как при прочих равных условиях выгоднее будет вкладывать деньги в финансовые институты ?
2.Можно ли придумать простой способ расчета удвоения вложенной суммы?
Принцип сложных процентов - ваша золотая курица
Итак, разговор у нас сегодня пойдет о настоящих деньгах, точнее об универсальном законе создания мегасостояний - принципе сложных процентов.
Лучше всего суть этого принципа отражает фраза, сказанная Полом Эрдманом относительно американской мечты: «Американская мечта: начать делать деньги, затем начать делать деньги при помощи денег и, наконец, делать большие деньги при помощи больших денег».
Действительно, практически все крупнейшие современные миллиардеры создавали свои финансовые империи, опираясь на принцип работы сложных процентов. Механизм действия этого закона прост: проценты, начисленные на вложенный капитал по итогам года, увеличивают стартовый размер ваших вложений на начало следующего периода, а значит, и суммы будущих доходов.
Наглядно это можно продемонстрировать на следующем примере:
Если вы вложите в банк 1 000 рублей под 10 процентов годовых сегодня, то через год сумма на вашем счете составит 1100 рублей. Однако в следующем году та же процентная ставка приведет к появлению на вашем счете уже 1210 рублей, так как проценты будут начисляться не только на базовый вклад (1000 руб.), но и на приращенный доход (100 руб.).
Этот, на первый взгляд, простой и очевидный принцип «работы» денег на самом деле является золотым пропуском в мир миллионеров.
Ниже мы приводим таблицу, где указано, сколько потребуется лет, чтобы ежедневные вклады различного достоинства превратились в миллион долларов:
вклад в долларах
3% годовых
10% годовых
20% годовых
1 доллар
147
56
32
2 доллара
124
49
28
3 доллара
112
45
26
4 Доллара
102
42
25
5 долларов
95
40
24
6 долларов
90
38
22
7 долларов
85
37
22
8 долларов
81
36
21
9 долларов
77
35
21
10 долларов
74
34
20
Вот как описывает механизм работы сложных процентов Роберт Г.Аллен, автор американского бестселлера «Множественные источники дохода»:
«Мой калькулятор утверждает, что 200 долларов ежемесячного вклада под 20% годовых за 20 лет приведут к накоплению суммы, равной 632 тысячам долларов. Неплохо!
Теперь предположим, что вместо того, чтобы начать немедленно, вы решили дождаться следующего года. В итоге у вас на все останется 19 лет вместо запланированных 20. На сей раз мой калькулятор утверждает, что по прошествии этих 19 лет на вашем счете будет всего 516 тысяч долларов. Это на 116 тысяч долларов меньше, чем вы имели бы, если бы начали точно в срок.
Иными словами, промедление длиною в год стоило вам суммы 116 тысяч в будущих долларах.
Промедление стоит дорого! За каждый из 365 дней, что вы сидели сиднем, ваш будущий портфель с деньгами худел на 300 долларов (116 тысяч : 365 = 317,81 доллара). Иначе говоря, каждый день промедления стоит вам 300 долларов (или 13 долларов в час, круглые сутки).
А что, если бы вы клали ежемесячно под проценты те же 200 долларов, но в течение 30 лет? Цена промедления длиною в один год составила бы теперь ошеломительные 842803 доллара. Трата впустую одного года обошлась бы вам почти в 1 миллион долларов!»
Итак, не будем медлить и начнем подыскивать подходящий финансовый институт, который обеспечит вам максимальную процентную ставку. Определясь с выбором, стоит учитывать, что, кроме прочего, определенное влияние на будущую доходность ваших вложений может оказать такая на первый взгляд незначительная вещь, как частота начислений годовых процентных ставок:
Таблица фактических процентных ставок для 6% годовых
Частота Действующая годовая
начислений процентная ставка
Ежегодно 6,00000%
Каждые полгода 6,09000%
Ежеквартально 6,13614%
Ежемесячно 6,16778%
Еженедельно 6,17998%
Ежедневно 6,18313%
Непрерывно 6,18365%
Источник: Зви Боди, Роберт К.Мертон«Финансы».
Учебный элемент №1
Задачи с известным начальным и конечным количествами.
Учебный элемент №2
Задачи с неизвестным начальным и конечным количествами.
Реши самостоятельно задачи
1 уровень- 2 балла, 2 уровень - 4 балла , 3 уровень - 5 баллов
1. Пусть вкладчик положил на счет в банке 25000р. и в течение 3-х лет не будет снимать деньги со счета. Подсчитаем, сколько денег будет на счете вкладчика через 3 года, если банк выплачивает 30% в год, и проценты после каждого начисления присоединяются к начальной сумме 25000р., т.е. капитализируются. (1балл)
2. Зарплата служащему составляла 20000р. Затем зарплату повысили на 20%, а вскоре понизили на 20%. Сколько стал получать служащий? (2балла)
3. На товар снизили цену сначала на 20%, а затем еще на 15%. При этом он стал стоить 23,8 тыс.р. Какова была первоначальная цена товара? (3балла)
4. Завод увеличивал объем выпускаемой продукции ежегодно на одно и то же число процентов. Найти это число, если известно, что за 2 года объем выпускаемой продукции увеличивался на 21%.( ( 3 балла)
5. Цену товара первоначально понизили на 20%, затем новую цену снизили еще на 30% и, наконец, после пересчета произвели снижение на 50%. На сколько процентов всего снизили первоначальную цену товара? (2 балла)
В истории существует немало ярких примеров того, как небольшие суммы превращаются в огромное состояние.
Вы помните, Бенджамин Франклина? Этот человек был одним из тех, кто показал человечеству на что способны сложные проценты.
Перед своей смертью Франклин завещал по 5000$ двум своим любимым городам: Бостону и Филадельфии, положив эти деньги в банк.
Города могли снять эти деньги только за 2 раза. 1 раз через 100 лет и второй через 200. По условиям завещания, в первый срок города могли снять только 500.000$, что они и сделали.А во второй-уже всю оставшуюся сумму. Через 200 лет со счетов города сняли по 20.000.000$!. Здорово, не правда ли?
Домашнее задание:
Задача.
Клиент положил в банк денежную сумму в 100 тысяч рублей под 15% годовых на один год. Определите:
Какая сумма окажется на счете клиента в конце года? (2 балла)
Какая сумма окажется на счете клиента в конце года, если он будет перезакладывать всю сумму, имеющуюся на счете, каждый квартал? (4 балла)
Какая сумма окажется на счете клиента в конце года, если через полгода ставка процента уменьшилась до 12%? (5 баллов)
Какая сумма окажется на счете клиента через 2 года и 3 месяца при неизменной 15% ставке? (6 баллов)
Проверить выполнение «правила 72»
(5 баллов)
1 уровень- 2 балла, 2 уровень - 4 балла , 3 уровень - 5 баллов
удобный способ, позволяющий быстро подсчитывать будущую стоимость ваших денег, получивший название «правило 72». Согласно этому правилу, количество лет, необходимое для того, чтобы сумма денег удвоилась, примерно равно числу 72, поделенному на годовую процентную ставку.