Конспект урока Теорема обратная теореме Пифагора(8 класс)

Урок 25 8а,б (01.12.16)

Тема урока: «Теорема, обратная теореме Пифагора»

Тип урока: изучение нового материала.

Форма урока: комбинированный урок.

Оборудование: компьютер, проектор, экран.

Цели урока:

1) рассмотреть теорему, обратную теореме Пифагора, и показать её применение в процессе решения задач ;

2) закрепить умения применять теорему Пифагора и обратную ей при решении задач;

3) развивать логическое мышление, интерес к предмету, навыки самостоятельной и коллективной работы.

План урока:

1. Организационный момент. (1мин.)

2. Проверка домашнего задания. (10 мин.)

3. Изучение нового материала. (10 мин.)

4. Закрепление. (14 мин)

5. Подведение итогов. (3 мин.)

6. Домашнее задание. (1 мин.)

7. Рефлексия урока. (1 мин.)

Ход урока

1.Организационный момент.

Приветствие учащихся, сообщение темы, цели урока

2. Проверка домашнего задания.

1) Один из учеников доказывает теорему Пифагора способом, предложенным в учебнике.

Учитель: «Существует более ста способов доказательства теоремы Пифагора, поэтому она занесена в книгу рекордов Гиннеса».

Далее - проверка дополнительного домашнего задания. Ученики подготовили еще 2 способа доказательства теоремы Пифагора.

На экран проецируется слайд № 2 «Пифагоровы штаны» (доказательство Евклида).

Учитель: «В течение двух тысячелетий применяли доказательство, придуманное Евклидом, которое помещено в его знаменитых «Началах».

Далее на экран проецируется слайд № 3 «Доказательство основанное на использовании понятия равновеликости фигур».

2) Решение задач по готовым чертежам (устно). На экран проецируется слайд № 4 «Решение задач по готовым чертежам».

3. Изучение нового материала.

1) Практическая работа.

Трое учеников на доске (а остальные в тетрадях) строят треугольник по трем сторонам, если стороны равны: а) 3, 4, 5; б) 6, 8, 10; в) 5, 12, 13; (при этом вовсе не обязательно указывать единицу измерения). Затем ребята получают задание - измерить больший угол этих треугольников. Ответы оказываются близки к 90. Тогда учитель говорит: « Посмотрите, ребята! Треугольники у всех расположены по-разному, длины сторон разные, а результаты у всех получились примерно одинаковыми. Чем объясняются небольшие различия в данных? Тем ли, что здесь нет никакой закономерности, или тем, что закономерность есть, но нашими инструментами мы не можем установить ее с достаточной точностью?» Учащиеся склоняются к тому, что коль скоро у всех углы получились близкие к прямым, то, значит, какая-то закономерность существует. Но установить ее можно только путем доказательства. «Как же сформулировать утверждение, которое будем доказывать?» - спрашивает учитель. Класс постепенно находит нужную формулировку:

«Если треугольник имеет стороны а, в, с и а² + в² = с² , то угол, противолежащий стороне с, прямой».

Учитель: «Треугольник со сторонами 3,4,5 часто называют египетским треугольником. Для построения прямых углов египтяне поступали так: на веревке делали метки делящие её на 12 равных частей, связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Тогда угол между сторонами оказывался прямым».

Далее учитель демонстрирует слайд № 5.

Учитель: «Несмотря на то, что доказательства этой теоремы египтяне не знали, они применяли её при строительстве домов, дворцов и гигантских пирамид».

Учитель во время рассказа демонстрирует слайды № 6, 7, 8, 9, 10 с изображениями античных дворцов, храмов, египетских пирамид.

Учитель: «Существует очень много прямоугольных треугольников, у которых длины сторон выражаются целыми числами. Такие треугольники называются пифагоровыми треугольниками».

На экран проецируется слайд № 11 «Пифагоровы тройки чисел».

Учитель: «А сейчас мы докажем эту теорему».

На экран проецируется слайд № 12 «Доказательство теоремы, обратной теореме Пифагора».

4. Закрепление изученного.

1) Устная работа.

Не выполняя предложенных заданий, определить, когда необходимо воспользоваться теоремой Пифагора, а когда - обратной к ней.

На экран проецируется слайд № 13.

2) Работа с учебником.

№ 498 (а, б, в).

3) Решение задач № 49 и № 50 из рабочей тетради. (Групповая работа, с последующей фронтальной проверкой).

Задача № 49

Задача № 50

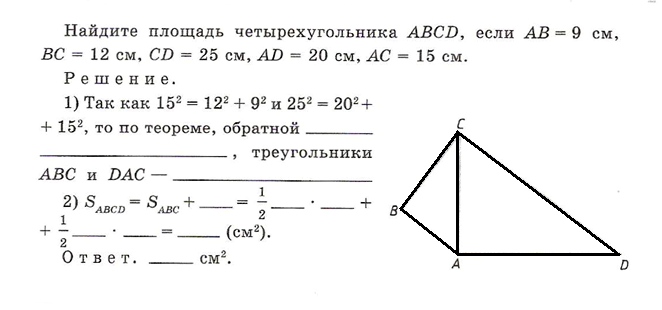
5. Подведение итогов.

1) Учитель: «Теорема Пифагора - одна из самых важных теорем геометрии. Значение ее состоит в том, что из неё или с её помощью можно вывести большинство теорем геометрии. Теорема Пифагора была первым утверждением, связавшим длины сторон треугольников. Потом узнали, как находить длины сторон и углы остроугольных и тупоугольных треугольников. Возникла целая наука тригонометрия ( «тригон» - по - гречески означает «треугольник»).

2) Выставляются и комментируются оценки за урок.

\6. Домашнее задание.

П. 55, № 498 (г, д, е), 499 (б), № 488 (б).

7. Рефлексия урока.

- Что нового узнали на уроке?

- Какие задания понравились?

- Какие задания вызвали затруднения?