Урок геометрии в 8 классе

МБОУ СОШ № 12 ст. Кавказская

Методическая разработка урока геометрии в 8-м классе по теме "Центральные и вписанные углы"

Учитель математики

Юдт Татьяна Владимировна

Конспект урока геометрии в 8 классе

Учебник Геометрия 7-9 А.С.Атанасян и др. «Просвещение» 2009

Тема урока «Центральные и вписанные углы»

Цели урока:

*Систематизировать теоретические знания по теме «Центральные и вписанные углы»

* Совершенствовать навыки решения задач.

Ход урока

I.Организационный момент.

II.Актуализация знаний учащихся.Тесты:

1) Точка равноудалённая от всех точек окружности, называется её:

1) Геометрическая фигура, все точки которой расположены на одинаковом расстоянии от заданной точки, называется:

2) Отрезок, соединяющий две точки окружности, называется её:

2) Хорда, проходящая через центр окружности, называется:

3) Все радиусы окружности:

3) Все диаметры окружности:

4) На рисунке О (r) окружность, AB касательная к ней;

точка B называется:

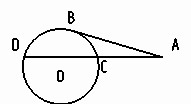
4) На рисунке О (r) окружность. В - точка касания прямой AB и окружности.

Прямая AB называется … к окружности.

5) Прямая , имеющая с окружностью только одну общую точку, называется … к окружности.

5) Прямая, имеющая с окружностью две общие точки, называется…окружности.

6) Угол между касательной к окружности и радиусом, проведённым в точку касания, равен…

6) Касательная к окружности и радиус, проведённые в точку касания…

7) На рисунке AB - диаметр окружности, C - точка, лежащая на окружности.

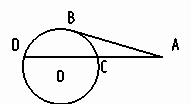
Треугольник ABC : (вид треугольника).

7) На рисунке AB - касательная, ОА - секущая, проходящая через центр окружности.

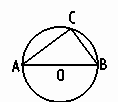
Треугольник ОВА …

(вид треугольника).

8) На рисунке AB=2ВС, AB - диаметр окружности.

Угол САВ равен…

8) На рисунке ОС=СА, AB - касательная к окружности с центром О.

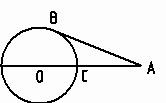
Угол ВАС равен…

III.Решение задач по готовым чертежам

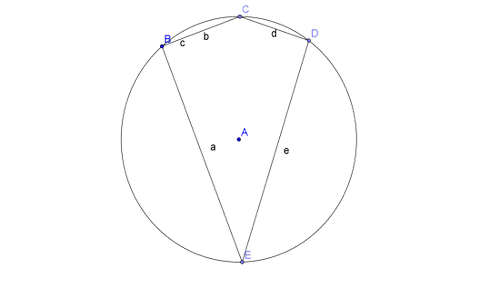
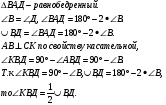№644

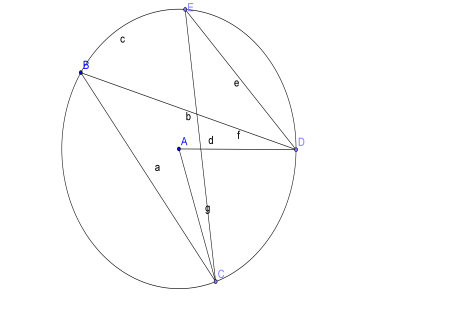
V.Физкультминутка

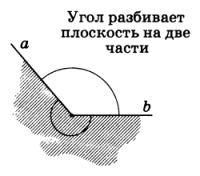
Угол разбивает плоскость на две части. Каждая из частей называется плоским углом. На рисунке заштрихован один из плоских углов со сторонами a и b.

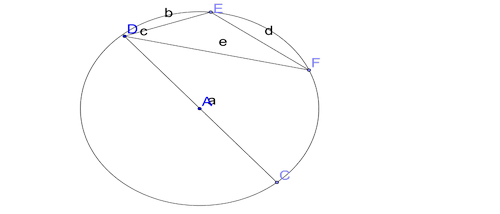
Плоские углы с общими сторонами называются дополнительными.

Если плоский угол является частью полуплоскости, то его градусной мерой называется градусная мера обычного угла с теми же сторонами.
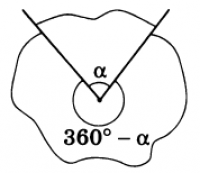
Если плоский угол содержит полуплоскость, то его градусная мера принимается равной 360° - α, где
α - градусная мера дополнительного плоского угла

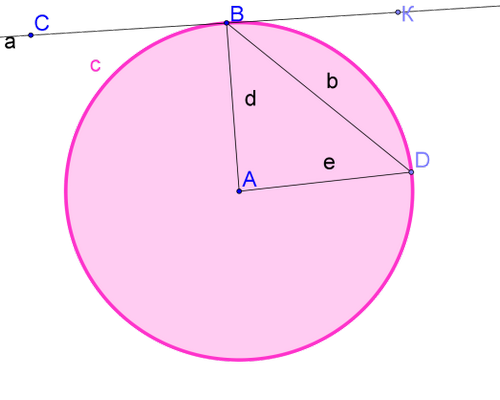
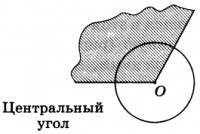
Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу

Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.

Угол, вершина которого лежит на окружности,

а стороны пересекают эту окружность, называется

вписанным в окружность.

Угол ВАС на рисунке 4 вписан в окружность.

Его вершина А лежит на окружности, а стороны пересекают окружность в точках В и С. Говорят также, что угол А опирается на хорду ВС.

Прямая ВС разбивает окружность на две дуги. Центральный угол, соответствующий той из этих дуг, которая не содержит точку А, называется центральным углом, соответствующим данному вписанному углу.

Теорема 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.

Следствие 1. Вписанные углы, стороны которых проходят через точки А и В окружности, а вершины лежат по одну сторону от прямой АВ, равны.

Пример 1.

Точки А, В, С лежат на окружности с центром О;

угол ABC равен 66°.

Найти центральный угол, соответствующий углу ABC.

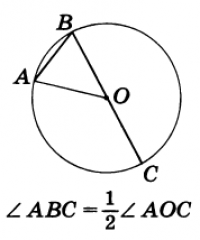
Решение. Пусть условию задачи отвечает рисунок

Угол ABC вписан в окружность. Поэтому согласно теореме о вписанном угле ∠ABC=1/2 ∠АОС или

∠АОС=2∠ABC.

Но ∠ABC=66° и, значит, ∠АОС=132° .

Пример 2.

Точки А, В, С лежат на окружности.

Чему равна хорда АС, если угол ABC равен 30°, а диаметр окружности 10 см?

Решение. Пусть условию задачи чертеж,

где ∠ABC=30° .

Так как вписанный угол ABC

равен ½ ∠АОС, то ∠АОС=60°. Следовательно, треугольник АОС равносторонний, и, значит, хорда АС равна радиусу данной окружности. А так как диаметр равен

10 см, то радиус равен 5 см.

Следствие 1.

Вписанные углы, стороны которых проходят через точки А и В окружности, а вершины лежат по одну сторону от прямой АВ, равны.

В частности, углы, опирающиеся на диаметр, прямые.

VII. Подведение итогов урока.
Оценить работу учащихся.

VIII. Задание на дом

П.68-71.№661.№663