Урок-практикум по математике в 10 классе по теме 'Тригонометрические функции'

Разработка урока по математике в 10 классе.

Урок-практикум по теме: «Тригонометрические функции»

Цель: проверить теоретические и практические знания по теме: «Тригонометрические функции».

Ход урока:

1. Организационный момент.

2. Решение контрольных заданий. Задания составлены в четырех вариантах. Учащиеся записывают ответы прямо на листе с заданием.

Вариант 1.

1. Найдите радианную меру угла

20°=

150°=

275°=

2. Найдите градусную меру угла

=

=

=

3. Выберите верные утверждения

Если 90°< α <180°, то α- угол II четверти

Если 180°< α <270°, то α- угол III четверти

Если 0< α <, то α- угол III четверти

4. Определите знак числа

sin 200°

tg 2

ctg (-150°)

5. Определите в какой четверти находится угол α, если:

sinα > 0, cosα <0

sinα > 0, tgα <0

ctgα > 0, cosα <0

6. Определите знак выражения

sin 93°· cos47°

-tg182°·ctg20°

sin 1· cos6·tg(-2)

7. Сравните числа

sin sin²

cos cos)

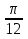tg tg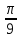

8. Упростите выражение

sin( - t)

cos(+t)

tg(t -)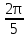

9. Найдите значение выражения

sin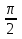

cos210°

ctg(-330°)

10. Найдите множество значений выражения

4cosx

sinx + 5

3-cosx

Вариант 2.

1. Найдите радианную меру угла

30°=

190°=

175°=

2. Найдите градусную меру угла

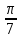
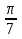
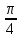
3. Выберите верные утверждения

Если 90°< α <180°, то α- угол I четверти

Если 180°< α <270°, то α- угол II четверти

Если < α <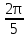, то α- угол III четверти

4. Определите знак числа

sin 230°

tg (-4)

ctg (-120°)

5. Определите в какой четверти находится угол α, если:

sinα < 0, cosα <0

sinα > 0, tgα >0

ctgα > 0, cosα >0

6. Определите знак выражения

-sin 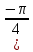· cos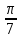

tg5·sin4·cos1

sin 12°· cos306°

7. Сравните числа

cos cos²

sin sin)

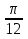ctg ctg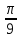

8. Упростите выражение

cos( - t)

tg(+t)

ctg(t -)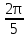

9. Найдите значение выражения

cos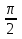

sin(-315°)

tg330°

10. Найдите множество значений выражения

2cosx

sinx + 2

8-cosx

Вариант 3.

1. Найдите радианную меру угла

120°=

15°=

270°=

2. Найдите градусную меру угла

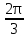
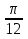
3. Выберите верные утверждения

Если 180°< α <270°, то α- угол II четверти

Если 270°< α <360°, то α- угол IV четверти

Если < α <��������������������������������

��������������������

���������

���

�������

����������������������������������

��< 0, cosα <0

sinα > 0, ctgα <0

tgα > 0, sinα <0

6. Определите знак выражения

sin 193°· cos67°

tg92°·ctg(-145°)

cos 2· sin4·ctg(-2)

7. Сравните числа

sin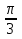 sin²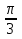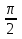

cos cos)

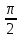tg tg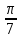

8. Упростите выражение

tg( - t)

sin(t+)

cos(t -)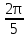

9. Найдите значение выражения

cos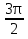

sin240°

tg(-300°)

10. Найдите множество значений выражения

-2cosx

sinx - 4

1-cosx

Вариант 4.

1. Найдите радианную меру угла

130°=

36°=

275°=

2. Найдите градусную меру угла

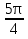
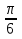
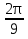
3. Выберите верные утверждения

Если 90°< α <180°, то α- угол II четверти

Если 0°< α <-90°, то α- угол I четверти

Если 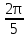< α <2, то α- угол IV четверти

4. Определите знак числа

sin (-167)°

ctg 5

cos (-240°)

5. Определите в какой четверти находится угол α, если:

sinα < 0, cosα >0

sinα < 0, ctgα >0

tgα > 0, cosα >0

6. Определите знак выражения

cos 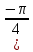· sin)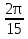

tg(-2)·cos3·sin1

sin 172°· cos36°

7. Сравните числа

cos70° cos²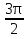

tg tg)

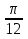sin sin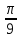

8. Упростите выражение

tg( - t)

cos(+t)

sin(t -)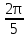

9. Найдите значение выражения

sin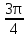

cos(-405°)

Ctg750°

10. Найдите множество значений выражения

13cosx

-sinx + 3

2-cosx

3. Выполнение творческого задания.

Найдите значение выражения. Ответ запишите под чертой. Положительный результат заштриховать красным цветом, а отрицательный результат - синим.

sin

cos (- )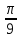

sin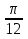

sin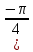

cos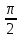

cos (- )

cos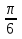

cos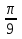

sin

cos

sin 2

cos 2

cos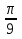

sin 0

sin (- )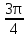

cos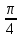

sin (-)

sin 

sin 4

sin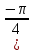

cos 3

cos (- )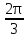

cos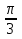

sin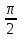

sin (- )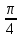

4. Подведение итогов урока.