- Учителю
- Практикум по элементам высшей математике
Практикум по элементам высшей математике
МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
Государственное бюджетное профессиональное образовательное
учреждение Московской области «Ногинский колледж»
подразделение «Балашиха»
И.А. Каверина
Практикум по элементам высшей математики
Балашиха
2016
Содержание
Глава 1. Теоретические сведения 3
Тема 1. Теория множеств 3
1.1. Множества и операции над ними 3
1.2. Числовые множества 4
Тема 2. Математический анализ 5
2.1. Функции. Предел функции 5
2.2. Непрерывность функции 9
2.3. Дифференциальное исчисление 11
2.4. Интегральное исчисление 15
Тема 3. Элементы комбинаторики 18
Тема 4. Элементы теории вероятностей 20
4.1. Случайные события 20
4.2. Случайные величины 21
Глава 2. Самостоятельная работа 25
Литература 34
Глава 1. Теоретические сведения
Тема 1. Теория множеств
-
Множества и операции над ними
Понятие множества принадлежит к числу первичных, не
определяемых через более простые и его можно определить как
совокупность объектов объединенных по определенному признаку.
Объекты, которые образуют множество, называются элементами этого
множества. Множества обозначаются большими буквами А, В, С, а их
элементы малыми а, b, с. Если элемент а
принадлежит множеству А, то используется запись аА, в
противном случае пишут ![]() .
.
Множество, содержащее конечное число элементов называется конечным, а множество, состоящее из бесконечного числа элементов, - бесконечным.
Множество, не содержащее ни одного элемента, называется пустым и обозначается символом .
Два множества называются равными, если они состоят из одних и тех же элементов, т.е. А=В.
Если множество А состоит из части элементов множества В или совпадает с ним , то множество А называется подмножеством множества В и обозначается АВ. АВ - множество А не включено в множество В.
Пусть дано множество U. Мы будем рассматривать всевозможные подмножества данного множества U. Исходное множество U в таком случае называют универсальным множеством.
Множество задают либо перечислением его элементов, либо описанием свойств множества, которые четко определяют совокупность его элементов.
Например, множество ![]() равно
равно
![]() или
или ![]() , где N множество
натуральных чисел.
, где N множество
натуральных чисел.
Алгебраические операции над множествами и их свойства обычно излагаются с применением кругов Эйлера.
Пусть имеются два множества А и В.
Объединением двух множеств А и В называется множество С,
состоящее из всех элементов, принадлежащих хотя бы одному из данных
множеств, т.е. ![]()
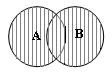
![]() .
.
П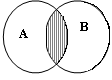 ересечением двух
множеств А и В называется множество С, состоящее из всех элементов,
одновременно принадлежащих каждому из данных множеств А и В, т.е.
С=
ересечением двух
множеств А и В называется множество С, состоящее из всех элементов,
одновременно принадлежащих каждому из данных множеств А и В, т.е.
С=![]() .
.
Р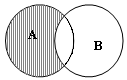 азностью множеств А
и В называется множество С, состоящее из всех элементов множества
А, которое не принадлежит множеству В, т.е. С=А\В=
азностью множеств А
и В называется множество С, состоящее из всех элементов множества
А, которое не принадлежит множеству В, т.е. С=А\В=![]() .
.
Пример 1. Пусть ![]() ,
,
![]() .Найти:
.Найти: ![]()
Решение: Если объединение ![]() включает в себя все
элементы, содержащиеся хотя бы в одном из множеств А или В, то
включает в себя все
элементы, содержащиеся хотя бы в одном из множеств А или В, то
![]() . Пересечение включает в
себя только те элементы, которые содержатся в обоих множествах,
поэтому
. Пересечение включает в
себя только те элементы, которые содержатся в обоих множествах,
поэтому ![]() . Разность множеств А и
В равна А\В =
. Разность множеств А и
В равна А\В =![]() , а В\А=
, а В\А=![]() . Очевидно, что А\ВВ\А.
. Очевидно, что А\ВВ\А.
1.2. Числовые множества
Множества, элементами которого являются числа, называются
числовыми множествами. Будем рассматривать: ![]() - натуральные числа;
- натуральные числа;
![]() - целые числа;
- целые числа;
![]() - рациональные числа; I
- иррациональные числа (бесконечные десятичные непериодические
дроби).
- рациональные числа; I
- иррациональные числа (бесконечные десятичные непериодические
дроби).
Множество R всех рациональных и иррациональных чисел называют множеством действительных чисел, т.е. R =QI . Таким образом, NZQR, и IR.
Между множеством действительных чисел и точками числовой оси существует взаимно однозначное соответствие, т.е. каждому действительному числу соответствует определенная точка числовой прямой.
Множество точек х прямой, удовлетворяющих условию а х b называется замкнутым промежутком или отрезком и обозначается [a;b].
Множество точек х прямой, удовлетворяющих условию а<x<b называется открытым промежутком или интервалом и обозначается (a;b).
Множество точек х прямой, удовлетворяющих неравенству ах<b или а<xb, называется полуинтервалом и соответственно обозначается [a;b) или (a;b]. Существуют бесконечные интервалы и полуинтервалы вида: (-;a), (b;+),(-;+),(-;a] и [b;+).
Окрестностью точки х0 называется любой интервал, содержащий эту точку:
![]()
Открытый интервал (а;b) служит окрестностью всякой принадлежащей ему точки.
-окрестностью точки х0 называется интервал с
центром в точке х0 длиной 2, т.е. интервал
(х0-; х0+)=![]() , где >0:
, где >0:
![]()
х0-e х0 х0+e
Абсолютной величиной (или модулем ) действительного числа х называется само число х , если х неотрицательно, и противоположное число -х, если х отрицательно:
![]() Очевидно, что
Очевидно, что ![]() .Запишем основные
свойства абсолютных величин:
.Запишем основные
свойства абсолютных величин: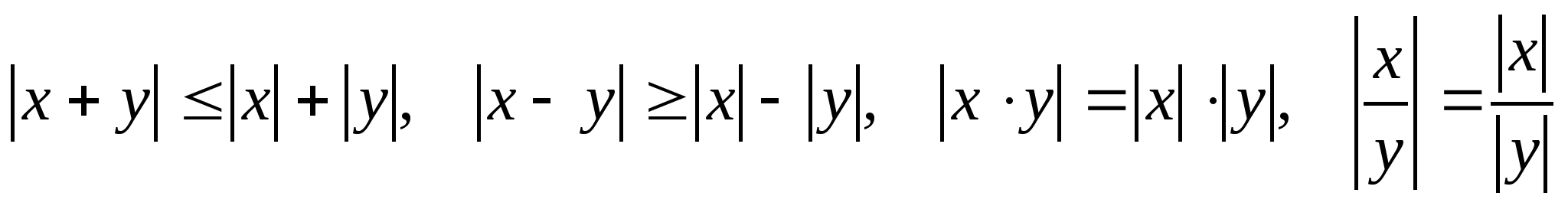 .
.
Абсолютная величина разности двух чисел ![]() означает расстояние
между точками х и х0 числовой прямой, как для случая
x<x0, так и для x>x0. Поэтому
-окрестность можно записать в виде неравенства
означает расстояние
между точками х и х0 числовой прямой, как для случая
x<x0, так и для x>x0. Поэтому
-окрестность можно записать в виде неравенства ![]() или
или ![]() .
.
Пример 2. Для множеств ![]() и
и ![]() найти АВ, АВ, А\В.
найти АВ, АВ, А\В.
Решение: Задачу решим графически и аналитически. Исходя из определения, получим
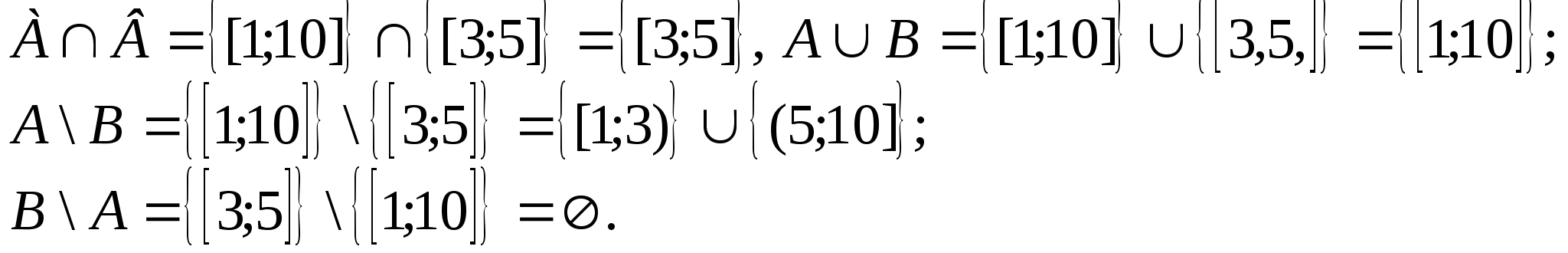
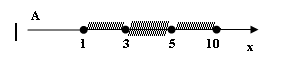
Для конечных множеств А и В состоящих
соответственно из числа элементов k(А) и k(В) имеет место следующее
равенство ![]() . Если
. Если ![]() = не пересекаются, то
k(АВ)=0 и k(АВ)=k(А)+k(В).
= не пересекаются, то
k(АВ)=0 и k(АВ)=k(А)+k(В).
Пример 3. На первом курсе обучаются 1500 курсантов. Известно, что 1050 курсантов изучают английский язык, 657 - немецкий, а 345 курсантов - оба языка, Сколько курсантов не изучают ни английского, ни немецкого языка.
Решение: А - множество курсантов изучающих английский язык, В -
множество курсантов изучающих немецкий язык, а АÇВ - множество
курсантов изучающих оба языка. Из условия задачи следует, что
k(А)=1050, k(В)=657, k(АÇВ)=345. Найдем k(АВ) - число курсантов,
изучающих хотя бы один из этих двух языков. ![]() =1050+675-345=1380.
Следовательно, не изучают ни английского, ни немецкого языка
1500-1380=120 курсантов.
=1050+675-345=1380.
Следовательно, не изучают ни английского, ни немецкого языка
1500-1380=120 курсантов.
Тема 2. Математический анализ
2.1. Функции. Предел функции
Переменная величина - это такая величина, которая в условиях изучения данного процесса может принимать различные значения. Постоянная величина - это та, которая в условиях изучения данного процесса остается неизменной.
Пусть Х и У -некоторые числовые множества. Если каждому элементу хХ по некоторому закону (правилу) f поставлен в соответствие один элемент уУ, то говорят, что определена функциональная зависимость у от х по закону у=f(x), при этом х называют независимой переменной или аргументом, а у - зависимой переменной или функцией.
Если для множества значений х Х определено множество значений у(х)У , то это множество называют областью определения функции и обозначают D(у). Множество значений, принимаемых переменной у, называют областью изменения функции и обозначают Е(y). Символ f(a) обозначает то значение, которое функция у=f(x) принимает при х=а.
Область определения D(у) находится только по соблюдению законности выполнения математических операций, входящих в формулу (знаменатель дроби не может быть равен нулю, выражение под знаком корня четной степени должно быть неотрицательным, выражение под знаком логарифма должно быть положительным и т.д.). Если множество X специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной х, т.е. множество таких значений х, при которых функция у =f(x) вообще имеет смысл.
Например, область определения функции ![]() есть полуинтервал (-;
10], так как 10 - х 0; если же переменная х
обозначает, предположим, время, то при естественном дополнительном
условии х 0 областью определения функции будет отрезок [0;
10].
есть полуинтервал (-;
10], так как 10 - х 0; если же переменная х
обозначает, предположим, время, то при естественном дополнительном
условии х 0 областью определения функции будет отрезок [0;
10].
Пусть задана прямоугольная система координат ОХУ и функция y=f(x).
Графиком функции f(x) называется множество всех точек плоскости с координатами (х;f(x)), где хD(у).
Основными элементарными функциями называются: постоянная функция
у=с; степенная функция у=х, R; показательная функция
у=ах, а>0, а1; логарифмическая
функция ![]() , а>0,
а1;тригонометричесчкие функции у=sinx, y=cosx,
y=tgx,y=ctgx,y=secx, y=cosecx; обратные тригонометрические функции
y=arcsinx, y=arccosx, y=arctgx, y=arcctgx.
, а>0,
а1;тригонометричесчкие функции у=sinx, y=cosx,
y=tgx,y=ctgx,y=secx, y=cosecx; обратные тригонометрические функции
y=arcsinx, y=arccosx, y=arctgx, y=arcctgx.
Элементарными функциями называются функции, которые получаются из основных элементарных функций с помощью конечного числа арифметических операций (+;-; ; :) и композиций.
Если переменная у зависит от переменной u (у=f(u)), а переменная u=(x) зависит от переменной х, то y=f((x)). Функцию у= f((x)) называют сложной функцией.
Пусть для любых значений х1,х2D(у) и х1,х2 справедливо, что f(x1)f(x2). Тогда для любого уЕ(y) найдется только одно значение х=g(y)D(y), такое, что у=f(x). Функция g(y), определенная на Е(у), называется обратной для функции f(x). График функции и обратной к ней симметричны относительно прямой у=х.
Существует несколько способов задания функции.
а) Аналитический способ, если функция задана
формулой вида y=f(x). Этот способ наиболее часто встречается на
практике. Так, функция ![]() ,
рассматриваемая выше, задана аналитически.
,
рассматриваемая выше, задана аналитически.
Не следует смешивать функцию с ее аналитическим выражением. Так, например, одна функция
![]()
имеет два аналитических выражения: х2 (при х < 0) и x + 3 (при х0).
б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента х и соответствующие значения функции f(x), например таблица логарифмов.
в) Графический способ состоит в изображении графика функции - множества точек (х, у) плоскости, абсциссы которых есть значения аргумента х, а ординаты - соответствующие им значения функции y=f(x).
г) Словесный способ, если функция описывается правилом ее составления, например, функция Дирихле: f(x)=1, если х - рационально; f(x) = 0, если х - иррационально.
Рассмотрим основные свойства функций.
1. Функция у=f(x) называется ограниченной на множестве X
D(у), если существует такое число М>0 , что ![]() для всех хХ.
для всех хХ.
2. Функция f(x) называется неубывающей (невозрастающей) на множестве ХD(f), если для любого значения х1, х2Х таких, что х1<х2, справедливо неравенство f(x1)f(x2) (f(x1)f(x2)).
3. Функция f(x) называется монотонной, если она невозрастающая или неубывающая на Х.
4. Функция называется четной (нечетной) если: а) множество D(у) симметрично относительной нуля; б) для любого хD(y) справедливо равенство f(-x)=f(x) (f(-x)=-f(x)).
Функция не являющаяся ни четной, и нечетной, называется функцией общего вида.
5. Функция f(x) называется периодической с периодом Т0, если для любого хD(y) справедливы условия: а) х-Т D(у), х+Т D(у); б) f(х-Т)=f(x+T)=f(x).
Число А называется пределом функции f(x) в точке
х=а, если для любого сколь угодно малого числа >0
найдется такое число![]() (зависящее от ), что для всех х
(зависящее от ), что для всех х ![]() , выполняется
неравенство
, выполняется
неравенство ![]() ,т.е.
,т.е. ![]() .
.
Число А называется пределом функции f(x) при х+, если
для любого числа >0 найдется такое число М>0 , что для всех
значений x>М выполняется неравенство ![]() ,т.е.
,т.е.![]() . Аналогично
определяется предел
. Аналогично
определяется предел ![]() .
.
Число А называется левосторонним (правосторонним) пределом
функции при ха слева (справа), если дл любого >0
существует ![]() такое, что при всех
ха и
такое, что при всех
ха и ![]() (
(![]() ), выполняется
неравенство
), выполняется
неравенство ![]() т.е.
т.е. ![]() - предел слева
(
- предел слева
(![]() -предел справа).
-предел справа).
Для того, чтобы функция f(x) имела предел в конечной точке
а, необходимо и достаточно, чтобы существовали пределы слева
и справа функции f(x) в этой точке и были равны между собой:
![]() .
.
Предел элементарных функций в точке ее определения равен
значению функции в этой точке: ![]() .
.
Нарушение ограничений, накладываемых на функции при вычислении
их пределов, приводит к неопределенностям вида![]() ,
,![]() . Элементарными
примерами раскрытия неопределенностей являются: 1) сокращение на
множитель, создающий неопределенность
. Элементарными
примерами раскрытия неопределенностей являются: 1) сокращение на
множитель, создающий неопределенность ![]() ; 2) деление числителя и
знаменателя на старшую степень аргумента
; 2) деление числителя и
знаменателя на старшую степень аргумента ![]() ; 3) применение
эквивалентных бесконечно малых и бесконечно больших величин;
; 3) применение
эквивалентных бесконечно малых и бесконечно больших величин;
4) использование двух - замечательных пределов: ![]()
![]() .
.
Функция (х) называется бесконечно малой при ха
(или в окрестности точки а); если ![]() .
.
Функция f(x) называется бесконечно большой при
ха, если ![]() .
.
Отметим так же, что ![]() , если
, если
![]() ; или
; или ![]() ,
, ![]() ,если
,если ![]() ; или
; или ![]() .При вычислении многих
пределов используют следующие эквивалентности, верные при х0:
sinxx; tgxx; arcsinxx; arctgxx; 1-cosx
.При вычислении многих
пределов используют следующие эквивалентности, верные при х0:
sinxx; tgxx; arcsinxx; arctgxx; 1-cosx![]() ; ln(1+x)x;
ax-1xlna, ex-1x,
(1+x)n-1nx,n>0;
loga(1+x)xlogae.
; ln(1+x)x;
ax-1xlna, ex-1x,
(1+x)n-1nx,n>0;
loga(1+x)xlogae.
Основные свойства пределов функции
-
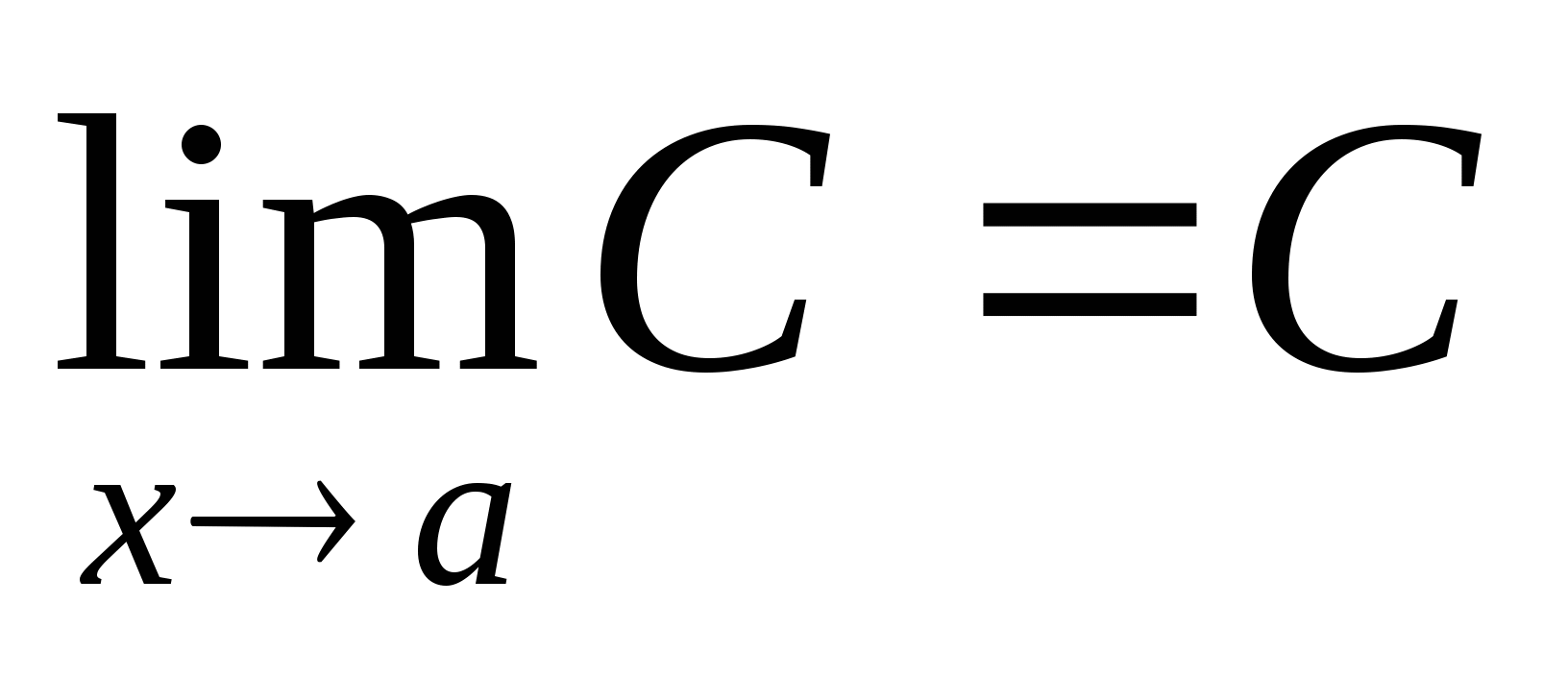 , где С=const. 4.
, где С=const. 4.
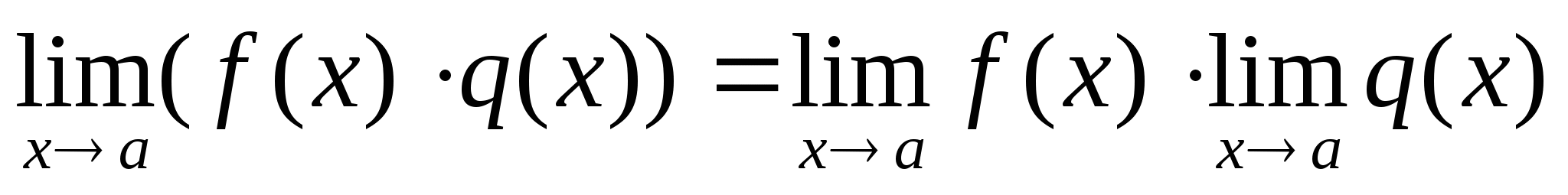 .
.
-
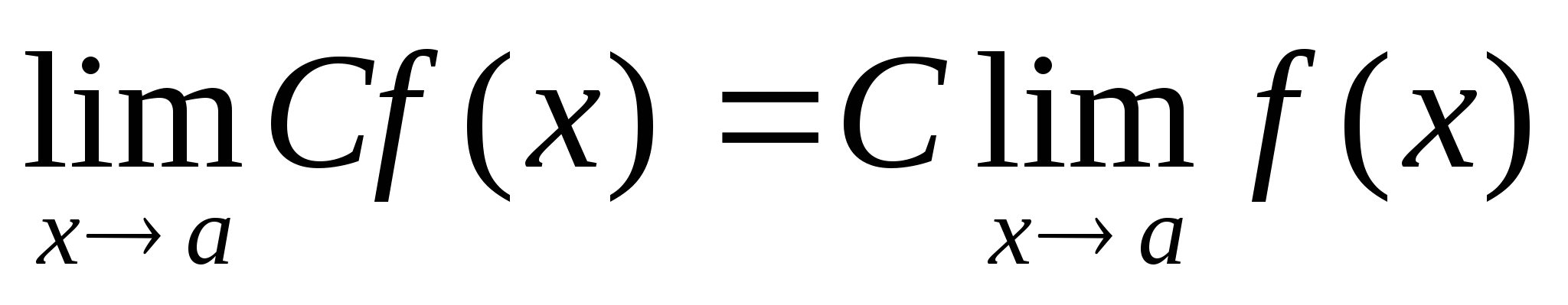 . 5.
. 5. 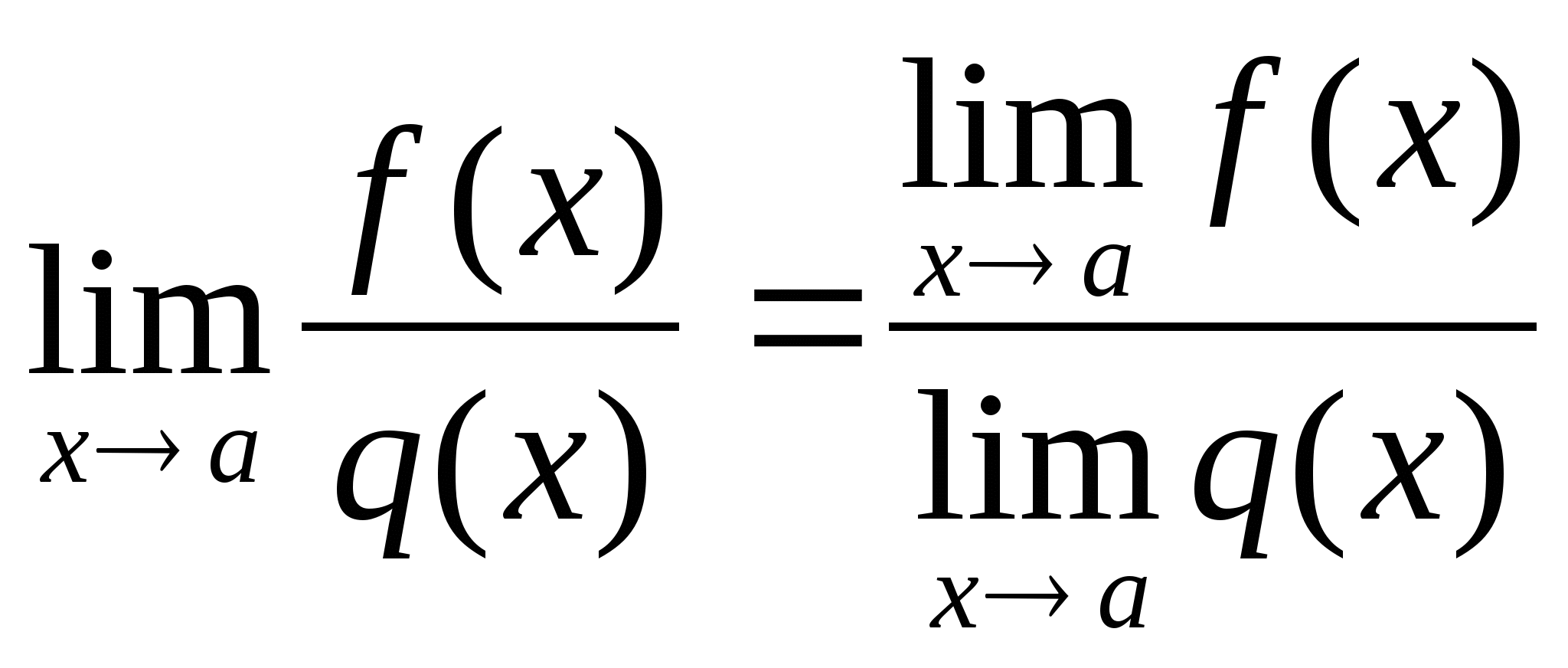 , если
, если 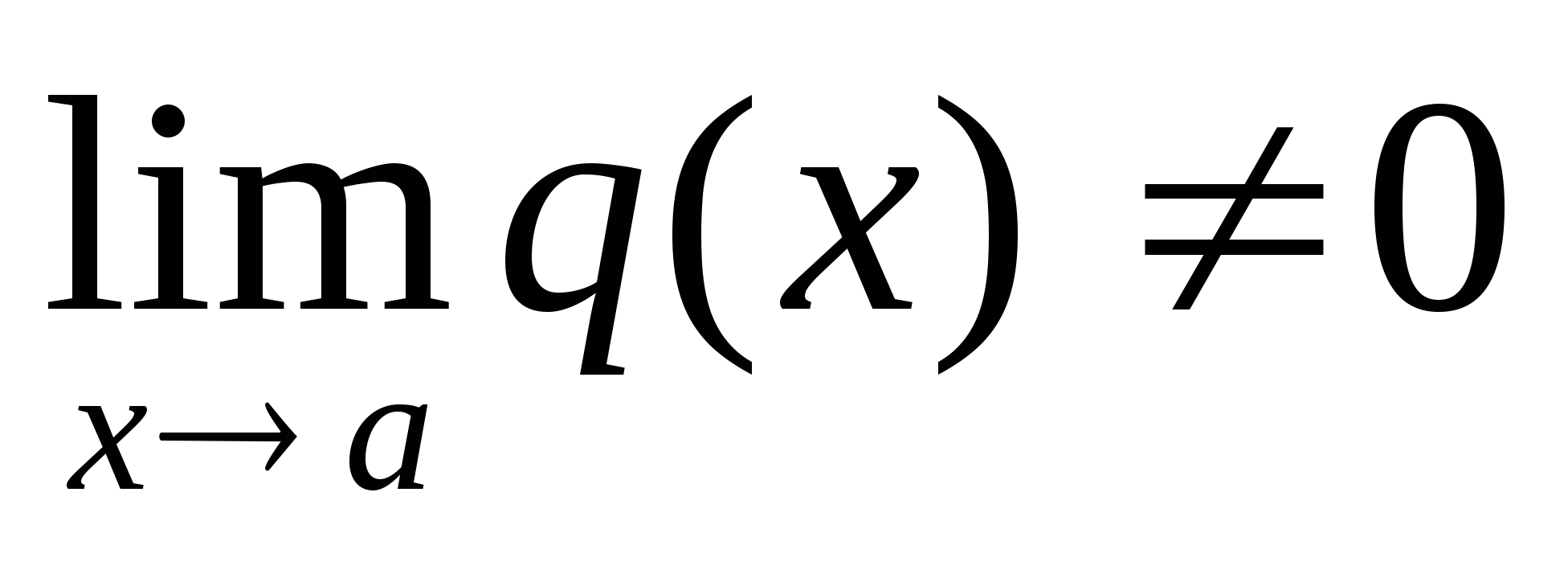 .
.
-
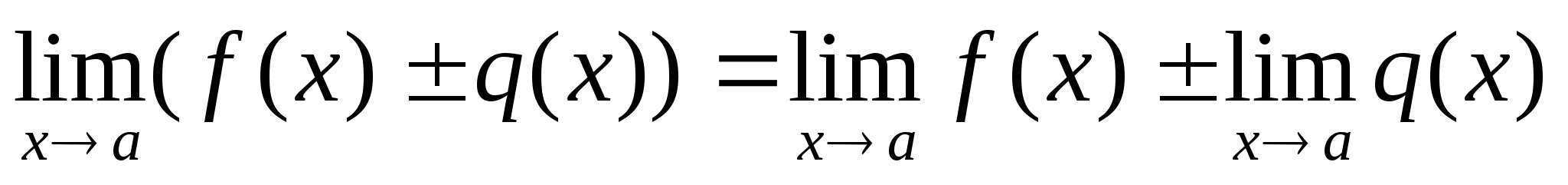 .
.
Пример 1: Вычислить пределы.
1. ![]() , при а=2; 1; +.
3.
, при а=2; 1; +.
3. ![]() . 5.
. 5. ![]() .
.
2. 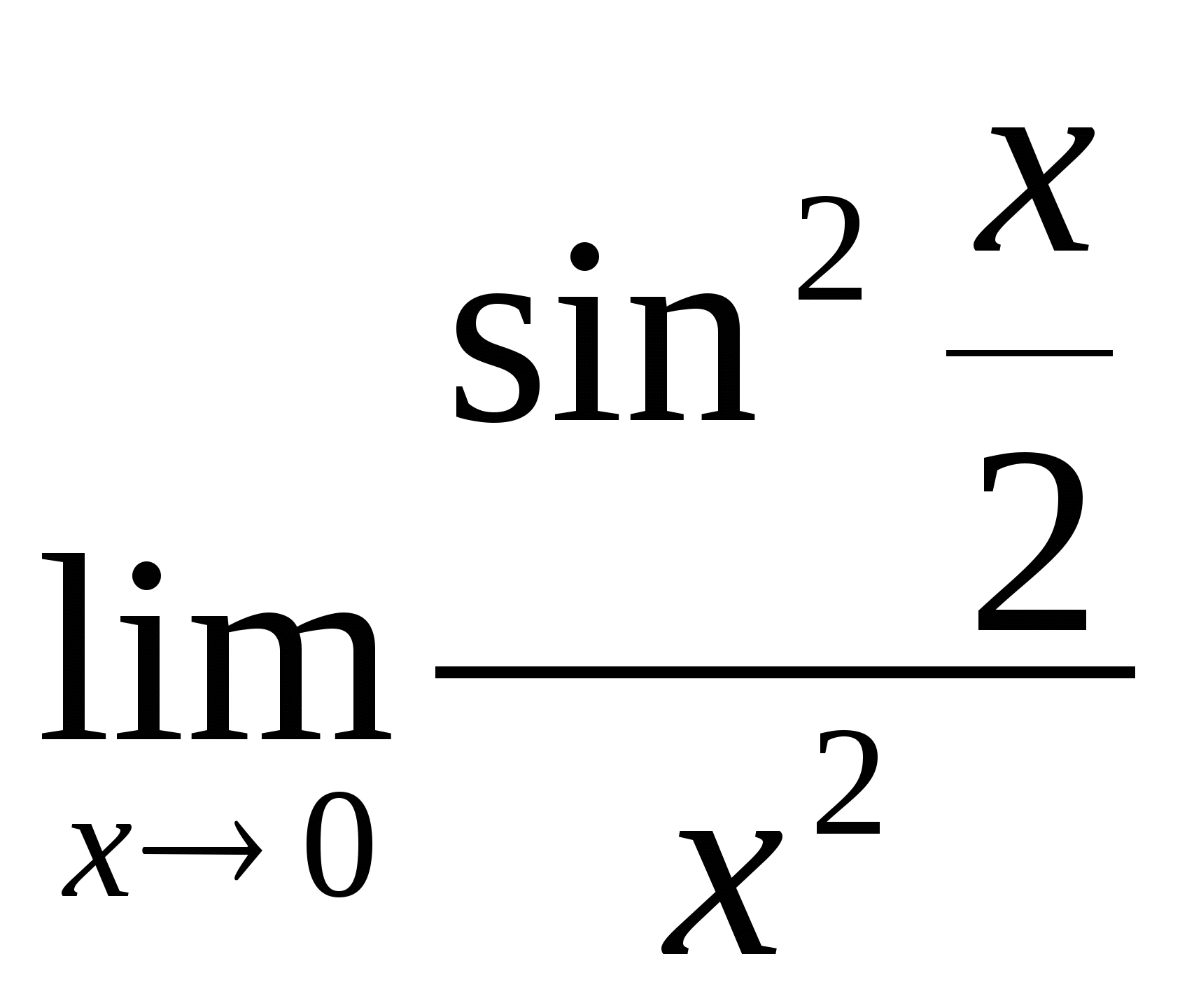 . 4.
. 4. ![]() . 6.
. 6. ![]() .
.
Решение: 1.Пусть х=2 ,разложим числитель и знаменатель на множители и сократив их далее на общий множитель х-2,получим
![]()
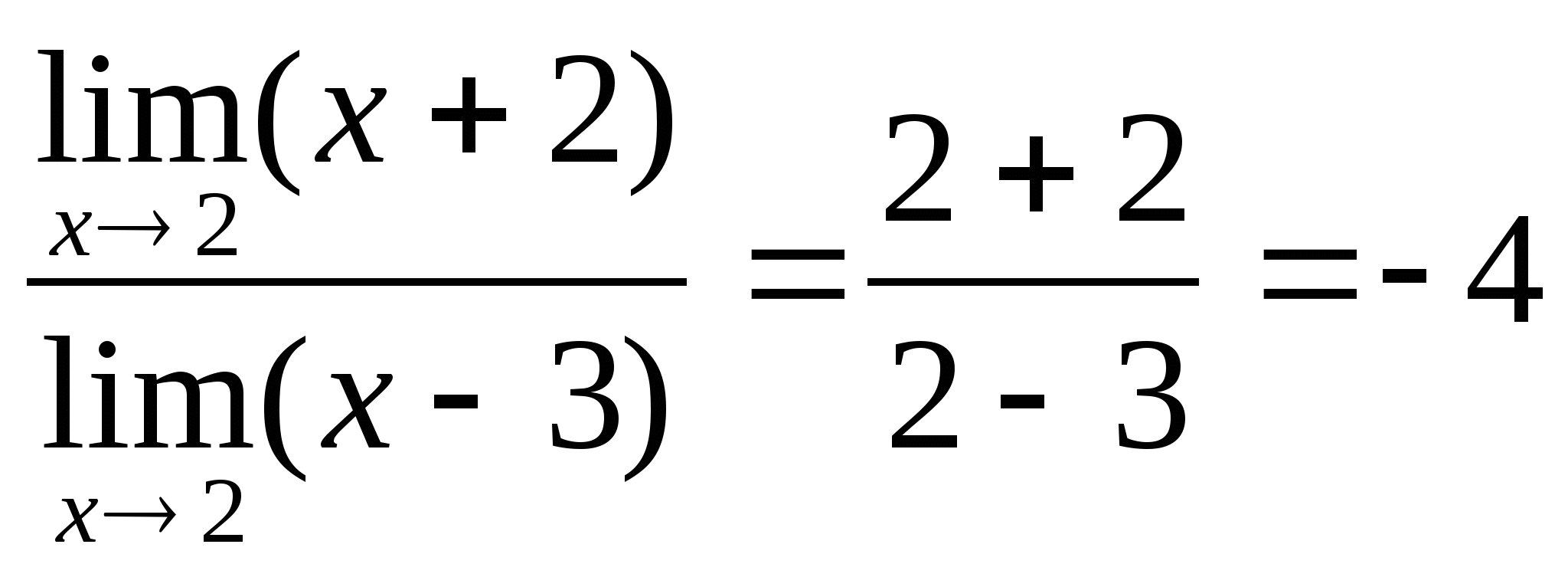 .
.
При а=1 ![]() , а при
х=,
, а при
х=, 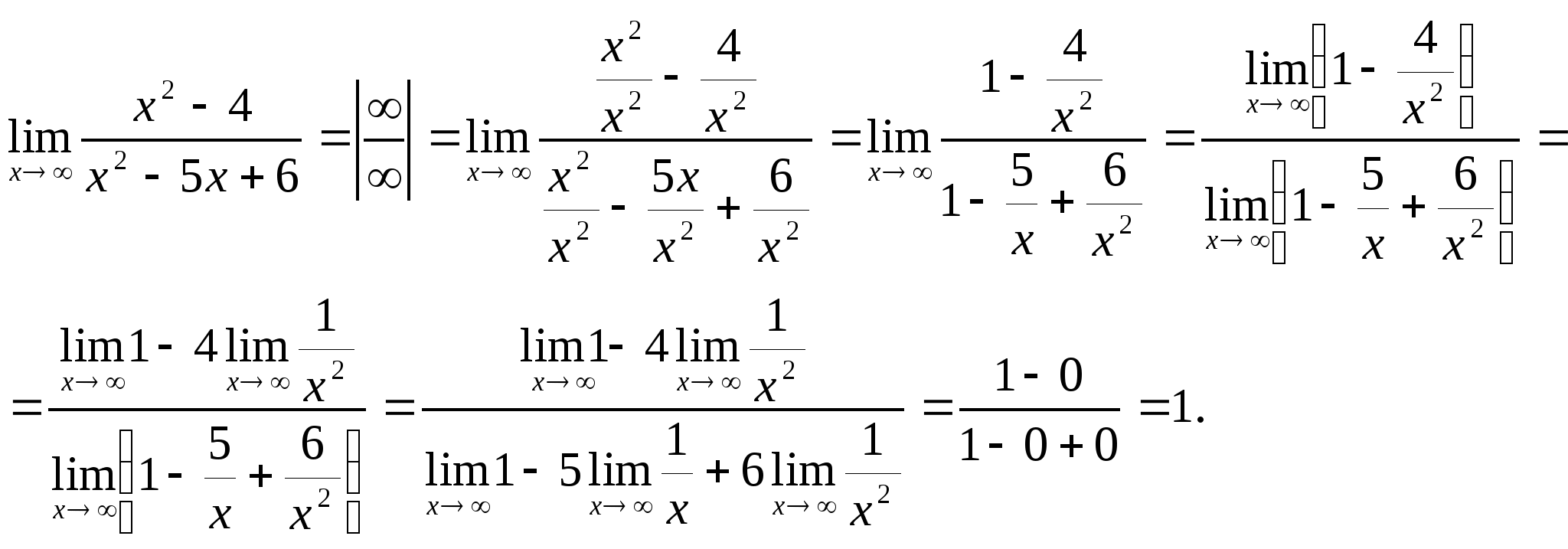
2. 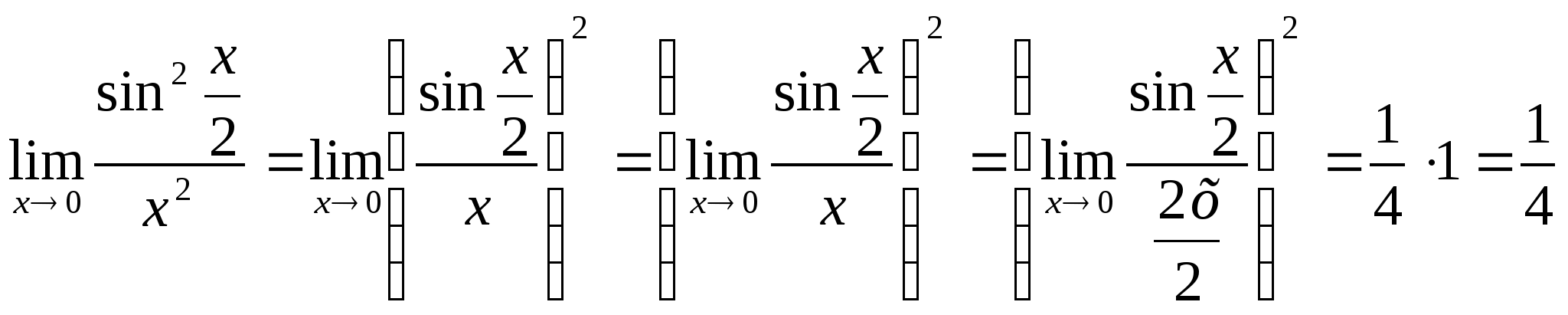 .
.
Так как 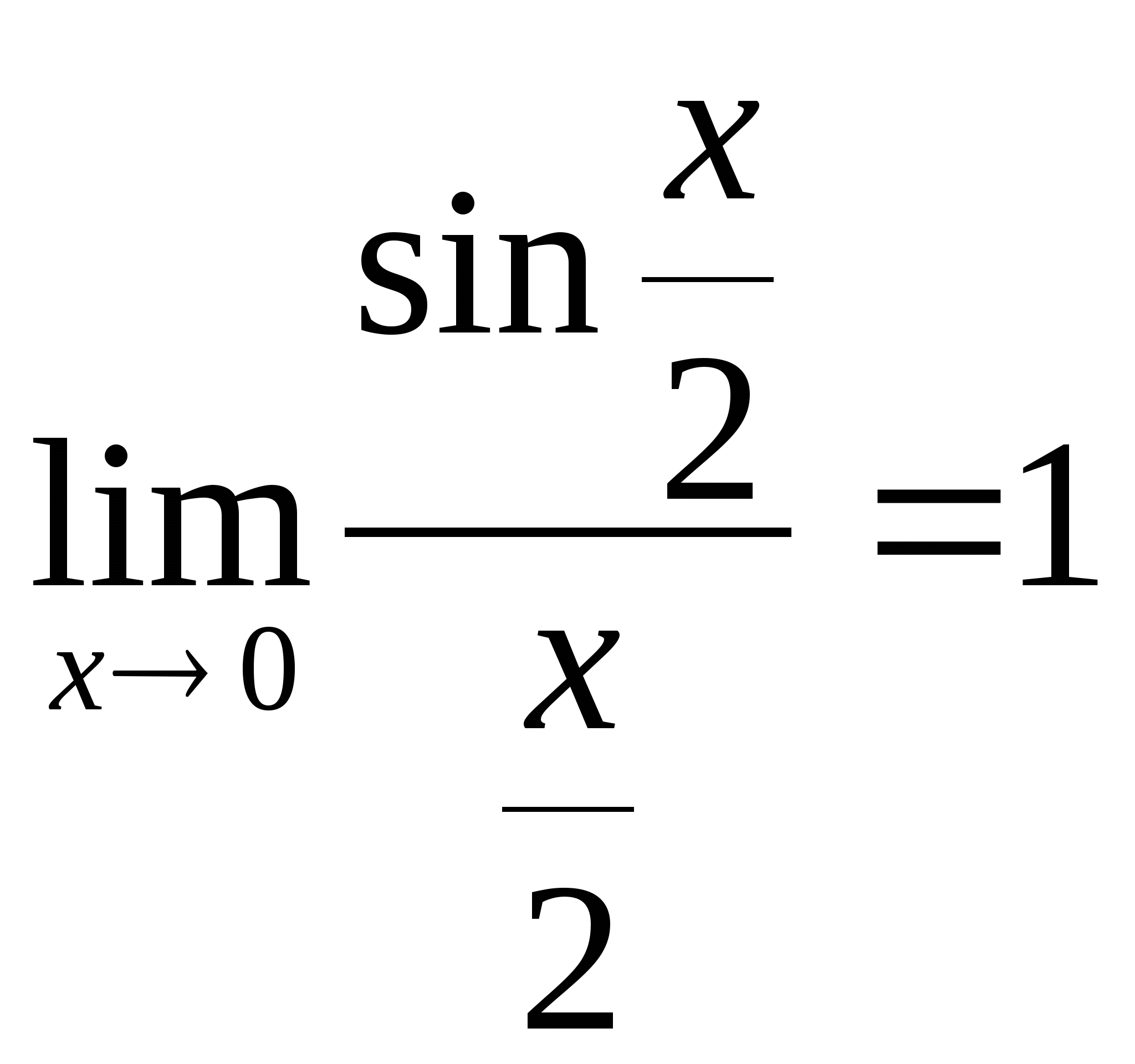 из первого
замечательного предела.
из первого
замечательного предела.
3. 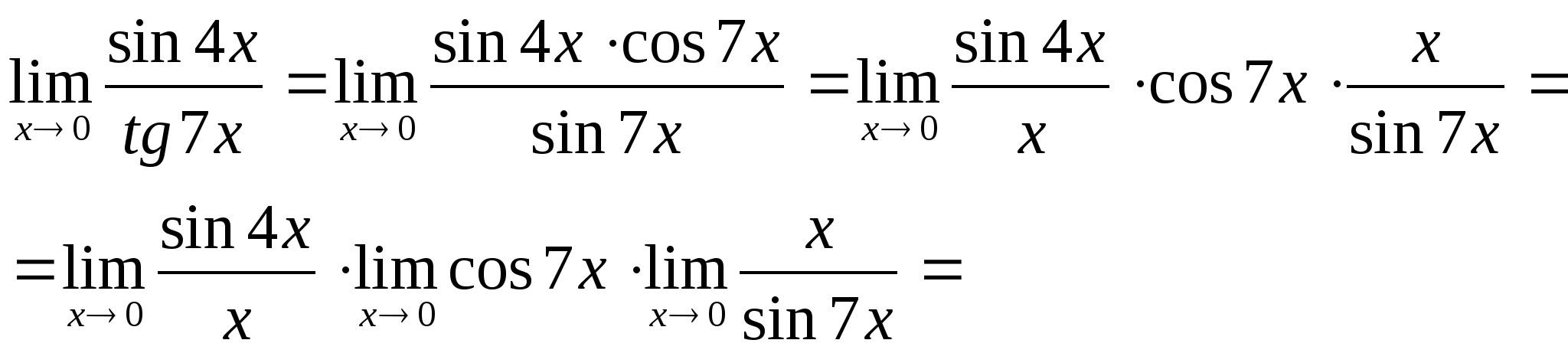
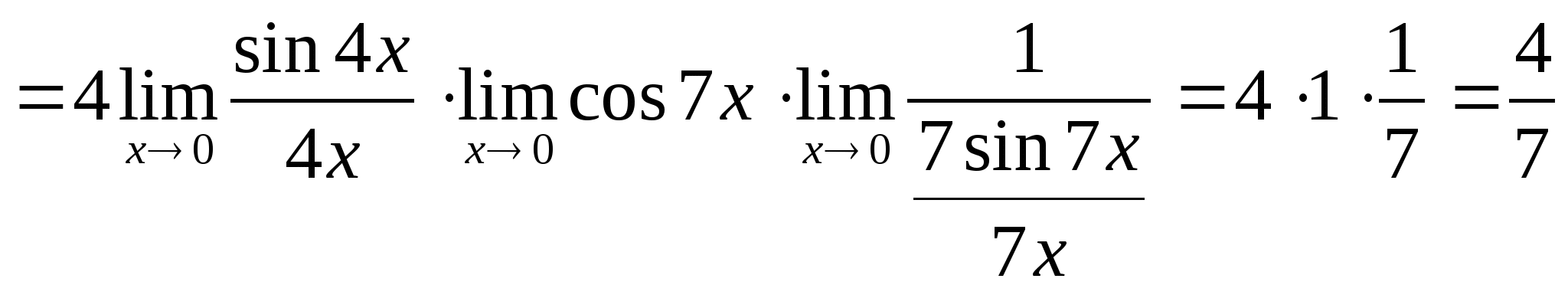 .
.
4. ![]() ln(1+2x)2x=
ln(1+2x)2x=![]() .
.
5. Вычислим предел справа ![]() .
.
6. 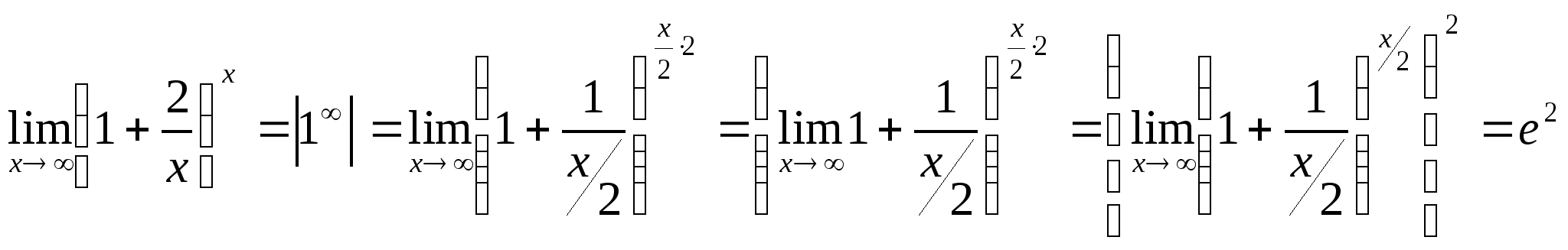 .
.
2.2. Непрерывность функции
Функция f(x) называется непрерывной в точке а, если для любого положительного числа найдется отвечающее ему положительное число , обеспечивающее справедливость неравенства
![]() ,
,
для всех значений аргумента х, удовлетворяющих условию ![]() .
.
Функция f(x) называется непрерывной на интервале, если она непрерывна в каждой его точке. Всякая элементарная функция непрерывна в своей области определения.
Для того, чтобы функция была непрерывна в точке а, необходимо и достаточно, чтобы односторонние пределы функции в точке совпадали со значением функции в этой точке:
![]() .
.
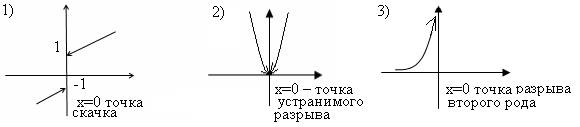
Точка а называется точкой разрыва функции f(x), если f(x) не является непрерывной в этой точке.
Точки разрыва подразделяются на точки разрыва первого рода и второго рода.
Если ![]() и односторонние пределы
конечны, то разрыв в точке а называется устранимым.
и односторонние пределы
конечны, то разрыв в точке а называется устранимым.
Если ![]() , и оба односторонних
предела конечны, то говорят о скачке функции в точке.
, и оба односторонних
предела конечны, то говорят о скачке функции в точке.
Устранимый разрыв функции и скачек называются разрывами первого рода.
Если один из односторонних пределов равен бесконечности или не существует, то разрыв называется разрывом второго рода.
Если функции f(x) и q(x) непрерывны в точке а, то функции f(x)q(x),f(x)q(x), f(x)/q(x) (если q(x)0) непрерывны в точке а.
Если функция u=(x) непрерывна в точке а, а функция y=f(u) непрерывна в точке u0=(x0), то сложная функция у=f((x)) непрерывна в точке а:
![]() .
.
Пример 2: Исследовать на непрерывность функцию ![]() .
.
Решение: Область определения D(у)=![]() ; т.е. в точке х=0
функция терпит разрыв. Вычислим односторонние пределы в точке х=0.
; т.е. в точке х=0
функция терпит разрыв. Вычислим односторонние пределы в точке х=0.
![]() , а
, а ![]() , таким образом
f(0-0)f(0+0). То есть х=0 является точкой разрыва первого рода,
точкой скачка.
, таким образом
f(0-0)f(0+0). То есть х=0 является точкой разрыва первого рода,
точкой скачка.
2.3. Дифференциальное исчисление
Производной функции y=f(x) в точке
х0называется предел отношения приращения функции
![]() к приращению аргумента
к приращению аргумента
![]() при произвольном
стремлении
при произвольном
стремлении ![]() к нулю, если такой
предел существует.
к нулю, если такой
предел существует.
Обозначение: ![]() .
.
Скорость![]() прямолинейного
движения материальной точки в момент времени t0 есть
производная от пути S(t) по времени
прямолинейного
движения материальной точки в момент времени t0 есть
производная от пути S(t) по времени
![]() .
.
В этом состоит механический смысл производной.
Пусть функция у=f(x) имеет производную в точке х0. Тогда существует касательная к графику этой функции в точке М0(х0;у0), уравнение которой имеет вид
![]() .При этом
.При этом ![]() , где - угол наклона
этой касательной к оси ОХ.
, где - угол наклона
этой касательной к оси ОХ.
Если функция в точке имеет конечную производную, то функция называется дифференцируемой в этой точке.
Функция, дифференцируема в каждой точке промежутка, называется дифференцируемой на этом промежутке. Операция вычисления производной называется дифференцированием.
Основные правила дифференцирования
Пусть С- константа, а u(x) и v(x) имеют производные в некоторой точке х. Тогда
1) ![]() ; 2)
; 2) ![]() , в частности,
(cu)'=cu'; 3)
, в частности,
(cu)'=cu'; 3) 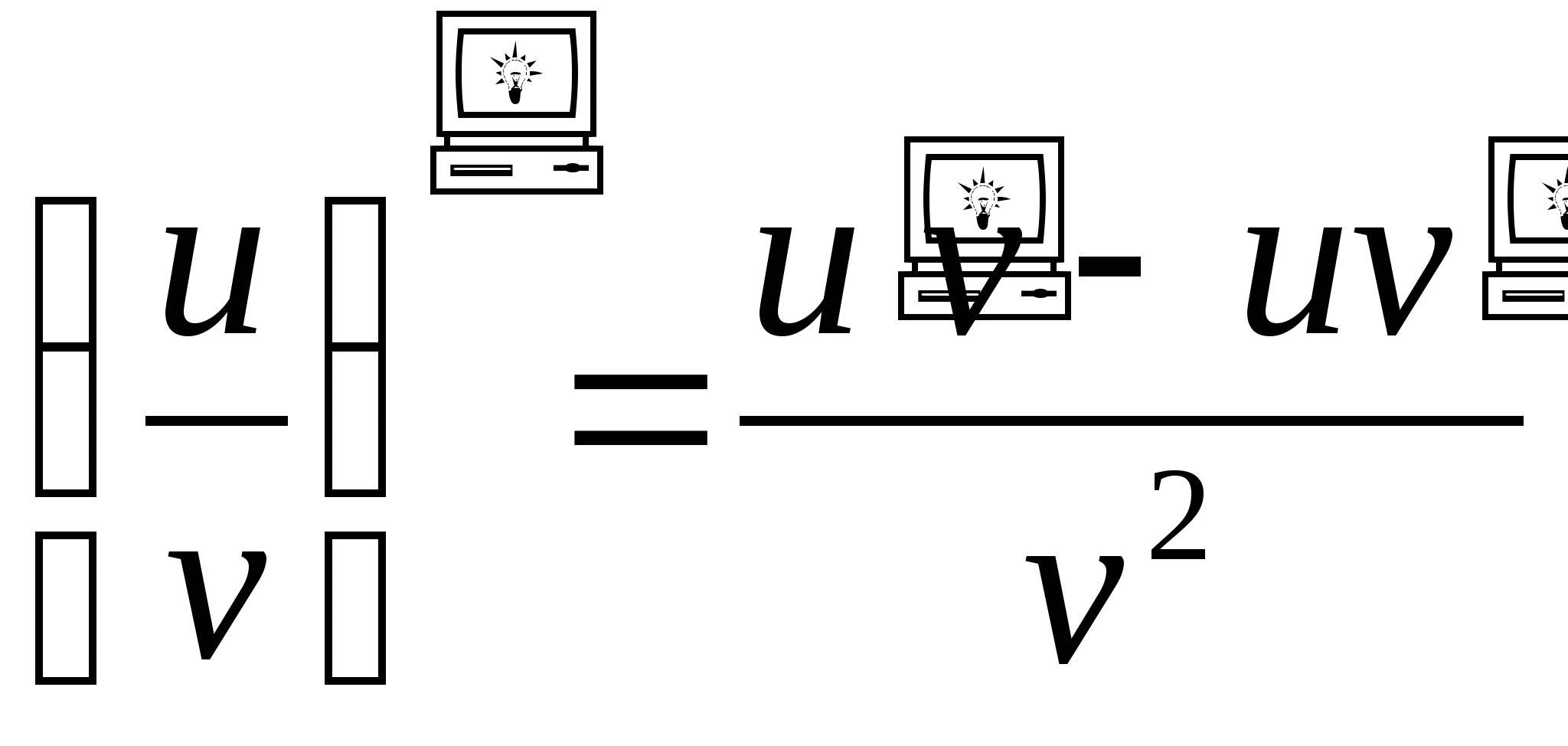 , в частности,
, в частности,
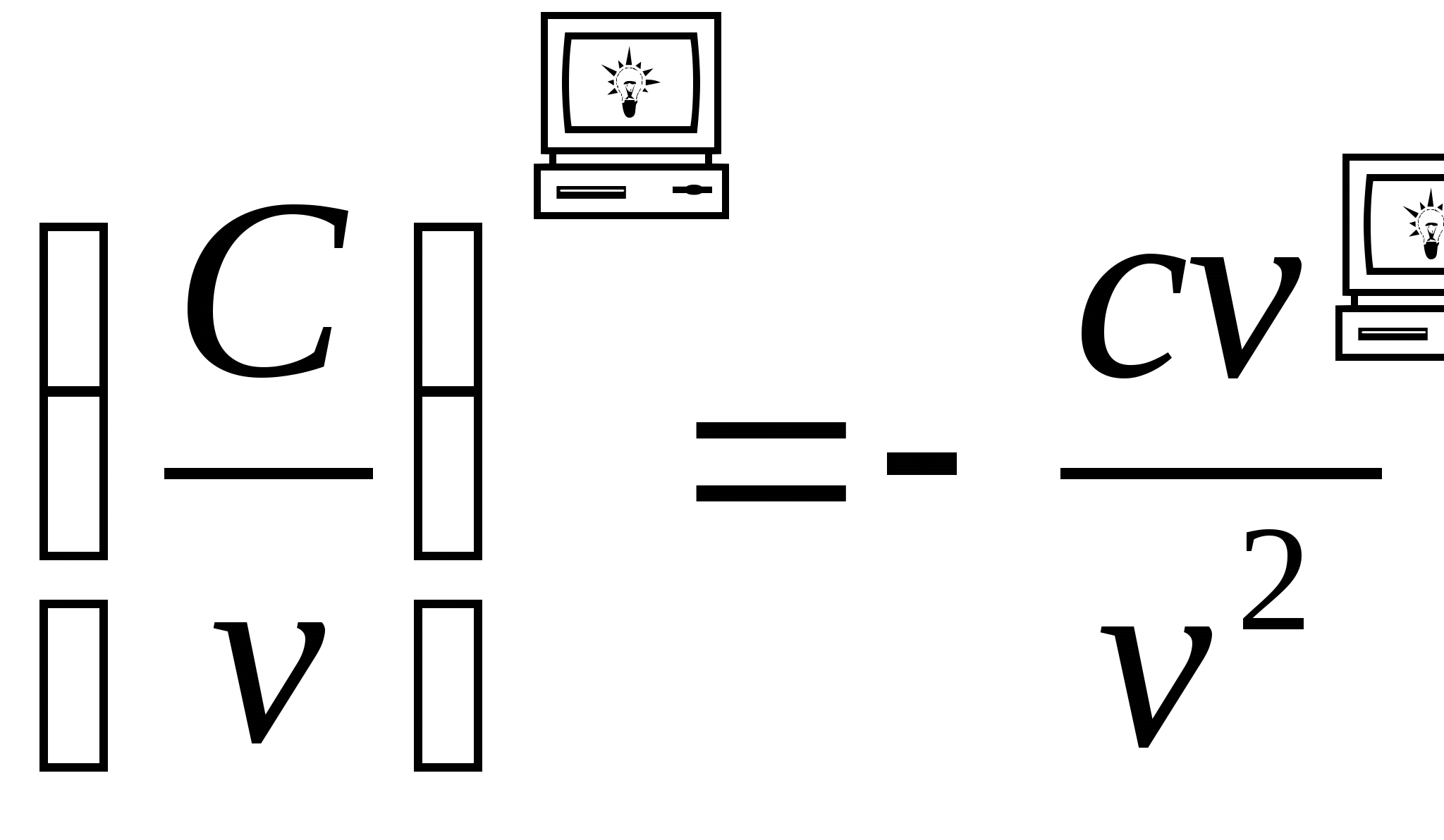 .
.
Если функция u=(x) имеет производную в точке х0, а
функция у=f(u) - в точке u0=(x0). Тогда
сложная функция у=f((x)) также имеет производную в точке
х0, причем ![]() .
.
Производной второго порядка функции у=f(x)
называют производную от ее первой производной ![]() , аналогично
y(n)=f(n)(x)
-n-я производная.
, аналогично
y(n)=f(n)(x)
-n-я производная.
Дифференциал функции у=f(x) равен
произведению ее производной и дифференциала независимой переменной,
т.е.![]() . Справедлива формула
приближенного вычисления значения функции
. Справедлива формула
приближенного вычисления значения функции![]() .
.
Таблица производных
-
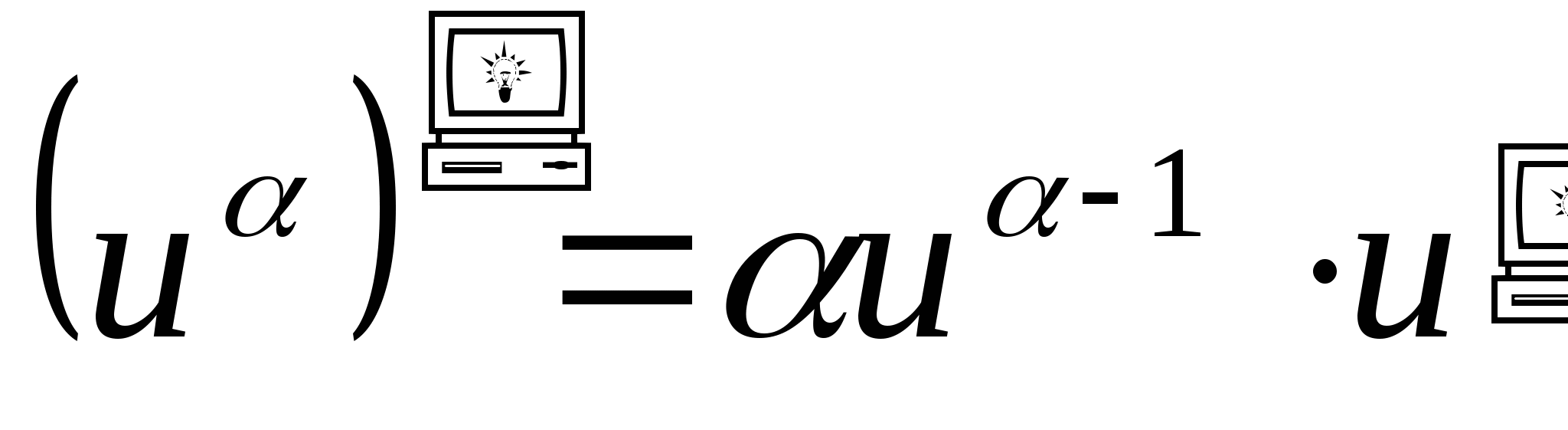 . 8.
. 8.
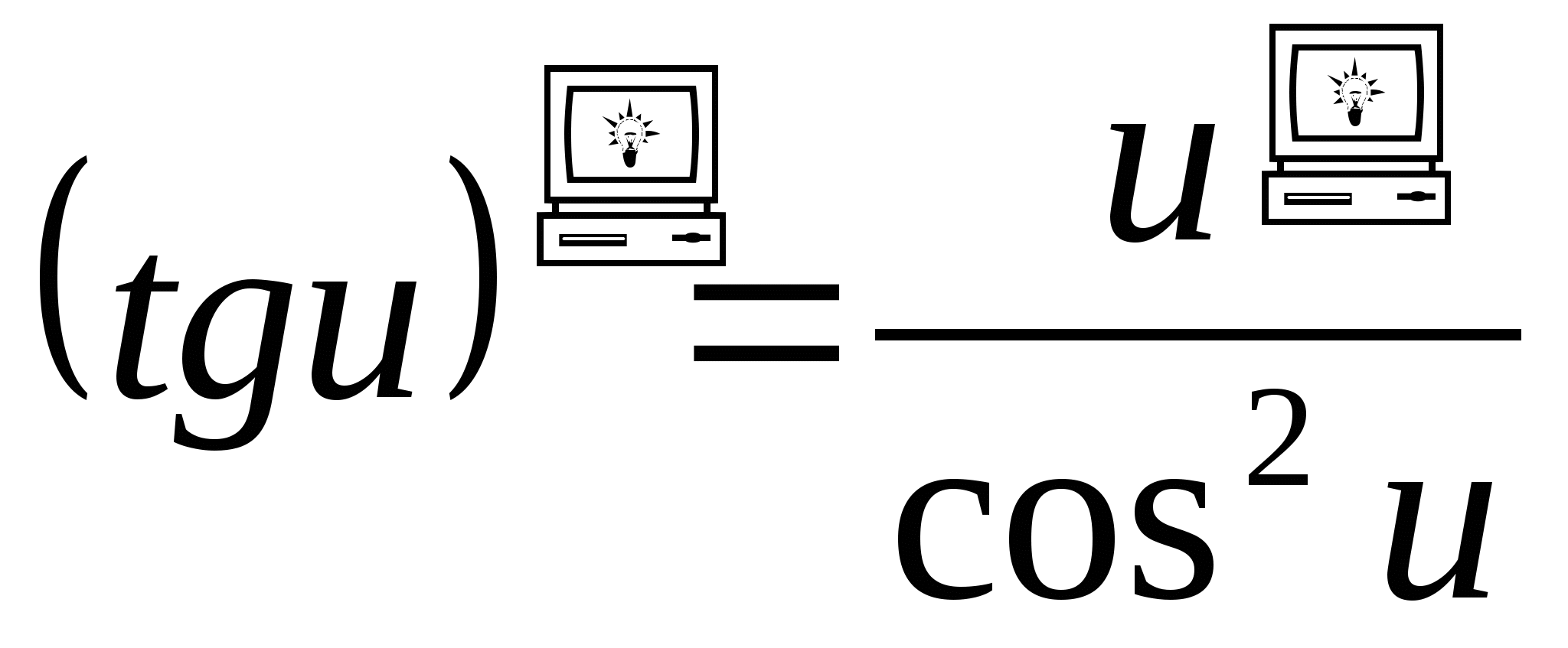 .
.
-
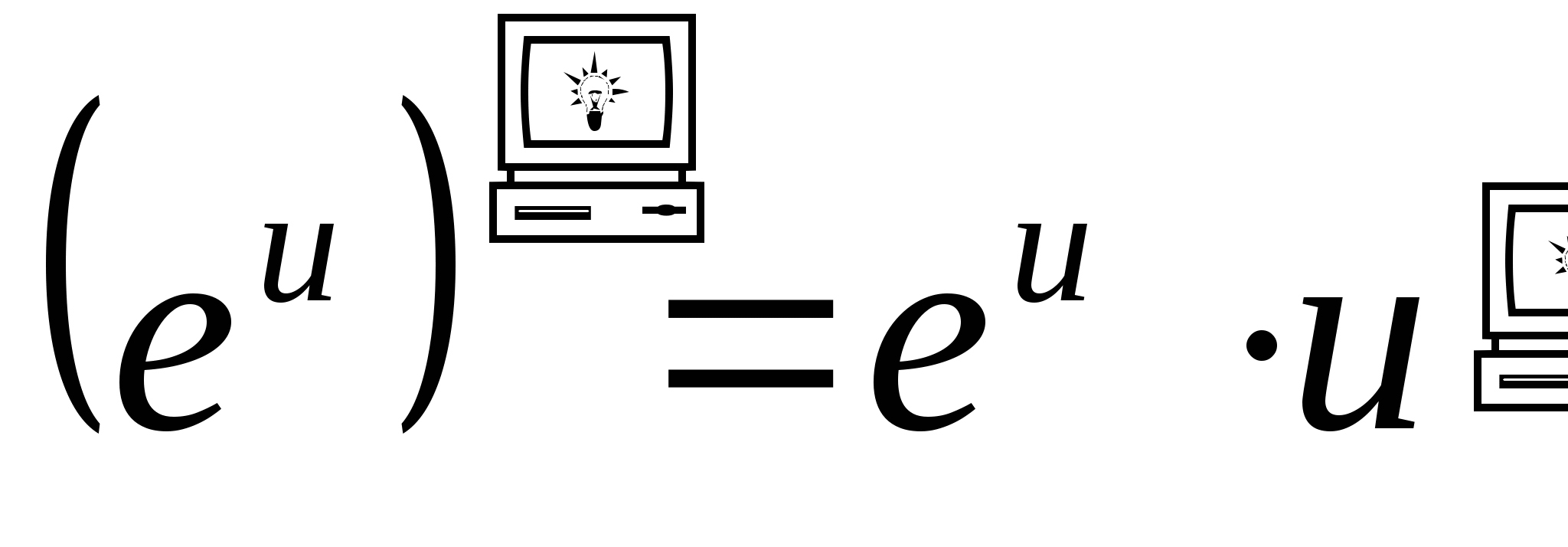 . 9.
. 9.
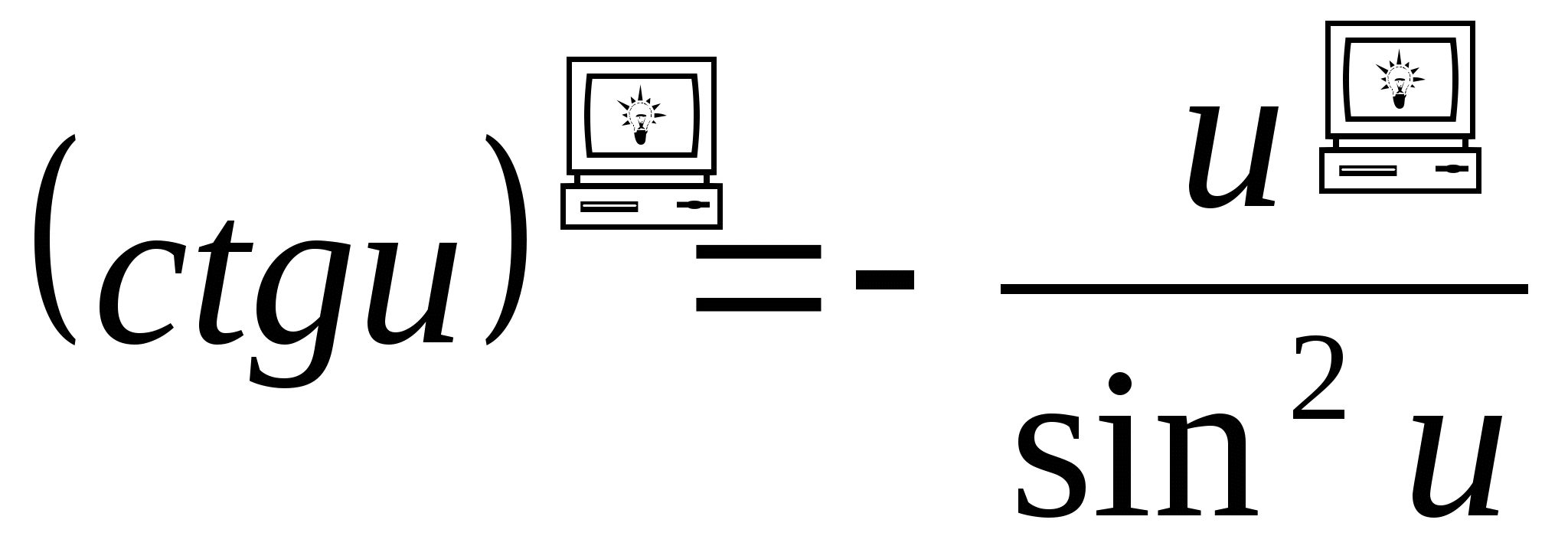 .
.
-
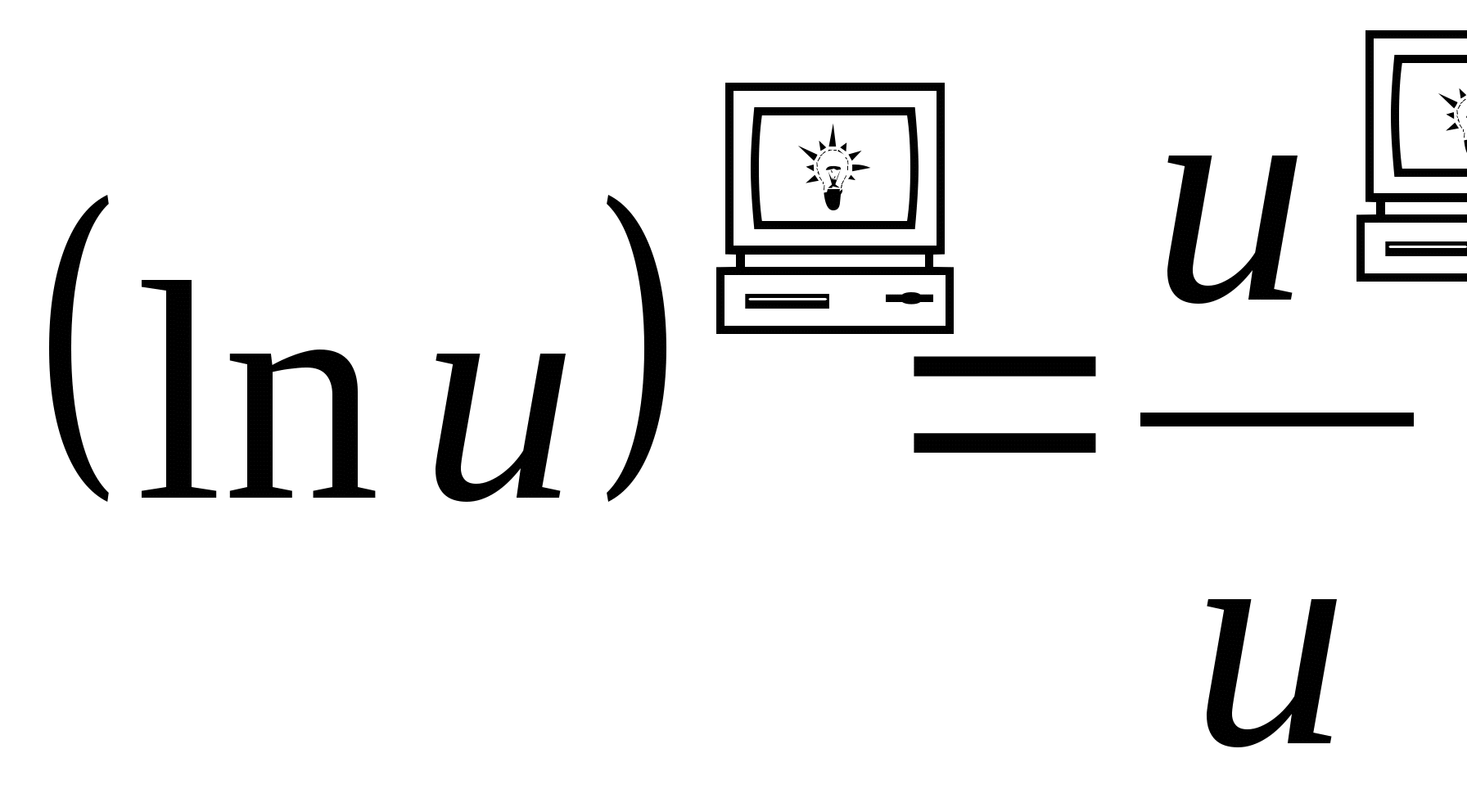 .
10.
.
10. 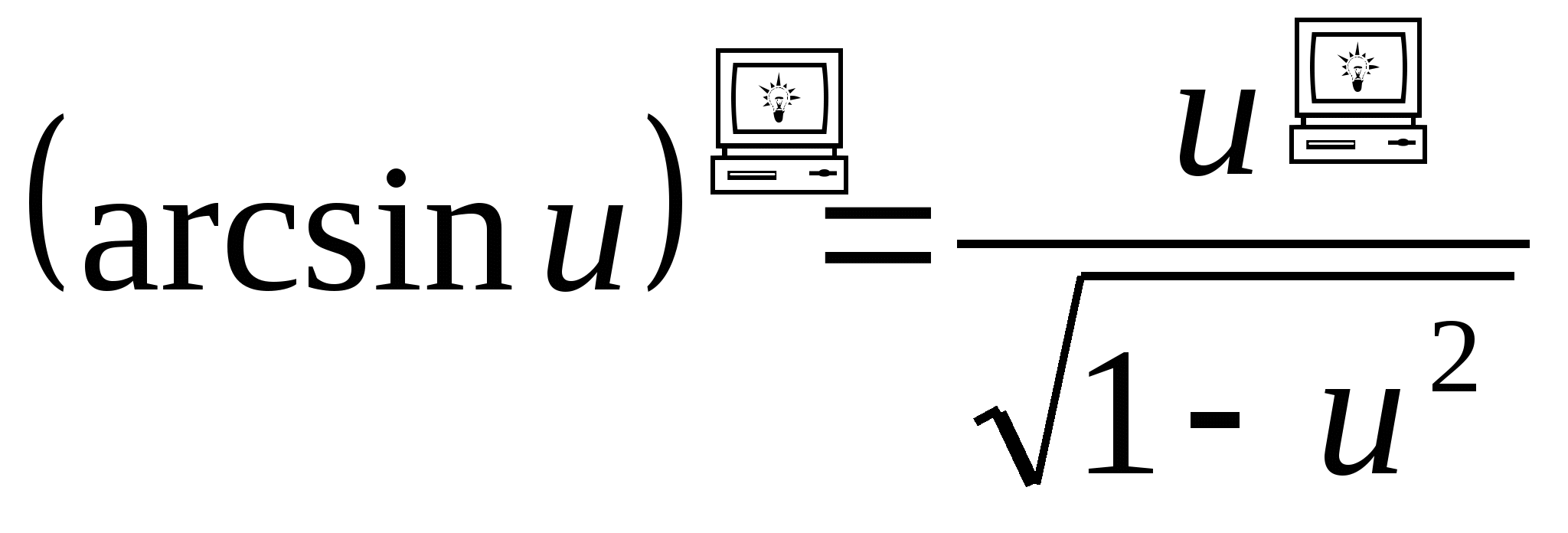 .
.
-
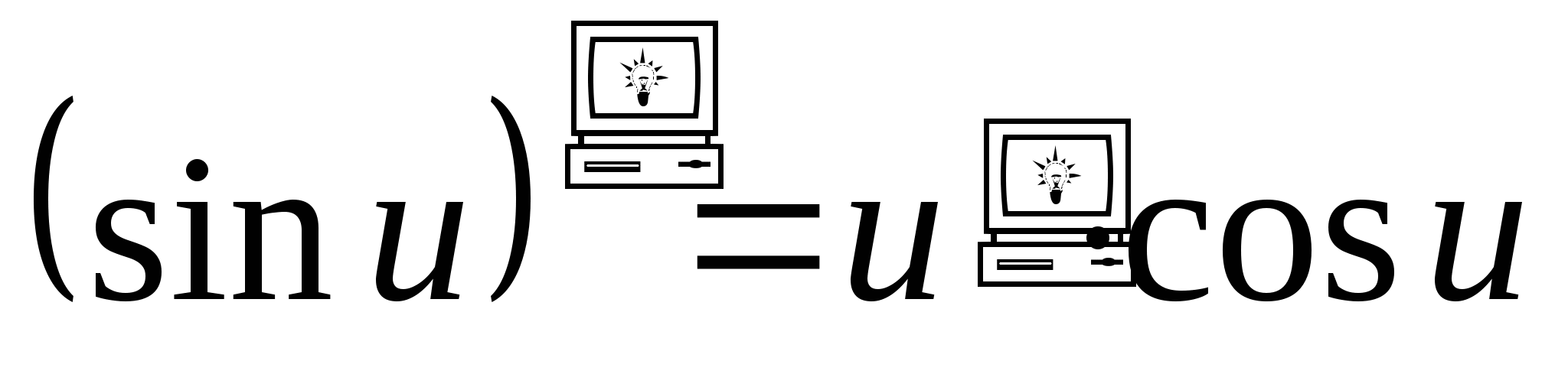 .
11.
.
11. 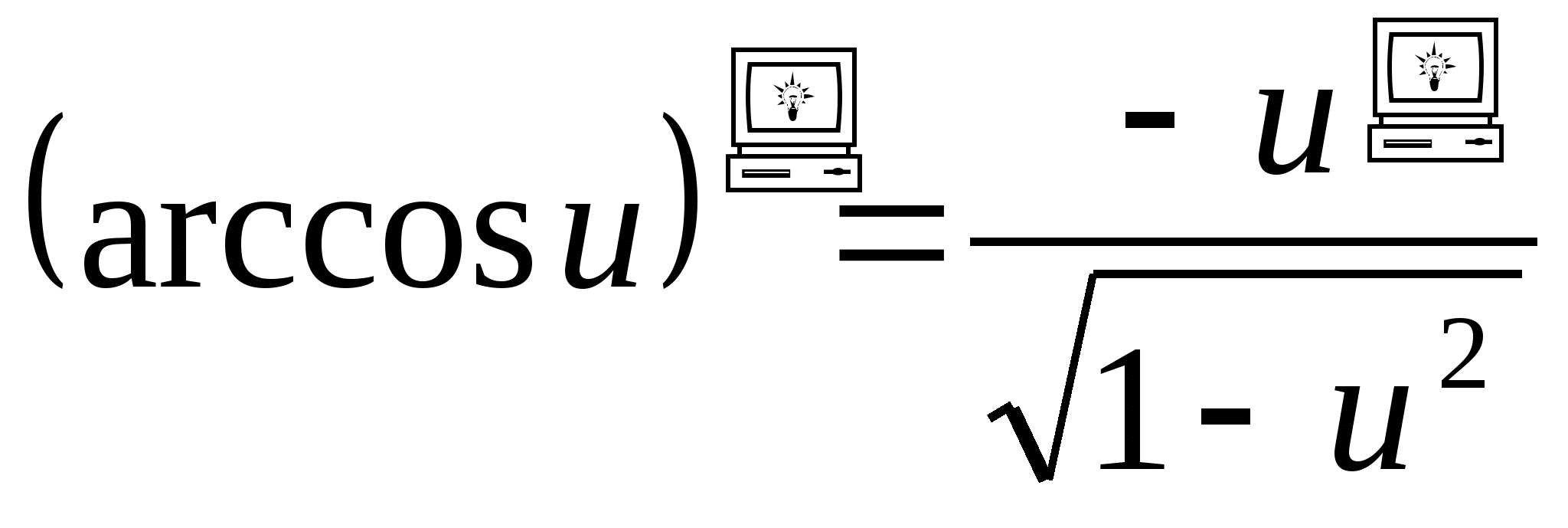 .
.
-
 .
12.
.
12. 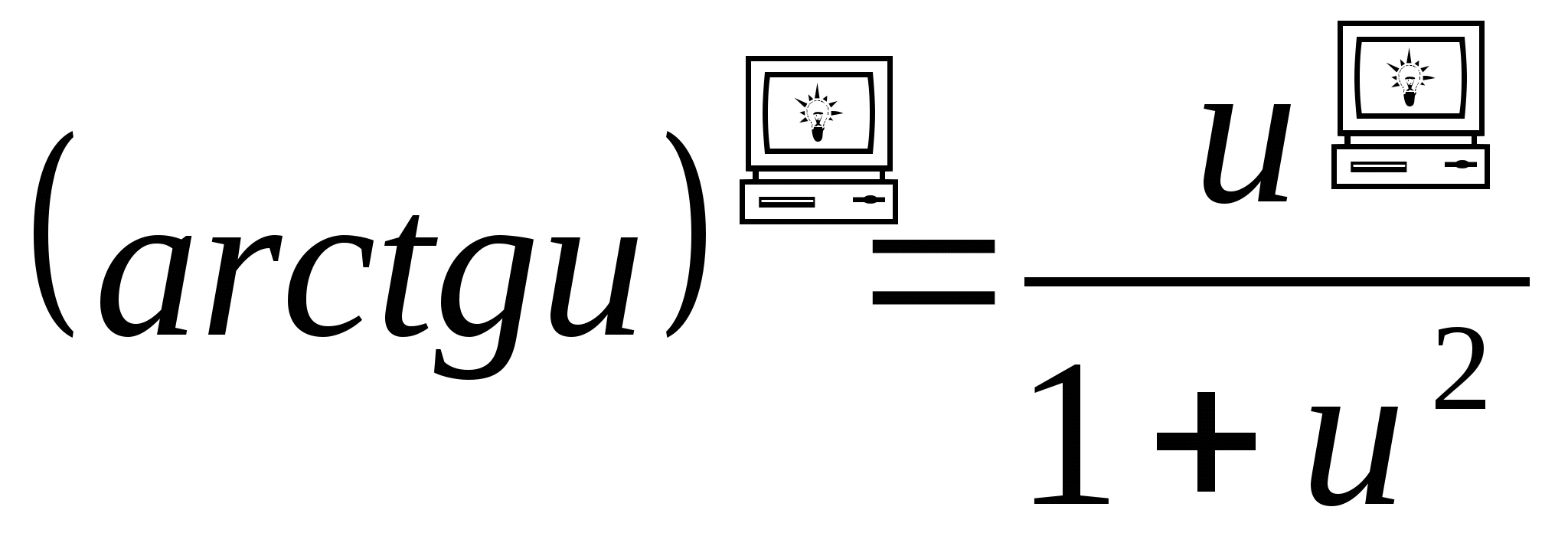 .
.
-
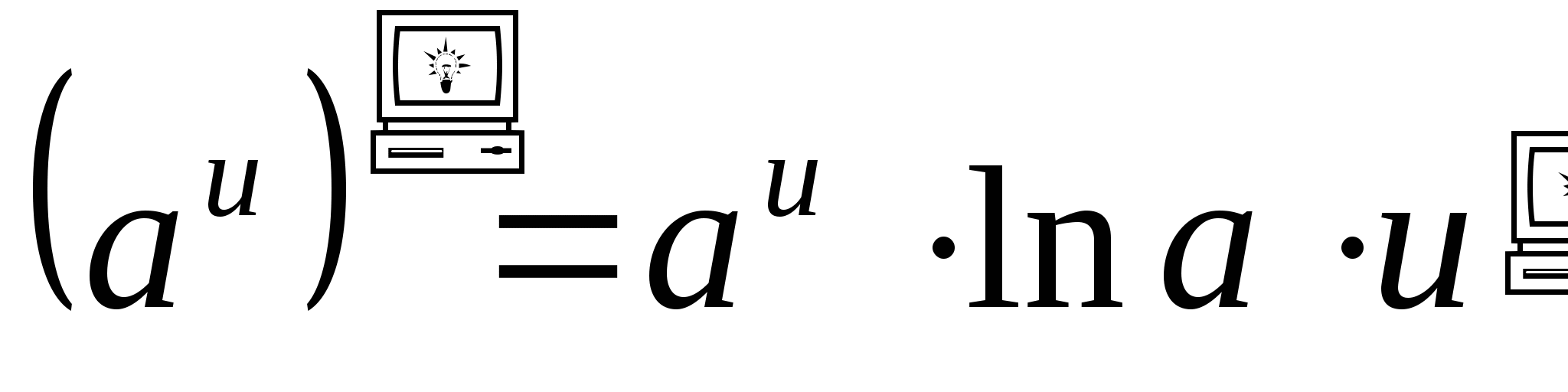 .
13.
.
13. 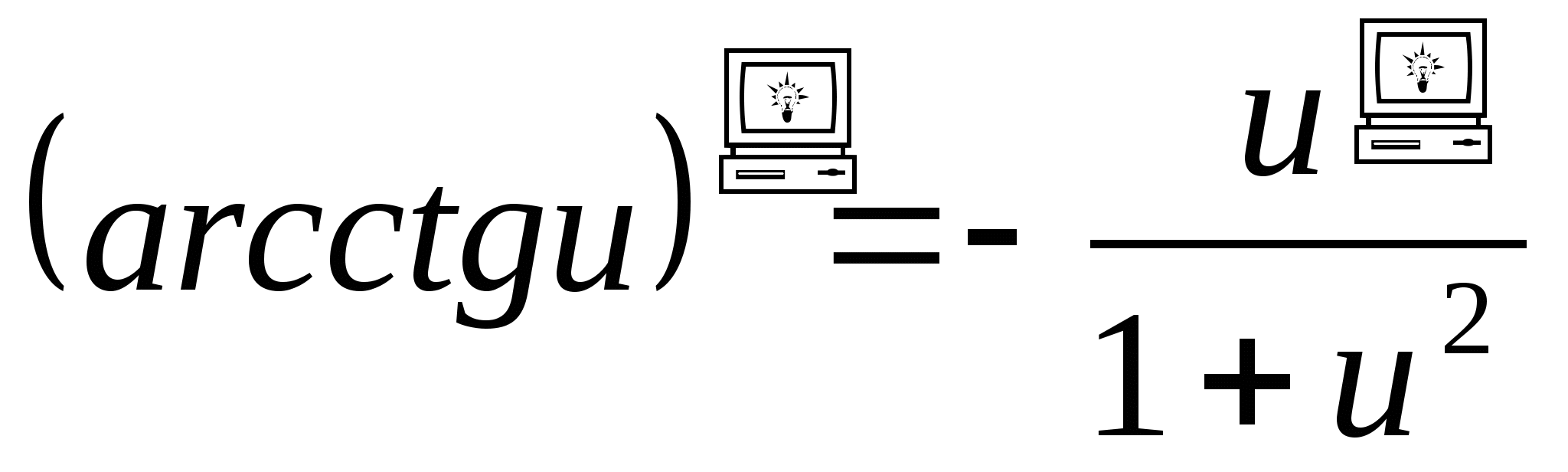 .
.
-
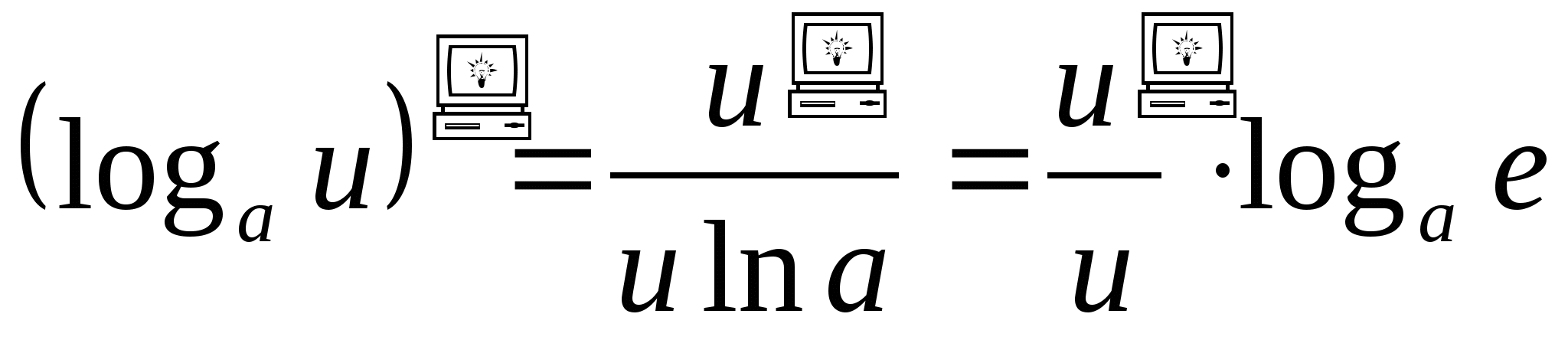 .
14.
.
14. 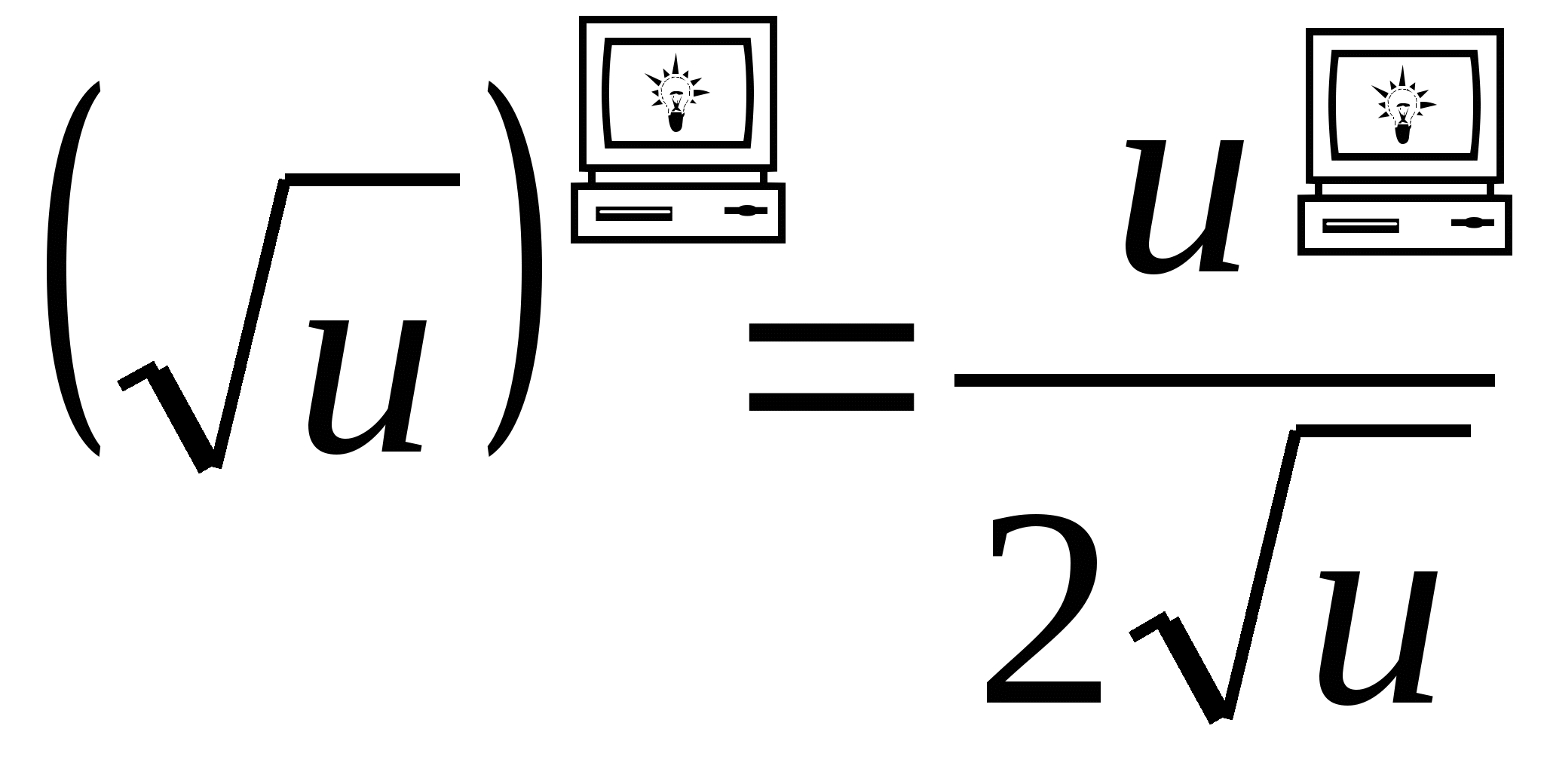 .
.
Здесь u=u(x) - дифференцируемая функция.
Пример 3. 1.Найти производную данных функций
а) ![]() ; в)
; в)
![]() .
.
2. Найти у'' и dy, если у=х2+3х.
3. Найти наибольшее и наименьшее значение функции у=х3 - 3х2 + 2 на отрезке [1;5].
4. Исследовать функцию ![]() и
построить ее график.
и
построить ее график.
Решение: 1.а) Преобразуем функцию к виду ![]() , тогда
, тогда
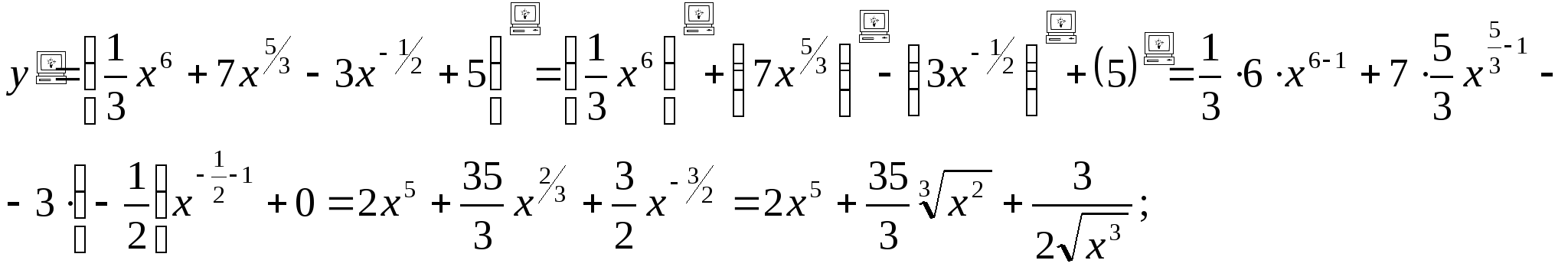
в)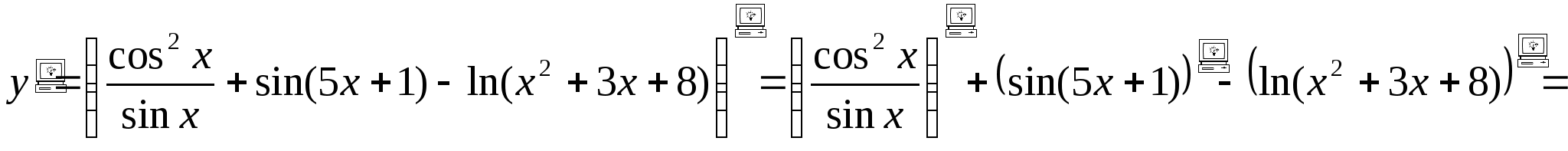
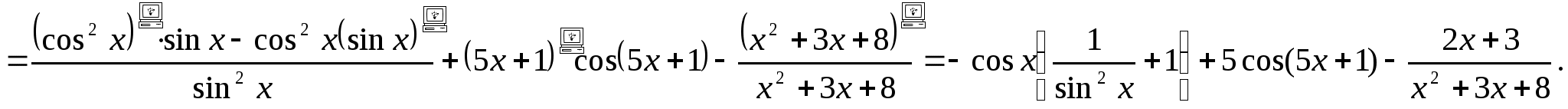 2. Вычислим первую и
вторую производную данной функции.
2. Вычислим первую и
вторую производную данной функции.
![]() ;
; ![]() . По определению
дифференциал равен
. По определению
дифференциал равен
![]() , т.е.
, т.е. ![]() .
.
3. 1. Найдем все стационарные точки и точки, в которых
производная не существует, и вычислим в них значения
функции.![]() . Приравняем к нулю
у',
. Приравняем к нулю
у',![]() =0 и найдем стационарные
точки х1=0, х2=2,тогда у(0)=2:у(2)=-2.
=0 и найдем стационарные
точки х1=0, х2=2,тогда у(0)=2:у(2)=-2.
2. Вычислим значения функции на концах отрезка, в точках х=1,х=5. То есть у(1)=0, у(5)=52.
3. Сравним между собой вычисленные значения функции, т. е. у(1)=0; у(2)=-2; у(5)=52, получим унаиб.(5)=52, унаим.(2)=-2. Значение у(0) не участвует в сравнении т.к. х=0 не принадлежит отрезку [1;5].
4. Для исследования функций и построения графика можно использовать следующую последовательность действий:
1. Найти область определения функции.
2. Определить четность, нечетность функции.
3. Исследовать функцию на периодичность.
4. Исследовать функцию на непрерывность; найти точки разрыва, асимптоты, точки пересечения графика с координатными осями.
5. Найти первую производную. Определить критические точки первого рода.
6. Определить интервалы монотонности и экстремумы функции.
7. Найти вторую производную, критические точки второго рода.
8. Определить интервалы выпуклости и точки перегиба.
9. Построить график функции.
Решение: 1. Данная функция определена на всей числовой оси, кроме значений х=2, т.к. в этих точках знаменатель равен нулю, т.е. функция не существует. D(у)= R /{2}.
2. Так как ![]() , то f(x)
нечетная, т.е. симметрична относительно начала координат.
, то f(x)
нечетная, т.е. симметрична относительно начала координат.
3. Непериодическая.
4. Функция f(x) непрерывна во всей области ее определения, кроме
значений х=2, являющимися точками разрыва II рода, т.к. 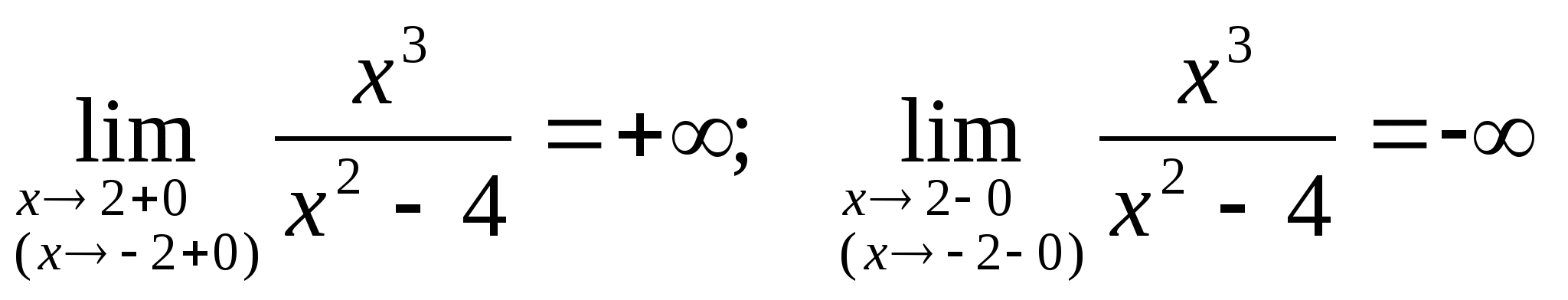
На основании выше указанных пределов прямые х=2 - являются
вертикальными асимптотами. По формулам: ![]() ,
, ![]() ,
, ![]() -найдем наклонную
асимптоту.
-найдем наклонную
асимптоту.
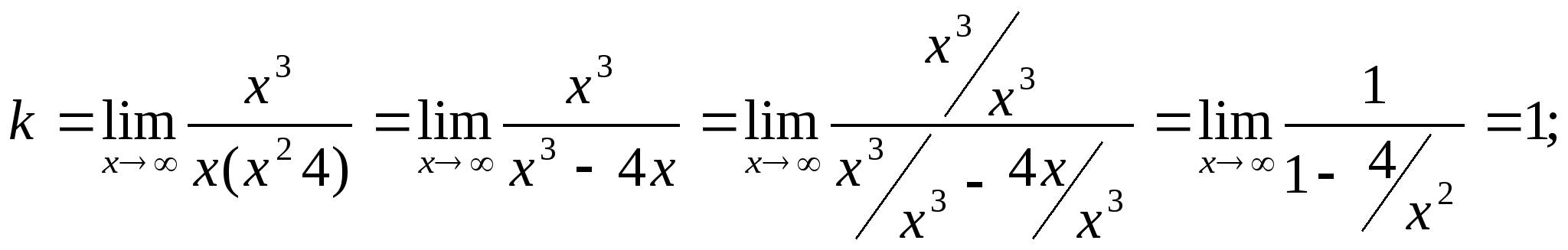
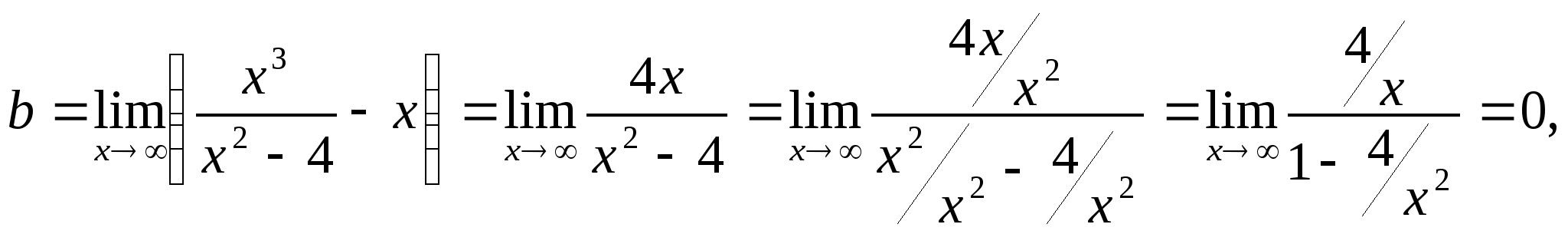
То есть у=х. Для определения точек пересечения графика функции с координатными осями необходимо решить системы уравнений:
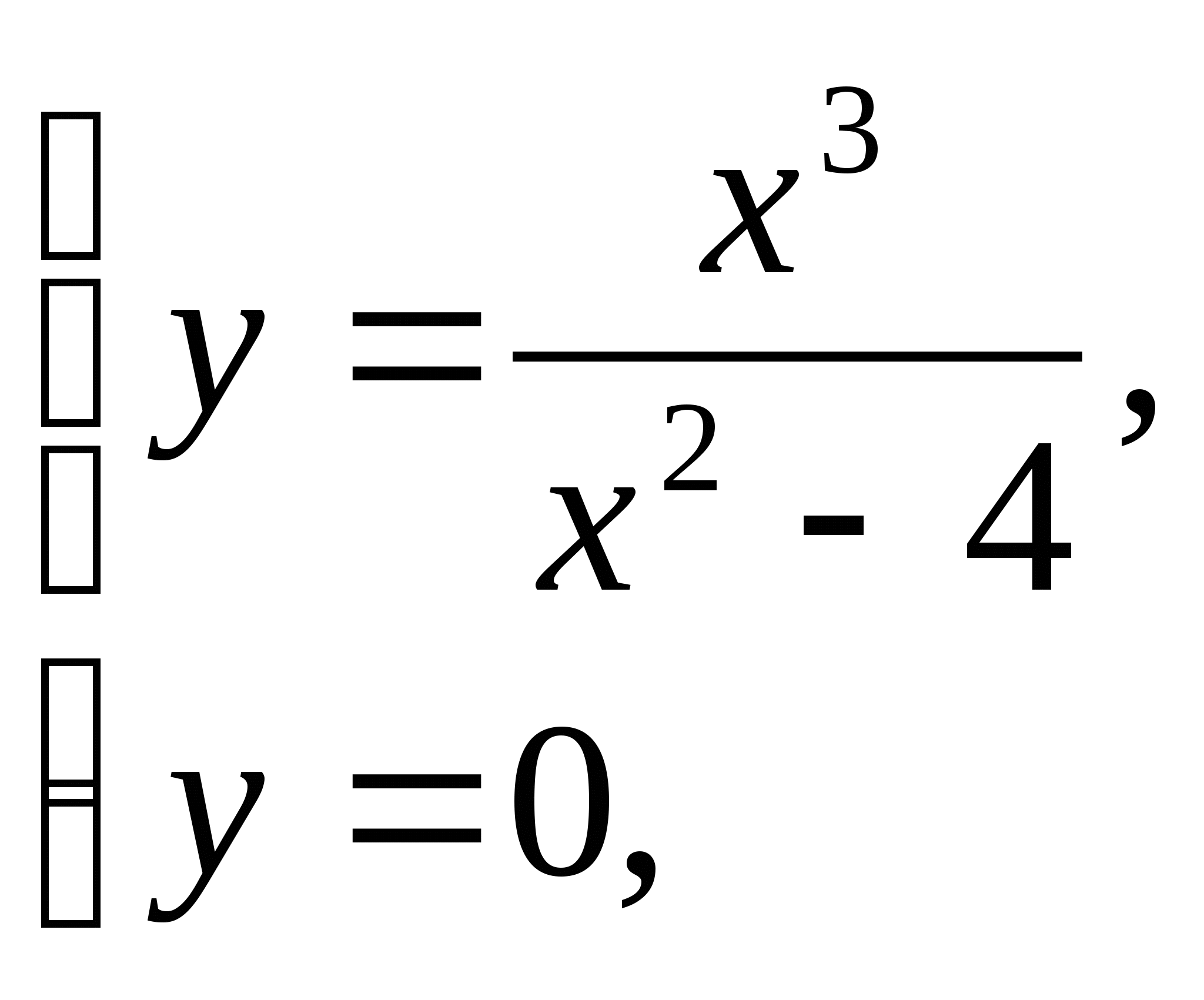 и
и 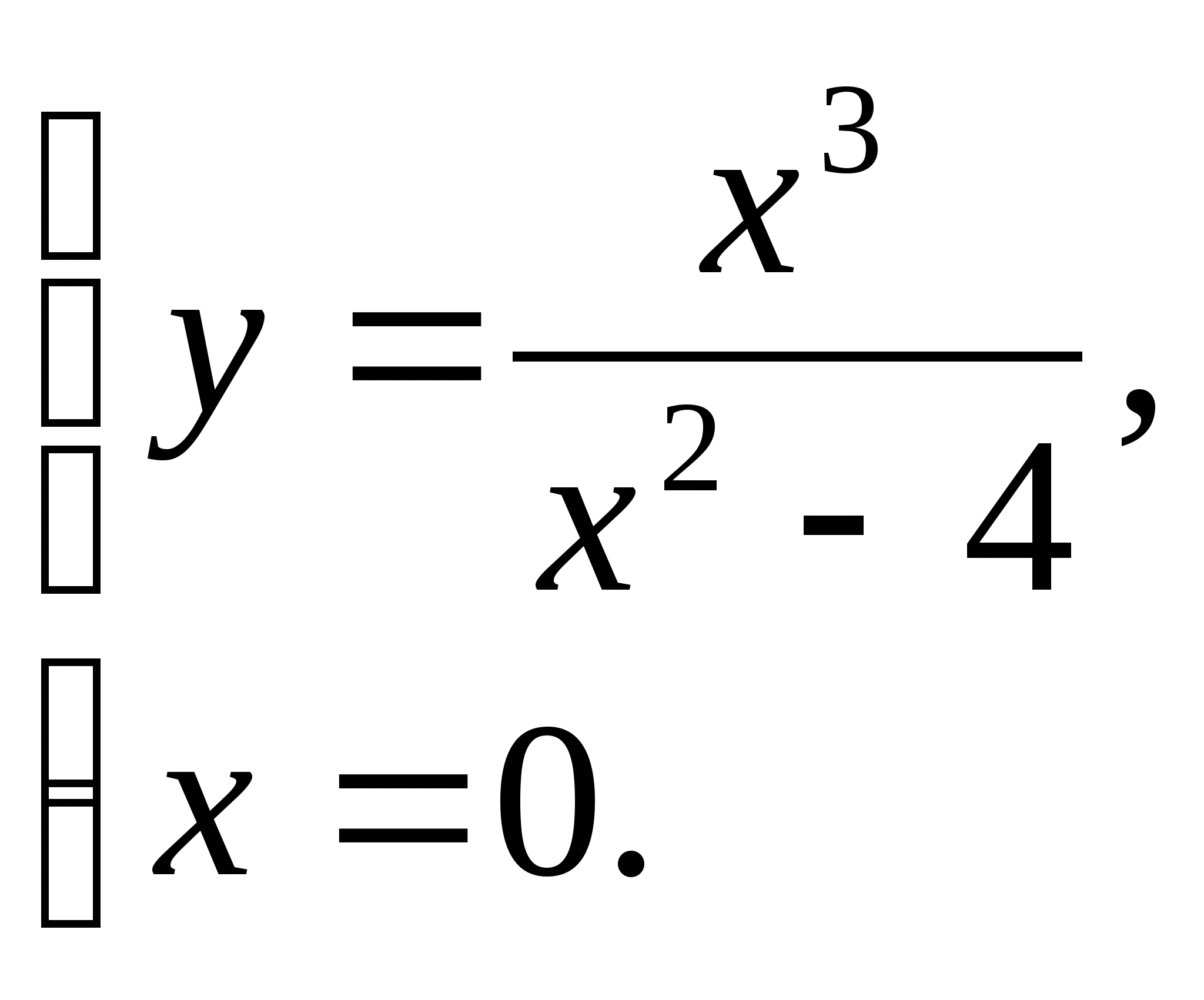
Обе системы имеют одно и то же решение х=0, у=0. В точке (0,0)функция пересекает систему координат.
5. Вычислим f'(x)=0.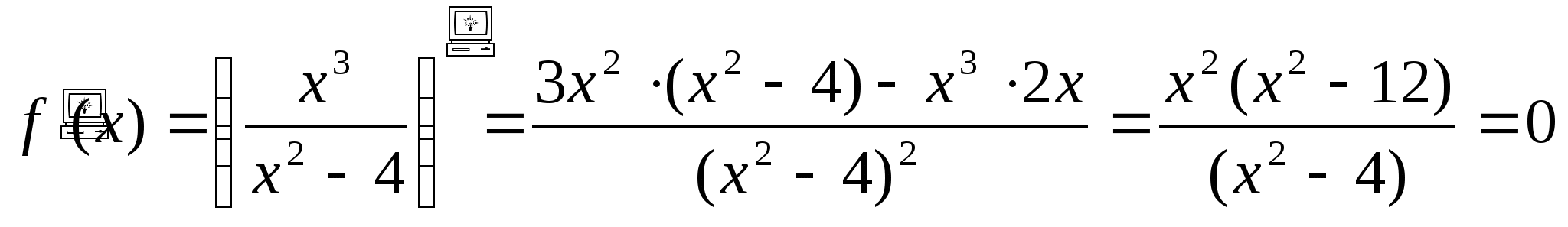 , отсюда
следует, что f'(x)=0 при х2(х2-12)=0, т.е.
при х=0 и х=2
, отсюда
следует, что f'(x)=0 при х2(х2-12)=0, т.е.
при х=0 и х=2![]() . В то же время
f'(x) не существует при х=2. Следовательно, функция f(x) имеет
следующие критические точки первого рода: х1=-2
. В то же время
f'(x) не существует при х=2. Следовательно, функция f(x) имеет
следующие критические точки первого рода: х1=-2![]() ; х2=-2;
х3=0; х4=2; х5=2
; х2=-2;
х3=0; х4=2; х5=2![]()
6. Методом пробных точек определим знаки первой производной в интервалах
![]()
т.е. данная функция f(x) в интервалах (-;-2![]() ) и (2
) и (2![]() ;+) возрастает, а в
интервалах
;+) возрастает, а в
интервалах
(-2![]() ;-2); (-2;0); (0;2);
(2;2
;-2); (-2;0); (0;2);
(2;2![]() )- убывает.
х1=-2
)- убывает.
х1=-2![]() точка
максимума, так как при переходе через эту точку производная меняет
знак с плюса на минус;
fmax(x)=fmax(-2
точка
максимума, так как при переходе через эту точку производная меняет
знак с плюса на минус;
fmax(x)=fmax(-2![]() )=-3
)=-3![]() , а точка
х5=2
, а точка
х5=2![]() - точка
минимума, так как при переходе через эту точку производная меняет
знак с минуса на плюс;
fmin(x)=fmin(2
- точка
минимума, так как при переходе через эту точку производная меняет
знак с минуса на плюс;
fmin(x)=fmin(2![]() )=3
)=3![]() .
.
В критической точке х3=0 первая производная не меняет знак, следовательно, в этой точке экстремума нет.
7. Вычислим 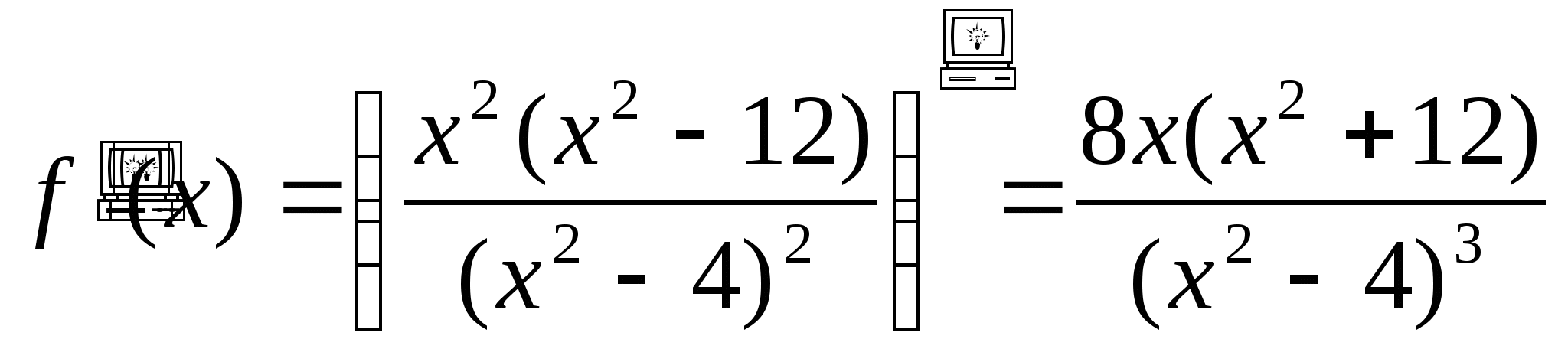 . f''(х)=0 при
х=0, а при х=2 f''(х) не существует, следовательно,
х2=-2; х3=0, х4=2 - есть
критические точки второго рода.
. f''(х)=0 при
х=0, а при х=2 f''(х) не существует, следовательно,
х2=-2; х3=0, х4=2 - есть
критические точки второго рода.
8. В интервалах (-;-2); (-2;0); (0;2); (2;+) определим знак второй производной методом пробных точек.
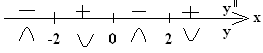
Таким образом, в промежутках (-; -2) и (0;2) график функции выпуклый вверх, а в (-2;0) и (2;+) - выпуклый вниз. Вторая производная в каждой из критических точек меняет знак, в то же время в точках х2=-2; х4=2 функция неопределенна, следовательно, только точка х=0 является точкой перегиба.
9. На основании полученных результатов построим график функции
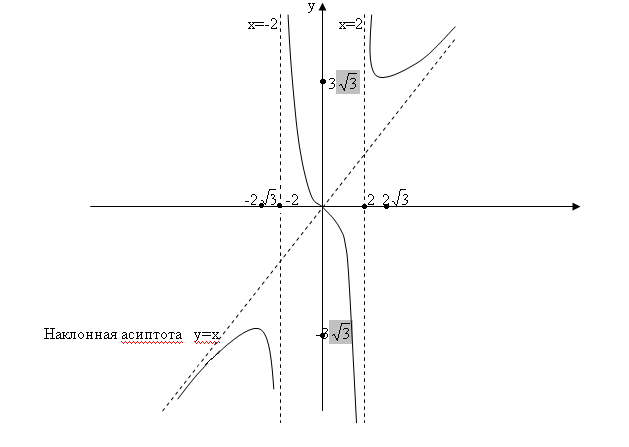
2.4. Интегральное исчисление
Функция F(x) называется первообразной для функции f(x) на интервале (a;b), если для любого х(a;b) функция F(x) дифференцируема и выполняется равенство F'(x)=f(x).
Если F(x) - первообразная функция для функции f(x), то функция F(x)+C, где С - произвольная постоянная, также первообразная для функции f(x).
Совокупность всех первообразных для функции f(x) называется неопределенным интегралом от функции f(x) и обозначается символом
![]() , где
F'(x)=f(x).
, где
F'(x)=f(x).
Операция нахождения неопределенного интеграла от данной функции называется интегрированием этой функции. Интегрирование - операция, обратная операции дифференцирования.
Основные свойства неопределенного интеграла
1. ![]() .
.
2. ![]() .
.
3. ![]() , где
k=const.
, где
k=const.
4. ![]() .
.
5. Если ![]() , то
, то
![]() , где а0.
, где а0.
Таблица интегралов
1. ![]() . 9.
. 9. ![]() .
.
2. ![]() . 10.
. 10. ![]() .
.
3. ![]() . 11.
. 11. ![]() .
.
4. ![]() . 12.
. 12. ![]() .
.
5. ![]() . 13.
. 13. ![]() .
.
6. ![]() . 14.
. 14. ![]() .
.
7. ![]() . 15.
. 15. ![]() .
.
8. ![]() . 16.
. 16. ![]() .
.
Если (t) - непрерывная и дифференцируемая функция, то, полагая х= (t), получим формулу интегрирования замены переменной
![]() . (1)
. (1)
Формула интегрирования по частям: ![]()
Определенный интеграл 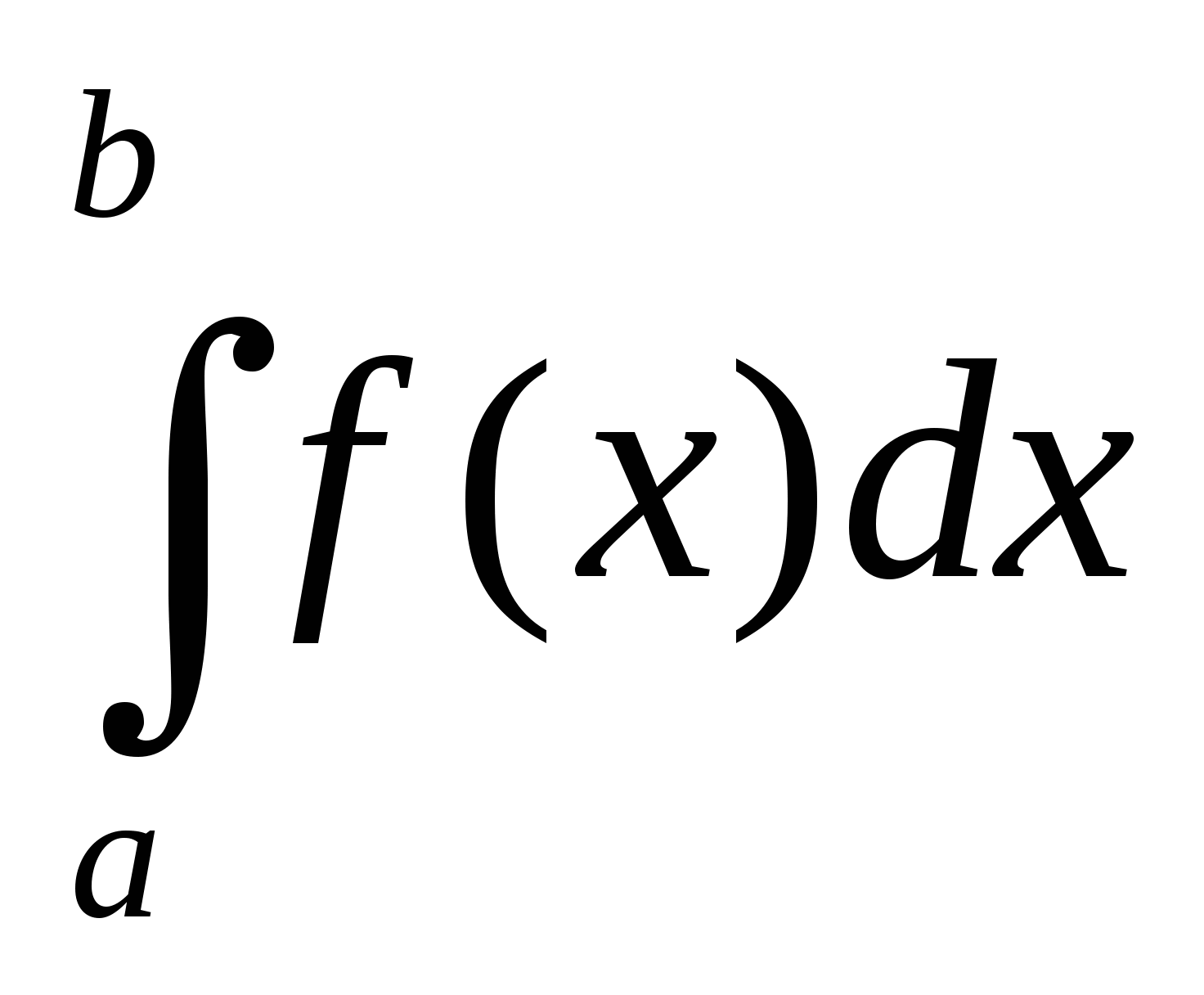 численно
равен площади криволинейной трапеции, ограниченной прямыми х=а,
х=b, у=0 и частью графика функции у=f(x), взятой со знаком
плюс, если f(x)0(минус, если f(x)0) (геометрическая интерпретация
определенного интеграла).
численно
равен площади криволинейной трапеции, ограниченной прямыми х=а,
х=b, у=0 и частью графика функции у=f(x), взятой со знаком
плюс, если f(x)0(минус, если f(x)0) (геометрическая интерпретация
определенного интеграла).
Формула Ньютона- Лейбница для вычисления
определенного интеграла имеет вид: 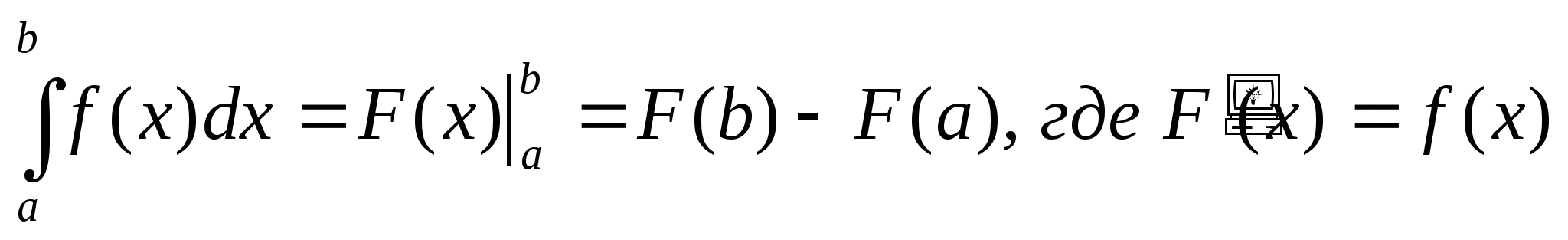 . (2)
. (2)
Интеграл с одним или обоими бесконечными пределами
интегрирования от непрерывной функции f(x) на всем промежутке
интегрирования называется несобственным интегралом первого рода,
т.е. 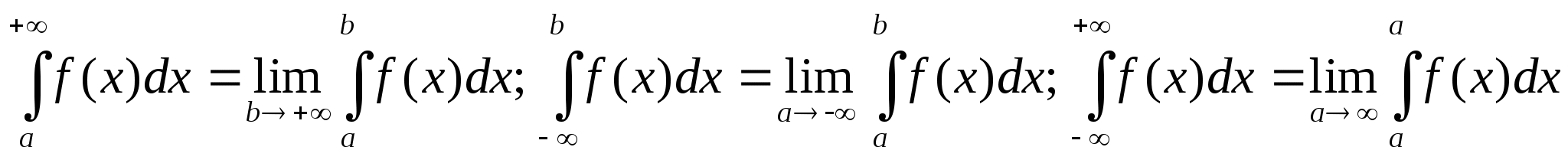 .
.
Пусть f(x) -функция, имеющая бесконечный разрыв в точке с[a,b], тогда
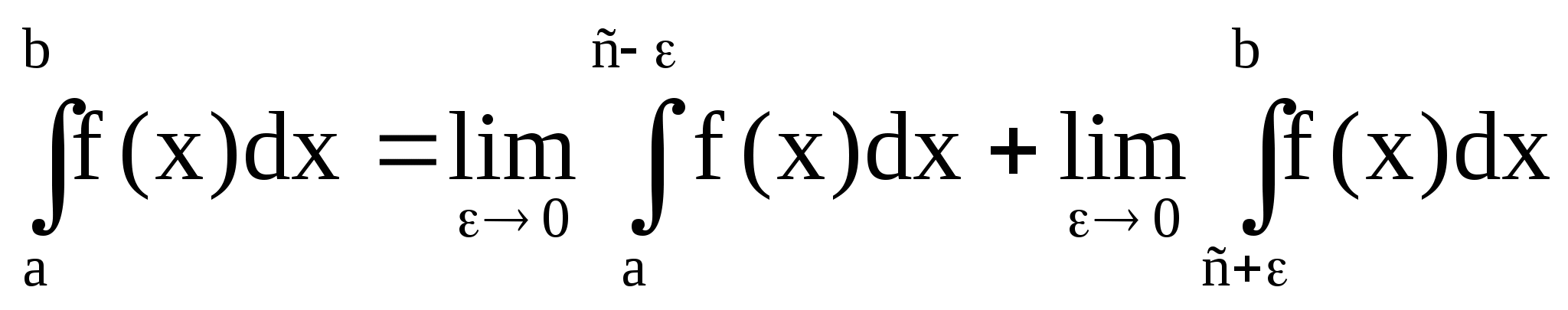 - называется
несобственным интегралом второго рода.
- называется
несобственным интегралом второго рода.
Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенств.
Если пределы бесконечны или не существуют, то говорят, что соответствующий несобственный интеграл расходится.
Пример 4. Найти
1) ![]() ; 5)
; 5) ![]() ;
;
2) ![]() ; 6)
; 6) ![]() ;
;
3) ![]() ; 7)
; 7) ![]() ;
;
4) ![]() ; 8)
; 8) ![]() .
.
Решение:1) непосредственным интегрированием получаем:
![]() ;
;
2) ![]() ,
,
заметим, что здесь и далее произвольные постоянные, входящие по определению, в
каждый из складываемых неопределенных интегралов, объединяются в одну произвольную постоянную;
3) вычислим данный неопределенный интеграл, используя формулу интегрирования заменой переменной (1)
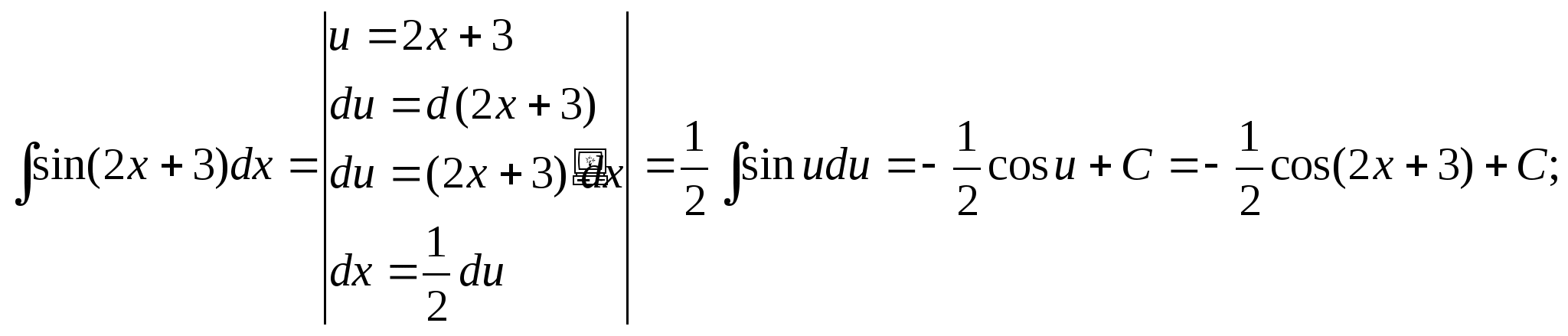
4) 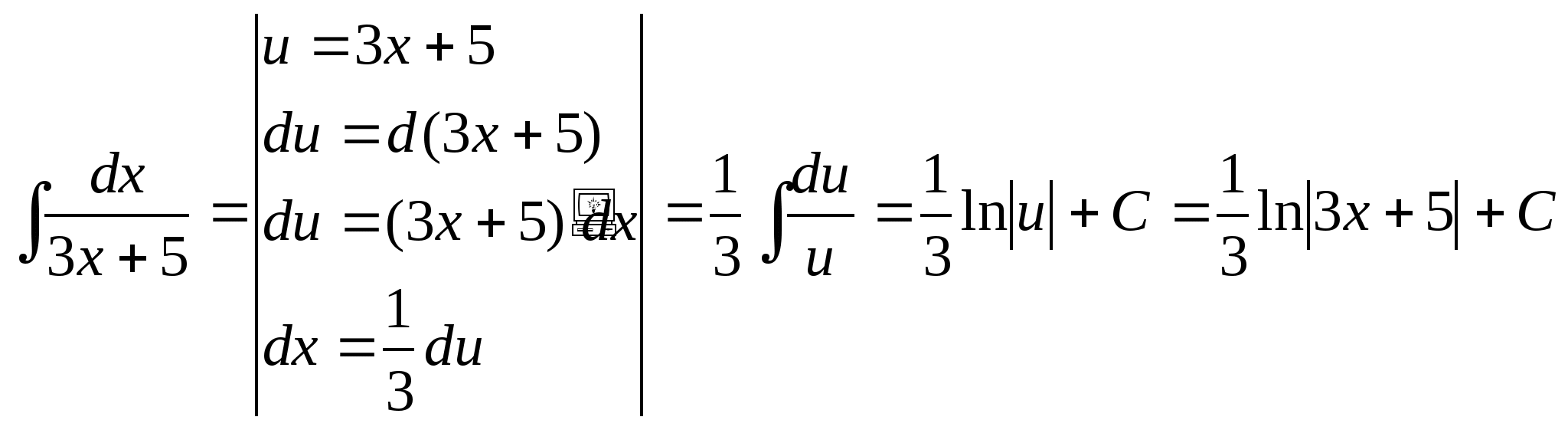 ;
;
5) ![]() .
.
Определенный интеграл вычислили при помощи формулы Ньютона-Лейбница (2).
6) ![]() ,
,
следовательно, данный несобственный интеграл I-го рода расходится;
7) 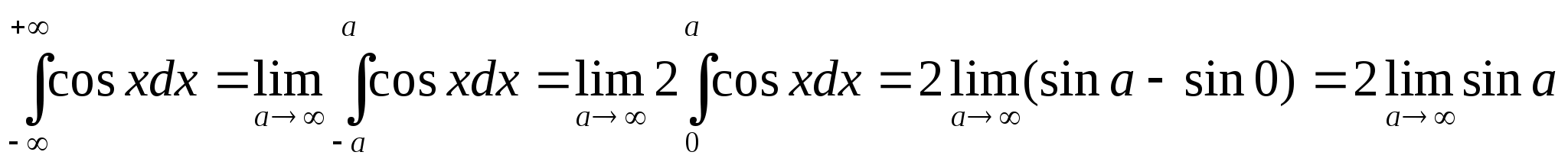 ,
,
т.е. несобственный интеграл первого рода расходится, так как при а последний предел не существует;
8)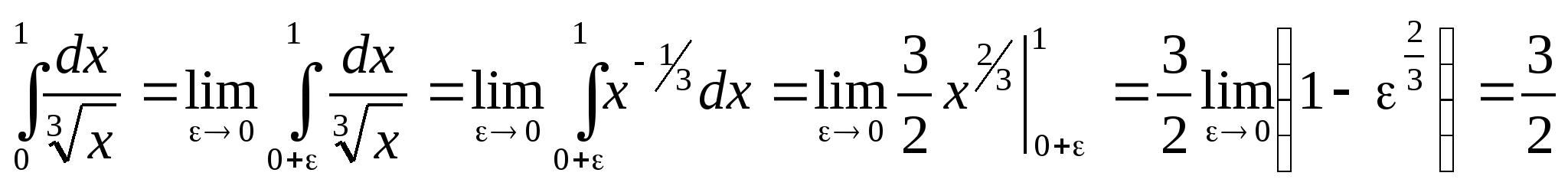 , таким
образом, несобственный интеграл второго рода от разрывной в точке
х=0 подынтегральной функции
, таким
образом, несобственный интеграл второго рода от разрывной в точке
х=0 подынтегральной функции ![]() сходится.
сходится.
Тема 3. Элементы комбинаторики
Комбинаторика - раздел математики, в котором изучаются задачи выбора элементов из заданного конечного множества и размещение этих элементов в каком - либо порядке.
Существуют три типа соединений: размещения, перестановки, сочетания.
Размещением из n элементов по m называется любое упорядоченное подмножество из m элементов множества, состоящего из n различных элементов.
Заметим, что размещения отличаются порядком входящих в них
элементов и их составом. Число размещений из n элементов по m равно
![]() .
.
Факториалом целого положительного числа n называют
произведение 123…(n-1)n, т.е. n!= 123…(n-1)n. Например:
8!=12345678 или 8!=7!8 или 8!=6!78. Верно, что 0!=1;
1!=1; (n+1)!=n!(n+1); (n-1)!=![]()
Размещения из n элементов по n элементов называется перестановками из n элементов. Число перестановок из n элементов равно Рn=n!.
Сочетаниями из n элементов по m элементов
называют подмножества, содержащие m элементов. Число сочетаний из n
элементов по m равно ![]() .
.
Размещение с повторениями из данных n элементов по
m называются всевозможные комбинации, содержащие m элементов. Число
размещений с повторениями из n элементов по m равно ![]() .
.
Правило сложения. Если выбор каждого из объектов
аi, i=![]() можно выполнить
ni способами, то выбор или «а1, или
а2 или а3,…, или
ак» можно произвести
n=n1+n2+n3+...+nk
способами.
можно выполнить
ni способами, то выбор или «а1, или
а2 или а3,…, или
ак» можно произвести
n=n1+n2+n3+...+nk
способами.
Правило умножения. Если выбор каждого из к объектов
аi, i=![]() можно
осуществлять niспособами, то выбор « и а1 и
а2 и а3, …,и ак» можно произвести
n=n1n2n3...nk
способами.
можно
осуществлять niспособами, то выбор « и а1 и
а2 и а3, …,и ак» можно произвести
n=n1n2n3...nk
способами.
Пример 1. Сколько существует способов отбора из 4 членов правления фирмы двух для замещения вакансий вице-президентов, отвечающих соответственно за производство, финансы.
Решение: Порядок при таком выборе играет существенную роль,
тогда число вариантов равно ![]() .
.
Пример 2. Сколько существует способов расстановки пяти различных учебников в один ряд?
Решение: Так как порядок учебников по условию - значения не имеет, то получим задачу о числе перестановок пяти различных книг. Следовательно, Р5=5!=12345=120.
Пример 3: В учебной группе 12 студентов. Сколько можно получить бригад по 5 человек?
Решение. Так как не имеет значение, какой студент будет первым,
а какой - вторым, число способов формирования бригад будем
вычислять с помощью ![]() по
формуле
по
формуле ![]() .
.
Пример 4: Бросаются две игральные кости. Найти общее число всевозможных результатов опыта.
Решение: При подбрасывании двух игральных костей общее число
результата опыта вычисляется по формуле размещения с повторением
![]() .
.
Пример 5: В группе 30 курсантов. Сколько существует способов выбора командира и его заместителя?
Решение: По условию задачи каждый курсант может быть выбран командиром, следовательно, существует 30 вариантов. Его заместителем может стать любой из оставшихся 29 курсантов. Таким образом, любой из 30 вариантов осуществляется вместе с любым из 29 вариантов выбора его заместителя. Следовательно, существует 3029=870 вариантов выбора командира и его заместителя (Правило умножения).
Пример 6: В группе 20 юношей и 10 девушек. Сколько существует способов формирования группы из трех юношей и двух девушек для участия в научной конференции.
Решение: Количество способов избрания трех юношей и двух девушек
равно произведению ![]()
![]() , где
, где ![]() - количество способов
выбора трех юношей из двадцати,
- количество способов
выбора трех юношей из двадцати, ![]() -количество способов
выбора двух девушек из десяти. Тогда
-количество способов
выбора двух девушек из десяти. Тогда ![]() - количество способов
выбора делегации из трех юношей и дух девушек.
- количество способов
выбора делегации из трех юношей и дух девушек.
Тема 4. Элементы теории вероятностей
4.1. Случайные события
В результате многократного повторения одних и тех же условий, которые носят название испытаний или опытов, можно наблюдать появление или не появление в них некоторого события. Такое событие, которое может произойти или не произойти в результате опыта, называется случайным.
Количественной мерой возможности появления некоторого случайного события А служит вероятность.
Вероятностью события А называется отношение числа благоприятных элементарных исходов к числу всех возможных исключающих друг друга исходов
Р(А)=![]() .
.
Здесь А - событие, n- число всех возможных исходов, m число благоприятных исходов событию А; Р(А) - вероятность события А .
Число ![]() называется
относительной частотой, где N(A) - число случаев наступления
события (частота); N - общее число испытаний (статистическое
определение вероятности).
называется
относительной частотой, где N(A) - число случаев наступления
события (частота); N - общее число испытаний (статистическое
определение вероятности).
Основные свойства вероятностей
1) 0Р(А)1;
2) P(U)=1, где U - достоверное событие;
3) Р(А+В)=Р(А)+Р(В) - есть правило сложения вероятностей несовместимых событий;
4) Р(А1)+Р(А2)+…+Р(Аn)=1, если А1,А2,А3,…,Аn-образуют полную систему событий;
5) Р(![]() )=1-Р(А) - вероятность
противоположного события;
)=1-Р(А) - вероятность
противоположного события;
6) Р(![]() )=
)=![]() - условная
вероятность,(Р(А)0);
- условная
вероятность,(Р(А)0);
7) Общее правило умножения вероятностей
Р(АВ)=Р(А)Р(В)=Р(В)Р(![]() );
);
8) Умножение вероятностей независимых событий Р(АВ)=Р(А)Р(В);
9) Общее правило сложения вероятностей Р(А+В)=Р(А)+Р(В)-Р(АВ);
10) Формула полной вероятностей
Р(А)=Р(Н1)Р(А/Н1)+Р(Н2)Р(А/Н2)+…+Р(Нn)Р(А/Нn)=![]() , где
Н1,Н2,…,Нn - попарно несовместные
события, причем событие А может осуществляться только с одним из
них;
, где
Н1,Н2,…,Нn - попарно несовместные
события, причем событие А может осуществляться только с одним из
них;
11) Формула вероятностей гипотез (формула Бейеса)
Р(Нi/A)=![]() .
.
4.2. Случайные величины
Действительная функция ![]() определенная на
пространстве элементарных исходов называется случайной величиной
(с.в.).
определенная на
пространстве элементарных исходов называется случайной величиной
(с.в.).
Функция распределения случайной величины
![]() определяется равенством
F(x)=
определяется равенством
F(x)=![]() .
.
Случайная величина множество значений которой конечно или счетно, называется дискретной.
Случайная величина называется непрерывной, если
существует неотрицательная функция f(x), такая, что для любого
действительного х функция распределения с.в. ![]() может быть представлена
в виде F(x)=
может быть представлена
в виде F(x)=![]() , при
этом f(x) называют плотностью распределения вероятностей.
, при
этом f(x) называют плотностью распределения вероятностей.
Таблица вида
х1
х2
…
р
р1
р2
…
![]() , где
x1,x2,… возможные значения случайной
величины, а р1,р2,…-вероятности этих значений
(т.е.
, где
x1,x2,… возможные значения случайной
величины, а р1,р2,…-вероятности этих значений
(т.е. ![]() ), называется рядом
распределения с.в..
), называется рядом
распределения с.в..
Справедливы свойства:
1) ![]() ; 2)
F(x) не убывает; 3)
; 2)
F(x) не убывает; 3) ![]() .
.
Математическим ожиданием дискретной с.в.
![]() , называется
число
, называется
число![]() . Математическое
ожидание непрерывной с.в.
. Математическое
ожидание непрерывной с.в. ![]() определяется равенством
определяется равенством ![]() ; здесь
f(x) плотность распределения вероятности.
; здесь
f(x) плотность распределения вероятности.
Свойства математического ожидания
1. М(С)=С, где С постоянная.
2. М(С)=СМ().
3. М(+µ)=М()+М(µ) для любых с.в. и µ.
4. М(µ)=М()М(µ) для независимых с.в. и µ.
Дисперсия дискретной случайной величины
![]() равна
D()=М(-а)2=М(2)-а2,
(М()=а),а непрерывной D
равна
D()=М(-а)2=М(2)-а2,
(М()=а),а непрерывной D![]() .
.
()=![]() -
среднее квадратическое отклонение.
-
среднее квадратическое отклонение.
Свойства дисперсии
1. D(С)=0.
2. D(С)=С2D().
3. D(+µ)=D()+D(µ) для независимых с.в. и µ.
4.Начальный момент к-го порядка ![]() .
.
5.Центральный момент к-го порядка ![]() ,где М()=а.
,где М()=а.
6.Коэффициент вариации ![]() .
.
7.Коэффициент асимметрии ![]() .
.
Дискретная с.в. ![]() , принимающая целые
неотрицательные значения
, принимающая целые
неотрицательные значения
к=0, 1, 2,…,n, имеет биномиальное распределение с параметрами (n,p) если
Р(=к)=![]() , где
q=1-p,
, где
q=1-p, ![]() .М()=np, D()=npq,
()=
.М()=np, D()=npq,
()=![]() .
.
Дискретная с.в. принимающая целые неотрицательные
значения к=0,1,2,… имеет распределение Пуассона с параметром
![]() , если Р(=к)=
, если Р(=к)=![]() ,(к=0,1,2,…), где
М()=, D()=,
,(к=0,1,2,…), где
М()=, D()=,![]() .
.
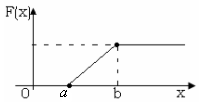
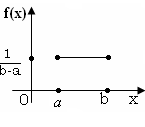
С.в. имеет равномерное распределение на отрезке [а,b], если она
имеет плотность распределения вероятности 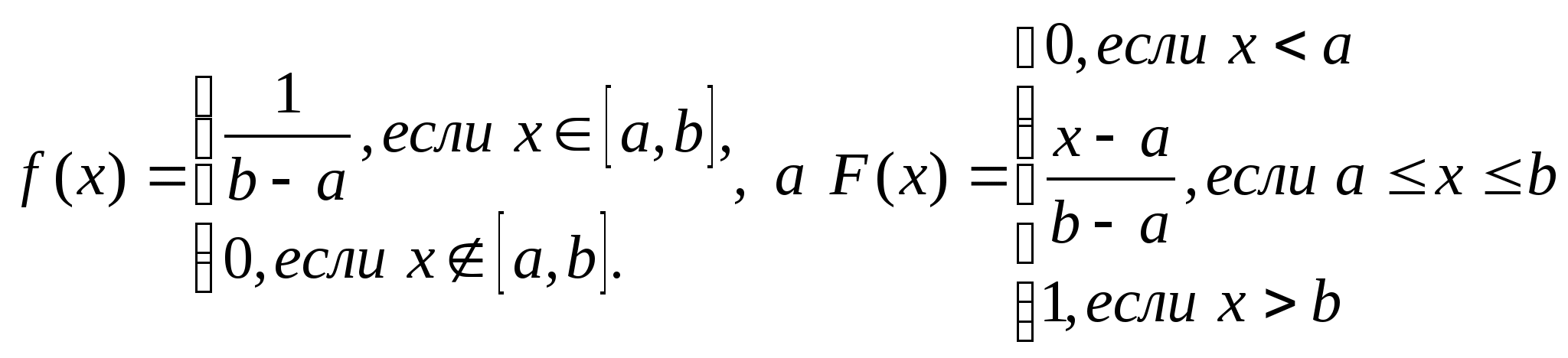 .
.
![]() .
.
С.в. имеет показательное распределение
(экспоненциональное) с параметром >0, если она имеет плотность
распределения вероятности 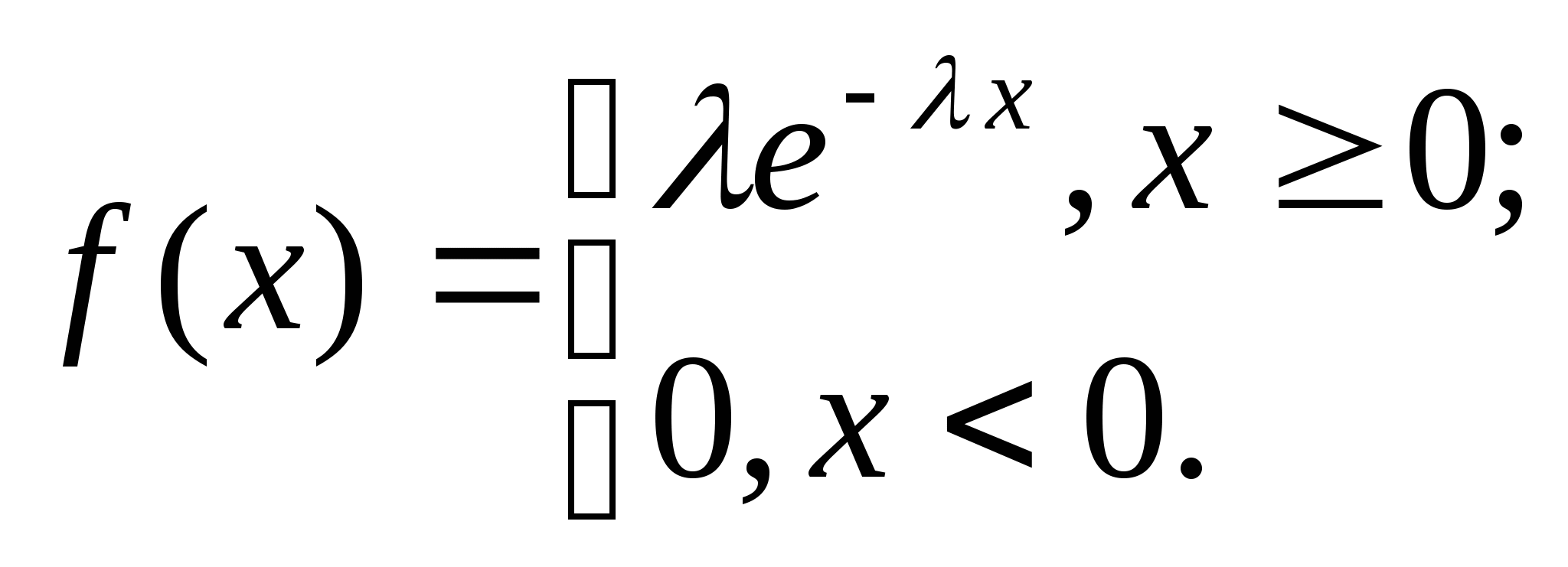 .
Тогда функция распределения с.в. F(x)=
.
Тогда функция распределения с.в. F(x)=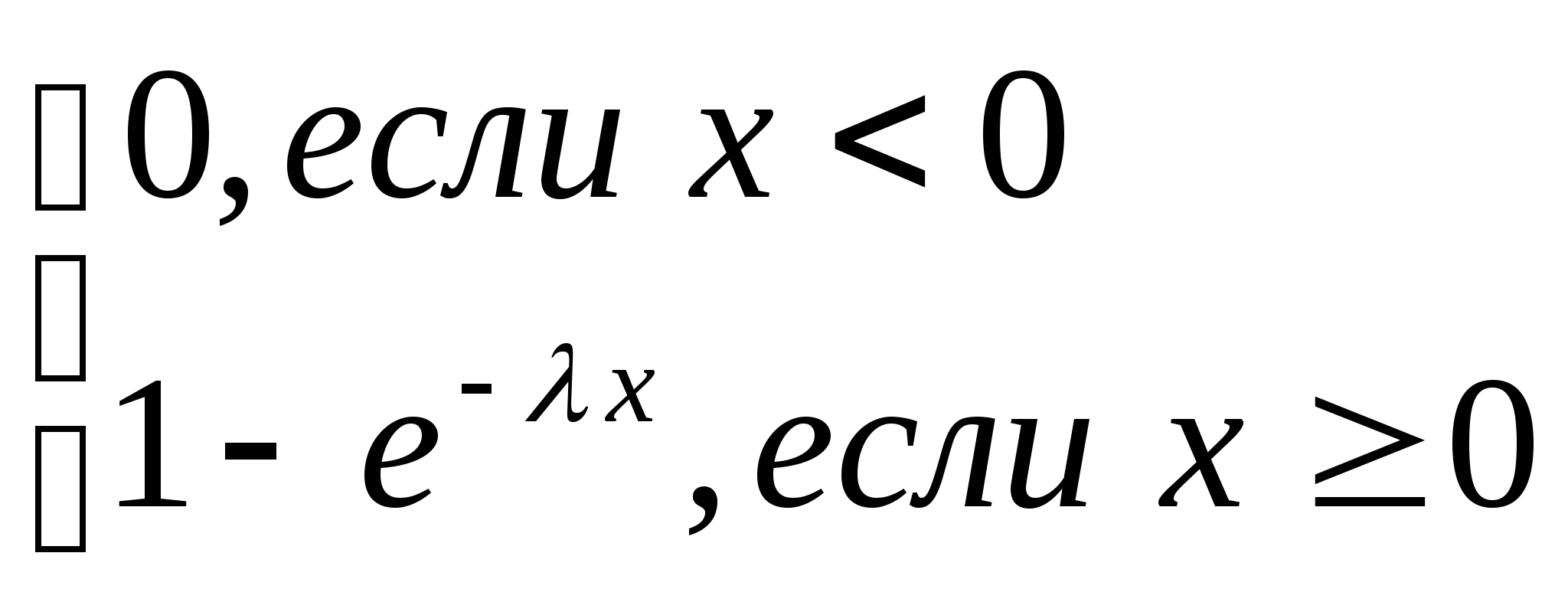 .
. ![]() .
.
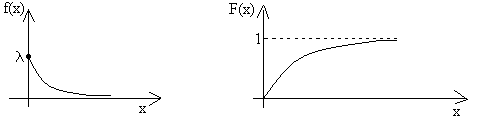
Показательное распределение часто используется в
теории надежности. Обозначим через ![]() - время безотказной
работы некоторого устройства, а через - интенсивность отказов
(среднее число отказов в единицу времени), тогда среднее время
между соседними отказами равно
- время безотказной
работы некоторого устройства, а через - интенсивность отказов
(среднее число отказов в единицу времени), тогда среднее время
между соседними отказами равно ![]() . Функция распределения
. Функция распределения
![]() определяет вероятность
отказа устройства за время t.
определяет вероятность
отказа устройства за время t.
Функцией надежности R(t) называют функцию ![]() , определяющую
вероятность безотказной работы устройства за время t.
, определяющую
вероятность безотказной работы устройства за время t.
С.в. имеет нормальное (гауссовское) распределение
c параметрами a,2( N(a,2) ![]() ), если она имеет
плотность вероятности
), если она имеет
плотность вероятности 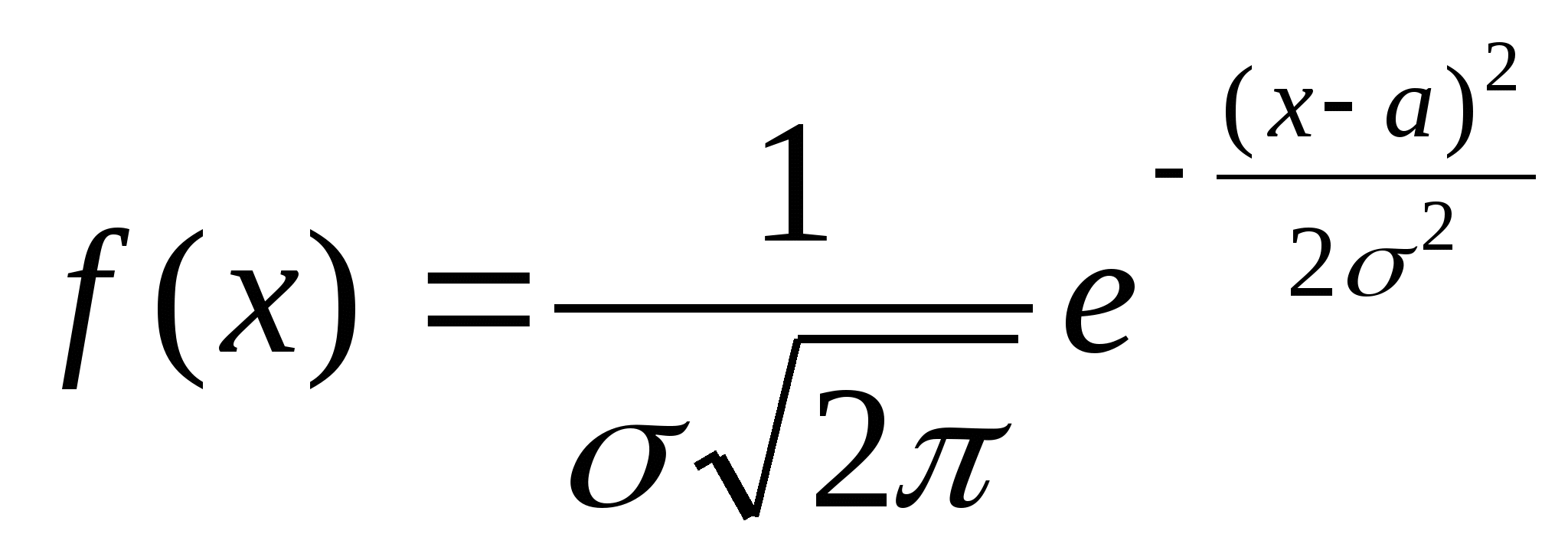 .
.
Плотность нормально распределенной случайной величины можно записать в виде
![]() ,где (х)
=
,где (х)
=![]() - четная функция.
- четная функция.
Функция распределения нормально распределенной случайной величины имеет вид:
![]() , где
Ф(х)=
, где
Ф(х)=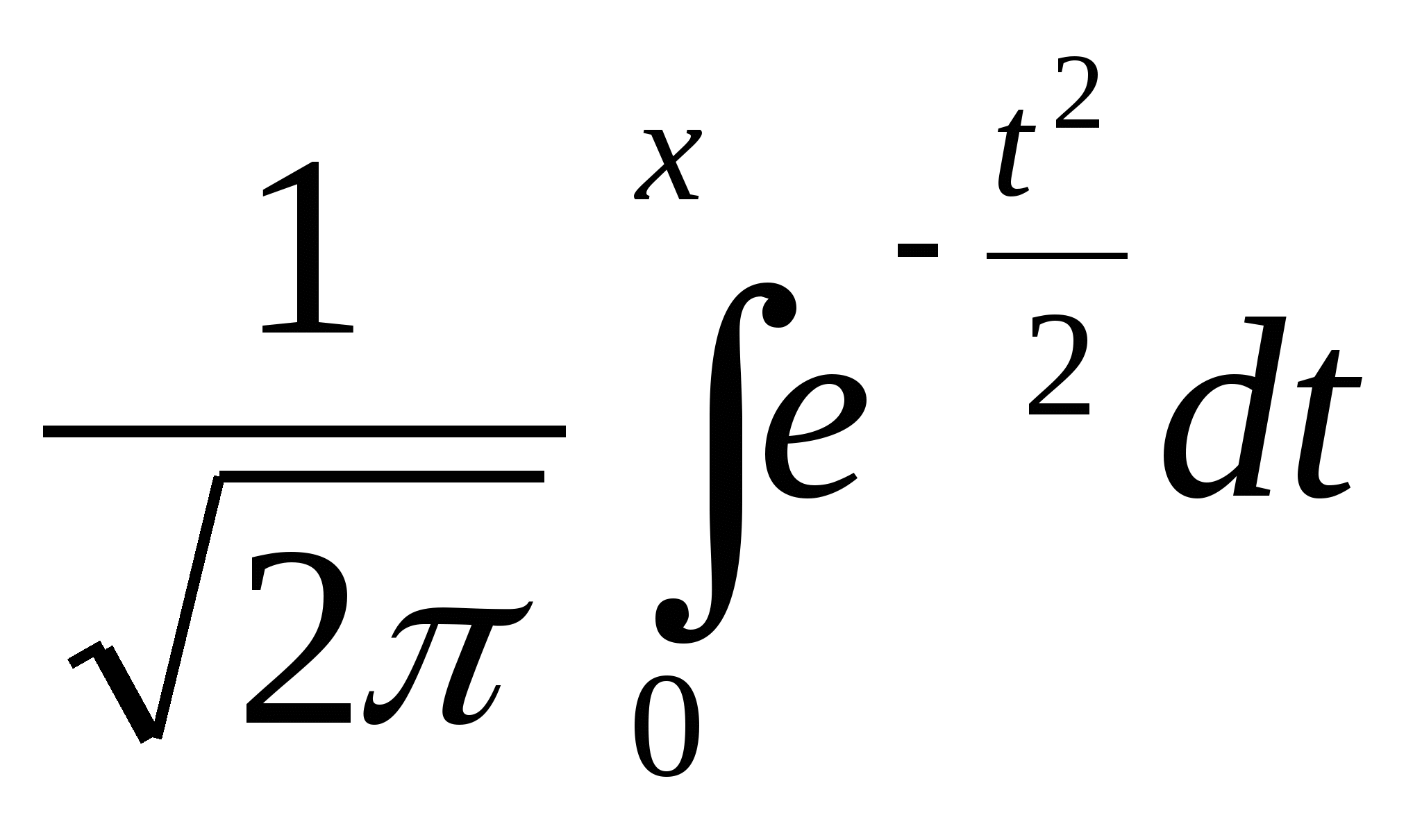 - функция Лапласа.
М(х)=а, D(x)=2, (х)=, m0=a
- функция Лапласа.
М(х)=а, D(x)=2, (х)=, m0=a
Вероятность попадания на промежуток нормально
распределенной случайной величины х:![]() ,
, ![]() .
.
Пример1. Студент знает 15 вопросов из 30. Наудачу ему задается вопрос. Найти вероятность того, что он его знает.
Решение: Данная задача на применение классического
определения вероятности. Обозначим событием А={студент знает
предложенный вопрос . Ясно, что все исходы опыта равновозможны и их
конечное число. Тогда m=15 - число исходов благоприятствующих
событию А, n=30 - общее число исходов. По классическому определению
вероятности Р(А)=![]() .
.
Пример 2. Стрелок произвел 100 выстрелов по мишени, причем поразил мишень в 25 случаях. Найти вероятность того, что стрелок поразил мишень .
Решение: А{стрелок поразил мишень при одном выстреле}. Применим статистическое определение вероятности и вычислим относительную частоту события А.
![]() , где N(A)=25 -
число опытов в которых А произошло, N=100 - общее число опытов.
, где N(A)=25 -
число опытов в которых А произошло, N=100 - общее число опытов.
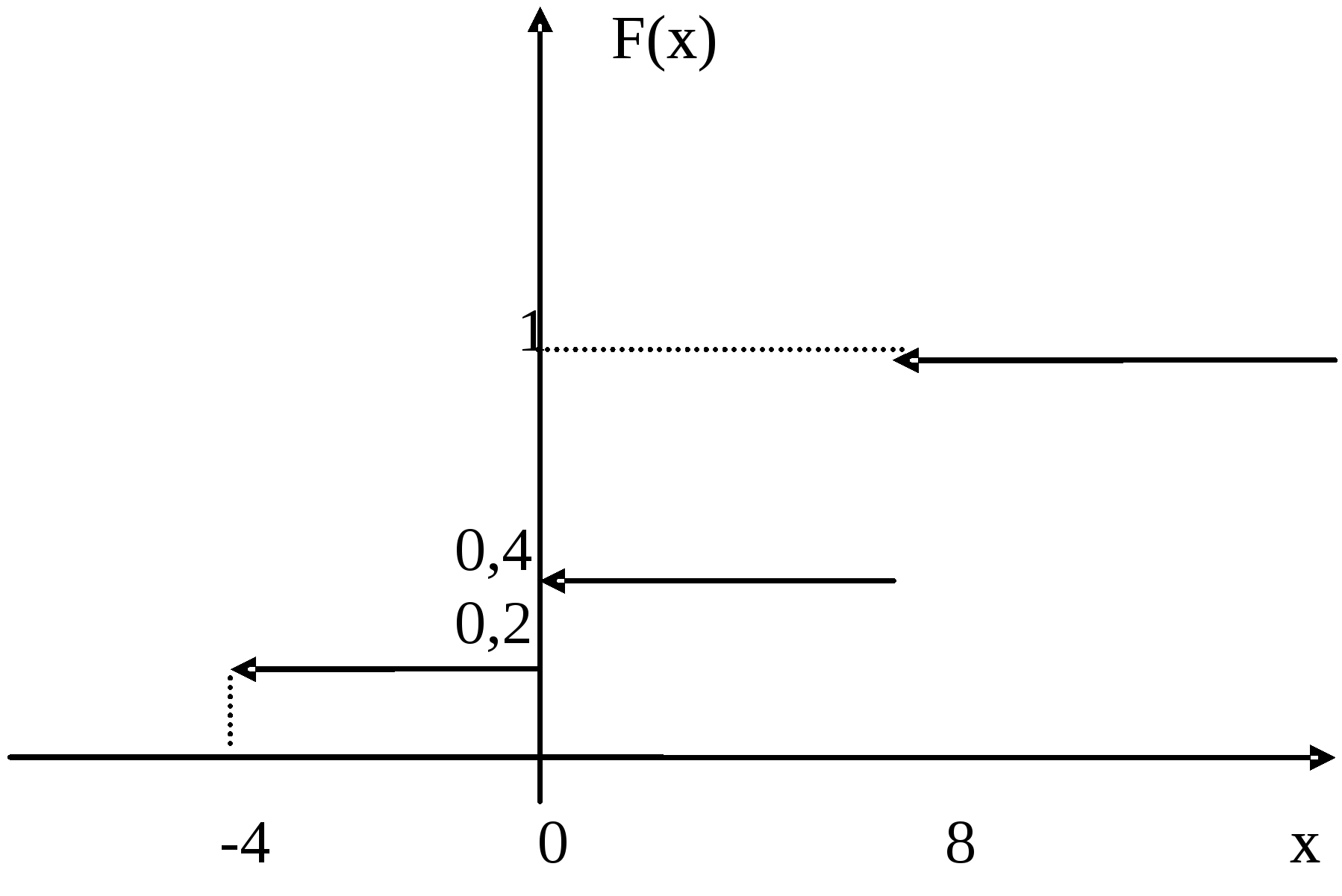
Пример 3. Построить функцию распределения. Найти
математическое ожидание, дисперсию, среднее квадратическое
отклонение и другие числовые характеристики для дискретной
случайной величины .
-4
0
8
Р
0,2
р
0,6
Решение: р=1-(0,2+0,6)=0,2. Построим график функции распределении рассматривая различные промежутки изменения аргумента Х,
1)если х-4, то F(x)=P(X<-1)=0;
2) если-4 <х0, то F(x)=P(X<0)=P(X=-4)=0,2;
3) если0 <х8, то F(x)=P(X<8)=P(X=-4)+P(X=0)=0,4;
4) если8 <х, то F(x)=P(X<x)=P(X=-4)+P(X=0)+P(X=8)=1.
М(х)=-40,2+00,2+80,6=4.
D(х)=M(х2
)-(M(х))2=(-4)20,2+020,2+820,6-(4)2=25,6.
Среднее квадратическое отклонение ![]() . Коэффициент вариации
. Коэффициент вариации
![]() . Мода(Х)=8,
т.к. 8 имеет наибольшую вероятность, равную 0,6. Коэффициент
асимметрии
. Мода(Х)=8,
т.к. 8 имеет наибольшую вероятность, равную 0,6. Коэффициент
асимметрии
![]() .
.
Пример 4. С.в. Х имеет нормальное распределение с параметрами а=150, 2=36
а) найти числовые характеристики с.в. Х;б) найти границы за которые практически не выходит с.в. Х; в) выпишите плотность с.в. Х и изобразите эскиз графика плотности;
г) вычислить Р(135
Решение:
г) Р(135=
![]() .
.
Здесь Ф()-функция Лапласа, Отметим свойство функции Ф(х):Ф(-х)=-Ф(х),поэтому Ф(-2,5)=- Ф(2,5)=-0,49379.
Глава 2. Самостоятельная работа
Задание 1. Заданы два множества: А и
В. Определить множества ![]() .
.
Задание 2. По данным промежуткам А и В на числовой прямой определить
![]() .
.
-
Найти предел функции
 при различных
значениях а.
при различных
значениях а.
Задание 6. Вычислить неопределенный, определенный и несобственный интегралы.
Задание 7. Вычислить вероятность события.
-
В ящике находится 60 красных и 30 белых шаров. Наудачу извлекается один шар. Какова вероятность, что он а) красный б) белый.
-
Брошена стандартная игральная кость. Какова вероятность того, что выпадет а) три; б) меньше трех.
-
Случайным образом выбирается число из множества 1,2,3,4,5,6,7,8. Какова вероятность, что а) оно четно; б) четное и делится на 4.
-
Студент знает 15 вопросов из 25. Какова вероятность того, что предложенный вопрос студент а) знает б) не знает.
-
Монета подбрасывается дважды. Построить множество элементарных исходов. Рассчитать вероятность того, что хотя бы один раз выпадет "герб".
-
Из колоды в 36 карт случайным образом достается одна. Какова вероятность того, что а) эта "картинка"; б) дама черви или король черви.
-
Из слова "математика" наугад выбирается одна буква. Какова вероятность, что это будет а) буква "М"; б) гласная буква
-
В лотерее 1000 билетов, из них на 1 билет, попадает выигрыш 500 руб., на 10 билетов по 50 руб. и на 60 билетов по 10 руб. Некто покупает 1 билет. Какова вероятность, что он выиграет а) 50 рублей; б) не менее 50 рублей.
-
Некто, набирая номер телефона, забыл последнюю цифру. Какова вероятность, что набирая ее случайным образом, он правильно наберет номер.
-
Подбрасывают три монеты. Найти вероятность того, что выпадет не более двух гербов.
-
Для определения доли бракованных изделий были взяты случайным образом 200 изделий. При проверке оказалось, что среди них 5 бракованных. Какова вероятность, что произведенная деталь является а) бракованной б) стандартной.
-
Обследование показало, что из 1000 зашедших в магазин потенциальных покупателей, действительно приобрело товар 190. Какова вероятность того, что зашедший в магазин человек а) приобретет товар б) не приобретет товар.
-
Стрелок произвел 100 выстрелов по мишени, причем поразил мишень 57 раз. Какова вероятность, что стрелок поразит мишень.
-
Из 500 телевизоров 490 проработало без поломок 10 000 часов и более. Какова вероятность, что произведенный по данной технологии телевизор проработает не менее 10 000 часов без поломок.
-
За последние 100 дней курс доллара повышался 25 раз. Какова вероятность, что на следующих торгах курс доллара повысится.
-
Статистика показала, что из последних 1000 новорожденных 560-мальчики. Какова вероятность того, что следующий новорожденный будет мальчик.
-
Из 1000 случайно отобранных семей у 350 доходы были выше 1000 у.е. Какова вероятность, что отдельная семья имеет доход выше 1000 у.е.
-
При аттестации 100 сотрудников не аттестованными оказались 8. Какова вероятность пройти аттестацию у данной категории сотрудников.
-
Относительная частота появления бракованных изделий на автоматической срочной линии составляет 0,02. Сколько проверялось изделий, если известно, что бракованных было 8?
-
Из 1000 проверенных деталей оказалось, что 110 из них с дефектом. Какова вероятность, что приобретенный товар является с дефектом?
-
В ящике 15 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
-
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,7 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает хотя бы один сигнализатор.
-
Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,69, для второго 0,85, а для третьего 0, 7.Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
-
Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,85. Найти вероятность того, что из двух проверенных изделий только одно стандартное.
-
В ящике 10 деталей, среди которых шесть окрашенных. Сборщик наудачу извлекает четыре детали. Найти вероятность того, что все извлеченные детали окажутся окрашенными.
Задание 8. Построить функцию распределения. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение для дискретной случайной величины .
14)
Х
-2
0
 2
2
р
0,5
0,2
0,3
р
2/5
1/5
2/5
2)
Х
10
20
40
15)
Х
30
60
70
р
0,6
0,3
0,1
р
0,2
0,3
0,5
3)
Х
30
40
50
16)
Х
0,1
0,4
0,5
р
0,2
0,1
0,7
р
0,2
0,3
0,5
4)
Х
10
11
12
17)
Х
0,5
3
5
р
0,4
0,5
0,1
р
0,8
0,1
0,1
5)
Х
11
15
20
18)
Х
1
2
4
р
0,4
0,1
0,5
р
0,1
0,3
0,6
6)
Х
21
23
25
19)
Х
2
4
7
р
0,1
0,1
0,8
р
0,5
0,2
0,3
7)
Х
10
20
30
20)
Х
2
4
5
р
0,5
0,4
0,1
р
0,1
0,5
0,4
8)
Х
40
50
60
21)
Х
-4
0
4
р
0,2
0,3
0,5
р
0,1
0,3
0,6
13)
Х
1
3
5
р
0,7
0,1
0,2
Задание 9. Число преступлений за неделю можно считать случайной величиной Х, имеющей нормальное распределение с параметрами а, . Выписать функцию распределения и плотность распределения с.в. Х. Найти вероятность того, что на следующей неделе число преступлений будет в пределах от с до d если:
1. а=200,
 =0,5, с =199,
d=20. 14. а=520,
=0,5, с =199,
d=20. 14. а=520, =6, с =508, d=532.
=6, с =508, d=532.
2. а=50,
 =2, с =46,
d=54. 15. а=300,
=2, с =46,
d=54. 15. а=300, =5, с =290, d=310.
=5, с =290, d=310.
3. а=100,
 =2, с =96,
d=104. 16. а=730,
=2, с =96,
d=104. 16. а=730, =10, с =710,
d=750.
=10, с =710,
d=750.
4. а=300,
 =0,5, с =299,
d=301. 17. а=800,
=0,5, с =299,
d=301. 17. а=800, =50, с =700,
d=900.
=50, с =700,
d=900.
5. а=700,
 =20, с =660,
d=740. 18. а=770,
=20, с =660,
d=740. 18. а=770, =30, с =710,
d=830.
=30, с =710,
d=830.
6. а=300,
 =2, с =294,
d=304. 19. а=690,
=2, с =294,
d=304. 19. а=690, =5, с =680, d=700.
=5, с =680, d=700.
7. а=400,
 =0,5, с =399,
d=401. 20. а=930,
=0,5, с =399,
d=401. 20. а=930, =1,5, с =927,
d=933.
=1,5, с =927,
d=933.
8. а=630,
 =0,5, с =629,
d=631. 21. а=652,
=0,5, с =629,
d=631. 21. а=652, =5, с =642, d=662.
=5, с =642, d=662.
9. а=330,
 =3, с =324,
d=336. 22. а=358,
=3, с =324,
d=336. 22. а=358, =4, с =350, d=366.
=4, с =350, d=366.
10. а=530,
 =5, с =520,
d=540. 23. а=850,
=5, с =520,
d=540. 23. а=850, =5, с =840, d=860.
=5, с =840, d=860.
11. а=150,
 =0,5, с =149,
d=151. 24. а=780,
=0,5, с =149,
d=151. 24. а=780, =3, с =774, d=786.
=3, с =774, d=786.
12. а=460,
 =4, с =452,
d=468. 25. а=315,
=4, с =452,
d=468. 25. а=315, =15, с =285,
d=345.
=15, с =285,
d=345.
13. а=456,
 =9, с =438,
d=464.
=9, с =438,
d=464.
</ Литература
1. Богатов Д.Ф., Богатов Ф.Г. "Математика для юристов в вопросах и ответах"- М.: ПРИОР, 2001г.
2. Гмурман В.Е.. "Руководство к решению задач по теории вероятностей и математической статистике".- М.: Высшая школа, 1999г.
3. Грес П.В.. "Математика для гуманитариев". - М.: Юрайт, 2000г.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я.. "Высшая математика в упражнениях и задачах" ч. 1. 2. -М.: Высшая школа, 1996г.
5. Турецкий В.Я. . "Математика и информатика"- М.: ИНФРА, 2000г.
6. Высшая математика для экономистов. Под ред. Кремера Р.Ш - М.: Банки и биржи, ЮНИТИ, 2001 г.
35
-