- Учителю
- Разработка практического занятия для СПО по математике по теме Матрицы для 2 курса
Разработка практического занятия для СПО по математике по теме Матрицы для 2 курса
ФИНАНСЫ Практическое занятие № 1
Практическое занятие №1
Тема: Действия над матрицами, вычисление определителей
Цель: формировать навыки выполнения операций над матрицами: сложение, вычитание, умножение матрицы на число, произведение матриц; формировать умения находить определители матриц.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
План практического занятия.
-
Организационные моменты.
Приветствует обучающихся. Проверяет подготовленность к учебному занятию, организует внимание обучающихся. Обеспечивает благоприятный настрой.
-
Актуализация опорных знаний.
-
Проверка домашнего задания (Разбор нерешенных примеров).
-
Вопросы для закрепления теоретического материала к практическому занятию:
-
Понятие матрицы и ее элементы
-
Основные виды матриц
-
Понятие ранга матрицы, минора и определителя матрицы. Виды определителей и их свойства
-
Применение и значение матриц в практической деятельности
-
Практический этап.
Требования к выполнению практической работы:
-
Оформить задания в тетради для практических работ.
-
Выполнить индивидуальную работу по варианту.
-
Ответить на один контрольный теоретический вопрос по варианту.
Содержание практической работы.
-
Выполнение заданий совместно с преподавателем.
Упражнения к практическому занятию:
-
Даны матрицы:
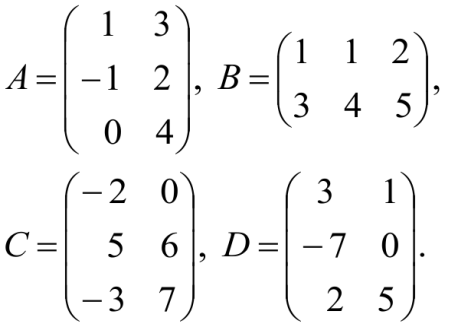
Можно ли сложить матрицу А: с матрицей В; с матрицей С; с матрицей D?
Решение:
Матрицу А нельзя сложить с матрицей В, так как матрица А имеет
размеры ![]() , матрица В - размеры
, матрица В - размеры ![]() , а складывать можно только матрицы одинаковых размеров. Матрицы А
и С имеют одинаковые размеры, поэтому их можно складывать.
, а складывать можно только матрицы одинаковых размеров. Матрицы А
и С имеют одинаковые размеры, поэтому их можно складывать.
Матрицы А и D имеют одинаковые размеры, следовательно, их можно
складывать.
-
Найти А+В , если
![]()
Решение:
![]()
Так как матрицы имеют одинаковый размер, то их можно складывать. При сложении матриц надо сложить элементы, стоящие на одинаковых местах, т.е.
![]()
-
Дано:
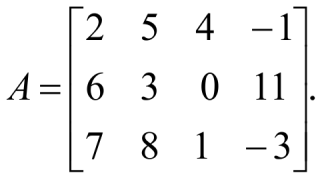
Найти: -3A.
Решение:
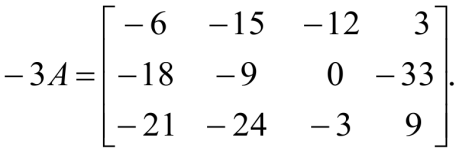
Для того, чтобы -3 умножить на матрицу A нужно каждый элемент матрицы A умножить на -3.
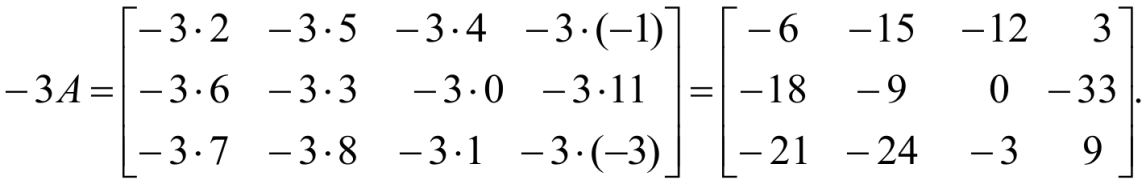
-
Даны матрицы:
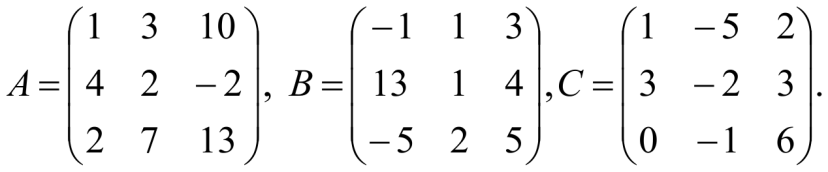
Найти: 2A+В-3С.
Решение:
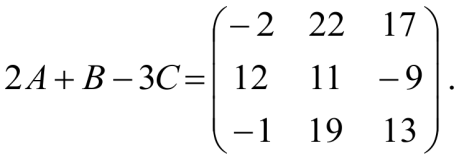
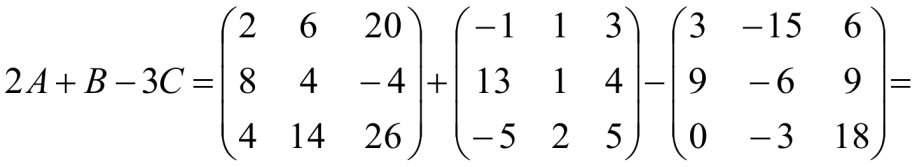
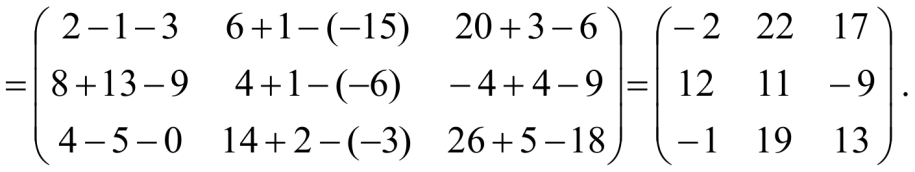
-
Найти матрицу Х, если:
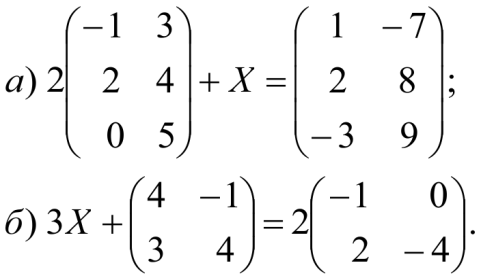
Решение:
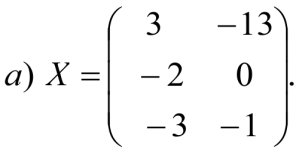
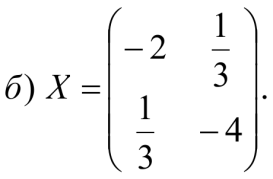
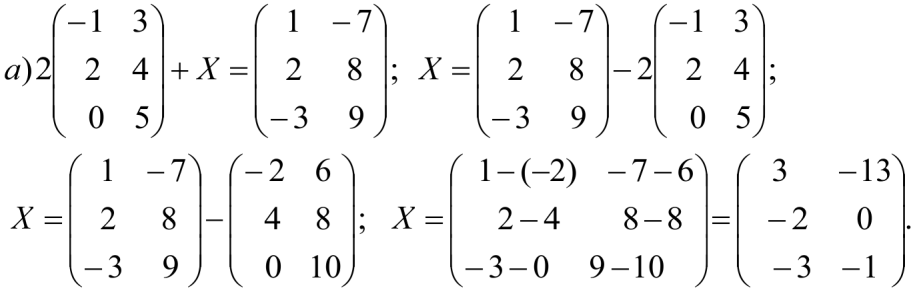
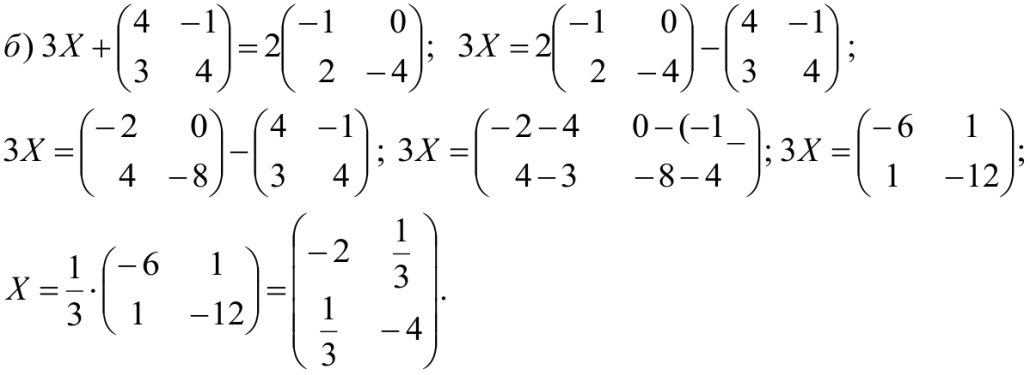
-
Матрицы А и В имеют вид
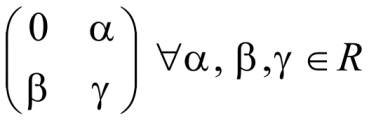
(знак![]() - любой, любые). Будет ли матрица А+В такого же вида?
- любой, любые). Будет ли матрица А+В такого же вида?
Решение:
Да. Так как в результате сложения матриц элемент ![]()
-
Матрицы А и В имеют вид
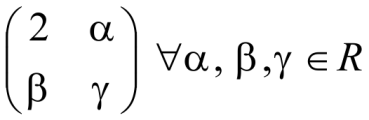
(знак![]() - любой, любые). Будет ли матрица А+В такого же вида?
- любой, любые). Будет ли матрица А+В такого же вида?
Решение:
Нет. Так как в результате сложения матриц элемент ![]()
-
Даны четыре матрицы:
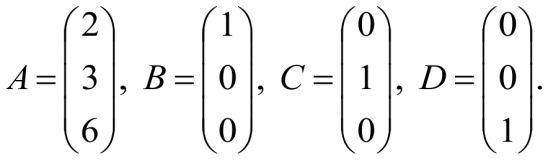
Подберите ![]() так, чтобы выполнялось равенство
так, чтобы выполнялось равенство![]()
Решение:
![]()
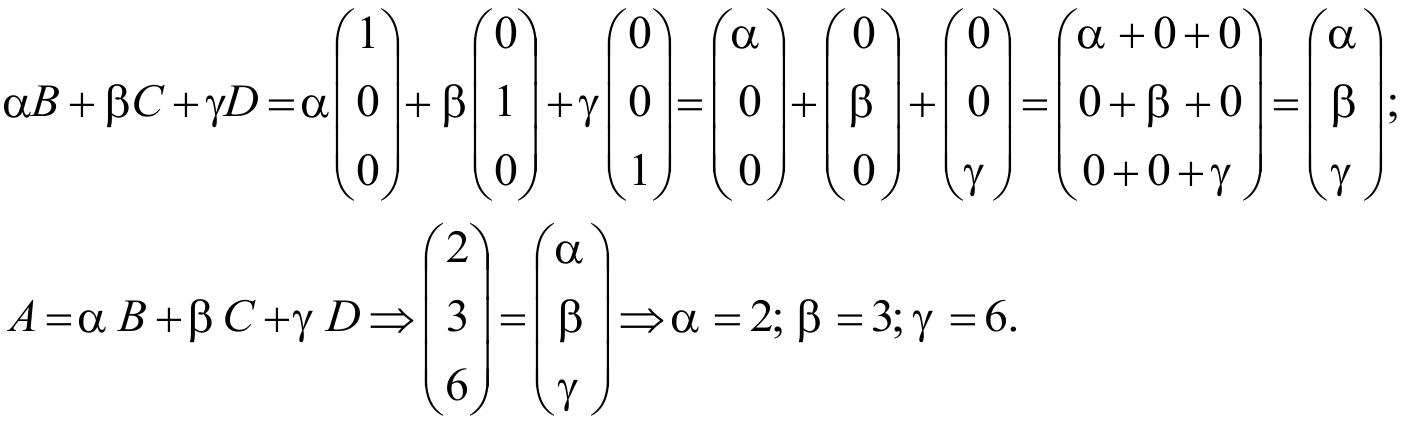
-
Даны матрицы:
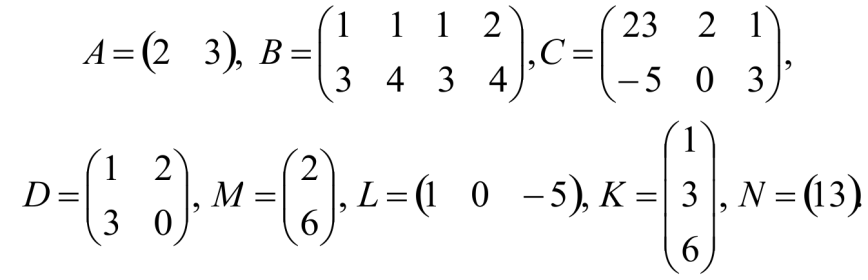
Определить размер матрицы-произведения матриц AB, CC, DM, NL, LK,
LM, DD.
Решение:
![]() не
существует, т.к. число столбцов первой матрицы не равно числу строк
второй матрицы;
не
существует, т.к. число столбцов первой матрицы не равно числу строк
второй матрицы; ![]()
![]() не
существует, т.к. число столбцов первой матрицы не равно числу строк
второй матрицы;
не
существует, т.к. число столбцов первой матрицы не равно числу строк
второй матрицы; ![]()
-
Дана матрица А размера
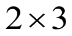 .
.
Какие из указанных действий можно выполнить над матрицей А:
![]()
Решение:
Операция произведение матрицы на число всегда выполнима, поэтому
![]() можно выполнить;
можно выполнить;
складывать можно матрицы одинаковых размеров,
следовательно,![]() можно
выполнить;
можно
выполнить;
матрицы можно умножать, если число столбцов первой матрицы равно
числу строк второй матрицы, поэтому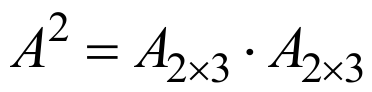 нельзя выполнить.
нельзя выполнить.
-
Найти a, b, c из уравнения
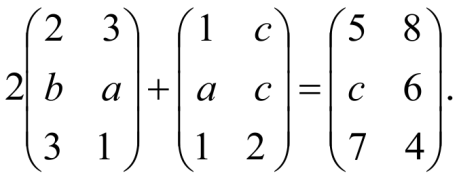
Решение:
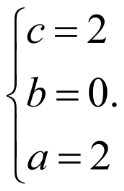
Учитывая определения операций сложения матриц и умножения матрицы на число, можно записать следующие равенства:
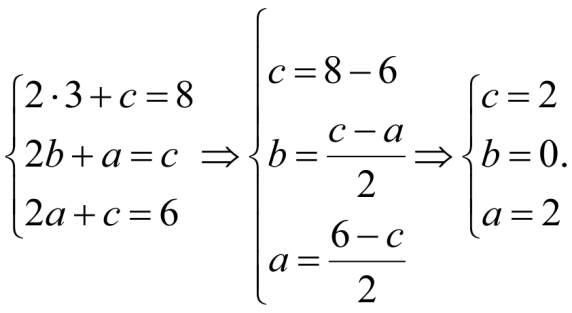
-
Выполнить действия:
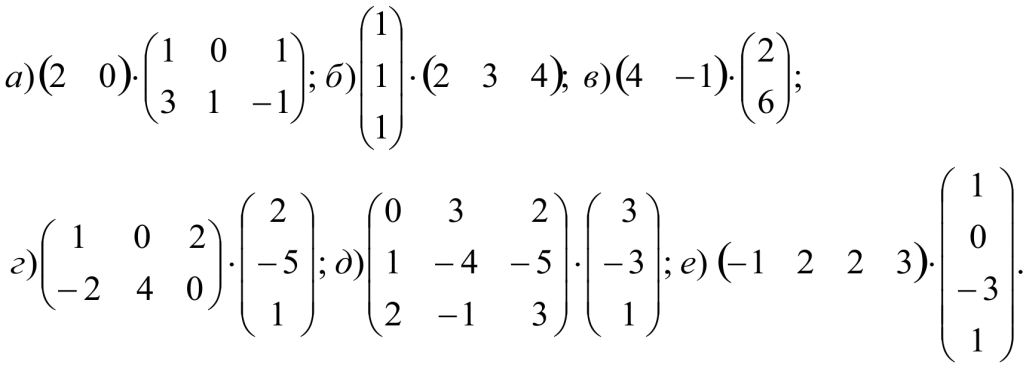
Решение:
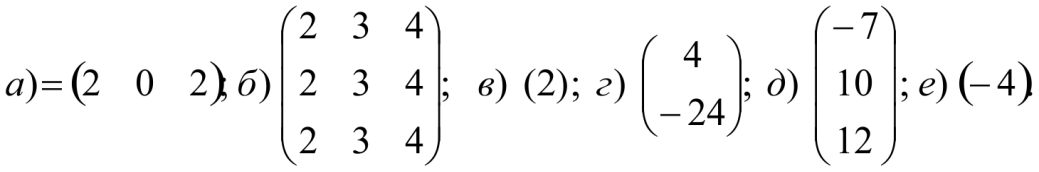
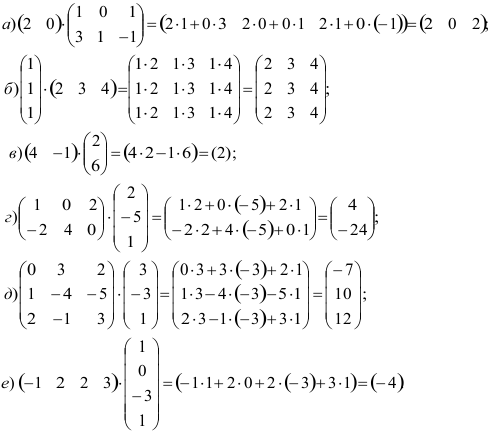
-
Известно, что
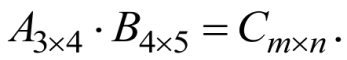 Найти m и n .
Найти m и n .
Решение:
По правилу умножения матриц: Матрица-произведение имеет строк
столько, сколько первая матрица, и столбцов - сколько вторая (пункт
два), следовательно, ![]()
-
Известно, что
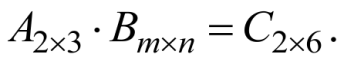 Найти m и n .
Найти m и n .
Решение:
По правилу умножения матриц
![]()
-
Известно, что
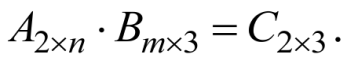 Найти m и n .
Найти m и n .
Решение:
По правилу умножения матриц ![]() (m, n - натуральные числа).
(m, n - натуральные числа).
-
Известно, что
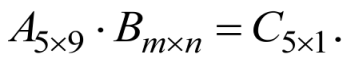 Найти m и n .
Найти m и n .
Решение:
По правилу умножения матриц
![]()
-
Известно, что
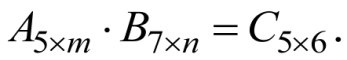 Найти m и n .
Найти m и n .
Решение:
По правилу умножения матриц
![]()
-
Найти матрицу
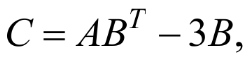 если
если
![]()
Решение:
![]()
Выполним по действиям:
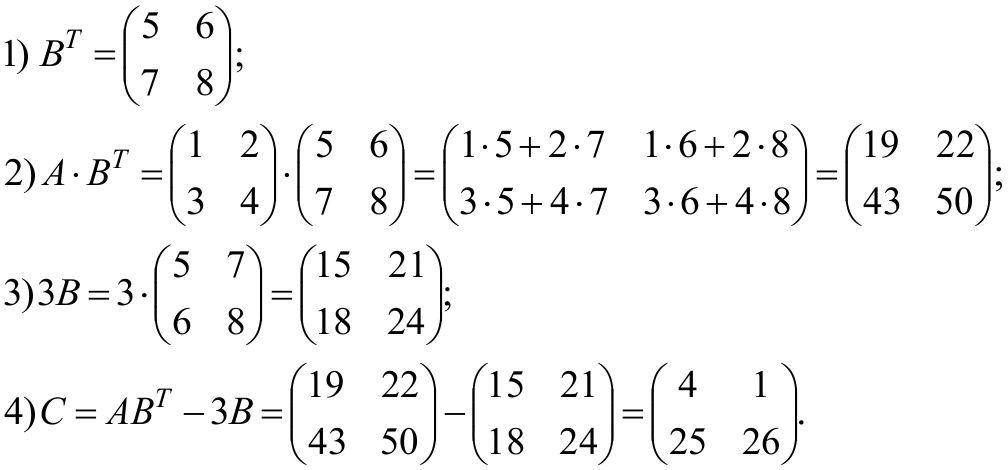
Выполнение заданий под руководством
преподавателя.
1.Вычислить произведение матриц:
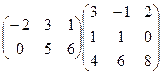 .
.
Решение. Первая матрица имеет размеры 2´3, а вторая размеры 3´3, поэтому произведение существует. В результате умножения получится матрица С = (cij) размеров 2´3. Вычислим ее элементы.
с11 = (-2)×3 + 3×1 + 1×4 = 1, с12 = (-2)×(-1) + 3×1 + 1×6 = 11,
с13 = (-2)×2+3×0+1×8 = 4, с21 = 0×3 + 5×1 + 6×4 = 29,
с22 = 0×(-1) + 5×1 + 6×6 = 41, с23 = 0×2+5×0+6×8 = 48.
Ответ: ![]() .
.
2.Вычислить произведение матриц:
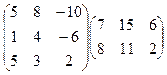 .
.
Решение. Первая матрица имеет размеры 3´3, а вторая размеры 2´3. Число столбцов в первой матрице (3) не совпадает с числом строк во второй матрице (2), поэтому произведение не существует,
Ответ: произведение не существует.
3.Вычислить произведение матриц:
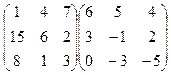 .
.
Ответ: 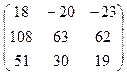 .
.
4.Вычислить произведение матриц:
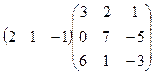 .
.
5.Вычислить произведение матриц:
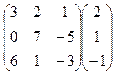 .
.
6.Вычислить произведение матриц:
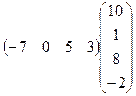 .
.
7.Вычислить произведение матриц:
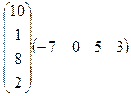 .
.
8.Вычислить произведение матриц:
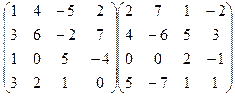 .
.
9.Вычислить степень матрицы:
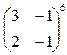 .
.
10. Вычислить степень матрицы:
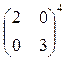 .
.
11. Вычислить значение многочлена f(x) = 2x2 + x - 3
от матрицы ![]() .
.
Указание. f(А) = 2А2 + А - 3Е, где Е - единичная матрица размеров 2´2. Далее использовать определения операций умножения матриц, умножения матрицы на число и сложения матриц.
Ответ: ![]() .
.
12. Вычислить значение многочлена f(x) = x3 - x2 + x + 2 от матрицы
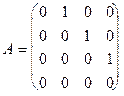 .
.
Ответ: 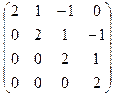 .
.
2. Самостоятельное выполнение заданий студентами.
-
Найдите сумму матриц и .
-
Транспонируйте матрицу . Укажите размеры данной и транспонированной матриц.
-
Даны матрицы: , . Произведите указанные действия, а в случае, когда это невозможно, указать причину: 1) ;
2) .
-
Даны матрицы и . Найдите матрицу .
-
Индивидуальная работа по вариантам.
Выполнить индивидуальную работу по теме «Действия с матрицами»
Задание. Выполнить указанные действия с матрицами А и В, если
Вариант №1
Вариант №2
Вариант №3
Вариант №4
Вариант №5
Вариант №6
Вариант №7
Вариант №8
Вариант №9
Вариант №10
Вариант №11
Вариант №12
Вариант №13
Вариант №14
Вариант №15
Вариант №16
Вариант №17
Вариант №18
Вариант №19
Вариант №20
Вариант №21
Вариант №22
Вариант №23
Вариант №24
Вариант №25
Вариант №26
Вариант №27
Вариант №28
Вариант №1
Вариант №2
Вариант №3
Вариант №4
Вариант №5
Вариант №6
Вариант №7
Вариант №8
Вариант №9
Вариант №10
Вариант №11
Вариант №12
Вариант №13
Вариант №14
Вариант №15
Вариант №16
Вариант №17
Вариант №18
Вариант №19
Вариант №20
Вариант №21
Вариант №22
Вариант №23
Вариант №24
Вариант №25
Вариант №26
Вариант №27
Вариант №28
-
Подведение итогов практического занятия.
Вопросы для самоконтроля:
-
Что называется матрицей? Запишите общий вид матрицы размером mxn.
-
Какие матрицы называются равными?
-
Назовите виды матриц.
-
Назовите линейные операции над матрицами.
-
Какие матрицы можно перемножать? Как выполняется умножение?
-
Домашнее задание.
Вычислить:
Дом. задание 1. Даны матрицы
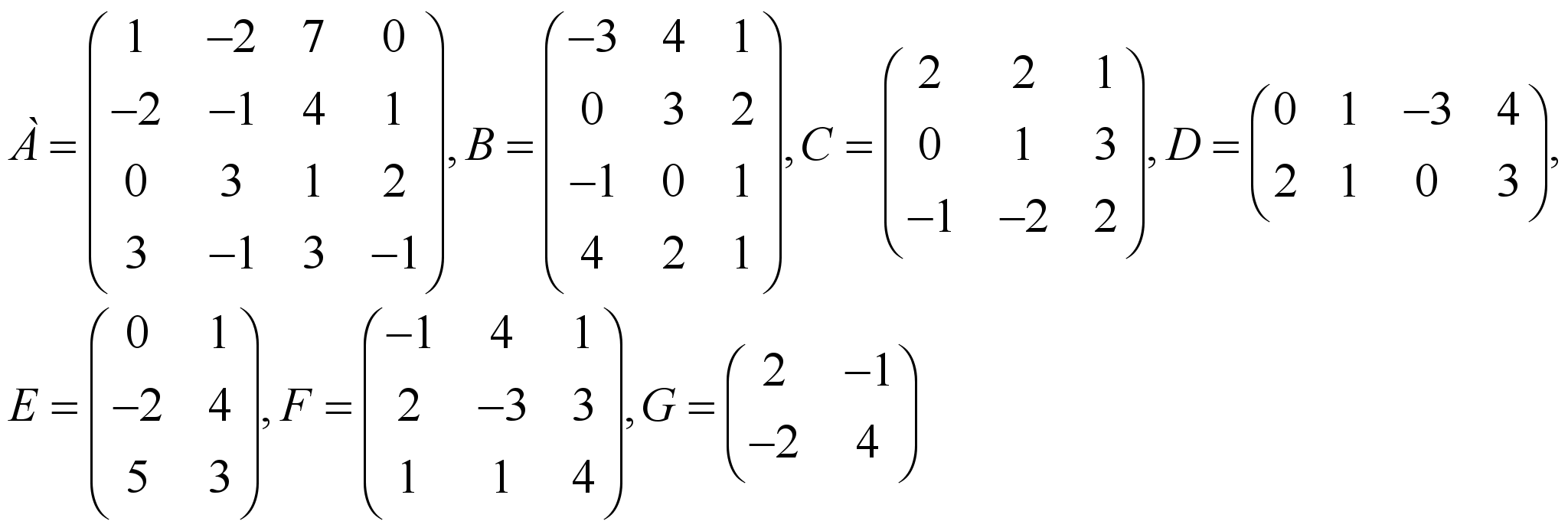
Найдите а) все произведения матриц, которые имеют смысл, б)
![]() в)
в) ![]() , г)
, г) ![]() .
.
Дом. задание 2. Вычислить ![]() .
.
Дом. задание 3. Вычислить 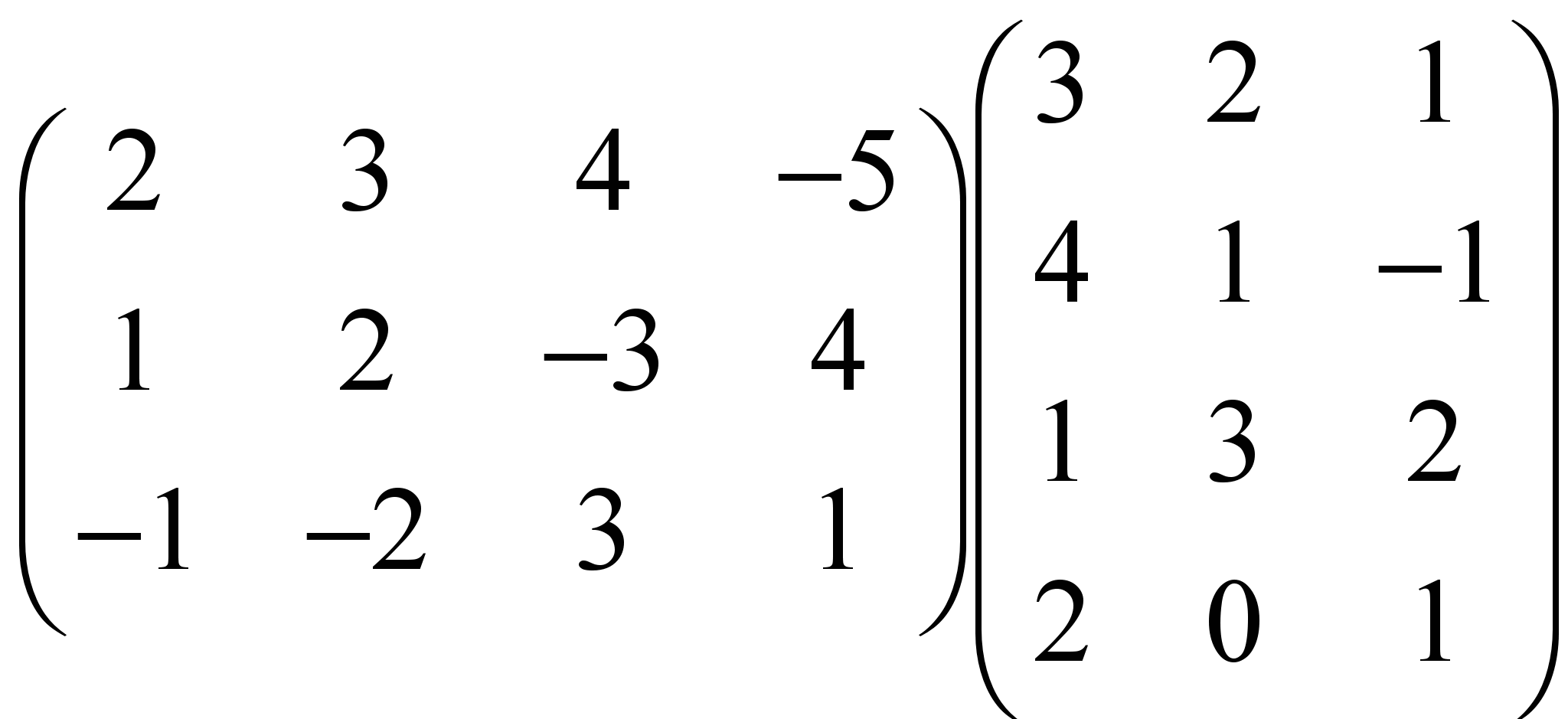 .
.
Дом. задание 4. Найдите произведение матриц
а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) 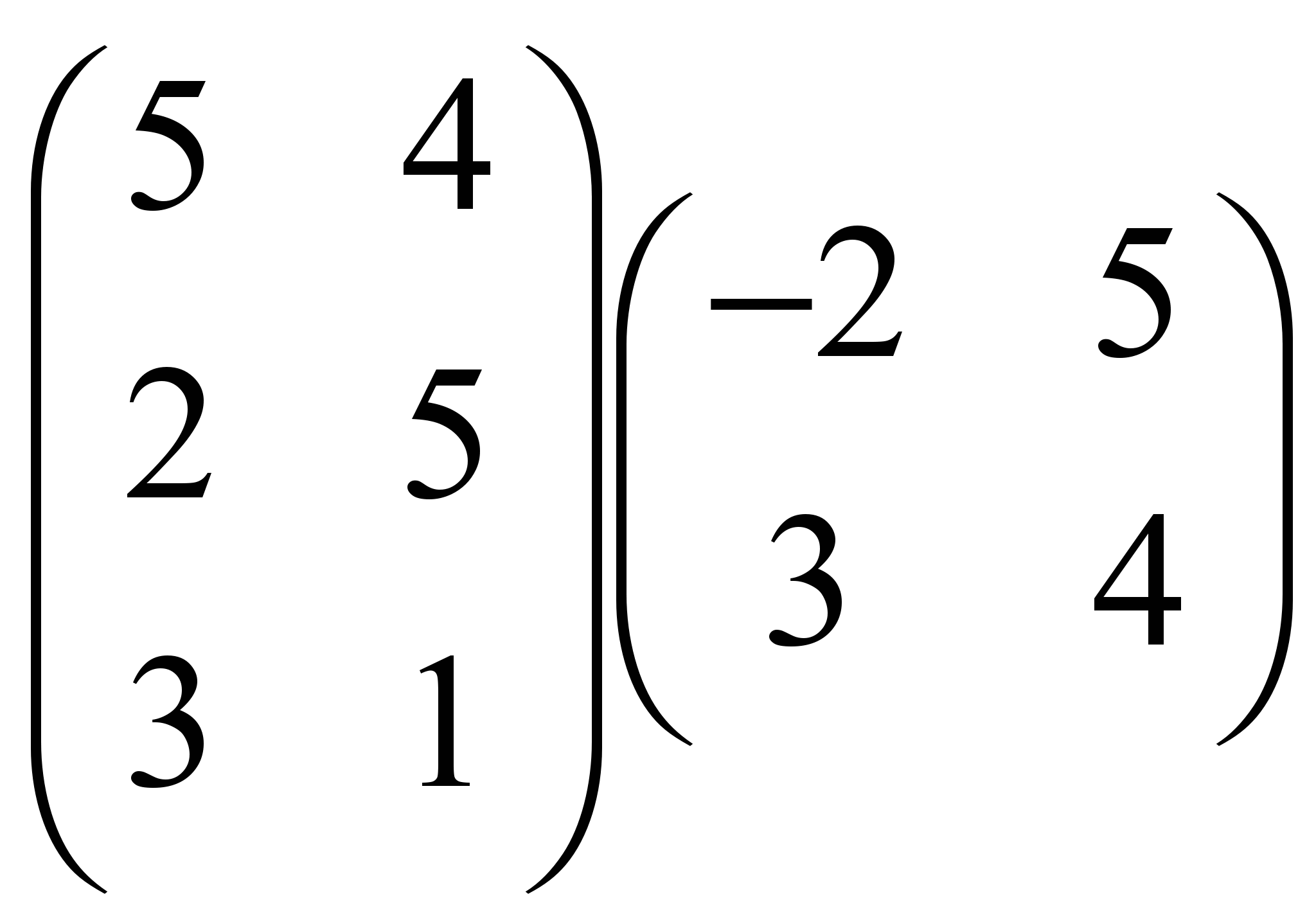 ,
,
д) 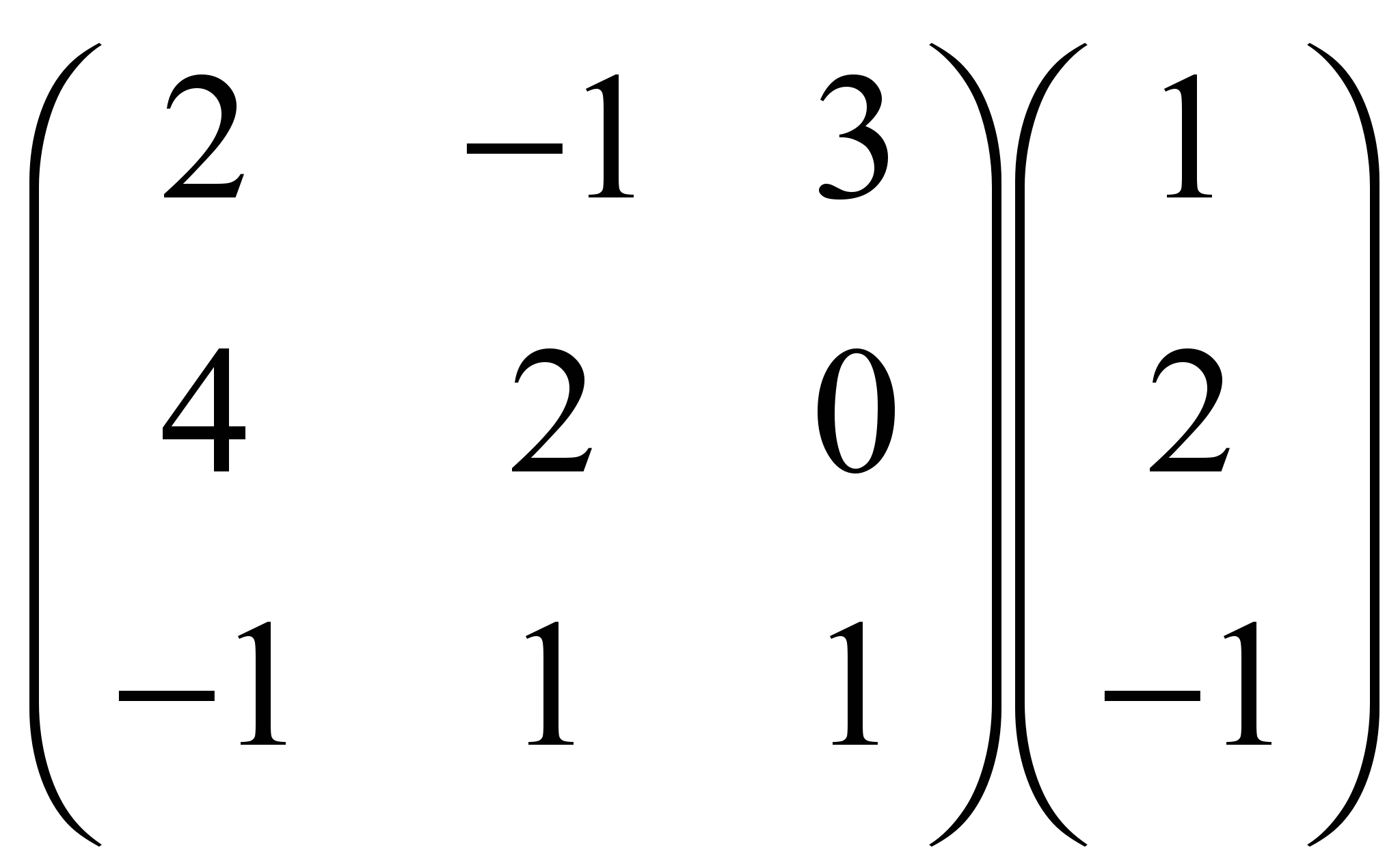 , е)
, е) 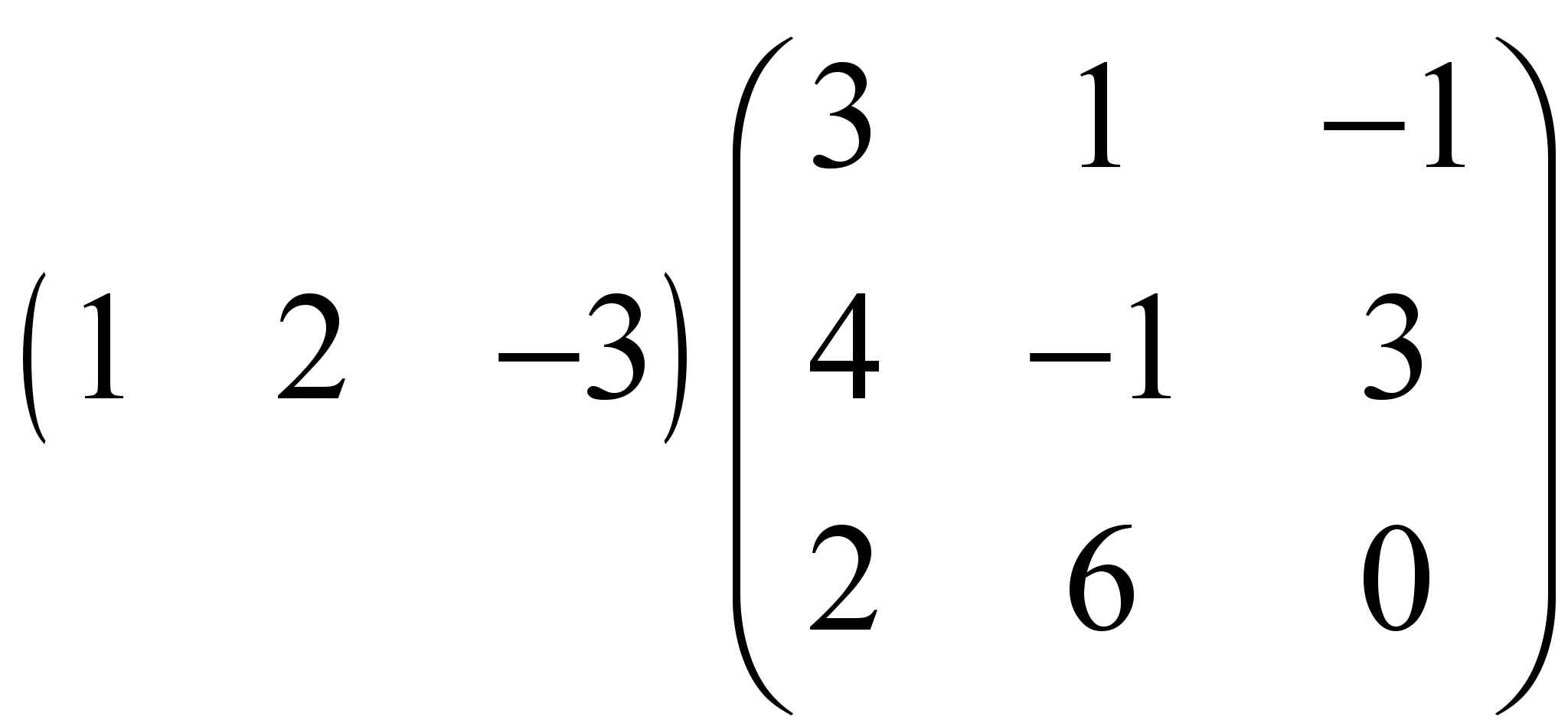 , ж)
, ж) 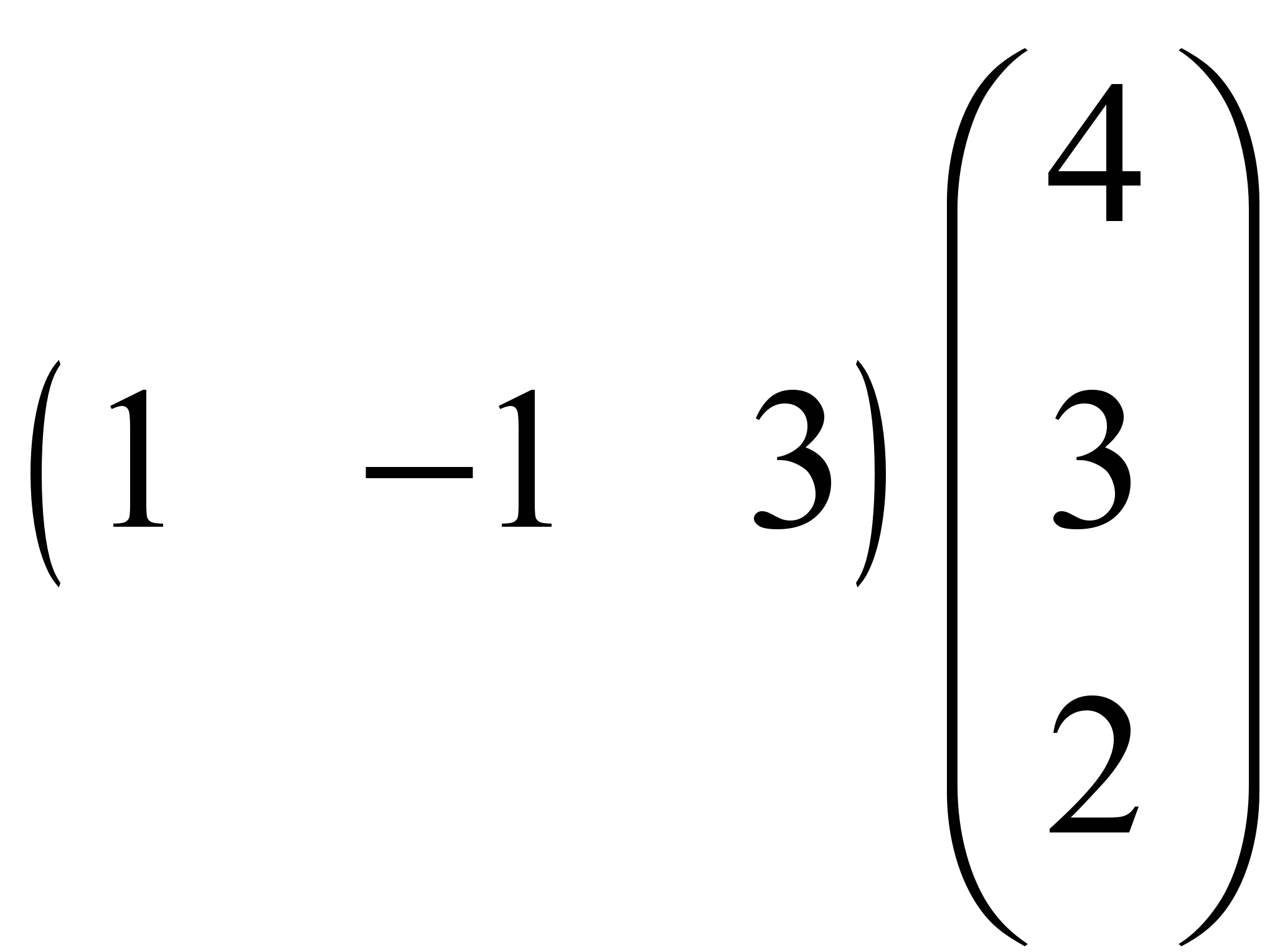 , з)
, з) 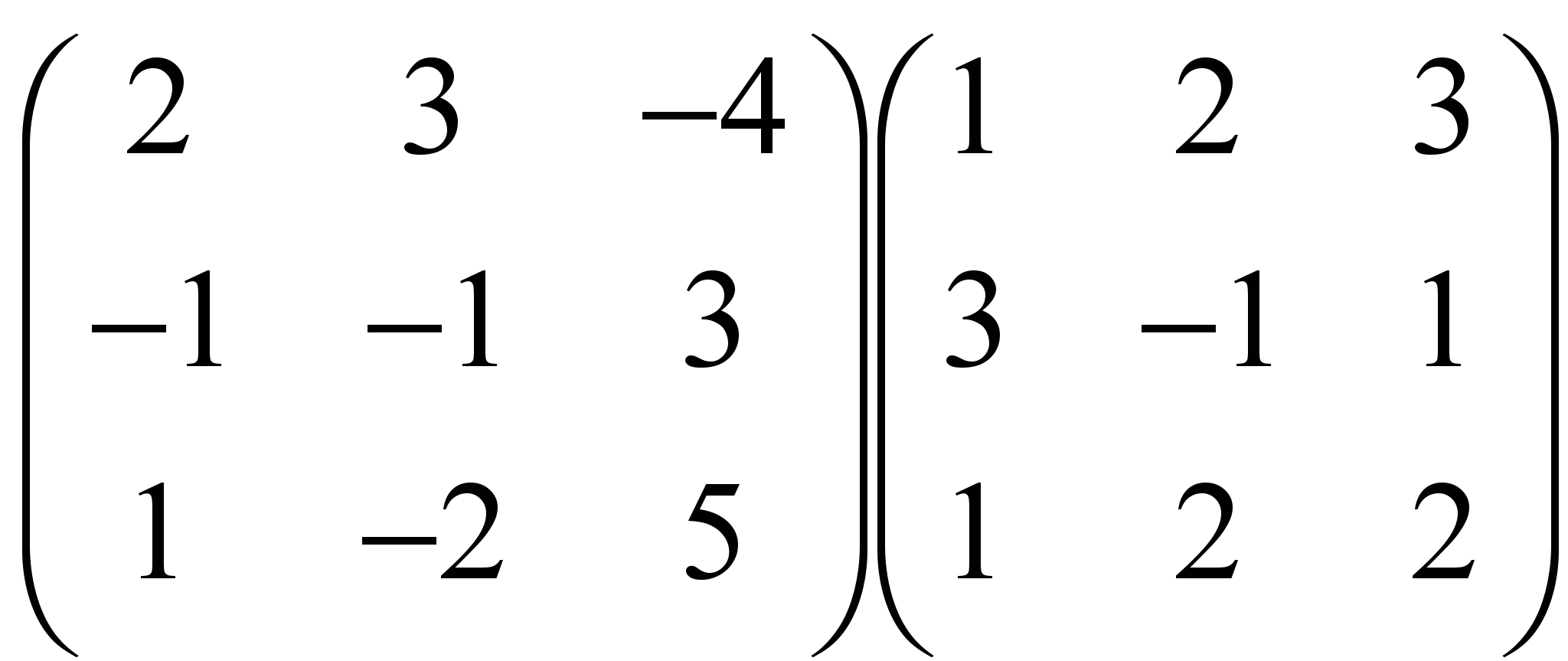 ,
,
и) 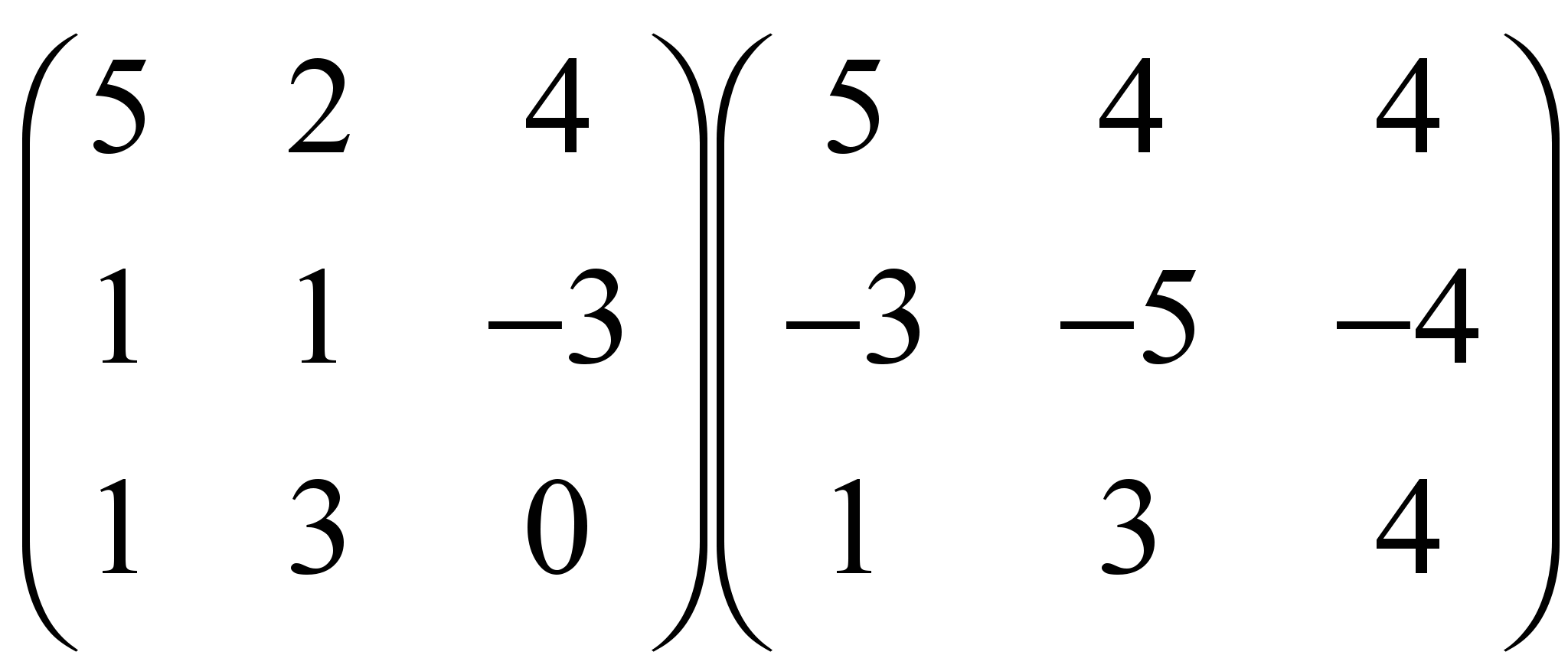 , к)
, к) 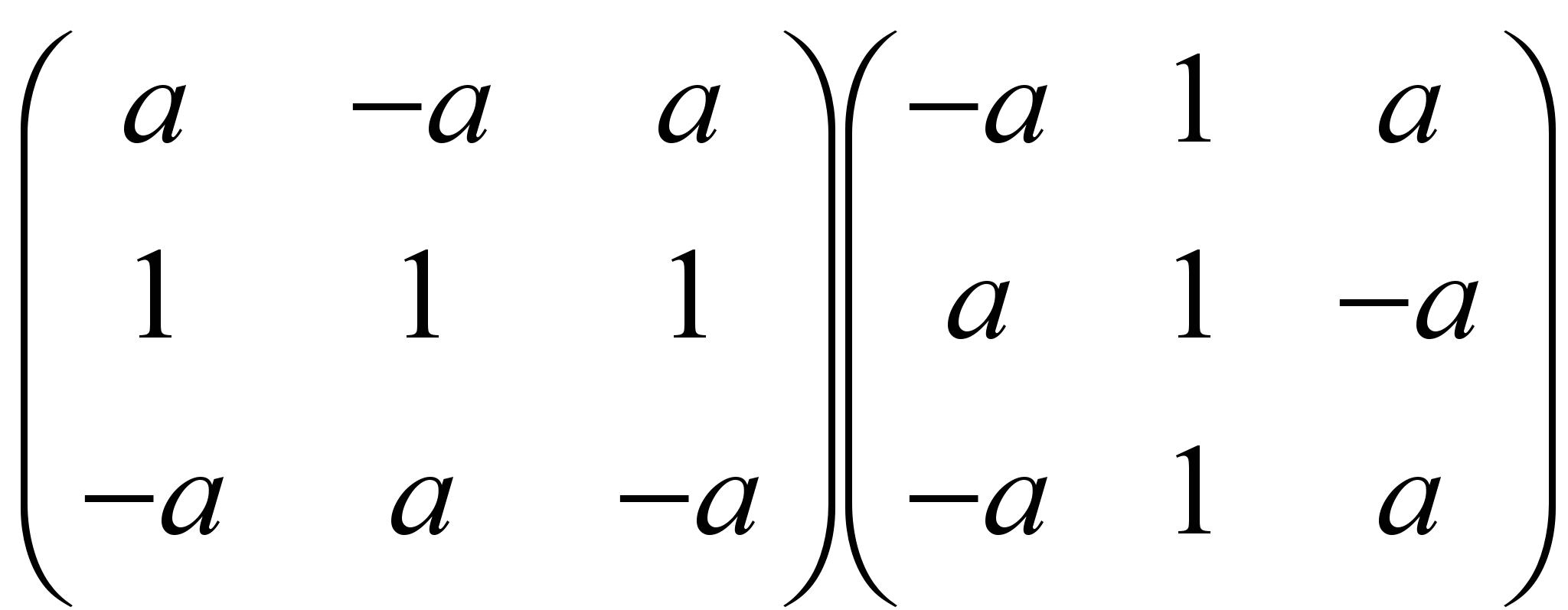 .
.
Дом. задание 5. Вычислить а) 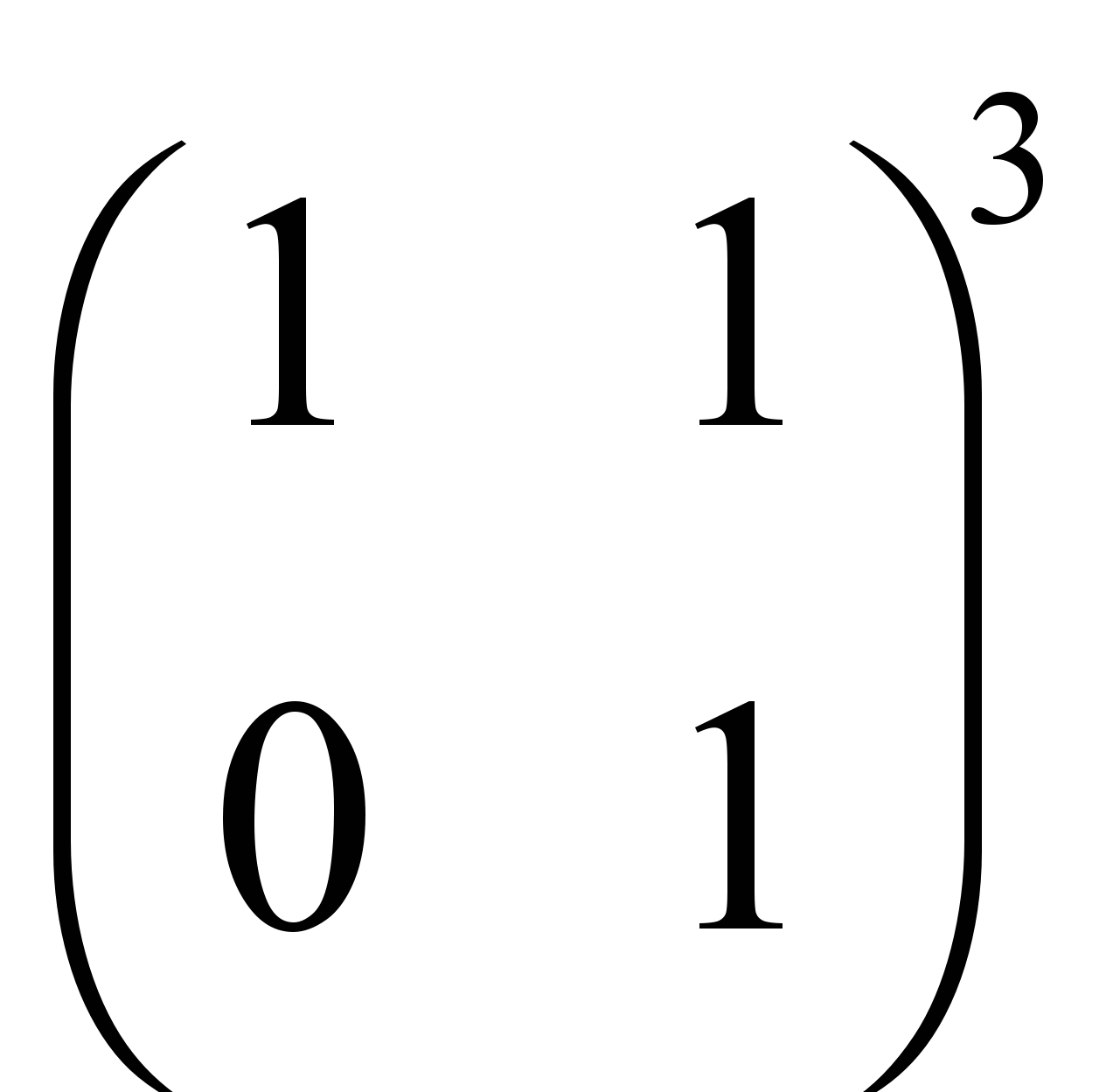 , б)
, б) 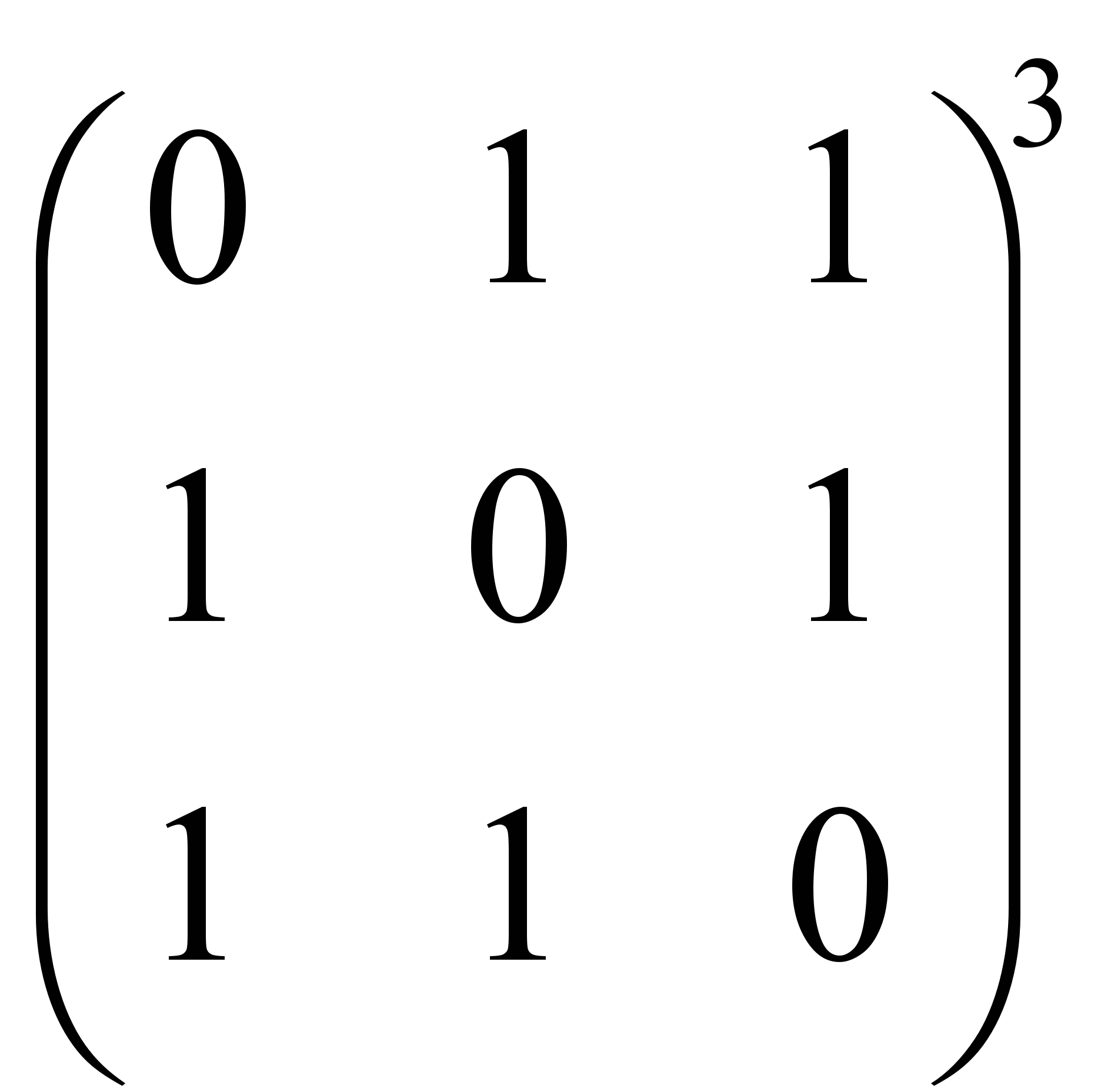 .
.
-
Рефлексия.
Продолжи фразу
1. Я повторил …
2. Я узнал …
3. Я научился…
4. Я могу…
</
Литература.
-
Элементы высшей математики: учебник для студентов учреждений сред. проф. образования / В.П. Григорьев, Ю.А. Дубинский. - 3-е изд., стер. - М.: Издательский центр «Академия», 2007. - 320 с.
-
Богомолов Н.В. Самойленко П.И. «Математика»,- М.: Дрофа, 2010.
-
Богомолов Н.В. «Практические занятия по математике»,- М.: Дрофа, 2010.
-
Высшая математика для экономистов: Практикум / Под ред. Н.Ш. Кремера. - 2-е изд. - М.: ЮНИТИ-ДАНА, 2007. -484 с
-
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. - М.:Высш. Школа, 2008г.
17