- Учителю
- Конспект урока: Предел функции в точке и на бесконечности
Конспект урока: Предел функции в точке и на бесконечности
Тема: «Предел функции в точке и на бесконечности».
Тип урока: Изучение нового материала
Оснащение урока: раздаточный материал, презентация, видео-, аудиоматериал
Литература.
-
Богомолов Н.В. Математика: учебник для ссузов. - М.: Дрофа,2009 г.
-
Богомолов Н.В. Математика: задачник для ссузов. - М.: Дрофа,2009 г
kopilkaurokov.ru/matematika/uroki/144866
sheisama.ru/publ/iskusstvo_krasivo_odevatsja/3_chto_nuzhno_uchityvat_pri_modelirovanii_odezhdy/38-1-0-261
Цели:
Уметь: самостоятельно вычислять предел функции.
Знать: основные формулы для вычисления предела функции.
ОК2. Умение организовать собстенную деятельность.
Ход урока:
-
Мотивация. (10)
-
Основная часть:
-
Изучение нового материала. (15)
-
Решение заданий. (10+10+10)
-
Итоговая работа. (15)
-
Подведение итогов. Рефлексия (10)
-
Домашнее задание.
Результат урока: выполнение самостоятельной работыДеятельность педагога
Деятельность обучающегося
-
Мотивация
Проверяет готовность обучающихся к уроку; формулирует тему урока.
Мотивация:
Девиз урока: " Мы не знаем, каковы пределы человеческих возможностей. Никакие тесты, секундомеры и финишные ленточки не могут измерить потенциал человека. В погоне за мечтой люди</<font face="Times New Roman, serif"> заходят намного дальше того, что казалось их пределом. Потенциал заключённый в каждом из нас, безграничен и ещё не задействован. Когда вы думаете о пределе, вы сами его создаёте.". (обсудить со студентами)
Объявление темы урока.
Логическая цепочка
Тема «Предел» - Тема «Производная» - Тема «Интеграл» - Тема «?»
- Посмотрите на список данных тем. Скажу по секрету, что мы начинаем изучать одну из главных тем математики. Как Вы считаете, есть ли между ними связь? А нужны ли они вам в профессии?
- Давайте проверим наши предположения. (картинки с темой)
1) тема «предел»: выбор и анализ образа модели;
2) тема «производная»: расчет размера образа модели;
3) тема «интеграл»: построение чертежа модели.
4) «?»
Что бы вы пришли к такому результату, были успешными и специалистами высокого класса, начнем изучение нашей темы.
Готовятся к восприятию материала, записывают тему урока.
-
Основная часть
1.Изучение нового материала
Предел функции на бесконечности.
Пусть существует функция y=f(x) и пусть она определена на луче
![]() , и
пусть она сходится к точке b
, и
пусть она сходится к точке b ![]() .
.
Если же эта функция определена и на луче ![]() , т.е.
, т.е.
![]() ,
то говорят, что она имеет предел на бесконечности и выражения (1) и
(2) можно объединить в одно:
,
то говорят, что она имеет предел на бесконечности и выражения (1) и
(2) можно объединить в одно: ![]() .
.
Вычисление предела функции на бесконечности выполняется по правилам. Вот эти правила:
![]()
Если ![]() ,
,![]() , то:
, то:
а) предел суммы равен сумме пределов:
![]()
б) предел произведения равен произведению пределов:
![]()
в) предел частного равен частному предела (при условии
c![]() ):
):
![]()
г) постоянный множитель можно вынести за знак предела:
![]()
Предел Функции в точке.
Примеры. Вычислить предел функции:
а) ![]() =
=
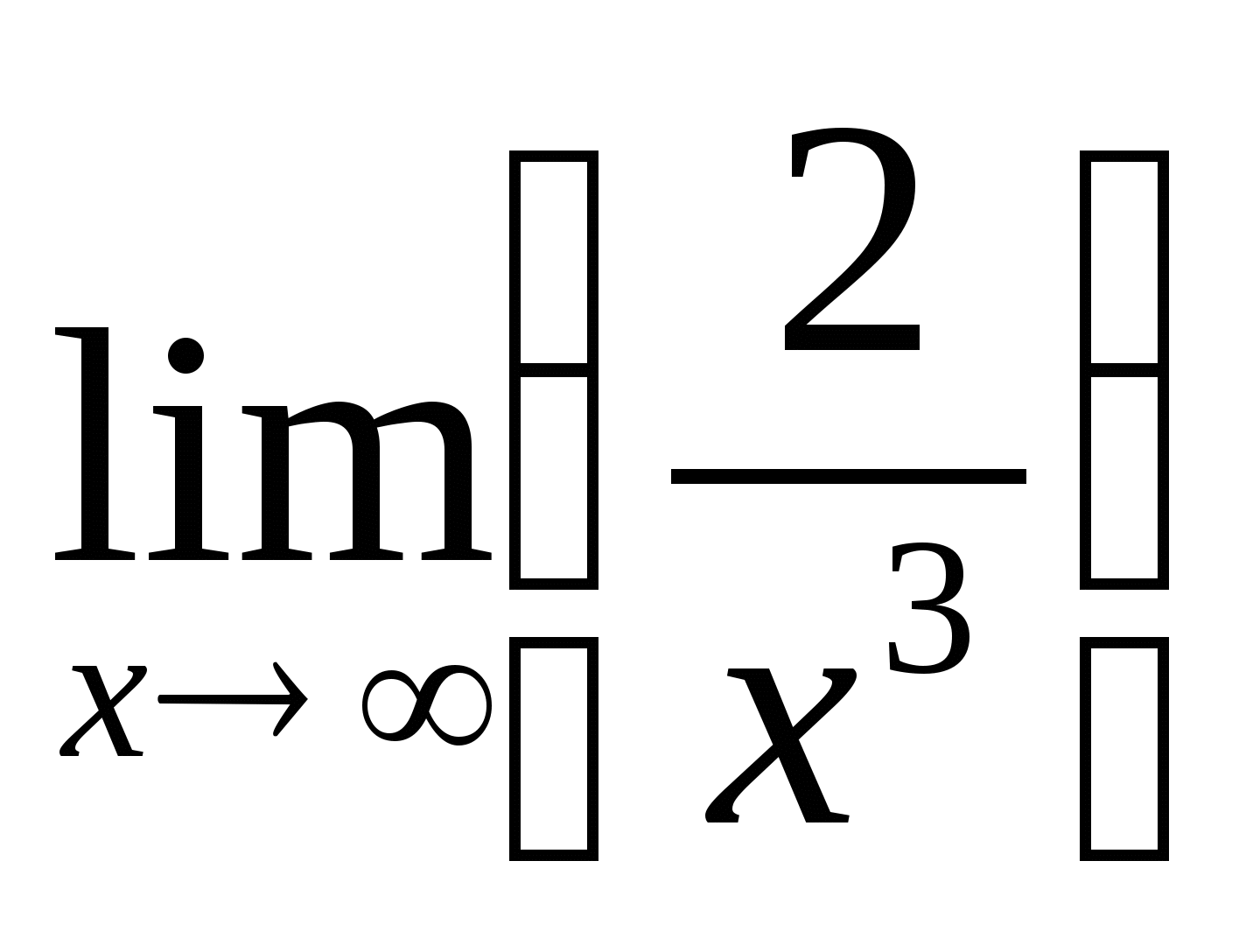 +
+
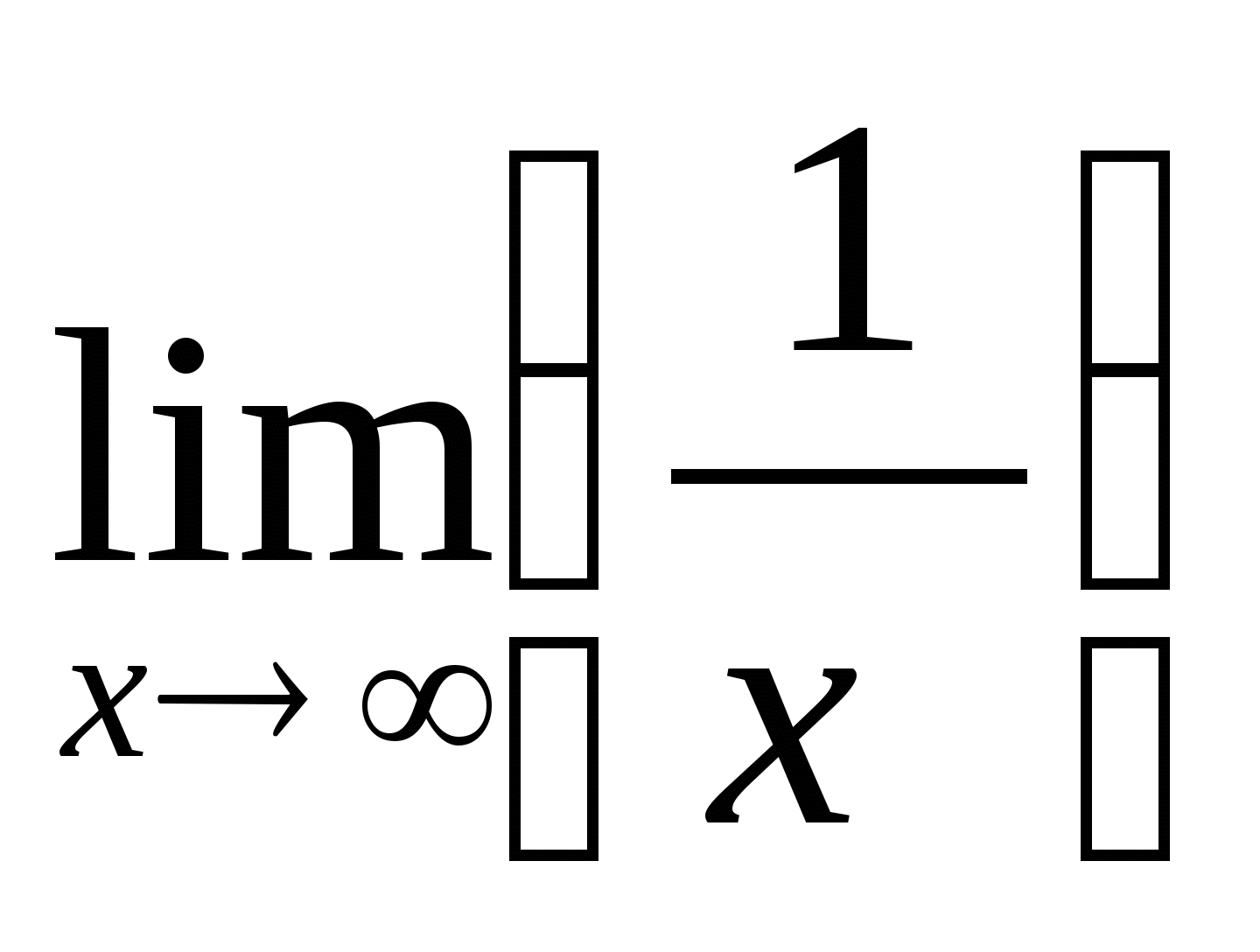 =0+0=0
=0+0=0
б) ![]() =
=
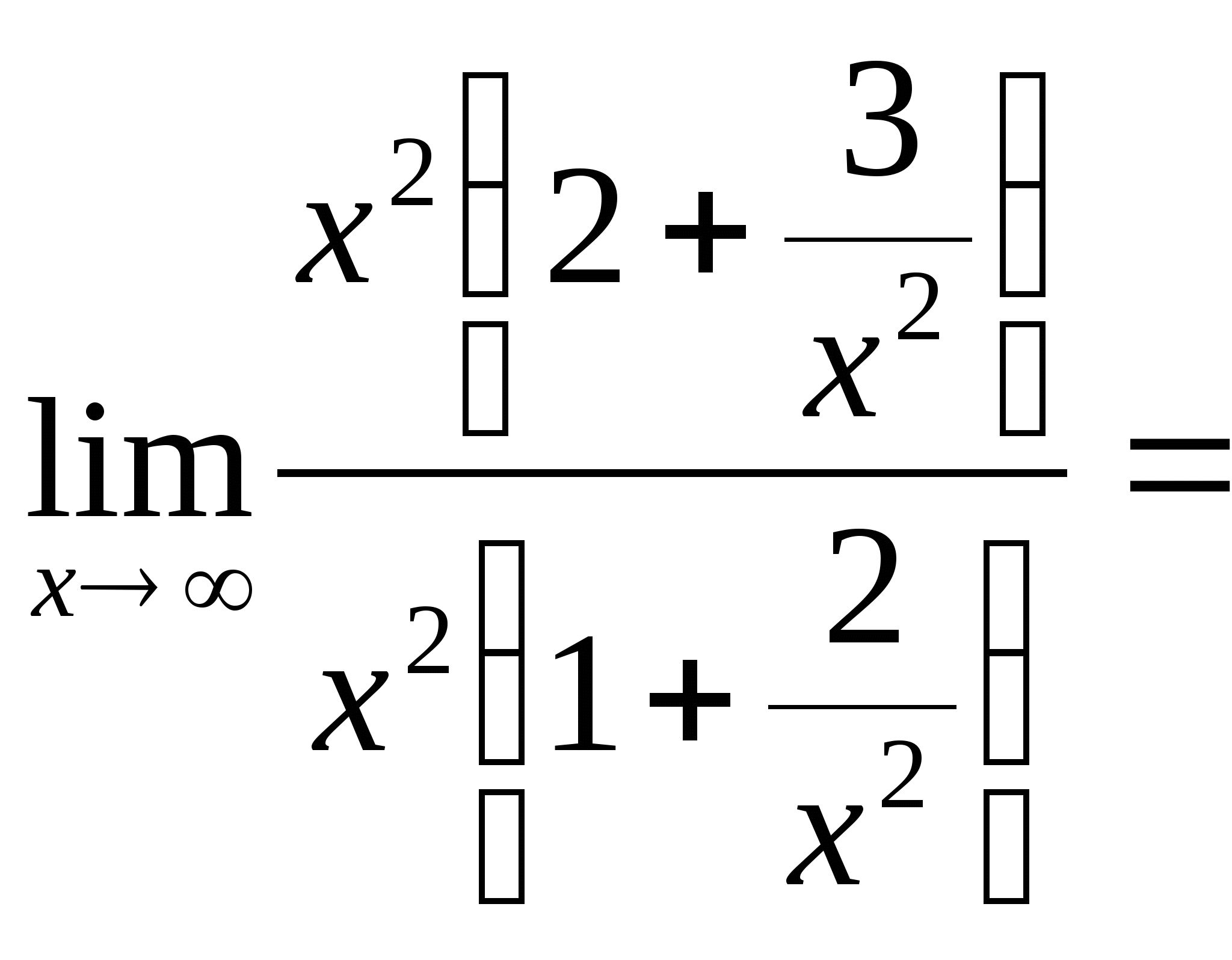
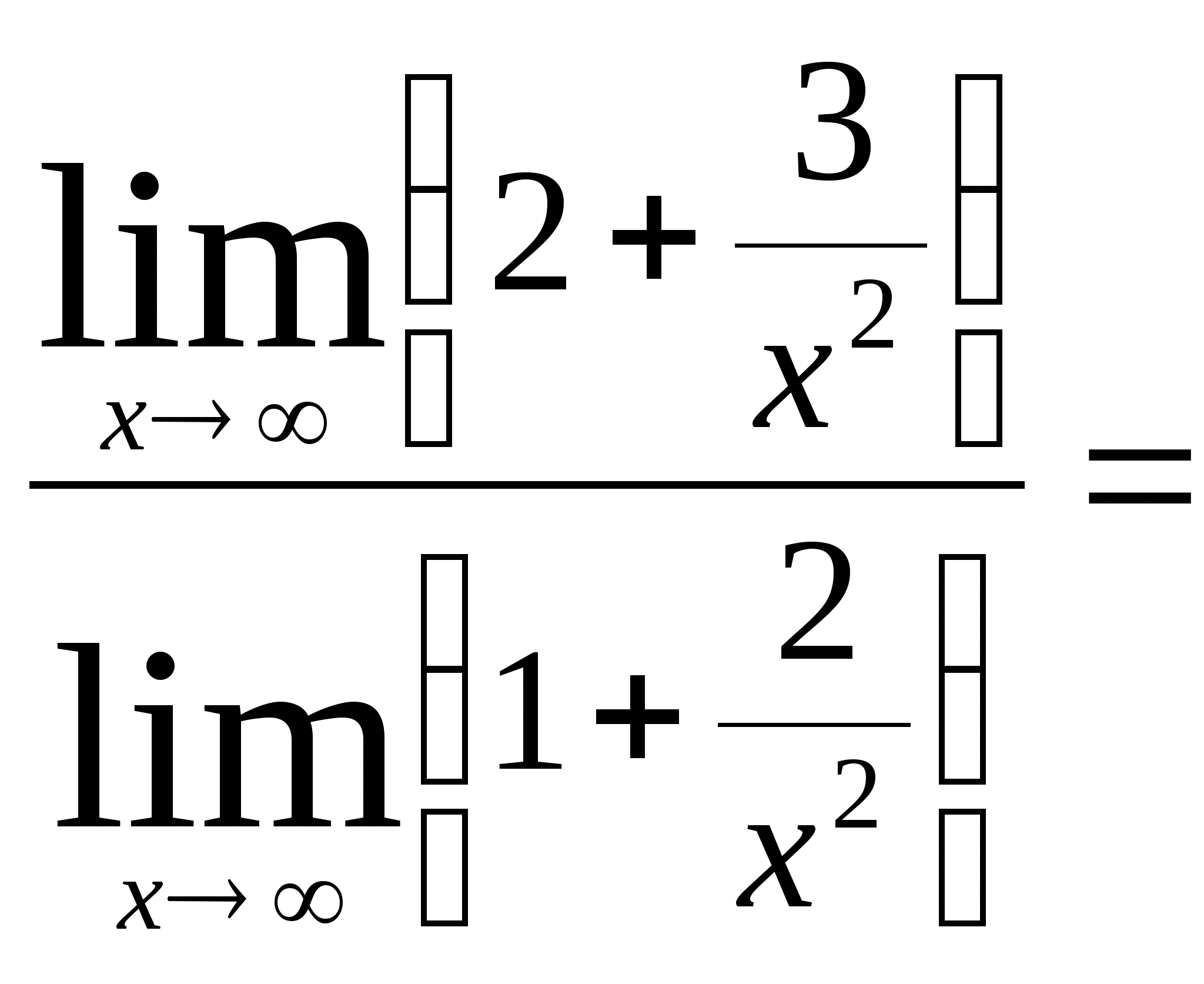
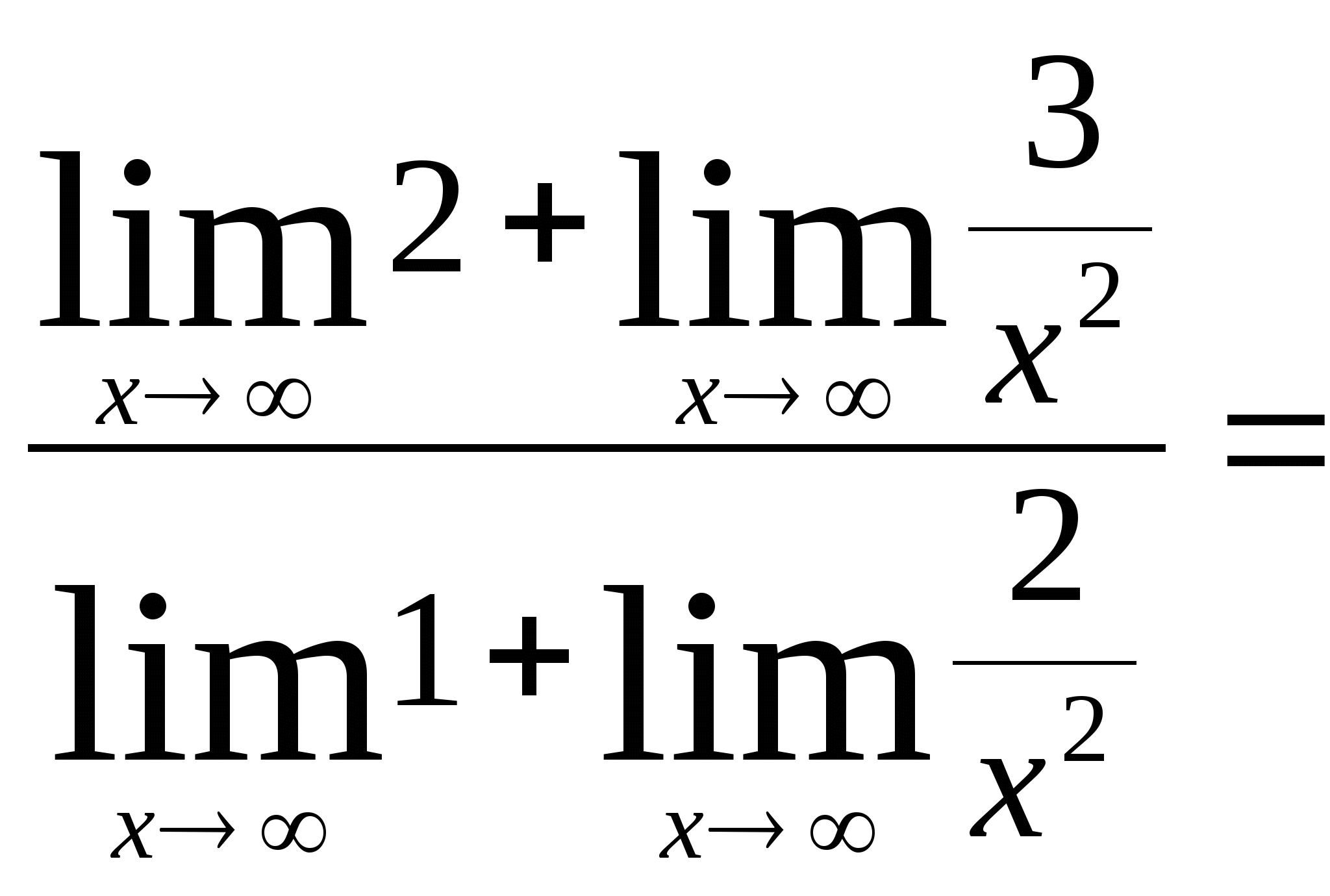
![]()
в) ![]()
![]() = -1
= -1
2.Решение заданий.
Вычислить предел функции:
![]() ;
;
![]() ;
;![]()
Самостоятельная работа. Вычислите:
Вариант 1.
Вычислить: ![]() ;
;
![]() ;
;![]()
![]() .
.
Вариант 2.
Вычислить:![]() ;
;![]() ;
;![]()
![]() .
.
Один у доски остальные в тетради.
Проверка ведется студентами под руководством преподавателя.
3.Отработка изученного. (работа в группах)
Задания в листах самоконтроля.
Студенты защищают свои проекты.
IV. Подведение итогов.
Рефлексия.
Студентам объявляются оценки с пояснением.
11 - 12 - 5
8 - 10 - 4
6 - 7 - 3
Ребята поднимают руки соответственно оценке.
V.Задания для самостоятельной работы.
![]() гл.6§1-3№36-40(2)
гл.6§1-3№36-40(2)
Лист самоконтроля._______________________Ф. И.
![]()
![]()
2.
Вариант 1.
Вычислить: ![]() ;
;
![]() ;
;
![]()
![]() .
.
3.
Вычислите предел и определите деталь чертежа одежды:
Итого:
Лист самоконтроля._______________________Ф. И.
![]()
![]()
2.
Вариант 2.
Вычислить:![]() ;
;
![]() ;
;
![]()
![]() .
.
3.
Вычислите предел и определите деталь чертежа одежды:
Итого:
Вычислите предел и определите деталь чертежа одежды:
1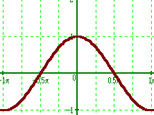 .
.
![]() при
при
![]() .
.
_____________________________________________________
2.________________(применение в образе)
-
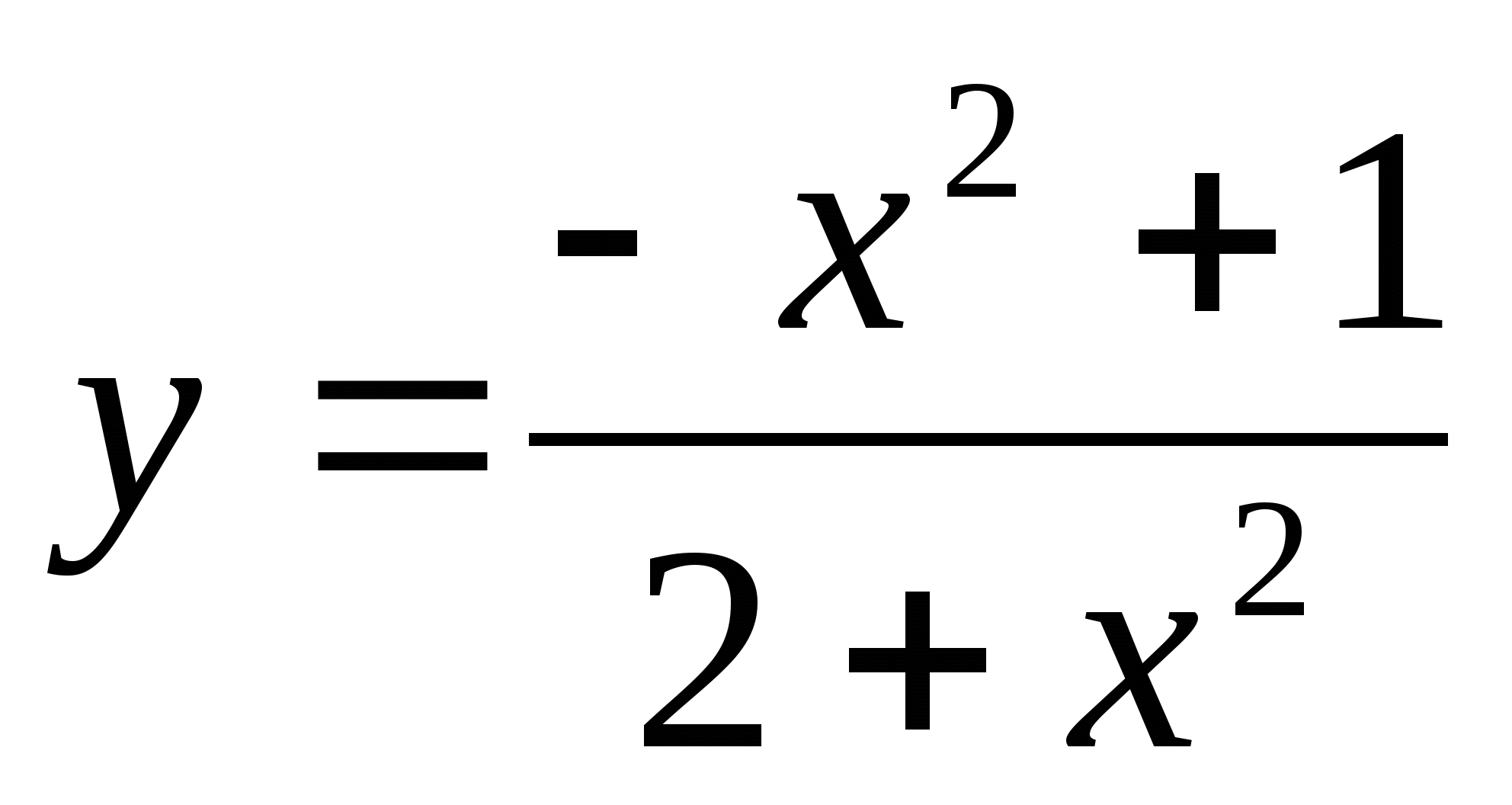 ,
при
,
при  .
_______________________________
.
_______________________________
_______________________________________
2._________________( применение в образе)
-
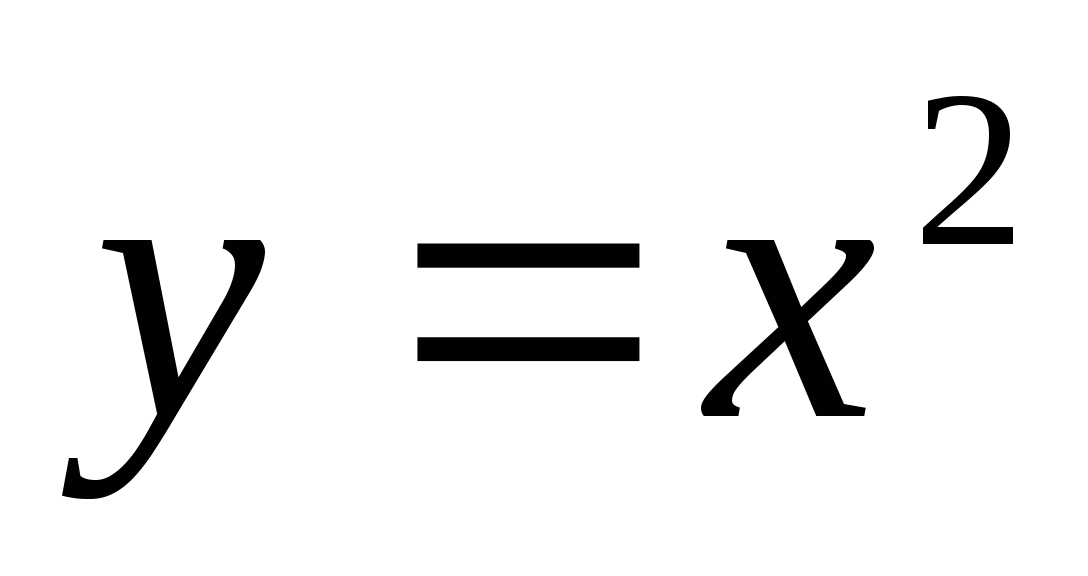
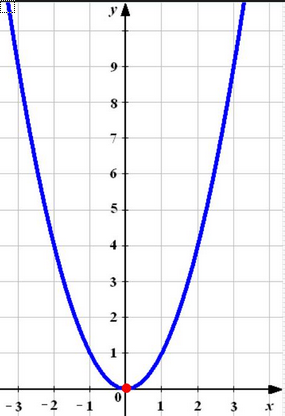 при
при

__________________________________________________
-
________________( применение в образе)
Изобразите согласно предложенным функциям образ модели.
Вычислите предел и определите деталь чертежа одежды:
-
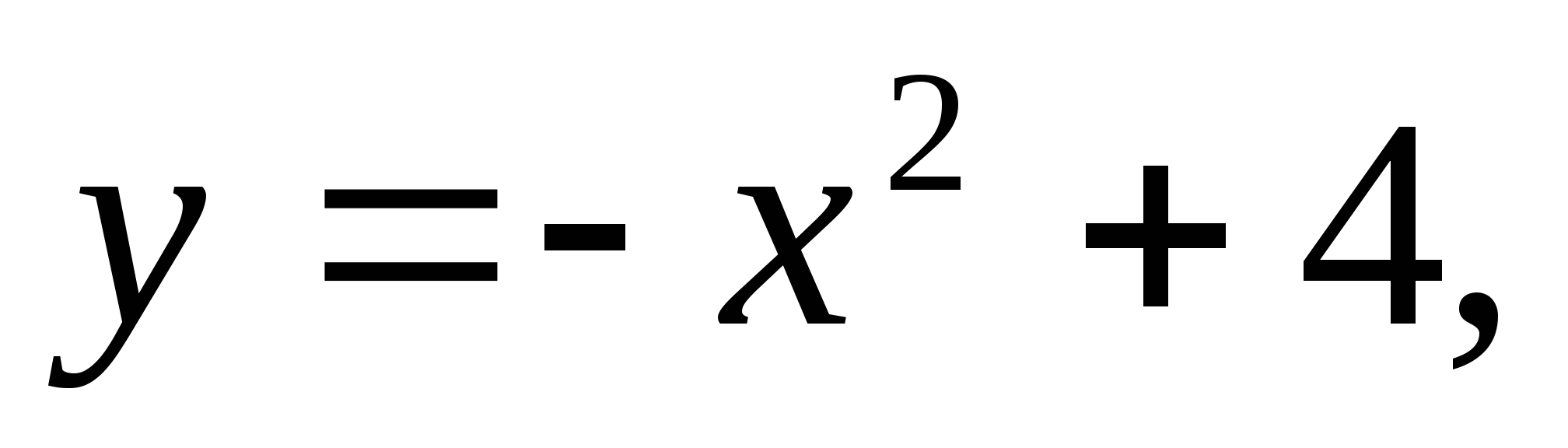 п
п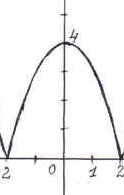 ри
ри
 .
.
_________________________________________________________
-
________________( применение в образе)
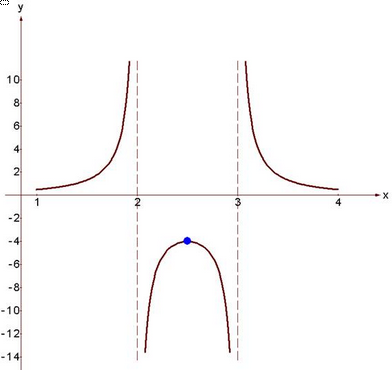
-
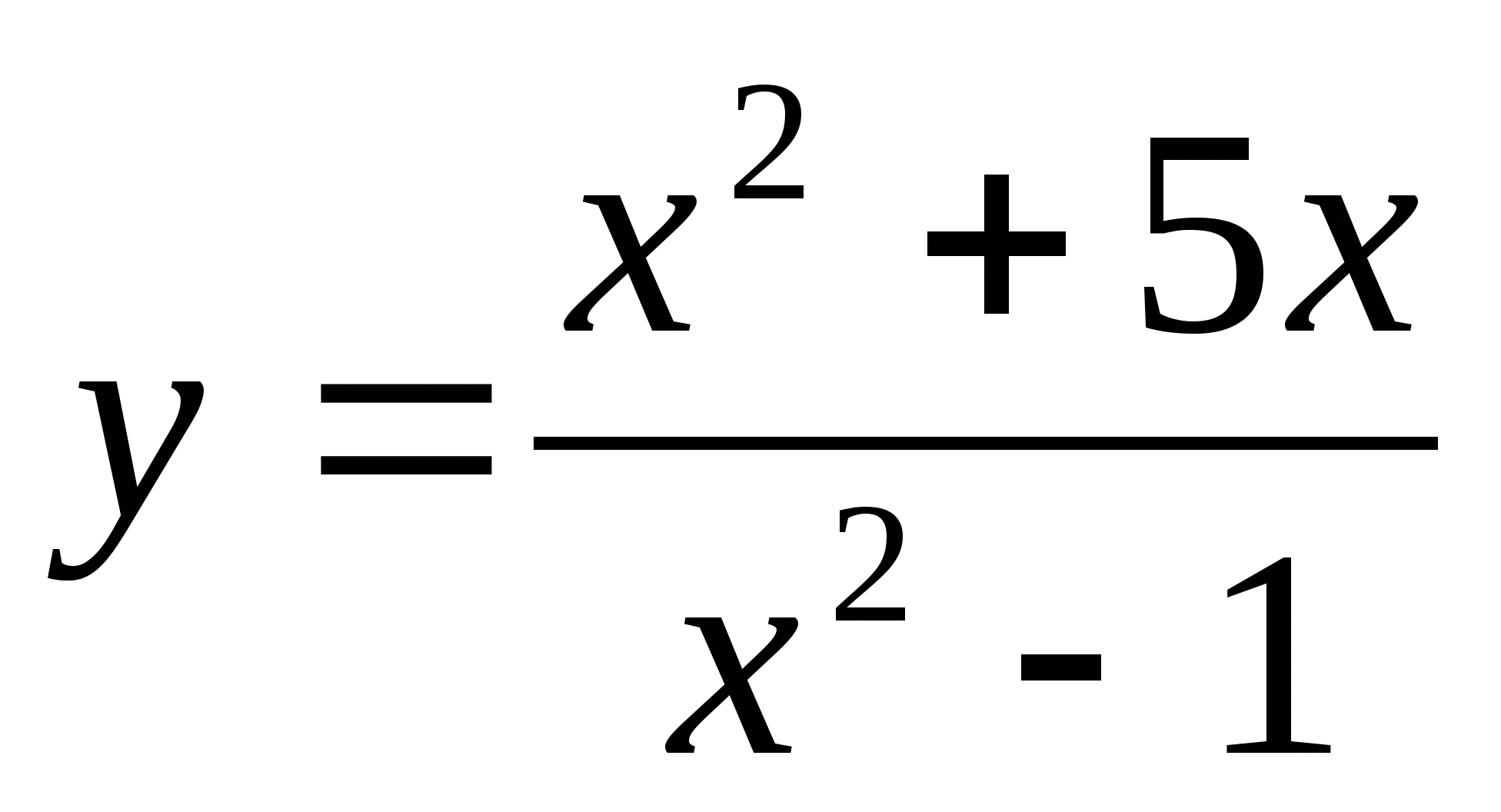 ,
при
,
при  .
.
____________________________________________
____________________________________________
-
_________________( применение в образе)
1 .
.![]() при
при
![]()
__________________________________________________
2.________________( применение в образе)
Изобразите согласно предложенным функциям образ модели.
Вычислите предел и определите деталь чертежа одежды:
1.![]() п
п ри
ри
![]() .
.
_________________________________________________________
2.________________( применение в образе)
1.![]() ,
,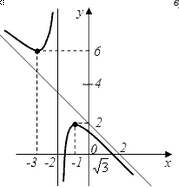 при
при
![]() .
.
____________________________________________
____________________________________________
2._________________( применение в образе)
1 .
.![]() при
при
![]()
__________________________________________________
2.________________( применение в образе)
Изобразите согласно предложенным функциям образ модели.
Вычислите предел и определите деталь чертежа одежды:
1.![]() п
п ри
ри
![]() .
.
_________________________________________________________
2.________________( применение в образе)

1.![]() , при
, при
![]() .
.
____________________________________________
____________________________________________
2._________________( применение в образе)
1 .
.![]() при
при
![]()
__________________________________________________
2.________________( применение в образе)
Изобразите согласно предложенным функциям образ модели.
Вычислите предел и определите деталь чертежа одежды:
1 .
.
![]() при
при
![]() .
.
_____________________________________________________
2.________________( применение в образе)

1.![]() , при
, при
![]() .
_______________________________
.
_______________________________
_______________________________________
2._________________( применение в образе)
1 .
.![]() при
при
![]()
__________________________________________________
2.________________( применение в образе)
Изобразите согласно предложенным функциям образ модели.