- Учителю
- Уро по геометрии для 9 класса по теме «Соотношение между сторонами и углами треугольника»
Уро по геометрии для 9 класса по теме «Соотношение между сторонами и углами треугольника»
Тема: «Соотношения между сторонами и углами треугольника»
(9 класс, учебник Атанасяна Л.С).
Цели:
образовательная
- проверить теоретические знания учащихся по изученной теме;
- повторить формулировки теоремы синусов и косинусов, определения синуса,
косинуса, тангенса в прямоугольном треугольнике;
- познакомить учащихся с использованием тригонометрических функций cos![]() ,
,
sin![]() , tg
, tg![]() в измерительных работах на местности на примере задач №1036,
в измерительных работах на местности на примере задач №1036,
№1037;
- формировать навыки решения задач с использованием теоремы синусов.
развивающая
- развитие памяти, внимания, мышления учащихся;
воспитательная
- воспитание самостоятельности, аккуратности, интереса к математике.
Тип урока: комбинированный урок.
Форма: урок-практикум.
План:
-
Организационный момент.
-
Самостоятельная работа.
-
Подготовительный этап.
-
Решение задач.
-
Подведение итогов урока.
-
Информация о домашнем задании.
Ход урока:
1) Организационный момент.
Цель: создать благоприятную обстановку в классе, психологически настроить учащихся на работу.
Приветствие!!!
2) Самостоятельная работа.
Цель: проверить теоретические знания учащихся по изученной теме.
Форма: тестирование.
Деятельность
Учителя
Учащихся
Самостоятельная работа проводится в форме теста. Каждый получит лист с заданиями. Всего 2 варианта, в каждом варианте 8 заданий, 3 варианта ответа один из которых верный. Время на выполнение заданий теста 8-10 мин.
(Учащиеся выполняют тест на листочках . После выполнения учитель собирает работы, листы с заданиями остаются у ребят. Проверка теста устно).
Задания теста:
Вариант №1.
1) Для ![]() АВС справедливо равенство:
АВС справедливо равенство:
-
АВ2=ВС2+АС2- 2*ВС*АС*cos
 BCA;
BCA; -
BC2=AB2 +AC2-2*AB*BC*cos
 ABC;
ABC; -
AC2=AB2+BC2-2*AB*BC*cos
 ACB.
ACB.
2) Площадь ![]() MNK равна:
MNK равна:
-
 ;
; -
 ;
; -
 .
.
3) Если квадрат стороны треугольника равен сумме квадратов двух других сторон, то эта сторона лежит против:
-
тупого угла;
-
прямого угла;
-
острого угла.
4) По теореме синусов:
-
стороны треугольника обратно пропорциональны синусам противолежащих углов;
-
стороны треугольника пропорциональны синусам противолежащих углов;
-
стороны треугольника пропорциональны синусам прилежащих углов.
5) Площадь параллелограмма АВСД равна:
-
АВ*ВС*sin
 ;
; -
A B*BC*sin
 ;
; -
 .
.
6) Треугольник со сторонами 5, 6 и 7 см.:
-
остроугольный;
-
прямоугольный;
-
тупоугольный.
7) Если в треугольнике АВС ![]() ,
, ![]() , то наибольшей стороной треугольника является сторона:
, то наибольшей стороной треугольника является сторона:
-
АВ;
-
АС;
-
ВС.
8) В ![]()
![]() ВС=3. Радиус описанной около
ВС=3. Радиус описанной около![]() АВС окружности равен:
АВС окружности равен:
-
1,5;
-
2
 ;
; -
3.
Вариант №2.
1) Для ![]() АВС справедливо равенство:
АВС справедливо равенство:
-
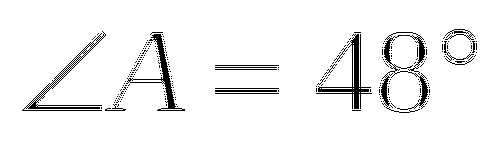 ;
; -
 ;
; -
 .
.
2) Площадь ![]() СДЕ равна:
СДЕ равна:
-
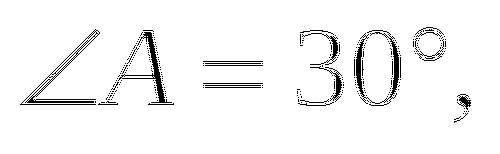 ;
; -
 ;
; -
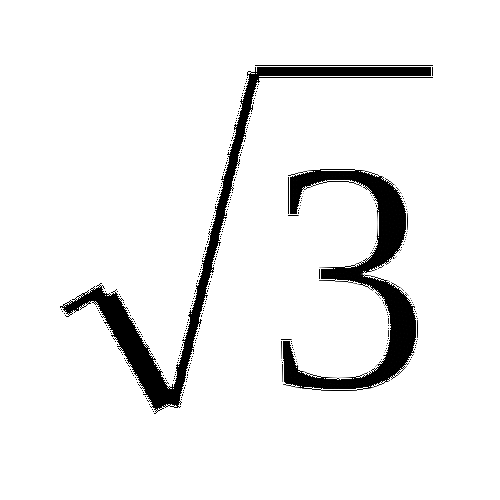 .
.
3) Если квадрат стороны треугольника больше суммы квадратов двух других его сторон, то эта сторона лежит против:
-
острого угла;
-
прямого угла;
-
тупого угла.
4) По теореме о площади треугольника:
-
площадь треугольника равна произведению двух его сторон на синус угла между ними ;
-
площадь треугольника равна половине произведения двух его сторон на угол между ними ;
-
площадь треугольника равна половине произведения двух его сторон на синус угла между ними .
5) Площадь параллелограмма АВСД равна:
-
 ;
; -
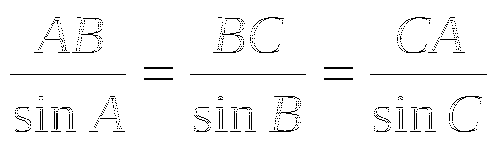 ;
; -
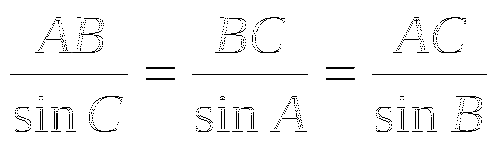 .
.
6) Треугольник со сторонами 2, 3 и 4 см.:
-
остроугольный;
-
прямоугольный;
с) тупоугольный.
7) Если в ![]()
![]() ,
, ![]() , то наименьшей стороной треугольника является сторона:
, то наименьшей стороной треугольника является сторона:
-
MN;
-
NK;
-
MK.
8) В ![]() MN=2,
MN=2,![]() . Радиус описанной около
. Радиус описанной около ![]() окружности равен:
окружности равен:
-
4;
-
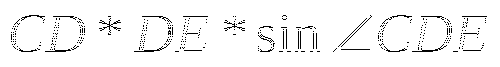 ;
; -
2.
Ключ к тесту.
1
2
3
4
5
6
7
8
Вариант №1
а
в
б
б
а
а
б
в
Вариант №2
б
а
в
в
б
в
а
б
Оценка
5-«3»
6-7-«4»
8-«5»
3) Подготовительный этап.
Цель: повторить формулировки теоремы синусов и косинусов, определения синуса,
косинуса, тангенса в прямоугольном треугольнике.
Форма: устная работа.
Деятельность
Учителя
Учащихся
Сейчас работаем устно.
Выполнить следующие упражнения.
1) Чему равен sin![]() , cos
, cos![]() , tg
, tg![]() в прямоугольном треугольнике .
в прямоугольном треугольнике .
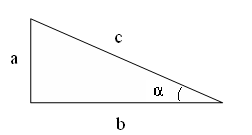
2) Как найти а, если известны с угол ![]() , b и угол
, b и угол![]()
3)Найдите MP, если известны сторона NP прямоугольного треугольника MNP и угол![]() .
.
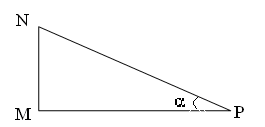
sin![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4) Решение задач.
Цель: познакомить учащихся с использованием тригонометрических функций cos![]() ,
,
sin![]() , tg
, tg![]() в измерительных работах на местности ;формировать навыки решения
в измерительных работах на местности ;формировать навыки решения
задач с использованием теоремы синусов
Деятельность
Учителя
Учащихся
Иногда измерить высоту какого-либо предмета или найти расстояние до точки невозможно или очень трудно. в таких случаях используют тригонометрические формулы sin, cos, tg угла. Сейчас на примере рассмотрим, как это можно сделать.
№1036.
Прочитайте условие задачи. Посмотрите на рис. 289 учебника.
Как этот рисунок можно преобразовать в геометрический чертеж?
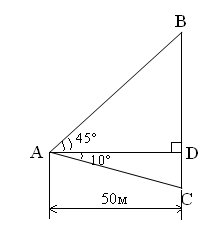
Что дано?
Что требуется найти?
Как найдем ВС?
Из какого треугольника найдем ВС?
Что известно об этом треугольнике?
Чему равен ![]()
![]() ?
?
Т.е. ![]()
![]() , значит какой это треугольник ?
, значит какой это треугольник ?
Из какого треугольника найдем DC?
Что известно об этом треугольнике?
Как найти DC?
(известен катет и прилежащий угол, как найти другой катет ?)
Чему равен отрезок ВС?
Т.е. высота башни равна ![]()
![]() м.
м.
Ответ: ![]()
![]() м.
м.
№1037
Прочитайте условие задачи. подумайте, как можно изобразить геометрически чертеж?
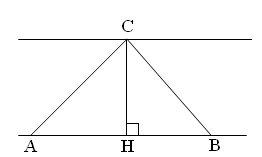
Что дано в задаче?
Что нужно найти?
Посмотрим: АВ из каких отрезков состоит?
Попробуем их выразить.
Рассмотрим ![]() -прямоугольный.
-прямоугольный.
Как можем найти АН?
( известен катет и противолежащий угол, как найти другой катет?)
Рассмотрим ![]() -прямоугольный.
-прямоугольный.
Как можем найти НВ?
Т.е. АВ=АН+НВ=![]()
Выразим СН.
![]() ;
;
![]() м.
м.
Таким образом, ширина реки равна ![]()
![]() м.
м.
Ответ:![]()
![]()
![]() м.
м.
№1027.
Прочитайте условие задачи.
Построим ![]()
![]()
Какой это треугольник- остроугольный, тупоугольный или прямоугольный ?
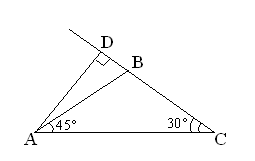
Высота AD куда будет проведена?
Что дано в задаче?
Что требуется найти?
![]() уже нашли.
уже нашли.
Рассмотрим ![]() -прямоугольный.
-прямоугольный.
Известен катет AD=3 м. и ![]() .
.
Что можем найти?
Чему она равна?
Сторону АС нашли.
Как найти остальные стороны ![]() ?
?
Запишем соотношение:
![]()
![]() ;
;
 м.
м.
![]() ;
;
![]() ;
;
![]() м.
м.
Ответ: 6 м.,![]() м.,
м., ![]() м.
м.
ВС- высота башни,
А- наблюдатель,
![]() -угол, под которым наблюдатель видит основание башни,
-угол, под которым наблюдатель видит основание башни,
АD- расстояние, на котором он находится.
![]()
Дано: ![]()
![]()
AD=50 м.
Найти: ВС
BC= BD+DC.
Из треугольника ABD.
![]() ,
, ![]() ,AD=50 м.
,AD=50 м.
![]()
Равнобедренный, тогда AD=BD=50м.![]()
Из треугольника ADC.
![]()
![]() м.
м.
DC=AD*tg100![]()
DC=50*0,1763![]() 8,815 м.
8,815 м.
BC=50+8,815![]()
![]() м.
м.
Дано: АВ=70 м.
![]()
![]() ',
',
![]() '
'
Найти: СН
из АН и НВ
АН=![]()
![]()
![]()
![]()
Тупоугольный т. к. ![]()
![]() >900
>900
На продолжение стороны ВС.
Дано: ![]()
![]() ,
,
![]()
AD-высота, AD=3 м.
Найти: АВ,ВС,АС.
![]()
Гипотенузу АС.
АС=2*AD=6 м. т.к. катет, лежащий против угла в 300 равен половине гипотенузы.
По теореме синусов.
5) Подведение итогов.
Цель: подвести итоги урока.
Деятельность
Учителя
Учащихся
Итак, сегодня на уроке вы убедились, что можно найти высоту предмета или расстояние до точки, не используя измерительных приборов. При этом, какими тригонометрическими формулами пользовались?
tg![]() .
.
6) Информация о домашнем задании.
Дома: №1038, №1060(в).
№1038.
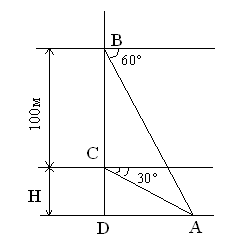
![]() ,
,![]() .
.
Из прямоугольного треугольника DCA
DA=DC*tgDCA=H*tg ![]() .
.
В прямоугольном треугольникеDBA
DB=DC+CB=H+100 и DA=DB*tg![]() =(H+100)*
=(H+100)*![]() .
.
Составим уравнение Н*![]() =(100+Н)*
=(100+Н)*![]() ;
;
Отсюда Н=50 м.
Ответ: 50 м .
№1060(в)
в) По теореме синусов ![]() и sin C=
и sin C=![]() и
и ![]()
Ответ: 0,6809; 88035'