- Учителю
- Олимпиады по математике для школьного этапа с решениями 5-11 класс
Олимпиады по математике для школьного этапа с решениями 5-11 класс
Задачи школьной олимпиады по математике
5 класс
-
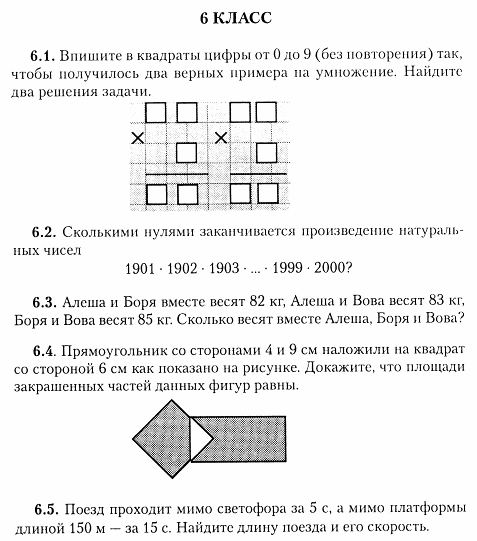
Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов? (2 балла)
-
Митя, Коля, Сеня, Юра и Костя пришли в музей и встали в очередь. Если бы Митя встал посередине очереди, то он оказался бы между Сеней и Костей, а если бы Митя встал в конце очереди, то рядом с ним мог быть Юра, но Митя встал впереди всех своих товарищей. Кто за кем стоит? (2 балла)
-
Дочери в настоящее время 8 лет, а матери 38 лет. Через сколько лет мать будет втрое старше дочери? (3 балла)
-
Как с помощью двух бидонов 5л и 8л отлить из молочной цистерны 7л молока? Молоко разрешается выливать обратно в цистерну. (5 баллов)
-
Катя и Юра купили лотерейные билеты с номерами: 625517 и 322324, и обнаружили, что в каждом из номеров можно расставить знаки арифметических действий и скобки так, что в каждом случае результат будет равняться 100. Как это можно сделать? (3 балла)
Ответы:
-
Перевернуть обои часы. Когда пройдет 3 минуты, в семиминутных часах останется 4 минуты. Поставить яйцо в данный момент вариться. Когда 4 минуты закончатся, перевернуть семиминутные часы обратно. Получим 4+7=11.
-
1 решение: Митя, Толя, Сеня, Костя, Юра
2 решение: Митя, Толя, костя, Сеня, Юра.
-
Через 7 лет.
-
1) Налить молоко в пятилитровый бидон и перелить в восьмилитровый.
2) Снова налить молоко в пятилитровый бидон и долить восьмилитровый бидон. Тогда в пятилитровом бидоне останется 2л молока.
3) Вылить молоко в цистерну из восьмилитрового бидона.
4) Перелить 2л молока из пятилитрового бидона в восьмилитровый бидон.
5) Налить молоко в пятилитровый бидон и перелить его в восьмилитровый.
В результате в восьмилитровом бидоне получим 2+5=7 (л) молока.
-
62+55-17 и (3+22) · (3-2)· 4
6 класс
-
Разместите восемь козлят и девять гусей в пяти хлевах так, чтобы в каждом хлеве были и козлята и гуси, а число их ног равнялось 10. (5 баллов)
-
Расшифруйте запись. Одинаковыми буквами обозначены одинаковые цифры, разными буквами- разные цифры. (2 балла)
УДАР
+УДАР
 ДРАМА
ДРАМА
-
Разместите на трех грузовиках 7 полных бочек, 7 бочек, наполненных на половину, и 7 пустых бочек так, чтобы на грузовиках был одинаковый по массе груз. (2 балла)
-
В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая из жидкостей? (3 балла)
-
В записи 52*2* замените звездочки цифрами так, чтобы полученное число делилось на 36. укажите все возможные варианты. (3 балла)
Ответы:
-
В двух хлевах по 1 козленку и 3 гусям, в трех хлевах - по 2 козленка и 1 гусю.
-
8126
 +8126
+8126
16252
-
На первый грузовик поместить 3 полных бочки, 1 наполненную наполовину и 3 пустых бочки; на второй грузовик- 3 полных, 1 наполненную наполовину и 3 пустых; на третий - 1 полную, 5 наполненных наполовину и 1 пустую.
-
Молоко в кувшине, лимонад в бутылке, квас в банке, вода в стакане.
-
52524, 52128, 52020, 52920.
7 класс
-
4 черные коровы и 3 рыжих дают за 5 дней столько молока, сколько 3 черные коровы и 3 рыжих за 4 дня. У каких коров удои больше: у черных или у рыжих? (3 балла)
-
Натуральное число умножили на каждую из его цифр. Получилось 1995. Найдите исходное число. (2 балла)
-
Число 56 разложите на два слагаемых так, чтобы
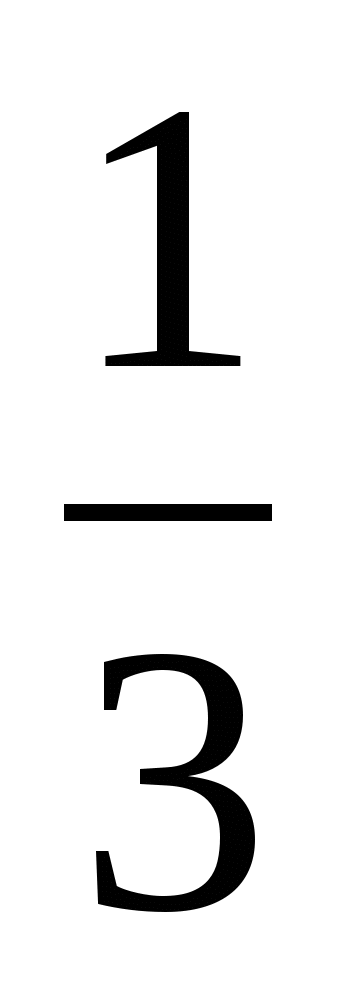 первого слагаемого была равна
первого слагаемого была равна
![]() второго. (2 балла)
второго. (2 балла)
-
Из корзины яиц взяли половину всего количества яиц, потом еще половину остатка, затем половину нового остатка и, наконец, половину следующего остатка. В итоге в корзине осталось 10 яиц. Сколько яиц было в корзине первоначально? (3 балла)
-
Какой угол образуют стрелки часов в 12 часов 20 минут? (5 баллов)
Ответы:
-
Из условия следует, что 20 черных коров и 15 рыжих дают за 1 день столько же молока, что и 12 черных и 20 рыжих коров. Тогда 8 черных коров дают столько же молока, сколько 5 рыжих. Поэтому у рыжих коров удои больше.
-
Разложим 1995 на множители: 1995=3·5·7·19. Так как искомое число не может быть ни однозначным, ни трехзначным, то оно является двузначным. Рассматривая возможные варианты для двузначного числа, получаем ответ: 57·5·7=1995.
-
24+32=56
-
160 яиц.
-
В 12.00 стрелки сходятся вместе. После этого за 20 минут минутная стрелка проходит
![]() окружности, то есть описывает угол в 120º. Часовая стрелка движется
в 12 раз медленнее минутной (так как описывает круг за 12 часов).
Поэтому она за 20 минут опишет угол в 120º : 12=10º и будет
образовывать с минутной стрелкой угол в
окружности, то есть описывает угол в 120º. Часовая стрелка движется
в 12 раз медленнее минутной (так как описывает круг за 12 часов).
Поэтому она за 20 минут опишет угол в 120º : 12=10º и будет
образовывать с минутной стрелкой угол в
120º -10º=110º
Задачи школьной олимпиады по математике 9 класс
1. Решите неравенство:
х 2 - 5х + 6 < 0 .
х 2 -7х + 12
2. Путь из села в город таков: сначала 15 км в гору, потом 6 км с горы. Велосипедист едет без остановок в гору с одной постоянной скоростью, с горы - с другой. В один конец он ехал 3,1 ч, обратно 2,5 ч. какова скорость велосипедиста в гору и с горы?
3. Уравнение х + 1__ = 30 имеет решение в целых числах ( 4;3;2 ).
у + 1 7
z
Найдите еще одно решение уравнения в целых числах.
Задачи школьной олимпиады по математике 8 класс
-
Решите уравнение
| х -1999| + | 1999 - х | = 2000.
-
В классе послушных девочек столько же, сколько непослушных мальчиков. Кого в классе больше: послушных детей или мальчиков? ( Объясните ваш ответ ).
-
На птицеферму привезли корм, которого хватило бы уткам на 30 дней, а гусям - на 45 дней. Рассчитайте, на сколько дней хватит привезенного корма и уткам, и гусям вместе?
8 класс
-
Поставьте знаки модуля так, чтобы равенство стало верным:
1-2-4-8-16=19. (2 балла)
-
Постройте график функции:
y=![]() (3 балла)
(3 балла)
-
В школе 30 классов и 1000 учащихся. Докажите, что есть класс, в котором не менее 34 учеников. (3 балла)
-
Найдите значения a и b, при которых равенство
![]()
Выполняется при всех допустимых значениях переменной x. (4 балла)
-
Найдите все пары натуральных чисел, удовлетворяющих уравнению x²-y²=69. (3 балла)
9 класс
1. Найдите значение выражения:
(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1-
)(1-![]() )
при а=2003 (3 балла)
)
при а=2003 (3 балла)
-
При каких значениях a квадратные трехчлены x²+ax+1 и x²+x+a имеют общий корень?
(4 балла)
-
Сколько цифр содержит число
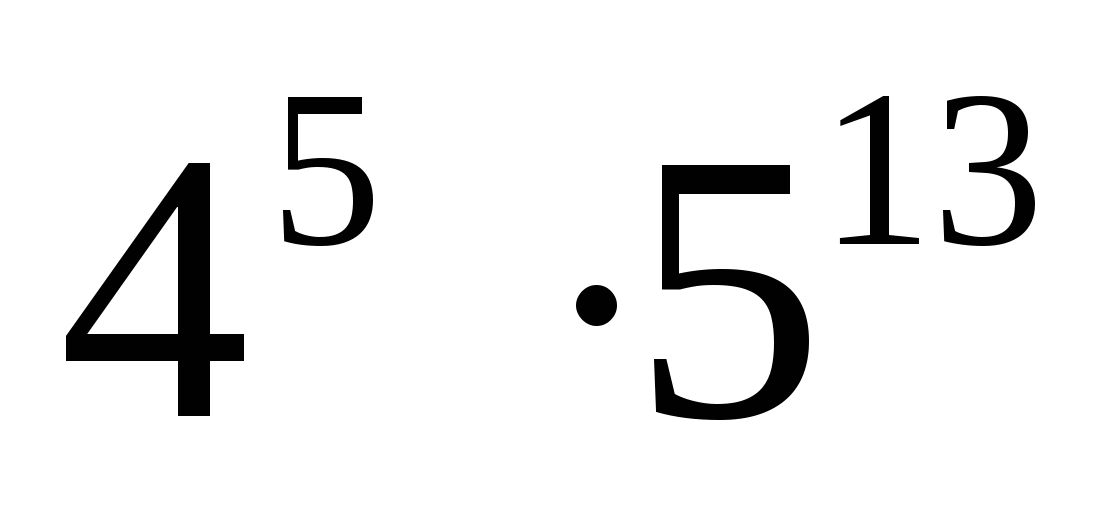 ? (2 балла)
? (2 балла)
-
Четыре семьи, дружившие между собой, держат по 10 различных животных. Их питомцы - белки, кролики, хомяки и ежи. Каждая семья держит разное число животных разных видов - от одного до четырех, и в разных семьях разное количество зверушек одного вида. Определите, сколько и каких животных в каждой семье, если известно, что:
-
у Ивановых, Сидоровых и Петровых ежей не по два;
-
у Ивановых и Петровых кроликов, а у Кузнецовых кроликов и хомяков не по одному;
-
в семьях Сидоровых, Петровых и Кузнецовых живут не по три белки;
-
В семьях Ивановых и Петровых хомяков не по два и не по четыре. (4 балла)
-
Разрежьте квадрат на 5 прямоугольников так, чтобы у соседних прямоугольников стороны не совпадали. (2 балла)
10 класс
-
Решите систему уравнений:
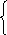
(x+y)(x+y+z)=72,
(y+z)(x+y+z)=120,
(x+z)(x+y+z)=96. (3 балла)
-
При каком целом k неравенство
х²+2(4k-1)х+15k²-2k-7>0 верно при любом действительном х? (4 балла)
-
Решите в целых числах уравнение x²-3xy+2y²=7. (3 балла)
-
Малыш и Карлсон разделили круглый торт двумя перпендикулярными разрезами на 4 части. Карлсон взял себе одну наименьшую часть и одну наибольшую часть, а остальные две отдал Малышу. Кому торта досталось не меньше половины?
(3 балла)
-
О
 тгадайте
ребус:
тгадайте
ребус:
 - ******* **
- ******* **
 *** **8**
*** **8**
-**
 **
**
- ***
 ***
***
0

 (2 балла)
(2 балла)
11 класс
1. Представьте числа от 1 до 10 с помощью числа π, используя скобки, знаки действий, извлечение квадратного корня, а также символ функции [x], где [x] - целая часть
числа x. Например, 11=[![]() +
+![]() ].
(3 балла)
].
(3 балла)
-
</ Постройте график функции: у =
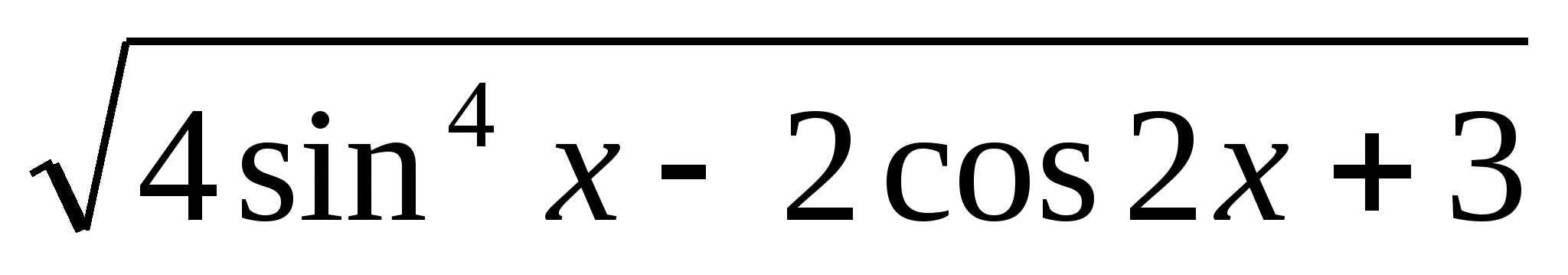 +
+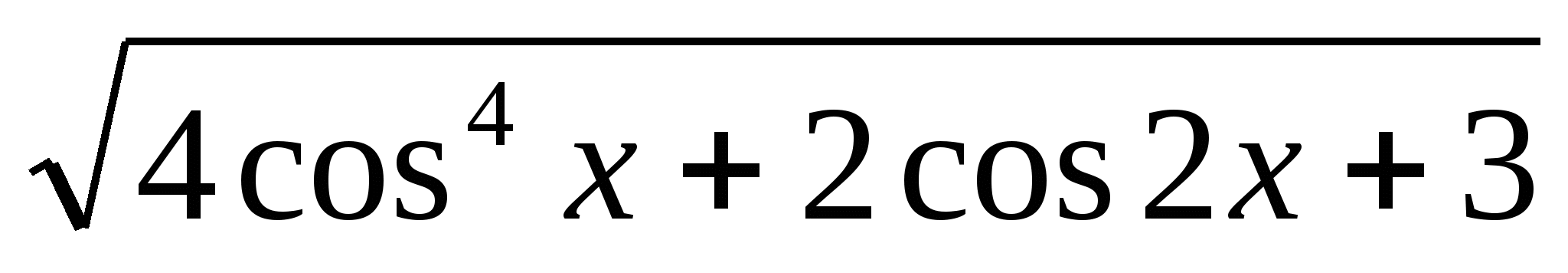 (2балла)
(2балла)
-
Решите уравнение |x-1|-|x-2|=1. (4 балла)
-
Найти четырехзначное число, которое в 4 раза меньше числа, записанного теми же цифрами, но в обратном порядке. (3 балла)
-
Десять машин выпускают одинаковые резиновые мячи массой по 10 г каждый. Одна из машин испортилась и стала выпускать мячи массой по 5 г. Как найти испортившуюся машину с помощью одного взвешивания мячей? (3 балла)
Ответы и решения
8 класс
1. ||1-2|-|4-8|-16|=19.
2. Упрощая правую часть, имеем: y=x, где x≠±1. Таким образом, графиком указанной функции является прямая, заданная формулой y=x, без 2 точек: А(1;1) и В(-1; -1).
3. Пусть такого класса в школе нет, т.е. во всех классах будет 33 и менее учащихся. Тогда во всей школе будет не более 33·30=990 учащихся, что противоречит условию задачи (в школе 1000 учащихся). Значит, наше предположение неверно, поэтому в школе есть класс, в котором не менее 34 учеников.
4. Приводя в правой части равенства дроби к общему знаменателю и учитывая, что знаменатели у дробей в левой и правой частях равны, получим:
5х+31=ах+2а+вх-5х;
5х+31=(а+в)х+(2а-5в).
 Откуда
имеем: а+в=5,
Откуда
имеем: а+в=5,
2а-5в=31.
Решая полученную систему, получаем: а=8, в=-3.
Ответ: при а=8, в=-3.
5. х²-у²=69
(х-у)(х+у)=69
6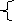
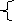 9=1·69=69·1=3·23=23·3,
учитывая, что х>у, имеем:
9=1·69=69·1=3·23=23·3,
учитывая, что х>у, имеем:
х-у=1, х-у=3,
х+у=69, или х+у=23.
Решая данные системы, находим два решения: (35,34) или (13,10).
Ответ: (35,34) или (13,10).
Ответы и решения
9 класс
1. Применяя формулу (х-у)(х+у)=х²-у² последовательно для последних двух множителей, в результате получим:
(1-![]() )(1+
)(1+![]() )=1-a.
)=1-a.
При а=2003 получим 1-а=1-2003=-2002.
Ответ:-2002.
-
Пусть
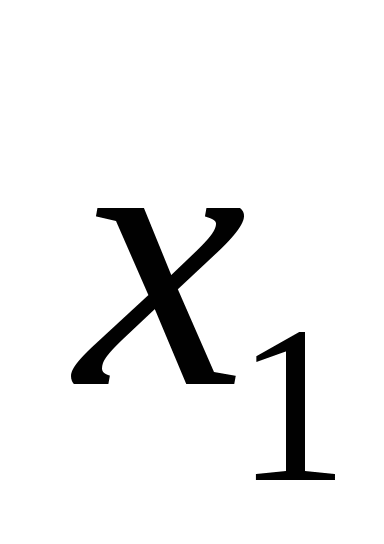 - общий корень данных трехчленов, тогда
- общий корень данных трехчленов, тогда
![]() +a
+a![]() +1=0
и
+1=0
и ![]() +
+![]() +а=0,
т.е.
+а=0,
т.е.
![]() +a
+a![]() +1=
+1=![]() +
+![]() +а
+а
![]() a
a![]() +1=
+1=![]() +а
+а![]() а(
а(![]() -1)=
-1)=
![]() -1
-1![]() (
(![]() -1)(а-1)=0.
-1)(а-1)=0.
Тогда а=1 или ![]() =1.
=1.
Если а=1, то трехчлены оба имеют вид х²+х+1 и не имеют действительных корней.
Если ![]() =1, то 1²+а·1+1=0 и 1²+1+а=0. В обоих случаях а=-2.
=1, то 1²+а·1+1=0 и 1²+1+а=0. В обоих случаях а=-2.
Ответ: а=-2.
3. ![]() =(
=(![]() )
)![]() =
=![]() =1
250 000 000 000.
=1
250 000 000 000.
Ответ: 13 цифр.
4.
-
животные
итого
белки
кролики
хомяки
ежи
Ивановы
3
2
1
4
10
Сидоровы
4
1
2
3
10
Петровы
2
4
3
1
10
Кузнецовы
1
3
4
2
10
5.
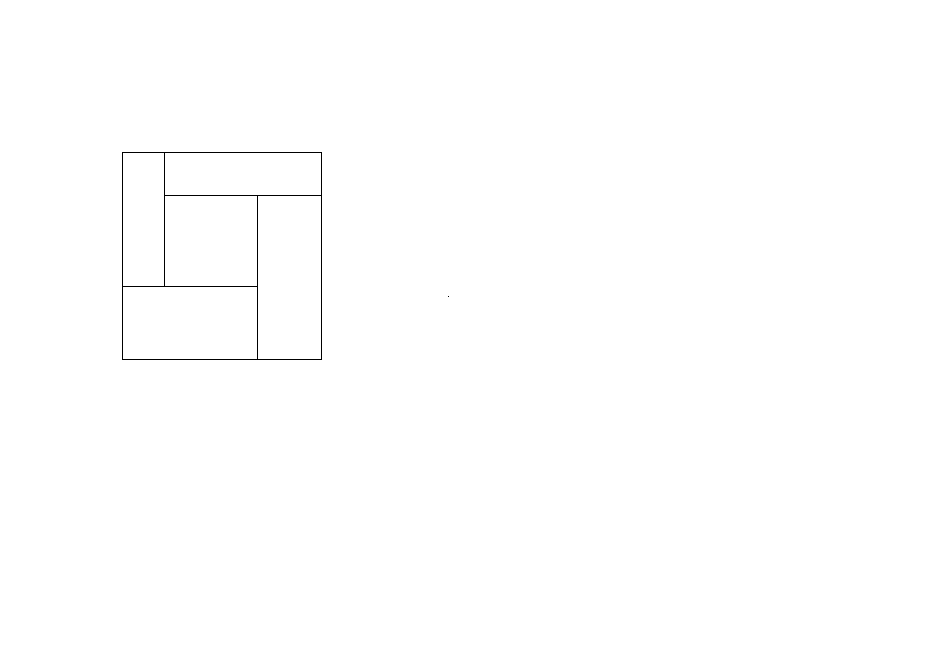
Ответы и решения
10 класс
1. Сложив все три уравнения системы, получим уравнение (х+у+z)(2x+2y+2z)=288, из которого найдем х+у+z=12 или х+у+z=-12. Подставляя вместо х+у+z числа 12 и -12, получим в первом случае: x=2,y=4,z=6, а во втором: x=-2,y=-4,z=-6.
Ответ: (2;4;6),(-2;-4;-6).
-
Неравенство будет верно, если D<0. Найдя дискриминант и учитывая, что он должен быть отрицательным, получим неравенство k²-6k+8<0, которое будет иметь решения при 2<k<4, то есть при k=3.
Ответ: при k=3.
-
Р


 азложим
-3ху на два слагаемых -ху и -2ху. Тогда получим:
х²-ху-2ху+2у²=7. Сгруппируем и вынесем за скобки (х-у) и
получим: (х-у)(х-2у)=7. Учитывая, что
7=1·7=7·1=-1·(-7)=-7·(-1), получим следующие четыре системы
уравнений:
азложим
-3ху на два слагаемых -ху и -2ху. Тогда получим:
х²-ху-2ху+2у²=7. Сгруппируем и вынесем за скобки (х-у) и
получим: (х-у)(х-2у)=7. Учитывая, что
7=1·7=7·1=-1·(-7)=-7·(-1), получим следующие четыре системы
уравнений:
х-у=1, х-у=7, х-у=-1, х-у=-7,
х-2у=7, х-2у=1, х-2у=-7, х-2у=-1.
Решая данные системы, найдем решения уравнения: (-5;-6), (5;6), (13;6), (-13;-6).
Ответ: (-5;-6), (5;6), (13;6), (-13;-6).
-
Проведем два разреза, центрально симметричные уже сделанным. Куски 1, 2, 6, 9 достались Малышу, а симметричные им 7, 8, 4 и 3 - Карлсону, которому отошла еще и середина 5. поэтому Карлсону досталось не менее половины торта.
 - 1089708 12
- 1089708 12
108 90809
 -
97
-
97
 96
96
- 108
 108
108
0
Ответы и решения
11 класс
1. 1=[![]() ];
2=[
];
2=[![]() +
+![]() ];
3=[π]; 4=[ π+
];
3=[π]; 4=[ π+![]() ];
5=[ π
];
5=[ π![]() ];
6=[ π+ π]; 7=[ π+
];
6=[ π+ π]; 7=[ π+![]() ]+
[π];
]+
[π];
8=[( π· π)- ![]() ]; 9=[( π· π)]; 10=[
]; 9=[( π· π)]; 10=[![]() ]+[(
π· π)].
]+[(
π· π)].
2. y=![]() +
+![]()
y=![]() +
+![]()
y= ![]() +
+![]()
y= 2sin²x+1+2cos²x+1
y=4
Ответ: графиком функции является прямая, заданная уравнением у=4.
-
Ответ: х
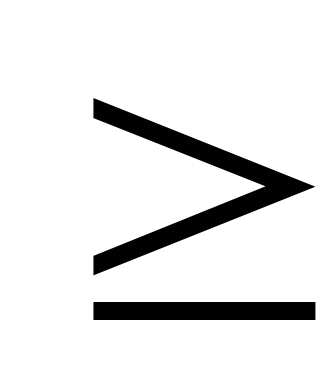 2
2
4. Обозначим искомое число за 1000a+100b+10c+d. По условию задачи имеем:
4(1000a+100b+10c+d)=1000d+100c+10b+a.
Так как левая часть - число четное, то и правая часть - число четное, поэтому a- четная цифра. Тогда a=2, так как в других случаях получим в левой части пятизначное число. Так как 4d оканчивается на 2, то d=8. В итоге имеем:
4(1000·2+100b+10c+8)=1000·8+100c+10b+2.
Тогда 4(10b+c)+3=10c+b или 40b+4c+3=10c+b.
После упрощения получим: 13b+1=2c.
Решением данного уравнения будут: b=1,c=7. Тогда искомое число будет 2178.
Ответ: 2178
5. Возьмем от первой машины один мяч, от второй - два, от третьей - три и т.д., от десятой - десять. Найдем их общую массу. Это взвешивание будет единственным.
Если бы все мячи были массой по 10г, то весы показали бы
10(1+2+3+4+5+6+7+8+9+10)=550 (г).
Если первая машина допускает брак, то общая масса станет меньше на 5г, если вторая, то на 10г, и т.д., если десятая, то на 50г. Таким образом, по массе 55 мячей можно узнать, какая машина испортилась.
ОЛИМПИАДА
6 класс
-
Выразите число 16 с помощью четырех пятерок, соединяя их знаками действий.
(2 балла)
-
В летний лагерь приехали отдыхать три друга- Миша, Володя и Петя. Известно, что каждый из них имеет одну из следующих фамилий: Иванов, Семенов, Герасимов. Миша - не Герасимов. Отец Володи - инженер. Володя учится в 6 классе. Герасимов учится в 5 классе. Отец Иванова - учитель. Какая фамилия у каждого из трех друзей? (3 балла)
-
Школьник прочитал книгу за три дня. В первый день он прочитал 0,2 всей книги и еще 16 страниц, во второй день - 0,3 остатка и еще 20 страниц. В третий день - 0,75 остатка и последние 30 страниц книги. Сколько страниц в книге? (5 баллов)
-
Расшифруйте запись. Одинаковыми буквами обозначены одинаковые цифры, разными буквами - разные цифры. (2 балла)
КОКА
+ КОКА

ВОДА
-
Разрежьте клетчатый прямоугольник размером 5х8 клеток на фигурки из четырех клеток вида: (3 балла)
-
ОЛИМПИАДА 10 КЛАСС
-
Найдите значение выражения:
(1+
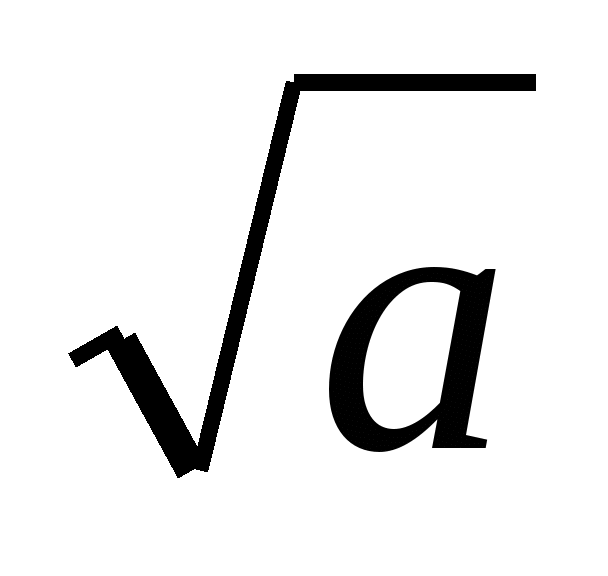 )(1+
)(1+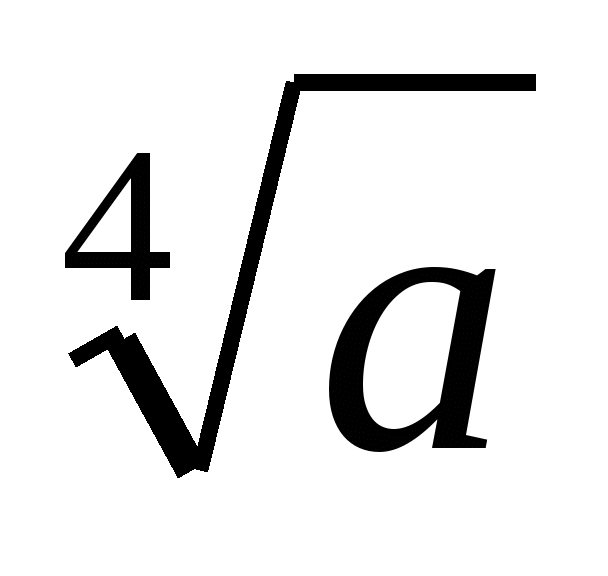 )(1+
)(1+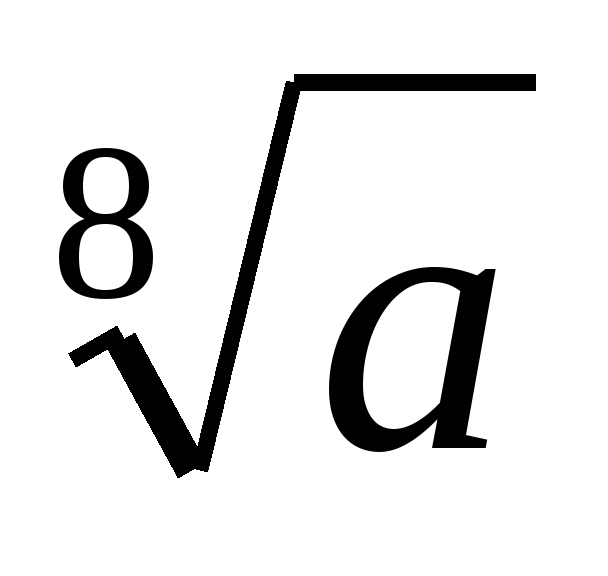 )(1+
)(1+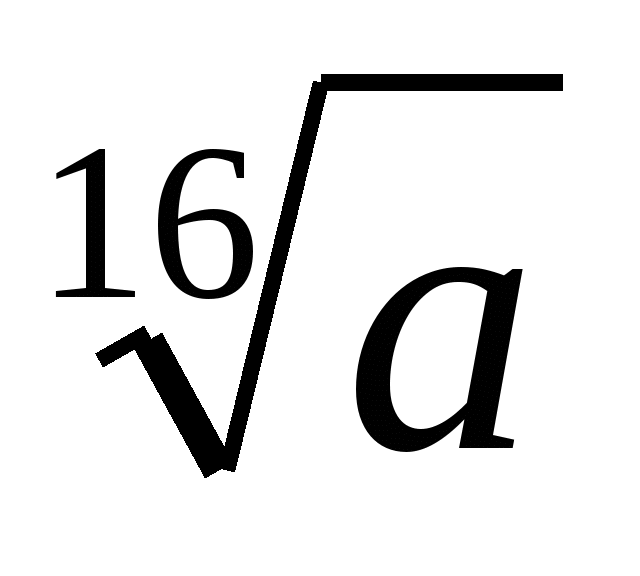 )(1+
)(1+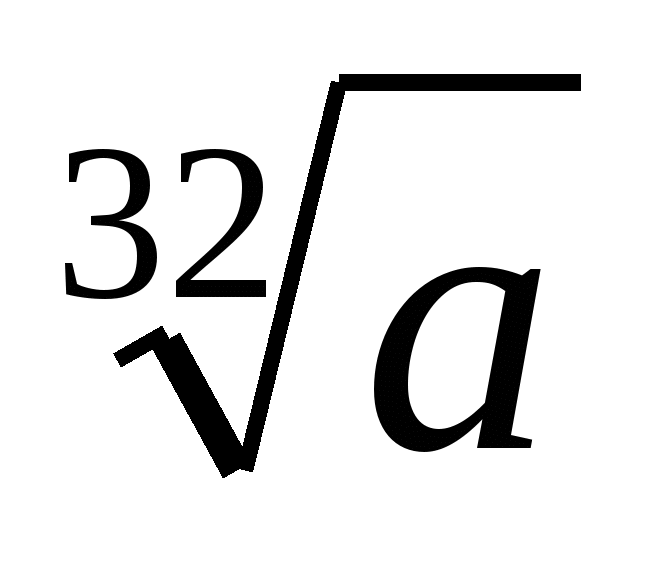 )(1-
)(1-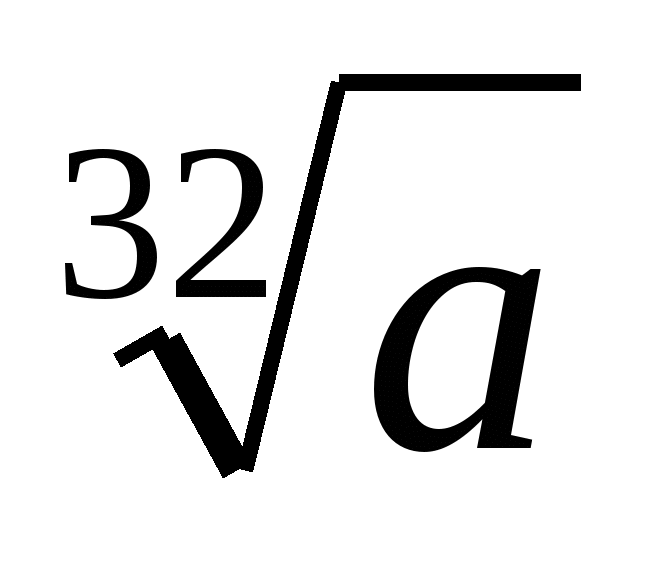 )
при а=2003 (3 балла)
)
при а=2003 (3 балла)
-
Листок календаря частично закрыт предыдущим листком. Какая его часть больше -закрытая или открытая? (3 балла)
-
Автомобиль проехал 600 км. Первую половину пути он двигался со скоростью 100 км/ч, а вторую - 60 км/ч. Найдите среднюю скорость движения автомобиля. (2 балла)
-
Сколько цифр содержит число 4
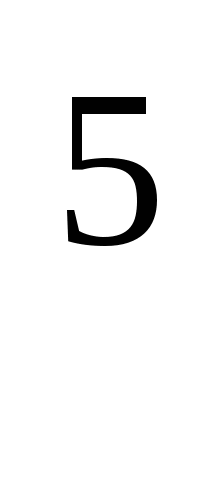 *5
*5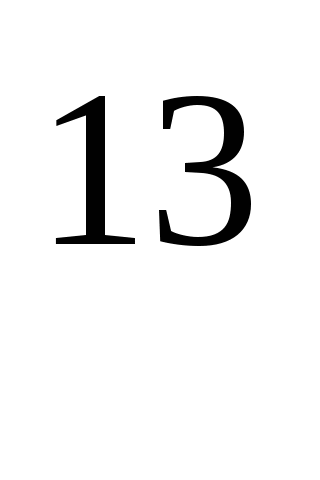 ?
(3 балла)
?
(3 балла)
-
При каком целом k неравенство
х²+2(4k-1)х+15k²-2k-7>0 верно при любом действительном х? (4 балла)

-