Поурочный по геометрии на тему Дөңес көпбұрыштар

1 сабақ

Сабақтың тақырыбы: Дөңес төртбұрыш. Көпбұрыш.

Сабақтың мақсаты:

Дөңес төртбұрыштың қасиеттерін зерттеуде оқушылардың танымдылық ой-өрістерін кеңейту.

Дөңес көпбұрыштың және дөңес төртбұрыштың анықтамаларын беру және олардың элементтерін көрсету.

Дамытушы мақсат: Дөңес және дөңес емес көпбұрыштардың қасиеттерін үйрету арқылы оқушыларды оларды зерттеуге үйрету.

Сабақтың жоспары:

1. Ұйымдастырушылық кезең

2. Жаңа сабақ өту

3. Сабақтың мақсатын түсіндіру

4. Жаңа сабақты өту

5. Жаңа тақырыпқа есептер шығару

6. Жаңа тақырыпты бекіту

7. Үйге тапсырма беру және сабақты қорытындылау.

Сабақтың көрнекілігі:

Сызғыш, циркуль, интерактивті тақта.

Сабақтың өту барысы:

І Ұйымдастыру кезеңі:

Сыныпты түгендеу. Сабақтан қалыс қалған оқушыларды белгілеу.

ІІ Жаңа тақырыпты баяндау

Алдымен сабақта сынық ұғымы енгізіледі.

сынығы деп нүктелерінен және оларды қосатын .... кесінділерінен құралатын фигураны атайды. нүктелері - сынықты төбелері деп, ал кесінділері сынықтың буындары деп аталады. Сынық жай сынық болу үшін оның буындары өзара қиылыспауы керек.

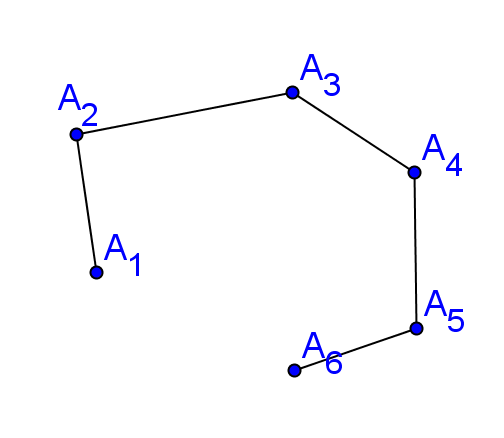
а) жай сынық

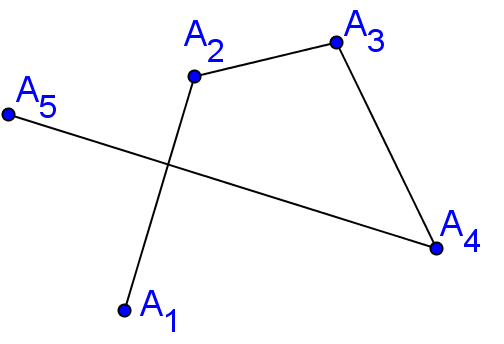
ә) жай сынық емес

Сынықтың ұзындығы деп оның буындарының ұзындықтарының қосындысын айтады.

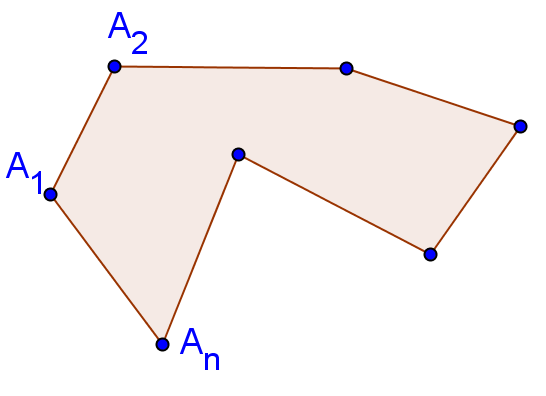
Егер сынықтың бас нүктесі оның соңғы нүктесімен беттессе, онда ол тұйықталған сынық деп аталады. Сынықтың төбесі екі буын үшін ортақ болса, онда ол екі буын көршілес деп аталады. Тұйықталған сынықты көпбұрыш деп атайды. Бір буынның екі төбесі көршілес төбелер деп аталады. Көпбұрыштың көршілес емес төбелерін қосатын кесіндіні диагональ деп атайды.

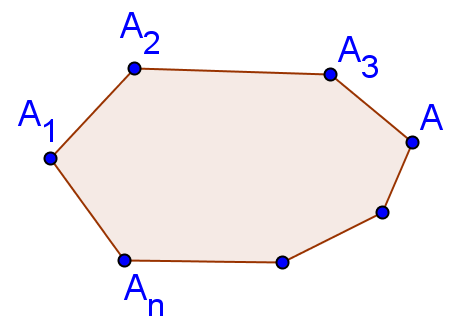
Егер көпбұрыштың кез-келген қабырғасы арқылы түзу жүргізгенде көпбұрыш сол түзудің бір ғана жарты жазықтығында жатса, онда оны дөңес көпбұрыш деп атайды.

Тек қана дөңес көпбұрыштарды қарастыратын болғандықтан бұдан былай дөңес сөзін жазбаймыз.

Дөңес көпбұрыштың берілген төбесіндегі бұрышы деп оның осы төбеде қиылысатын қабырғаларының арасындағы бұрышты атайды.

Төртбұрыш деп төрт нүктеден және оларды тізбектей қосатын ешқандай екеуі өзара қиылыспайтын бір түзудің бойында жатпайтын 4 кесіндіден тұратын фигураны айтады. Берілген нүктелер төртбұрыштың төбелері деп, ал оларды қосатын кесінділер төртбұрыштың қабырғалары деп аталады. Осыдан кейін дөңес және дөңес емес көпбұрыштың анықтамасы төртбұрышқа да орынды екені айтылады. Келесі фигураларды қайсысы төртбұрыш болатыны және болғанның өзінде қай түріне жататынын оқушылар анықтау керек.

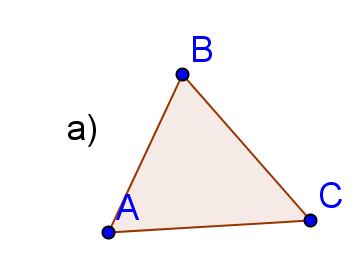
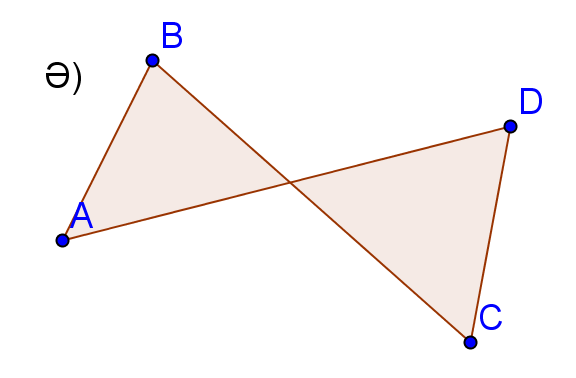
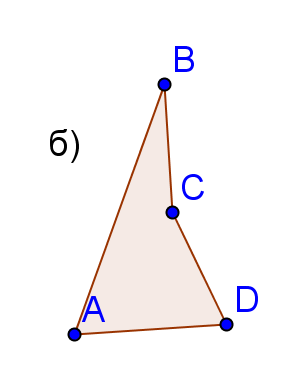
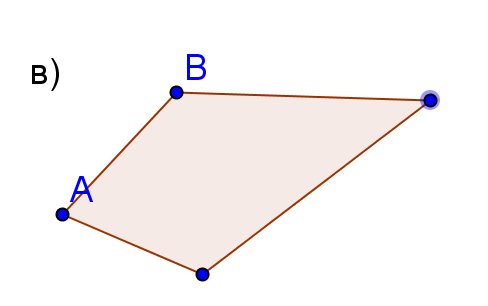а), ә) - төртбұрыш емес ( және кесінділері қиылысады)

б) дөңес емес төртбұрыш

в) дөңес төртбұрыш.

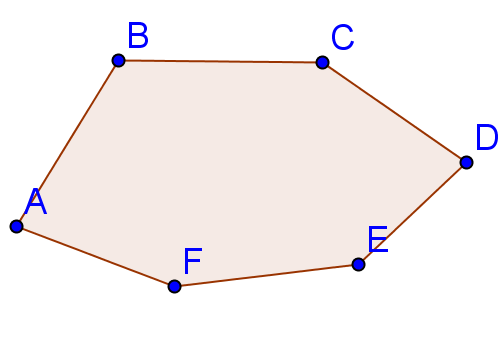
Төртбұрыштың көршілес қабырғалары қарама-қарсы қабырғалары, көршілес төбелері қарама-қарсы төбелері көрсетіледі.

мен , мен, мен , мен көршілес қабырғалары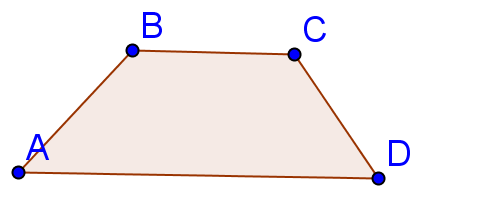

мен , мен қарама-қарсы қабырғалар.

мен , мен , мен , мен көршілес төбелер. мен , мен қарама-қарсы төбелер төртбұрыштың периметрі деп оны барлық қабырғаларының ұзындықтарының қосындысын айтады.

Сабақта бақылау сұрақтары қойылады:

1. Қандай фигура сынық деп аталады?

2. Қандай фигура көпбұрыш деп аталады, элементтерін атаңдар?

3. Қандай фигура төртбұрыш деп аталады? Оның элементтерін атаңдар?

4. Дөңес емес төртбұрыштың бір бұрышы басқаларынан ерекше болады. Неліктен?

5. Төртбұрышта қанша жұп көршілес төбелер және қанша жұп қарама-қарсы қабырғалар болады?

6. Төртбұрышта қанша жұп көршілес қабырғалар және қанша жұп қарама-қарсы қабырғалар болады?

Сабақта келесі есептер шығарылады.

Кез-келген сынығын салыңдар. Сынықтың ұзындығы кесіндісінен ұзын болатынын дәлелдеңдер.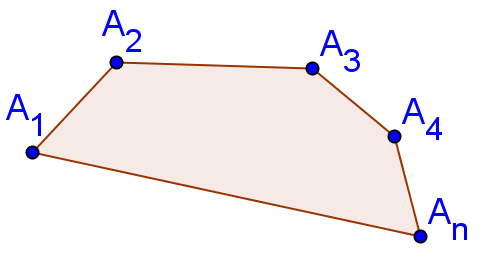

Дәлелдеу мен буындарын бір ғана буынымен алмастырамыз. Үшбұрыш теңсіздігі бойынша

Енді алынған сынығында тағы да буынын буынымен алмастыралық тап осылайша әрі қарай жалғастыра отырып аламыз. Бұдан бастапқы сынығының ұзындығы буынының ұзындығынан үлкен болатынын аламыз. Сынықтың ұзындығы кесіндісінің ұзындығына тең болуы үшін сынықтың төбелері бір түзудің бойында жатуы керек.

2 есеп. Тұйықталған сынықтың кез-келген екі төбесінің ара қашықтығы сынық жарым ұзындығынан кем болатынын дәлелдеңдер. Тұйықталған сынық көпбұрыш болады. Алдымен үшбұрыш үшін дәлелдейік.

Айталық берілген болсын. < <,

< екендігін дәлелдеу керек болсын. < жағдайын қарастырайық.

2<

< үшбұрыш теңсіздігі орындалады. Қалған екі жағдай осылайша дәлелденеді. Сынықтың буындары 3-тен артық болған жағдайлары дәлелденген теңсіздіктегі теңсіздіктің оң жағының сан мәнін үлкейтеді. Бұл жағдайларда да теңсіздік тура болады.

n=4 болғанда <

2<

<

еңсіздігінен шығады.

Әрі қарай да солай кете береді. Теорема дәлелденді.

3 есеп. төртбұрышында және диагональдары жүргізілген. Диагональдардың ұзындықтарының қосындысы төртбұрыштың периметрінен кіші болатынын дәлелдеңдер.

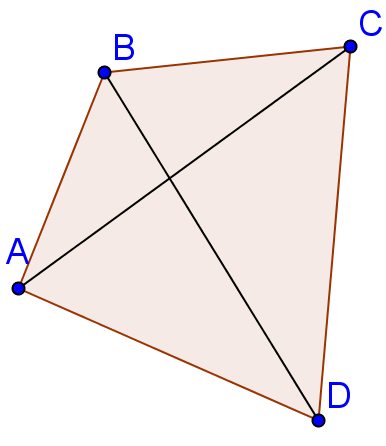
Дәлелдеу және диагональдарын жүргіземіз. Үшбұрыш теңсіздігі бойынша , , , үшбұрыштарында <

<

<

<

Теңсіздіктердің сол және оң жақтарын мүшелеп қосамыз. Сонда 2 + 2 < 2 +2 +2 + бұдан + < + + + . Дәлелденді

Қорытындылау.

Үй тапсырмасы:

1. Бес буынды сынық сызыңдар. Оның қанша төбесі, бұрышы, көршілес төбелер жұбы, көршілес буындар жұбы бар болатындығын табыңдар.

2. Алты бұрыш сызыңдар. Оның қанша диагоналы бар болады? Жауабын түсіндіріңдер.

3. Дөңес және дөңес емес төртбұрыштар сызыңдар. Олардың диагональдарын жүргізіңдер. Диагональдар қиылысады ма? Жауабын түсіндіріңдер.