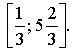Контрольная работа № 8 по теме «Отыскание наибольшего и наименьшего значений» (2 ЧАСА)

Контрольная работа № 8 (2 часа)

Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.

Вариант 1

1. Найдите наименьшее и наибольшее значения функции.

а) 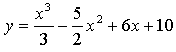на отрезке [0; 1];

б) на отрезке [-; 0].

2. Найдите диагональ прямоугольника наибольшей площади, вписанного в прямоугольный треугольник с катетами 18 см и 24 см и имеющего с ним общий прямой угол.

3. Исследуйте функцию 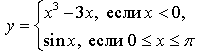на монотонность и экстремумы.

4. При каких значениях параметра а уравнение 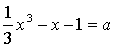имеет три корня?

Вариант 2

1. Найдите наименьшее и наибольшее значения функции.

а) на отрезке [-2; 1];

б) на отрезке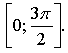

2. В прямоугольном треугольнике с катетами 36 и 48 на гипотенузе взята точка. Из неё проведены прямые, параллельные катетам. Получился прямоугольник, вписанный в данный треугольник. Где на гипотенузе надо взять точку, чтобы площадь такого прямоугольника была наибольшей?

3. Исследуйте функцию 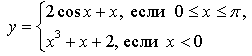на монотонность и экстремумы.

4. При каких значениях параметра а уравнение имеет два корня?

Вариант 3

1. Найдите наименьшее и наибольшее значения функции.

а) на отрезке [0; 3];

б) на отрезке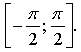

2. Сумма катетов прямоугольного треугольника равна 15 см. Каковы должны быть их длины, чтобы гипотенуза треугольника была наименьшей?

3. Исследуйте функцию 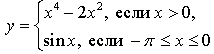на монотонность и экстремумы.

4. При каких значениях параметра а уравнение имеет менее трех корней?

Вариант 4

1. Найдите наименьшее и наибольшее значения функции.

а) на отрезке [-2; 2];

б) на отрезке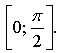

2. Периметр равнобедренного треугольника равен 18 см. Какими должны быть его стороны, чтобы площадь треугольника была наибольшей?

3. Исследуйте функцию 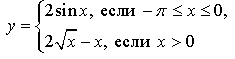на монотонность и экстремумы.

4. При каких значениях параметра а уравнение имеет более одного корня?

Решение вариантов контрольной работы

Вариант 1

1. а) [0; 1]

у (0) = 10

Ответ:

б) [-; 0].

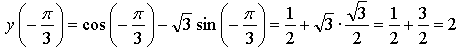
Ответ:

2.

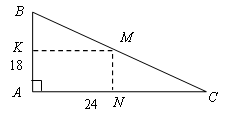
Пусть дан прямоугольный , в котором АВ = 18, АС = 24. Пусть AKMN - прямоугольник, вписанный в .

1) Оптимизируемая величина - площадь прямоугольника AKMN. Обозначим её буквой S.

Пусть KM = х, тогда NС = 24 - х. Треугольники АВС и NMС подобны. Составим пропорцию:

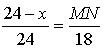
Откуда

Выразим площадь прямоугольника AKMN:

2)

Найдем производную полученной функции:

х = 12

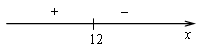
3) При х = 12 функция достигает наибольшего значения. Найдем стороны прямоугольника AKMN:

По теореме Пифагора найдем диагональ прямоугольника:

Ответ: 15 см.

3.

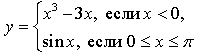
1) Если то

Если то

Получим: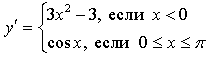

2) х = 0 - критическая точка.

Найдем стационарные точки:

3)

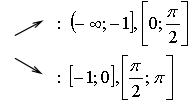
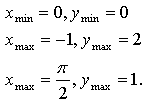
4. - 3 корня.

Решим это уравнение графически. Построим график функции

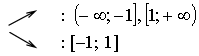
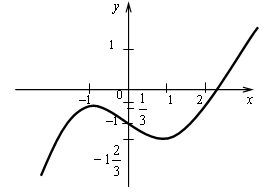
Прямая у = а будет пересекать график этой функции в трёх точках, если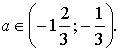

Ответ: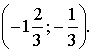

Вариант 2

1. а) [-2; 1]

или х + 1 = 0

х = 0 х = -1

Ответ:

б)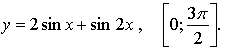

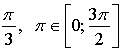
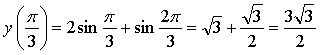
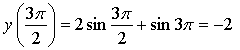
Ответ:

2.

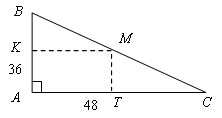
Пусть дан прямоугольный треугольник АВС, в котором Пусть AKMT - прямоугольник, вписанный в  АВС.

1) Оптимизируемая величина - площадь прямоугольника AKMT. Обозначим её буквой S.

Пусть KM = х, тогда ТС = 48 - х. Треугольники АВС и СТМ подобны. Составим пропорцию:

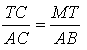
Находим, что

Выразим площадь прямоугольника AKMT:

2)

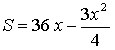
Найдем производную полученной функции:

х = 24

3) При х = 24 функция принимает наибольшее значение. Значит, KM = 24 см. Это говорит о том, что точку М нужно взять на середине гипотенузы.

Ответ: на середине.

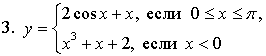
1) Если то

Если то

Получим: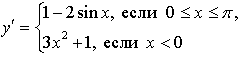

2) х = 0 - критическая точка.

Найдем стационарные точки:

функция монотонно возрастает

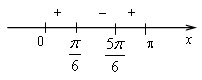
3)

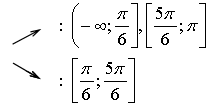
4. , два корня.

Построим график функции

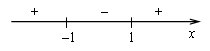
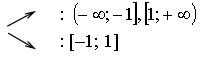
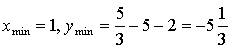
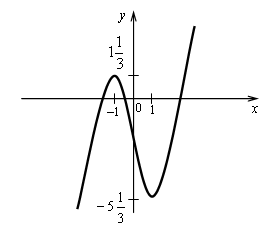
Прямая у = а будет пересекать график этой функции ровно в двух точках, если или

Ответ:

Вариант 3

1. а) , [0; 3]

или

х = 0

0; 2  [0; 3]

Ответ:

б)

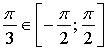
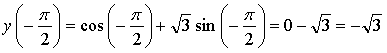
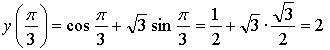
Ответ:

2.

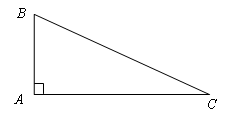
Пусть дан прямоугольный  АВС, в котором и

АВ + АС = 15.

1) Оптимизируемая величина - гипотенуза  АВС, обозначим её буквой с.

Пусть один из катетов равен х см, тогда второй катет равен (15 - х) см.

Выразим гипотенузу треугольника:

2) Найдем производную полученной функции:

3) При х = 7,5 функция достигает наименьшего значения. Значит, катеты должны быть равны по 7,5 см.

Ответ: 7,5 см и 7,5 см.

3.

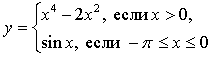
1) Если то

Если то

Получим: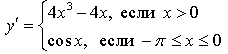

2) х = 0 - критическая точка.

Найдем стационарные точки:

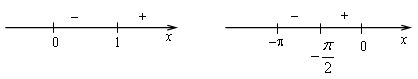
3)

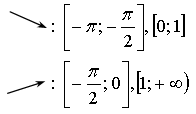
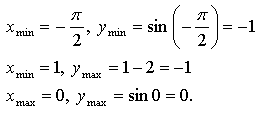
4. , менее трех корней.

Построим график функции

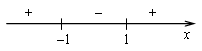
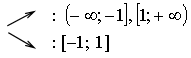
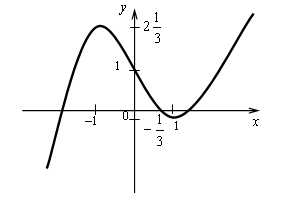
Прямая у = а будет пересекать график этой функции менее чем в трех точках, если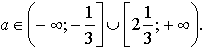

Ответ: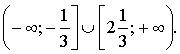

Вариант 4

1. а) , [-2; 2]

Ответ:

б)

или

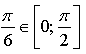
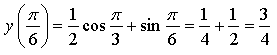
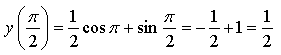
Ответ:

2.

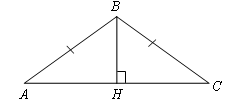
Пусть дан  АВС, в котором АВ = ВС и периметр которого равен 18.

1) Оптимизируемая величина - площадь треугольника. Обозначим её буквой S.

Пусть АВ = ВС = х см, тогда см и см. Из  СНВ найдём ВН:

Выразим площадь  АВС:

2) Найдём производную полученной функции:

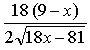
3) При х = 6 функция принимает наибольшее значение. Значит, стороны треугольника должны быть равны по 6 см, то есть  АВС - равносторонний.

Ответ: 6 см, 6 см, 6 см.

3.

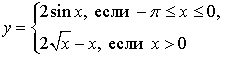
1) Если то

Если то

Получим: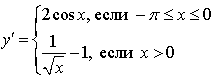

2) х = 0 - критическая точка.

Найдем стационарные точки:

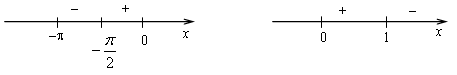
3)

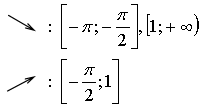
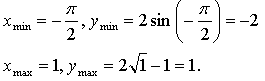
4. , более одного корня.

Построим график функции

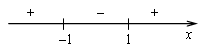
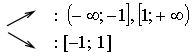
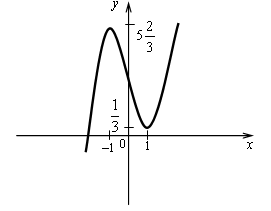
Прямая у = а будет пересекать график этой функции более чем в одной точке, если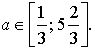

Ответ: