- Учителю
- Конспект по алгебре для 11 класса «Решение показательных уравнений»
Конспект по алгебре для 11 класса «Решение показательных уравнений»
Урок-путешествие по теме
«Показательные уравнения» (слайд №1)
Цели урока:
-
образовательные: обобщить знания по теме «Показательные уравнения», создать разноуровневые условия контроля (самоконтроля) усвоения знаний и умений, проверить практические навыки и умения студентов при решении уравнений, научить применять знания, умения в новой ситуации;
-
развивающие: развивать логическое мышление, вычислительные навыки, умение пользоваться таблицами, расширить кругозор учащихся, развивать любознательность, самостоятельность мышления.
-
воспитательные: воспитывать стремление к овладению знаниями, интерес к предмету, потребность в самостоятельном приобретении знаний, культуру мышления, культуру речи, познакомить с практическим применением показательной функции в различных областях деятельности человека, воспитывать умение выполнять самоконтроль, воспитывать чувство ответственности, уверенности в себе.
Оборудование: мультимедийный проектор, таблицы «Свойства степени с рациональным показателем, «Показательная функция», карточки с дополнительным заданием, карточки для домашней работы.
План урока:
1. Организационный момент - вводное слово учителя.
2. Актуализация опорных знаний:
а) повторение изученного материала;
б) устная работа.
3. Практическая часть - решение упражнений.
а) работа в группах, решение уравнений у доски;
б) дифференцированная самостоятельная работа с самопроверкой;
в) выполнение задания на применение знаний, умений и навыков в новой ситуации.
4. Защита проектов - сообщение ребят: «Практическое применение показательной функции».
5. Итог урока.
6. Домашнее задание.
Ход урока.
-
Организационный момент - вступительное слово учителя (слайд №2).
Учитель. Добрый день, ребята! Сегодня мы заканчиваем изучение показательных уравнений и проведем необычный урок - совершим путешествие по очень важному разделу курса алгебры и начал анализа. А эпиграфом к нашему уроку я взяла слова С.Коваля: «Уравнения - это золотой ключ, открывающий все математические сезамы». Т.е другими словами можно сказать, что, если вы будете уметь решать уравнения, то экзамена по математике вам не стоит бояться.
Отправляясь в путешествие, каждый из нас возьмет с собой багаж, а состоять он будет из знаний, умений и навыков, накопленных вами за время изучения данной темы. Как и в любом путешествии, сегодня нас ждет не только много интересного и неизвестного, на пути всегда встречаются какие-то препятствия, трудности, которые нужно преодолевать. (Сегодня мы обобщим, закрепим и проверим умения и навыки решения показательных уравнений, попробуем выполнить задание на применение знаний, умений и навыков в новой ситуации, пока еще для вас незнакомой, рассмотрим примеры практического применения показательной функции). И к концу урока постараемся ответить на вопрос «Так ли важна изучаемая нами тема в жизни каждого из нас?»
-
Актуализация опорных знаний:
а) повторение изученного материала.
Учитель. Собираясь в путешествие, необходимо хотя бы немного знать о той стране, куда вы отправляетесь. Поэтому начнем мы свое путешествие с повторения.
-
Станция «Повторение - мать учения» (слайд №3).
-
Какое уравнение называется показательным?
-
Какова область определения показательной функции? (слайд №4)
-
При каком условии показательная функция возрастает? Убывает?
-
В
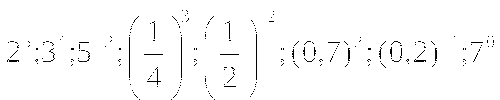
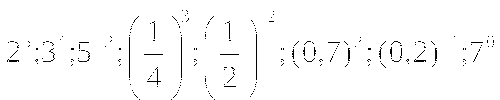 ычислите: (слайд №5)
ычислите: (слайд №5)
-
Ответы: 32, 81, ![]() , 4; 0,49; 5; 1.
, 4; 0,49; 5; 1.
-
Перечислите основные свойства степени с рациональным показателем - свойства в буквенном виде записаны в таблице, учащиеся должны их сформулировать (при умножении степеней с одинаковым основанием, основание остается прежним, а показатели складываются; при делении степеней с одинаковым основанием основание остается прежним, а показатели вычитаются; при возведении степени в степень, основание остается прежним, а показатели перемножаются; любое число в нулевой степени равно 1; чтобы возвести число в отрицательную степень, основание необходимо перевернуть и возвести его уже в положительную степень; чтобы произведение (частное) нескольких множителей возвести в некоторую степень, необходимо каждый множитель возвести в эту степень (и числитель, и знаменатель возвести в эту степень).
б) устная работа.
II. Станция «Внимательная» (слайд №6)
У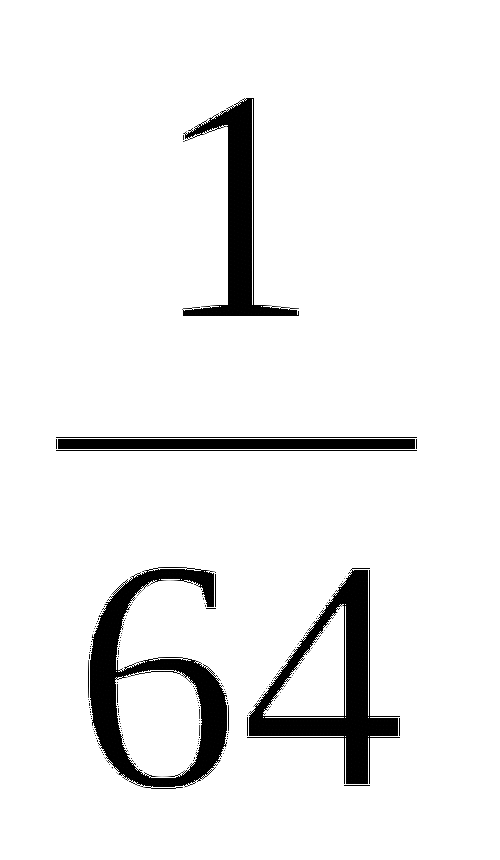
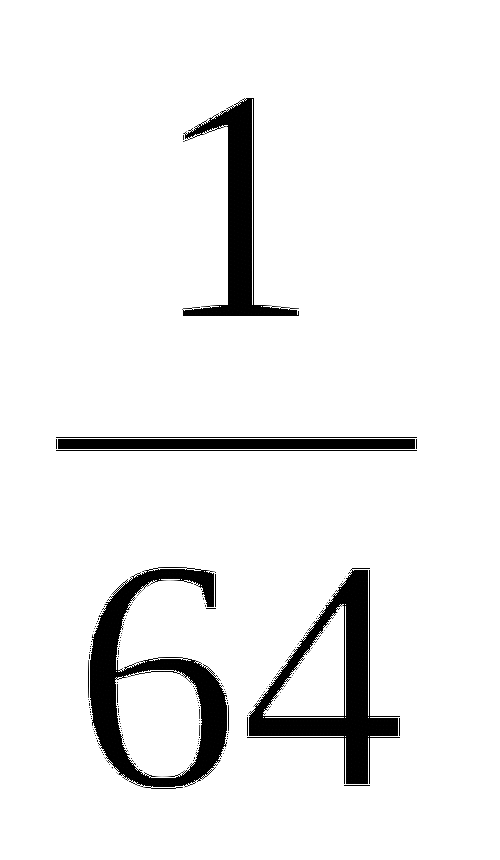 читель. Во время путешествия нужно быть предельно внимательными, чтобы багаж ваших знаний не достался случайному попутчику, и все путешествие не стало для вас разочарованием. Продолжаем наше путешествие и следующая наша станция «Внимательная». Давайте проверим, насколько вы внимательны, выполнив следующее упражнение. Посмотрите внимательно на доску. (Слайд №7) А. Энштейн говорил так: «Мне приходится делить время между политикой и уравнениями. Однако, уравнения, по - моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно. И решать их нужно правильно». Я предлагаю вам решенные уравнения. (Слайд №8) Ребята, посмотрите внимательно на уравнение, его решение, корни. Выясните, нет ли ошибок; если есть, то какова их причина?
читель. Во время путешествия нужно быть предельно внимательными, чтобы багаж ваших знаний не достался случайному попутчику, и все путешествие не стало для вас разочарованием. Продолжаем наше путешествие и следующая наша станция «Внимательная». Давайте проверим, насколько вы внимательны, выполнив следующее упражнение. Посмотрите внимательно на доску. (Слайд №7) А. Энштейн говорил так: «Мне приходится делить время между политикой и уравнениями. Однако, уравнения, по - моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно. И решать их нужно правильно». Я предлагаю вам решенные уравнения. (Слайд №8) Ребята, посмотрите внимательно на уравнение, его решение, корни. Выясните, нет ли ошибок; если есть, то какова их причина?
Ответы: а) неправильно представлено число 8 в виде степени с основанием 2; б) ошибок нет; в) основания можно отбрасывать только в том случае, когда в обеих частях уравнения основание стоит в гордом одиночестве, без всяких соседей и коэффициентов, сначала нужно было применить свойство 1º степени; г) неверно вынесен за скобки общий множитель 5х, в скобках должно получиться (2+1).
3. Практическая часть - решение упражнений.
а) работа в группах, решение уравнений у доски.
III. Станция «Эрудит» (слайд №9).
Учитель. Время не ждет. Нужно отправляться дальше. Много трудностей и опасностей подстерегает нас в этом путешествии. (слайд №10) М.В.Ломоносов говорил «Теория без практики мертва и бесплодна, практика без теории невозможна и пагубна. Для теории нужны знания, для практики сверх того, и умения». И вот теперь вы должны проявить свои умения при решении различных показательных уравнений. Выполнение этого задания потребует от вас применения знаний, умений и навыков изученного материала, а также поможет развить вычислительные способности. Откройте тетради, запишите число, тему урока. Посмотрите внимательно на доску: (слайд №11). Задание. Здесь приведены несколько показательных уравнений. Я вам предлагаю разделиться на три группы (по колонкам) и распределить уравнения на три группы в зависимости от способа решения: I группа - приведение обеих частей уравнения к одному основанию; II группа - вынесение за скобки общего множителя; II группа - замена переменной. Запишите в тетрадях название своего метода решения показательных уравнений и выпишите номера только уравнений своего типа.


Задание студенты выполняют в группах, затем результаты заносят в таблицу (на ватмане), затем проверяем, правильно ли дети распределили уравнения по слайду. (слайд №12)
Приведение к одному
основанию
Вынесение общего
множителя за скобки
Замена переменной
(приведение к квадратному)
2, 5, 10, 12
1, 7, 9, 11
3, 4, 6, 8
А сейчас я предлагаю представителю каждой группы показать решение одного уравнения (номер уравнения, которое предстоит решить на доске вытягивают с помощью жребия) на доске.
К доске выходят трое учащихся, вытягивают карточку с заданием и выполняют решение на доске с комментированием и объяснением. Остальные учащиеся выполняют на местах по одному уравнению своей группы, сверяются с доской; внимательно слушают объяснения других учащихся и записывают их решения в тетради (по желанию).
б) дифференцированная самостоятельная работа с самопроверкой.
Учитель. Внимание! Контроль! В поезд вошли ревизоры, которые проверяют в своих ли вагонах едут пассажиры. Согласно приобретенным билетам, нам достались места в общем, плацкартном и купейных вагонах. Следующее задание, с которым вам предстоит справиться на этой станции - это выполнить дифференцированную самостоятельную работу (слайд № 13). Данное задание направлено на то, чтобы выяснить степень усвоения вами материала по теме «Решение показательных уравнений». Идея заключается в том, что каждый из вас сам выберет уровень сложности задания. За верное выполнение задания вы получаете соответствующую данному уровню оценку. Вам предлагается 2 варианта. Билеты желтого цвета - это места в общем вагоне (соответствуют оценке «3»), зеленого - в плацкартном вагоне (оценке «4»), розового - в купейных вагонах (оценке «5»). Но если вы выполняете задание неверно, то получаете оценку «2» и вам придется заплатить штраф контролеру (вы получите дополнительное домашнее задание по карточке). Если вы хотите подстраховаться и не получить «двойку», то можете выполнить задание из своего варианта, но уровнем ниже того, что выбрали первоначально. Поскольку каждому из вас нужно решить только одно уравнение, то отводимое время на выполнение задания - 5 минут. Желаю всем удачи.
Вариант №1
Вариант №2
«3»
![]()
![]()
«4»
![]()
![]()
«5»
![]()
![]()
(Выполнение самостоятельной работы сопровождается тихой спокойной инструментальной музыкой).
Учитель. А сейчас я предлагаю вам еще раз перепроверить билеты, чтобы избежать недоразумений. (Слайд №14). Сверьте ответы с предложенными на доске и выставьте соответствующую уровню сложности оценку за верное выполнение задания. Если же ответ получен неправильный, то выставляете оценку «2». А теперь давайте подведем итоги и посмотрим, сколько человек из нас едут в общем вагоне? (поднимают руки учащиеся, получившие оценку «3»), в плацкартном вагоне (оценку «4»), в купейных вагонах (оценку «5»). А есть ли среди нас пассажиры, которые перепутали свои места и которым необходимо заплатить штраф? (оценку «2», им дается небольшое дополнительное задание).
в) выполнение задания на применение знаний, умений и навыков в новой ситуации.
IV. Станция «Новая» (слайд №15).
Учитель. Мы подъезжаем к станции «Новая». Путешествуя, человек узнает всегда что-то новое. И наш урок сегодня - не исключение. Рассмотрим пример решения смешанного уравнения. Порой сама задача решения уравнений бывает менее важна, чем нахождение частных корней, удовлетворяющих некоторому условию. Эта проблема стала наиболее актуальной в связи с введением ЕГЭ. В заданиях базового и повышенного уровня сложности этого экзамена все чаще встречаются задания, требующие более глубокого анализа условия: найти корни, принадлежащие заданному отрезку, найти сумму или произведение корней уравнения из заданного промежутка и пр., которых почти не встретишь в учебнике. И на этой станции вам предстоит применить все имеющиеся у вас знания, умения и навыки в новой для вас ситуации. Я предлагаю вам такое задание. Но прежде, чем приступить к его выполнению, мне бы хотелось услышать от вас алгоритм выполнения, все логические шаги. Пожалуйста, вдумайтесь внимательно в условие и постарайтесь понять, что от вас требуется. Внимание на доску.
(Слайд № 16) Найти сумму корней уравнения: ![]()
Учащиеся предлагают план решения:
-
Приравнять к нулю каждый из множителей
-
Решить по отдельности каждое уравнение
-
Найти сумму всех корней данных уравнений
-
Записать ответ
Учитель. Произведение множителей равно нулю, когда один из множителей равен нулю, а другой при этом имеет смысл. Поэтому необходимо будет проверить, что корни каждого из уравнений входят в область определения другого. Сделать это можно несколькими способами: оформить задание через равносильные переходы; решить уравнение и в конце сделать проверку; либо найти ОДЗ уравнения, входящих в него множителей; решить уравнение и посмотреть, какие корни удовлетворяют ОДЗ. Какова область допустимых значений переменной первого множителя? (все числа, так как это показательная функция и ее областью определения являются все действительные числа). Второго множителя? Областью определения дроби являются все числа, при которых знаменатель не равен 0.
ОДЗ: ![]()
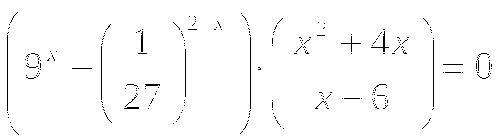 или
или 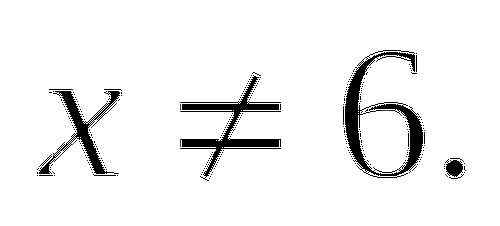
В ОДЗ входят только числа -4 и 0, их сумма равна -4. Ответ. -4.
4. Защита проектов - сообщение ребят: «Практическое применение показательной функции».
V. Станция «Практического применения» (слайд №17).
Учитель. Всякая дорога немного утомляет, и я думаю, что нам пора немного отдохнуть. Сейчас мы проезжаем станцию «Практического применения» и предлагаем вам окунуться в мир практической стороны показательной функции. Квасникова Ксения и Галиева Юлия познакомят вас с применением данной темы в различных областях деятельности человека.
Сообщение учащихся сопровождается показом слайдов. (Квасникова Ксения). Порой многие понятия курса алгебры и математического анализа носят абстрактный характер, и мы задаёмся вопросом: «А где применяются те знания, которые мы получаем на уроках математики?» Так возникла идея: исследовать, в каких областях науки, техники нашла применение показательная функция. Задавшись целью, мы провели небольшую исследовательскую работу и выяснили, что показательная функции имеет прикладное значение в следующих областях естествознания: физика, химия, биология, география, астрономия, а так же экономика банковского дела и производства. Приведем в качестве доказательства только некоторые примеры.
Биология. (Слайд №18) Рост количества бактерий происходит по закону N=5t, где N - число колоний бактерий в момент времени t, t - время размножения. Это закон органического размножения при благоприятных условиях (отсутствие врагов, большое количество пищи), живые организмы размножались бы по закону показательной функции.
(Слайд №19) Так, например, одна комнатная муха может за лето произвести потомство 8*1014 особей потомства, их вес составил бы несколько миллионов тонн (вес потомства пары мух превысил бы вес нашей планеты). Они бы заняли огромное пространство, а если выстроить их в цепочку, то ее длина будет больше, чем расстояние от Земли до Солнца. По такому же принципу распространились завезенные в Австралию кролики, которые стали экологической катастрофой для этого уникального континента. Рост различных видов микроорганизмов и бактерий, дрожжей, ферментов подчиняются одному и тому же закону - N=N0ekt. Процессы выравнивания - именно так называются процессы, изменяющиеся по законам показательной функции, часто встречаются в химии и биологии. Например, при испуге в кровь внезапно выбрасывается адреналин, который впоследствии разрушается. Причем скорость разрушения примерно пропорциональна количеству этого вещества, еще остающемуся в крови. Примером обратного процесса может служить восстановление концентрации гемоглобина в крови у донора или раненого, потерявшего много крови.
География. (Слайд №20) (Галиева Юлия) Для планирования развития городов, других населённых пунктов, строительства жилья, дорог, других объектов мест проживания людей, необходимы расчёты - прогнозы на 5, 10, 20 лет вперёд.
Для решения этих задач используется формула сложных процентов ![]() .
.
Экономика производства. (Слайд №21) Приведём примеры, демонстрирующие применение показательной функции в экономических расчётах производства. Так, стоимость оборудования цеха через t лет может быть найдена по формуле ![]() , где
, где ![]() - первоначальная стоимость оборудования в рублях, p - ежегодный процент амортизации, В - стоимость оборудования в рублях через t лет.
- первоначальная стоимость оборудования в рублях, p - ежегодный процент амортизации, В - стоимость оборудования в рублях через t лет.
Физика. Тема «Показательная функция» является основополагающей при изучении таких тем физики, как, «Термодинамика», «Электромагнетизм», «Ядерная физика», «Колебания», используется для решения некоторых задач судовождения.
(Слайд №22) Все, наверное, замечали, что если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо медленнее. Дело в том, что скорость остывания пропорциональна разности между температурой чайника и температурой окружающей среды. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала температура чайника равнялась То, а температура воздуха T1, то через t секунд температура Т чайника выразится формулой: T=(T1-T0)e-kt+T1,
где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.
(Слайд №23) Много трудных математических задач приходится решать в теории межпланетных путешествий. Одной из них является задача об определении массы топлива, необходимого для того, чтобы придать ракете нужную скорость v. Эта масса М зависит от массы m самой ракеты (без топлива) и от скорости v0, с которой продукты горения вытекают из ракетного двигателя.
Если не учитывать сопротивление воздуха и притяжение Земли, то масса топлива определится формулой: M=m(ev/v0-1) (формула К.Э.Циолковского).
Как видите, во всех приведенных выше исследованиях использовалась показательная функция.
(Слайд №24) Вот некоторые из Нобелевских лауреатов, получивших премию за исследования в области физики с использованием показательной функции: (Слайд №25) Пьер Кюри - 1903 г. ; Ричардсон Оуэн - 1928 г.; (Слайд №26) Игорь Тамм - 1958 г.; Альварес Луис - 1968 г.; (Слайд №27) Альфвен Ханнес - 1970 г.; Вильсон Роберт Вудро - 1978 г.
5. Итог урока. VI. Станция «Итоговая» (слайд №28).
Учитель. Ну вот и подошёл к концу наш урок. Мы с вами обобщили решение показательных уравнений, выяснили степень усвоения материала, но путешествие по разделу «Показательная функция» можно еще продолжать бесконечно. Нам еще неведомы многие темы этого раздела: решение показательных неравенств, более сложных уравнений, систем уравнений и неравенств. А мне бы хотелось услышать ответы на вопросы: был ли наш урок для вас познавательным? Что вам больше всего запомнилось? (слайд №29). А закончить наш урок мне бы хотелось словами великого педагога Яна Амоса Каменского «СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС, В КОТОРЫЙ ТЫ НЕ УСВОИЛ НИЧЕГО НОВОГО И НИЧЕГО НЕ ПРИБАВИЛ К СВОЕМУ ОБРАЗОВАНИЮ». Очень надеюсь, что во время нашего урока каждый из вас пополнил свои знания.
Давайте вернемся к эпиграфу нашего урока «Решение уравнений это золотой ключ, открывающий все сезамы». Мне хотелось бы вам пожелать, чтобы каждый из вас нашел в жизни свой золотой ключик, с помощью которого перед вами открывались бы любые двери, и все ваши мечты и желания сбывались. Выставляются оценки за урок, комментируются.
6. Домашнее задание.
У![]() читель. Спасибо большое всем за урок. Запишите домашнее задание. Есть ли вопросы?
читель. Спасибо большое всем за урок. Запишите домашнее задание. Есть ли вопросы?
Найдите произведение корней уравнения:
О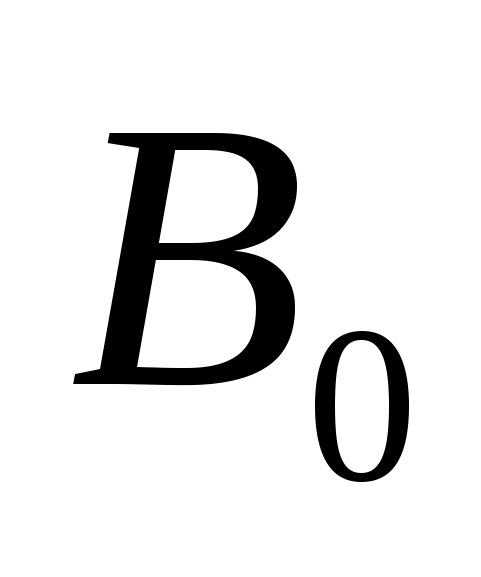 ДЗ:
ДЗ: 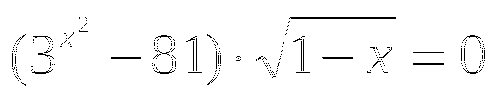
Ответ: -2.
Дополнительные уравнения для тех, кто не справился с самостоятельной работой: