Конспект урока Расстояние от точки до плоскости 10 класс

</ Конспект урока.

Геометрия 10 класс

Тема урока: «Расстояние от точки до плоскости»

Для изучения темы отведено часов

Тема: расстояние от точки до плоскости.

Тип урока: урок изложения нового материала.

Цели урока.

Дидактические:

- обобщить и систематизировать знания учащихся по теме;

- продолжить формирование умений и навыков по решению задач;

- стимулировать учащихся к овладению решением задач;

- проконтролировать степень усвоения знаний, умений и навыков по теме.

Развивающие:

- совершенствовать, развивать умения и навыки по решению задач на нахождение расстояния от точки до плоскости;

- развивать логическое мышление, учить анализировать и обобщать;

- продолжить работу по развитию математической речи и памяти.

Воспитательные:

- продолжить формирование навыков эстетического оформления записей в тетради и выполнения чертежей;

- приучать к умению общаться и выслушивать других;

- воспитание сознательной дисциплины;

- развитие творческой самостоятельности и инициативы.

Задачи урока:

• Обеспечить усвоение новых понятий, изображать и определять на рисунке перпендикуляр, наклонную, проекцию наклонной, расстояние от точки до плоскости

• применить знания при решении задач базового уровня

• развивать пространственное воображение;

• развивать навыки как самостоятельной деятельности, так и работы в паре, выслушивать объяснения и самому объяснять, проводить самоанализ своей работы

Планируемые образовательные результаты:

предметные

• знать определения понятий: перпендикуляр, наклонная, проекция;

• знать план решения задачи

личностные

• развитие познавательных интересов, учебных мотивов;

• проявление дисциплинированности, трудолюбия и упорства в решении поставленных целей;

метапредметные

• умение ставить перед собой цель и планировать деятельность в соответствии с поставленной целью;

• сличение способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;

• умение вступать в сотрудничество с учителем и сверстниками, работать в группе;

• формирование научного мировоззрения

Оборудование урока:

• презентация к уроку;

• карточки с задачами;

• лист самооценки для каждого ученика

Литература:

«Геометрия. 10-11 класс», Л. С. Атанасян и др., М.: Просвещение, 2006 г. 256 с.;

«Изучение геометрии в 10-11 классах. Книга для учителя», С. М. Саакян, В. Ф. Бутузов, 2010 г., 248 с.

Ход урока

1. Организационный момент: разъяснение учащимся темы, цели и организацию работы в парах , рассказывает о заполнении листа самооценки

2. Изложение нового материала:

Объяснение ведется с помощью презентации, в результате на экране и в тетрадях учащихся появляются записи: (см. слайд 2,3)

3. Решение задач, работая в парах:

Задача 1

-решить задачу самостоятельно и оформить решение в тетради

- обсудить решение в паре, заполнить лист самооценки

Задача: Доказать, что проекции равных наклонных, проведенных из одной точки равны.

Обсудить вместе с классом алгоритм решения следующей задачи: (см. слайд 5, 6, 7)

Найти расстояние от точки Р до плоскости треугольника, если точка Р равноудалена от его вершин. (см. слайд 5)

Вопросы к классу:

-Где находится точка О ?

-Каким свойством она обладает ? (она равноудалена от вершин треугольника, т.е. является центром описанной около треугольника окружности)

-От чего зависит местонахождение центра описанной окружности (от типа треугольника)

-Что нужно знать, чтобы найти искомое расстояние РА и РО, где РО- радиус описанной окружности)

Составим план решения задачи:

1. Определить тип треугольника и местонахождение точки о

2. Сделать рисунок к задаче

3. Найти радиус описанной окружности:

прямоугольный

равносторонний

остроугольный

тупоугольный

О - середина гипотенузы

О - точка пересечения медиан, высот, биссектрис

О - точка пересечения серединных перпендикуляров

О - точка пересечения серединных перпендикуляров

R=c/2

R=

R=

S=

P=(a+b+c)/2

R=

S=

P=(a+b+c)/2

4. Найти расстояние по теореме Пифагора : РО=

4. Тест. Работа в паре: решить тест, поменяться тетрадями, проверить правильность

Тест по теме «Расстояние от точки до плоскости».

1.Отрезок АН называется__перпендикуляром___________________,

проведенным из точки А к плоскости , если прямая АН и пересекает ее в точке Н. Точка Н - основание перпендикуляра______________________

2.Отрезок АМ называется __наклонной___________________________,

проведенной из точки А к плоскости , если прямая АМ не перпендикулярна плоскости и пересекает ее в точке М. Точка М - ___основание наклонной_

3. Перпендикуляр, проведенный из данной точки к плоскости, __меньше__________любой наклонной, проведенной из той же точки к этой плоскости.

4. Длина перпендикуляра, проведенного из точки А к плоскости называется _расстоянием от точки А к плоскости_________________

5. Через точку М проведены прямые c и d , пересекающие плоскость в точках С и Д, причем прямая с . Тогда МС - _перпендикуляр______, МД - _____наклонная__________, СД - __проекция наклонной____________

6. Расстояние от точки А до плоскости равно 3 см. Длина перпендикуляра, проведенного из точки А к плоскости равно _____3 см________.

7. Установите соответствие по рисунку.

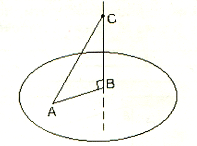
1. АС А. Проекция наклонной.

2. СВ В. Перпендикуляр.

3. АВ С. Наклонная.

Ответ: 1 __С__ 2 __В___ 3 ___А___

8. Из точки А к плоскости проведены наклонная АВ длиной 5 см. Найдите ее проекцию, если расстояние от точки до плоскости 3 см.

Ответ: _4 см.____

9. Расстояние между параллельными плоскостями - это расстояние _____расстояние от точки одной плоскости до другой_____________

10. Расстоянием между скрещивающимися прямыми называют __длину их общего перпендикуляра___________________________

11. Прямая NM параллельна плоскости . Расстоянием от точки N до плоскости равно 6 см. Расстояние от точки М до плоскости равно _ 6 см__

12. Точка В лежит в плоскости , а точка А находится от плоскости на расстоянии 8 см. Найдите расстояние от середины отрезка АВ до плоскости .

Ответ: 4 см.

Внести данные в лист самооценки.

Задача 3.Вернуться к своей паре и совместно решить следующие задачи:

1пара: Точка К находится на расстоянии 7 см от вершин треугольника со сторонами 5 см, 5 см и 6 см. Найдите расстояние от точки К до плоскости треугольника.

2 пара: Точка К находится на расстоянии 8 см от вершин треугольника со сторонами 5 см, 5 см и 8 см. Найти расстояние от точки К до плоскости треугольника.

Поменяться парами, объяснить решение своей задачи, разобрать другую задачу, проверить правильность решения, заполнить лист самооценки

5. Итог урока

Тетради сдать на проверку учителю.

6. Рефлексия

7. Домашнее задание

§2. П.19 № 114, № 140.

Д.п. Из точки S проведены на плоскость перпендикуляр SO и наклонные SAи SB. Длины наклонных соответственно равны 13 см и 20 см. Длина проекции наклонной AS равна 5 см. Найдите расстояние от точки S до плоскости и длину проекции наклонной SB.

Лист самооценки знаний ученика 10 класса______________________________

задачи

Не приступил к решению

(0 баллов)

Не успел решить

(1 балл)

Решил с ошибкой

(2 балла)

Решил полностью

(3балла)

Объяснил

решение

(3 балла)

1

2

3

Посчитай количество набранных баллов:

16-18 баллов - «Молодец, очень хорошо!»

12-15 баллов - «Не плохо!»

9-11 баллов - « Можно и получше ! »

менее 9 баллов - «Сегодня не твой день!»