Конспект факультативного занятия по математике на тему 'Введение в топологию. Лист Мёбиуса' (6 класс)

Тақырып / Тема: "Введение в топологию. Лист Мёбиуса". (1час)

Мақсат / Цель:

1. Познакомить учащихся с листом Мёбиуса, его свойствами и применением в технике. Эстетическое значение листа Мёбиуса.

2. Развить внимание, наблюдательность, умение обоснованно делать выводы, а также познавательный интерес учащихся. Развить навыки групповой работы.

3. Воспитание аккуратности, внимательности и чувства взаимовыручки.

Құрал-жабдықтар, көрнекті құралдар / Оборудование, наглядные пособия: интерактивная доска, готовая презентация к уроку, раздаточный материал, бумага, ножницы, фломастер и клей.

Оқулық / Учебник: «Наглядная геометрия 5-6», И.Ф. Шарыгин, Л.Н. Ерганжиева, издательский дом «Дрофа» 1999 г.

Сабақ түрі / Тип урока: урок-практикум получения новых знаний.

Методические замечания:

К занятию, посвященному листу Мёбиуса, полезно подготовить достаточное количество бумажных лент, с которыми будут проводиться эксперименты. Хороши ленты, у которых длина примерно в 4 раза больше ширины. При разрезании листов Мёбиуса, склеенных из более узких лент, получатся слишком тонкие "кольца". Предложите набор лент, клей и ножницы каждому школьнику для экспериментальной работы сначала параллельно с учителем, а потом самостоятельно.

Сабақ барысы / Ход урока:

Организационный момент.

Девизом нашего урока я взяла слова Козьмы Пруткова «Глядя на мир, нельзя не удивляться».

У каждого из нас есть интуитивное представление о том, что такое "поверхность". Поверхность листа бумаги, поверхность стен класса, поверхность земного шара известны всем. Может ли быть что-нибудь неожиданное и даже таинственное в таком обычном понятии? Ответ на этот вопрос мы постараемся получить сегодня на уроке, тема урока « Введение в топологию. Лист Мёбиуса».

ТОПОЛОГИЯ (по-другому - "геометрия положения") является одним из самых «молодых» разделов современной геометрии. Чтобы получить некоторое представление о топологии, рассмотрим несколько топологических опытов с поверхностями, полученной из бумажной полоски.

Изготовление и знакомство с листом Мёбиуса.

Смотрите, я беру бумажную ленту АВСD, разделенную по ширине пополам пунктирной линией. Прикладываю ее концы АВ и СD друг к другу и склеиваю. Но не как попало, а так, чтобы точка А совпала с точкой D, а точка B с точкой С. Перед склейкой я перекрутила ленту один раз. Получилось знаменитое в математике бумажное кольцо. У него есть даже особое название - "Лист Мёбиуса". Изучение листа Мёбиуса - хорошее введение к элементам топологии.

1.Сколько сторон у листа Мёбиуса?

У ленты, из которой сделан лист Мёбиуса, две стороны. А у него самого, оказывается, есть только одна сторона!

Попробуйте покрасить одну сторону листа Мёбиуса - кусок за куском, не переходя за край ленты. И что же? Вы закрасите весь лист Мёбиуса!

Историческая справка.

Таинственный и знаменитый лист Мебиуса (иногда говорят: "лента Мёбиуса") придумал в 1858 г. немецкий геометр Август Фердинанд Мёбиус (1790-1868), ученик "короля математиков" Гаусса. Мёбиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика была обязана своим развитием. В те времена занятия математикой не встречали поддержки, а астрономия давала достаточно денег, чтобы не думать о них, и оставляла время для собственных размышлений. И Мёбиус стал одним из крупнейших геометров XIX в. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Это открытие односторонних поверхностей, одна из которых - лист Мёбиуса. Лист Мёбиуса - один из объектов области математики под названием "топология". В топологии изучаются свойства фигур и тел, которые не меняются при их непрерывных деформациях (как если бы они были сделаны из резины). Сама топология, можно сказать началась именно с листа Мёбиуса. Слово это придумал Иоган Бенедикт Листинг, профессор Геттингенского университета, который почти в тоже время, что и его лейпцигский коллега, предложил в качестве первого примера односторонней поверхности уже знакомую нам, единожды перекрученную, ленту.

Эксперименты для всех.

Опыт №1 и №2. Возьмем нами приготовленный лист Мёбиуса и разрежем склеенную ленту посередине, вдоль пунктирной линии. Как вы думаете, что получится? Конечно, если бы мы не перекрутили ленту перед склейкой, все было бы просто: из одного широкого кольца получилось бы два узких (это тоже лучше продемонстрировать). А что сейчас?

Получилось не два кольца, а одно, вдвое уже, но зато вдвое длиннее. К тому же перекручено оно не один раз, а два. Предлагаю детям результат эксперимента занести в таблицу.

Число полуоборотов

Результат разрезания

Свойства

Рисунок

0

2 кольца

Длина окружности кольца та же, но кольцо в 2 раза уже

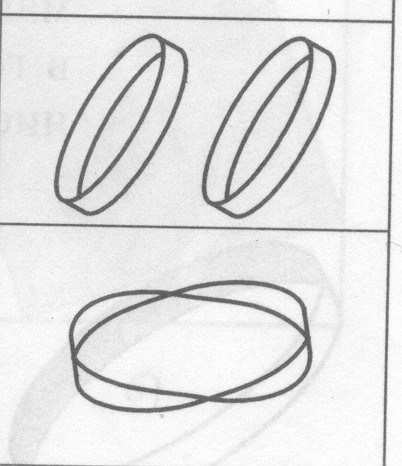
1

1 кольцо

Кольцо перекручено на 2 полуоборота, длина его окружности в 2 раза больше, и кольцо уже исходного

2

2 сцепленных кольца

Кольцо перекручено на 2 полуоборота, длина его окружности та же, но кольца в 2 раза уже

3

1 кольцо

1 кольцо вдвое длиннее и уже с множеством перегибов.

Продолжаю эксперименты

Опыт №3 Дважды перекрученное кольцо. А ну-ка, разрежем это кольцо еще раз посередине. Получится два сцепленных друг с другом кольца, каждое из которых дважды перекручено (заносим результат в таблицу).

Опыт№4 Возьмем кольцо с тремя перекрутами и разрежем опять посередине. получим одно кольцо вдвое длиннее и уже с множеством перегибов.

Может быть кто-то сумеет их пересчитать? (Заканчиваем заполнение таблицы).

(если успеем)

Опыт N 5 Склейте два кольца- одно простое и лист Мёбиуса. Разрежьте каждое из них пополам вдоль. Что у Вас получилось:

2 простых и 1 кольцо Мёбиуса

1 простoе и 2 кольца Мёбиуса

Опыт N 6

Попробуйте прорезать в полосе щель и продеть сквозь нее один конец полосы. (как показанно на рисунке) А теперь попробуйте продолжить разрез вдоль всей ленты. Что у вас получилось, если не секрет:

Два кольца Мёбиуса

Вывернутое но простое кольцо

Топология как наука.

Наука эта молодая и потому озорная. Иначе не скажешь о тех правилах игры, который в ней приняты. Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать - делать с ней всё что угодно, только не разрывать и не склеивать. И при этом он будет считать, что ничего не произошло, все её свойства остались неизменными. С точки зрения топологии баранка и кружка - это одно и то же. Сжимая и растягивая кусок резины, можно перейти от одного из этих тел ко второму. А вот баранка и шар - разные объекты: чтобы сделать отверстие, надо разорвать резину.

Применение листа Мёбиуса в технике и его эстетическое значение.

Полоса ленточного конвейера выполненная в виде ленты Мёбиуса, позволяет ему работать дольше, потому что вся поверхность ленты равномерно изнашивается. Также в системах записи на непрерывную плёнку применялись ленты Мёбиуса (чтобы удвоить время записи). В матричных принтерах красящая лента имела вид листа Мёбиуса для увеличения срока годности. Если у ременной передачи ремень сделать в виде ленты Мёбиуса, то его поверхность будет изнашиваться вдвое медленнее, чем у обычного кольца. Это дает ощутимую экономию. Лист Мёбиуса привлек к себе внимание не только ученых, но и художников, скульпторов, филателистов.

Үйге тапсырма беру / Задание на дом : Эксперимент на дом.

а) На обеих сторонах ленты на равном расстоянии от краев провести по две пунктирные линии.

Склеить лист Мёбиуса. Разрезать по пунктирным линиям. Описать полученный результат.

(Получается 2 кольца. Одно из них вдвое длиннее первоначальной ленты и вдвое перекручено. Оно получилось из краев исходной ленты. Другое - лист Мёбиуса - состоит из центральной части исходного листа Мёбиуса.

Прошу дать прогноз для подобного эксперимента, но когда лента не была перекручена. (Два тонких кольца и центральная часть).

б) Приготовьте ленту шириной 5 см, на которой нанесите пунктир, отступив от края на

1 см, 2 см, 3 см и 4 см. Сделайте из неё лист Мёбиуса. Что получится, если разрезать его по пунктиру?

Получим 3 кольца:

кольцо - лист Мёбиуса - 1 перекрут, ширина 1 см, длина равна длине исходного кольца.

II, III - кольца кольца с двумя перекрутами, ширина 1 см, длина в 2 раза больше исходного листа.

II и III кольцо сцеплены с I кольцом и между собой.

Можно ставить еще немало экспериментов по разрезанию лент. Попросите учеников придумать и поставить свой эксперимент, суть которого отразить на отдельном листе бумаги.

Урок хочу завершить стихотворением автор Юрий Юркий

Лист Мёбиуса

Лист Мёбиуса. Мёбиуса лента,

Что некая туманность между звёзд,

Полна чудес, как старая легенда.

Извив змеи, во рту держащей хвост.

В науке точной мистики нет места.

Лист Мёбиуса замкнут, как темляк.*

Пересекать не надо край - известно:

В любую точку попадёшь и так.

"Конец" в единой точке и "начало"...

Парадоксален Мёбиуса лист!

Нас эта лента меж собой связала.

Был путь к любви и долог и тернист!

Подведение итогов урока.

Мы много интересного узнали о листе Мёбиуса, но конечно же главная ценность листа Мёбиуса состоит в том, что он дал толчок новым обширным математическим исследованиям. Именно поэтому его часто считают символом современной математики и изображают на различных эмблемах и значках, как, например, на значке механико-математического факультета Московского университета.