Обобщающий урок по теме "Методы решения квадратных уравнений"

• Образовательная: закрепление и обобщение знаний учащихся полученные при изучении темы. Выработка умений и навыков по решению квадратных уравнений различного вида разными способами. Выработка умения выбрать нужный рациональный способ решения.

• Развивающие: развитие логического мышления, памяти, внимания, умений сравнивать и обобщать, умения выступать с самостоятельными суждениями и отстаивать их.

• Воспитательные: воспитание трудолюбия, взаимопомощи, математической культуры. Умение работать в группах, развивать познавательную активность и логическое мышление учащихся, развитие интереса к предмету.

Тип урока: Урок обобщения и систематизации.

Оборудование: Интерактивная доска, проектор, планшеты для построения графика, раздаточный материал, цветной мел.

Ход урока

I. Организационный момент.

Добрый день! Рада приветствовать Вас на нашем уроке, прошу всех вас улыбнуться друг другу, и мысленно пожелать успехов себе и товарищам. Садитесь.

II. Повторение пройденного материала.

1) Предлагаю начать урок со следующего задания: на слайде - анаграммы (слова даны на слайде).

Ребята что вы видите? (Дискриминант, уравнение, коэффициент, корень)

- Какая тема объединяет данные слова? ( Квадратные уравнения)

-Какие цели мы поставим к уроку? (вспомним и обобщим все те знания, которые мы получили на предыдущих уроках).

- Ребята, скажите, что должен уметь делать каждый из вас на сегодняшнем уроке? (уметь правильно, быстро и рационально решать квадратные уравнения)

Великий, немецкий ученый А. Эйнштейн говорил о себе: «Мне приходится делить своё время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только до данного момента, а уравнения будут существовать вечно»

Квадратные уравнения - тема очень важная в курсе математики, она является первой ступенькой в изучении более сложного материала.

На доске уравнение: 7х²+2х+2013=0

- Назовите вид данного уравнения. Назовите его коэффициенты.

О каком событии говорят коэффициенты уравнения? (Дата проведения урока)

Итак, откройте тетради и запишите сегодняшнее число, классная работа, тема урока: «Квадратные уравнения»

3) Установите соответствие между уравнениями и их типом. (Интерактивная доска) .

А теперь обратите внимание на доску. Что вы видите? А на какие типы делятся квадратные уравнения.?(Полные и неполные)

1) 2x²=0 2) 5х²+10х-3=0 3) m²+7m-18=0 4) -576z²=0

5) 2x²-6=х 6) x²=4 7) 3d²+7d-6=0 8) n²+4n=0 9) x²+25=0

Устный опрос. Вопросы:

1 Какие уравнения называются неполными квадратными уравнениями?

Ответ: Уравнения называются неполными квадратными уравнениями если b = 0 или с = 0.

2. Какое квадратное уравнение называется приведенным?

Ответ: Квадратное уравнение называют приведенным, если его старший коэффициент равен 1; Квадратное уравнение называют не приведённым, если старший коэффициент отличен от 1.

3. Что называют корнем квадратного уравнения?

Ответ: Корнем квадратного уравнения называют всякое значение переменной х, при котором квадратный трёхчлен обращается в нуль. Такое значение переменной х называют также корнем квадратного трёхчлена.

4. Что значит решить квадратное уравнение?

Ответ: Решить квадратное уравнение - значит найти все его корни или установить, что корней нет.

Формулы:

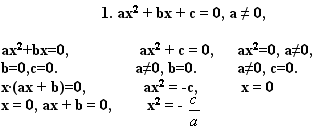
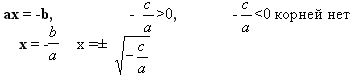
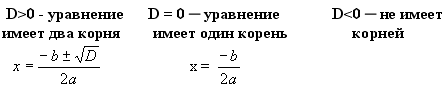
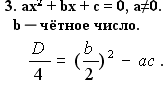
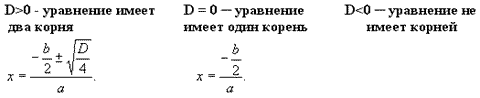
Теорема Виета.

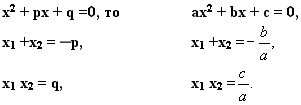
Геометрическая задача.

На катетах прямоугольного треугольника построены квадраты. Стороны одного из них на 2 больше сторон другого. Найти длины сторон данного треугольника, если площадь квадрата построенного на гипотенузе равно 20.

(Решение задачи сводится к решению квадратного уравнения)

А) по формуле корней

Б) графический способ

В) выделение полного квадрата

IV.Физминутка 7х²+2х+2013=0

На доске дано квадратное уравнение.

1)В данном уравнении все коэффициенты четные.(-)

2) Это уравнение полное.(+)

3) Свободный член равен 0 (-)

4) Второй коэффициент положительный (+)

5) Уравнение приведенное(-)

Молодцы ребята, вы очень внимательны.

Мы немного отдохнули, а теперь мы продолжим.

Тест: "Квадратные уравнения"

1 вариант

1.Установите соответствие.

а) 3х² =-5х + 4; в) 3х² +5 = 8;

б) х² + 1 = 0; г) -3х² - 11х = 0.

2. Решите уравнение: х² - 8х + 7 = 0 в ответе запишите больший из корней.

а) -1 б) 7 в) -7 г) 1

3. Найдите сумму корней уравнения: 4х² + 22х - 7 = 0.

а) -22; б) корней нет; в) 22; г) -5,5.

4.При каком значении v уравнение х² + vх + 12 = 0 имеет 2 корня, если один из корней равен 2.

Тест: "Квадратные уравнения"

2 вариант

1. Установите соответствие

а) 2х² =-7х ; в) -2х² +7х= 30

б) х -5х + 1 = 0; г) -х² - 9х + 5 = 0.

2. Решите уравнение: х² - 5х - 6 = 0 в ответе запишите меньший из корней

а) 6; б) 1; в) -1; г) -6.

3. Найдите сумму корней уравнения: 5х² - 13х + 9 = 0.

а) 13; б) -13; в) корней нет; г) 2,6.

4. При каком значении t уравнение х² + tх + 12 = 0 имеет 2 корня, если один из корней равен 4.

Выполняется взаимопроверка.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Ребята, подведем итоги урока. Послушайте притчу о мудрецах, которые заблудились в лесу. Один решил пойти назад, говоря о том что дорога которая привела его в лес обязательно выведет его из леса. Второй мудрец сказал, что он пойдет вперед, так как надо двигаться дальше и лес непременно закончится. А третий мудрец залез на самое высокое дерево, откуда увидел самый кротчайший путь выхода из леса. Спустя некоторое время все мудрецы вышли из леса и выбор каждого из них был правильным Тот кто пошел назад проложил через лес тропинку, которая вскоре превратилась в дорогу для всех. Тот кто пошел вперед стал первооткрывателем и открыл для людей прекрасные новые возможности. Тот же, что влез на дерево, стал специалистом по нахождению коротких путей.

У каждого была цель: выйти из леса и каждый из них достиг цели разными путями.

ВОПРОС: А какую цель преследовали вы сегодня на протяжении всего урока?

Рефлексия:: Ребята вы сегодня плодотворно поработали, и в знак того что урок для вас прошел хорошо и интересно, я бы хотела чтобы вы наградили друг друга аплодисментами.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.

Домашнее задание:

1) Составьте квадратное уравнение с корнями х_1,х_2, где: х₁=3_, х₂=-2.

2) Решите это квадратное уравнение способами, которые мы рассмотрели на уроке.