- Учителю
- Материал для подготовки к уроку по теме Вписанная и описанная окружность
Материал для подготовки к уроку по теме Вписанная и описанная окружность
УРОК 60.
Тема: Вписанная и описанная окружность.
Прежде чем перейти к теме урока, повторим теоремы о серединном перпендикуляре к отрезку.
Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Теорема 2 (Обратная к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
В этом случае треугольник называют треугольником, описанным около окружности.
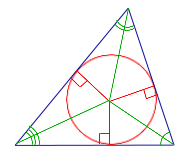
Рис. 1
Следствие. В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.
Рисунок
Формула
Обозначения
Произвольный треугольник
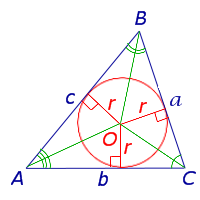
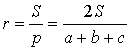
Посмотреть вывод формулы
a, b, c - стороны треугольника,
S -площадь,
r - радиус вписанной окружности,
p - полупериметр
![]() .
.
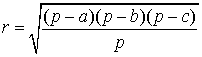
Посмотреть вывод формулы
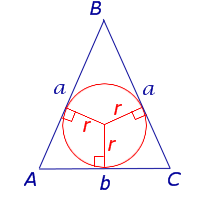
Равнобедренный треугольник
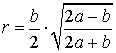
Посмотреть вывод формулы
a - боковая сторона равнобедренного
треугольника,
b - основание, r - радиус вписанной окружности
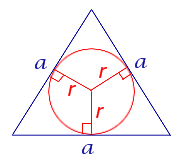
Равносторонний треугольник
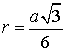
Посмотреть вывод формулы
a - сторона равностороннего треугольника, r - радиус вписанной окружности
Прямоугольный треугольник
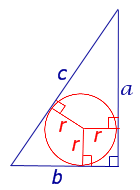
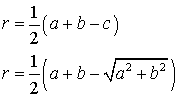
Посмотреть вывод формул
a, b - катеты прямоугольного треугольника,
c - гипотенуза, r - радиус вписанной окружности
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 3 . Для произвольного треугольника справедливо равенство
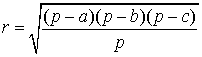 ,
,
где a, b, c - стороны треугольника, r - радиус
вписанной окружности,![]() -
полупериметр (рис. 6).
-
полупериметр (рис. 6).

Рис. 2
Доказательство. Из формулы
![]()
с помощью формулы Герона получаем:
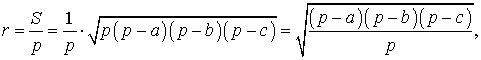
что и требовалось.
Теорема 4. Для равнобедренного треугольника справедливо равенство
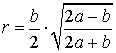 ,
,
где a - боковая сторона равнобедренного треугольника, b - основание, r - радиус вписанной окружности (рис. 3).

Рис. 3
Доказательство. Поскольку для произвольного треугольника справедлива формула
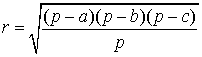 ,
,
где
![]() ,
,
то, в случае равнобедренного треугольника, когда
![]()
получаем
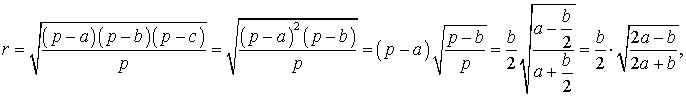
что и требовалось.
Теорема 5 . Для равностороннего треугольника справедливо равенство
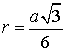
где a - сторона равностороннего треугольника, r - радиус вписанной окружности (рис. 4).

Рис. 4
Доказательство. Поскольку для равнобедренного треугольника справедлива формула
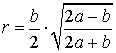 ,
,
то, в случае равностороннего треугольника, когда
b = a,
получаем
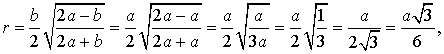
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 6. Для прямоугольного треугольника справедливо равенство
![]()
где a, b - катеты прямоугольного треугольника, c - гипотенуза, r - радиус вписанной окружности.
Доказательство. Рассмотрим рисунок 5.
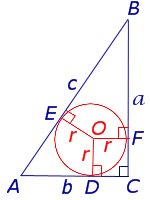
Рис. 5
Поскольку четырёхугольник CDOF является прямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник - квадрат. Следовательно,
СВ = СF= r,
В силу теоремы 3 справедливы равенства
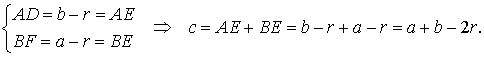
Следовательно, принимая также во внимание теорему Пифагора, получаем
![]()
что и требовалось.
В этом случае треугольник называют треугольником, вписанным в
окружность, или вписанным треугольником.
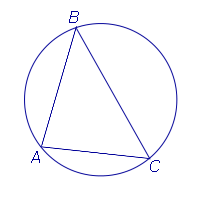
Рис.6
Свойства описанной около треугольника окружности
![]()
где a, b, c - стороны треугольника, S - площадь треугольника, R - радиус описанной окружности.
Теорема 7. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC, и обозначим точку их пересечения буквой O (рис. 7).
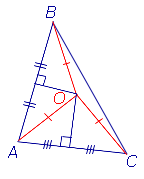
Рис. 7
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC, то в силу теоремы 1 справедливо равенство:
CO = AO .
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB, то в силу теоремы 1 справедливо равенство:
AO = BO .
Следовательно, справедливо равенство:
CO = BO ,
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
</ Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство. Рассмотрим точку O, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC(рис. 2).
При доказательстве теоремы 3 было получено равенство:
AO = OB = OC ,
из которого вытекает, что окружность с центром в точке O и радиусами OA, OB, OC проходит через все три вершины треугольника ABC, что и требовалось доказать.
Выполните задания.

