Урок Общие методы решения уравнений

Тема: «Общие методы решения уравнений».

Вид урока: обобщение и систематизация знаний.

Тип урока: комбинированный, концентрированное повторение с выходом на обобщение и систематизацию знаний.

Форма проведения: семинар, работа в группах, индивидуальная.

Педагогические технологии: Обучение в сотрудничестве, метод проектов, компьютерная технология, личностно-ориентированный подход в обучении, интернет - технологии.

Цели:

• Повторить и расширить сведения об уравнениях и способах их решения;

• Формировать умения выполнять обобщения и конкретизацию, правильно отбирать способы решения уравнений;

• Развивать качества мышления, гибкость, целенаправленность, рациональность, воспитание чувства ответственности за коллектив в процессе творческой работы.

• учить осуществлять исследовательскую деятельность;

• продолжить формирование психологической готовности учащихся к применению имеющихся знаний в заданиях ЕГЭ.

Задачи:

• Продолжить работу по формированию умения решать уравнения.

• Подготовить к ЕГЭ (задания типа № 5, 13).

Осуществлять контроль своих знаний с помощью компьютерных тестов.

• Развивать и совершенствовать культуру математического труда, математическую речь.

  • Воспитывать умение объективно оценивать свои знания (оценивать чужой ответ).

Оборудование урока:

ПК учителя, мультимедийный проектор, персональные компьютеры учащихся,

презентация, содержащая материал для повторения и закрепления теоретических знаний, для отработки навыков практического применения теории к решению упражнений, создания проблемной ситуации, для самоконтроля.

Формы организации познавательной деятельности:

• фронтальная

• групповая

Методы обучения:

• по источнику приобретенных знаний:

• словесный

• практический

• наглядный

• по уровню познавательной активности:

• проблемный

• поисковый

Планируемый конечный результат:

Учащиеся знают алгоритмы методов решения уравнений (замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x),метод разложения на множители, метод введения новой переменной, функционально-графический метод).

При решении уравнений аргументировано выбирают наиболее удобный способ решения.

Перечень критериев проверки достижения планируемых результатов:

Знание теоретического материала (умение устно ответить на поставленные вопросы)

Умение решать уравнения различными способами.

Подготовительная работа:

Творческое задание. Решить уравнение различными способами. Оценить достоинства и недостатки каждого способа. Оформить запись выводов в виде таблицы.

В течение выполнения творческого задания провести по (необходимости) консультации для учащихся, у которых возникают вопросы по заданию.

Структура урока:

1. Организационный момент;

2. Актуализация опорных знаний;

3. Проверка домашнего задания;

4. Исследовательская работа в творческих разноуровневых группах;

5. Защита каждой группой своего способа решения уравнений;

6. Проверка знаний и умений (самоконтроль). Самостоятельная работа за ПК.

7. Итог урока;

8. Домашнее задание.

Ход урока

1. Организационный момент:

2. Актуализация опорных знаний. Сегодня на уроке мы с вами повторим основные методы решения уравнений, выполним самостоятельную работу за ПК, работу в группах.

С учетом подготовки учащихся возникла необходимость повторения теоретического материала. Фронтальный опрос проводился по следующим вопросам:

- какие уравнения называются равносильными?

- что можно сказать о корнях равносильных уравнений?

- что называют областью допустимых значений уравнения f(x) = g(x)?

- какие способы решения уравнений вы знаете?

Должны прозвучать ответы:

1) два уравнения называются равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

2) корни равносильных уравнений совпадают.

3) областью допустимых значений (ОДЗ) уравнения f(x) = g(x) называют множество тех значений переменной х, при которых одновременно имеют смысл выражения f(x) и g(x).

4) графический метод и аналитический: вынесение общего множителя за скобки, введение новой переменной, сведение к простейшему путем тождественных преобразований.

Учитель: "Когда возникает необходимость в проверке полученных корней уравнения?"

(Должен прозвучать ответ: если при решении уравнения, мы на каком-то шаге выполняем преобразования без учета ОДЗ (вводим новую переменную, возводим в квадрат или четную степень, освобождаемся от знаменателя (умножаем на общий знаменатель), сокращаем на общий множитель.)

3. Проверка домашнего задания.

Учащиеся получили творческую работу: подобрать из разных источников такие уравнения, которые выходили бы за рамки традиционных уравнений, предлагаемых в школьных учебниках.

4. Исследовательская работа в творческих разноуровневых группах.

Класс разбивается на три группы.

После того как каждой группе дано задание, идет обсуждение и поиск решения уравнения. Группа решает: кто представляет решение у доски для всего класса.

5. Представление и защита своего задания каждой группой.

1-я группа

Представили уравнение . Решили методом разложения на множители.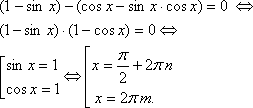

Ответ:

2-я группа

Представили показательное уравнение, сводящееся к однородному.

Перепишем уравнение в виде

Получилось уравнение однородное относительно . Разделим обе части уравнения на

Пусть , причем y>0. Получим , откуда

Вернемся к исходной переменной и решим уравнения

Ответ:

3-я группа

Представили уравнение: Это уравнение можно решить вполне стандартным способом. Но мы применили свойство монотонности функции. В левой части уравнения - возрастающая функция, в правой части - убывающая функция. Следовательно, данное уравнение не может иметь более одного корня. Число 5- корень уравнения, что проверяется подстановкой. Представили графический способ.

Ответ: 5.

Вот эти задания взяты из вариантов ЕГЭ прошлых лет. На одном из слайдов учащимся предлагаются адреса сайтов Интернет (www.fipi.ru, www.mathege.ru, www.ege.edu.ru, www.mioo.ru</<font face="Times New Roman, serif"> ), где можно найти информацию по самоподготовке к ЕГЭ, принять участие в on-line тестировании.

6. Проверка знаний и умений (самоконтроль). Самостоятельная работа за ПК.

Самый важный этап - этап самостоятельной работы. Учащиеся работают за компьютером с интерактивными обучающими и контролирующими программами, которые дают возможность выбора задания, метода решения, анализа ошибок, обращения к справочному теоретическому материалу, демонстрации верного хода решения.

В тесте предусмотрено сообщение об общем количестве заданий и верно выполненных заданий, зачетном минимуме, выраженном в процентах.

7. Итог урока. Релаксация.

Притча. Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» Тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?» И тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»

Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.

Кто работал так, как первый человек? (поднимают жёлтые кружочки)

Кто работал добросовестно? (синие)

Кто принимал участие в строительстве храма? (зелёные)

Рефлексивно-оценочный этап.

1. Оценка:

а) за фронтальную работу.

б) за самостоятельную работу.

2. Какой момент был наиболее интересен на уроке?

3. Где пришлось более всего концентрироваться, задумываться?

Корзина знаний:

1. Виды уравнений.

2. Общие методы решения уравнений.

3. Всегда ли переход от h(f(x)) = h(g(x)) к

f(x) =g(x) равносилен?

4. Алгоритм метода разложения на множители.

5. Когда целесообразно применять метод замены переменной?

6. В чем состоит графический метод?

8. Задание на дом. Домашнее задание даётся на карточках по материалам ЕГЭ. Подборка заданий типа №5: уметь решать уравнения и неравенства, дополнительно сильным ученикам задания №13

Проверяемые требования: решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения.

.