- Учителю
- Сборник задач краевой физмат школы 8-11 класс
Сборник задач краевой физмат школы 8-11 класс
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
Нижнетамбовского сельского поселения
Комсомольского муниципального района Хабаровского края
Задачи с решениями, предлагаемые краевой заочной физико-математической школой
Составил: Жмеренецкая Е.А.,
руководитель в школе обучением в Краевой заочной физико-математической школе, учитель 1 категории.
От составителя
Настоящий сборник составлен в соответствии с материалами Краевой физико-математической школы. В нём содержатся задачи по следующим разделам: прогрессии, алгебраические уравнения и неравенства, тригонометрические уравнения.
Пособие включает рекомендации по решению задач повышенного уровня, что будет способствовать активизации самостоятельной работы учащихся, улучшению их подготовки к ЕГЭ по математике, закреплению их теоретических знаний и выработке практических навыков, более качественной подготовке для поступления в ВУЗы.
Содержание
-
Решение уравнений и неравенств 8 класс.
-
Тригонометрия 10 класс.
-
Тригонометрические уравнения 11 класс.
-
Прогрессии 10 класс.
1.Решение уравнений и неравенств
1.Решить уравнение (х+1)(х+4)=(х-2)(х-3)
Решение:
(х+1)(х+4)=(х-2)(х-3)
х2+4х+х+4=х2-3х-2х+6
10х=2
х=![]()
Ответ: х=![]()
2.Решить уравнение: (х-1)(х-2)(х+3)=(х-2)(х-3)(х+5)
Решение:
(х-1)(х-2)(х+3)=(х-2)(х-3)(х+5)
х3+3х2-2х2-6х-х2-3х+2х+6=х3+5х2-3х2-15х-2х2-10х+6х+30
-7х+6=-19х+30
12х=24
х=2
Ответ:х=2
3. Решить уравнение: 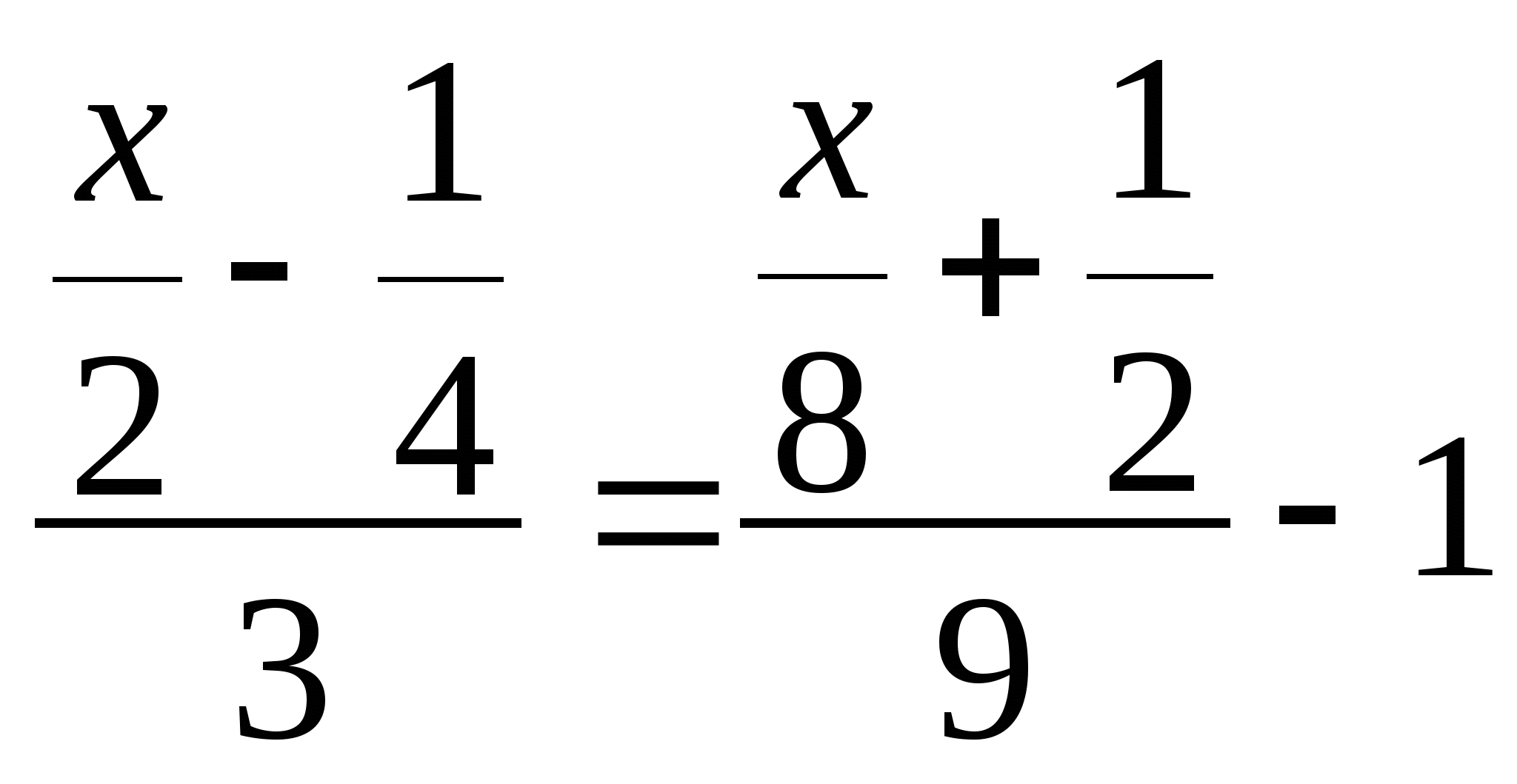
Решение:
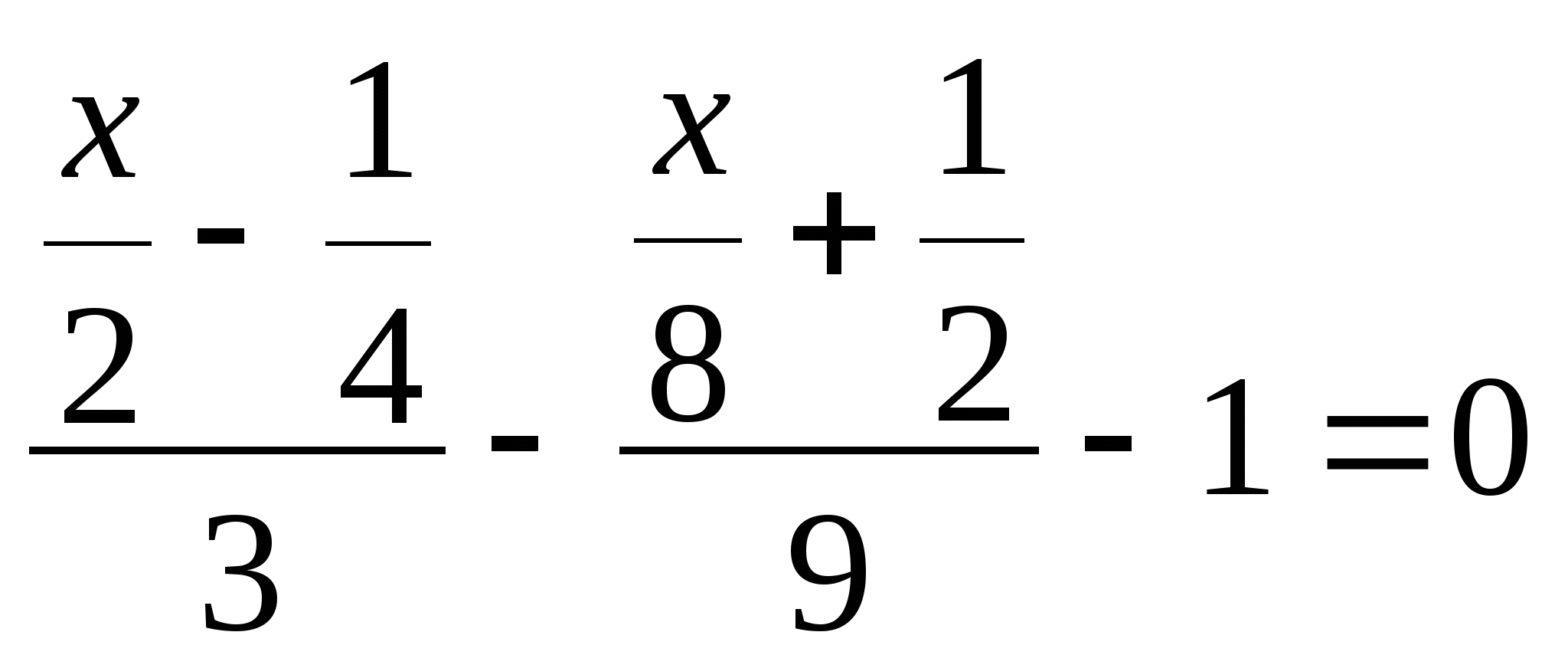
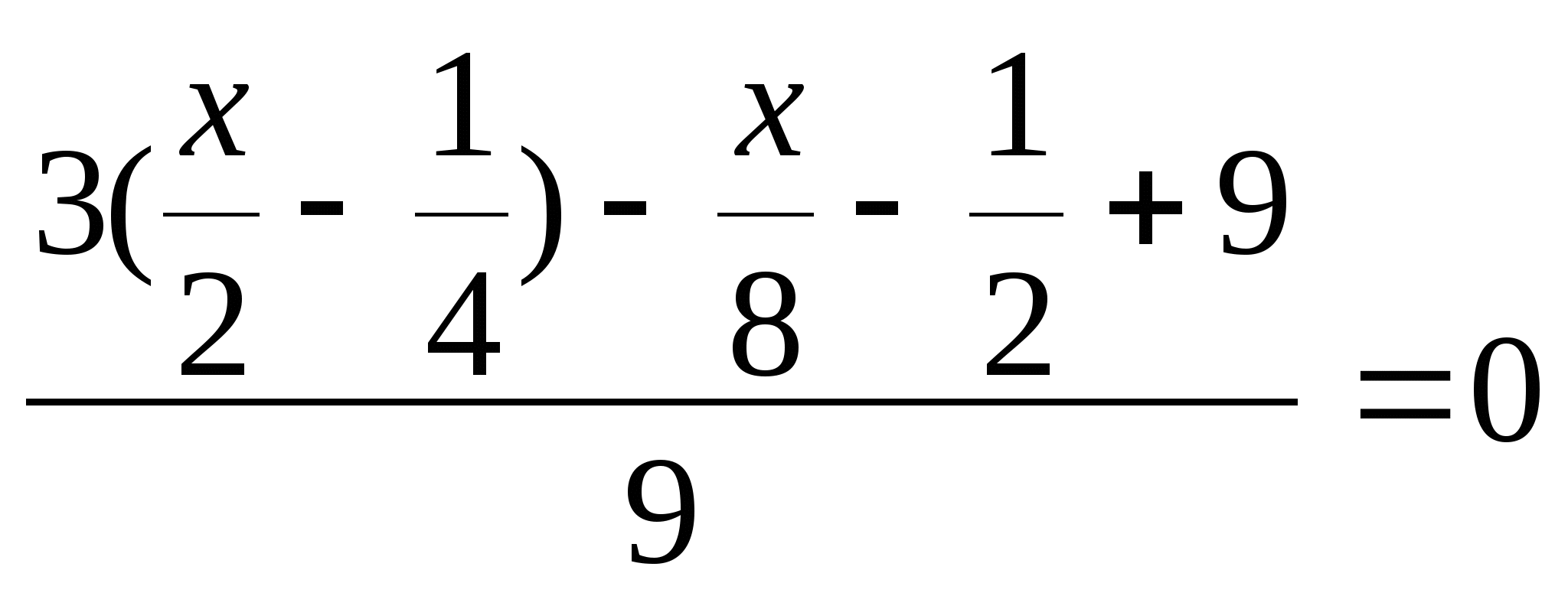
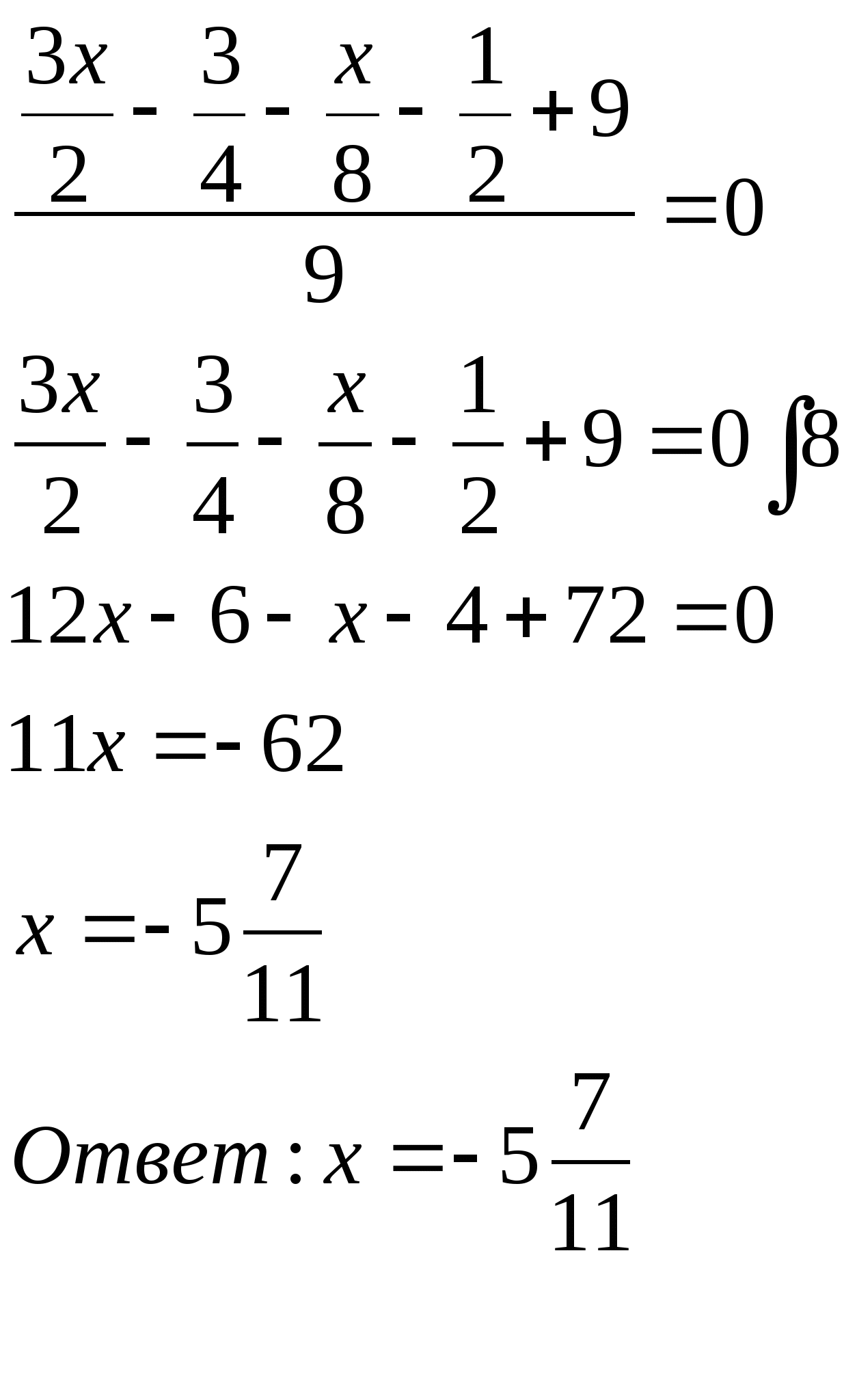
4. Решить уравнение:![]()
Решение:
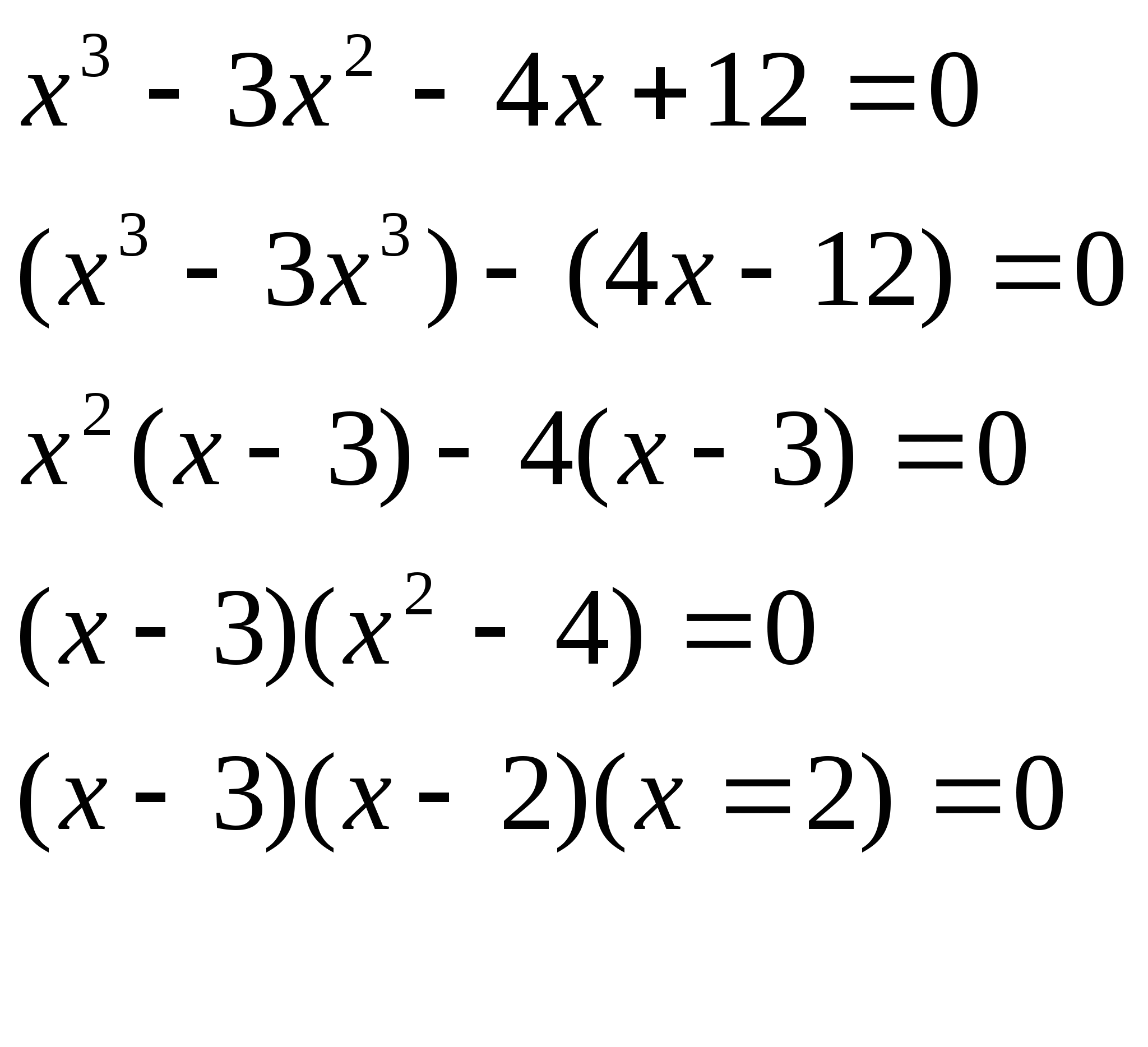
х-3=0 или х-2=0 или х+2=0
х=3 х=2 х=-2
Ответ: х1=3;х2=2;х3=-2
5. Решить уравнение: 3х+4=ах-8, а-параметр
Решение:
3х+4=ах-8
-ах+3х=-12
х(3-а)=-12
1).3-а=0, т.е. а=3
![]() 0=-12 уравнение
решений не имеет
0=-12 уравнение
решений не имеет
2).3-а![]() 0, т.е.
а
0, т.е.
а![]() 3
3
х=![]()
![]()
Ответ: при а=3 решений нет;
при а![]() 3
3 ![]()
6. Решить уравнение: ![]() ,
а- параметр
,
а- параметр
Решение:
![]()
![]()
(х+а)(2+а)=(х-а)(1+а)
2х+ах+2а+а2=х+ах-а-а2
2х-х=-а-а2-2а-а2
х=-3а-2а2
х=-а(3+2а)
1) а=-1 и а=-2 уравнение не имеет корней
2) а=0,то х=0
3) ![]() ,то х=-а(3+2а)
,то х=-а(3+2а)
Ответ: при а=-1,а=-2 нет решения;
при а=0,х=0
при![]() ,х=-а(3+2а)
,х=-а(3+2а)
7. Решить уравнение: ![]()
Решение:
![]()
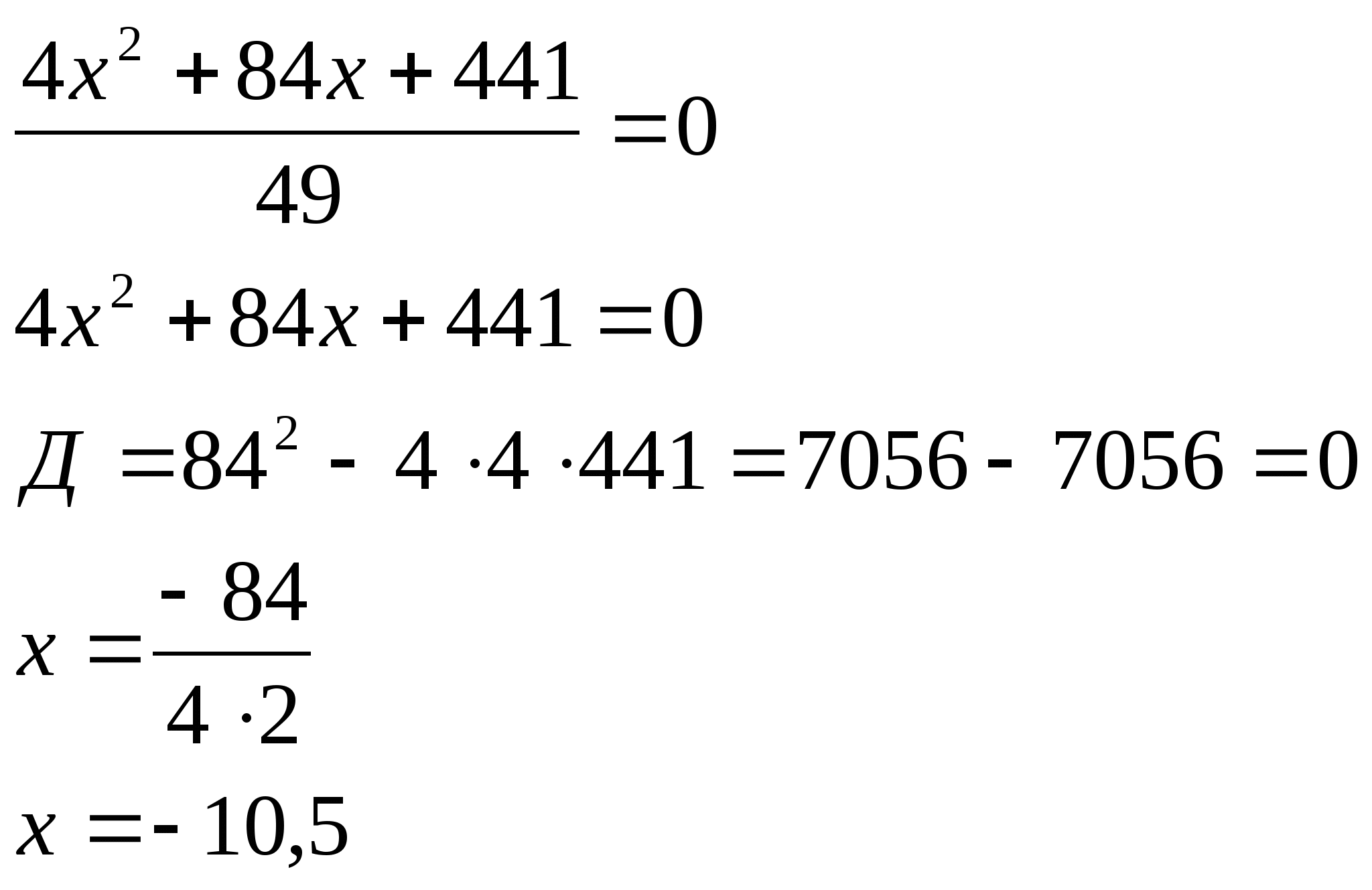
Ответ: х=-10,5
9. Решить уравнение: ![]()
Решение:
![]()
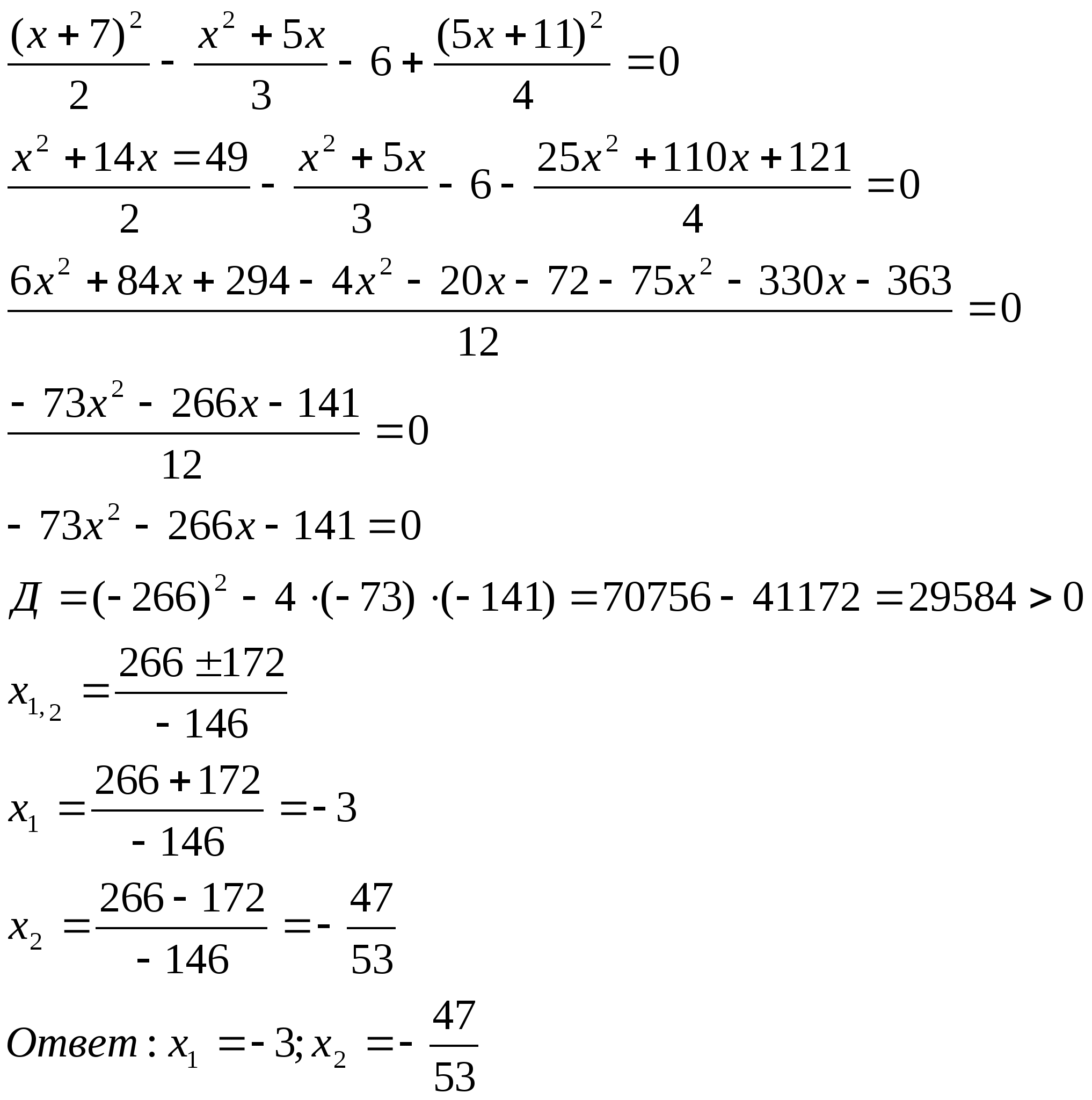
10. Решить уравнение: ![]()
Решение:
![]()
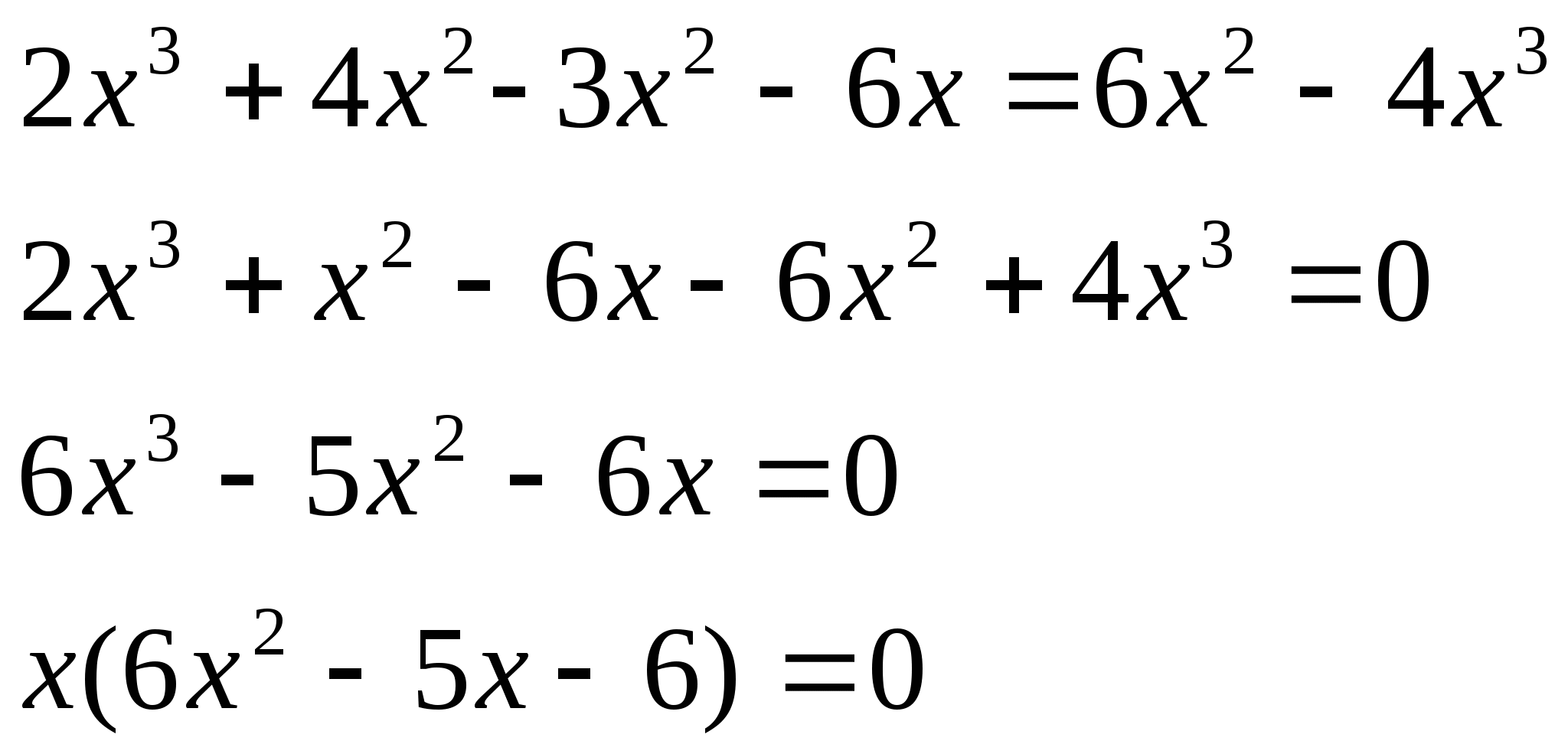
х=0 или 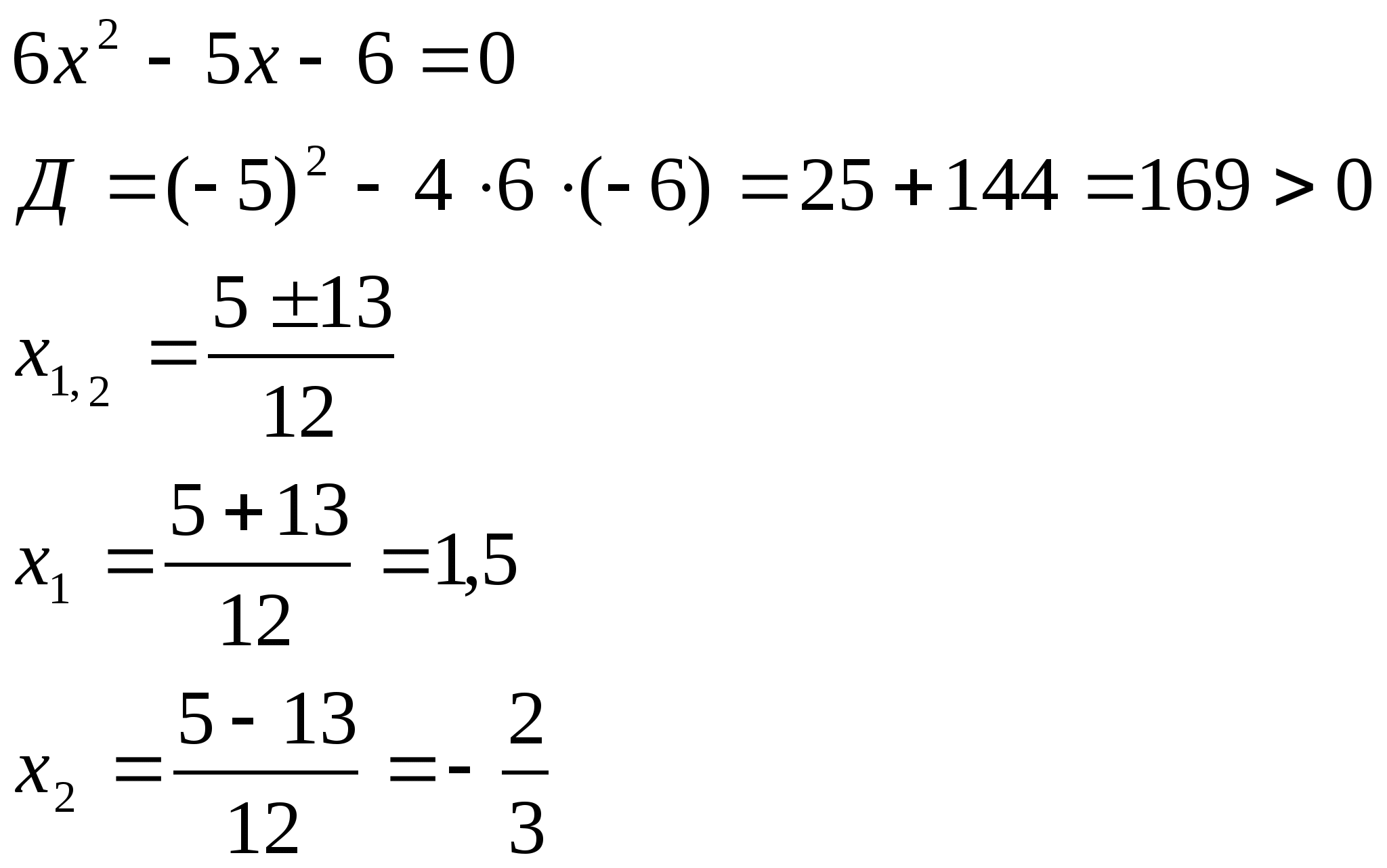
Ответ:![]()
11. Решить уравнение: ![]()
Решение:
![]()
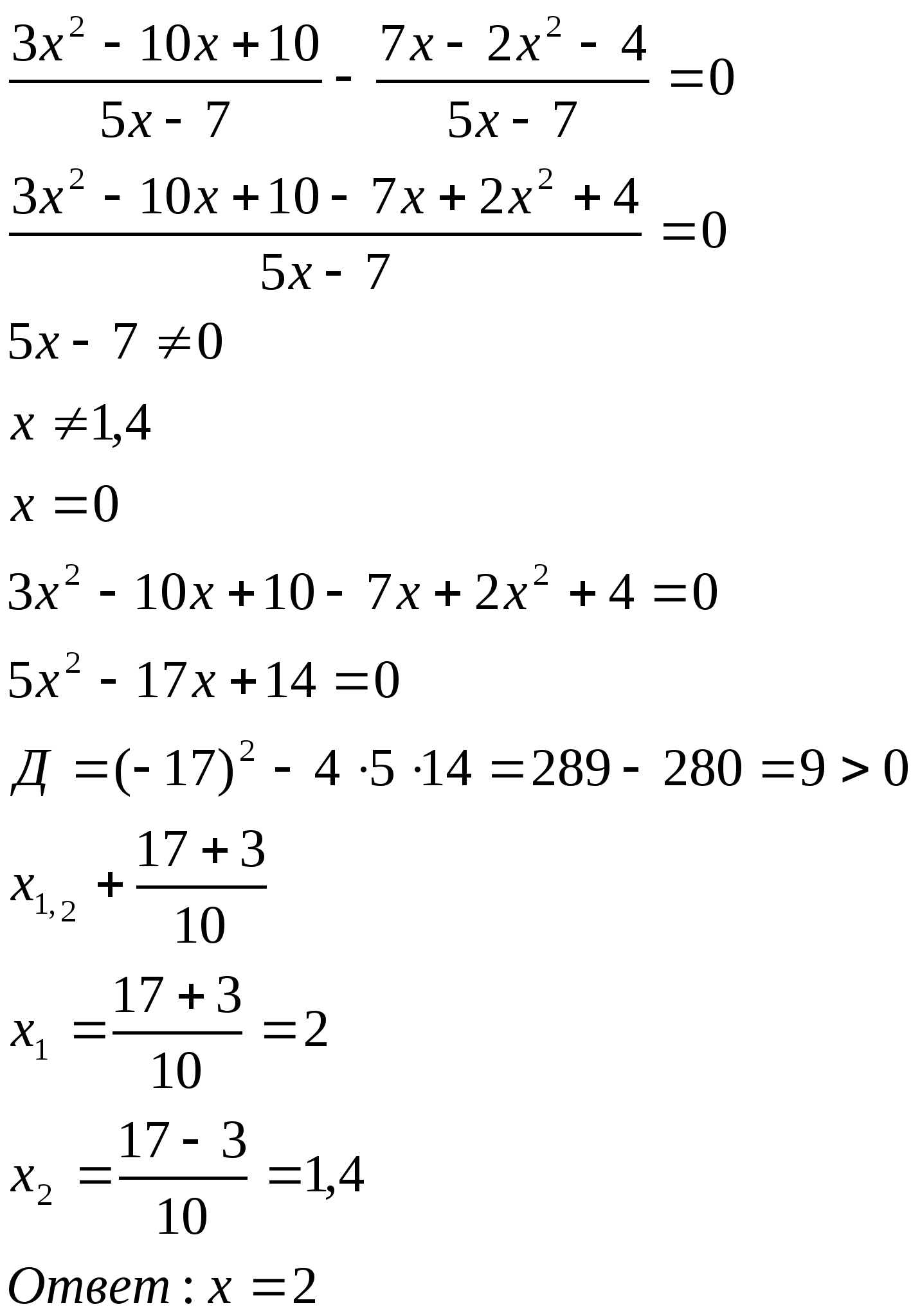
12. Решить уравнение: ![]()
Решение:
![]()
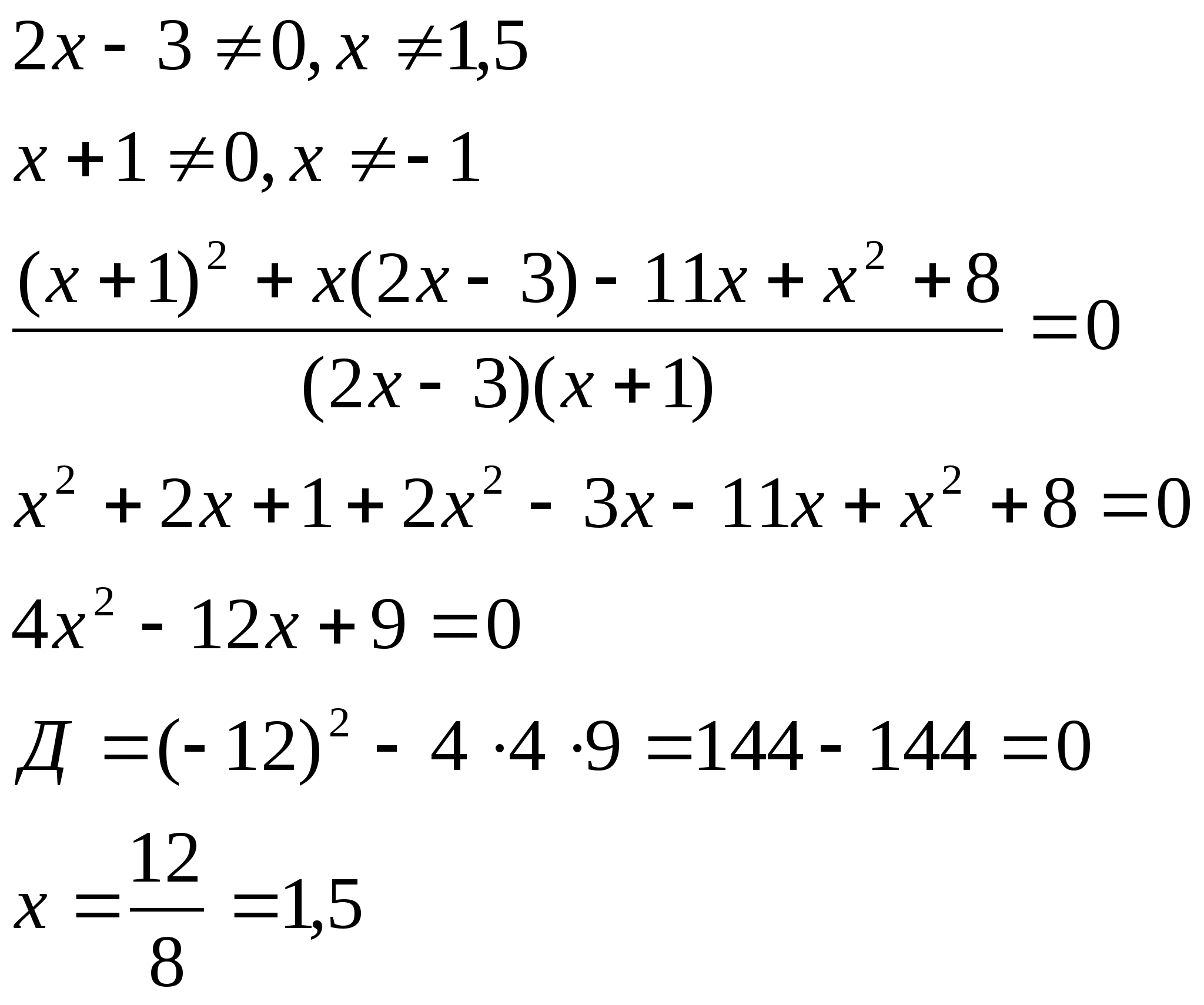
Ответ: нет решений.
13. Решить неравенство: ![]()
Решение:
![]()
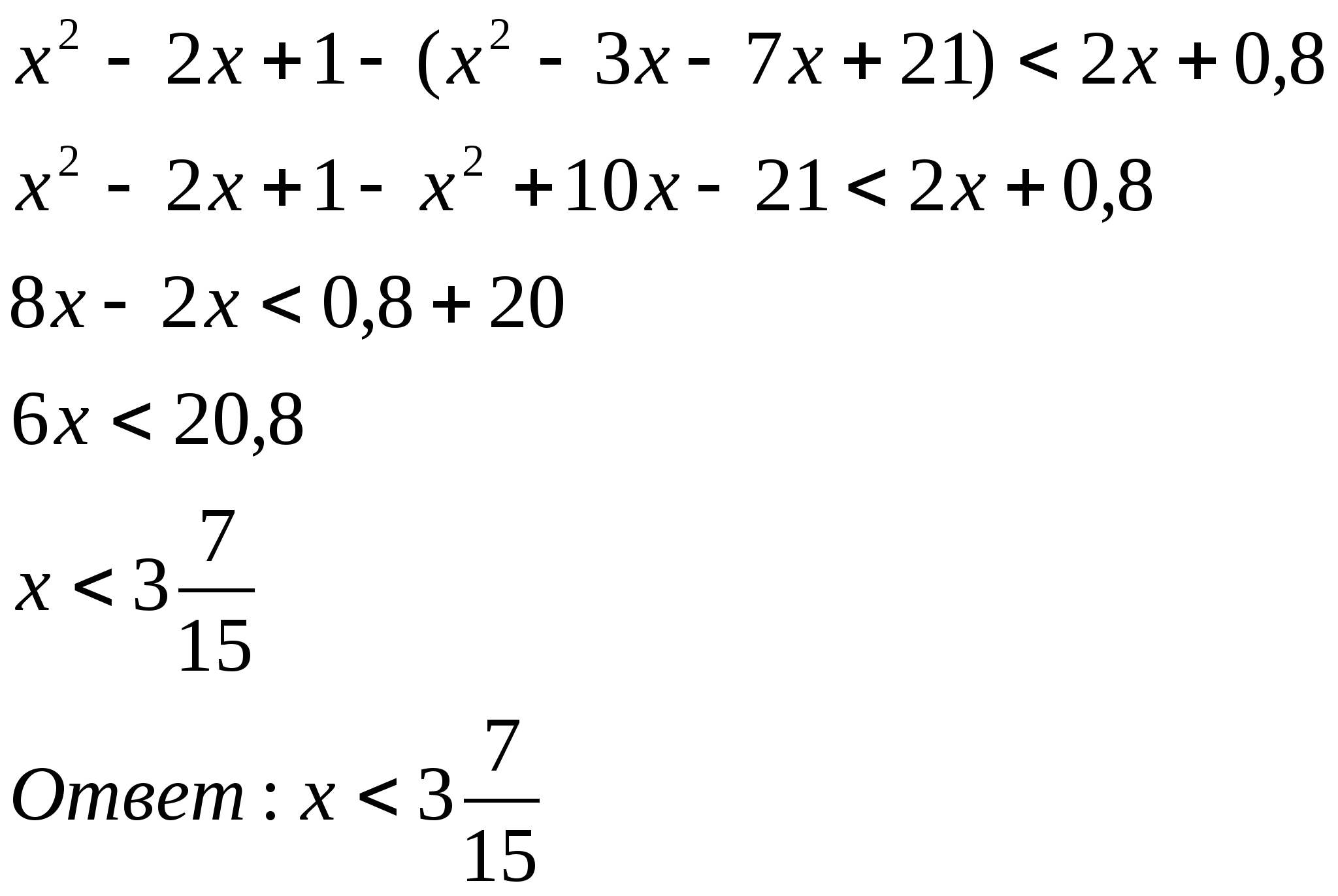
14. Решить неравенство:![]()
![]()
Решение:
![]()
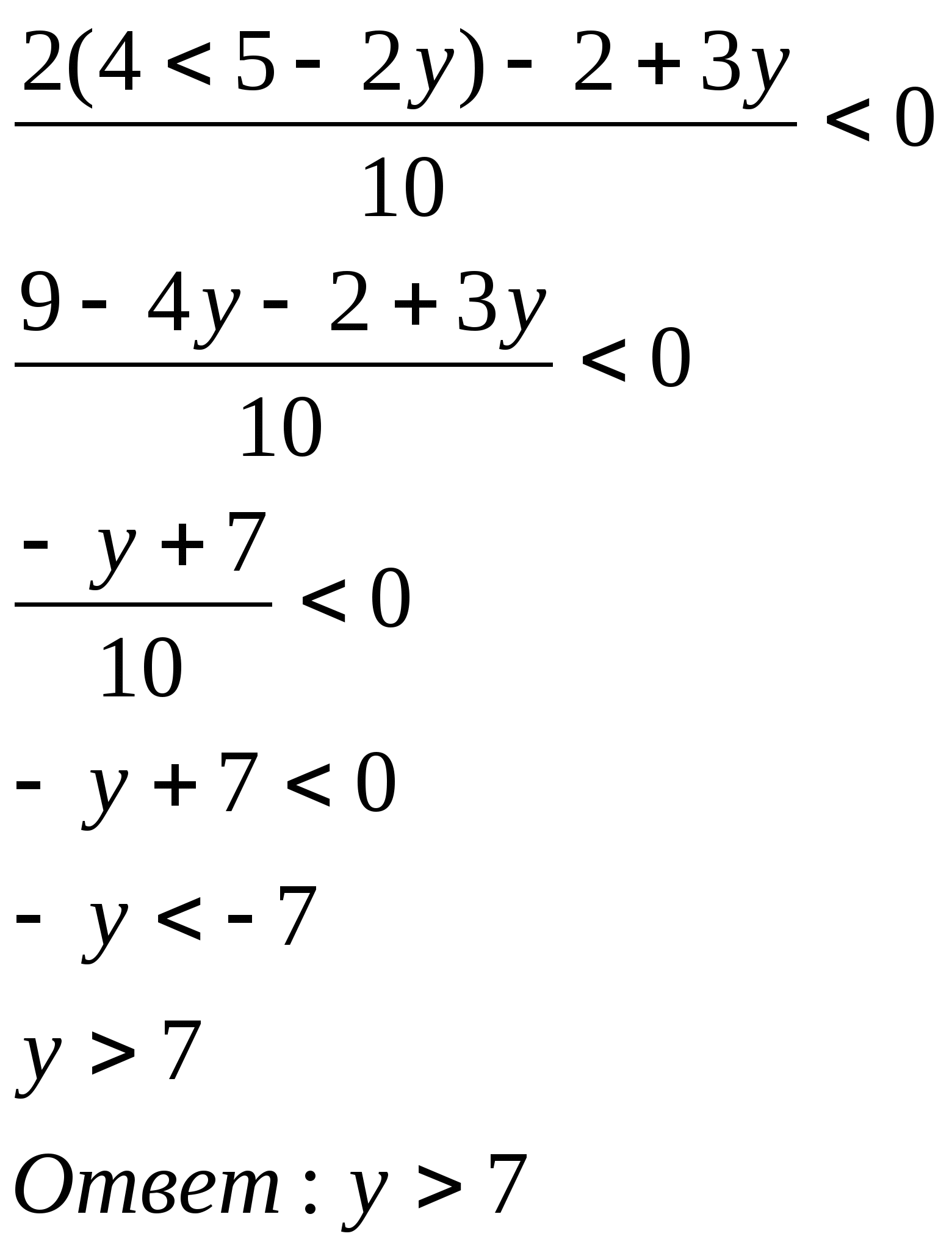
15. Решить неравенство: ![]()
Решение:
![]()
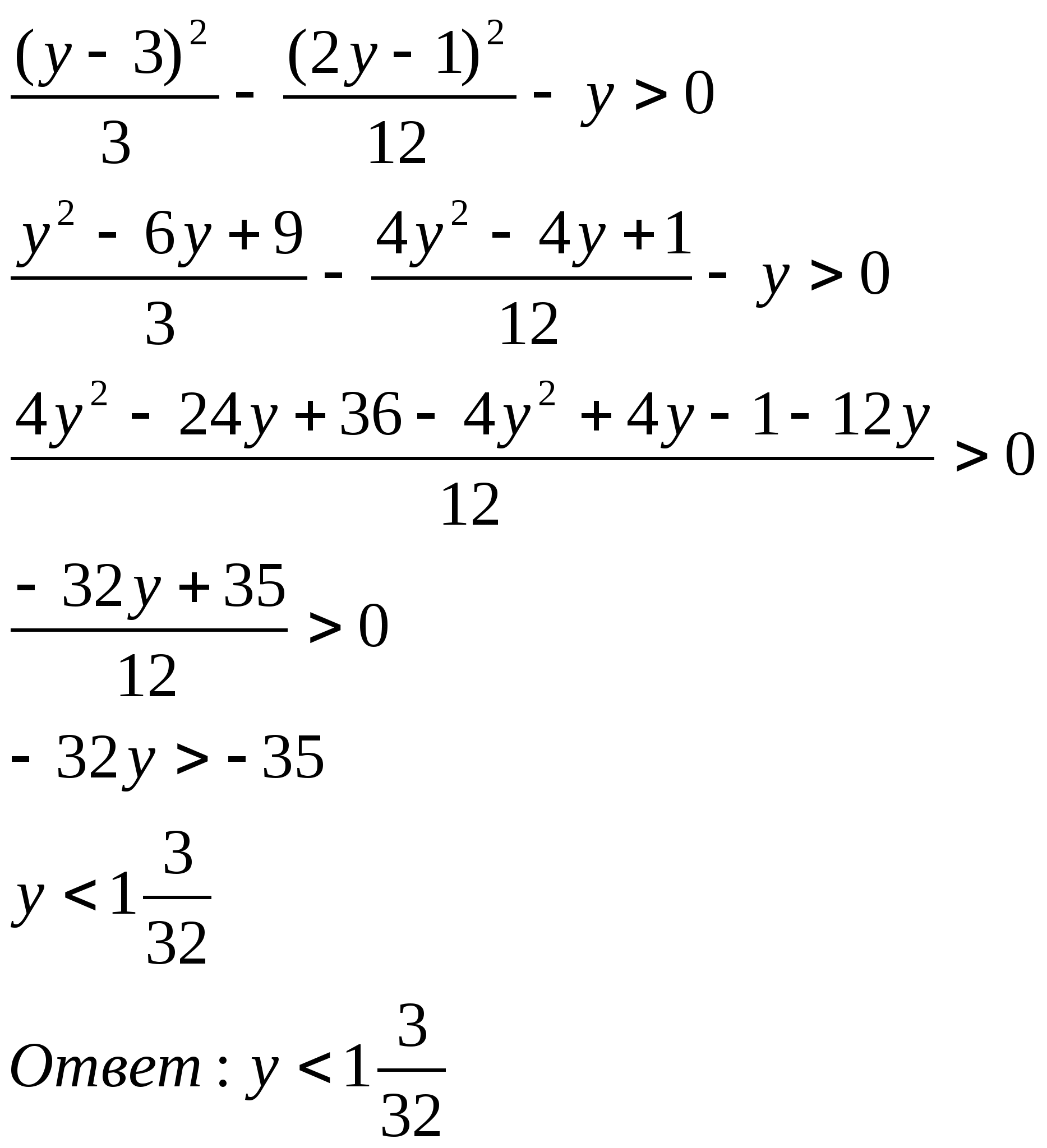
16. Решить уравнение: ![]()
Установить, когда уравнение имеет два различных действительных корня.
Решение:
![]()
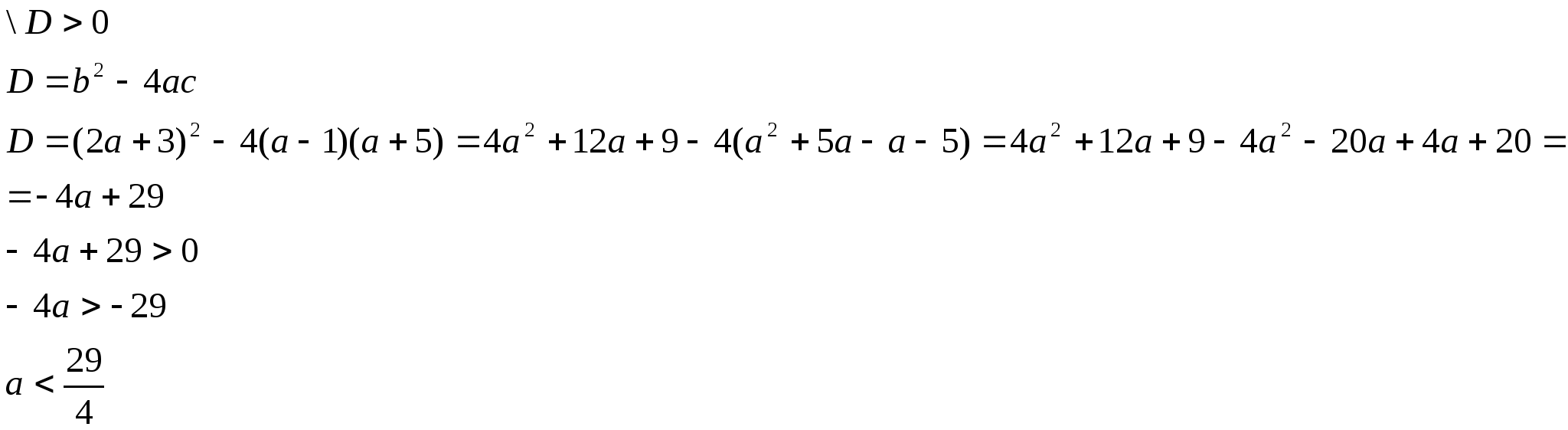 Ответ: уравнение
имеет два различных действительных корня при
Ответ: уравнение
имеет два различных действительных корня при ![]()
17. Решить систему неравенств: 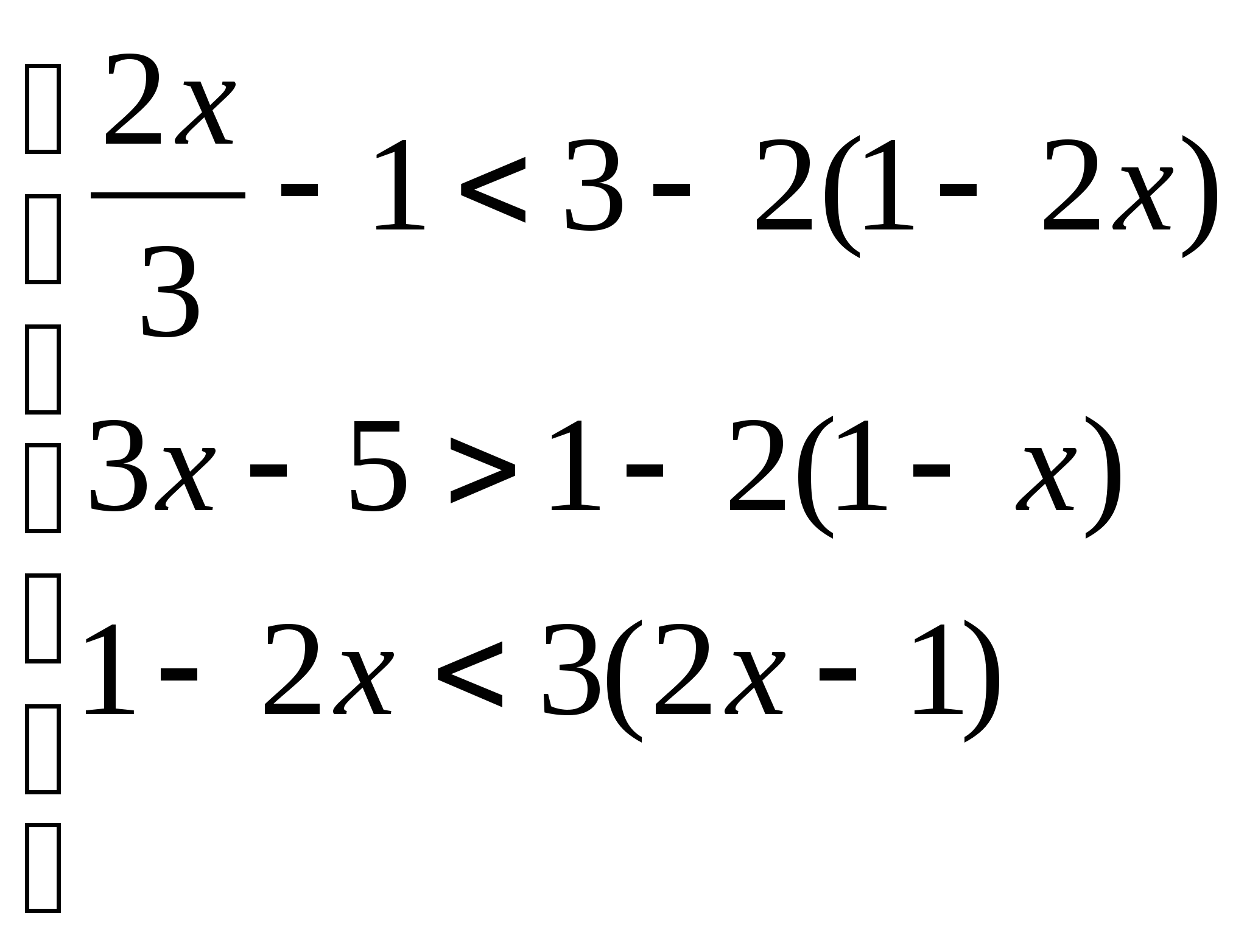
Решение:
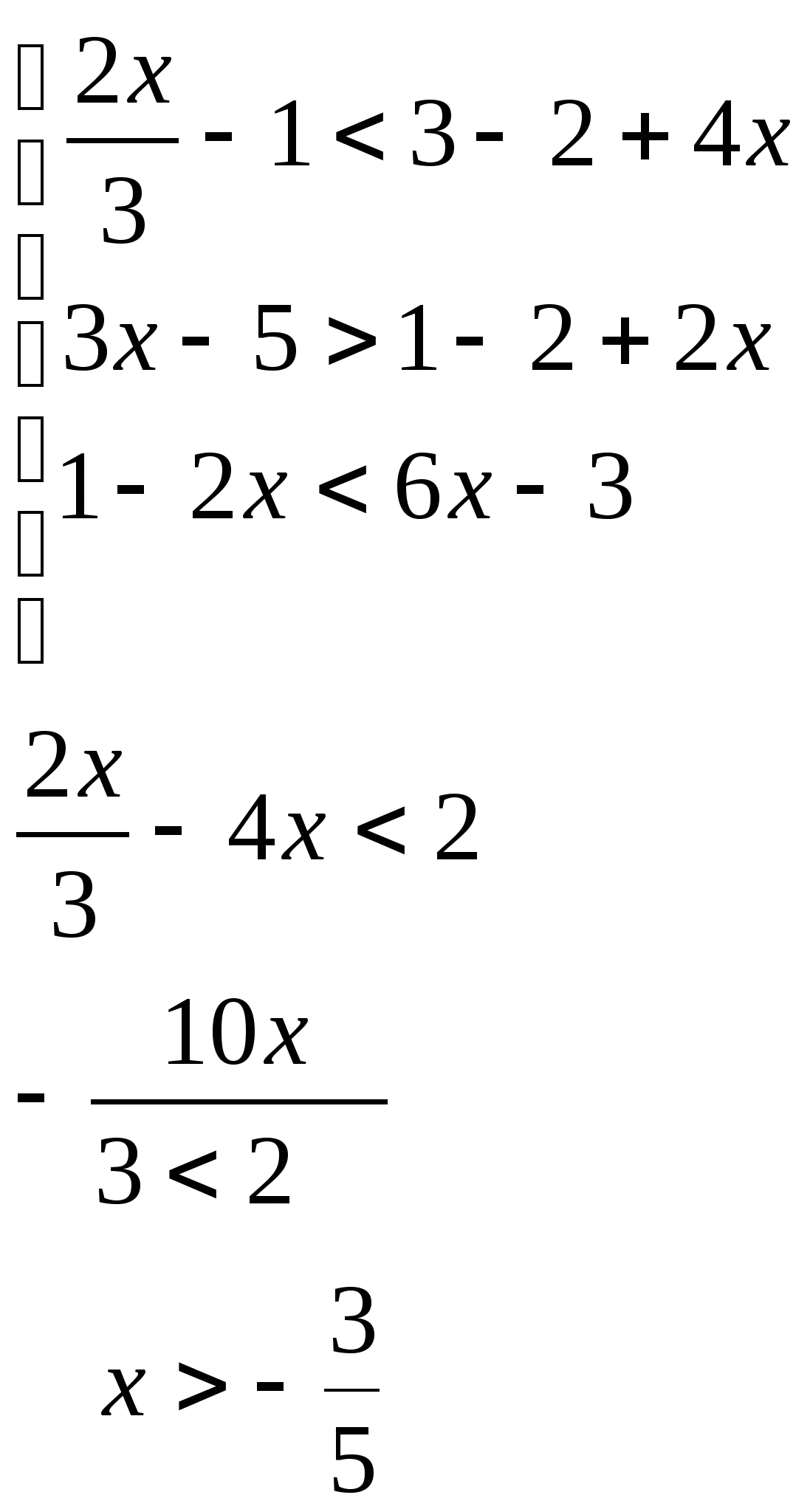
![]()
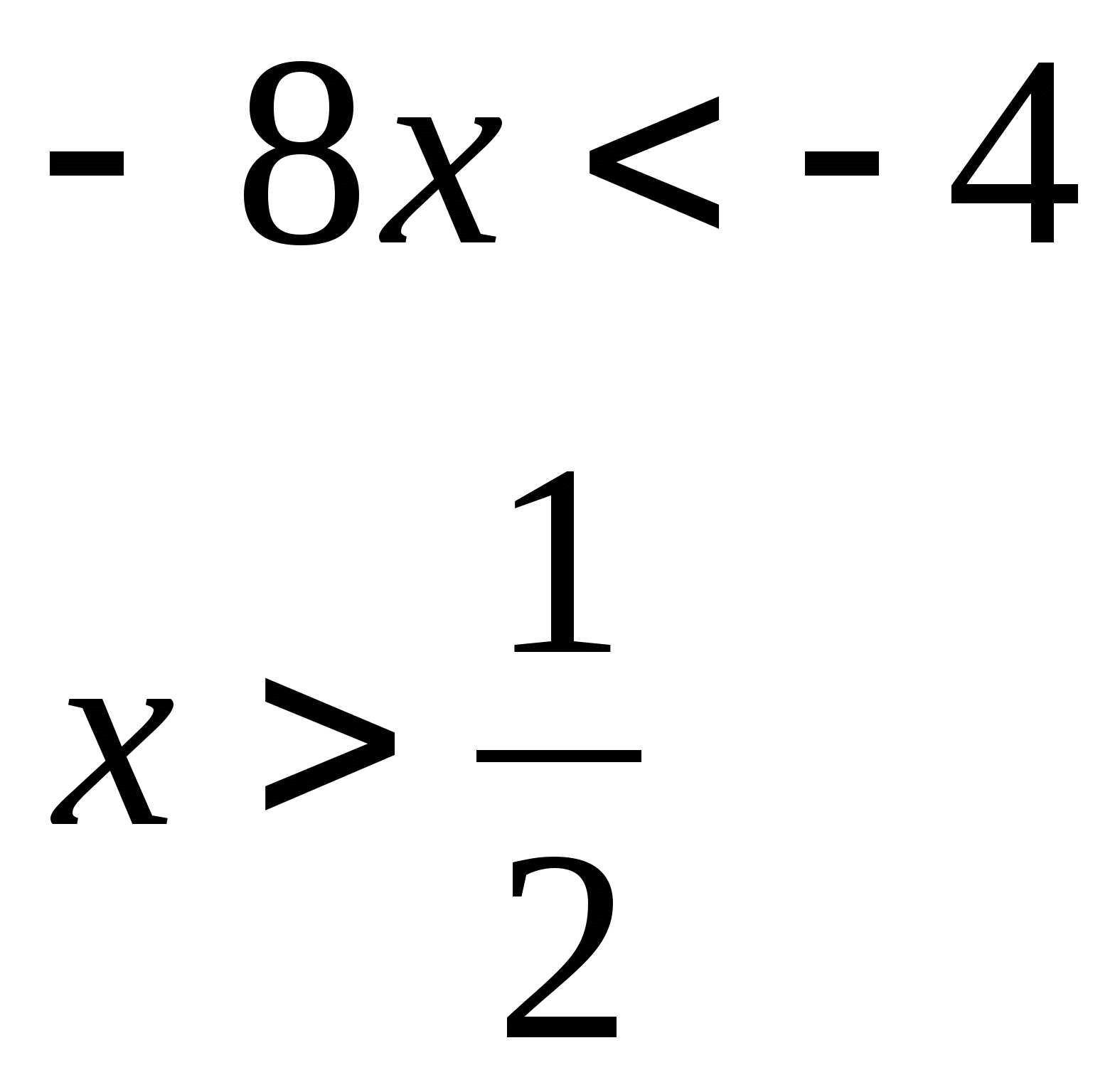
Ответ: х>4
18. Решить систему неравенств:
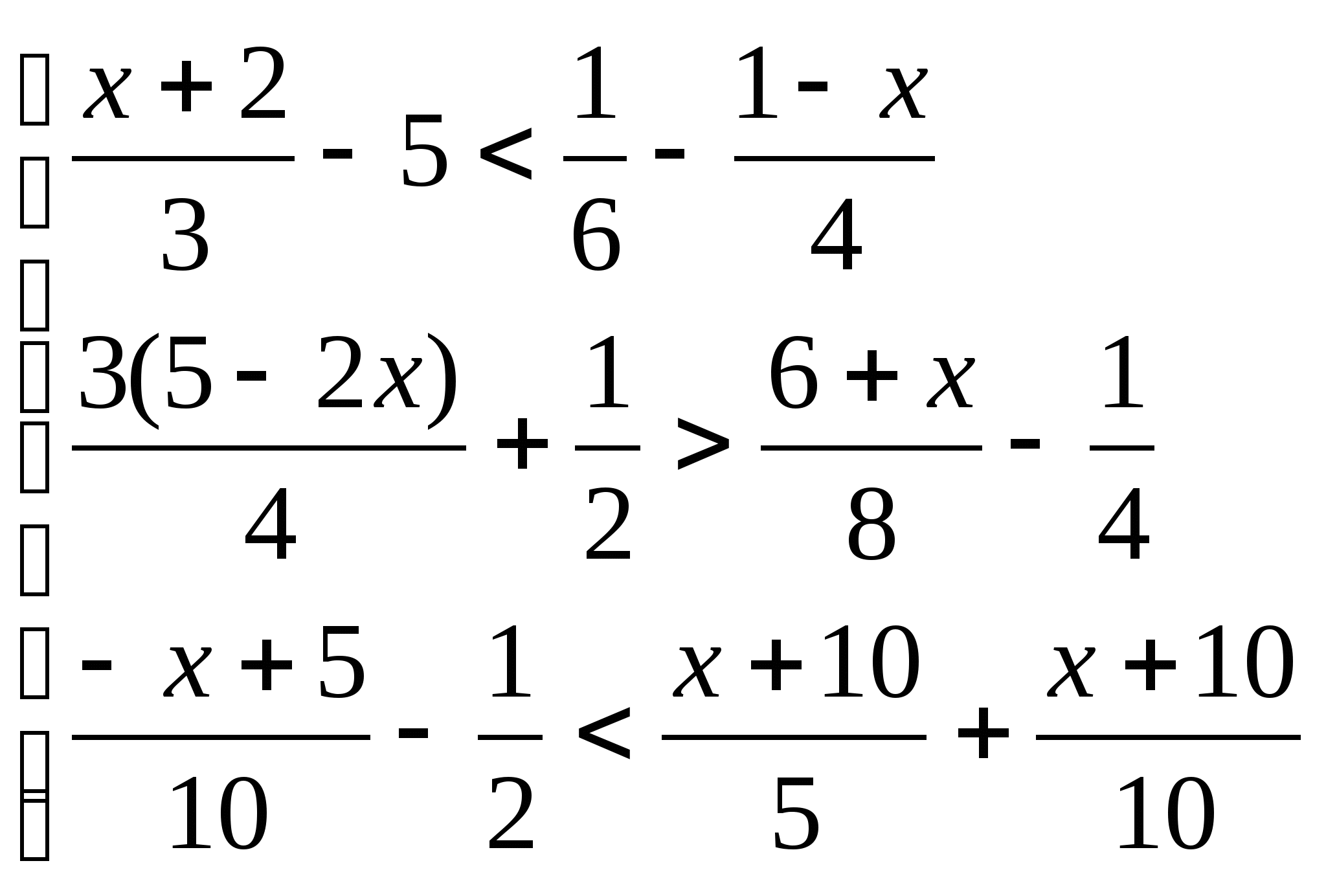
![]()
Решение: ![]()
![]()
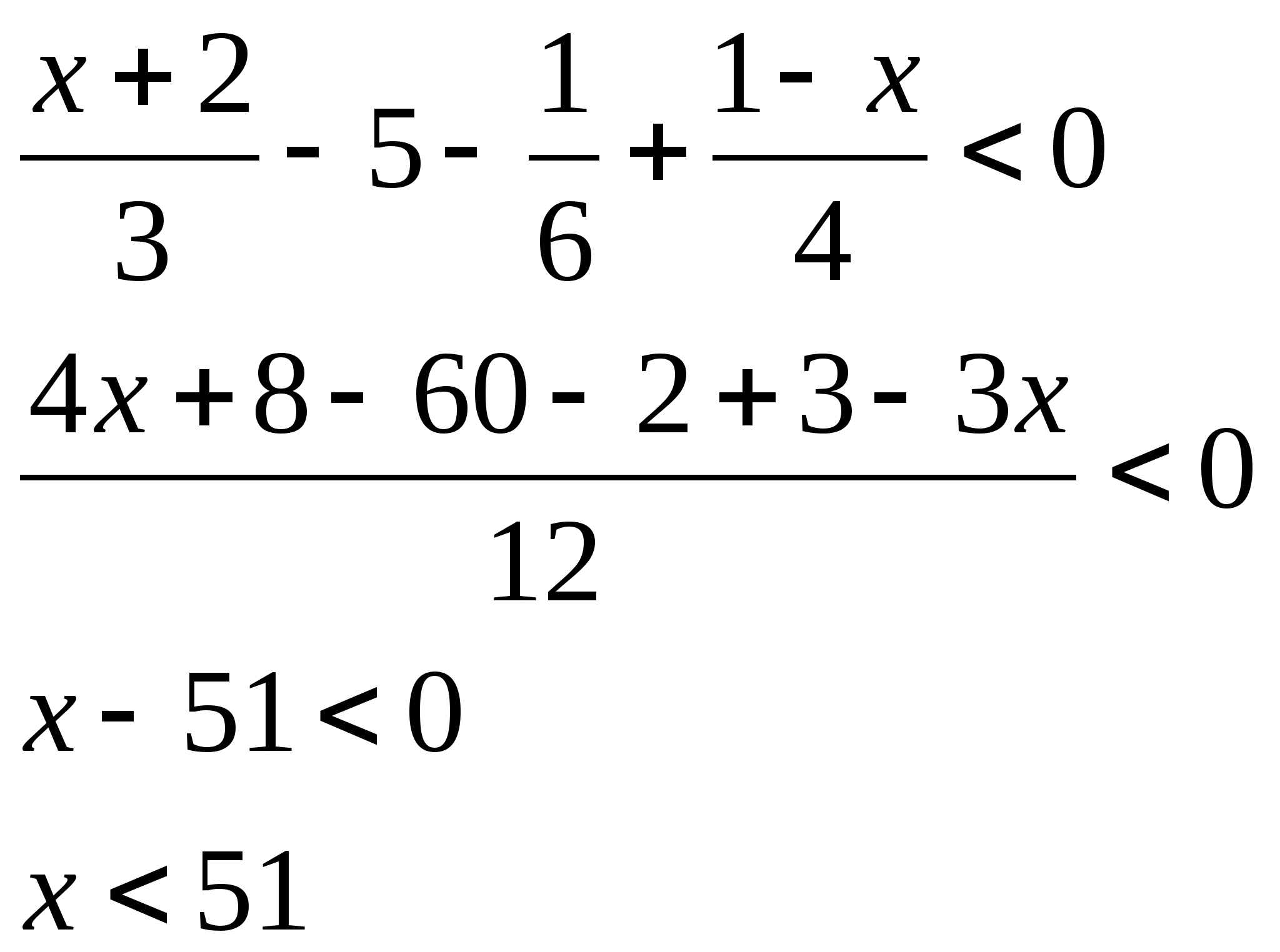
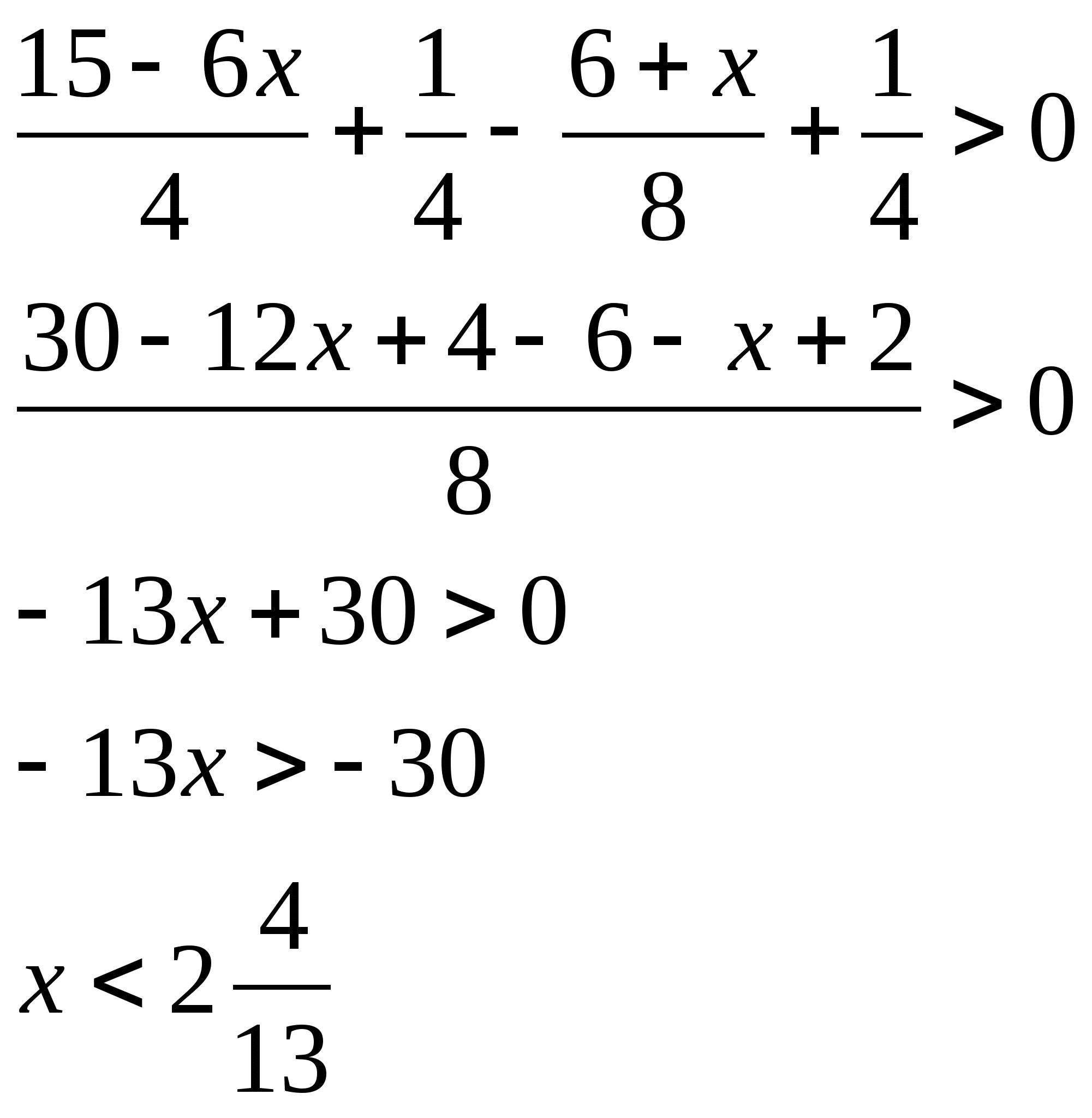
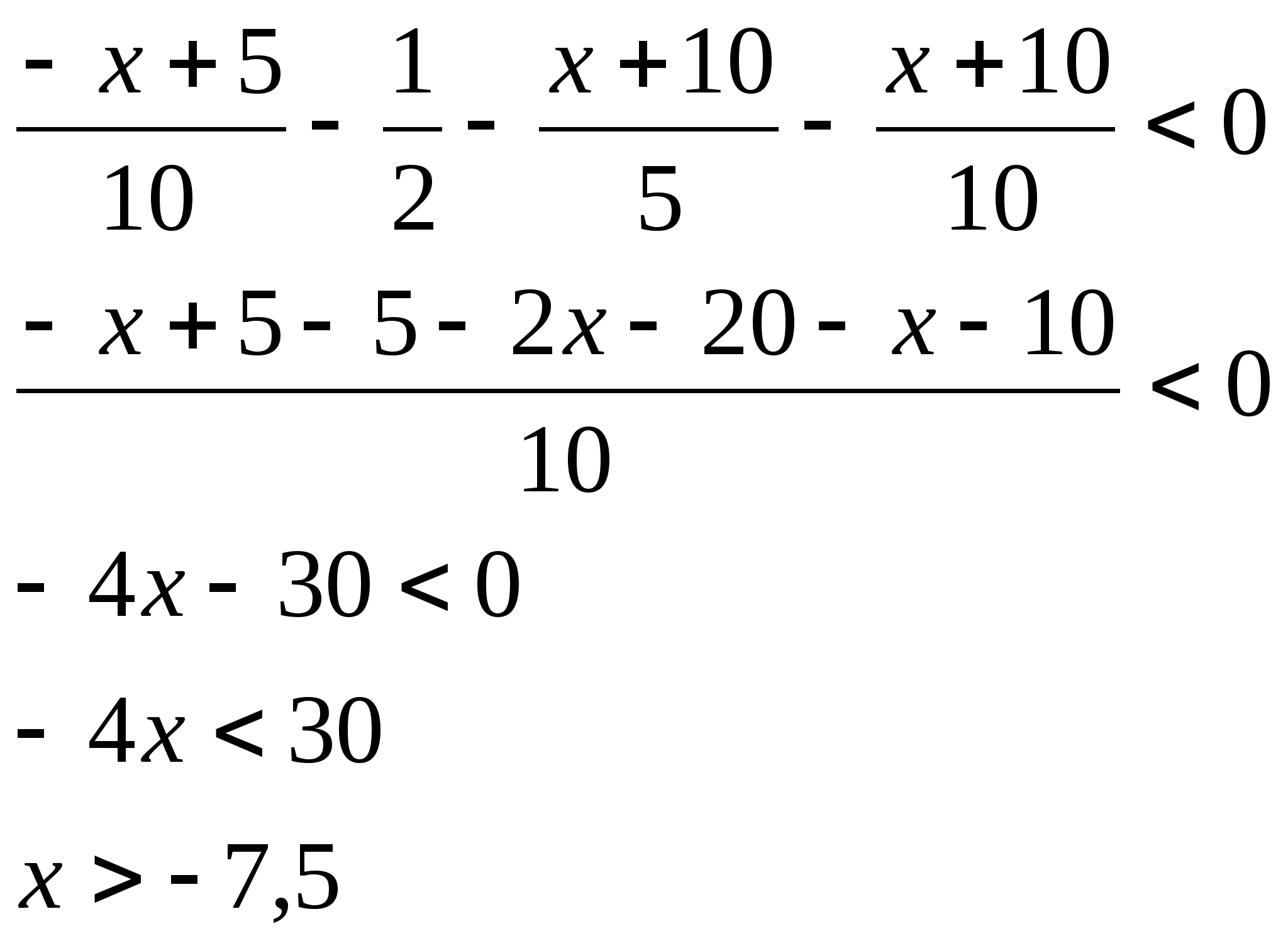
![]()
Ответ: ![]()
19. Решить уравнение: ![]()
Решение:
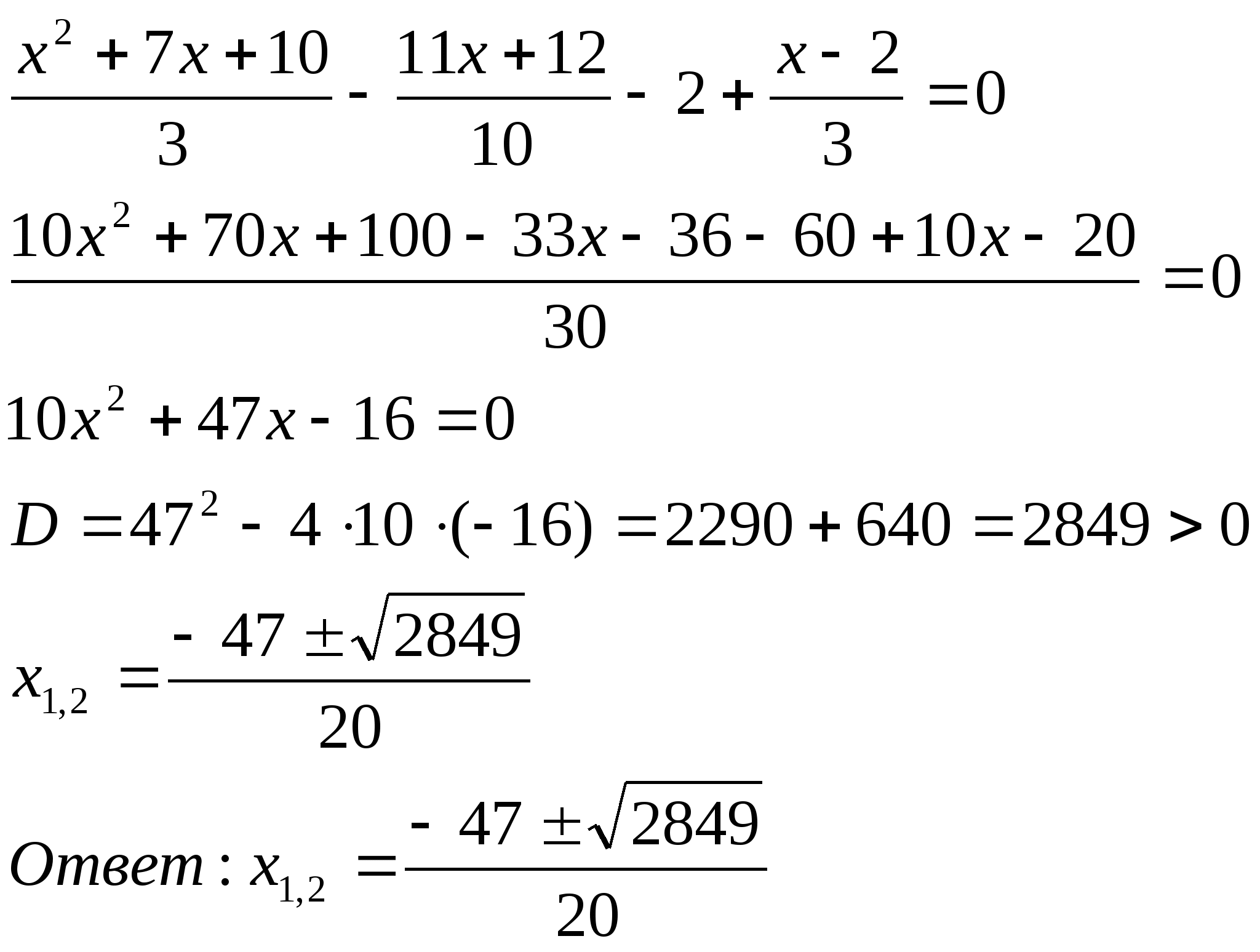
20. Решить уравнение: ![]()
Решение:
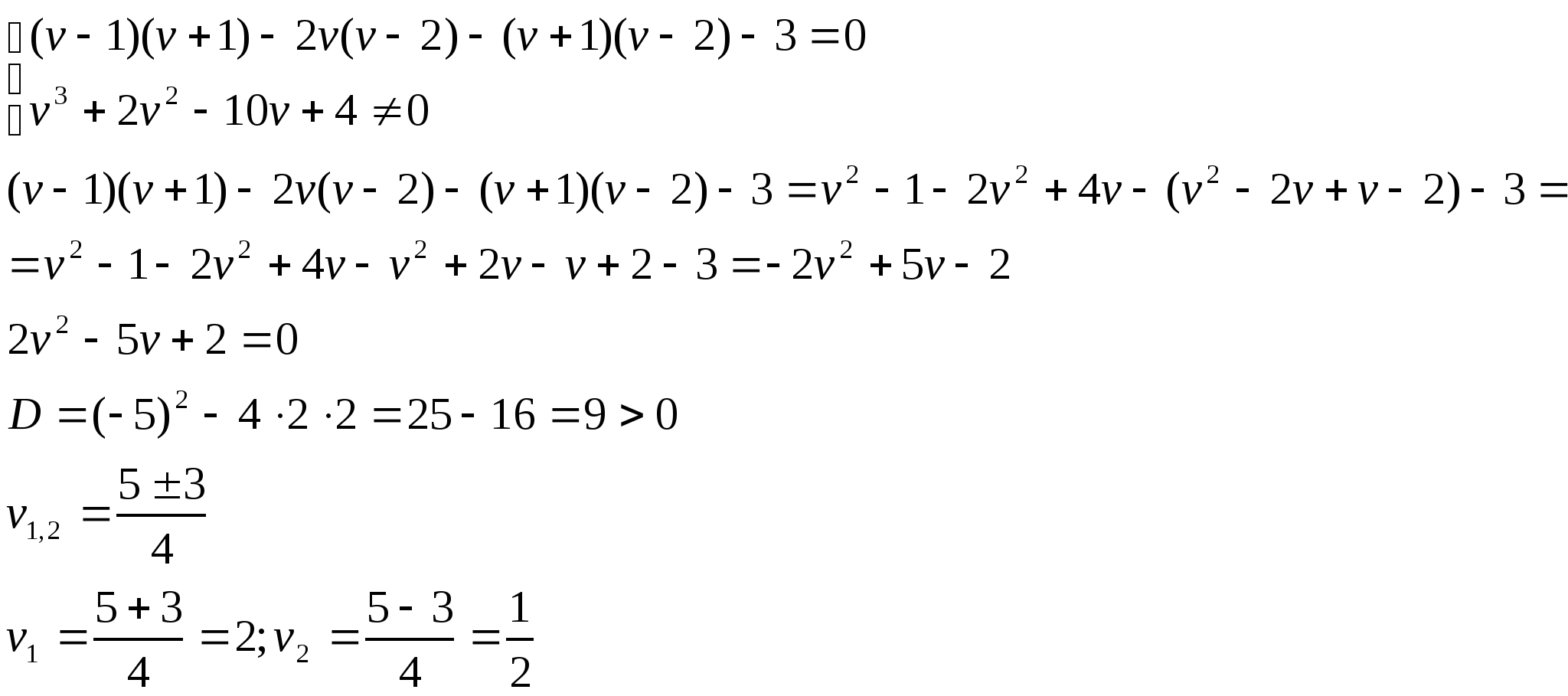
При подстановки ![]() в
знаменатель выражения, получим число, равное 0;
в
знаменатель выражения, получим число, равное 0;
При подстановке ![]() в
знаменатель выражения, получим число, не равное 0;
в
знаменатель выражения, получим число, не равное 0;
Следовательно, корнем уравнения является число ![]() .
.
Ответ: ![]() .
.
2. Тригонометрия
1.Доказать справедливость тождества:
sin6![]() -cos6
-cos6![]() =
=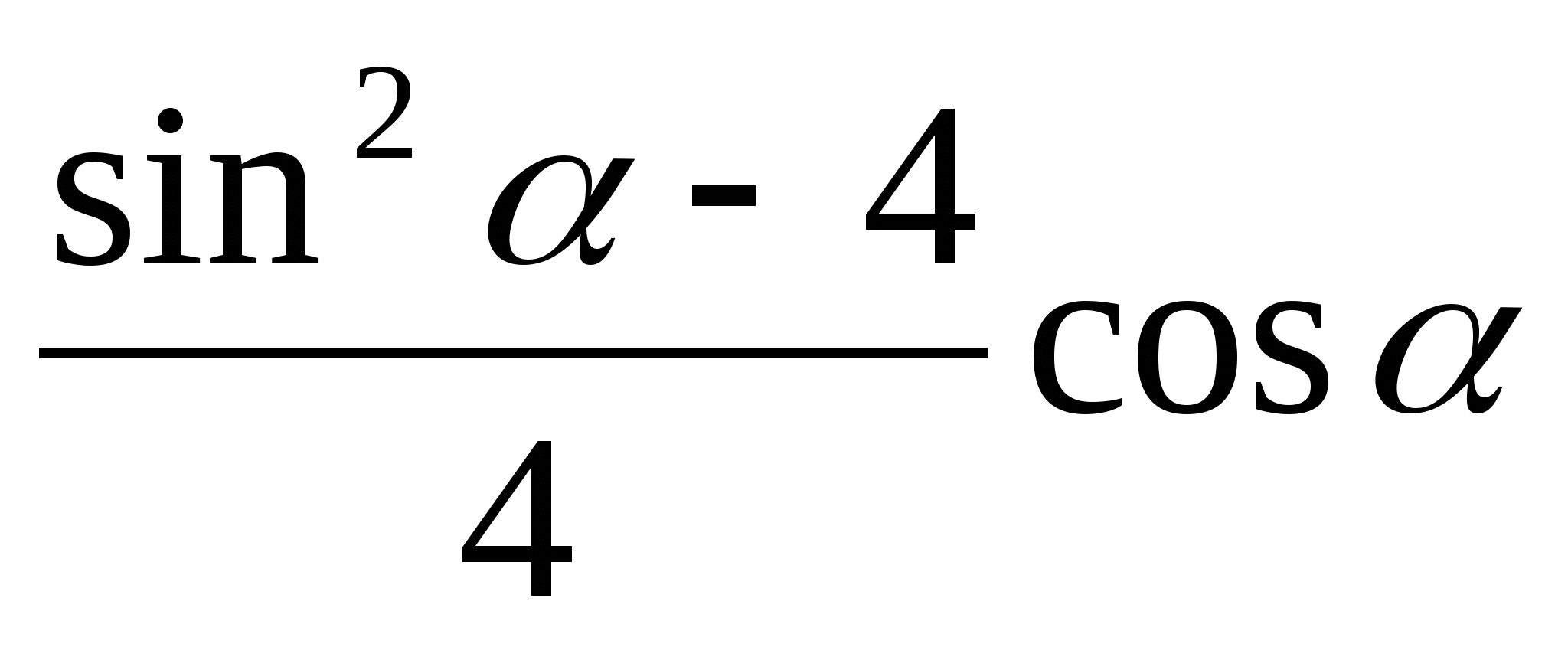
I Способ
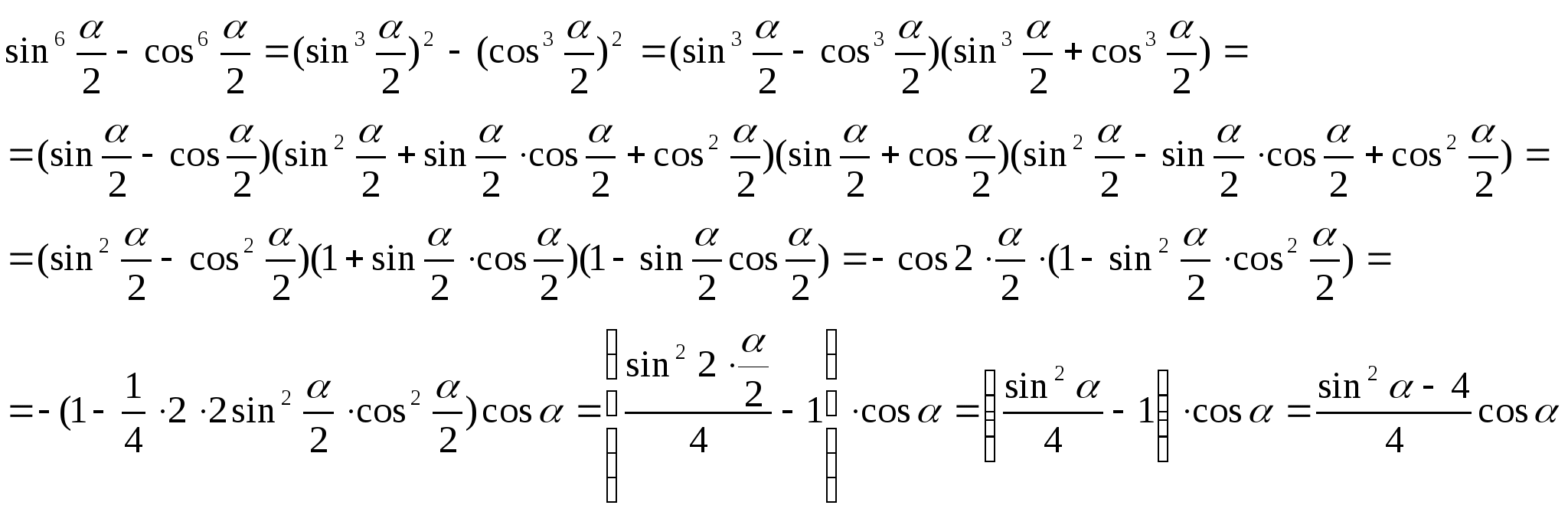
![]() II Способ
II Способ
Используя формулы понижения степени ![]() и
и ![]() получим:
получим:
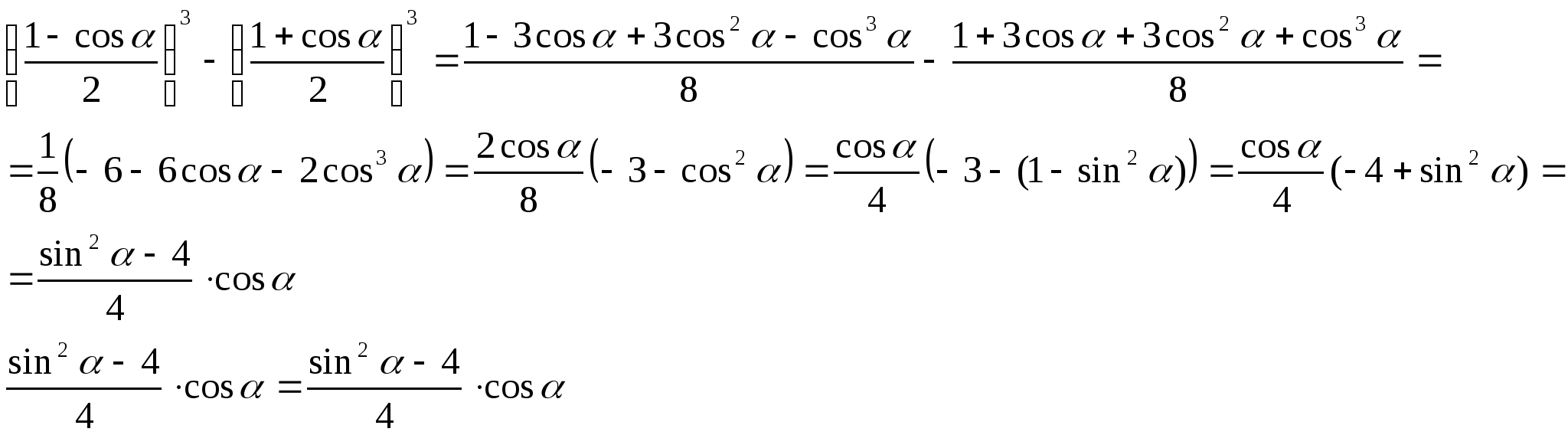 что и требовалось
доказать.
что и требовалось
доказать.
2. Вычислить ![]() ,
если
,
если![]()
Решение:
Возведём обе части уравнения во вторую степень:
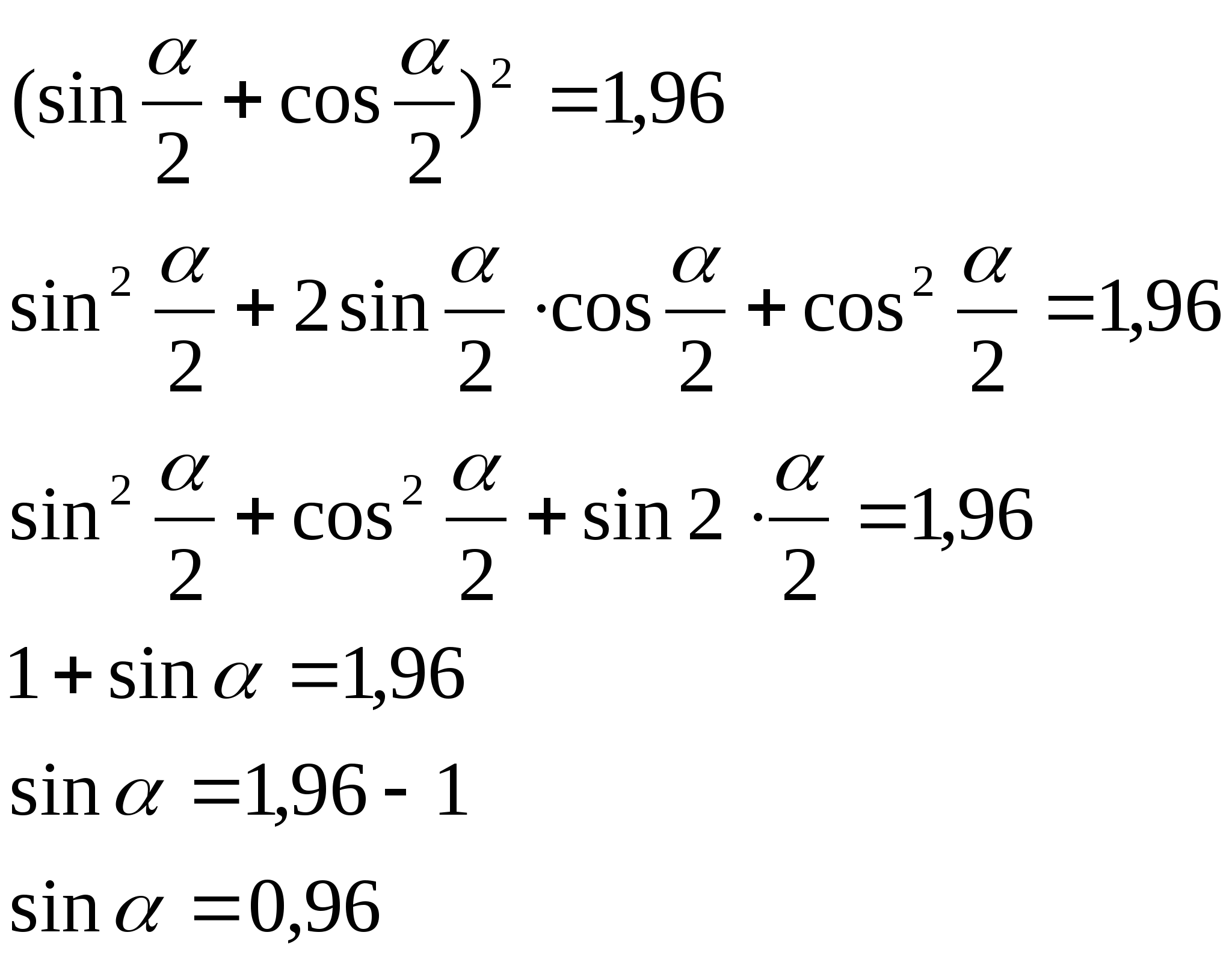
Ответ:![]()
3. Решить уравнение, сводя его к алгебраическому относительно одной тригонометрической функции:
![]()
![]() Решение:
Решение:
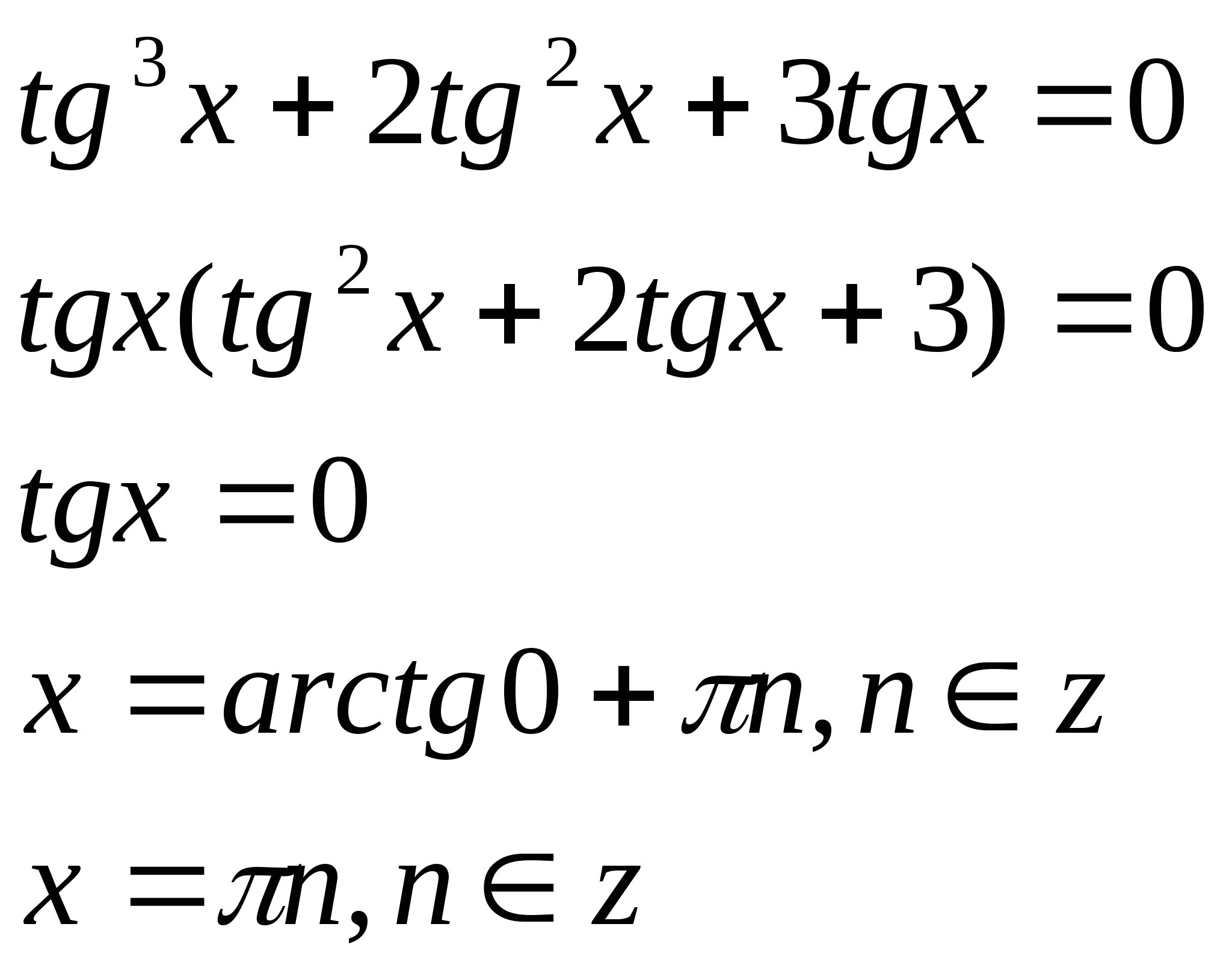
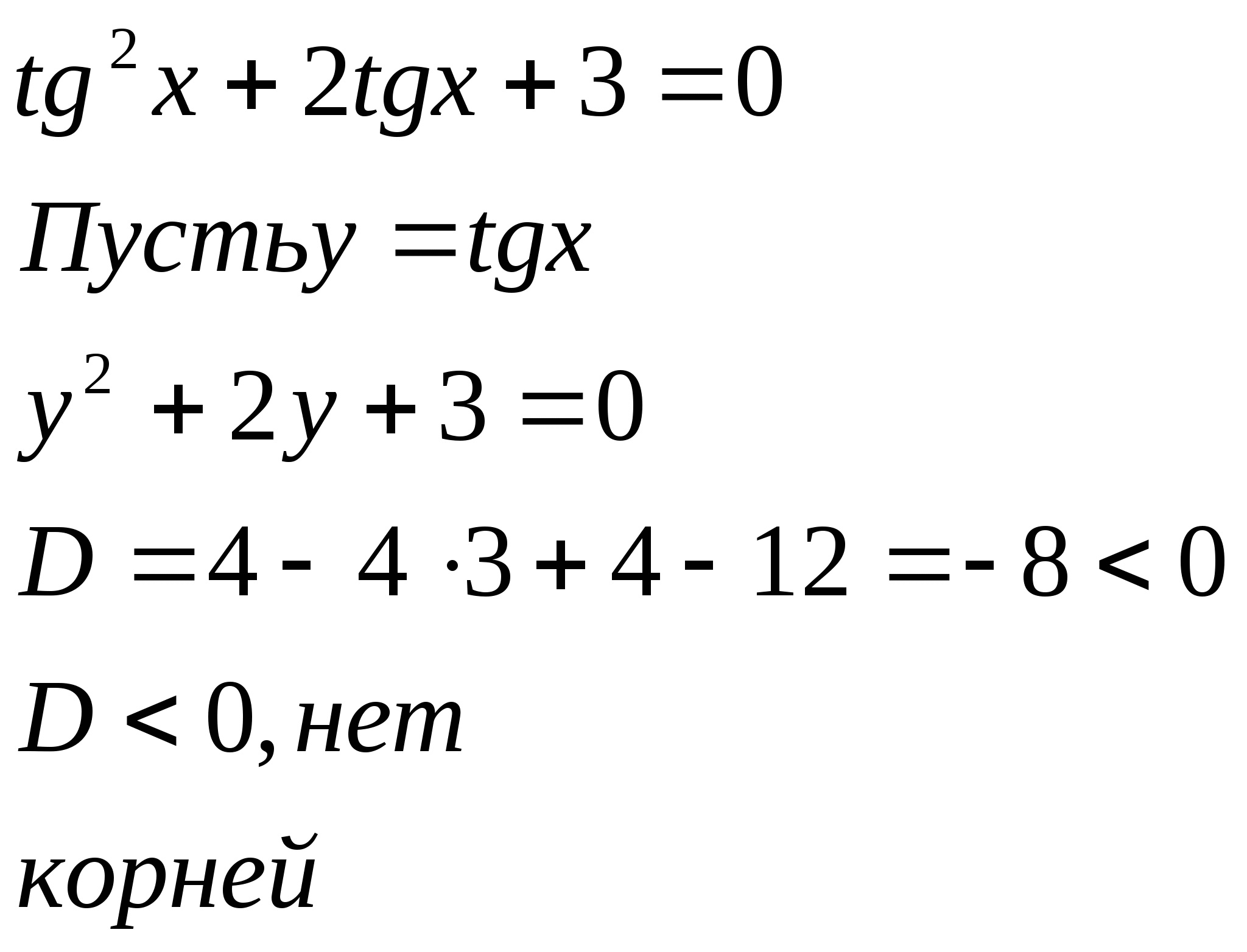
Ответ:![]()
4.Решите уравнение, сведением к однородному
![]()
Решение:
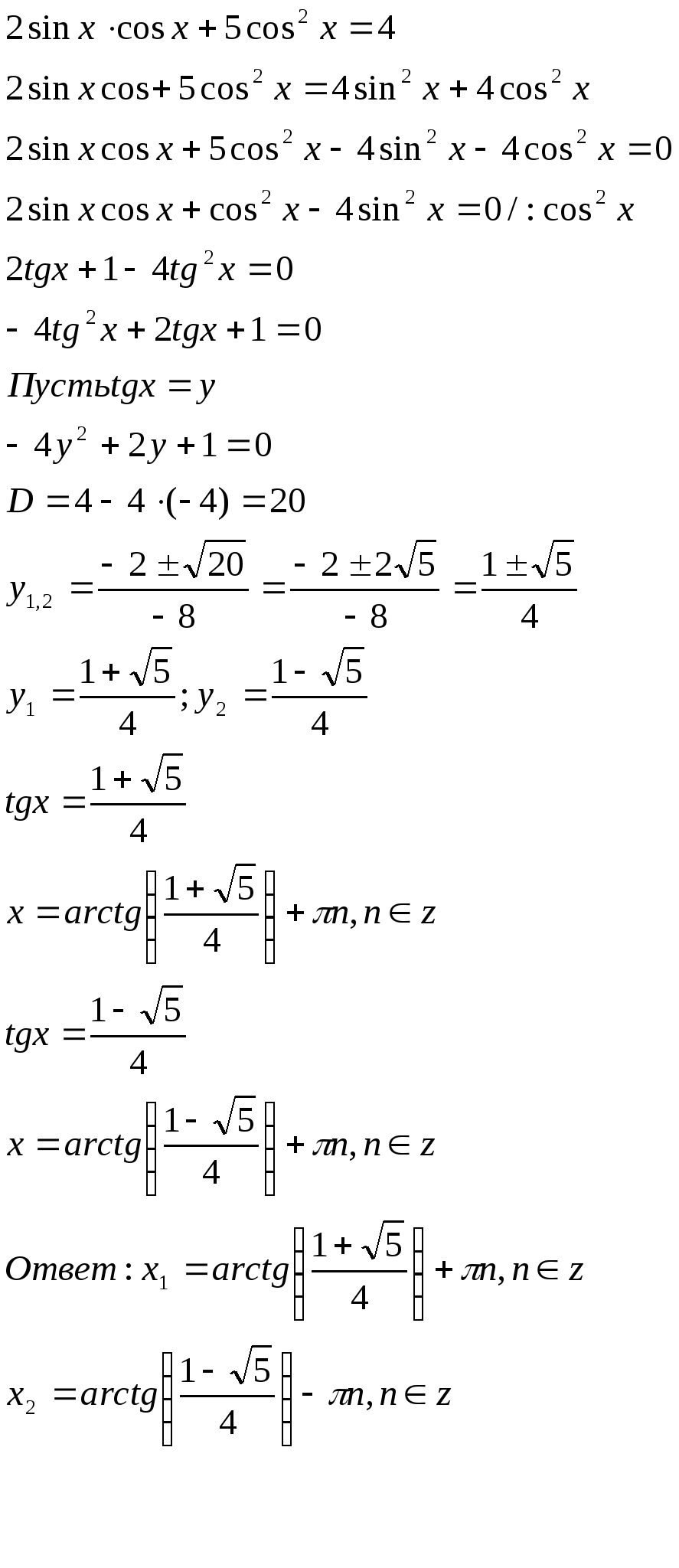
5. Решить уравнение методом универсальной тригонометрической
подстановки: ![]()
а) ![]()
Решение:
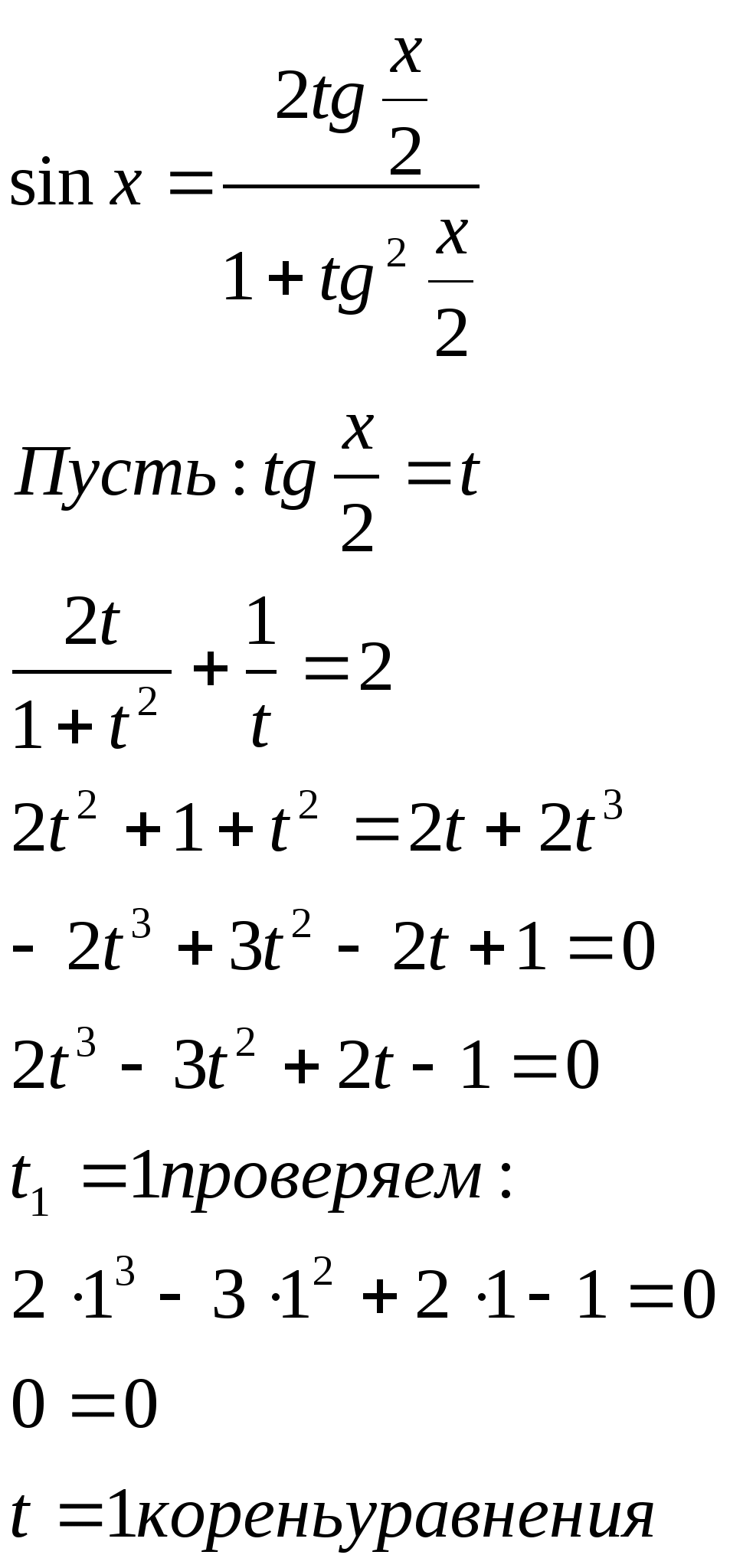
Поделим данный многочлен на ![]()
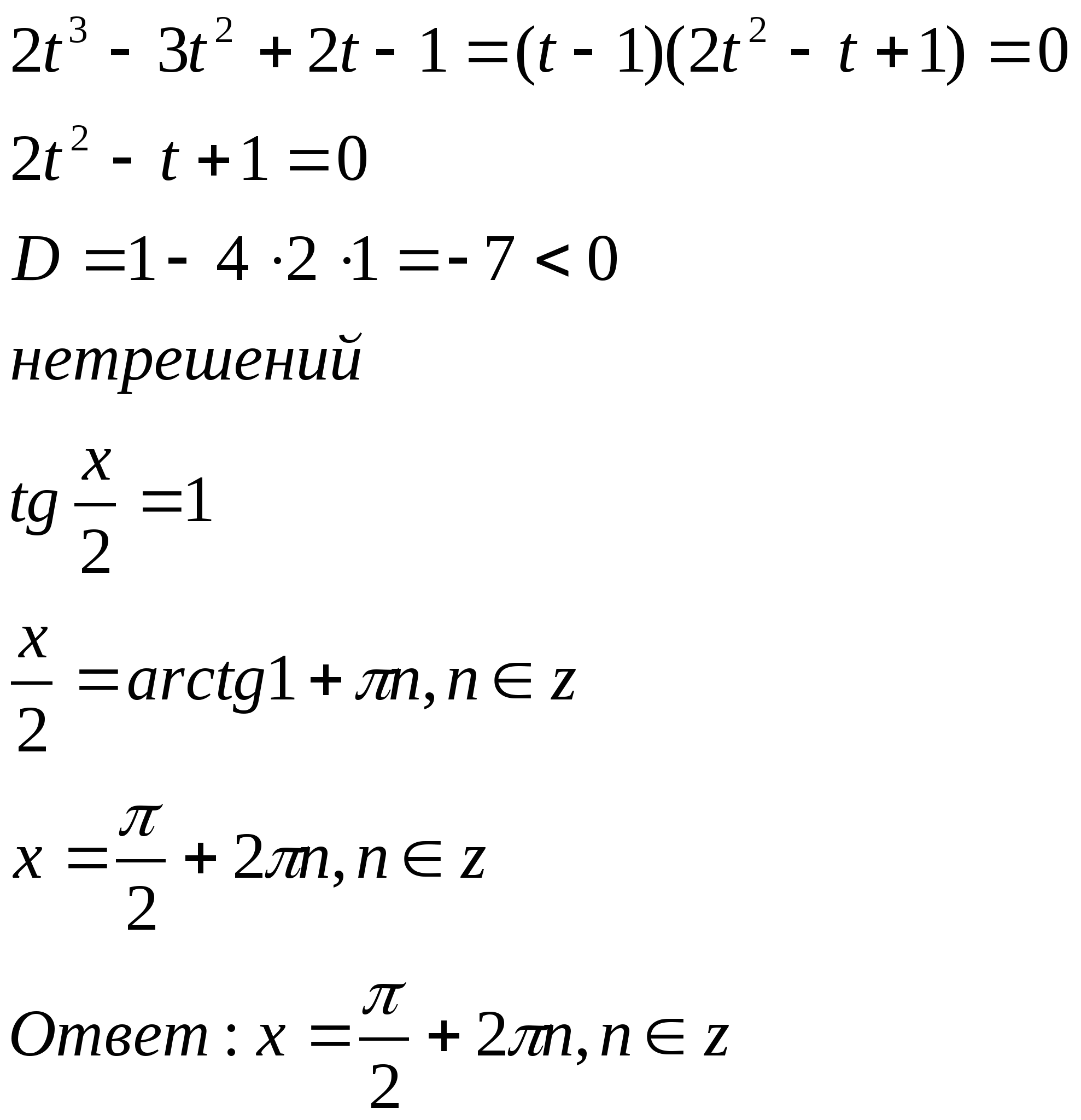
б)![]()
Решение:
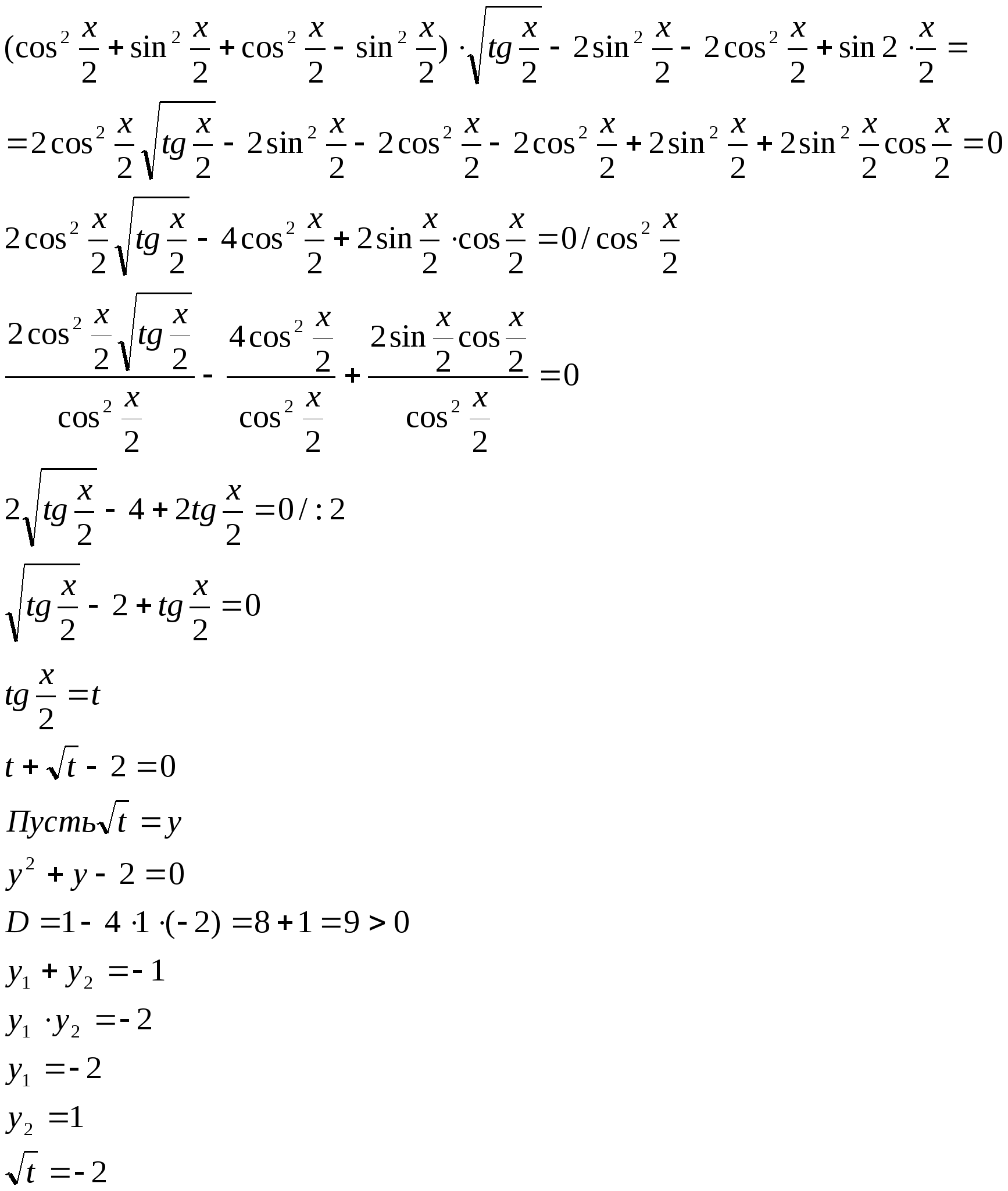
нет решений
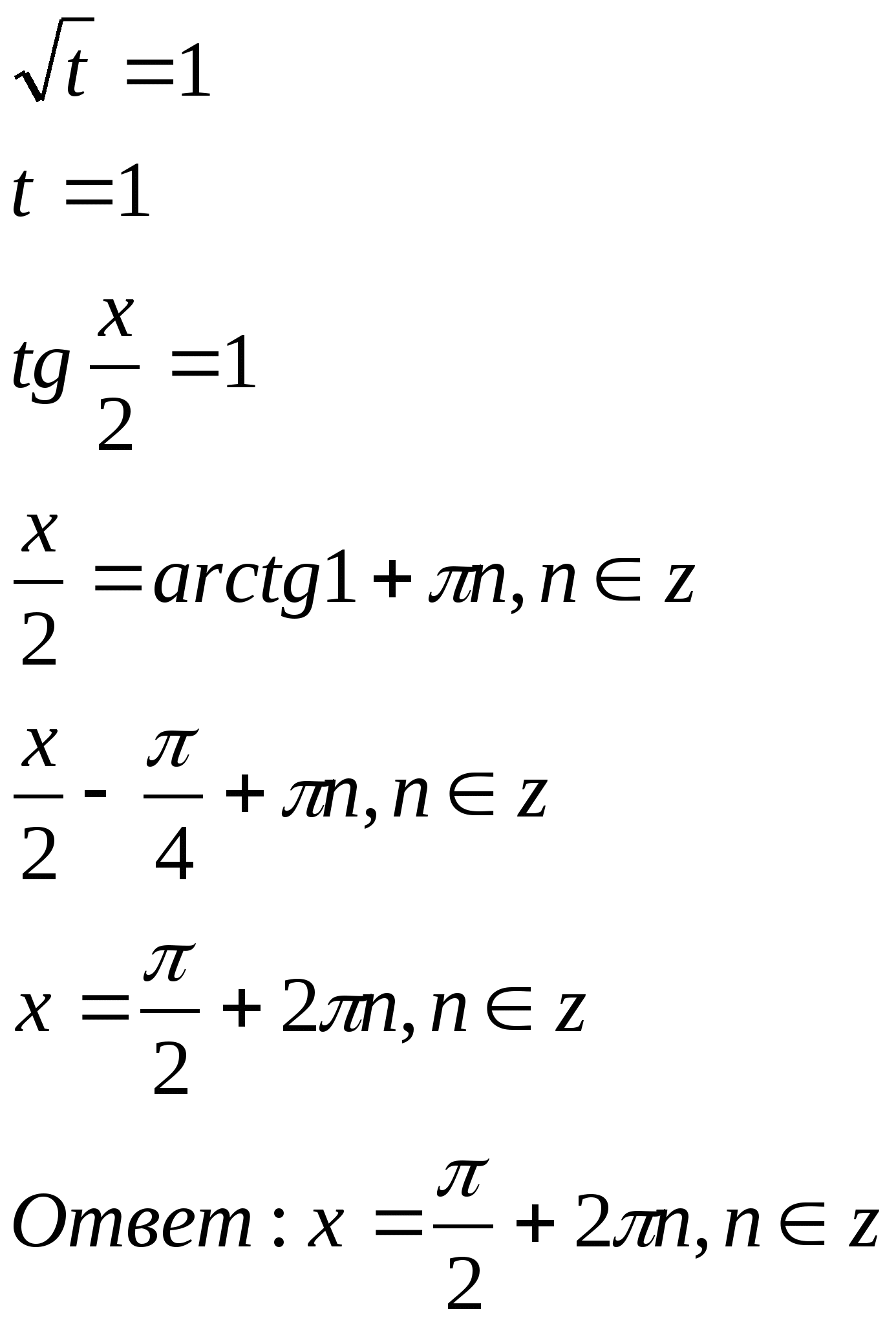
6. Сведение к уравнению относительно неизвестного
![]()
Решение:
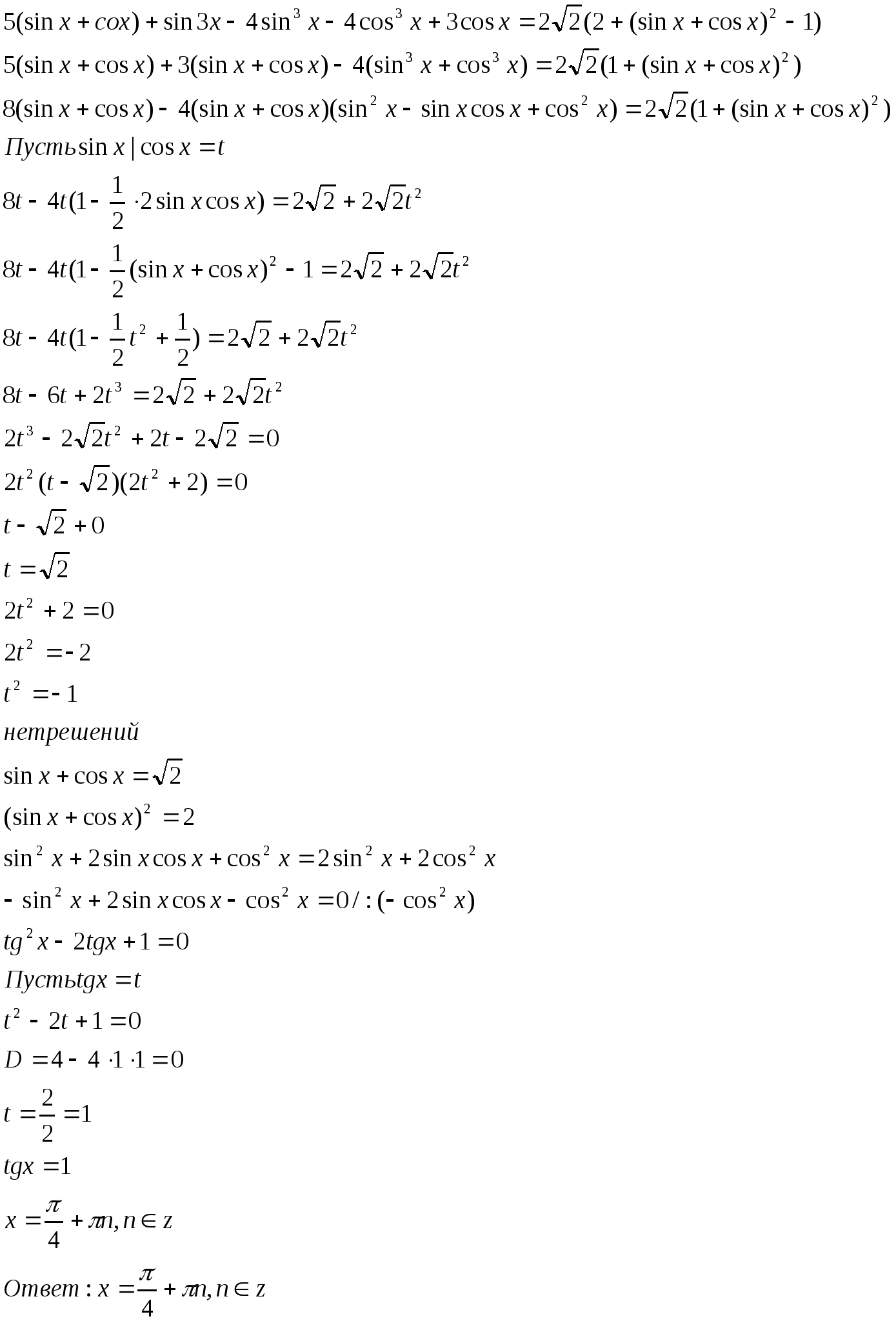
7.Метод понижения степени по формулам половинного аргумента
![]()
Решение:
![]()
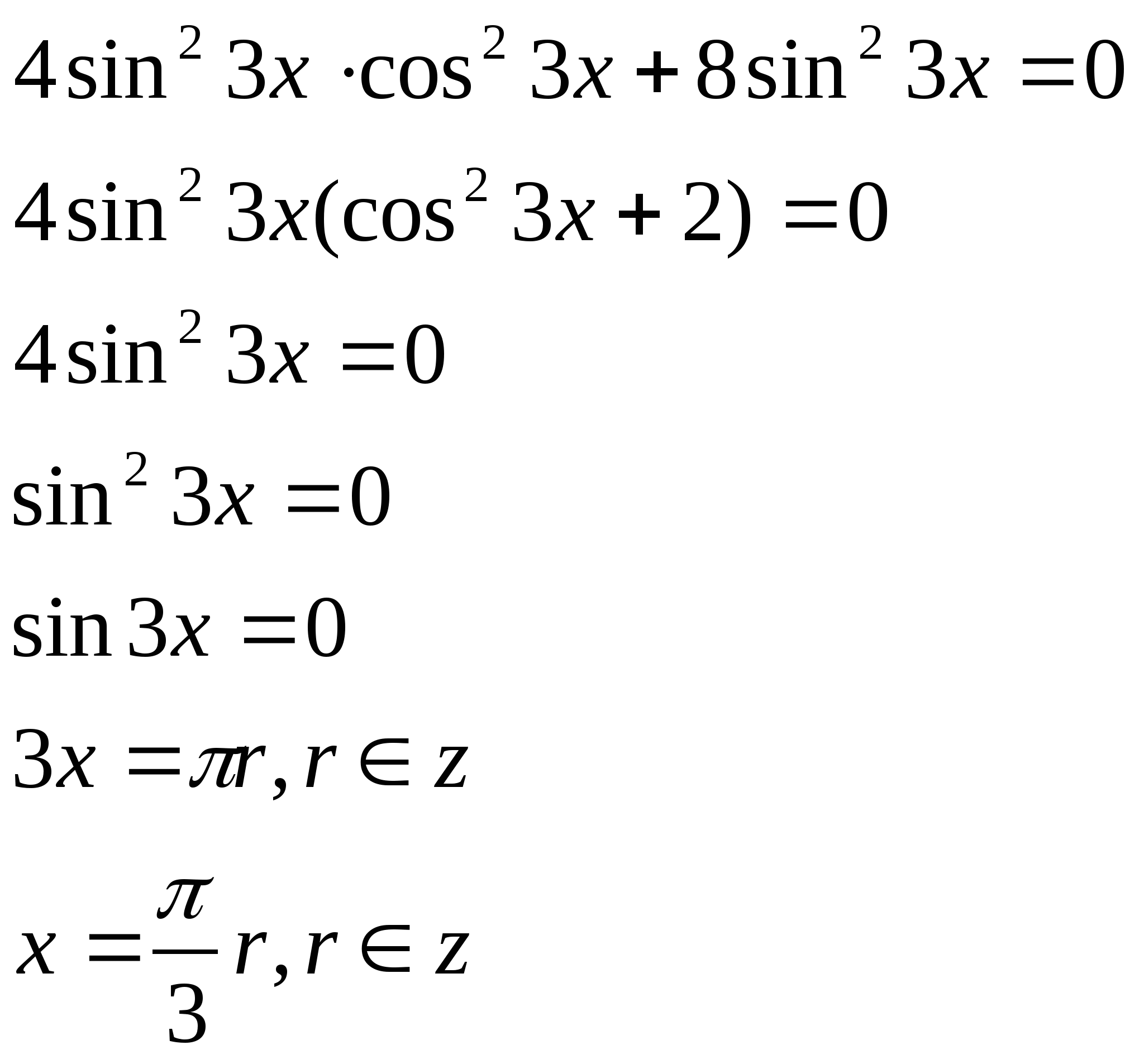
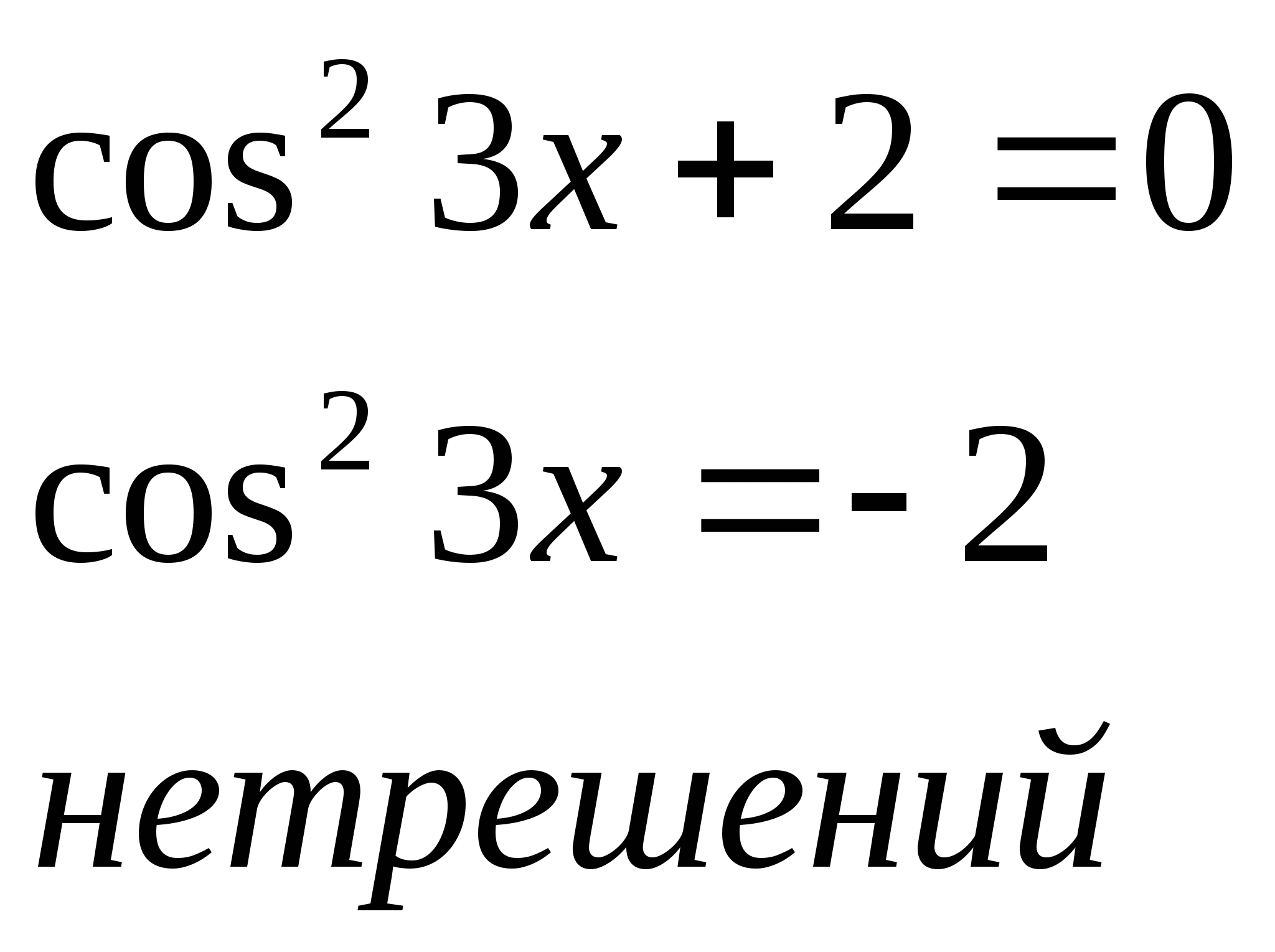
Ответ:![]()
3. Тригонометрические уравнения. 11 класс
1. Решить уравнение: ![]()
Решение:
О.О.У. cos2x≠0
2x≠![]()
x≠![]()
sinx + cosx = 0 /: cosx
Проверка cosx = 0
x= ![]()
![]() 1 + 0 ≠ 0
1 + 0 ≠ 0
cosx ≠ 0
tgx + 1 = 0
tgx = -1
x = -arctg1 +πκ, κ![]() Z
Z
x = -![]() +πκ, κ
+πκ, κ![]() Z - не является
решением
Z - не является
решением
Проверка x= ![]()
![]()
![]()
Ответ: нет решений.
2. Решить уравнение: tg3x + tg2x - 3tgx = 3
Решение:
О.О.У. ![]() x ≠
x ≠ ![]() + πκ, κ
+ πκ, κ![]() Z
Z
tg3x + tg2x - 3tgx - 3=0
tg2x·( tgx + 1 ) - 3·( tgx + 1) =0
( tgx + 1 ) ·( tg2x - 3) = 0
tgx + 1 =0 tg2x - 3 =0
tgx = -1 tg2x = 3
![]() x = -
x = -![]() + πκ, κ
+ πκ, κ![]() Z tgx =
Z tgx = ![]() , tgx = -
, tgx = -![]()
x = ![]() + πn, n
+ πn, n ![]() Z x = -
Z x = -![]() + πn, n
+ πn, n ![]() Z
Z
Ответ: x = -![]() + πκ,
κ
+ πκ,
κ![]() Z; x = ±
Z; x = ±![]() + πn, n
+ πn, n ![]() Z
Z
3. Решить уравнение: sin3x = cos2x
Решение:
sin3x = cos2x
т.к. cos2x = sin(![]() -
2x)
-
2x)
sin3x = sin(![]() - 2x)
- 2x)
sin3x - sin(![]() - 2x) = 0
- 2x) = 0
2sin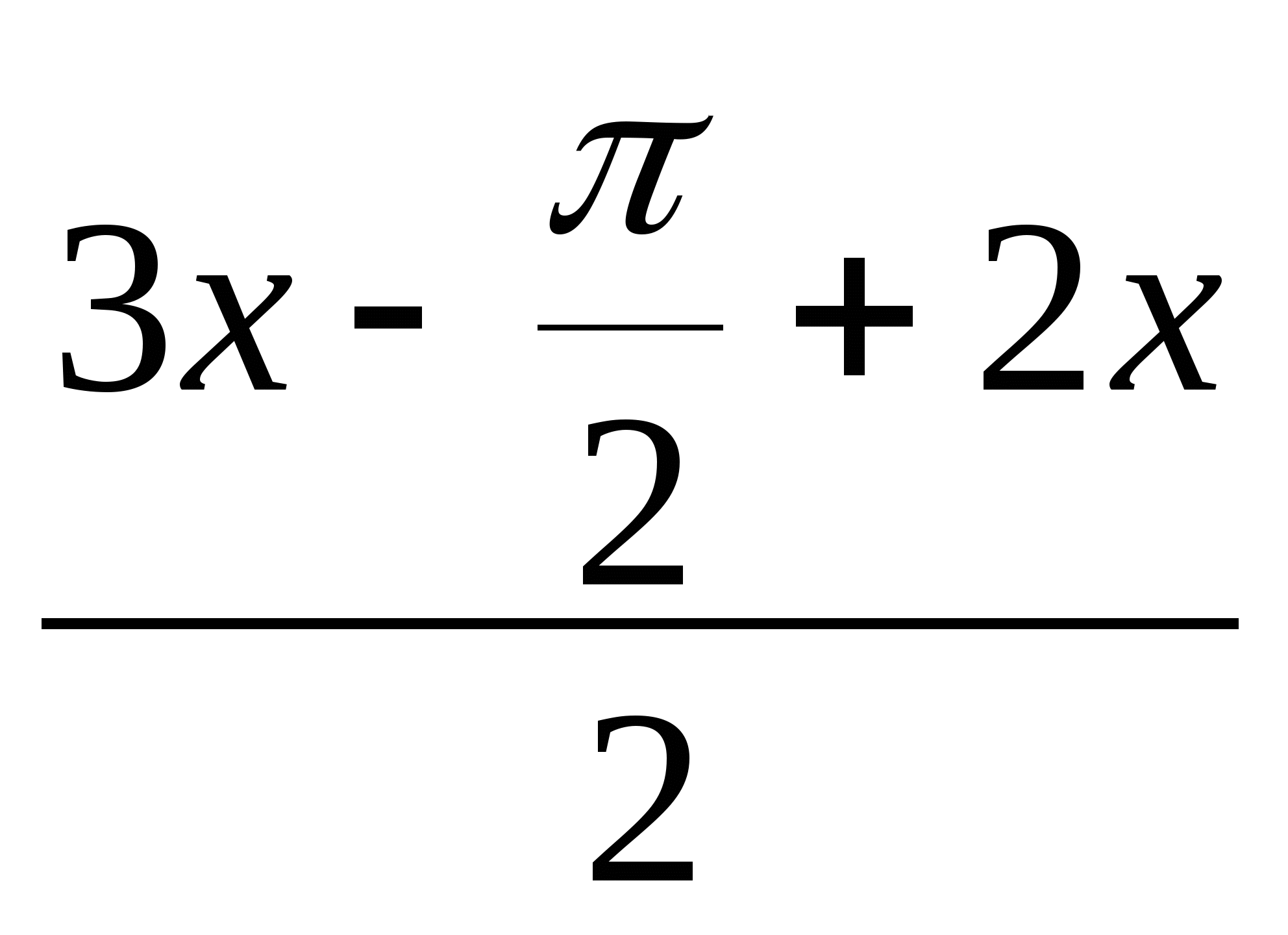 ·cos
·cos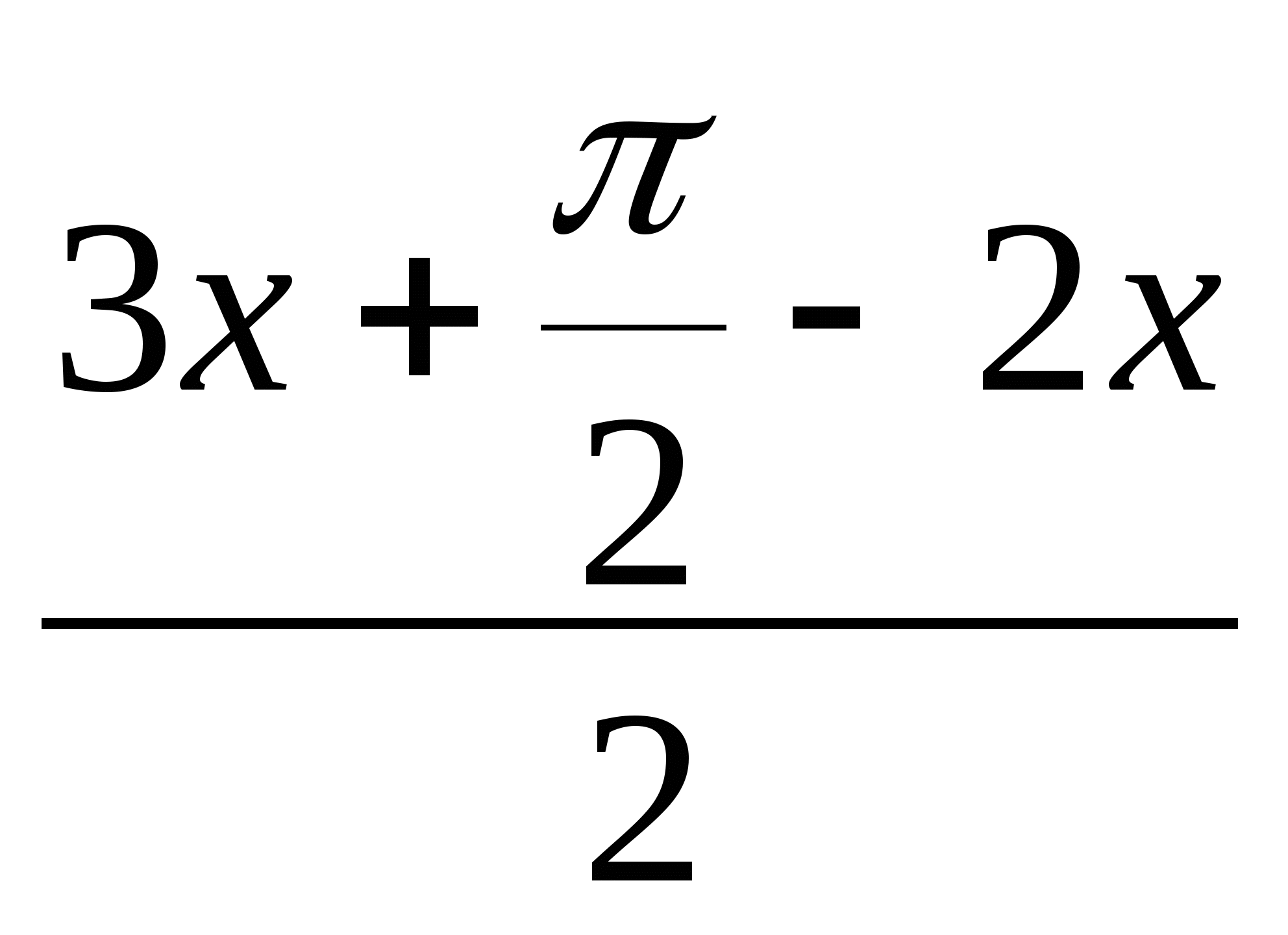 = 0
= 0
2sin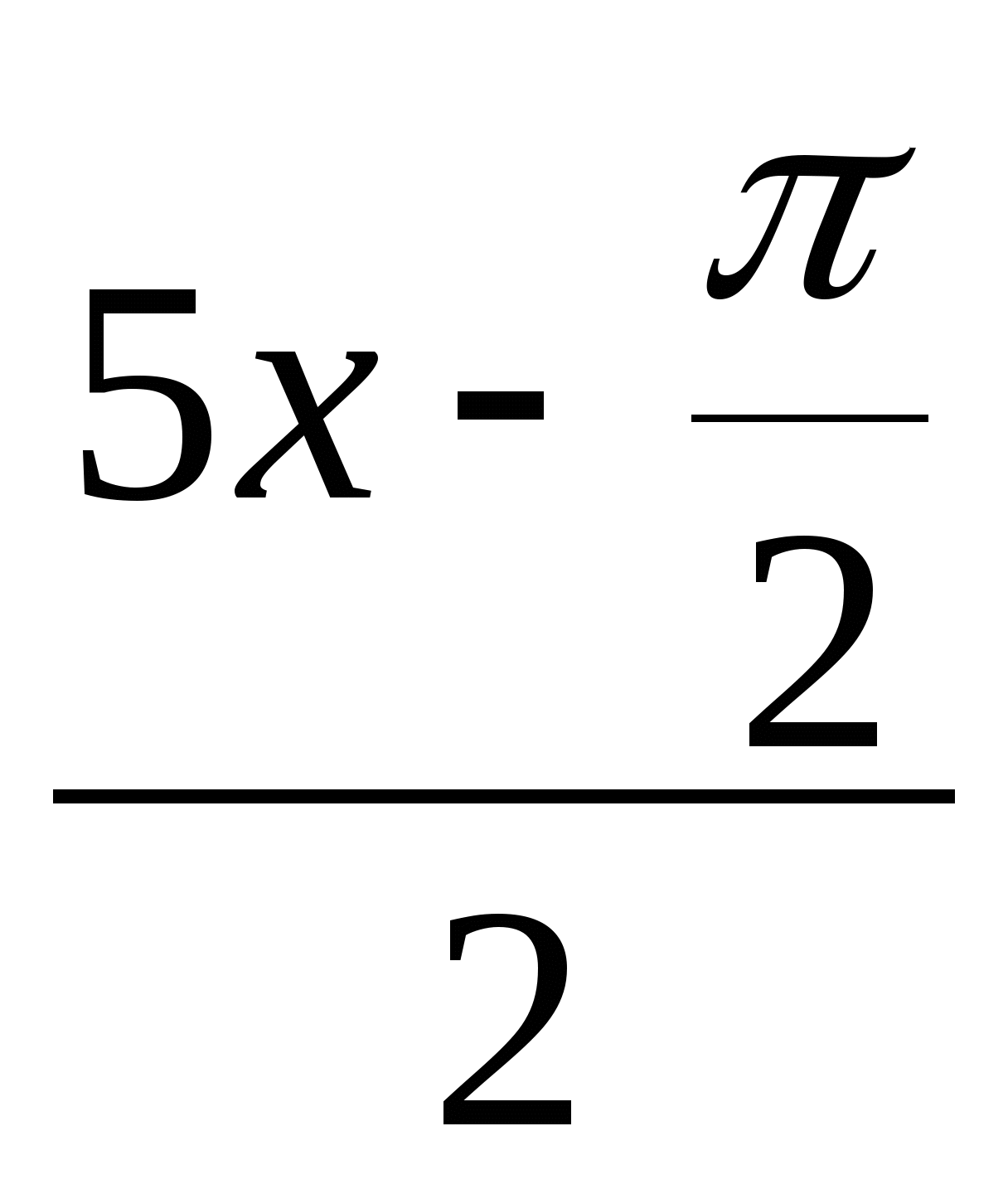 ·cos
·cos![]() = 0
= 0
sin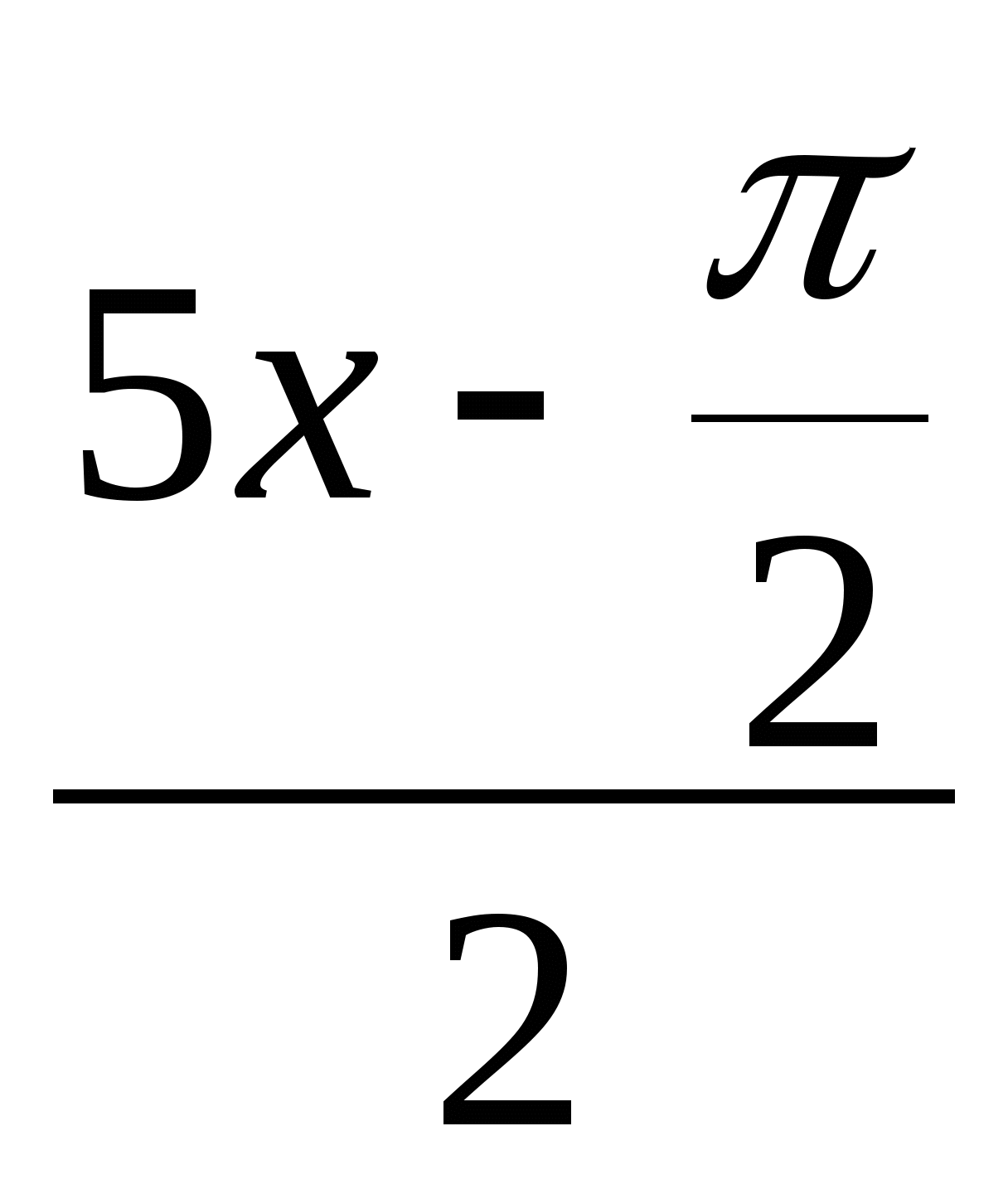 = 0 cos
= 0 cos![]() = 0
= 0
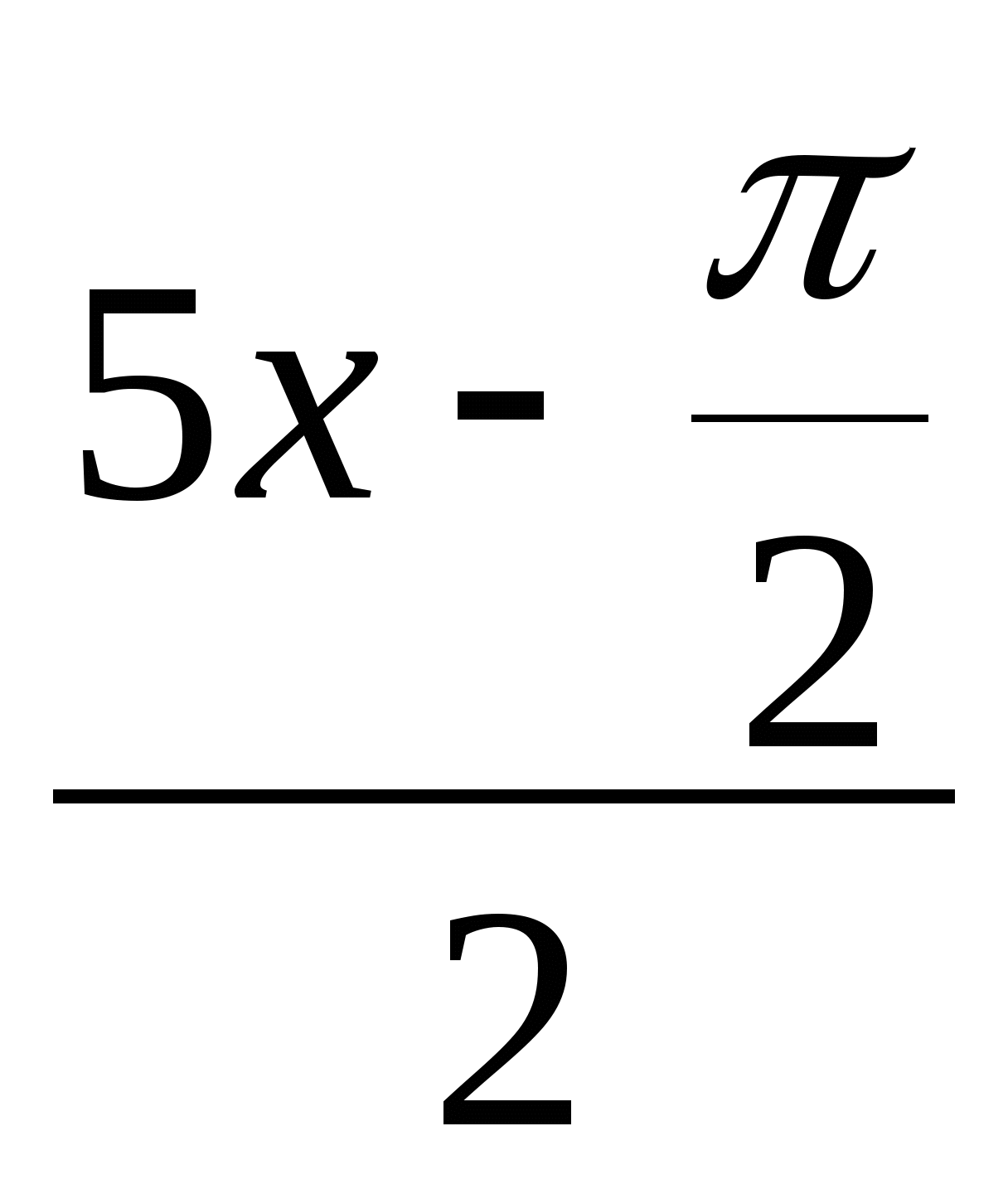 =πκ, κ
=πκ, κ![]()
![]() =
=![]() + πn, n
+ πn, n![]()
![]() =2πκ, κ
=2πκ, κ![]()
![]() + 2πn, n
+ 2πn, n![]()
![]() + 2πκ, κ
+ 2πκ, κ![]()
![]() + 2πn, n
+ 2πn, n![]()
![]() +
+ ![]() πκ, κ
πκ, κ![]()
![]() + 2πn, n
+ 2πn, n![]()
Ответ: ![]() +
+ ![]() πκ, κ
πκ, κ![]() ;
; ![]() + 2πn, n
+ 2πn, n![]()
4. Решить уравнение: sin5x·cos3x = sin9x·cos7x
Решение:
sin5x·cos3x = sin9x·cos7x
sin5x·cos3x - sin9x·cos7x = 0
![]()
![]()
![]()
sin8x - sin16x = 0
sin8x -2sin8xcos8x = 0
sin8x (1 - 2cos8x) = 0
sin8x = 0 1 - 2cos8x = 0
8x = πκ, κ![]() Z cos8x =
Z cos8x =
![]()
x = ![]() κ, κ
κ, κ![]() Z 8x =
Z 8x = ![]() + 2 πn, n
+ 2 πn, n![]()
x = ![]() +
+ ![]() πn, n
πn, n![]()
Ответ: x = ![]() κ, κ
κ, κ![]() Z; x =
Z; x = ![]() +
+ ![]() πn, n
πn, n![]() .
.
5. Решить уравнение: 2cos2x + sinx = 2
Решение:
2cos2x + sinx = 2
2(1 - sin2x) + sinx - 2 = 0
2 - 2sin2x + sinx - 2 = 0
- 2sin2x + sinx = 0
sinx(- 2sinx +1) = 0
sinx = 0 - 2sinx + 1 = 0
x = πκ, κ![]() Z - 2sinx = -1
Z - 2sinx = -1
sinx = ![]()
x = (-1)n![]() +
πn, n
+
πn, n![]() .
.
Ответ: x = πκ, κ![]() Z;
x = (-1)n
Z;
x = (-1)n![]() +
πn, n
+
πn, n![]() .
.
6. Решить уравнение: 2sinx - 3cosx = 3
Решение:
2sinx - 3cosx = 3
sinx = 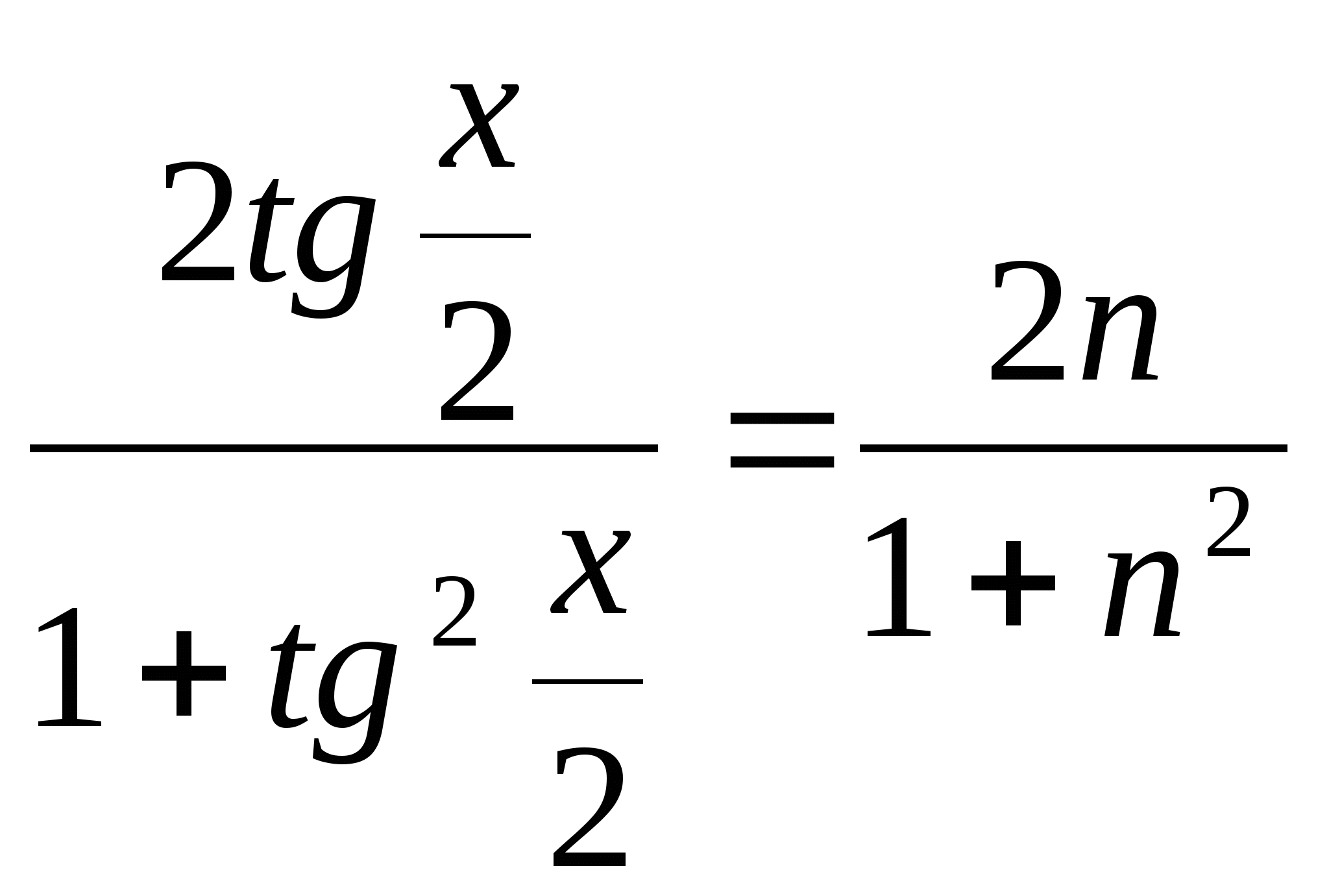 ; cosx =
; cosx =
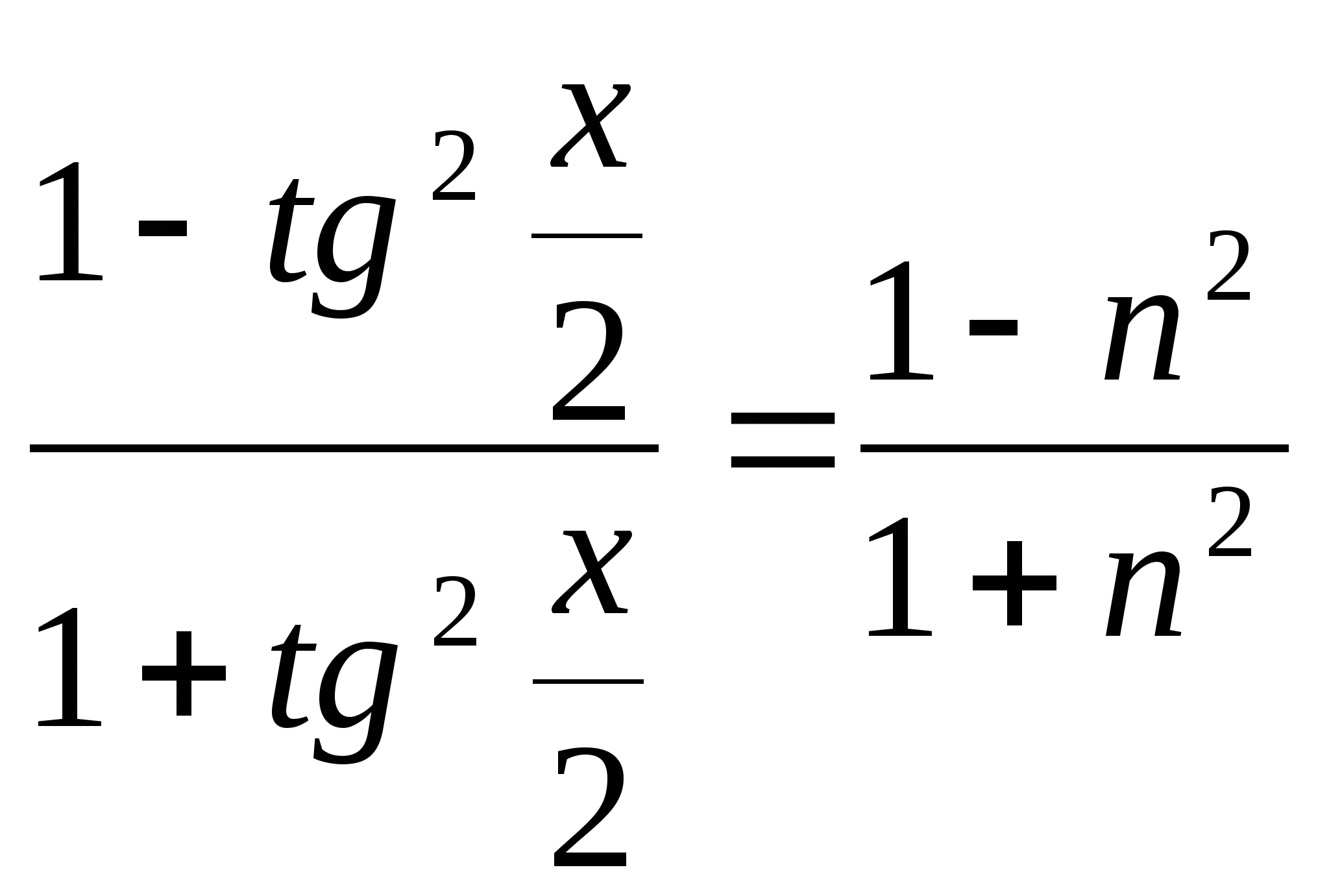
![]()
![]() /·
/·![]() т.к.
т.к. ![]()
4n - 3 + 3n2 = 3 + 3n2
4n + 3n2 - 3n2 = 3 + 3
4n = 6
n = ![]()
tg![]() =
= ![]()
![]() = arctg
= arctg![]() + πκ, κ
+ πκ, κ![]() Z
Z
x = 2 arctg![]() + 2πκ,
κ
+ 2πκ,
κ![]() Z
Z
Проверка x =π + 2πn, n![]()
2·0 - 3· (-1) = 3
0 + 3 = 3
3 = 3
Ответ: x =π + 2πn, n![]() ; x
= 2 arctg
; x
= 2 arctg![]() + 2πκ, κ
+ 2πκ, κ![]() Z.
Z.
7. Решить уравнение: sin(5π - x) = cos(2x + 7π)
Решение:
sin(5π - x) = cos(2x + 7π)
sin(4π + π - x) = cos(6π + π + 2x)
sin(π - x) = cos(π + 2x)
sin x = -cos2x
sin x = -cos2x + sin2x
sin x + cos2x - sin2x = 0
sin x + 1 - sin2x - sin2x = 0
- 2sin2x +sin x + 1 = 0
sin x = t
-2t2 + t + 1 = 0
Д = b2 - 4ac = 12 + 4·2·1 = 1 + 8 = 9
t1,2 = ![]()
t1 = 1; t2 = -0,5
sin x = 1 sin x = -0,5
x = ![]() + 2π κ, κ
+ 2π κ, κ![]() Z x = (-1)n +
1
Z x = (-1)n +
1![]() + πn, n
+ πn, n ![]()
Ответ: x = ![]() + 2π κ,
κ
+ 2π κ,
κ![]() Z; x = (-1)n +
1
Z; x = (-1)n +
1![]() + πn, n
+ πn, n ![]() .
.
8. Решить уравнение: 2cos2x - 3sinx·cosx + 5sin2x = 3
Решение:
2cos2x - 3sinx·cosx + 5sin2x = 3
2cos2x - 3sinx·cosx + 5sin2x = 3· (cos2x + sin2x)
2cos2x - 3sinx·cosx + 5sin2x - 3cos2x + 3sin2x = 0
-cos2x - 3sinx·cosx + 2sin2x = 0 /: cos2x
Проверка: cos2x = 0
cosx = 0
0 - 3sinx·0 + 2·(±1) = 0
2 ≠ 0
-1 - 3tgx + 2tg2x = 0
2tg2x - 3tgx - 1 = 0
tgx = t;
2t2 - 3t - 1 = 0
Д = 9 - 4·2·(-1) = 17
t1,2 = ![]()
tgx = ![]() tgx =
tgx = ![]()
x = arctg![]() + π κ,
κ
+ π κ,
κ![]() Z x =
arctg
Z x =
arctg![]() + πn, n
+ πn, n ![]()
Ответ: x = arctg![]() +
π κ, κ
+
π κ, κ![]() Z; x =
arctg
Z; x =
arctg![]() + πn, n
+ πn, n ![]() .
.
9. Найти корни уравнения: cos4x - sin4x + sin2x = 1 из интервала (0°; 90°)
Решение:
cos4x - sin4x + sin2x = 1
(cos2x - sin2x)(cos2x - sin2x) + sin2x = 1
cos2x + 2sinx·cosx - sin2x - sin2x - cos2x = 0
2sinx·cosx - 2sin2x = 0
2sinx·(cosx - sinx) = 0
sinx = 0 cosx - sinx = 0 /: cosx
x= π κ, κ![]() Z Проверка cosx
= 0
Z Проверка cosx
= 0
0 < π κ < ![]() /:
π 0 - (±1) = 0
/:
π 0 - (±1) = 0
0 < κ < ![]() ±1 ≠ 0
±1 ≠ 0
нет решений, т.к.
к - целое число 1 - tgx = 0
tgx = 1
x = ![]() + π κ, κ
+ π κ, κ![]() Z
Z
0 < ![]() + π κ <
+ π κ <
![]()
-![]() < π κ <
< π κ <
![]()
-![]() < κ <
< κ <
![]()
κ = 0
x = ![]() + π·0 =
+ π·0 = ![]()
![]() (0; 90°)
(0; 90°)
Ответ: x= π κ; x = ![]() +
π κ, κ
+
π κ, κ![]() Z; x =
Z; x = ![]()
![]() (0; 90°).
(0; 90°).
10. Найти в градусной мере наименьший положительный корень уравнения cos3x + cosx = cos2x
Решение:
cos3x + cosx = cos2x
2cos2x cosx = cos2x / :cos2x
Проверка cos2x = 0
2·0· cosx = 0
0 = 0
2x = ![]() + π κ, κ
+ π κ, κ![]() Z
Z
x = ![]() +
+![]() κ, κ
κ, κ![]() Z
Z
2cosx = 1
cosx = ![]()
x = ±![]() + 2π κ, κ
+ 2π κ, κ![]() Z
Z
Ответ: x = ![]() +
+![]() κ, κ
κ, κ![]() Z; x = ±
Z; x = ±![]() + 2π κ, κ
+ 2π κ, κ![]() Z , наименьший
положительный корень равен 45°.
Z , наименьший
положительный корень равен 45°.
11. Решить уравнение: 4sin4x + cos4x = 1 + 12cos4x
Решение:
4sin4x + cos4x = 1 + 12cos4x
4sin4x + cos22x - sin22x = 1 + 12cos4x
4sin4x + cos2x·cos2x - sin2x·sin2x = 1 + 12cos4x
4sin4x + (cos2x - sin2x) · (cos2x - sin2x) - 2sinx·cosx·2sinx·cosx = 1 + 12cos4x
4sin4x + cos4x - cos2x·sin2x - cos2x·sin2x + sin4x - 4sin2x·cos2x = 1 + 12cos4x
4sin4x + cos4x - 6cos2x·sin2x + sin4x - 1 - 12cos4x = 0
5sin4x - 6cos2x·sin2x - 11cos4x - 1= 0
5sin4x - 6sin2x·(1- sin2x) - 11cos4x - 1= 0
5sin4x - 6sin2x + 6sin4x - 11cos4x - 1 = 0
11sin4x - 11cos4x - 6sin2x - sin2x - cos2x = 0
11·(sin2x - cos2x) ·(sin2x + cos2x) - 7sin2x - cos2x = 0
11sin2x - 11cos2x - 7sin2x - cos2x = 0
4sin2x - 12cos2x = 0
4sin2x - 12· (1 - sin2x) = 0
4sin2x - 12 + 12sin2x = 0
16sin2x = 12
sin2x = ![]()
sin2x = ![]()
sinx = ![]()
sinx = ![]() sinx =
sinx =
![]()
x = (-1)κ ![]() +
π κ, κ
+
π κ, κ ![]() x = (-1)n +
1
x = (-1)n +
1![]() + π n, n
+ π n, n ![]()
Ответ: x = (-1)κ ![]() + π κ, κ
+ π κ, κ ![]() ; x = (-1)n +
1
; x = (-1)n +
1![]() + π n, n
+ π n, n ![]() .
.
12. Решить уравнение:
2sinx·cos (![]() + x) - 3sin (π
- x) ·cosx + sin (
+ x) - 3sin (π
- x) ·cosx + sin (![]() + x)
·cosx = 0
+ x)
·cosx = 0
Решение:
2sinx·sinx - 3sinx·cosx + cosx·cosx = 0
2sin2x - 3sinx·cosx + cos2x = 0 /: cos2x
Проверка cos2x = 0
2·1 - 3sinx·0 + 0 ≠ 0
2tg2x - 3 tgx + 1 = 0
tgx = t
2t2 - 3t + 1 = 0
Д = (-3)2 - 4·2·1 = 9 - 8 = 1
t1,2 = ![]()
t1 = 1; t2 = 0,5
tgx = 1 tgx = 0,5
x = ![]() + πκ, κ
+ πκ, κ![]() Z x = arctg0,5 +
πn, n
Z x = arctg0,5 +
πn, n ![]()
Ответ: x = ![]() + πκ,
κ
+ πκ,
κ![]() Z; x = arctg0,5 +
πn, n
Z; x = arctg0,5 +
πn, n ![]() .
.
4.Арифметическая и геометрическая прогрессия.
1. Найти а13, если а5 = 2, а40 = 142
an =a1 + d (n - 1) формула n-го члена(n ≥ 2)
a5 = а1 + d (5 - 1) a40 = a1 + d (40 - 1)
a5 = a1 + 4d a40 = a1 + 39d
_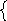 a1 + 4d
= 2
a1 + 4d
= 2
a1 + 39d = 142
-
35d = -140
d = -140 :(-35)
d = 4
a1 + 4·4 = 2 a13 = a1 + d (13 - 1)
a1 + 16 = 2 a13 = -14 + 12d
a1 = 2 - 16 a13 = -14 + 12·4
a1 = -14 a13 = 34
Ответ: a13 = 34
2. Найти а1 + а20, если а3 + а18 = 50
ak =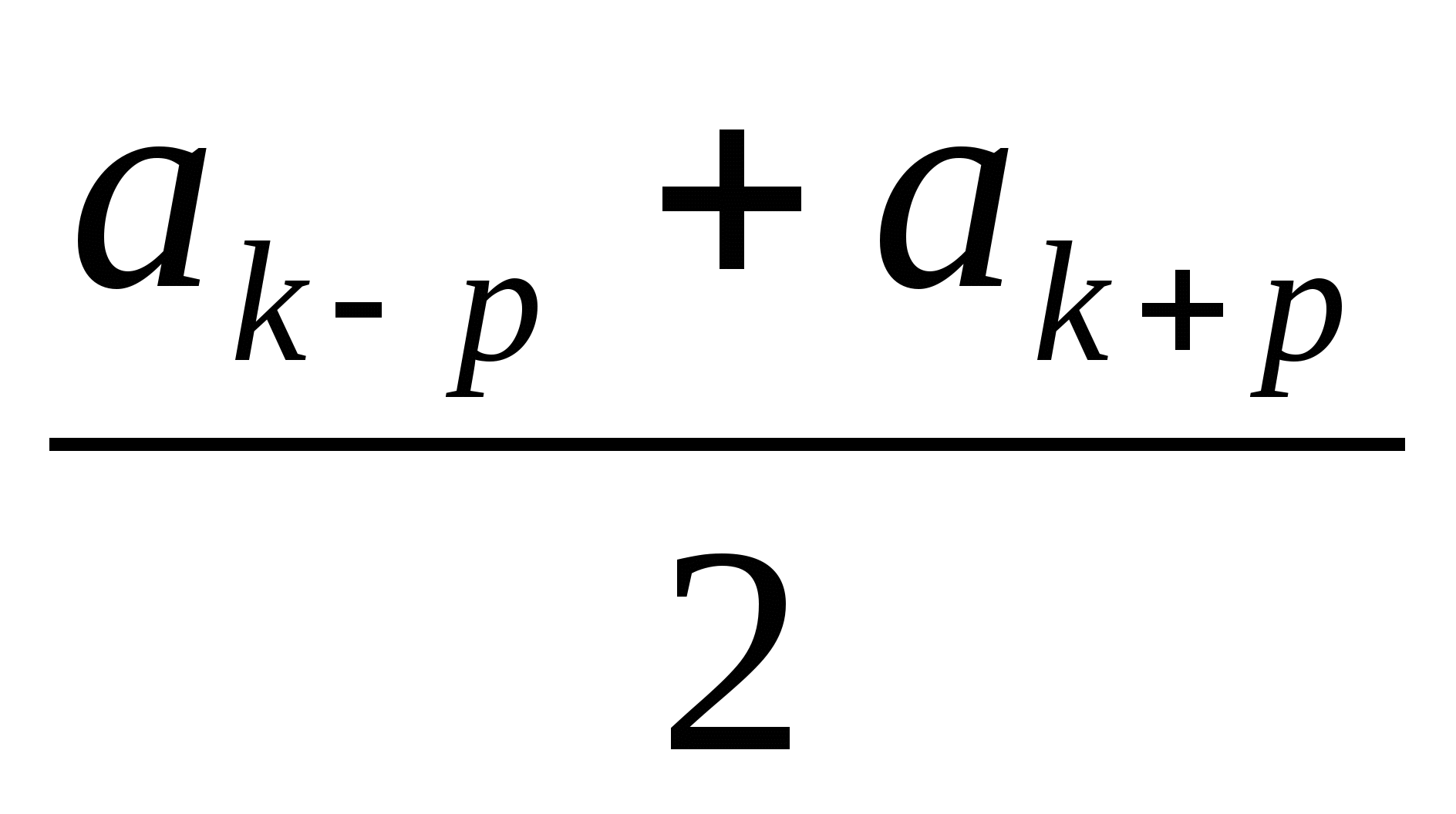 , (p <
k), в частности
, (p <
k), в частности
a3 + a18 = 50
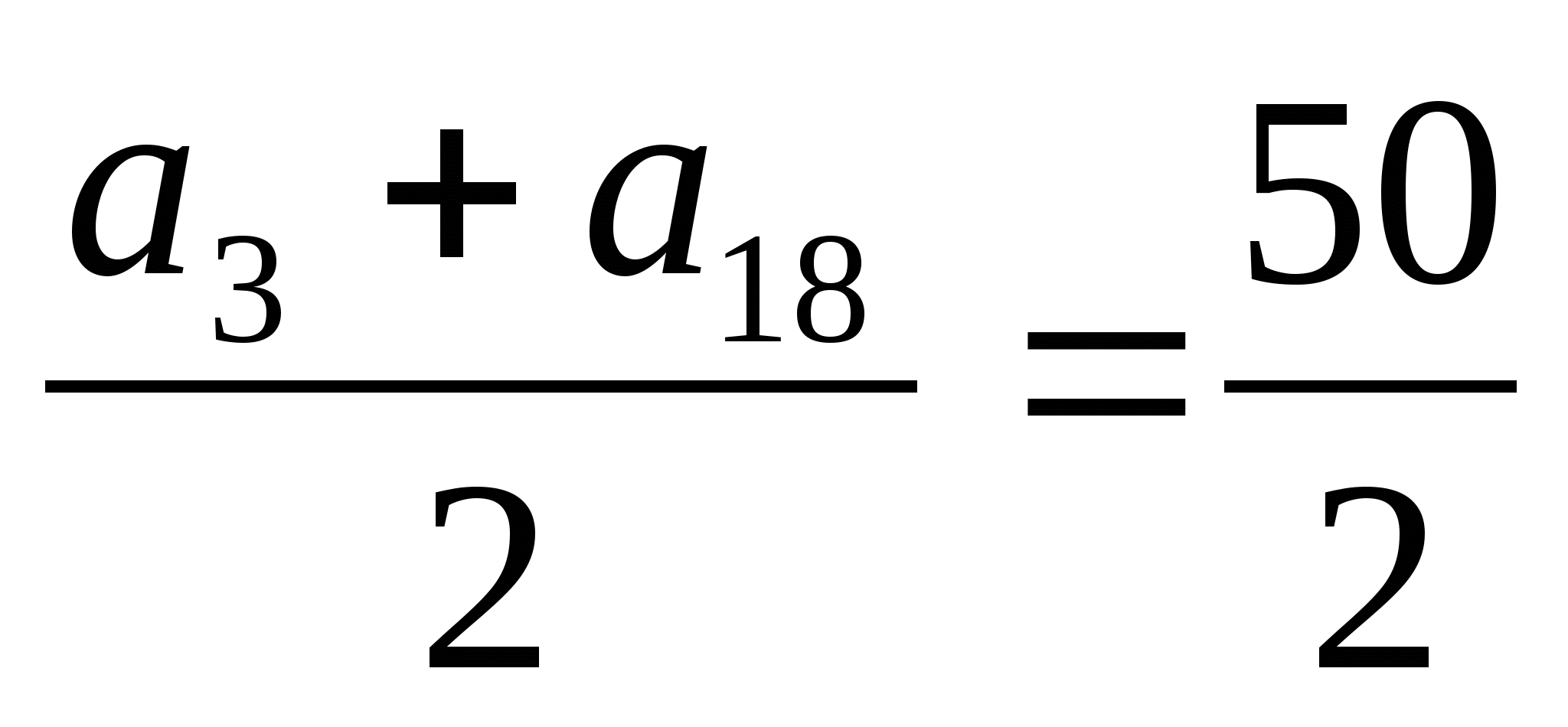 p = 2
p = 2
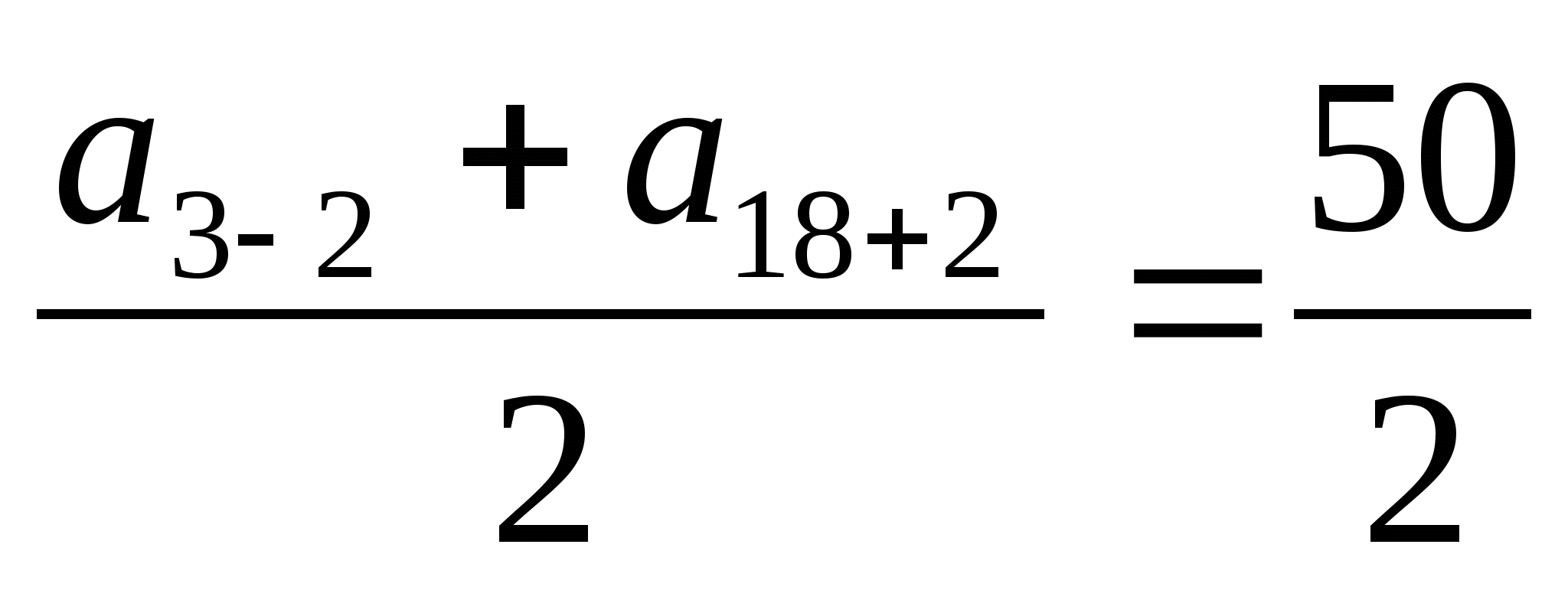
![]()
a1 + a20 = 50
Ответ: a1 + a20 = 50
3. Найти n, если а1 = 3, а2 = 5, Sn = 360
a2 - a1 = d an = a1 + d (n - 1)
5 - 3 = 2 Sn = 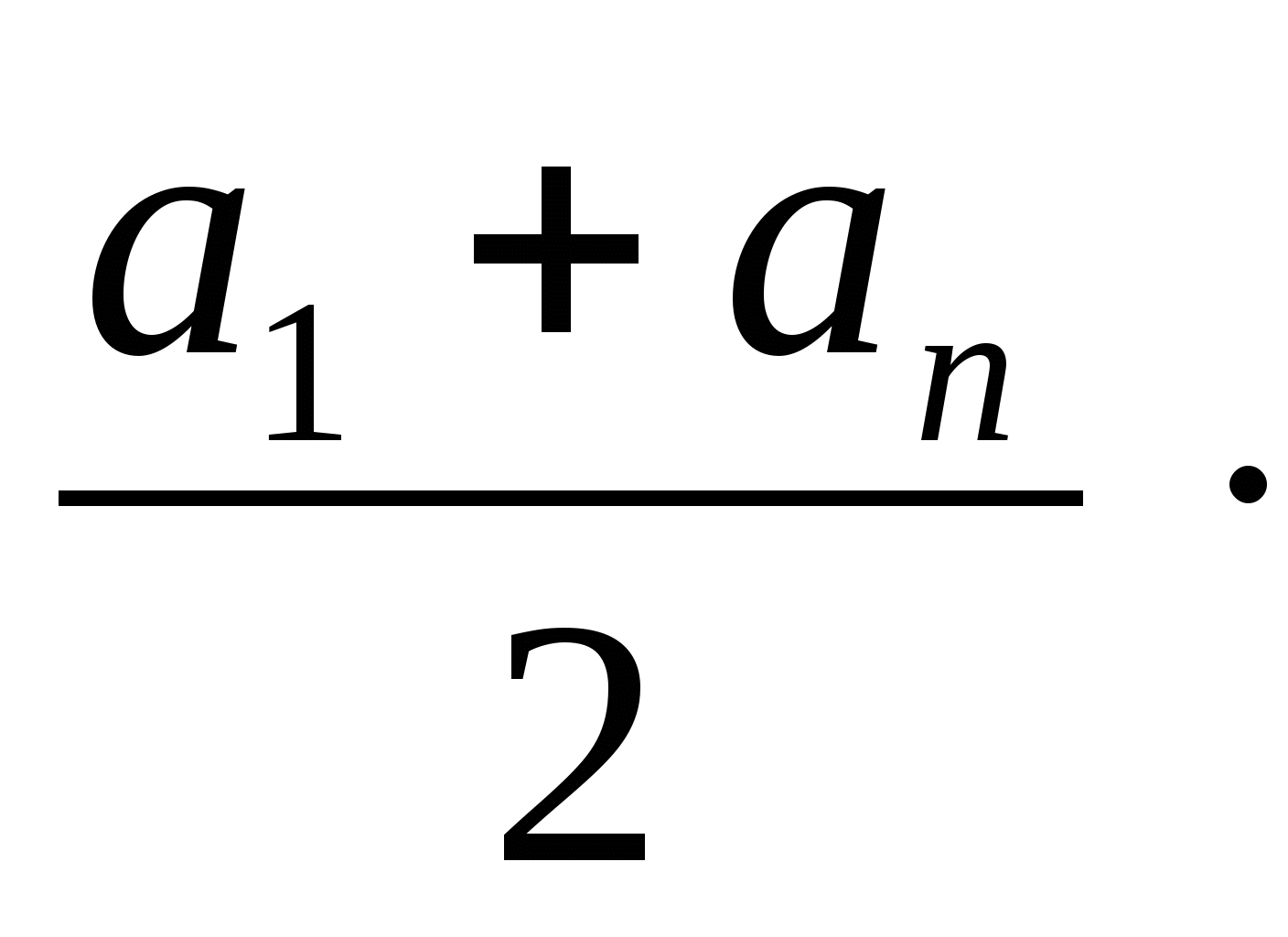 n
n
d = 2 Sn = ![]() n
n
![]() = 360
= 360
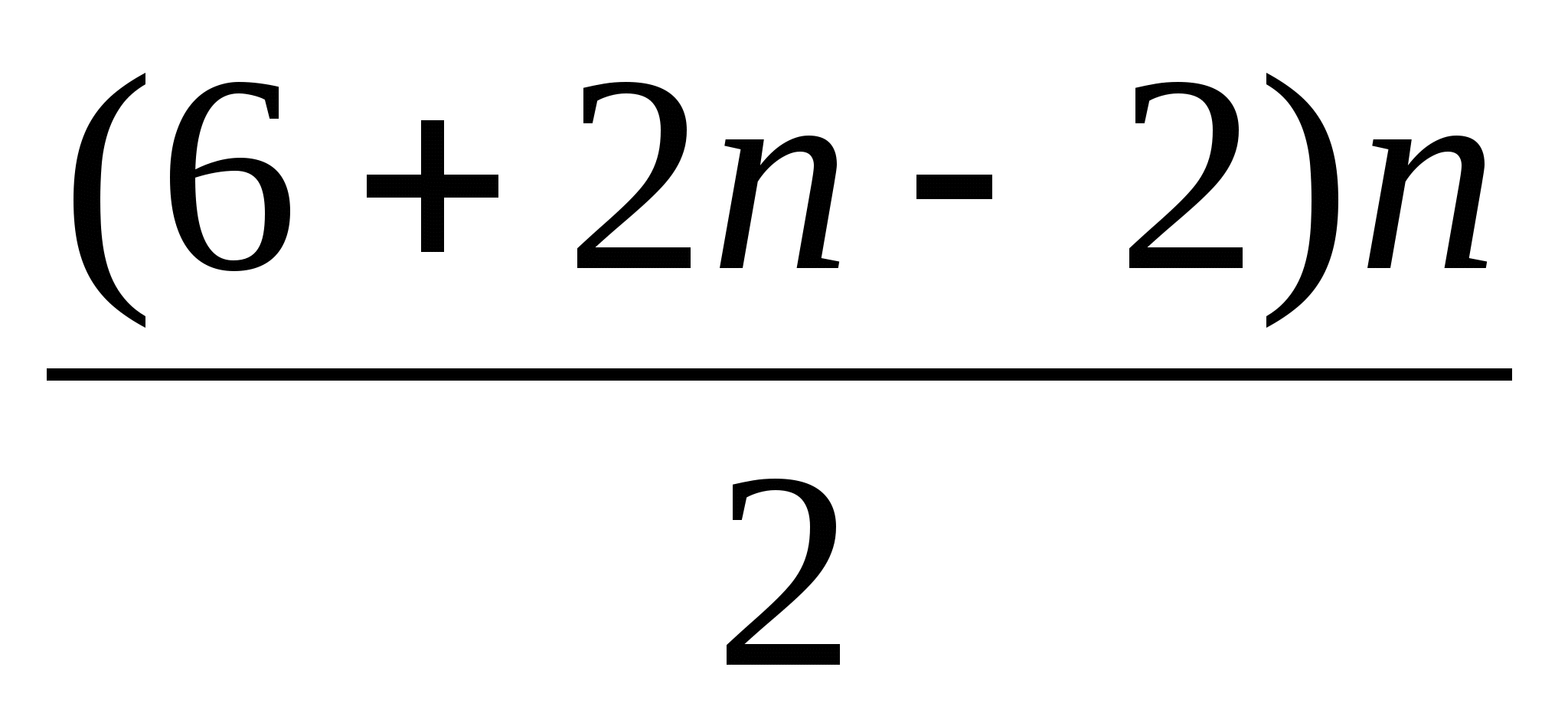 = 360
= 360
6n +2n2 - 2n = 720
2n2 + 4n - 720 = 0
Д = 16 - 4·2·(-720) = 16 + 5760 = 5776 = 762
n1 = ![]() =
18
=
18
n2 =![]() =
-20
=
-20
Ответ: n = 18.
4. Найти а1 и d, если Sn = 2n2 - 3n
S1 = 2·12 - 3·1 S2 = 2·22 - 3·2
S1 = -1 S2 = 2
S1 -a1 S2 = a1 + a2
a1 = -1 a1 + a2 = 2
-1 + a2 = 2
a2 = 3
d = a2 - a1
d = 3 + 1
d = 4
Ответ: a1 = -1; d = 4.
5. Найти сумму всех натуральных трехзначных чисел, не делящихся на 3 100, 101, 102…..999.
а1 = 100 n -?
an = 99
an = a1 + d (n - 1)
999 = a1 + d (n -1) 999 = 100 + (n - 1)
100 = n - 1 = 999 99 + n = 999
n = 999 - 99 n = 900
S900 = 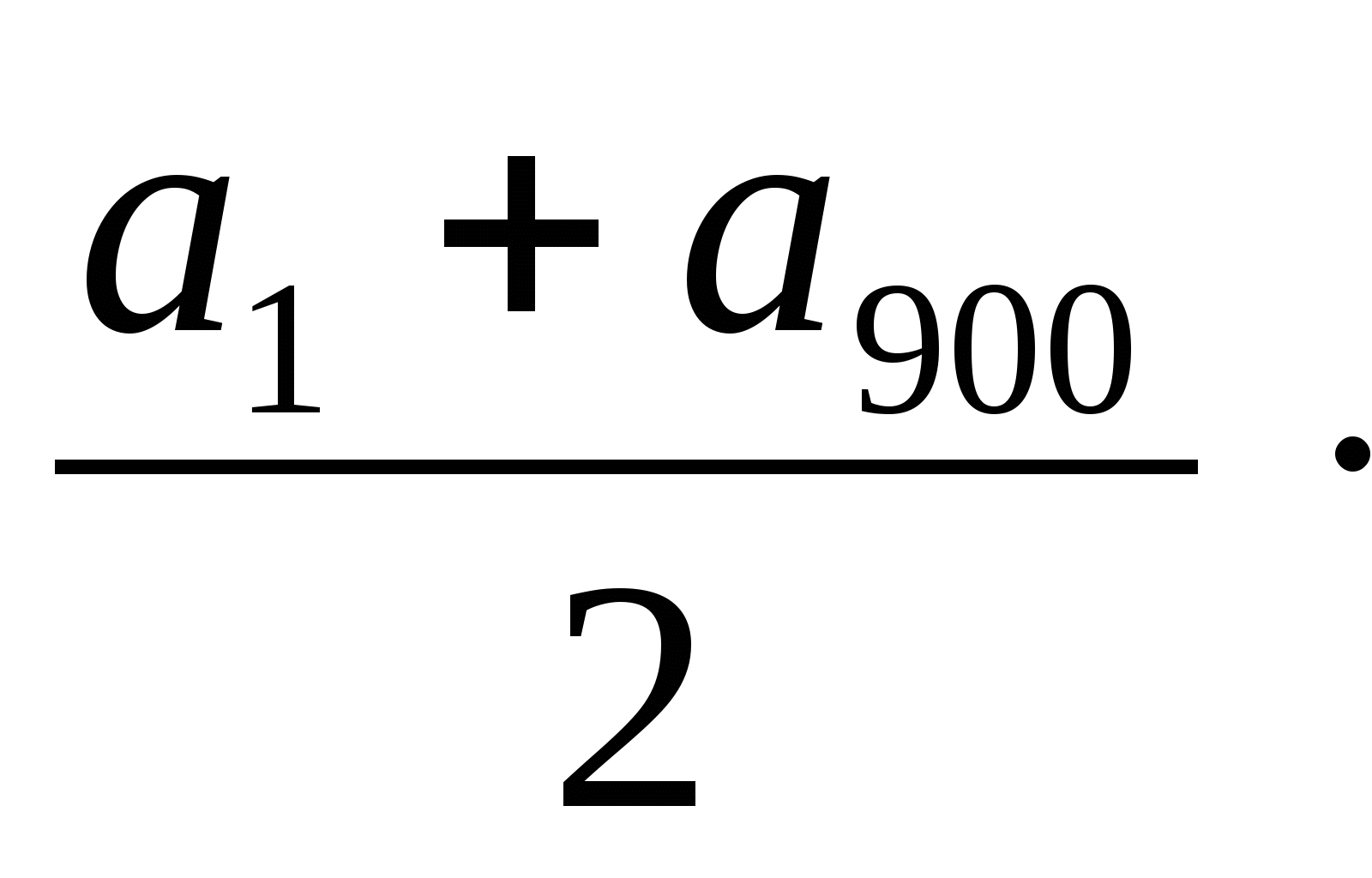 900
S900 =
900
S900 = 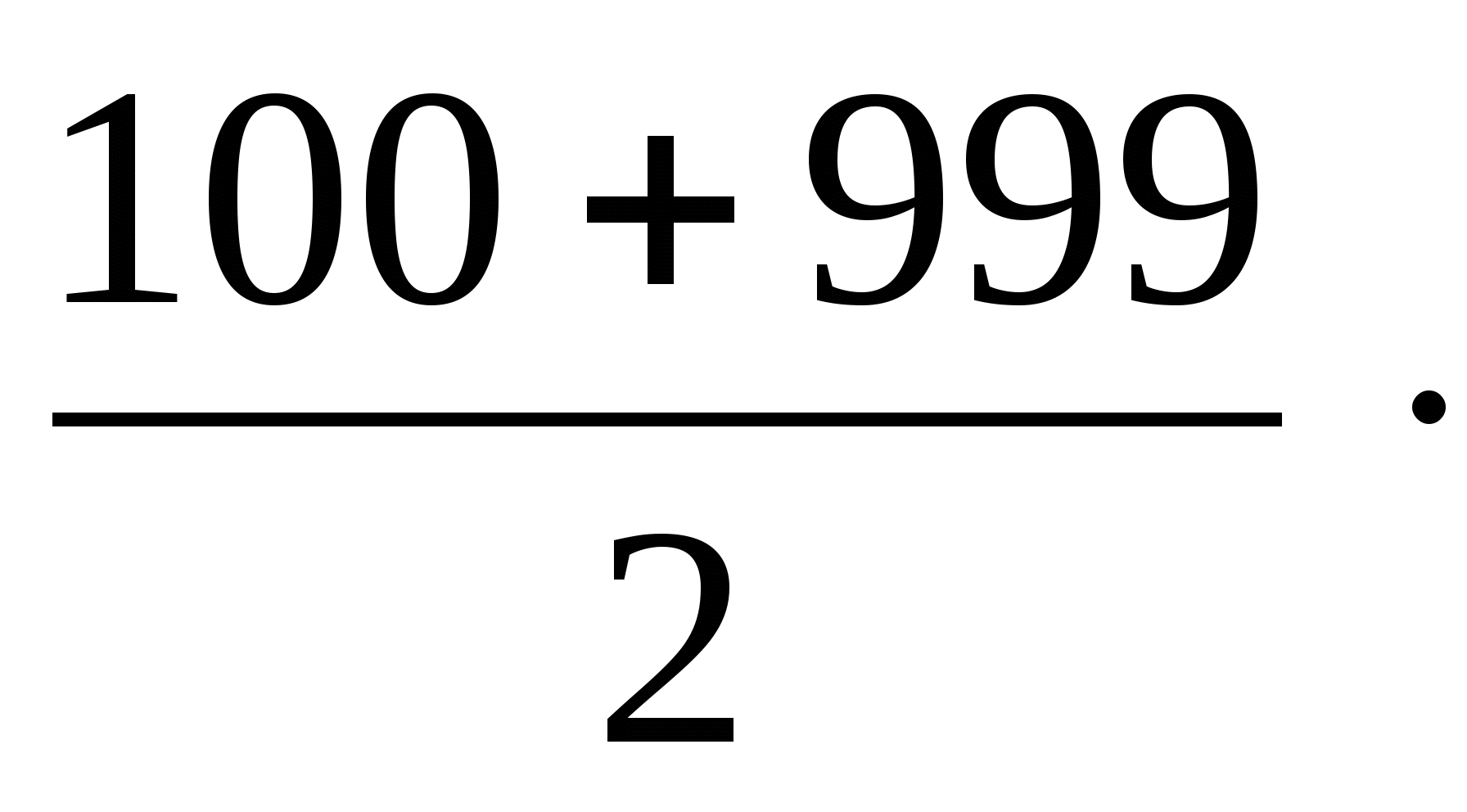 900
900
S900 = 1099·450 S900 = 494550
999 = 102 +3 (n - 1) 999 = 102 + 3n - 3
3n + 99 = 999 3n = 999 - 99
3n = 900 n = 300
S300 = 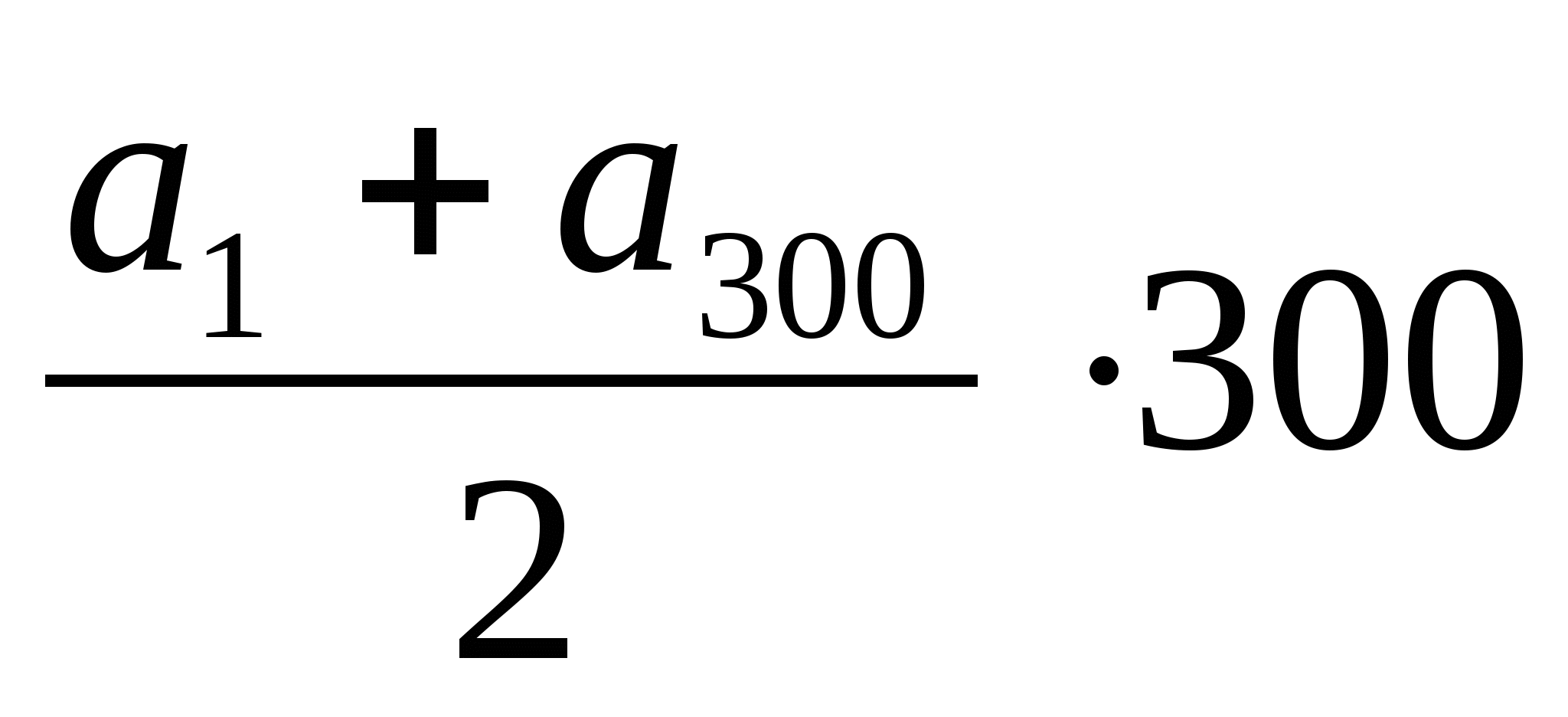 S300 = 1101·150 = 165150
S300 = 1101·150 = 165150
Находим исходную сумму
S = S900 - S300 S = 494550 - 165150 = 329400
Ответ: S = 329400.
6. Найти b6, если b5 = 36, b7 = 114
b2k = bk - 1·bk + 1 (k ≥ 2)
b26 = b5·b7
b26 = 36·144 b6 = ![]() b6 =
b6 =
![]()
Ответ: b6 = ![]() .
.
7. Найти q, если b1 = 10, b2 + b3 = 60
b2 = b1·q b3 = b1·q2
b1·q + b1·q2 = 60
10q + 10q2 = 60 /: 10
q2 + q - 6 = 0
q1 + q2 = -1
q1·q2 = -6
q1 = -3 q2 = 2
q = -3
b2 = 10· (-3) = -30 b3 = 10·(-3)2 = 90
b2 + b3 = 60 -30 + 90 = 60
q = 2
b2 = 10·2 = 20 b3 = 10·22 = 10·4 = 40
20 + 40 = 60
Ответ: q = -3; q = 2.
8. Найти b13, если b11 = 25, b15 = 400
b213 = b12·b14
b2k = bk-p·bk + p, p = 2
b213 = b11·b15 b13 = 25·400 b13 = 5·20 b13 = 100
Ответ: b13 = 100.
9. Найти S6, если b1 = -2, b6 = -486
Sn = 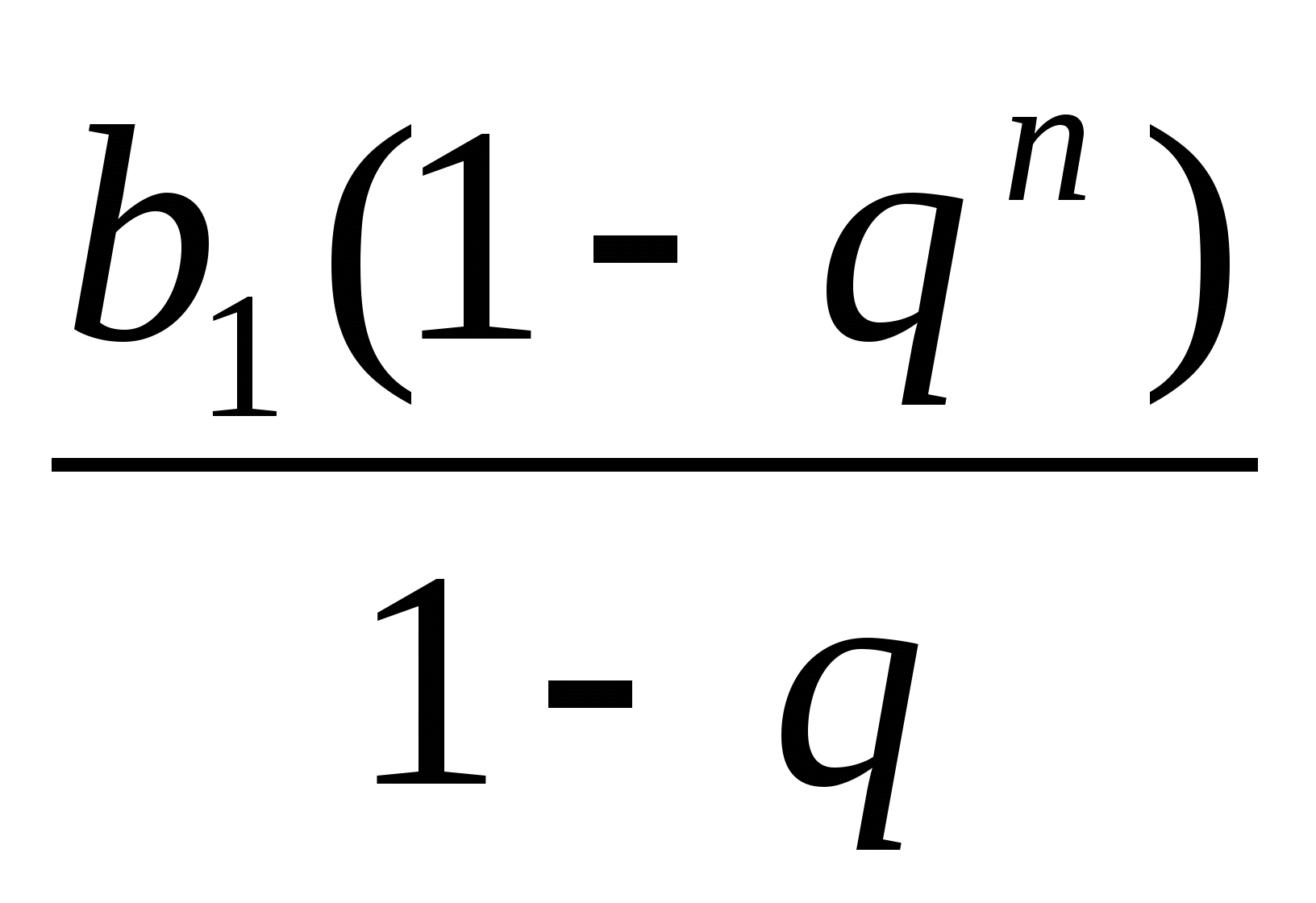
Находим q
b6 = b1·q5
-2·q5 = -486
q5 = -486: (-2)
q5 = 243
q = 3
S6 = ![]() 1
- 729 = -728
1
- 729 = -728
Ответ: S6 = -728.
10.Найти n, если b1 = 9, bn = ![]() , Sn =
, Sn =
![]()
bn = b1·qn - 1
![]() = 9·qn -
1
= 9·qn -
1
qn - 1 = ![]()
qn - 1 = ![]()
qn - 1 = ![]()
q = ![]()
n - 1 = 6
n = 7
Ответ: n = 7.