Софизмы и парадоксы в математике

МБОУ Мугудайская СОШ им Д.Д.Красильникова

СОФИЗМЫ И ПАРАДОКСЫ В МАТЕМАТИКЕ

Выполнила ученица 6 класса

МБОУ Мугудайской СОШ

им. Д.Д.Красильникова

Захарова Света

Руководитель: учитель математики

Кондратьева А.Т

2012

Введение

Почему я взялась за эту работу?

Я очень люблю решать задачи и разгадывать математические ребусы, но в математике есть «задачи-ловушки», которые не похожи на другие, они как будто - бы правильные, но в то же время неправильные. Это софизмы!

Я увлеклась темой «Софизмы и парадоксы в математике». Во время работы мне было очень интересно.

Поиск заключенных в софизме ошибок, ясное понимание их причин ведут к осмысленному постижению математики и, кроме того, показывает, что математика - это живая наука.

Надеюсь, что моя работа будет интересен и принесёт пользу ребятам.

Цель:

1) Дать определение софизмам и парадоксам.

2) Определить сферу их применения.

3) Понять в чем различие и сходство между софизмами и парадоксами.

4) Выяснить, как разбор математических софизмов развивает умение и навыки логического мышления.

Задачи:

1. привести примеры софизмов и парадоксов.

2. разобрать несколько примеров.

3. понять, как найти ошибку в них.

4. проведя разбор софизмов, сделать вывод.

Софизм

Софизм (от греч. слова, «мастерство, умение, хитрая выдумка, уловка») - это рассуждение, формально кажущееся совершенно безупречным, но содержащее на самом деле ошибку, в результате чего конечный вывод оказывается абсурдным. Софизм основан на преднамеренном, сознательном нарушении правил логики.

А теперь немного истории…

В Древней Греции «софисты» (от греческого слова sofos, означающего мудрость) - мыслители, люди, авторитетные в различных вопросах.

Их задачей обычно было научить убедительно защитить любую точку зрения.

Математический софизм - удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.

Особенно часто в софизмах выполняют "запрещенные" действия или не учитываются условия применимости теорем, формул и правил.

Пример софизма:

5 есть 2+3 («два» и «три»). Два - число четное, три - нечетное, выходит, что пять - число и четное и нечетное.

Кроме математических софизмов, существует множество других, например: логические. Понять абсурдность таких утверждений проще, но от этого они не становятся менее интересными. Очень многие софизмы выглядят как лишенная смысла и цели игра с языком; игра, опирающаяся на многозначность языковых выражений, их неполноту, недосказанность, зависимость их значений от контекста и т.д. Эти софизмы кажутся особенно наивными и несерьезными.

Парадокс

Парадокс (греч. "пара" - "против", "докса" - "мнение") близок к софизму</<font face="Times New Roman, serif">. Но от него он отличается тем, что это не преднамеренно полученный противоречивый результат.

Парадокс - странное умозаключение, расходящееся с общепринятым мнением, высказывание, а также мнение, противоречащее здравому смыслу, на самом деле справедливо.

Математический парадокс - высказывание, которое может быть доказано и как истинна, и как ложь.

Логические парадоксы:

Это парадоксы, которые затрагивают сферы логики и здравого смысла.

Казалось бы, парадокс - и парадокс себе, и стоит ли сильно по его поводу переживать.

Однако некая легенда гласит, что древнегреческий философ Кронос, не в силах разрешить его, от огорчения умер.

Парадокс «Парадокс лжеца»

Этот древнегреческий логический парадокс имеет множество вариаций. Я приведу одну из них.

Человек произносит: « Я лгу».

Он обманывает или говорит правду?

С одной стороны, он говорит неправду, т.к. это утверждает. Но это означает, что он утверждает правду, а, следовательно, лжет.

Чем полезны софизмы и парадоксы?

Разбор софизмов и парадоксов:

• развивает логическое мышление,

• прививает навыки правильного мышления,

• помогает сознательному усвоению математического материала,

• развивает наблюдательность, вдумчивость,

• изящная гимнастика для ума!!!

В своей работе я рассмотрела несколько математических софизмов и парадоксов, и сейчас приведу разбор некоторых из них.

Примеры

Софизм №1 «пять равно шести»

Возьмем тождество 35+10-45=42+12-54.

В каждой части вынесем за скобки общий множитель:

5(7+2-9)=6(7+2-9).

Теперь, получим, что 5=6. Где ошибка?

Разбор софизма.

Ошибка допущена при делении верного равенства 5(7+2-9)=6(7+2-9) на число

7+2-9, равное 0. Этого нельзя делать.

Любое равенство можно делить только на число, отличное от 0.

Софизм №2 «140=150»

Допустим, я у друга взяла 100 рублей, пошёл в магазин и потерял их. Встретил подругу и занял у неё 50 рублей, купил 2 шоколадки по 10 рублей, у меня осталось 30 рублей, я их отдал другу и остался должен ему 70 руб., и подруге 50 руб., итого 120 руб. Плюс у меня две шоколадки за 20 рублей.

Итого 140 рублей!

Где остальные 10 рублей?

Парадокс №1.

«Парадокс кучи»

Имеется утверждение:

Разница между "кучей" и "не кучей" не в одном элементе.

Возьмем некоторую кучу, например, орехов. Теперь начнем брать из нее по ореху:

50 орехов - куча,

49 - куча,

48 - тоже куча и т.д.

Так дойдем до одного ореха, который тоже составит кучу.

Вот тут-то и парадокс - сколько орехов бы мы не взяли, они все равно будут кучей.

Такое рассуждение нельзя применять, так как не определено само понятие «куча».

Парадокс №2.

«Загадочное исчезновение»

Какая линия исчезла и куда?

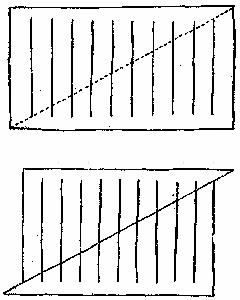
После небольшого размышления становится ясно, что никакая отдельная линия после передвижения не исчезает и не появляется. Просто каждая линия становится чуточку длиннее и на глаз незаметно. Так что исчезновение 10-й палочки только на первый взгляд кажется загадочным.

Парадоксы из жизни

Количество развлечений растет с каждым днем, а количество радостей уменьшается

Мы стали покупать больше вещей, но меньше ими пользоваться

Мы увеличили свою собственность, но уменьшили свои ценности

Много медикаментов, но мало здоровья…

Мы говорим очень много, любим очень редко и ненавидим слишком часто.

У нас очень много ученых званий, но слишком мало рассуждений.

Мы добавили годы к жизни, но не жизнь к годам.

Заключение

Итак я познакомилась с увлекательной темой, узнала много нового, научилась решать задачки на софизмы, находить в них ошибку, разбираться в парадоксах.

Тема моей работы далеко не исчерпана. Я рассмотрела лишь некоторые, самые известные примеры софизмов и парадоксов. На самом деле их намного больше. Я продолжу изучение этой темы в дальнейшем.