- Учителю
- Урок- практическое занятие на тему 'Многогранники' (1 курс)
Урок- практическое занятие на тему 'Многогранники' (1 курс)
Практическое занятие по теме "Многогранники"
Цели:
-
Образовательная - повторить весь пройденный материал по теме, обобщить и систематизировать знания учащихся, проверить умения учащихся в решении задач на применение теоретического материала.
-
Развивающая - развивать математически грамотную устную и письменную речь, способствовать развитию логического мышления, умения самостоятельно работать (при подготовке к уроку) с различными источниками информации.
-
Воспитательная - воспитывать чувство ответственности за свои знания, за своих товарищей, учиться поддерживать друг друга, формировать коммуникативные качества учащихся.
Форма организации учебной деятельности: фронтальная, парная, групповая, индивидуальная.
Методы обучения: репродуктивный, частично-поисковый.
Средства обучения: тела многогранников, карточки с задачами, листы с кроссвордом.
Ход урока
1. Мотивация и целеполагание.
1) Задание учащимся.
Назовите фигуры, которые изображены на рисунке.
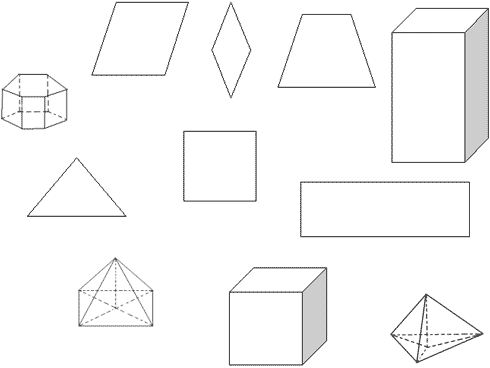
2) На какие две группы их можно разделить?
Какую группу фигур мы изучали на последних уроках?
Сегодня на уроке наша цель - обобщить и систематизировать знания по теме: "Многогранники", закрепить умения решать задачи по этой теме.
2. Актуализация знаний.
Идёт работа в парах - разгадывание кроссворда (листы с кроссвордом на каждой парте).
Кроссворд, можно по вариантам.
Вариант 1
Задание1. Отгадайте кроссворд.
-
1.
2.
3.
4.
5.
6.
7.
8.
9.
-
Одно из видов сечений цилиндра. 2.Многогранник, состоящий из 2-х равных многоугольников, лежащих в параллельных плоскостях, называемых основаниями и прямыми, соединяющими вершины этих многоугольников, называемые ребрами.3. Египетский многогранник. 4. Раздел геометрии, изучающий фигуры в пространстве. 5. Фигура, которая образуется при пересечении тела плоскостью. 6. Правильный многогранник с наименьшим количеством граней. 7. Поверхность, составленная из многоугольников. 8. Геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов. 9. Виды цилиндров: наклонный и …….. .
Вариант 2
Задание1. Отгадайте кроссворд.
-
1.
2.
3.
4.
5.
6.
7.
8.
9.
-
Мера измерения углов. 2. Основные фигуры в пространстве: точка, прямая и ……
3. Один из видов правильных многогранников. 4. Вид сечения цилиндра.
5. ……… плоскость многогранника - это плоскость, по обе стороны от которой имеются точки данного многогранника. 6. Призма, основанием которой является параллелограмм . 7. Правильный многогранник, полученный из двух правильных четырехугольных пирамид с общим основанием. 8. Геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов. 9. ……. поверхности цилиндра состоит из прямоугольника и двух кругов.
Ответы.
Вариант 1
-
1.о
с
е
в
о
е
2.п
р
и
з
м
а
3.п
и
р
а
м
и
д
а
4.с
т
е
р
е
о
м
е
т
р
и
я
5.с
е
ч
е
н
и
е
6.т
е
т
р
а
э
д
р
7.м
н
о
г
о
г
р
а
н
н
и
к
8.ц
и
л
и
н
д
р
9.п
р
я
м
о
й
Вариант 2
-
1.г
р
а
д
у
с
2.п
л
о
с
к
о
с
т
ь
3.г
е
к
с
а
э
д
р
4.о
с
е
в
о
е
5.с
е
к
у
щ
а
я
6.п
а
р
а
л
л
е
л
е
п
и
п
е
д
7.о
к
т
а
э
д
р
8.ц
и
л
и
н
д
р
9.р
а
з
в
е
р
т
к
а
3. Систематизация и обобщение знаний. Творческие отчёты групп.
1 группа: "Пирамида".
Ребята представляют изготовленные ими модели пирамид: треугольная, правильная треугольная, четырёхугольная, правильная четырёхугольная, шестиугольная, усечённая. Пирамида- это многогранник, состоящий из многоугольника, называемого основанием, точки, не лежащей в плоскости этого многоугольника, называемой вершиной, и всех отрезков, соединяющих вершину с точками основания.
На рисунке представлена пирамида SABCD.(Рисунок заранее приготовлен на доске).
ABCD- основание;
S - вершина пирамиды;
AS, BS, CS, DS- боковые рёбра;
![]() ASB,
ASB, ![]() BSC,
BSC, ![]() CSD,
CSD, ![]() DSA -боковые грани
DSA -боковые грани
SO - высота.
Рассказ сопровождается показом по рисунку.

пирамида треугольная, потому что в основании у меня лежит треугольник. (Держит в руках треугольную пирамиду). А если моя высота будет соединять вершину с центром правильного треугольника, то я буду правильной треугольной пирамидой (показывает соответствующую модель). Высота боковой грани правильной пирамиды называется апофемой (показывает на модели).
пирамида четырёхугольная, т.к. у меня в основании лежит четырёхугольник. А если моя высота будет соединять вершину пирамиды с центром квадрата, то я буду называться правильной четырёхугольной пирамидой (демонстрирует модель правильной четырёхугольной пирамиды) Это моя апофема (показывает на модели). Площадь боковой поверхности правильной пирамиды можно найти по формуле: Sбок =![]() , где k-апофема (формула записывается на доску рядом с рисунком пирамиды).
, где k-апофема (формула записывается на доску рядом с рисунком пирамиды).
Доклад на тему: Египетский многогранник
2 группа: "Призма".
В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Евклид даёт следующее определение призмы: "Призма есть телесная, т.е. пространственная фигура, заключённая между плоскостями, из которых две противоположные равны и параллельны, остальные же - параллелограммы". Термин "призма" греческого происхождения и буквально означает "отпиленное тело".
2-й: На рисунке призма ABCDEFA1B1C1D1E1F. (Рисунок призмы заранее приготовлен на доске)
ABCDEF - нижнее основание;
A1B1C1D1E1F1 -верхнее основание;
AA1; BB1;:;FF1- боковые рёбра;
AA1B1B; BB1C1C; :;FF1A1A-боковые грани;

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы.
A1C; A1D; A1E- диагонали (все названные элементы показывает на рисунке).
1 студент рассказывает о прямо йпризме (демонстрирует модель),
боковое ребро перпендикулярно основанию (показывает).
высотой является боковое ребро.
Площадь боковой поверхности можно найти по формуле:Sбок=Pосн*h (записывает формулу рядом с рисунком на доску).
2 студент призма наклонная (демонстрирует модель)
3 студент призма правильная,
не только боковое ребро перпендикулярно основанию, но и в основании лежит правильный многоугольник (показывает модель).
4 студент- вывод
Призмы бывают треугольные, четырёхугольные, пятиугольные и т.д., смотря потому какой многоугольник лежит в основании. Четырёхугольная призма имеет особое название- параллелепипед. А площадь полной поверхности любой призмы вычисляется по формуле: Sполн=Sбок+2Sосн (формула записывается на доску).
Задачи по теме: "Многогранники".
1 группа.
1. В прямоугольном параллелепипеде стороны основания равны 12см и 5см.
Диагональ параллелепипеда образует с плоскостью основания угол 45![]() .
.
Найдите площадь боковой поверхности параллелепипеда.[1]
2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота 12см. Найдите площадь полной поверхности пирамиды.
2 группа.
1. Найдите сторону основания и высоту правильной четырёхугольной призмы, если Sполн=90см2, Sбок=40см2.
2. В правильной четырёхугольной пирамиде высота равна 12см, а апофема - 15см. Найдите площадь полной поверхности пирамиды.
3 группа.
1. Сторона основания правильной четырёхугольной пирамиды равна 12см, а высота пирамиды - Найдите боковое ребро пирамиды.
2. В основании прямой призмы ABCDA1B1C1D1 лежит параллелограмм со сторонами 3см и 6см и углом между ними 60![]() . Диагональ B1D образует с плоскостью основания угол 30
. Диагональ B1D образует с плоскостью основания угол 30![]() . Найдите площадь боковой поверхности призмы.
. Найдите площадь боковой поверхности призмы.
5. Итоги урока.
Сегодня на уроке мы повторили, обобщили и систематизировали знания по теме "Многогранники", проверили умения решать задачи по этой теме. Я думаю, каждый для себя сделает выводы, насколько близка нам математика, как важно её изучать.
Какая часть урока показалась вам самой интересной? Какие вопросы урока вызвали у вас затруднения?
Домашнее задание: Составить геометрический кроссворд, используя предметный указатель на стр. 249 - 251 учебника: Л.С.Атанасян «Геометрия 10-11 классы».
Требования: минимум 10 слов, задания к кроссворду должны быть оформлены грамотно.
Литература
-
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10 - 11 Кл. - М.: Просвещение.
-
Виленкин Н.Я. и др. За страницами учебника математики 10-11 класса.- М.: Просвещение, 1996.
-
Иванова О. Многогранники вокруг нас //Математика, 2005, № 3.Скворцова Н. В. Учась - твори! Нетрадиционные формы проведения уроков математики. - Йошкар-Ола. Педагогическая инициатива, 2003.