Конспект урока на тему: ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ (10 класс)

Урок на тему:

ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ

Цель: сформировать навык применения теоремы о трех перпендикулярах к решению задач.

Ход урока

I. Проверка домашнего задания (теорема, №№ 155, 159).

II. Устная работа.1. АМ (АВС), АВ = АС, CD = DB.

Докажите, что MD ВС.

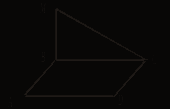
2. ABCD - параллелограмм,

BM (АВС), МС DC.

Определите вид параллелограмма ABCD.

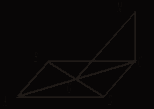
3. ABCD - параллелограмм,

CM (АВС), МO BD.

Определите вид параллелограмма ABCD.

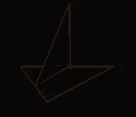
4. Δ АВС, С = 90°, О - центр описанной окружности, АМ = МС,

OD (АВС), АВ = 5, АС = 3.

Найдите DM.

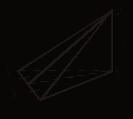
5. Δ АВС, АВ = ВС = АС, CD (АВС),АМ = МВ, DM = 15, CD = 12.

Найдите S_ADB.

6. Δ АВС, С = 90°, BD (АВС),

AD = 2 BD.

Найдите 1 +2.

7. ABCD - квадрат, ВЕ (АВС),

ЕАВ = 45°, S_ABCD = 4.

Найдите S_ΔAЕС.

III. Решение задач.

1. Если точка равноудалена от всех сторон многоугольника, то она проецируется на его плоскость в центр вписанной окружности.Дано: ML АВ, MN АС,

МK ВС, МО (АВС).

Доказать, что О - центр вписанной

в Δ АВС окружности.

Доказательство

1)

2) Аналогично ОK ВС, ON АС.

3) OL = OK = ON (как проекции равных наклонных).

4) Точка О равноудалена от всех сторон треугольника, следовательно, является центром вписанной в него окружности.

2. Докажите обратное утверждение: «Если через центр вписанной в n-угольник окружности проведена прямая, перпендикулярная плоскости этого n-угольника, то каждая точка этой прямой равноудалена от сторон этого n-угольника». (Для доказательства можно использовать тот же рисунок). №№ 157, 158.

Домашнее задание: №№ 160, 205.