- Учителю
- Применение производной при решении задач с практическим содержанием
Применение производной при решении задач с практическим содержанием
29
Применение производной при решении задач с практическим содержанием
В сборнике представлены задачи, связанные с различными сферами деятельности человека. Ко всем задачам даны решения.
Составитель Шумилова М.В., учитель математики
Содержание
Предисловие…………………………….….……….3
§1. Производная в химии…………………………..4
§2. Производная в биологии………………..……...4
§3. Производная в физике……………………..…...4
§4. Производная в технике …..…………………….5
§5. Производная в строительстве…..……………...6
§6. Производная в экономике……..…………….....7
§7. Производная в медицине………..…………….10
§8. Производная в быту…..……………………….10
Ответы……………………………………………...13
Источники информации и иллюстраций…….......29
Предисловие
В школьном курсе математики изучается множество правил, определений, доказываются теоремы. Многие школьники задают вопрос: зачем все это нужно? И это естественный вопрос, т.к. школьные учебники не всегда дают на него полный ответ.
Предлагаемые в сборнике задачи помогут учителю в иллюстрации применения школьных знаний по теме «Производная» при решении задач, взятых из смежных с математикой учебных предметов - физики, химии; задач экономического содержания и др.
Решение задач с практическим содержанием будет способствовать развитию интереса школьников к математическим знаниям.
§1. Производная в химии
Задача № 1
Газовая смесь состоит из оксида азота (NO) и кислорода (О2). Требуется найти концентрацию О2, при которой, содержащийся в смеси оксид азота окисляется с наибольшей скоростью.
§2. Производная в биологии
Задача № 1
В питательную среду вносят популяцию из 1000 бактерий.
Численность популяции возрастает по закону P(t)=1000 + 
, где t - время в часах. Найдите максимальный размер этой
популяции.
§3. Производная в физике
Задача № 1
Составляется электрическая цепь из двух параллельно соединенных сопротивлений. При каком соотношении между этими сопротивлениями сопротивление всей цепи максимально, если при последовательном соединении этих сопротивлений оно равно R.
Задача № 2
П
ри
извержении вулкана камни горной породы выбрасываются
перпендикулярно вверх с начальной скоростью 120 м/ с.
Какой наибольшей высоты достигнут камни, если сопротивлением ветра пренебречь?
Задача № 3
Известно, что тело массой m = 5кг движется
прямолинейно по закону 
. Найдите кинетическую энергию тела через 2с после начала движения.
§4. Производная в технике
Задача № 1
Известно, что прочность на горизонтальный изгиб балки прямоугольного горизонтально сечения пропорциональна произведению ширины балки на квадрат высоты. Найти отношение ширины к высоте поперечного сечения наиболее прочной балки, которую можно вырезать из цилиндрического бревна диаметром d см
§5. Производная в строительстве
З
адача
№1
Чтобы уменьшить трение жидкости о стенки и дно канала, нужно смачиваемую ею площадь сделать возможно малой. Требуется найти
размеры открытого прямоугольного канала с площадью сечения 4,5м2, при которых смачиваемая площадь будет наименьшей.
Задача № 2
Д
ля
конструкторского бюро строится зал в форме прямоугольного
параллелепипеда, одна из граней, которая должна быть сделана из
стекла, а остальные из обычного материала. Высота зала должна быть
4м, а площадь, 80м². Известно, что 1м² стеклянной стены стоит 75
руб., а обычной 50 руб.
Какими должны быть размеры зала, чтобы общая стоимость всех стен была наименьшей?
Задача № 3
О
пределить
размер такого открытого бассейна с квадратным дном и объемом 32см³,
чтобы на облицовку его стен и дна было истрачено наименьшее
количество материала.
Задача № 4
Под каким углом надо
сделать въезд на мост,
если его высота 10 м, а
пролёт составляет
120 м ?
§6. Производная в экономике
З
адача№1
Предприятию поручается погрузка 100 стаканов и выделяется на это
1000 рублей. Но из этой суммы вычитается 40 рублей за каждый час
погрузки. Предприятие заключает договор с бригадой грузчиков, по
которому они получают премию в 10 v рублей, 
-скорость погрузки. При какой скорости предприятие получит
максимальную прибыль, и какова величина этой прибыли?
З
адача
№ 2
Цементный завод производит
х т цемента в день. По договору
он должен ежедневно поставлять
строительной фирме не менее
20 т цемента. Производственные
мощности завода таковы, что
выпуск цемента не может превышать 90 т в день. Определить, при каком объеме производства удельные затраты будут наибольшими (наименьшими), если функция затрат имеет вид: К=-х3+98х2+200х.
Задача № 3
П
редприятие
производит Х единиц некоторой однородной продукции в месяц.
Установлено, что зависимость финансовых накоплений предприятия от
объема выпуска выражается формулой
f(x)=-0,02x3+600x-1000.
Задача № 4
Рассмотрим применение производной к решению следующей
экономической задачи: в математической модели экономического роста
хозяйства производящего, например, цветы для потребления.
Р - ежегодное потребление продукта на душу занятых в производстве;
Х - число занятых в производстве рабочих.
, где M, b - постоянные, характеризующие производственные
возможности хозяйства. При M=250, b=8464 определить число рабочих,
соответствующее наибольшему значению Р в хозяйствах с 80,90,120 и
150 рабочими местами.
З
адача
№ 5 Оборот предприятия за истекший год описывается через функцию
U(t)=0,15t² - 2t² +200, где t - месяцы, U-миллионы. Исследуйте оборот предприятия.
§7. Производная в медицине
Задача № 1
Р
еакция
организма на введенное лекарство может выражаться в повышении
кровяного давления, уменьшения температуры тела, изменении пульса
или других физиологических показателей. степень реакции зависит от
назначенного лекарства, его дозы. Предположим, что Х обозначает
дозу назначенного лекарства, У - функция степени реакции
описывается функцией у=R(x)=x2(a-x), где а - некоторая
положительная постоянная. При каком значении Х реакция максимальна?
§8. Производная в быту
Задача № 1
Над центром круглого стола радиуса r висит лампа. На какой высоте следует подвесить эту лампу, чтобы на краях стола получить наибольшую освещенность?
Задача № 2
Нагруженные сани движутся по горизонтальной поверхности под действием силы F, приложенной к центру тяжести. Какой угол α должна составлять линия действия силы F с горизонтом, чтобы равномерное движение саней происходило под действием наименьшей силы? Коэффициент трения саней о снег равен к.
Задача № 3
Р
асход
горючего легкового автомобиля (литр на 100 км.) в зависимости от
скорости Х км/ч при движении на 4-й передаче приблизительно
описывается функцией: F(x)=0,007х-0,18х+10,2, х>30. При какой
скорости расход горючего будет наименьшим?
Задача № 4
У
часток,
площадью 2400м2, надо разбить на два участка
прямоугольной формы так, чтобы длина изгороди была наименьшей.
Найти размеры участков.
Задача № 5
У
часток
прямоугольной формы одной стороной прилегает к зданию. При заданных
размерах периметра 20 м, надо огородить участок так, чтобы площадь
была наибольшая. Найти длины сторон участка.
Ответы
§1.
№1.
Решение:
Напишем уравнение реакции окисления оксида кислородом
2NO + O2
2NO2
Пусть х - концентрация оксида азота, у - концентрация кислорода, тогда vпрямой=Кх2у, где К - константа скорости реакции, зависящая только от температуры и не зависящая от концентрации реагирующих веществ.
Концентрацию газов выразим в объемных процентах.
Весь объем газовой смеси возьмем за 100%.
В этом случае у=100-х и v=Кх2(100-х), где х принадлежит [0;100].
Найдем наибольшую скорость
D(v) = R
v'(x)=200K - 3Kx2
200K - 3Kx2=0
x=0
x=66,7%
Ответ: при концентрации О2, равной 33,3% оксид азота окисляется с наибольшей скоростью.
§2.
№ 1.
Решение.
D(P)=R
P'(t)=
=
=
P'(t)=0
100-t2=0
t=
P(10)=1000+
=1005
Ответ: через 10 часов популяция достигнет максимального размера 1005 бактерий.
§3.
№ 1.
Решение:
Пусть сопротивление одного х, другого - у. Сопротивление всей цепи при параллельном соединении r, тогда
При последовательном х + у = R
y= R-x
Имеем
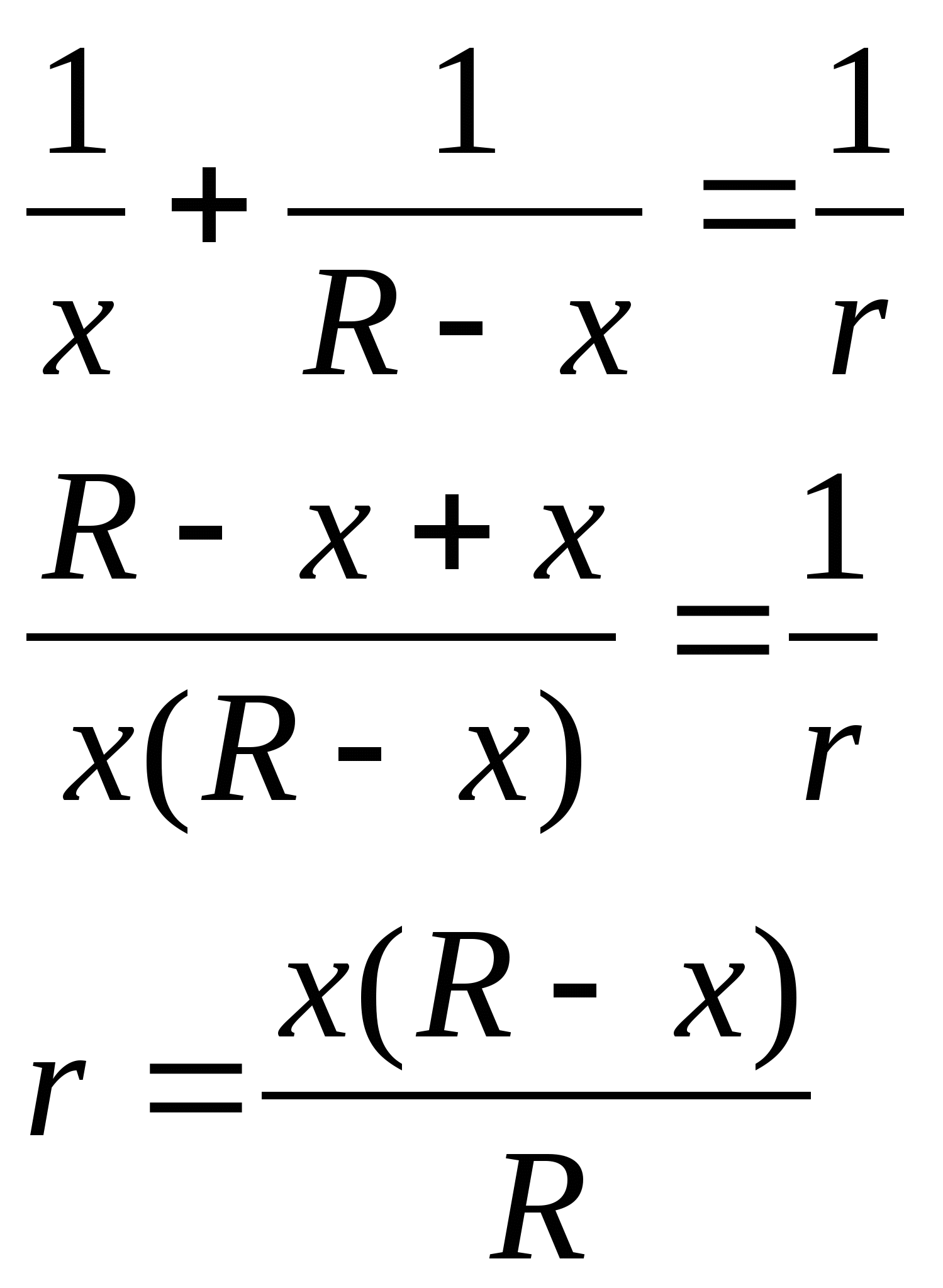
Сопротивление r - является функцией от х, х
принадлежит [0;R]; F(x)=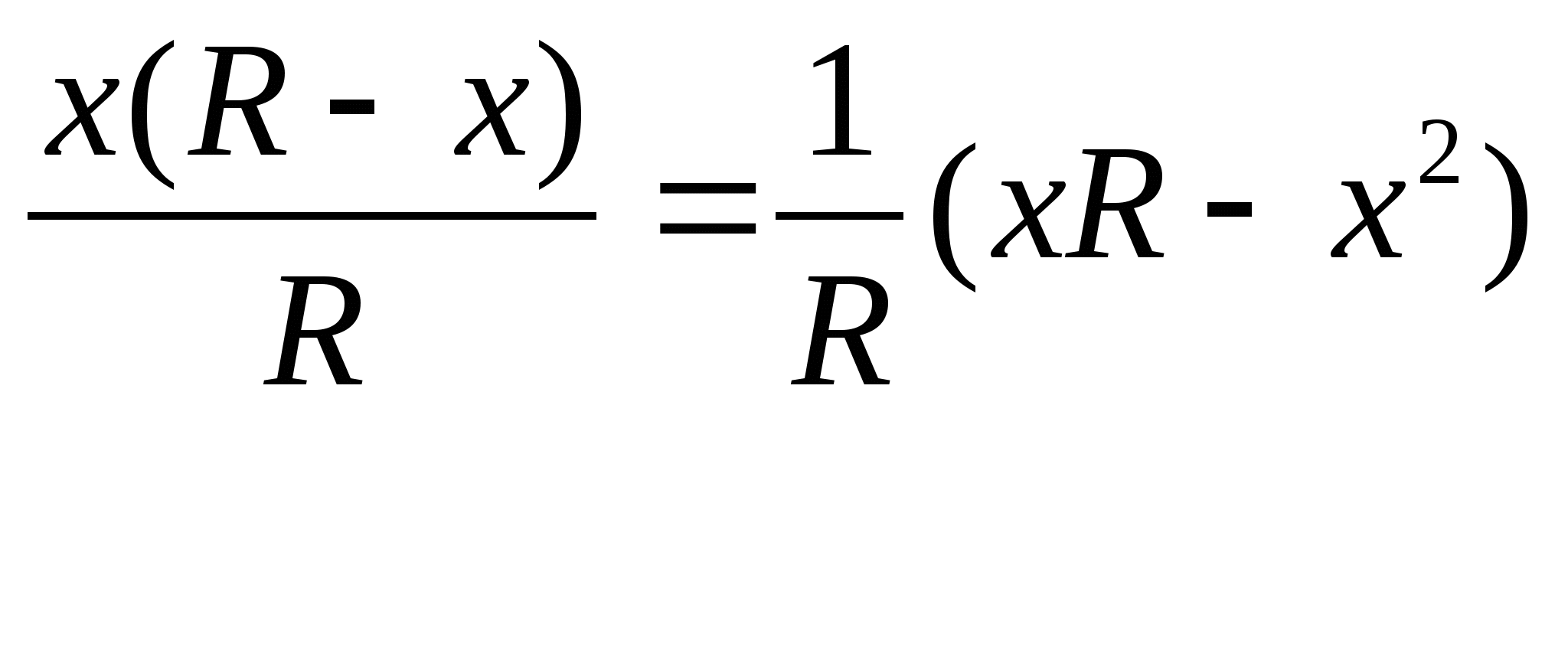
D(f)=R
f'(x)=
f'(x)=0, x=
f(0)=0, f(R)=0, f()=
при х=
сопротивление
всей цепи при параллельном соединении будет наибольшим.
Ответ: сопротивления должны быть одинаковыми.
№ 2.
Решение:
Вещество выбрасывается перпендикулярно вверх. Высота камня h,
функция времени 
. Откуда следует: 
. Следовательно, 0 = 120 - 9,8t и t≈13 сек. Тогда h = 745м, т.е.
камни горной породы достигают уровня 720 м от края вулкана.
Ответ: 720 м.
№ 3.
Решение: E(t)= 
, 
,
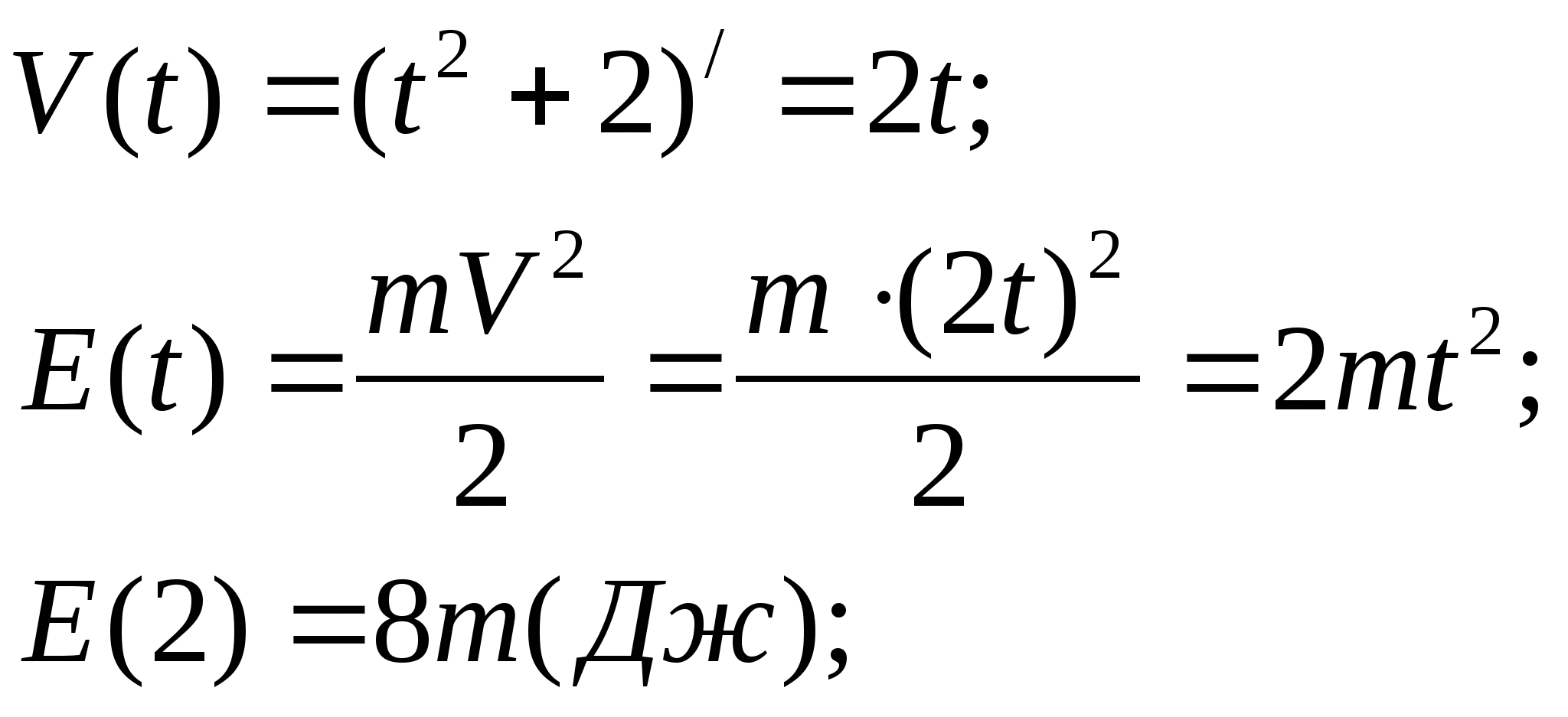
Если 
то Е(2)
Ответ:
40 Дж
§4.
№ 1.
Решение:
Пусть x см - ширина, y см - высота сечения балки. По теореме Пифагора d²=x²+y².
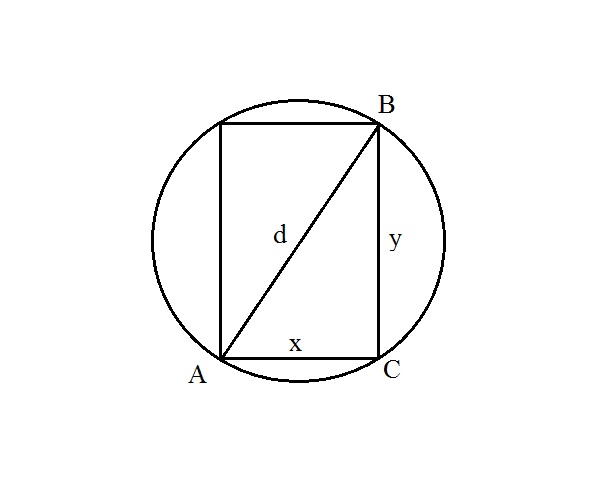
Прочность σ балки определяется соотношением σ= kxy², где k-коэффициент прочности, зависящий от материала. σ=kxy²=kx(d²-x²) = kd²-kx³
Исследуем функцию σ(х)=kd²x-kx³ на максимум и минимум.
1)σ`(х)=kd²-3kx²=k(d²-3x²)
2)σ`(x)=0;
k(d²-3x²)=0
k≠0 d²=3x²;
3) x= -
не удовлетворяет условию задачи.
σ`(х)
+ - x
σ (x) 
max
Знак производной меняется с «+» на «-», значит, при х=
функция имеет максимум и балка имеет максимальную прочность.
x=
>0
x=
<0
y=
=
=
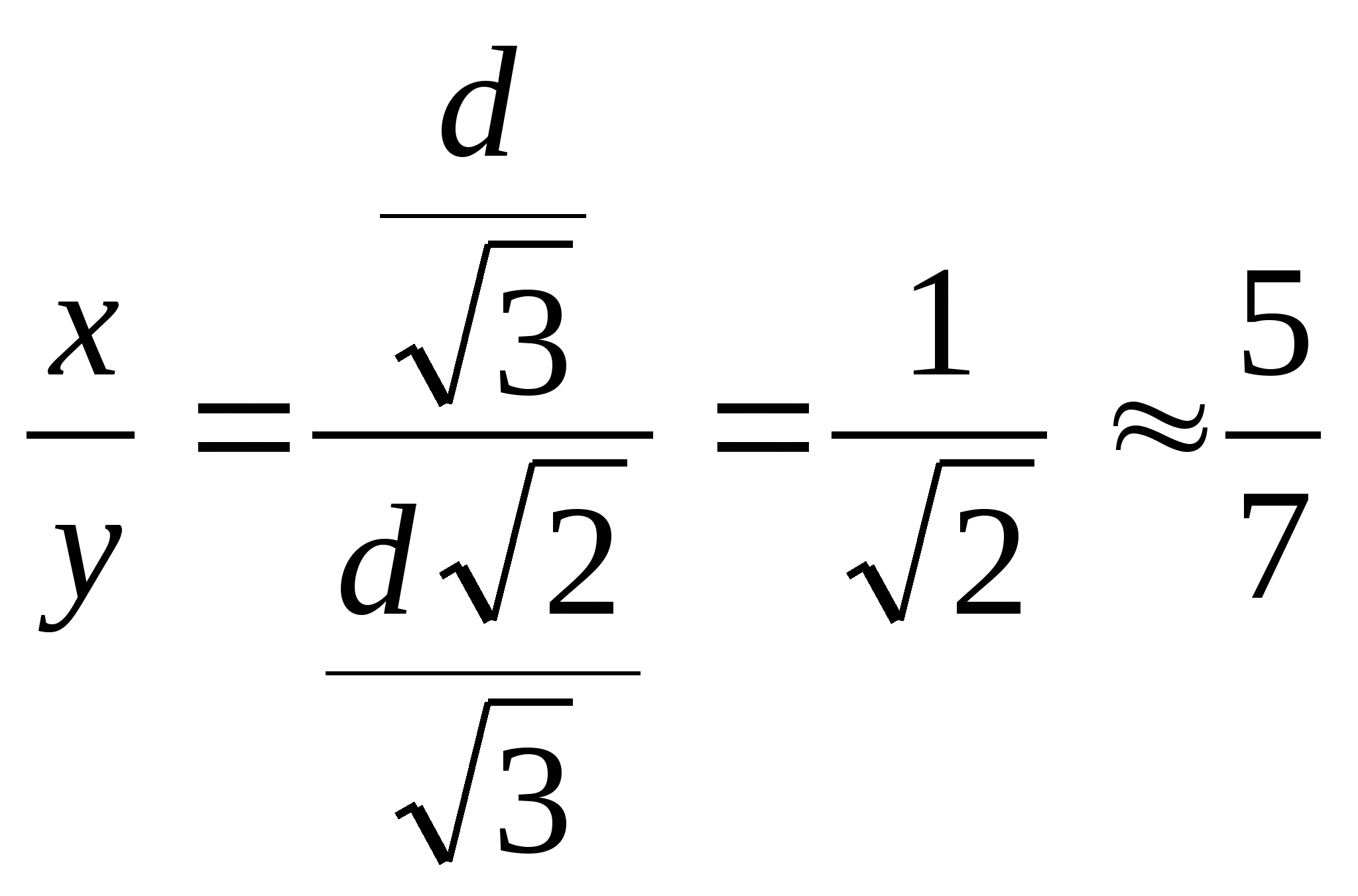
Ответ: 
§5.
№1.
Решение:
Обозначим глубину канавы через х м, тогда ширина будет 
м, Р(х)=2х+
;
Р/(х)=2-
;
Р/(х)=0;2х2=4,5; х=1,5. Берем только
положительное значение по условию задачи, т.е. х 
(0; 
). Найдем знак производной на промежутке (0;1,5) и на промежутке
(1,5; ?). Производная меняет знак с "-" на "+". Отсюда х=1,5 точка
минимума, следовательно, Р(1,5)=6м наименьшее значение, значит,
одна сторона канавы 1,5м, вторая
=3м.
Ответ: глубина - 1,5 м, ширина - 3 м.
№2.
Решение:
Пусть стеклянная стена представляет собой прямоугольный, одно
измерение, которого рано 4 м, а другое примем за x м. Тогда площадь
стеклянной стены равна
4хм². Суммарная площадь остальных стен равна
м²,
а их стоимость 
руб. Общая стоимость всех стен K=K₁+K₂. То получим функцию
Минимум которой требуется найти.
и 
Следовательно,м.
Поскольку 
при 
и
при
,
то.
Тогда наименьшее значение функции 
руб.min
При этом размеры зала 8x10x4.
Ответ: 4 м, 8 м, 10 м.
№ 3.
Решение:
Обозначим длину стороны квадрата x м,
а высоту бассейна y м. Тогда 
м3.
Площадь боковой поверхности бассейна с площадью дна равна
Найдем
м2,
тогда
.
Найдем производную этой функции:
; 
; 
Поскольку
при
, а 
при 
, то 
- точка минимума (наименьшего знания функции). Значит наименьше
размеры бассейна, заданного объема V=32м³ такие;
y=
м.
Ответ: 2м; 2м и 4м
№ 4.
Решение: необходимо ввести прямоугольную систему координат и
рассмотреть график функции 
графиком является парабола, ветви направлены вниз;
b = 10; 
;
.
Ответ :
§6.
№1.
Решение:
Заметим, что скорость ѵ погрузки, станков предполагается
постоянной. За час погружается 100/ѵ станков. Поэтому прибыль Ρ
предприятия такова:
отсюда
-
По смыслу задачи видно, что 
- точка наибольшего значения для функции 
При этом 
руб.
Ответ: 20 
; 600руб.
№ 2.
Решение:
Удельные затраты составят К/х=-х2+98х+200.
Наша задача сводится к отысканию наибольшего и наименьшего значения функции Y= -х2+98х+200.
Таким образом, при выпуске 49 тонн цемента в день удельные издержки максимальны, это экономически не выгодно, а при выпуске 90 тонн в день минимально, следовательно, можно посоветовать работать заводу на предельной мощности и находить возможности усовершенствовать технологию, так как дальше будет действовать закон убывающей доходности. И без реконструкции нельзя будет увеличить выпуск продукции.
№3.
Решение:
Решение исследуется с помощью производной. Получаем, что при Х=100 функция достигает максимума.
Вывод: финансовые накопления предприятия растут с увеличением объема производства до 100 единиц, при х =100 они достигают максимума и объем накопления равен 39000 денежных единиц. Дальнейший рост производства приводит к сокращению финансовых накоплений.
№4.
Решение:
(раскроем
скобки и представим дробь в виде разности трёх дробей). Исследуем
функцию на наибольшее значение при х>0. Для этого найдём
производную и прировняем её к нулю:
Так как х>0, то 
.
Исследуя
знак производной, легко убедиться в том, что 
функция монотонно
возрастает, а при х >92- монотонно убывает =>
.
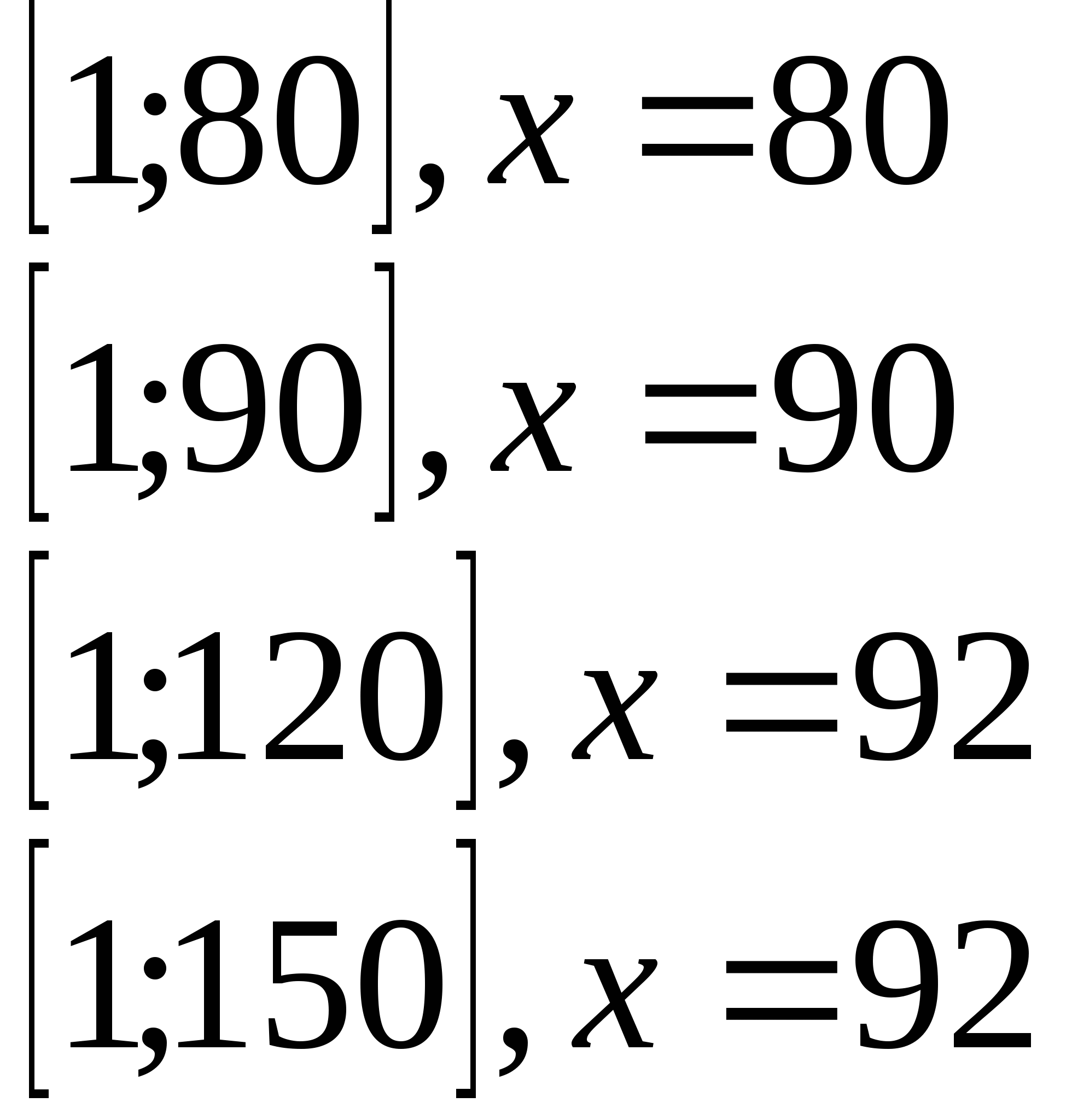Следовательно на отрезке от 1 до 80 функция возрастает и её наибольшее значение достигается на правом конце х=80. и др
А на отрезках от 1 до 120 и от 1до 150 функция меняет характер монотонности, => наибольшее значение достигает в точке х = 92. Производная помогла определить, что хозяйству нет смысла набирать 120 и 150 человек для достижения наибольшей прибыли.
Ответ: 92 рабочих
№5.
Решение:
Исследуем оборот предприятия с помощью производной: U'(t)=0,45t2 - 4t, U''(t)=0,9t - 4, U'''(t)=0,9. Момент наименьшего оборота при U(t)=0, т.е. при t=8,9. Наименьший оборот был на девятом месяце. Первая производная показывает экстремальное изменение оборота. Из U(t)=0 следует t=4,4. Так как U'''(t)>0, то на пятом месяце имеется сильное снижение оборота.
Точки перегиба важны в экономике, так как именно по ним можно определить, в какой конкретно момент произошло изменение.
Так, например, по решению предложенной задачи можно сделать выводы:
-
В начале исследуемого периода у предприятия было снижение оборота;
-
Предприятие пыталось выйти из этого состояния и для этого использовало определенные средства.
Ответ: На пятом месяце (точка перегиба) что-то было предпринято и предприятие стало выходить из кризиса, а на девятом месяце стало набирать обороты.
§7.
№1.
Решение: 0<x<а. R(x)=x2(a-x)=ax2
-x3
D(x)=R
R'(x)=2ax-3x2
2ax-3x2=0; x=0; x=
.
Точки перегиба важны в биохимии, так как они определяют условия, при которых некоторая величина, например скорость процесса, наиболее ( или наименее) чувствительна к каким-либо воздействиям.
Ответ: при х=
максимальную реакция организма на введенное лекарство максимальна.
§8.
№ 1.
Решение:
Из физики известно, что освещенность обратно пропорциональна квадрату расстояния до источника света и пропорциональна синусу угла наклона луча света к освещаемой маленькой площадке.
r
φ
h
Иными словами, E=k
, где E- освещенность на краю стола, 
, h- расстояние от лампы до стола.
Вместо функции E=k
рассмотрим функцию T=
При этом вместо h можно взять переменную
z=
и найти критические точки T как функции от z:
T=
, 
=
;
T'=0, 
-2
,
, т.е.
и 
.
Итак, освещенность максимальна, если
, т.е. если 
.
Ответ: 
№2.
Решение:
Разложим силу F на горизонтальную и вертикальную составляющие. Сила нормального движения саней и вертикальной составляющей силы F:N=P-F sinα, поэтому сила трения F тр = kN = k(P-Fsinα). Сани будут двигаться равномерно при условии компенсации горизонтальных сил:
Fx=Fтр., то есть Fcosα=k (P-Fsinα). Далее находим силу как функцию угла α:
F(α)= kP/(ksinα+cosα).
F′(α) =kP(sinα-kcosα)/(ksinα+cosα)2. Тогда F′(α)=0 при k=tgα. Определим знак второй производной в этой точке.
Из решения этой задачи можно сделать практический вывод: когда необходимо везти на санях груз по дороге с большим коэффициентом трения, нужно тянуть сани за короткую веревку. Если же коэффициент трения мал, веревка должна быть длинной.
№3.
Решение:
Исследуем расход горючего с помощью производной:
F`(х)=0,007х-0,18х+10,2
F(х)=0,0034х-0,18
0,007х-0,18=0
Х=53
Определим знак 2-й производной в критической точке: F`(х)=0,0034х>0, следовательно, расход горючего при скорости 53км/ч будет наименьшим. F(53)=5,43(л.)
Ответ: 53км/ч
№4.
Решение:
Обозначим одну сторону участка через х м, тогда
вторая будет 
м, длина изгороди Р(х)=3х+
Р/(х)=
3-
;
Р/(х)=0; 3х2=4800; х2=1600; х=40.
Берем только положительное значение по условию задачи, т.е. х
(0;
). Найдем знак производной на промежутке (0;40). Производная меняет
знак с "-" на "+". Отсюда х=40 точка минимума, следовательно,
Р(40)=240м наименьшее значение, значит, одна сторона 40м, вторая
=60м.
Ответ: 40 м и 60 м.
№5.
Решение:
Обозначим одну сторону прямоугольника через х м, тогда вторая будет (20 -2х) м, площадь
S(х)= (20-2х)х=20х -2х2;
S /(х)= 20 -4х; S/(х)=0;
20 -4х =0; х = 
=5;
По условию задачи х
(0; 10)
Найдем знак производной на промежутке (0; 5) и на промежутке (5; 10). Производная меняет знак с "+" на "-". Отсюда х = 5точка максимума. Следовательно, одна сторона участка = 5м, вторая 20 -2х= 10м.
Ответ: 5 м, 5 м, 10 м.
Источники информации:
-
Апанасов П.Т., Апанасов Н.П. Сборник математических задач с практическим содержанием. - М.: Просвещение, 1987.
-
Башмаков М.И. Алгебра и начала анализа, 10-11 кл. - М.: Просвещение, 1993.
-
Приложение к газете «Первое сентября», « Производная в физике и технике», 2008.
Источники иллюстраций:
1. geraldica.ru/names/143-l-r-lr
2. dianetics-books.ru/category/dianetika-i-pamyat/
3. www.sevmash.ru/rus/proekt/pkb.html
4. mkonline.ru/2000-03/2000-03-4.html
5. taksi-aeroport-moskva.ru/wp-content/uploads/2010/06/pereezdi.jpg
6. dearhome.ru
7. www.mallex.info/auto/Rabotniki-IzhAvto-nedovolny-antikrizisnymi-zarplatami-top-menedzhmenta
8. www.shampan.by/belarus/?ELEMENT_ID=119
9. sob.ru/uyut/kusochek-morya-v-vashem-dvore
10. www.avto.goodfon.ru/bmw/index-30.html
11. kbtm.ru/stroitelstvo/kak-ogorodit-dachnyj-uchastok.html
12. mn.ru/moscow/20121008/328341221.html
13. ostroymaterials.ru/zabor-iz-setki-rabicy-svoimi-rukami.html
14. www.phenomenonsofhistory.com/site/?p=3014
15.kabefor.at.ua/news/novaja_ofisnaja_mebel_ehto_vashe_samoe_mudroe_reshenie/2012-04-23-3</</u>