Разработка урока на тему : «Применение производной для нахождения наибольших и наименьших значений непрерывной функции на промежутке».

14.04.2016 г. 10 класс

Тема урока: «Применение производной для нахождения наибольших и наименьших значений непрерывной функции на промежутке».

Цель урока: Организовать деятельность учащихся, направленную на овладение системой математических знаний и умений по теме «Отыскание наибольшего и наименьшего значений непрерывной функции не промежутке», необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования.

Задачи:

1. Дать представление о связи свойств функции с её производной, учить чтению и анализу графиков функций.

2. Развивать умение анализировать, сопоставлять, сравнивать, формулировать выводы по результатам собственной деятельности..

3. Развивать такие качества личности, как ясность и точность мысли, логическое мышление, алгоритмическая культура, интуиция, критичность.

4. Воспитывать средствами математики культуру личности: умения выслушать и принимать во внимание взгляды других людей, умение справляться с неопределённостью и сложностью.

Тип урока: Урок формирования новых знаний.

Структура урока:

1. Организационный момент.

2. Актуализация опорных знаний и фиксация затруднений в деятельности.

3. Постановка учебной задачи.

4. Выполнение лабораторной работы и фиксация результатов.

5. Обсуждение результатов деятельности учащихся, теоретическое обоснование этих результатов.

6. Первичное закрепление.

7. Включение в систему знаний и повторение.

8. Рефлексия деятельности (итог урока)

9. Домашнее задание.

Ход урока

1. Организационный момент.

Какой раздел математики мы сейчас изучаем? Какую главу данного раздела? Тема сегодняшнего урока откроет нам еще одно из приложений производной «Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке».

- Знакомы ли вы с данной темой? Сформулируйте цель нашей учебной работы.

Эпиграфом к уроку взяты слова датского математика Цейтена

«Правильному применению методов можно научиться только применяя их на разнообразных примерах».

О каком методе мы ведем сегодня речь? Какие приложения производной вы знаете?

Учебные задачи сформулируем позже, а сейчас повторим основные моменты

2. Актуализация опорных знаний

1. Найдите производные данных функций:

(слайд)

По графику функции найдите: а) Область определения функции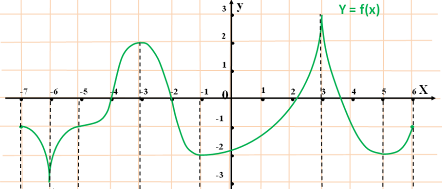

б) точки, в которых производная равна нулю. Как называются эти точки?

в) точки, в которых производная не существует. Как называются эти точки?

г) назовите наибольшее значение функции

д) найдите наименьшее значение функции

3. -Приведите пример функции, имеющей только одну стационарную точку. Имеет ли эта функция наибольшее, наименьшее значение?

- приведите пример функции, имеющей множество стационарных точек. Имеет ли эта функция наибольшее, наименьшее значение?

- приведите пример функции, имеющей только одну критическую точку, а стационарных точек нет. Имеет ли эта функция наибольшее, наименьшее значение?

4. Вы видите, когда функция задана графически, наибольшее и наименьшее ее значения на заданном отрезке найти несложно. Как быть, когда функция задана аналитически? (постановка проблемной ситуации) Требуется найти наибольшее и наименьшее значения функции у=х³-3х²-45х+1 на отрезке .Построить график этой функции процесс трудоемкий и поэтому давайте сформулируем учебные задачи урока. Моя подсказка состоит в следующем - вспомните эпиграф урока и главу математики, которая нами изучается(учащиеся формулируют задачу: научиться по аналитическому заданию функции с помощью производной находить наименьшее и наибольшее значения функции, разработать алгоритм нахождения наиб. и наим. значений.

3) Изучение нового материала .

Ставим задачу: составить алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на отрезке

(слайд) Теорема Вейерштрасса : Непрерывная на отрезке функция принимает на этом отрезке наибольшее и наименьшее значения

(слайд)

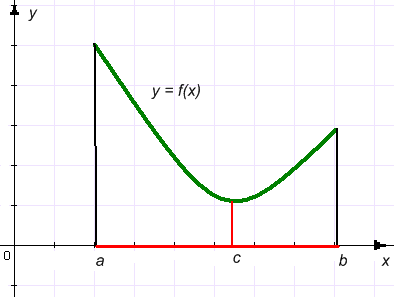
У_наиб=f(в), в - конец отрезка

У_наим= f(Х₁), Х₁ - стационарная точка, в ней f¹(х₁)=о

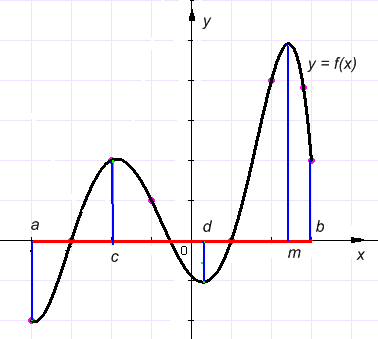
У_наим=f(а), а - конец отрезка

У_наиб= f(m), m- стационарная точка, в ней f^'(m)=о

У_наим=f(-1)=f(5), x=-1, x=5 - стационарные точки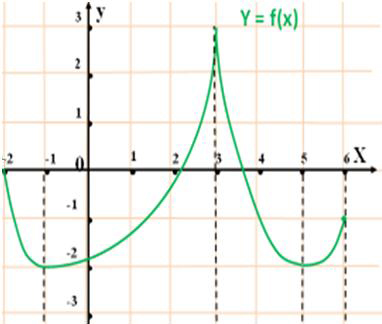

У_наиб= f(3), х=3- критическая точка, в ней f^'(3) не существует

Проанализируем полученные данные и составим алгоритм отыскания наибольшего и наименьшего значений функции

Вернуться к примеру и показать его решение на доске:

Требуется найти наибольшее и наименьшее значения функции у=х³-3х²-45х+1 на отрезке . (учитель представляет образец решения, записывая ход рассуждений согласно разработанному алгоритму)

4. Первичное закрепление

Работа по учебнику задание №32.1(а,б) у доски с подробным объяснением 1 уч-ся, остальные решают в тетрадях, затем задание № 32.2(а,б) на местах и 1 чел на открывающейся части доски, проверка решения, оценивание. Сильные уч-ся разбирают пример

5.Домашнее задание п. 32 учить №32.1 (в,г), №32.8 (в,г).

6. Самостоятельная работа учащихся 32.6 (а,в) - 1 вариант; 32.6 (б,г) - 2 вариант

7.Подведение итогов урока

Имеет ли данный тип задач практическое применение? (слайд)

"…Особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды".

Чебышев Пафнутий Львович

(обсудить, какая выгода имеется ввиду)

8. Рефлексия

Изобразите смайликом свое впечатление от работы на уроке и изученного материала (веселый или грустный)Узнал много нового, интересного

Хочу узнать больше, заинтересовался

Остались вопросы по изученной теме