- Учителю
- Справочные материалы по теме Некоторые приемы решения тригонометрических уравнений
Справочные материалы по теме Некоторые приемы решения тригонометрических уравнений
Некоторые приёмы решения тригонометрических уравнений.
cos x=a ![]() , пÎZ
, пÎZ
![]()
tg x=a ![]() , пÎZ
, пÎZ
сtg x=a ![]() , пÎZ
, пÎZ
-Функции разных аргументов привести к функции одного аргумента.
-Разные функции одного аргумента привести к одной функции.
-Обозначить эту функцию новой переменной.
-Привести уравнение к алгебраическому виду и решить.
-Перейти к старым переменным.
-Найти корни исходного уравнения.
cos 2x+3 sin x=2;
cos2 x- sin2 x+3 sin x=2;
1-2 sin2 x+3 sin x-2=0;
sin x=y 2y2-3y+1=0;
y1=0,5; y2=1;
sin x=0,5 или sin x=1
х=![]()
х=![]()
2 cos2 3x - sin 3x =1;
2(1 - sin2 3x) - sin 3x = 1;
2 sin2 3x - sin 3x - 1 = 0;
sin 3x=у 2у2 - у - 1 = 0;
у1=1; у2= - 0,5;
sin 3x = 1; sin 3x = - 0,5
3х=![]() ;3х=
;3х=![]()
х=![]() ;
х=
;
х=![]()
![]()
2.Однородные уравнения.
a sin x + b cos x = 0 - I степ.
a sin2 x + b sin x cos x + c cos2 x = 0 - II степ.
cos x=0 не является корнем исходного уравнения, т.к. если cos x=0, то в силу исходного уравнения и sin x=0, что противоречит основному тригонометрическому тождеству. Поэтому можно разделить обе части уравнения на cos x (на cos2 x) или на sin x (на sin2 x).
2 sin x - 3 cos x = 0;
![]() ;
;
2 tg x - 3 = 0;
tg x =1,5
х= arctg1,5+p п; пÎZ
sin2 x - 3 sin x cos x + 2 cos2 x=0;
![]()
tg2 x - 3 tg x + 2 = 0;
tg x =у у2 - 3у + 2=0;
у1=1 у2=2
tg x=1 tg x=2
х=![]() х= arctg2+p k
х= arctg2+p k
п,kÎZ
При оформлении решения нужно пояснять, почему можно делить на cos x (cos2 x)
3. Уравнения, решаемые с помощью разложения на множители.
- Перенести все слагаемые в левую часть уравнения.
- Разложить левую часть уравнения на множители (с помощью вынесения общего множителя за скобки, группировки, формул сокращённого умножения и др.)
- Каждый множитель приравнять к нулю.
- Решить полученные уравнения.
sin 4x=3cos 2x
2sin 2xcos 2x-3cos 2x=0
cos 2x(2sin 2x - 3)=0
cos 2х=0 или 2 sin 2x- 3=0
2х=![]() sin2x=1,5
sin2x=1,5
![]() ,
пÎZ
,
пÎZ ![]()
cos2 x+sin xcos x=0
cos x(cos x+sin x)=0
cos x=0 или cos x+sin x=0
![]() 1+
tg x=0
1+
tg x=0
![]()
п,kÎZ
sin x + cos x - 1 - sin 2x = 0
sin x + cos x - (cos2 x+sin2 x +
+ 2sin xcos x )=0
(sin x+cos x) - (sin x+cos x)2=0
(sin x+cos x)(1-sin x-cos x)=0
![]()
………
4. Линейные тригонометрические уравнения.
a sin x + b cos x =с где
а2+b2 с2 (т.е. с ≤![]() )
- иначе уравнение не будет иметь решения.
)
- иначе уравнение не будет иметь решения.
1 способ: применение универсальной
подстановки: ![]() . Тогда
. Тогда
![]()
При таком переходе возможна потеря решений:
следует помнить, что ![]() (в этих
(в этих ![]() не существует). Поэтому значения х= p +2p т нужно проверять,
подставляя в исходное уравнение.
не существует). Поэтому значения х= p +2p т нужно проверять,
подставляя в исходное уравнение.
2 способ: введение дополнительного аргумента:
-
Обе части уравнения разделить на
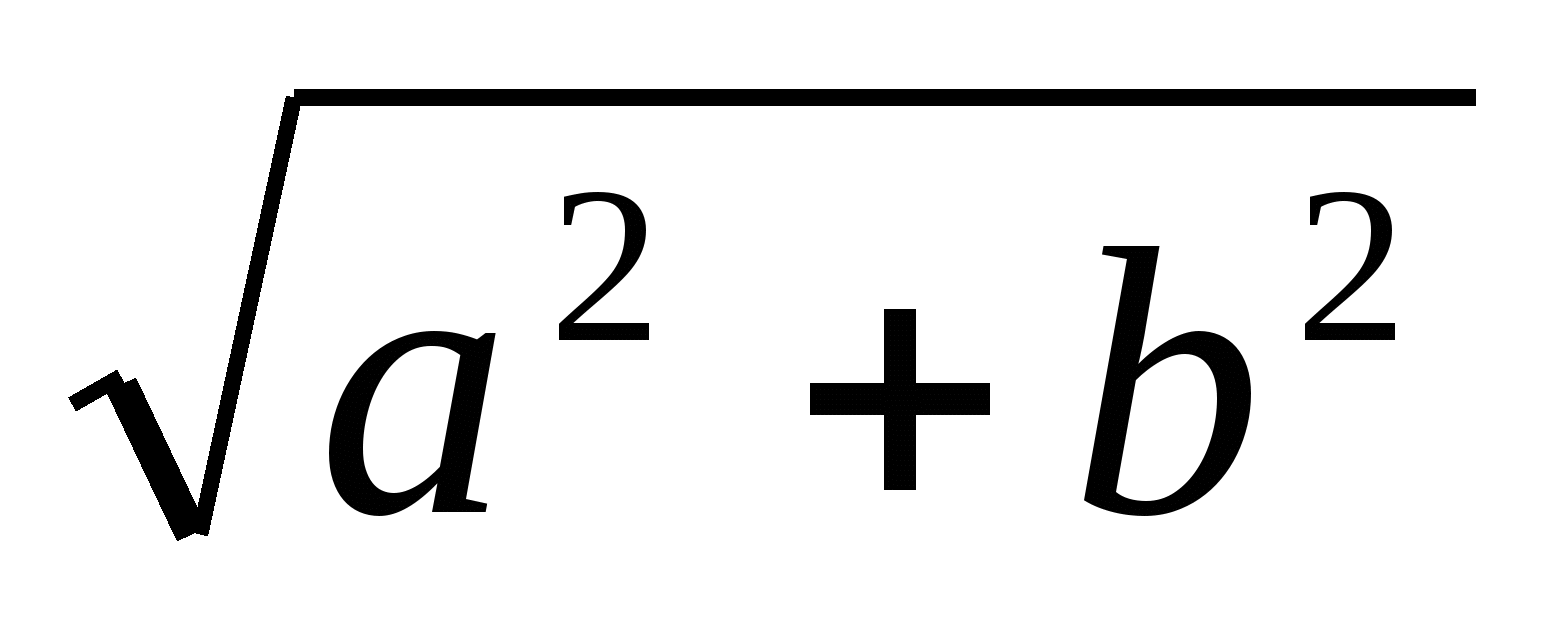 .
.
![]()
-
Ввести дополнительный аргумент - угол α такой, что
![]() и
и
![]() тогда
тогда ![]()
![]()
-
Если ввести угол b такой, что
![]() и
и
![]() , то получим
, то получим
![]()
![]() .
.
sin x + cos x= - 1
![]()
![]()
2t+1- t2= - 1 - t2
2t = -2
t = -1
![]() ,
,
![]()
Подставив в исходное уравнение
![]() убеждаемся,
что эти числа также являются его решениями.
убеждаемся,
что эти числа также являются его решениями.
Ответ: ![]()
![]() ,
п,тÎZ
,
п,тÎZ
sin x + cos x= - 1
a=1, b=1, c= - 1.
a2+b2=2
![]() .
.
Учитывая, что ![]()
получим
![]()
![]()
![]()
![]()
При данном способе решения нет риска потери корней.
3sin x +4 cos x= 2
a=3, b=4, c=2. a2+b2=25, с2=4, т.е. a2+b2 > с2
![]()
![]()
![]()
![]() .
Значит
.
Значит ![]() .
.
5. Уравнения вида Р(sin x cos x,
sin x cos x)
Уравнения вида Р(sin x± cos x, sin x cos x), где Р(х,у) - многочлен, удобно решать при помощи введения новой переменной t= sin x ± cos x. Тогда 1± 2sin x cos x = t2.
sin x+cos x+4sin xcos x - 1 =0
t=sin x+cos x; t2=(sin x+cos x)2=1+2sin xcos x
Значит 4sin xcos x=2t2 - 2
2t2 + t - 3=0 sin x+cos
x=1![]()
t1=1 t2=-1.5 sin x + cos
x= - 1,5![]()
6. Уравнения, решаемые с помощью формул понижения степени.
![]()
![]()
2 sin2 x+ cos 4x=0
1- cos 2x+ cos 4x=0; Þ 1- cos 2x+2 cos2 2x-1=0; cos 2x(2 cos 2x-1)=0
cos 2x=0 ![]() или
или ![]()
7. Уравнения, решаемые преобразованием суммы или разности в произведение.
![]()
![]()
![]()
![]()
![]()
![]()
sin 5x=sin 3x
cos 2x - cos 8x+cos 6x=1
cos 3x+sin 2x - sin 4x=0
8. Уравнения, решаемые преобразованием произведения в сумму и с помощью формул сложения.
![]()
![]()
![]()
![]()
![]()
![]()
cos 3x cos 2x=sin 3x sin 2x
cos 3x cos 2x - sin 3x sin 2x=0
cos (3х+2х)=0
cos 5х=0
![]() ,
пÎZ
,
пÎZ
sin 5x cos 3x=sin 6x cos 2x
0,5(sin 8x+ sin 2x)=0,5(sin 8x+ sin 4x)
sin 2x - sin 4x=0
-2 sin x cos 3x=0
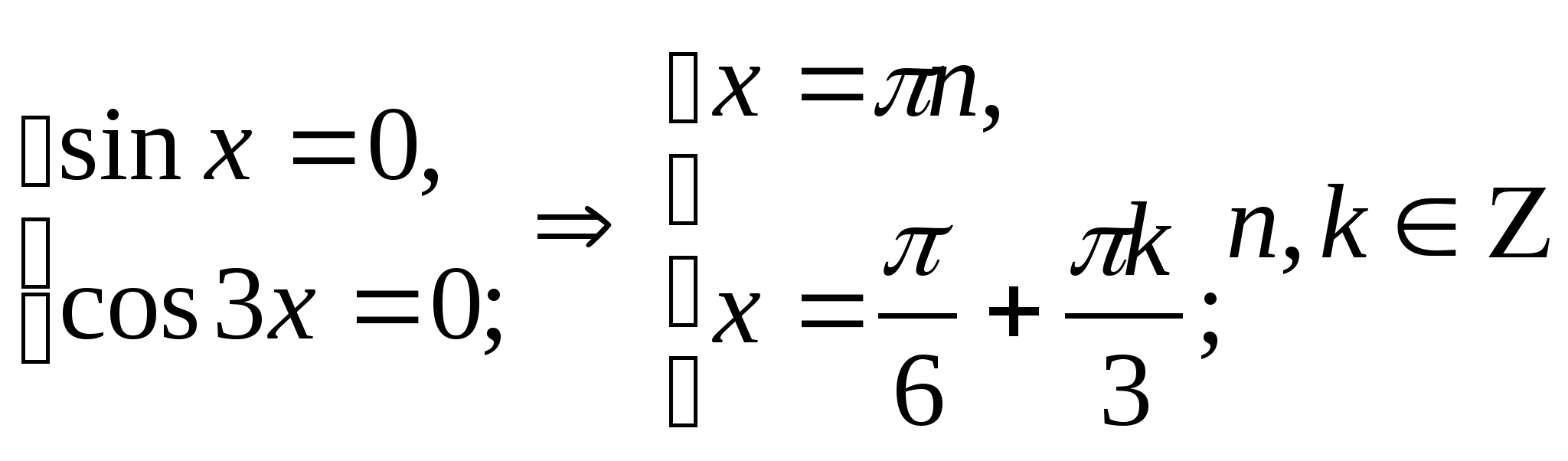
![]()
9. Уравнения, решаемые с помощью равенства одноимённых тригонометрических функций
sin α=sin ![]() cos α=cosb
cos α=cosb![]()
tg α=tgb 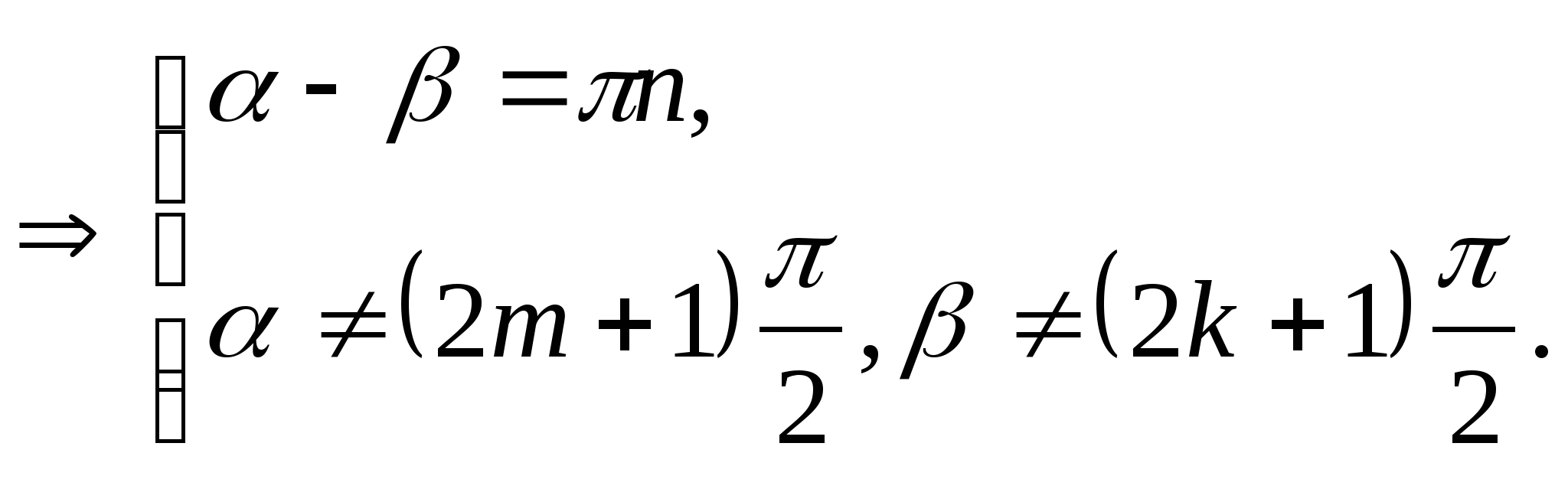
cos 3x= sin x
cos 3x= cos (0,5p - х)
3х - (0,5p - х)=2p п
4х=![]() ,
,
![]() , пÎZ
, пÎZ
3х + (0,5p - х)=2p k, ![]() , kÎZ
, kÎZ
sin 3x=sin 5x
5х-3х=2лp 2х=2лp, х=лp, лÎZ
3х+5х=(2т+1)p, 8х=(2т+1)p
х =![]() ,
пÎZ
,
пÎZ
Другое решение:
3х=(-1)п5х+pп, пÎZ
п-чётн. х=…
п-нечётн. х=…
10. Использование ограниченности функций у= sin x и у= cos x.
![]() и
и
![]()
![]()
sin sin x=1
![]()
Модуль полученного выражения больше 1 при любых k корней нет
sin x+ sin 9x=2