Урок-мастерская для 7 класса по теме: «Сумма углов треугольника»

Разработка урока для 7 класса по теме: «Сумма углов треугольника»

Пояснительная записка:

Вашему вниманию предлагается урок-мастерская по геометрии для 7 класса по учебнику Л. С. Атанасяна, В.Ф.Бутузова , где знания ученики не получают уже в готовом виде, а самостоятельно добывают их, активно используя исследовательский метод. Большую часть работы дети выполняют самостоятельно, учитель выполняет лишь роль помощника.

Не секрет, что с каждое новое поколение отличается от предыдущего, и подходы к их обучению, а также средства обучения должны трансформироваться в соответствии с новыми требованиями и правилами жизни. Мотивация школьников к учебе остается одной из самых актуальных задач современного учителя. Именно исследовательская деятельность, а также ненавязчивость и легкость подачи материала является приоритетом в обучении.

I Организационный момент

Форма проведения урока: мастерская

Цели урока: доказать теорему сумме углов треугольника, ее следствие, научиться решать задачи на применение нового материала.

Оборудование: тетради, чертежные инструменты, транспортир.

Опорная литература : Л. С. Атанасян, В.Ф.Бутузов геометрия 7-9 классы.- М.:Просвещение, 2012, Н. Ф. Гаврилова универсальные поурочные разработки по геометрии, 7 класс.

Класс разбивается на рабочие группы по 5-6 человек и присаживается за заранее приготовленные столы.

II Изучение нового материала

«Тема нашего занятия «Сумма углов треугольника». Сегодня мы узнаем, чему она равна, а также попробуем доказать это, а также решим задачи по этой теме. И так начнем»

На каждом столе будут лежать вырезанные из бумаги треугольники, различные по типу (прямоугольные, остроугольные, тупоугольные) и размеру. Учащимся самостоятельно предлагается выбрать себе треугольники для исследования и измерить углы этих треугольников при помощи транспортира. Результаты измерений записать прямо на этих треугольниках.

Вопросы учащимся:

• Какова сумма углов треугольника?

• У всех ли треугольников сумма углов одинакова и равна 180°?

• Сформулируйте теорему

«Итак, давайте докажем теорему о том, что сумма углов треугольника равна 180°». Каждому из учащихся предлагается вспомогательный чертеж:

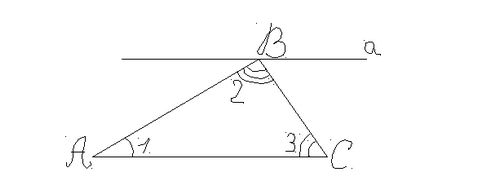
Подсказка: «Для того, чтоб произвести доказательство, необходимо вспомнить недавно изученную вами теорему о внутренних накрест лежащих углах и понятие развернутого угла».

Учащиеся думают, советуются друг с другом, выполняют тезисно доказательство теоремы, затем учитель обращает внимание учащихся на доску, где под диктовку учеников делает выкладки доказательства. Ученики перечерчивают рисунок и оформляют грамотно доказательство в тетрадь.

«Итак, вы доказали теорему о сумме углов треугольника».

Учитель обращает внимание учеников на внешние углы, обозначив их за третий и четвертый углы. Вопрос к ученикам: «Как бы вы назвали эти углы?»

Ответ: «Это внешние углы». Внешним углом называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол равен сумме двух углов треугольника, не смежных с ним. Запишите это следствие и самостоятельно сделайте к нему чертеж.

(Ученики пишут, чертят.)

III Закрепление изученного материала

«Предлагаю вашему решению задачи».

На каждый стол выкладываются задачи (условием вниз), ученики наугад тянут задачи и самостоятельно решают. Те, кто первыми решают верно задачи, получают «5», затем помогают решать задачи остальным «участникам стола».

В конце урока каждый ученик получает бумажный «смайлик» с домашним заданием на оборотной стороне.

III Подведение итогов

«Подведем итоги урока: сегодня вы сформулировали и доказали теорему о сумме углов треугольника, а также закрепили изученный материал решив задачи».

Задачи на карточках

1. Найдите угол В треугольника АВС, если ∟А=73°, ∟С=25°.

2. Найти углы треугольника АВС, если ∟А :∟В:∟С= 2:3:4

3. Докажите, что каждый угол равностороннего треугольника равен 60°

4. Найти углы равнобедренного треугольника, если угол при основании в три раза меньше, чем противолежащий угол.

5. Найти углы равнобедренного треугольника, если один из углов равен 80°

IV Задание на дом

Домашнее задание

№ 224, №228(а), 230 (Л. С. Атанасян, В.Ф.Бутузов геометрия 7-9 классы)

Замечание

Даже необычная расстановка столов невероятно пробуждает интерес учеников к учебному процессу. Позвольте детям проявить самостоятельность и фантазию в решении геометрических задач, ведь геометрия - это прекрасный инструмент для развития логики и мышления. Пусть дети сами измеряют, думают, доказывают, то есть ищут пути решения проблемы, ведь это так важно в дальнейшей жизни.