- Учителю
- Урок по алгебре на тему Неполные квадратные уравнения с использованием технологии модульного обучения
Урок по алгебре на тему Неполные квадратные уравнения с использованием технологии модульного обучения
Урок по технологии модульного обучения.
Предмет: математика.
Класс: 8.
Тема: «Определение квадратного уравнения. Неполные квадратные уравнения».
УМК Ю. Н. Макарычев
Цель урока: изучить определение квадратного уравнения, неполного квадратного уравнения; создать комфортный темп работы для каждого ученика.
Задачи:
Образовательные: развитие навыков решения неполных квадратных уравнений;
Развивающие: развитие ключевых компетенций мышления, понимания, самостоятельности.
Коррекционные: коррекция элементов внимания.
Воспитательные: воспитание умения работать в группе и самоорганизовываться.
Тип урока: изучение нового материала.
Метод ведения урока: использование модульной технологии.
Оборудование: индивидуальные карточки, алгоритм работы для учащихся.
Условные обозначения:
& - работа с учебником;
$ - цель урока;
? - вопрос;
! - письменное задание;
6 - физкультминутка;
% - помощь учителя;
J - «все получилось»;
L - неудача;
< - домашнее задание.
М-1 Неполные квадратные уравнения и их корни.
$
Знать: - что такое квадратное уравнение; неполное квадратное уравнение;
- виды неполных квадратных уравнений;
- алгоритмы решения неполных квадратных уравнений.
Уметь: - решать неполные квадратные уравнения.
УЭ-1
Изучение нового материала.
Задание 1
1. Внимательно прочитай п.19, стр. 105-106 (до примера 1).
Прочитай определение квадратного уравнения, выучи наизусть.
2. Расскажи выученное определение своему соседу.
3. Письменно ответь на следующие вопросы и запиши ответы в словарь:
-
Уравнение, какого вида называют квадратным?
-
Что такое коэффициенты квадратного уравнения?
-
Придумай и запиши несколько квадратных уравнений, укажи значения его коэффициентов.
Если у тебя возникли трудности, обратись к учителю!
Задание 2.
1. Внимательно прочитай п.19, стр. 105-106 (до примера 1).
Прочитай определение неполного квадратного уравнения, выучи наизусть.
2. Расскажи выученное определение своему соседу.
3. Письменно ответь на следующие вопросы и запиши ответы в словарь:
-
Какое уравнение называют неполным квадратным уравнением?
-
Запишите в общем виде 3 вида неполных квадратных уравнений?
-
Придумай и запиши все виды неполных квадратных уравнений, укажи значения его коэффициентов.
Если у тебя возникли трудности, обратись к учителю!
Задание 3
стр. 108.
Устно выполните №505.
Обсудите решение со своим соседом!
Если у тебя возникли трудности, обратись к учителю!
6 Физкультминутка.
УЭ-2
Изучение нового материала
(алгоритм решения неполного квадратного уравнения вида: а • х2 + с = 0).
Задание 1
Рассмотри образцы решения уравнений:
-
Решите уравнение №1:
-3х2 +27=0
Решение.
1.Перенесем свободный член в правую часть уравнения:
-3х2 = -27
2.Разделим обе части уравнения на коэффициент при х2:
х2= -27: (-3)
х2 = 9
х1 =
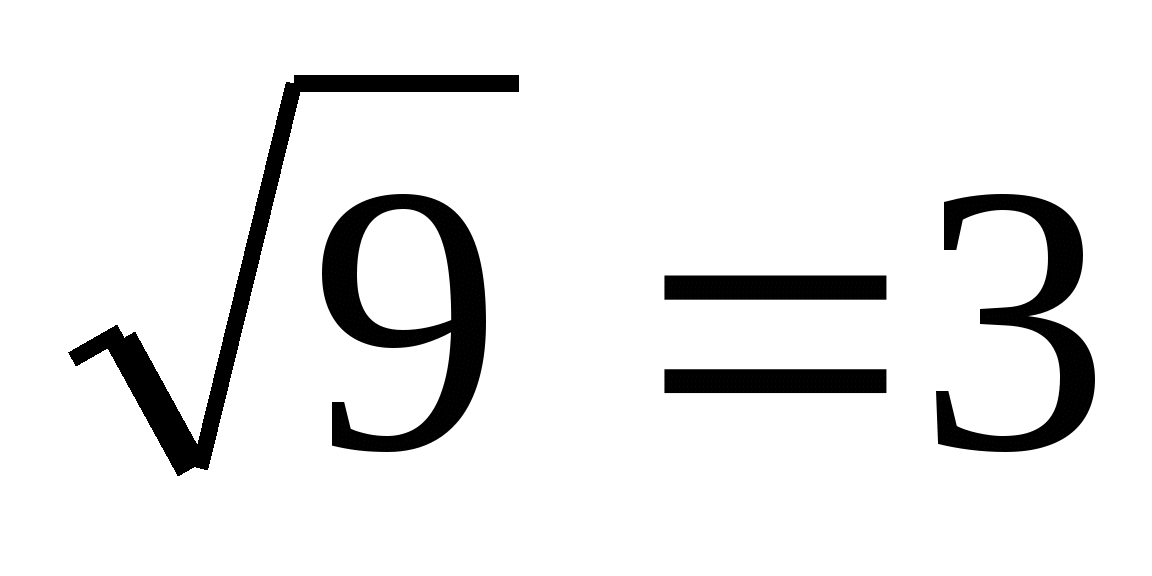 ,
х2 =-
,
х2 =-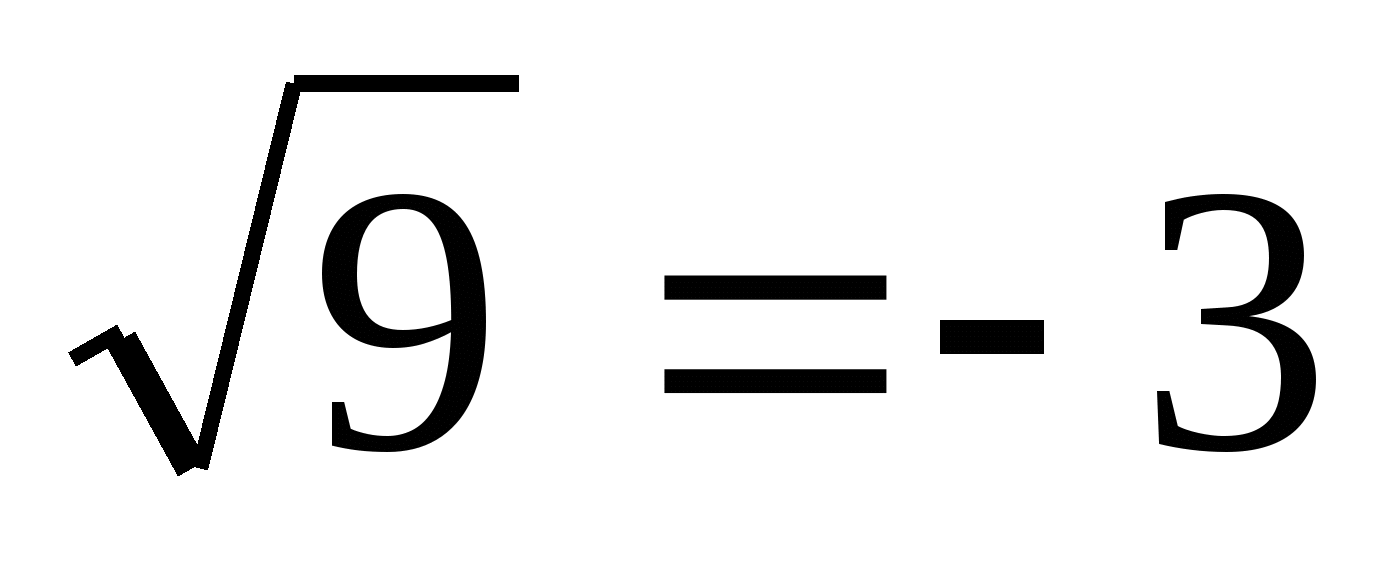 ,
,
Ответ: х1 =
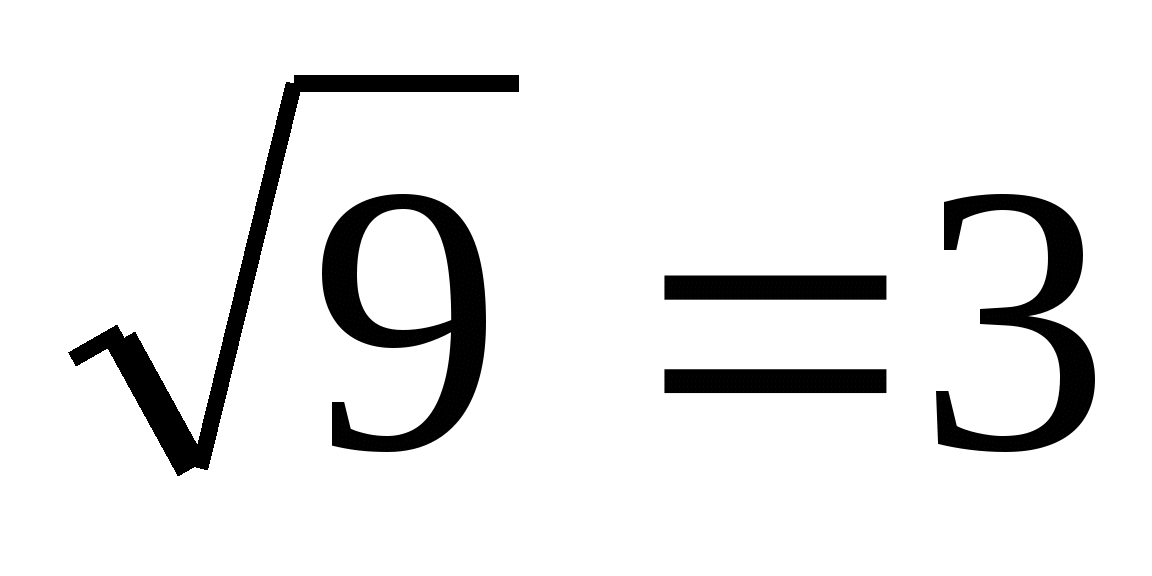 ,
х2 =-
,
х2 =-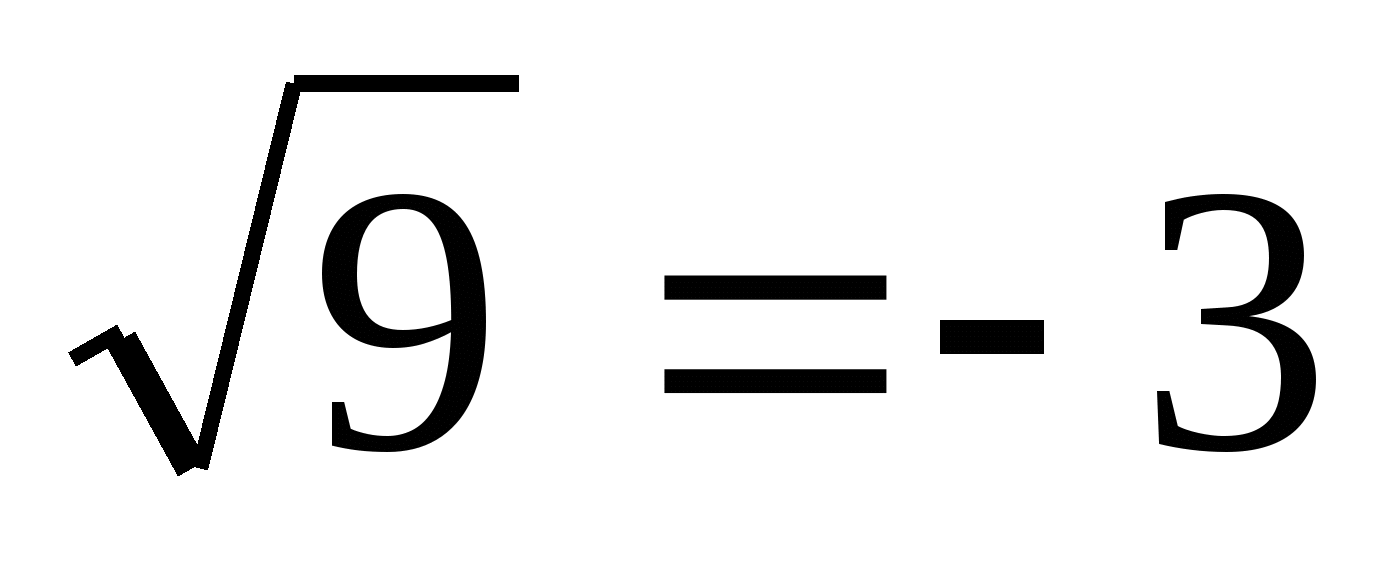 .
.Решите уравнение №2:
5х2 +25=0
Решение.
1.Перенесем свободный член в правую часть уравнения:
5х2 = -25
2.Разделим обе части уравнения на коэффициент при х2:
х2= -25: 5
х2 = -5
Ответ: корней нет.
? Почему уравнение не имеет корней?
Задание 2
стр. 106.
Разберите решение в общем виде неполного квадратного уравнения вида: а • х2 + с = 0.
? Сколько корней имеет неполное квадратное уравнение вида а • х2 + с = 0? Почему?
Запишите в словарь алгоритм решения неполного квадратного уравнения вида: а • х2 + с = 0.
В случае затруднения обратись к учителю.
Практическое применение знаний
Задание 3
Реши по образцу:
стр. 108. №509 (а, д).
Проверь свои ответы по приложению 1.
Если ответы совпали, то переходи к следующему заданию.
Если допустил ошибки, вернись к уравнениям №1 и №2.
В случае затруднения обратись к учителю.
6 Физкультминутка.
УЭ-3
Изучение нового материала
(алгоритм решения неполного квадратного уравнения вида а • х2 + b • х = 0:).
Задание 1
Рассмотри образец решения уравнения:
-
Решите уравнение №3:
6х2 +12х=0
Решение.
1.Разложим левую часть уравнения на множители:
х(6х+12)=0
2.Решаем уравнение через слово «или»:
х=0 или 6х+12=0
6х= -12
х= - 2
Ответ: х1 =0, х2 = -2.
Задание 2
стр. 107.
Разберите решение в общем виде неполного квадратного уравнения вида: а • х2 + b • х = 0.
? Сколько корней имеет неполное квадратное уравнение вида а • х2 + b • х = 0? Почему?
Запишите в словарь алгоритм решения неполного квадратного уравнения вида: а • х2 + b • х = 0.
В случае затруднения обратись к учителю.
Практическое применение знаний
Задание 3
Реши по образцу:
стр. 108. №510 (в, д).
Проверь свои ответы по приложению 2.
Если ответы совпали, то переходи к следующему заданию.
Если допустил ошибки, вернись к уравнению №3.
В случае затруднения обратись к учителю.
УЭ-4
Изучение нового материала
( решение неполного квадратного уравнения вида а • х2 = 0).
стр. 107.
Разберите решение в общем виде неполного квадратного уравнения вида: а • х2 = 0.
? Сколько корней имеет неполное квадратное уравнение вида а • х2 = 0? Почему?
УЭ-5
<
4.Домашнее задание.
П.19, стр. 105-107
Знать
- определения квадратного уравнения;
- неполного квадратного уравнения;
- алгоритмы решения неполных квадратных уравнений.
№ 511
Подведение итогов урока:
-
Что нового узнали на уроке?
-
Дайте определение квадратного уравнения, неполного квадратного уравнения.
-
Своими словами расскажите алгоритмы решения каждого вида неполных квадратных уравнений.
-
Выставление оценок за урок.
Рефлексия
Дети говорят по одному предложению, выбирая начало фразы:
-
Сегодня я узнал…
-
Было интересно…
-
Было сложно…
-
Теперь я могу…
-
Я приобрел…
-
Приложение №1.
а) х1=1
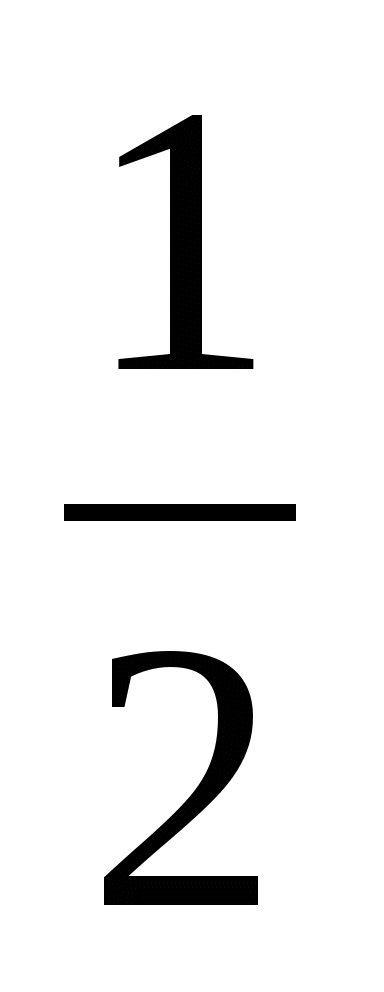 ;
х2=-1
;
х2=-1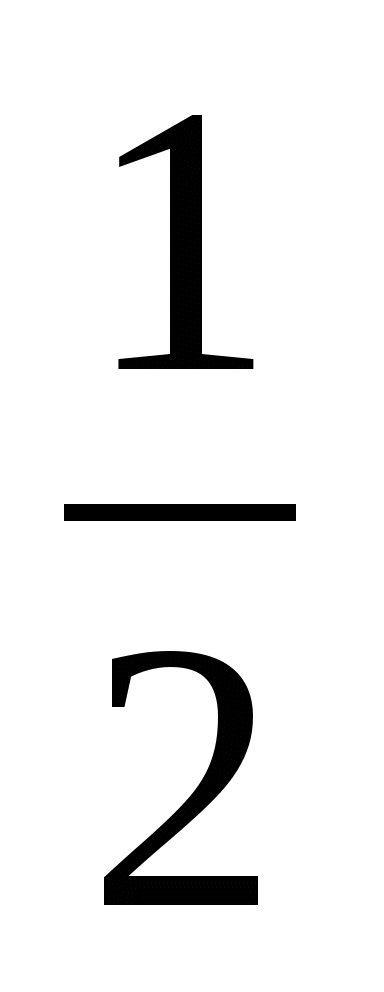
д) нет корней
Приложение №2.
в) х1=0; х2= - 0,7
д) z1=0; z2=
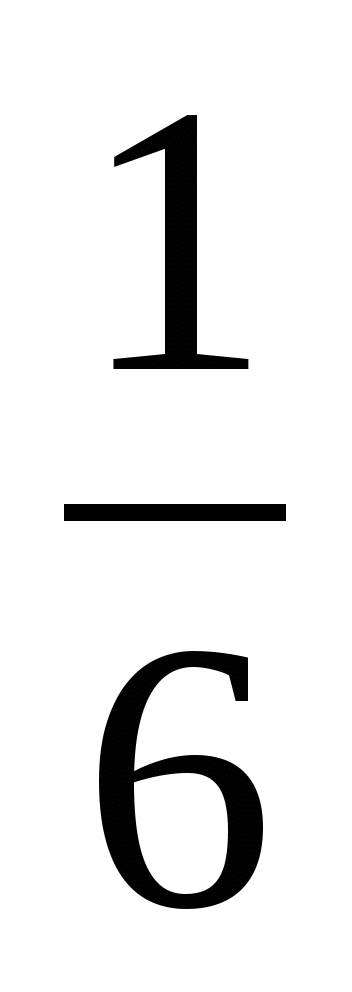
Индивидуальные карточки для коррекции знаний
Образец
Выполните упражнения по заданному алгоритму
Самостоятельно решите уравнение
Пример 1.
Решите уравнение №1:
-3х2 +27=0
Решение.
1.Перенесем свободный член в правую часть уравнения:
-3х2 = -27
2.Разделим обе части уравнения на коэффициент при х2:
х2= -27: (-3)
х2 = 9
3.Находим корни уравнения:
х1 =![]() ,
х2 =-
,
х2 =-![]() ,
,
Ответ: х1 =![]() ,
х2 =-
,
х2 =-![]() .
.
Решите уравнения:
5х2 -20=0
Решение.
1.Перенесем свободный член в правую часть уравнения:
2.Разделим обе части уравнения на коэффициент при х2:
3.Находим корни уравнения:
Ответ: х1 = , х2 = .
Решите уравнения:
-8х2 +32=0
Решение.
1.
2.
3.
Ответ:
Пример 2.
Решите уравнение №2:
5х2 +25=0
Решение.
1.Перенесем свободный член в правую часть уравнения:
5х2 = -25
2.Разделим обе части уравнения на коэффициент при х2:
х2= -25: 5
х2 = -5
Ответ: корней нет.
Решите уравнение:
6х2 +10=0
Решение.
1.Перенесем свободный член в правую часть уравнения:
2.Разделим обе части уравнения на коэффициент при х2:
Ответ:
Решите уравнение:
-х2 -9=0
Решение:
1.
2.
Ответ:
Пример 3.
Решите уравнение №3:
6х2 +12х=0
Решение.
1.Разложим левую часть уравнения на множители:
х(6х+12)=0
2.Решаем уравнение через слово «или»:
х=0 или 6х+12=0
6х= -12
х= - 2
Ответ: х1 =0, х2 = -2.
Решите уравнение:
3х2 +2х=0
Решение.
1.Разложим левую часть уравнения на множители:
2.Решаем уравнение через слово «или»:
х=0 или
Ответ: х1 =0, х2 = .
Решите уравнение:
8х2 - х=0
Решение.
1.
2.Решаем уравнение через слово «или»:
Ответ: