Конспект урока по теме Применение функции при решении задач на движение

Конспект урока по теме

«Применение функции в решении задача на движение»

Тип урока: обобщение и систематизация знаний.

Цели:

образовательные: совершенствование навыков решения задач на применение свойств функции, контроль уровня усвоения и применения знаний при решении различных видов задач;

развивающие: развитие познавательного интереса, творческой деятельности учащихся, логического мышления, интуиции.

воспитательные: воспитание самостоятельности и трудолюбия.

План урока.

1. Организационный момент

2. Актуализация знаний

3. Сообщение темы урока

4. Практическая работа

5. Задание на дом

6. Рефлексия

Ход урока

1. Организационный момент

Здравствуйте, ребята! Я рада вас видеть и очень хочу начать работу с вами! Хорошего вам настроения и успехов! Повторяем вместе со мной формулу успеха (Слайд 1):

Я в школе на уроке

Сейчас я начну учиться

Внимание мое растет

Я, как разведчик, все замечу

Память моя крепка

Голова мыслит ясно

Я хочу учиться

Я готов к работе

2. Актуализация знаний (Слайд 2)

Практика рождается из тесного

соединения физики и математики

Р. Бэкон

Роджер Бэкон говорил:

Связь двух наук физики и математики мы и увидим сегодня на уроке.

Для начала проведем небольшую интеллектуальную разминку.

(Слайд 3)

Учитель: Является ли y(x) = x + 1 функцией. Назовите зависимую и независимую переменные. Что является графиком функции?

Предполагаемый ответ: x - независимая переменная, y - зависимая переменная.

Учитель: Как может быть задана функция.

Предполагаемый ответ: графиком, формулой, таблицей.

Учитель: Как вы считаете, какой из способов задания функции является наиболее удобным.

Учащиеся предлагают варианты ответов.

Учитель: Какой вид имеет формула для нахождения пути?

Предполагаемый ответ: где время, скорость, пройденный путь.

(слайд 4). Перед вами функция, выраженная формулой: Y=2x-1

Восстановите пропуски в таблице.

3. Сообщение темы урока

А сейчас я предлагаю вам вспомнить решение задач на движение:

Задача 1 (слайд 5). Расстояние от Саранска до Москвы 637 км. Скорость автобуса, выехавшего из Саранска, равна 40 км/ч, а скорость автомобиля, выехавшего из Москвы, 60 км/ч. Какое расстояние будет между автобусом и автомобилем через три часа?

Решение: здесь недостаточно данных для решения задачи. Поэтому вопрос о расстоянии остается открытым. Каким образом можно изменить условие задачи, чтобы ее можно было решить? Какой информации не хватает в этой задаче? (ребята предлагают возможные ответы…)

Задача 2. Расстояние от села до города 180 км автомобиль проедет за 2 часа, а автобус за 3 часа. Сколько времени сэкономит человек, решивший проехать данный путь на автомобиле.

Решение: задача имеет лишнее условие.

Итак, ребята, вы видите, что не каждую задачу можно решить сразу и одним способом. Иногда нам нужно расширить условие, иногда убрать лишнее, а некоторые задачи имеют разные варианты решения, которые зависят от того, как сформулируем условие задачи. Значит вы всегда должны внимательно читать условие задачи, быть готовыми к тому, что у этой задачи может быть несколько решений, а может и не быть и ни одного. Так же, как и в жизни… когда мы сталкиваемся с проблемами.

А сейчас вернемся к словам Бэкона, с которых мы начали наш урок и попытаемся установить связь двух наук.

При изучении темы функция вы разбирали задачи на движение, которые помогали вам лучше понять эту тему, а можно ли использовать функцию и способы ее задания при решении задач на движение? Хотите этому научиться?

</ Давайте сформулируем тему нашего урока.

Запишем тему урока в тетради: «Применение функции в решении задач на движение»

4. Практическая работа

Задача 3. Автомобиль «Волга» движется по шоссе со скоростью 80 км/ч. Записать формулу, выражающую зависимость длины пути (в км) от времени (в ч). Чему равно: ? (Слайд 7)

Решение.

.

(км)

Ответ: ; 240 км, 432 км.

Задача 4. Движение автомобиля задано функцией За какое время автомобиль проедет 640 км? 800 км?(Слайд 8)

Решение.

=> . Так как то

При

Ответ: .

Мы видим, что в условии второй задачи используется функция, полученная при решении первой задачи. Т.е. на примере одной функции мы смогли найти путь, пройденный за определенный промежуток времени, а также время, за которое автомобиль пройдет определенное расстояние.

А сейчас я предлагаю вам еще одну задачу, решить которую можно блочным способом, суть которого состоит в том, что при решении более сложной задачи используются способы решения простых задач.

Задача 5 (№576). На рисунке изображены графики движения автомобиля и автобуса. Используя рисунок, ответьте на вопросы: (Слайд 9)

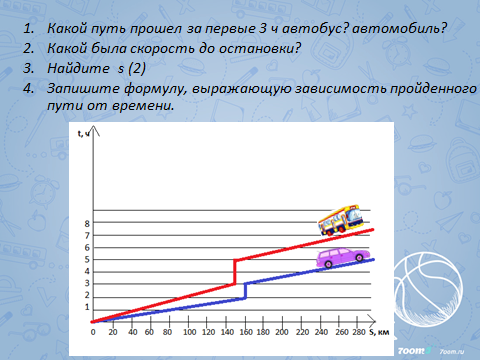
Рис. 1

1. Какой путь прошел за первые 3 ч автобус? автомобиль?

2. Какой была скорость до остановки?

3. Найдите s (2)?

4. Запишите формулы, выражающие зависимость пройденного пути от времени, для автобуса и автомобиля.

Ответ:

1. 150 км; 180 км.

2. ; .

3. 120 км; 160 км.

В данной задаче мы смогли перейти от графика функции к ее формуле.

А сейчас я попрошу вас объединиться в группы. Перед вами находится рисунок. Составьте вопросы к этому рисунку.

5. Домашнее задание

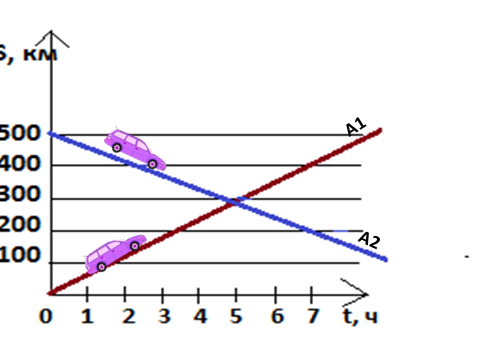
Задача 6 (№ 614 из учебника Ш. А. Алимова). Автомобили выезжают одновременно навстречу друг другу. По заданным графикам движения автомобилей найти: (Слайд 10)

1. время от начала движения автомобилей до их встречи;

2. путь, пройденный каждым из автомобилей до их встречи;

3. скорость движения каждого автомобиля.

Ответ:

1. 5 часов.

2. 350 км и 150 км соответственно автомобилями

3. 70 км/ч; 30 км/ч соответственно автомобилями

6. Рефлексия

Ребята, за небольшой отрезок времени мы с вами рассмотрели возможные варианты использования функции при решении задач на движение. Процесс познания - это движение вперед, вверх, к вершине знаний. А давайте оценим насколько каждый из вас на сегодняшнем уроке продвинулся к этой вершине. Перед вами система координат, на которой вы должны определить свою точку нахождения. Если сегодня на уроке вы ничего не поняли, то отметьте себя в точке начала координат М(0,0). Те, кто открыл для себя что-то новое, чему-то научился, но считает, что этих знаний еще недостаточно или остались вопросы - пусть отметит себя в любой точке графика. Те, кто усвоил тему полностью и готов применить полученные знания на следующих уроках, может отметить себя на высшей точке нашей горы.

Я желаю каждому из вас делать новые открытия для того, чтобы добраться до вершины знаний. Ведь …

Все в мире было бы мертво,

как будто мира самого совсем и не бывало

Когда б живое существо его не открывало!

Спасибо за активную работу!

Я была очень рада знакомству с вами.

7