ФГАОУ ВО «КРЫМСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ имени В.И. Вернадского» ГУМАНИТАРНО-ПЕДАГОГИЧЕСКАЯ АКАДЕМИЯ (ФИЛИАЛ) В Г. ЯЛТЕ

ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ

Бубнова А.А.

МЕТОДИЧЕСКОЕ ПОСОБИЕ

ПРОЕКТИВНАЯ ГЕОМЕТРИЯ

для студентов-бакалавров специальности «Математика»

Ялта, 2016

УДК 514.12(07)

ББК 22.151.54

Б 90

Рекомендовано ученым совета Гуманитарно-педагогической академии (филиал) «Крымский федеральный университет им. В.И. Вернадского» от «8» декабря 2015 года (протокол № 11)

Бубнова А.А.

Б 90 Проективная геометрия. / Бубнова А.А.:

Методическое пособие. - Ялта: РИО ГПА, 2016. - 84с.

Данное пособие предназначено для студентов математических и экономических специальностей, для учащихся старших классов, учителей школ и преподавателей вузов. Пособие содержит программный материал по проективной геометрии. Может быть использовано для подготовки к экзамену по геометрии и высшей математике.

Рецензенты:

Орлов В.Н., доктор физико-математических наук, профессор кафедры математики, теории и методики обучения математике Гуманитарно-педагогической академии (филиал) в г. Ялте «Крымского федерального университета им. В.И. Вернадского».

Овчинникова М.В., кандидат педагогических наук, доцент кафедры математики, теории и методики обучения математике Гуманитарно-педагогической академии (филиал) в г. Ялте «Крымского федерального университета им. В.И. Вернадского».

ББК 22.151.54

©Бубнова А.А., 2016 г.

©Гуманитарно-педагогическая академия (г. Ялта), 2016 г.

СОДЕРЖАНИЕ

Вступление 4

1 ПРОЕКТИВНАЯ ГЕОМЕТРИЯ 5

1.1.Построение проективного пространства 5

1.1.1.Центральное проецирование в евклидовом пространстве; 5

1.1.2. Построение проективного пространства; 8

1.1.3. Аксиомы принадлежности проективного пространства; 12

1.1.4 Аксиомы порядка проективного пространства; 15

1.1.5. Аксиома непрерывности проективного пространства. 20

1.2. Основные геометрические формы. Теорема Дезарга 21

1.2.1. Основные геометрические формы; 21

1.2.2. Принцип двойственности в проективной геометрии; 25

1.3. Координаты точки на проективной прямой 27

1.3.1. Двойное отношение четырех точек прямой и двойное отношение четырех прямых пучка; 27

1.3.2. Координаты точки на проективной прямой; 31

1.3.3. Проективные отображения форм первой ступени в координатах 34

1.4. Индивидуальные задания 50

2 НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ 54

2.1. Общие сведения про изображения фигур 54

2.1.1. Центральное проецирование; 54

2.1.2. Параллельное проецирование. 55

2.2. Метод Монжа 57

2.2.1. Понятие про метод Монжа; 57

2.2.2. Система трех плоскостей проекций; 58

2.3. Метод аксонометрии 60

2.3.1. Основные понятия аксонометрии; 60

2.3.2. Основная теорема аксонометрии. Теорема Польке-Шварца. 60

2.4. Метод основной плоскости 63

2.4.1. Основные понятия метода основной плоскости 63

2.4.2. Изображение пространственных фигур; 63

2.4.3. Сечение многогранников плоскостью. 66

2.5.Индивидуальные задания 72

3 ПРИЛОЖЕНИЯ 78

3.1.Образец выполнения контрольной работы 78

3.2.Темы рефератов 80

3.3.Вопросы на экзамен 81

ЛИТЕРАТУРА 82

Вступление

Дисциплина проективная геометрия является одной из базовых дисциплин высшей математики. Предметом проективной геометрии является изучение свойств геометрических фигур, которые сохраняются при центральном проецировании.

Понятие проективного пространства введено путем расширения евклидового пространства - дополнением его несобственными точками, несобственными прямыми и несобственной плоскостью. Построенное таким образом проективное пространство имеет все свойства, необходимые для объяснения проективных понятий. Кроме того, такой подход к построению проективного пространства дает возможность тесно связать новые понятия и теоремы проективной геометрии с соответствующим материалом евклидовой геометрии, что облегчает пониманию студентами новых проективных понятий.

Настоящее пособие призвано помочь студентам освоить фундаментальные факты проективной геометрии геометрии. Основная цель - научить студентов решать задачи. В связи с этим много примеров дано с подробным объяснением.

В пособии приведены основные теоретические сведения, которые необходимы для выполнения заданий. По каждой теме приведены примеры решения задач.

Пособие содержит две контрольных работы: по проективной геометрии и по начертательной геометрии. В приложении указаны темы рефератов и вопросы для экзамена, предложены решения контрольных работ.

1 ПРОЕКТИВНАЯ ГЕОМЕТРИЯ

1.1.Построение проективного пространства

1.1.1.Центральное проецирование в евклидовом пространстве;

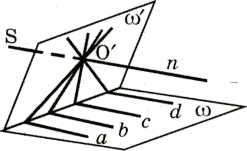
Проективная геометрия изучает свойства геометрических фигур, которые не изменяются при каком-нибудь центральном проецировании. Поэтому необходимо изучить свойства такого проецирования.

Центральное проецирование в пространстве

Пусть заданы две плоскости и точка S , которая не лежит ни в одной из этих плоскостей (рис. 1).

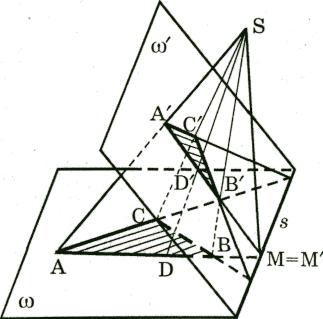Между точками этих плоскостей установим такое соответствие, что какой-нибудь точке А плоскости соответствует точка плоскости , которая является точкой пересечения прямой AS с плоскостью . Установленное таким образом соответствие между точками плоскостей называется центральным проецированием.

Точка S называется центром проецирования, точка называется центральной проекцией точки А на плоскость , прямая SA - проектирующей прямой, плоскость - плоскостью проекций.

Если в плоскости возьмем другую точку и построим ее центральную проекцию в плоскости , то отрезок - это центральная проекция отрезка АВ в плоскости . Точки пересечения плоскостей соответствуют самим себе, они называются двойными точками ( например, точка М=).

Точка D прямой АВ отображается в точку прямой .

Если в плоскости задана фигура F , все точки которой имеют образы в плоскости , то в плоскости получится фигура , которая называется центральной проекцией фигуры F.

Центральное проецирование на плоскости

Аналогично можно установить проективное соответствие между точками двух прямых на плоскости. Пусть имеем две прямые а и в плоскости . Возьмем в этой плоскости точку S, которая не принадлежит ни одной из этих прямых, за центр проектирования и будем проектировать точки прямой а на точки прямой . Например, точке А прямой а соответствует точка , точка пересечения прямой с проецирующей прямой SA. Точка - это центральная проекция точки А. Аналогично точка прямой

- это центральная проекция точки В прямой а, а прямая - центральная проекция прямой а (рис. 2).

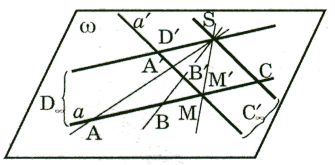
Из способа установления проективного отношения следует, что центральной проекцией точки есть точка, если она существует; проекцией прямой , что не проходит через центр проецирования, есть прямая; точки, которые лежат на одной прямой, отображаются на точки, которые лежат на соответствующей прямой; прямые, которые проходят через одну точку (пучок прямых), переходят в прямые, которые проходят через одну точку, таким образом инцидентность точек и прямых при центральном проектировании не нарушается.

Но не для каждой точки прямой а есть образ на прямой : точка , для которой проектирующая прямая SС параллельна прямой , не имеет образа, так как прямая SC не пересекает прямую . Аналогично точка прямой , для которой прямая параллельна прямой а, не есть образ никакой точки прямой а (рис. 2).

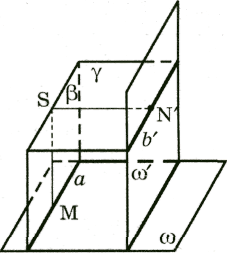
Пусть в пространстве между плоскостями установлено проективное отображение с центром S. Проведем через точку S плоскость параллельно плоскости и плоскость параллельно плоскости (рис. 3).

Тогда никакой точке М прямой а пересечения плоскостей не имеет образа на плоскости (║║), поскольку прямая SM параллельна плоскости . Все другие точки плоскости имеют образы в плоскости .

Аналогично, ни какая точка прямой пересечения плоскостей не имеет прообраз в плоскости , так как прямая параллельна плоскости и потому не имеет с этой плоскостью ни одной общей точки; все другие точки плоскости имеют прообразы в плоскости .

Таким образом, если взять фигуру F в плоскости , в состав которой входит прямая а, то ее изображение будет не полным в плоскости . С другой стороны, на изображении могут быть точки, прообразы которых нет у оригинала - это точки прямой .

Итак, проективное отображение в евклидовом пространстве не взаимно однозначно.

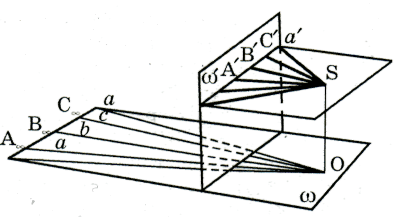
Пример 1.Дан треугольник АВС в плоскости и точка S, которая не лежит в плоскости . Построить центральную проекцию треугольника АВС в плоскости при условии, что центр S проектирования и вершина А треугольника АВС равноудалены от плоскости .

Решение. Центральной проекцией точки В будет точка , точки С - точка , стороны ВС - отрезок (рис. 4).

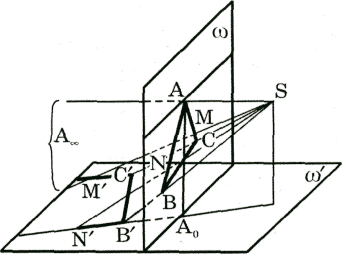
Поскольку проектирующий луч SA параллелен плоскости , то точка А не имеет в плоскости образа в виде обычной точки, образом будет бесконечно удаленная точка. Тогда . Итак, в евклидовом пространстве центральное проецирование не является взаимно однозначным.

1.1.2. Построение проективного пространства;

1. Проективная прямая

Наличие значительных недостатков отношения, которое устанавливается центральным проектированием в евклидовом пространстве, не дают возможности использовать метод центрального проектирования в полном объеме для изучения свойств фигур, которые не меняются при этом проектировании. Поэтому для изучения проективных свойств фигур евклидовое пространство необходимо дополнить некоторыми объектами так, чтобы в новом дополненном пространстве перспективное отображение было взаимно однозначным.

Впервые такое дополнение осуществил французский математик и архитектор Ж.Дезарг (1591-1661), который ввел понятие бесконечно удаленной точки и прямой.

Чтобы перспективное соответствие между точками двух прямых (смотри рис.2) стало взаимно однозначным, необходимо, чтобы прямая SC, параллельная прямой , теперь имела с ней общую точку, то есть надо допустить, что параллельные прямые пересекаются. За точку пересечения параллельных прямых договорились считать бесконечно удаленную точку этих прямых, то есть прямая дополняется бесконечно удаленной точкой, которую обозначают символом «», точкою .

Аналогично, прямую а дополняют бесконечно удаленной точкой как точку пересечения параллельных прямых а и . Бесконечно удаленную точку еще называют несобственной точкой.

Определение 1. Несобственной точкой называют общую точку параллельных двух прямых.

Итак, пучок параллельных прямых имеет одну общую несобственную точку (рис. 5).

Определение 2. Евклидова прямая, дополненная несобственной точкой, называется проективной прямой.

2.Проективная плоскость

Введем понятие несобственной прямой.

На евклидовой плоскости можно провести бесконечно много прямых разных направлений через какую-нибудь точку плоскости. Каждую из этих прямых дополняем несобственной точкой, их будет бесконечно много. Пусть на плоскости имеем прямые а, в, с, …, им принадлежат несобственные точки , соответственно. Выберем точку S за центр проектирования (рис. 6).

Чтобы провести луч до несобственной точки , надо провести прямую , где - точка пересечения плоскости с лучом . Аналогично, получим точки и т. д. в плоскости как точки пересечения с плоскостью лучей Все проектирующие лучи параллельны плоскости , поэтому они лежат в плоскости, которая пересекает плоскость по прямой, на которой лежат точки . Точки этой прямой - это центральные проекции несобственных точек прямых а, в, с,… разных направлений плоскости .

Итак, геометрическое место образов плоскости несобственных точек прямых а, в, с,… разных направлений плоскости есть собственная прямая плоскости . Поскольку построенное соответствие с несобственными точками будет взаимно однозначным, то все несобственные точки прямых плоскости должны лежать на одной прямой, которую называют бесконечно удаленной прямой или несобственной прямой.

Определение 3. Несобственной прямой плоскости называется множество всех несобственных точек данной плоскости.

Следствие. Параллельные плоскости пересекаются по несобственной прямой. Пучок параллельных плоскостей имеет одну общую несобственную прямую.

Определение 4. Евклидова плоскость, дополненная несобственной прямой, называется проективной плоскостью.

Определение 5. Множество всех несобственных точек и всех несобственных прямых называется несобственной плоскостью.

Каждая собственная прямая с несобственной плоскостью имеет одну общую точку - несобственную точку прямой. Каждая собственная плоскость имеет с несобственной плоскостью одну общую прямую - несобственную прямую плоскости. Других несобственных точек, не принадлежащих несобственной плоскости, в пространстве не существует.

3.Проективное пространство

Определение 6. Евклидово пространство, дополненное несобственными точками, несобственными прямыми и несобственной плоскостью, называется проективным пространством.

Построение проективного пространства с помощью дополнения евклидового пространства несобственными элементами есть одна из моделей проективного пространства. Эту модель еще называют основной моделью проективного пространства.

Несобственные элементы пространства определяют с помощью собственных элементов, а именно:

1)несобственная точка может быть задана собственной прямой а, или какой-нибудь прямой пучка параллельных прямых;

2)несобственная прямая может быть задана собственной плоскостью , которой она принадлежит, а также с помощью какой-нибудь плоскости, которая входит в состав пучка параллельных плоскостей. Несобственную прямую можно задать также с помощью двух несобственных точек, которые задаются двумя непараллельными прямыми.

Задача 1. Даны две несобственные точки прямыми, что не пересекаются, и собственная точка С. Построить плоскость, которой принадлежат точки .

Решение. Плоскость однозначно определяется тремя точками, которые не лежат на одной прямой. Несобственные точки заданы прямыми а и в, которые не пересекаются, поэтому прямые а и в скрещиваются.

Чтобы построить плоскость, проведем через точку С прямую , параллельно прямой а, и прямую , параллельно прямой в. Прямые , которые пересекаются в точке С и определяет искомую плоскость.

1.1.3. Аксиомы принадлежности проективного пространства;

1.Основные объекты и отношения проективной геометрии

Основными объектами проективной геометрии есть точки, проективные прямые и проективные плоскости проективного пространства.

Основными отношениями между основными объектами есть отношение принадлежности, отношение порядка и отношение непрерывности.

Поскольку в проективной геометрии не сохраняются метрические свойства фигур, а также отсутствует понятие параллельности, то отсутствуют соответствующие группы аксиом.

Система аксиом проективной геометрии складывается из трех групп:

1) принадлежности; 2) порядка; 3) непрерывности.

Проективная прямая и проективная плоскость отличаются от соответствующих понятий евклидовой геометрии наличием несобственных элементов, поэтому формулировки аксиом, которые лежат в основе проективной геометрии, отличаются от аксиом евклидовой геометрии большей общностью.

2. Аксиомы принадлежности проективной геометрии

В аксиомах принадлежности называются три основных отношения, которые связывают точки, прямые и плоскости: принадлежность точки прямой, принадлежность точки плоскости, принадлежность прямой плоскости.

В аксиомах 1.1-1.8 евклидовой геометрии идет речь лишь о тех свойствах точек, прямых и плоскостей, которые являются инвариантами центрального проектирования.

Но аксиомы принадлежности проективной геометрии удобней дать по другому, более общую формулировку.

1 группа. Аксиомы принадлежности

Н.1. Две различные точки А и В всегда принадлежат одной и только одной прямой.

Н.2. Две различные плоскости всегда принадлежат одной и только одной прямой.

Н.3. Точка А и прямая а, которая ей не принадлежит, всегда принадлежат одной и только одной плоскости.

Н.4. Плоскость и прямая а, которая ей не принадлежит, всегда принадлежат одной и только одной точке.

Н.5. Существует, по крайней мере, четыре точки, которые не принадлежат как одной прямой, так и одной плоскости.

Н.6. Если точка А принадлежит прямой а, а прямая а принадлежит плоскости , то точка А принадлежит плоскости .

Сформулированные аксиомы принадлежности справедливы как для собственных, так и для несобственных объектов, так что имеют большее значение, чем соответствующие аксиомы евклидовой геометрии.

Следствия из аксиом принадлежности

1.Три различные точки А, В и С, которые не принадлежат одной прямой, принадлежат одной и только одной плоскости.

По аксиоме Н.1 существует прямая АВ, которой принадлежат точки А и В. Так как точка С не принадлежит прямой АВ, то по аксиоме Н.3 прямая АВ и точка С определяют одну и только одну плоскость, которой принадлежат точки А, В, С.

2. Три различные плоскости , которые не принадлежат одной прямой, принадлежат одной и только одной точке.

Справедливость этого утверждения выходит из того, что по аксиоме Н.2 существует прямая а, которая принадлежит плоскостям , причем плоскость не принадлежит прямой а. По аксиоме Н.4 существует единственная точка А, которая принадлежит прямой а и плоскости . Итак, эта точка А принадлежит всем трем плоскостям, поскольку по аксиоме Н.6 точка А принадлежит плоскостям .

3.Если две точки прямой принадлежат плоскости, то и все другие точки прямой принадлежат этой плоскости.

Это следствие докажем методом от противного. По условию две точки А и В принадлежат плоскости . Допустим, что прямая АВ не принадлежит плоскости .Тогда по аксиоме Н.4 существует одна и только одна точка, которая принадлежит прямой а и плоскости . А это противоречит условию, поэтому допущение не верно.

4.Если две плоскости принадлежат одной точке, то и их общая прямая принадлежит этой точке.

Пусть А - общая точка двух плоскостей , существование вытекает из аксиомы Н.2. Допустим, что прямая а не проходит через точку А. Тогда по аксиоме Н.3 существует плоскость, которая определяется прямой а и точкой А, а это противоречит условию.

5.Существует четыре плоскости, которые не принадлежат одной прямой и не принадлежат одной точке.

Справедливость этого утверждения выходит из того, что по аксиоме Н.5 существуют четыре точки, которые не принадлежат как одной прямой, так и одной плоскости. Ни одна из троек не принадлежит одной прямой, так как в противном случае, с последней четвертой точкой эта прямая определяла бы плоскость, которой принадлежали бы все четыре точки.

Существует много других следствий из аксиом принадлежности проективного пространства, на которых мы остановимся дальше. Аксиомы принадлежности и их следствия используются для решения задач, доказательства теорем.

Задача 1. Даны две несобственные точки прямыми, что не пересекаются, и собственная точка С. Построить плоскость, которой принадлежат точки .

Решение. Плоскость однозначно определяется тремя точками, которые не лежат на одной прямой. Несобственные точки заданы прямыми а и в, которые не пересекаются, поэтому прямые а и в скрещиваются.

Чтобы построить плоскость, проведем через точку С прямую , параллельно прямой а, и прямую , параллельно прямой в. Прямые , которые пересекаются в точке С и определяет искомую плоскость.

1.1.4 Аксиомы порядка проективного пространства;

Отношение порядка точек на проективной прямой

Отношение порядка точек на проективной прямой определяется свойствами проективной прямой, которые значительно отличаются от свойств евклидовой прямой.

1. Проективная прямая есть замкнутая линия.

Это свойство можно объяснить следующими пояснениями. Пусть имеем прямую s и точку S, которая не лежит на прямой s. Возьмем точку S за центр пучка прямых S(a, b, c, …) и установим соответствие между прямыми пучка S и точками прямой s, считая образом прямой точку пересечений этой прямой с прямой s. Такое соответствие между прямыми пучка S и точками прямой s называется перспективним соответствием.

Например, точка А прямой s соответствует прямой SA и наоборот. Поскольку проективная прямая - это евклидова прямая, дополненная несобственной точкой, перспективное соответствие между пучком прямых S(a, b, c, …) и точками прямой s будет взаимно однозначным. Луч n пучка S, параллельный прямой s, соответствует несобственной точке прямой s - (рис. 7).

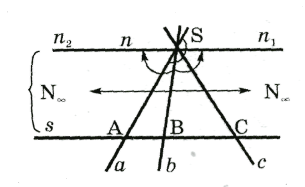
Все прямые пучка получим поворотом одной из прямых пучка на . Поворачивая луч SA против часовой стрелки, получим луч , параллельный s, в этом случае лучу соответствует точка прямой

Аналогично, поворачивая луч SA по часовой стрелке, достигаем положение луча прямой n, параллельной прямой s, которой соответствует несобственная точка. Поскольку прямая s имеет только одну несобственную точку, то это будет точка . Итак, проективная прямая замыкается в своей несобственной точке.

2. Проективная прямая двумя своими точками разбивается на два отрезка.

Известно, что евклидова прямая двумя своими точками разбивается на три части: отрезок и два луча. Поскольку проективная прямая - это замкнутая линия, то какая-нибудь точка не разбивает ее на части, а лишь разрезает, размыкает. На проективной прямой собственная и несобственная точки равноправны, поэтому отрезки АВ и тоже равноправны.

3. Понятие «отрезок прямой» есть инвариант центрального проектирования, то есть проективным понятием.

Рассмотри дальше расположение точек на проективной прямой. Известно, что в евклидовой геометрии принадлежность точек отрезку устанавливается отношением «лежать между».

При перспективном отображении это отношение ни есть инвариантом, поэтому не рассматривается в проективной геометрии.

Основным отношением, на котором основывается отношение порядка точек проективной прямой, есть разделяемость двух пар разных точек прямой. На рис. 8 пара точек (А,В) прямой s разделяется парой точек (С,Д).

При центральном проектировании прямой s на прямую с центром S получаем на прямой точки Точки поменялись местами относительно точек С и D на прямой s: точка С лежала между А и В, а точка не лежит между точками ; точка D не лежит между точками А и В, а точка лежит между точками Но и на прямой s пара (А,В) разделяет пару (С,D), и на прямой пара разделяет пару

4. Разделяемость ( или неразделяемость ) двух пар точек одной прямой есть инвариант при каком-нибудь проективном отображении этой прямой на другую прямую.

Аксиомы порядка проективной геометрии

В аксиомах порядка устанавливаются свойства разделяемости ( неразделяемости ) двух пар точек проективной прямой. Группу аксиом порядка сформулируем такими утверждениями.

П.1. Две разные точки А и В прямой разбивают все другие точки этой же прямой на два класса.

Определение 7. Каждый из классов, дополненных точками А и В, называется отрезком.

Определение 8. Если точки С и D принадлежат разным классам относительно точек А и В, то пары точек (А,В) и (С, D) называются разделяемыми. Пишут (С,D).

Если точки С и D принадлежат одному классу, то пары точек (А, В) и (С, D) называются неразделяемыми. Пишут: (А, В) (С, D).

П.2. Если (А, В) (С, D), то и (C, D) (A, B).

П.3. Какие-нибудь четыре точки прямой можно только одним способом разбить на пары разделяемых.

П.4. Центральное проецирование переводит две разделяемых пары в две разделяемые пары.

Задача 2. Даны пять точек проективной прямой А, В, С, D, E. С помощью аксиом порядка доказать, что если пара (А, В) разделяет пару (С, D) и пара (А, В) не разделяет пару (D,E), то пара (А, В) разделяет пару (С, Е).

Решение. По условию задачи пара точек (А, В) (С, D), поэтому точки С и D лежат в разных классах, на которые разбили прямую точки А и В. Пусть и . Кроме того, пара(А, В) (D, E), поэтому точки D,E лежат в одном классе. Пусть . Итак, точка , то есть пара (А, В) (, Е).(рис. 9)

Свойства отношения порядка на проективной плоскости

1. Какая-нибудь прямая а проективной плоскости не разбивает ее на две области.

1. Две прямые проективной плоскости разбивают ее на две области.

2. 
   
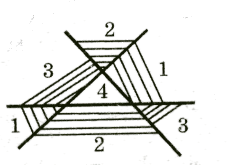
   Три прямые проективной плоскости разбивают ее на четыре области, (рис. 10).

3. 
   
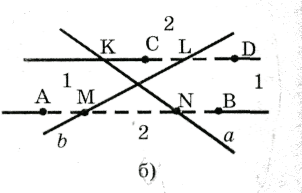
   Проективная плоскость является замкнутой и односторонней.

1.1.5. Аксиома непрерывности проективного пространства.

Отношение непрерывности проективного пространства

Аксиом первых групп - принадлежности и порядка не достаточно для изучения всех свойств проективного пространства, их необходимо дополнить аксиомой непрерывности, поскольку отношение непрерывности не вытекает из аксиом принадлежности и порядка. Такой аксиомой может быть проективная форма аксиомы Дедекинда (1831-1916).

Д.1. Пусть все точки отрезка АВ разбиты на два класса, причем точка А принадлежит первому, а точка В - второму классу. Обозначим через М произвольную точку первого класса, отличную от точки А, а через N - точку второго класса, отличную от В. Если для какой-нибудь пары точек М и N справедливо условие то существует такая точка С отрезка АВ, которая принадлежит одному из классов такая, что для всех точек М и N, отличных от точки С.

На основе сформулированных аксиом трех групп - принадлежности, порядка и непрерывности - можно самостоятельно построить проективное пространство и изучать его свойства.

1.2. Основные геометрические формы. Теорема Дезарга

1.2.1. Основные геометрические формы;

1. Основные геометрические формы

Основные геометрические формы проективной геометрии формируются по ступеням. К одной форме принадлежат те формы, между которыми можно установить взаимно однозначное соответствие.

Формы первой ступени

1.Прямолинейный ряд точек - это множество всех точек, которые принадлежат одной прямой, называется носителем ряда, и обозначают s(A, B, C, D, …), где s - дання прямая, А, В, С, … - точки на ней, (рис.11).

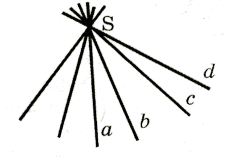
2..Пучок прямих - это множество всех прямых данной плоскости, которые принадлежат данной точке, которая называется носителем или центром пучка, обозначают S(a, b, c, d,…), (рис.12).

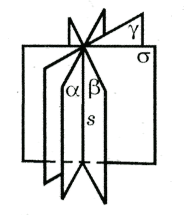
3.Пучок плоскостей - это множество всех плоскостей, которые принадлежат одной прямой, которая называется носителем пучка, или осью, обозначают , (рис.13).

Формы второй ступени

1. Плоское поле точек - это множество всех точек данной плоскости, которая называется носителем. Обозначается

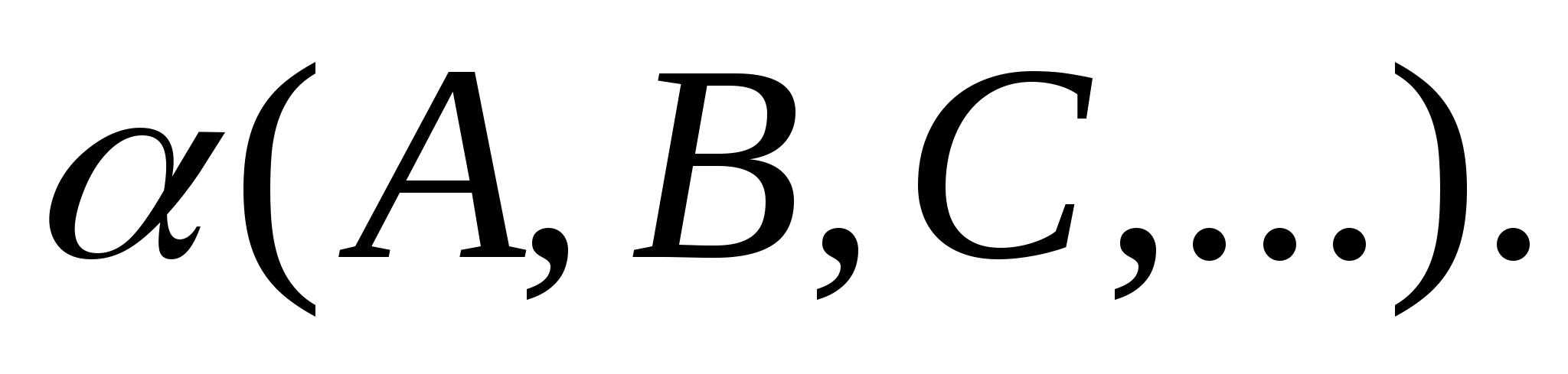
2. Плоское поле прямых - это множество всех прямых данной плоскости, которая называется носителем этого поля. Обозначается .

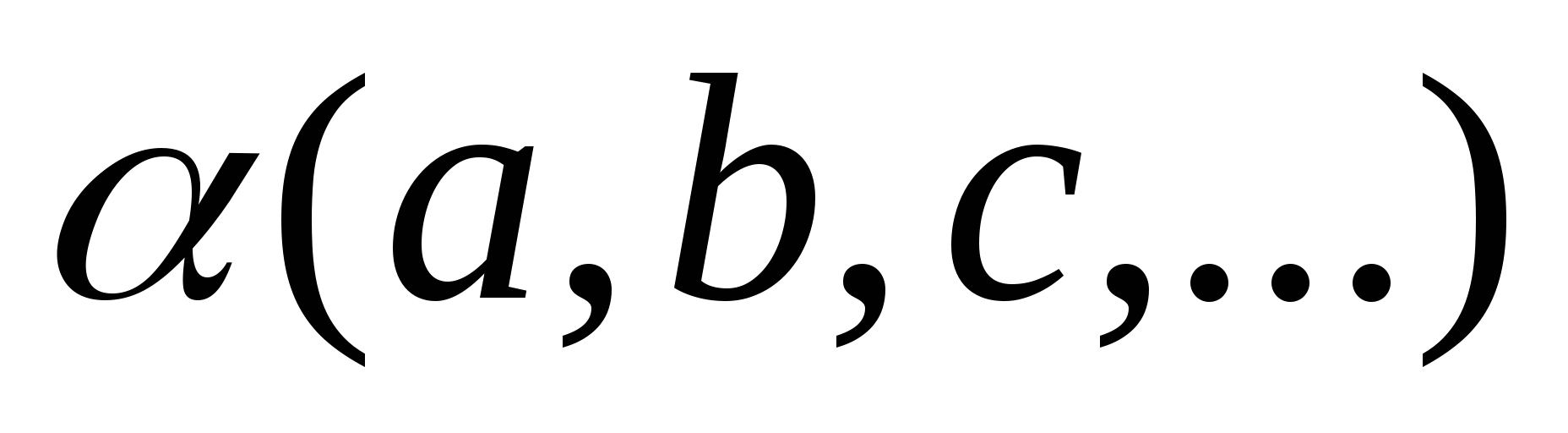3. Связка прямых - это множество всех прямых пространства, которые принадлежат данной точке, которая называется носителем, или центром связки.

4. Связка плоскостей - это множество всех плоскостей, которые принадлежат данной точке, которая называется носителем, или центром связки.

Формы третьей ступени

1.Пространство точек - это множество всех точек проективного пространства, которое играет роль носителя точек.

2.Пространство плоскостей - это множество всех плоскостей проективного пространства, которое является носителем плоскостей.

2. Теорема Дезарга

Одна из основных теорем проективной геометрии названа именем Ж . Дезарга (1591-1661) - французского математика и архитектора, основоположника проективной и начертательной геометрии.

Теорема Дезарга. Если три прямые, которым принадлежат соответствующие вершины двух данных треугольников, принадлежат одной точке, то три точки, принадлежащие парам соответствующих сторон этих треугольников, принадлежат одной прямой.

Доказательство.

Доказательство теорема рассмотрим для двух случаев.

1.Пусть два данных треугольника АВС и расположены в разных плоскостях , которые пересекаются по прямой s. Прямые пересекаются в точке S (рис. 14).

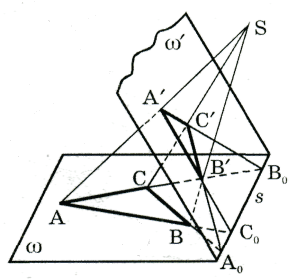
Можно считать, что треугольник - это образ треугольника АВС в проективном отображении с центром в точке S.

Прямые определяют плоскость , в которой лежит стороны АВ и данных треугольников, поэтому эти прямые, пересекаются в некоторой точке , которая принадлежит трем плоскостям - . Аналогично, докажем, что точка пересечения прямых точка принадлежит трем плоскостям - , а точка пересечения прямых точка принадлежит трем плоскостям . Итак, точки пересечения соответствующих сторон лежат одновременно в плоскостях , поэтому эти точки принадлежат прямой s пересечения плоскостей.

Теорема доказана.

Теорема, обратная теореме Дезарга. Если три точки, которые принадлежат соответствующим сторонам двух данных треугольников, принадлежат одной прямой, то три прямые, принадлежащие парам соответствующих вершин этих треугольников, принадлежат одной точке.

Доказательство. Пары соответствующих сторон данных треугольников АВС и образуют три плоскости: - плоскость , - плоскость , - плоскость , которые имеют общую точку S, то есть, образовался трехгранник с вершиной в точке S (рис. 14). Плоскости попарно пересекаются, образуя прямые , которые являются ребрами трехгранника, а значит, пересекаются в его вершине S.

Теорема доказана.

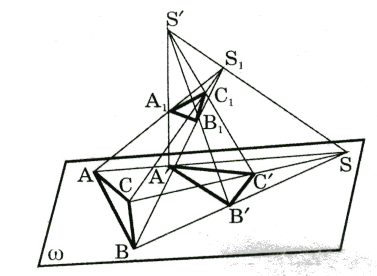
Даны треугольники , которые лежат в одной плоскости

(рис. 15).

Прямые пересекаются в одной точке S. Возьмем точку , которая не принадлежит плоскости , и на прямой возьмем точку , отличную от точек . Проведем прямые . Прямые принадлежат плоскости , поэтому пересекаются в точке . Аналогично получаем точки . Точки являются образами точек при центральном проектировании с центром в точке . Треугольники лежат в разных плоскостях и удовлетворяют условиям теоремы Дезарга в первом случае. Тогда точки пересечения пар прямых лежат на одной прямой.

При проектировании с точкой на плоскость отрезки перейдут в отрезки , а точки P,Q,R отрезки ВС, АСБ АВ останутся неизменными, поскольку лежат в плоскости . Поэтому точками пересечения прямых будут точки P,Q,R, которые лежат на одной прямой.

Теорема доказана.

1.2.2. Принцип двойственности в проективной геометрии;

Анализируя формулировки аксиом принадлежности, основных геометрических форм проективного пространства и следствия из них, легко заметить симметричность выражений относительно слов «точка» и «плоскость». Например, аксиому Н.2 получаем из аксиомы Н.1, заменив слово «точка» словом «плоскость». Аналогично, получаем аксиому Н.4 из аксиомы Н.3, при этом в обоих случаях слово «прямая» осталось без изменений. Такая же симметрия существует в определениях основных форм проективного пространства. Например, прямолинейный ряд точек - это множество всех точек, которые принадлежат одной прямой. Заменив слово «точка» на слово «плоскость», получим определение пучка плоскостей как множество всех плоскостей, который принадлежат одной прямой.

Этот факт в проективной геометрии известен под названием принципа двойственности в пространстве, который формулируется так.

Если в каком-нибудь истинном утверждении про принадлежность основных элементов проективного пространства (точек, прямых, плоскостей) всюду слово «точка» заменить словом «плоскость» и слово «плоскость» - словом «точка», а слово «прямая» оставить без изменений, то получим также истинное утверждение в проективном пространстве.

Принцип двойственности в пространстве еще называют большим принципом двойственности. Принцип двойственности имеет место и на плоскости. Его называют малым принципом двойственности на плоскости.

Если в каком-либо истинном утверждении про принадлежность основных элементов проективной плоскости (точек и прямых) всюду слово «точка» заменить словом «прямая», слово «прямая» - словом «точка», то получим истинное утверждение на проективной плоскости.

1.3. Координаты точки на проективной прямой

1.3.1. Двойное отношение четырех точек прямой и двойное отношение четырех прямых пучка;

1. Двойное отношение четырех точек прямой

К формам первой ступени принадлежит прямолинейный ряд точек, пучок прямых и пучок плоскостей. Наиважнейшим из них и одновременно наипростейшим является прямолинейный ряд точек.

Для установления порядка точек на прямой было введено понятие разделяемости (неразделяемости ) двух пар точек прямой. Поэтому четыре точки прямой, их двойное отношение, играют важную роль в установлении проективных свойств форм первой ступени.

Простое отношение трех точек А, В и С евклидовой прямой определяется как отношение двух отрезков АС и ВС и записывается

Простое отношение трех точек прямой есть инвариант при параллельном проектировании.

Инвариантом центрального проектирования есть так называемое двойное отношение четырех точек.

Определение 9. Двойным отношением четырех точек прямой называется отношение двух простых отношений:

Пара точек (А,В) называется основной парой, а пара (С,Д) - разделяющей парой.

Свойства двойного отношения четырех точек прямой

1. Если , то

Доказательство. Так как пара точек (А,В) разделяется парою (С,Д), то точки С и Д принадлежат разным отрезкам, образованным точками А и В. Пусть точка С принадлежит отрезку АВ, а точка Д - отрезку (рис. 16).

рис.16

Тогда простое отношение (АВ, С) (так как отрезки АС и ВС противоположно направлены), а отношение (отрезки одинаково направлены). Итак, .

2. Если , то

Доказательство. Если то точки С и Д принадлежат одному из отрезков - или АВ или . В обоих случаях простое отношение точек А, В, С, одного знака,

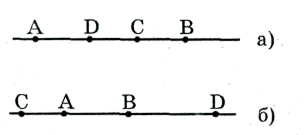(рис. 17а, б)

Рис.17

3.Величина двойного отношения не изменится, если пары поменять местами:

4.Величина двойного отношения не изменится, если переставить буквы в обеих парах:

5.Двойное отношение изменит свою величину на обратную, если поменять порядок букв только в одной паре: .

6.При перестановке средних или крайних букв величина двойного отношения четырех точек прямой получает значение, равное дополнению первой до единицы:

Поэтому будем иметь всего шесть разных по значению двойных отношений.

Если обозначим , то получим шесть случаев:

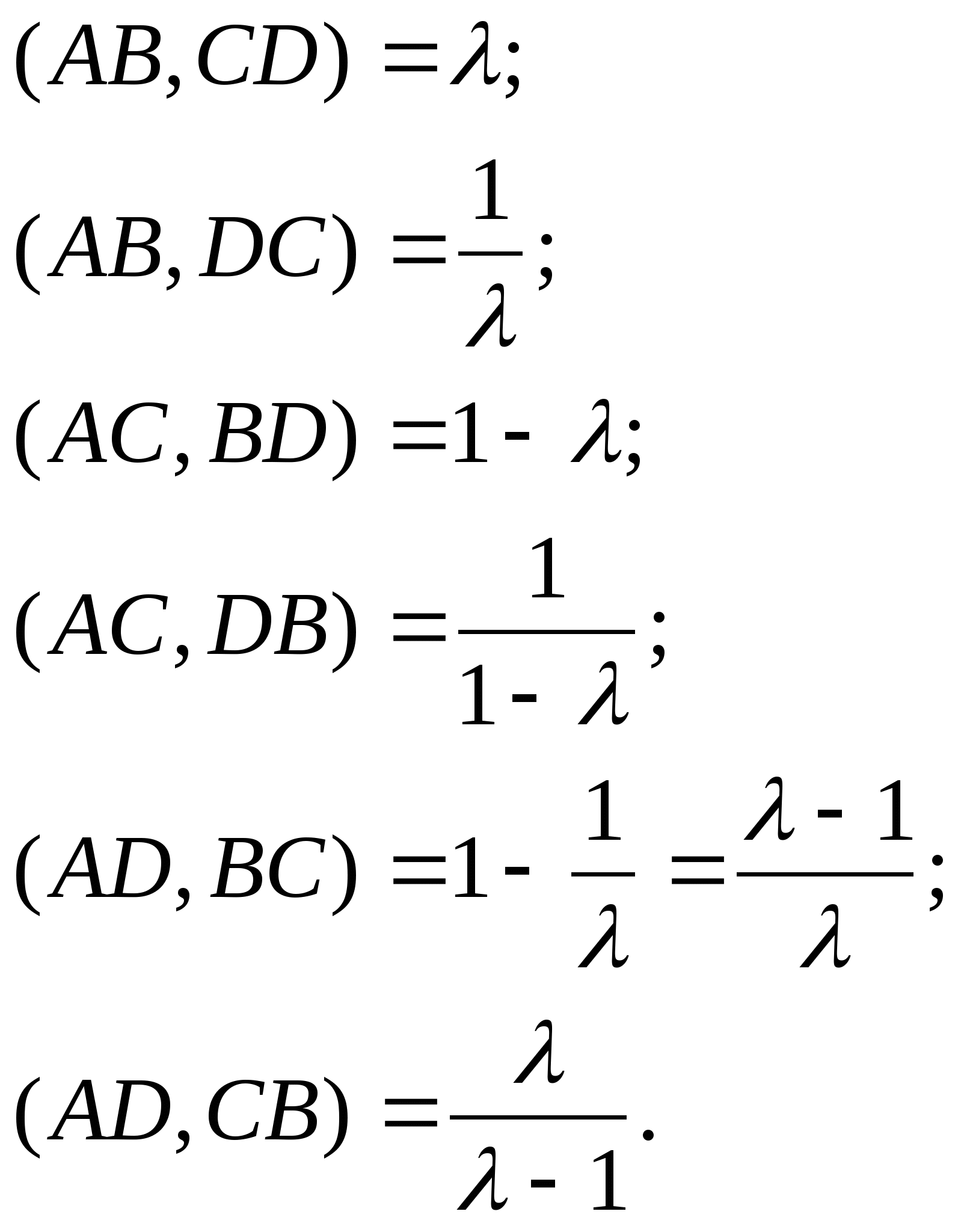
Пример 2. Даны четыре точки A, B, C, D прямой s такие, что расстояния между ними равны. Вычислить все значения, которые может принимать двойное отношение этих точек.

Решение. Обозначим расстояние между точками через а:

Тогда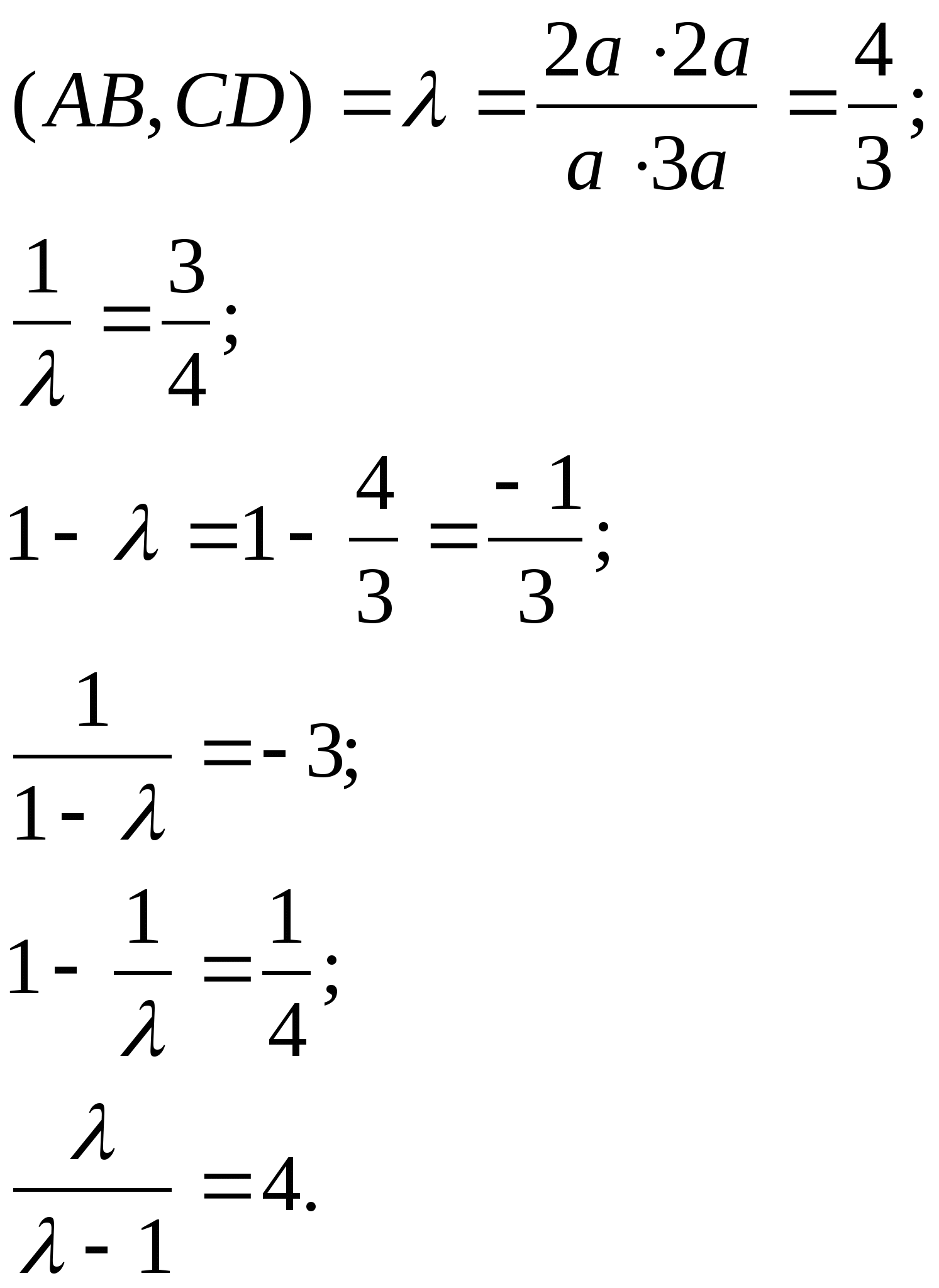

2. Двойное отношение четырех прямых пучка

Понятие пучка прямых есть двойственное понятие ряду точек по малому принципу двойственности. Поэтому понятие двойного отношения четырех прямых пучка можно ввести аналогично понятию двойного отношения четырех точек прямой.

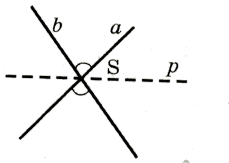Пусть имеем две произвольные прямые а и в пучка с центром в точке S. Какие-либо две прямые образуют два угла (две пары равных вертикальных углов). Проведем еще одну прямую р пучка и договоримся выбирать тот из углов, образованных двумя прямыми, который не содержит прямую р. Смотри рис. 19.

Рис.19

В таком способе выбранному углу присваиваем знак «+» или «-» в зависимости от того, сходится порядок его сторон с направлением против часовой стрелки или с направлением по часовой стрелке. Обозначим величину угла между прямыми а и в символом Возьмем три произвольных прямых а, в, с пучка с центром в точке S.

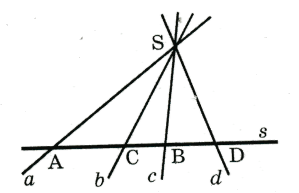
Определение 11. Простым отношением трех прямых пучка называют величину

Пара прямых (а, в) называется основой или базовой, а прямая с - разделяющей (рис 20).

Рис.20

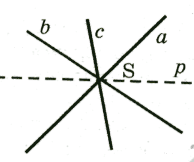В связи с договоренностью про знак угла простое отношение трех прямых а, в, с пучка будет отрицательным, если прямая с принадлежит углу (а, в).

Пусть a, b, c, d - четыре прямые пучка с центром в точке S.

Определение 12. Двойным отношением четырех прямых пучка называется величина

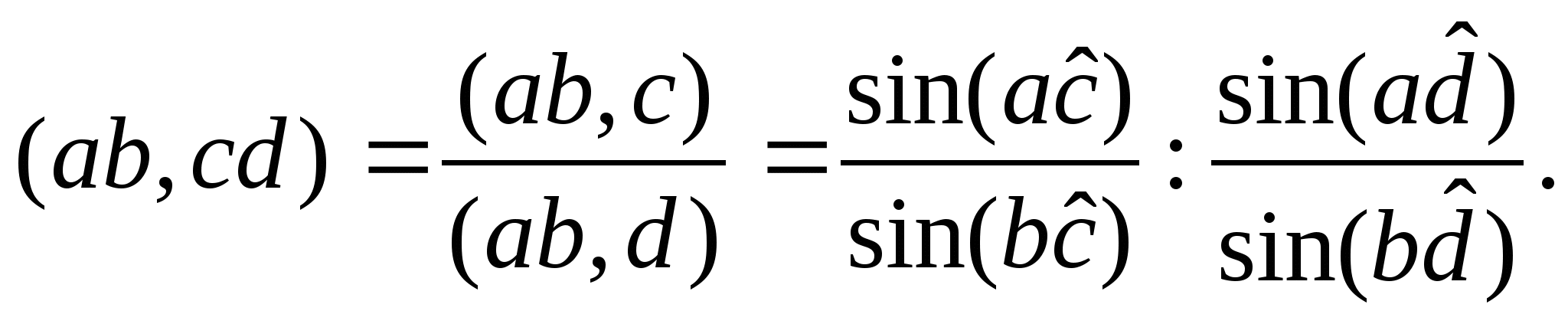
В двойном отношении (а в, c d) первая пара называется основной, или базовой, а вторая пара - разделяющей (рис. 21).

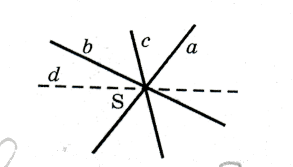Рис.21

Из малого принципа двойственности двойное отношение четырех прямых пучка имеют такие же свойства, что и двойное отношение четырех точек прямой.

Понятие двойного отношения четырех прямых пучка является инвариантным при центральном проектировании.

1.3.2. Координаты точки на проективной прямой;

Теорема 1. Если точки А, В, С - три фиксированные точки прямой, а точка Д перемещается по прямой, то каждому положению точки Д соответствсвует только одно значение двойного отношения (АВ, СД).

Доказательство. Допустим противоположное: пусть двум разным положениям точки соответствуют равные значения двойного отношения при фиксированных А, В, С так, что или . Тогда

НО полученное равенство можно лишь тогда, когда точки совпадают. Таким образом, предположение не верно.

Теорема доказана.

На основании доказанной теоремы можно ввести координаты точки на прямой.

Определение 10. Координатой точки Д, которая определяет положение точки на прямой при фиксированных точках А, В, С на этой прямой, называется двойное отношение четырех точек прямой

Рассмотрим различные случае для . Если точка Д совпадает с точкой С, то имеем:

Если точка Д совпадает с точкой В, то имеем:

Если точка Д совпадает с точкой А, то этот случай можно рассмотреть как предельный, то есть

Итак, фиксированные точки В, С, А имеют, соответственно, координаты 0, 1, Смотри рис. 18.

Рис.18

Три произвольные разные точки А, В, С прямой а, взятые в определенном порядке, образуют на ней проективный репер (АВС); точка А при этом называют первой точкой репера, ей соответствует координата , точка В - его вторая точка, ей соответствует координата 0, С - его третья точка, ей соответствует координата 1. С помощью репера каждой точке Д прямой а ставится в соответствие единственное действительное число х, которое называется неоднородной проективной координатой точки Д относительно выбранного репера.

На ряду с неоднородной проективной координатой точки вводят так называемую однородную проективную координату точки.

Пусть точка Д прямой а имеет неоднородную координату х, ее однородные координаты определяются равенством , в котором хотя бы одна из координат отлична от нуля. Записывают: Тогда первая точка А репера имеет координаты (1:0), вторая точка репера В имеет координаты (0:1), третья точка репера С - (1:1), произвольная точка Очевидно, что при каком-либо действительном числе поэтому точки с координатами совпадают.

Задача 2. Даны три точки А(-1), В(3), С(2) относительно декартовой системы координат на прямой. Найти координаты четвертой точки Д, если (АВ, СД)=-2.

Решение. По условию задачи

Отсюда В однородных координатах

Задача 3. Найти двойное отношение (АВ, СД) четырех точек прямой А(0), В(1), С(-2), Д(4), заданных декартовыми координатами.

Решение. По условию задачи

Пара точек (С,Д) не разделяет пару (А,В).

1.3.3. Проективные отображения форм первой ступени в координатах

1. Проективные ряды (и пучки) с общим носителем

Пусть имеем два проективных ряда точек

Если совместить носители этих рядов - прямые , то получим два проективных ряда точек с общим носителем, который обозначим буквой u:

Аналогично вводится понятие двух проективных пучков с общим носителем. Общим носителем двух пучков есть их центр.

При совмещении носителей двух проективных рядов или пучков часть соответствующих элементов может совпасть. Каждый элемент двух форм первой ступени с общим носителем, что совпадает со своим соответствующим элементом, называется двойным. Если все точки одного ряда совпадают с соответствующими точками другого ряда или все прямые одного пучка - с соответствующими прямыми другого пучка, то имеем тождественное отображение двух рядов или двух пучков.

Рассмотрим лишь нетождественные ряды точек. Ответ на вопрос, сколько двойных точек могут иметь два нетождественных проективных ряда точек общим носителем, дает теорема Штаудта.

Теорема 5. (Штаудта). Два нетождественных проективных ряда точек с общим носителем может иметь не больше двух двойных точек.

Доказательство. Пусть два проективных ряда с общим носителем u, причем совпадают три пары точек - и и . По свойствам проективных рядов для какой-нибудь другой пары точек имеет место равенство или по данным допущениям В последнем равенстве по теореме 1. выходит, что D совпадает с . Поскольку пара - произвольна, то все соответствующие пары данных рядов совпадают. Тогда эти ряды тождественны, что противоречит условию.

Теорема доказана.

Аналогичное утверждение имеет место для других форм первой ступени, их получают по малому или большому принципу двойственности.

Из теоремы Штаудта вытекает, что два проективных ряда точек с общим носителем могут иметь или два двойных элемента, или один, или ни одного.

В существовании каждого из этих случаев убедимся на примерах.

Задача 6. Построить проективное соответствие двух рядов с общим носителем, который имеет две двойные точки.

Построение. Пусть имеем прямолинейный ряд точек s(A, B, C, ) (рис. 28).

Рис.28

Спроектируем его на прямую u, которая пересекает прямую s в точке Х, из двух центров , выбранных так, что прямая пересекает прямую u в точке Y.

На прямой u получаем два проективных ряда точек:

.

Понятно, что эти два ряда точек имеют две двойных точки X,Y, которые принадлежат как одному ряду, так и другому.

Задача 7. Построить проективное соответствие двух рядов с общим носителем, которое имеет одну двойную точку.

Построение. Построение выполняется аналогично предыдущему. Но центры выберем так, чтобы прямая проходила через точку Х пересечения прямой s c прямой u (рис 29).

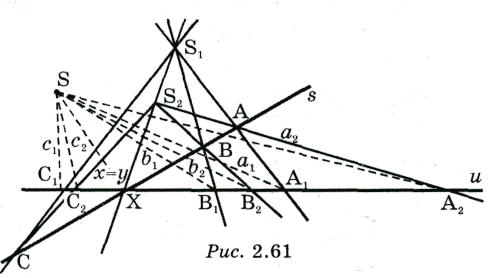рис.29

Задача 8. Построить проективное отношение двух рядов точек с общим носителем, чтобы не было двойных точек.

Построение. Для построения проективного отношения двух рядов точек с общим носителем, которое не имеет двойных точек, совместим центры , чтобы проектирование осуществлялось двумя пучками прямых из общего центра S так, что соответствующие прямые другого пучка получался с помощью поворота прямых первого пучка (а, в, с, …) в определенном направлении на один и тот же угол . Понятно, что такие два пучка прямых проективны и не могут иметь двойных прямых. В таком же самом соответствии будут и перспективные им ряды точек, то есть , у которых нет двойных точек (рис. 30).

Определение 15. Проективное соответствие двух форм первой ступени с общим носителем называется гиперболическим, если это отношение имеет два двойных элемента, параболическим, если оно имеет один двойной элемент, и эллиптическим, если двойных элементов у него нет.

В рассмотренных задачах имеем проективные отношения двух рядов с общим носителем гиперболическое (рис. 28), параболическое (рис. 29), эллиптическое (рис. 30).

Задача 9. Симметрия относительно точки на прямой есть гиперболическое соответствием двух рядов с общим носителем.

Решение. Пусть на прямой u задана центральная симметрия точкой О. Тогда какой-нибудь точке А соответствует точка , что , точке В - точка , что , точке С - точка , что (рис. 31).

Рис.31

Поскольку точка О есть середина всех образованных отрезков, то проективное отношение двух рядов точек с общим носителем u, определяется тремя парами соответствующих точек, точка О и несобственная точка прямой u сами себе соответствуют.

Задача !0. Пусть имеем два пучка прямых с общим носителем S. Между прямыми этих пучков установим такое отношение, что каждой прямой первого пучка соответствует перпендикулярная ей прямая второго так, чтобы .

Покажем, что этот способ устанавливает соответствие между пучками, которое является проективным, то есть

Правда,

Поскольку как острые с соответственно перпендикулярными сторонами, то их и синусы равных углов равны. Аналогично для остальных углов.

Итак, , поэтому в таком способе установлено проективное отношение между прямыми пучков

Перпендикулярные прямые не могут совпадать, поэтому это отношение не имеет двойных элементов - оно эллиптическое.

Задача 11. Сопряженные диаметры линий второго порядка образуют проективное отношение двух пучков прямых с общим носителем.

Решение. Из аналитической геометрии известно, что диаметром эллипса (гиперболы) называется прямая, которая делит пополам параллельные; такая прямая обязательно проходит через центр эллипса (гиперболы). Диаметром параболы называется прямая, параллельная ее оси, а также сама ось. Два диаметра эллипса (гиперболы) называются сопряженными, если один из них делит пополам все хорды, параллельные другому диаметру.

Можно доказать, что два пучка, соответствующие прямые которых есть сопряженные диаметры линий второго порядка, проективны.

У эллипса сопряженные диаметры не совпадают, так что пучки, образованные сопряженными диаметрами, не имеют двойных точек, они образуют эллиптическое отношение.

У гиперболы сопряженные диаметры, которые совпадают - это асимптоты гиперболы. Итак, сопряженные диаметры гиперболы образуют проективное гиперболическое отношение двух пучков с общим носителем.

В случае параболы ось, как диаметр, сам собой сопряжен, так что имеем параболическое отношение двух пучков с общим носителем (несобственная точка оси параболы).

Отсюда и взяты названия типов проективных отношений.

Теорема 6. Каждая пара соответствующих элементов гиперболического проективного отношения двух форм первой ступени образует с двумя двойными элементами постоянное двойное отношение.

Доказательство.

Докажем теорему для проективных рядов точек. Пусть - две пары соответствующих точек двух рядов с общим носителем, а X,Y - двойные точки этого отношения. Тогда

или Переставив средние члены пропорции, получим:

Итак, .Теорема доказана

2. Инволюция

Пусть

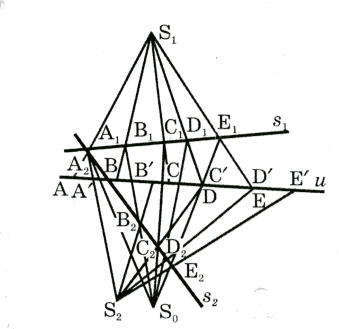
- два проективных ряда точек с общим носителем u, отношение между которыми задано тремя парами точек - и и . Каждую точку прямой u можно отнести как к первому так и ко второму ряду (рис. 32).

Рис.32

Выясним, как найти для произвольной точки Д, отнесенную к первому ряду соответствующую точку , отнесенную ко второму ряду.

Спроектируем точки А, В, С ряда u из произвольного центра , а точки ряда u - из произвольного центра . Получим два проективных пучка прямых .Через точку пересечения одной пары соответствующих прямых - точку проведем две прямые , на которых получим в пересечении с пучками два проективных ряда точек Поскольку ряды перспективны, то существует центр перспективы , который находится как точка пересечения прямых Заготовка для построения точки сделана. Проведем прямую которая пересекает прямую в точке , а затем прямую , которая пересекает прямую в точке . Искомая точка - это точка пересечения прямой с прямой u. При таком построении может быть случай, когда точке , отнесенная к первому ряду, соответствующей точкой будет точка D, отнесенная ко второму ряду. Про точки говорят, что они соответствуют одна другой взаимно.

Теорема 7. Если между точками двух рядов с общим носителем установлено такое проективное соответствие, при котором одна пара точек соответствует одна другой взаимно, то и каждая пара точек этих рядов соответствует одна другой взаимно.

Определение 16. Проективное отношение между двумя рядами точек с общим носителем, при котором каждая пара соответствующих точек есть взаимно соответствующей, называется инволюцией.

При инволюции каждая пара соответствующих элементов не зависит от того, какую точку отнести к первому, а какую ко второму ряду.

Теорема 8. Инволюция в формах первой ступени полностью задается двумя парами соответствующих элементов.

Доказательство. Пусть инволюция двух рядов с общим носителем задана двумя парами соответствующих точек и (рис. 33).

Рис.33

,то есть из двух пар инволюционно заданных точек имеем четыре пары соответствующих точек проективных рядов . Для задания проективного отношения двух рядов достаточно трех пар. Поэтому инволюция двух рядов на прямой u полностью задается двумя парами точек.

Теорема доказана.

Аналогично доказывается теорема для двух инволюционных пучков.

Инволюционные пары могут или разделять, или не разделять друг друга. Рассмотрим три случая:

1.Пусть пары разделяют друг друга (рис. 34):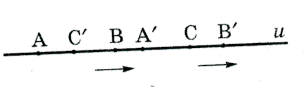

Рис.34

В этом случае, если точка А движется в определенном направлении, то ей соответствует точка , которая движется в том же направлении, поскольку, если бы она двигалась в другую сторону, она не прошла через соответствующую ей точку .

Возьмем еще одну пару соответствующих точек прямой u, причем, если точка С первого ряда лежит после , но перед , то во втором ряду ей соответствующая точка должна лежать после А, но перед В. Понятно, что в этом случае пару должна разделять другая пара - или . Тогда следует, что в данном случае две соответствующие одна другой точки не могут совпадать.

Аналогичную ситуацию имеем в инволюции для двух пучков.

Определение 17. Инволюция форм первой ступени, в которой не существует двойных элементов, называется эллиптичною

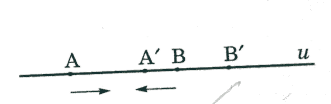2.Рассмотрим случай, когда инволюция точек прямой определяется двумя парами соответствующих точек, которые не разделяют друг друга (рис. 35): .

Рис.35

В этом случае, если точка А перемещается в определенном направлении, то точка , ей соответствующая, должна перемещаться в противоположном направлении. Правда, если точки движутся в одном направлении , то при присутствии точки на отрезке , который не содержит точек , соответственная ей точка вписалась бы в отрезок , на котором лежат точки , а это не возможно, поскольку при прохождении точки через точка А не может находиться у точки В. Итак, точки двигаются в противоположном направлении. Тогда и другие соответствующие пары тоже двигаются в противоположном направлении.

При таком движении точки могут совпасть, так что образуют двойную точку инволюции. По теореме Штаудта, проективное отношение не может иметь больше двух двойных элементов.

Итак, в случае, если инволюционные пары не разделяют друг друга, имеем две двойные точки.

Определение 18. Инволюция форм первой ступени, в которой есть два двойных элемента, называется гиперболической.

Теорема 9. Двойные элементы гиперболической инволюции гармонично разделяют каждую пару соответствующих элементов.

Доказательство. Пусть X,Y - двойные элементы инволюции, пара - соответствующие точки инволюции. Тогда

.

Из полученных равенств имеем

или

Но при точки совпадают, тогда пара будет третьей двойной точкой, что не возможно. Тогда,

Теорема доказана.

С понятием точки, инволюционно соответствующей несобственной точке прямой, связано понятие центра инволюции.

Определение 18. Центром инволюции на прямой u называется точка О, соответствующая точке прямой u.

Теорема 10. Произведение расстояний двух соответствующих точек до центра инволюции есть величина постоянная.

Доказательство. Пусть инволюция задана парой соответствующих точек О - центр инволюции. Тогда, поскольку инволюция есть частный случай проективного отношения, то

Запишем это равенство через отношение трех точек:

Считая, что , из предыдущего равенства получаем

или а тогда где k - постоянное число.

Теорема доказана.

Установим суть постоянной величины k.

Для двойной точки или отсюда .

Если , то имеем две действительных двойных точки X и Y, расположенных по разные стороны от центра О инволюции на расстоянии

В случае, если имеем гиперболическую инволюцию.

Для какой-нибудь пары соответствующих точек произведение , поэтому точки в гиперболической инволюции расположены по одну сторону от точки О на прямой u.

Если , то расстояние двойной точки Х от центра инволюции мнимая величина, тогда мы не имеем действительных точек, а значит, имеет место эллиптическая инволюция.

Если , то для какой-нибудь пары соответствующих точек . Это означает, что одна точка пары соответствующих точек совпадает с центром О инволюции. Поскольку в этом случае имеем одну двойную точку, то инволюция будет параболической.

3. Случай, когда оба двойных элемента инволюции совмещаются. Можно рассмотреть как предельный случай гиперболической инволюции. Практично этот случай не используют, поскольку он не отвечает понятию проективного отношения. Но для общности этот случай называют параболической инволюцией.

3. Проективные отображения форм первой ступени в координатах

3.1.Проективное отображение двух рядов точек в координатах

Понятие координаты на проективной прямой введено через двойное отношение.

Зависимость между координатами пары соответствующих точек двух проективных рядов с общим носителем устанавливаются такими утверждениями.

Теорема 11. Проективное отображение точки одного ряда в точку другого ряда выражается дробно-линейной функцией:

Где действительные числа, которые определяются координатами точек.. Причем .

Следствие. Если перейти к однородным координатам, обозначив

, то формула (1) будет выглядеть так:

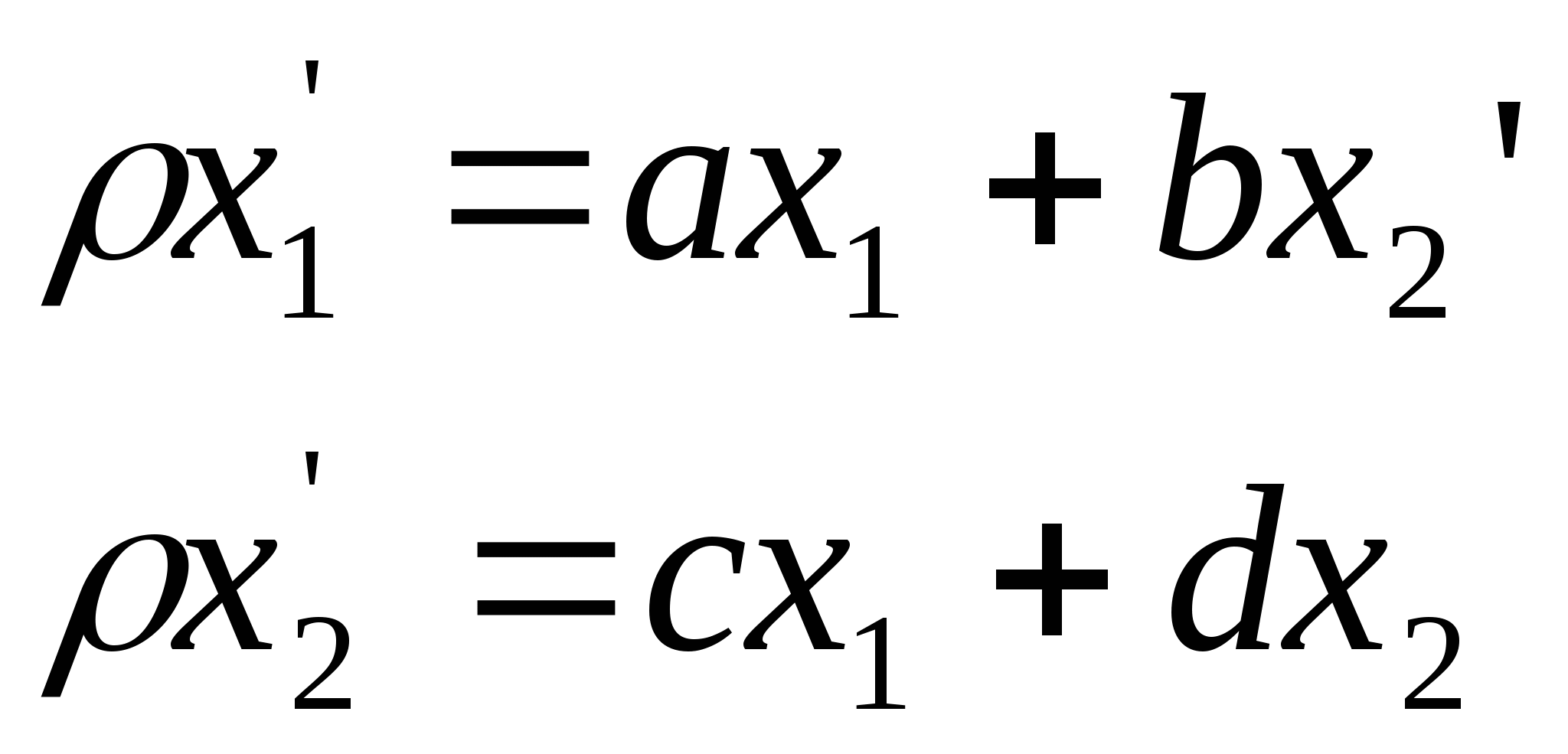(2).

Задача 12. Проективное отношение на прямой в обычных декартовых координатах задано формулой

Найти координаты точки , соответствующую точке А(2).

Решение. По условию х = 2, тогда по формуле найдем координаты точки :

Итак, точке А(2) соответствует точка

Задача 13. Проективное отношение на прямой в однородных координатах задано формулами:

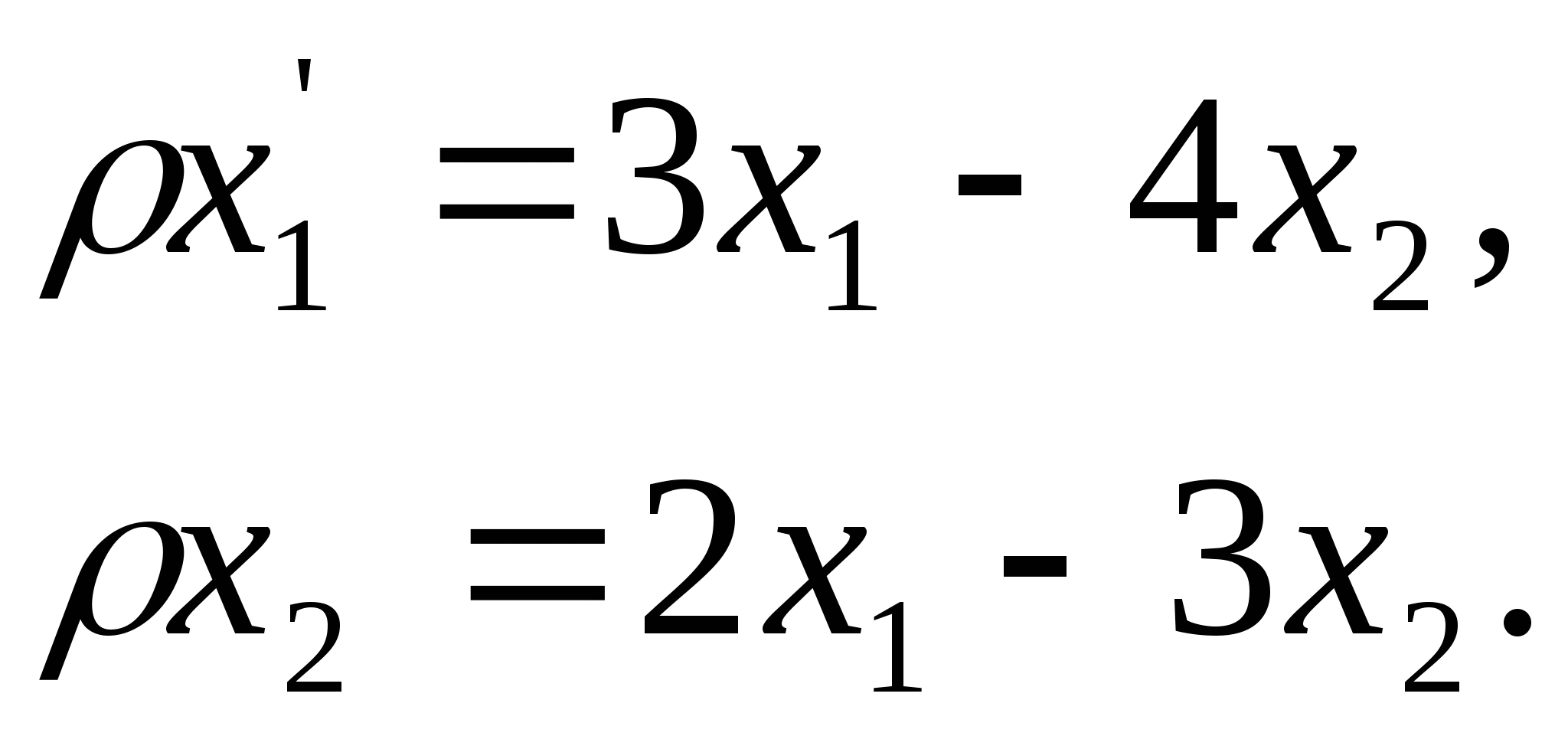Найти координаты точки , соответствующей точке В(3:1).

Решение. Подставляя в данные формулы вместо координаты точки В, получим

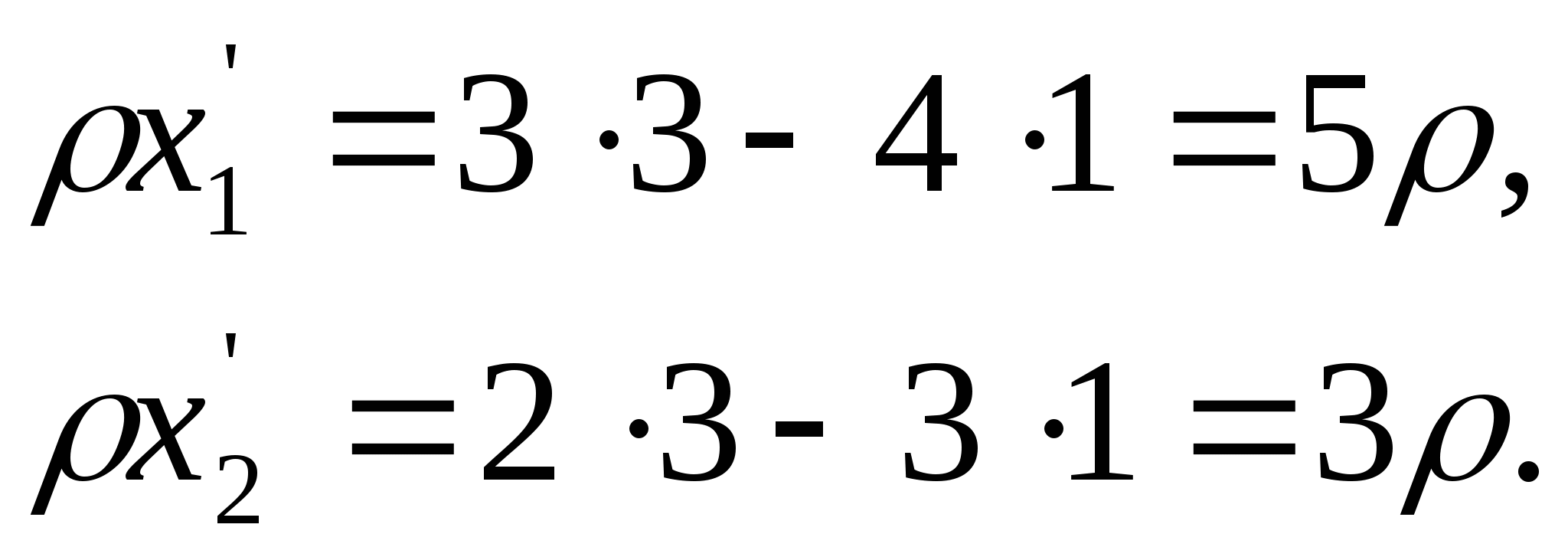
Итак, точке В(3:1) соответствует точка

3.2. Инволюция в координатах

Инволюция точек прямой двух рядов точек с общим носителем есть частный случай проективного отношения. Поэтому формулы (1) и (2) справедливы при некотором условии.

Запишем формулу (1) ввиде:

тогда для инволюционных точек левая часть будет симметричной относительно , то есть выполняется при замене буквы х на букву , и наоборот. Это выполняется при условии, если Тогда инволюция определяется формулой:

(3)

Для двойных элементов инволюции , тогда из равенства (3) получаем (4)

Корни этого уравнения будут координатами двойных точек. Количество корней уравнения (4) зависит от дискриминанта

Если , то уравнение (4) имеет два действительных корня, то есть инволюция имеет две двойных точки - будет гиперболическая инволюция.

Если то уравнение (4) не имеет решений, то есть двойных точек не существует - имеем эллиптическую инволюцию.

Если то уравнение (4) имеет один корень, то есть инволюция имеет одну двойную точку - имеем параболическую инволюцию.

Задача 14. Инволюция на прямой задана формулой

Определить тип инволюции.

Решение. Запишем данную формулу ввиде уравнения через х при условии, что , получим Корнями этого уравнения будут числа: -2;1. Итак, данная инволюция имеет две двойные точки, то есть, имеем гиперболическую инволюцию.

Задача 15. Инволюция на прямой задана формулой

Отнесите данную точку А(1) сначала к первому ряду, а затем ко второму, найти ее инволюционные образы.

Решение. Если точку А(1) отнесем к первому ряду, то х = 1. По данным формулам найдем

Отнесем точку А(1) ко второму ряду, то есть . Тогда по данным формулам х = -3. То есть, точки взаимно соответственны.

Задача 16. Инволюция на прямой задана двумя парами соответствующих точек и . Найти формулу этой инволюции.

Решение. Формула инволюции имеет вид:

Надо найти Для этого в формулу подставим сначала координаты точек , а затем . Получим систему двух уравнений с тремя неизвестными:

Решим эту систему в отношениях Получаем и получим формулу инволюции

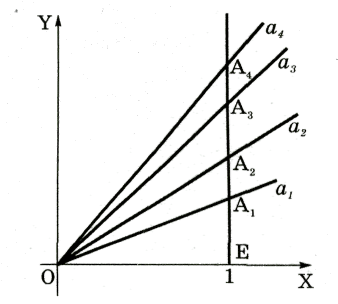Проективное отношение и инволюция пучков прямых в координатах может иметь аналогичное трактовку, выраженное через угловые коэффициенты прямых.

Для этого центр О пучка берем за начало координат (рис. 36)

Рис.36

и запишем уравнения прямых пучка через угловые коэффициенты , виде

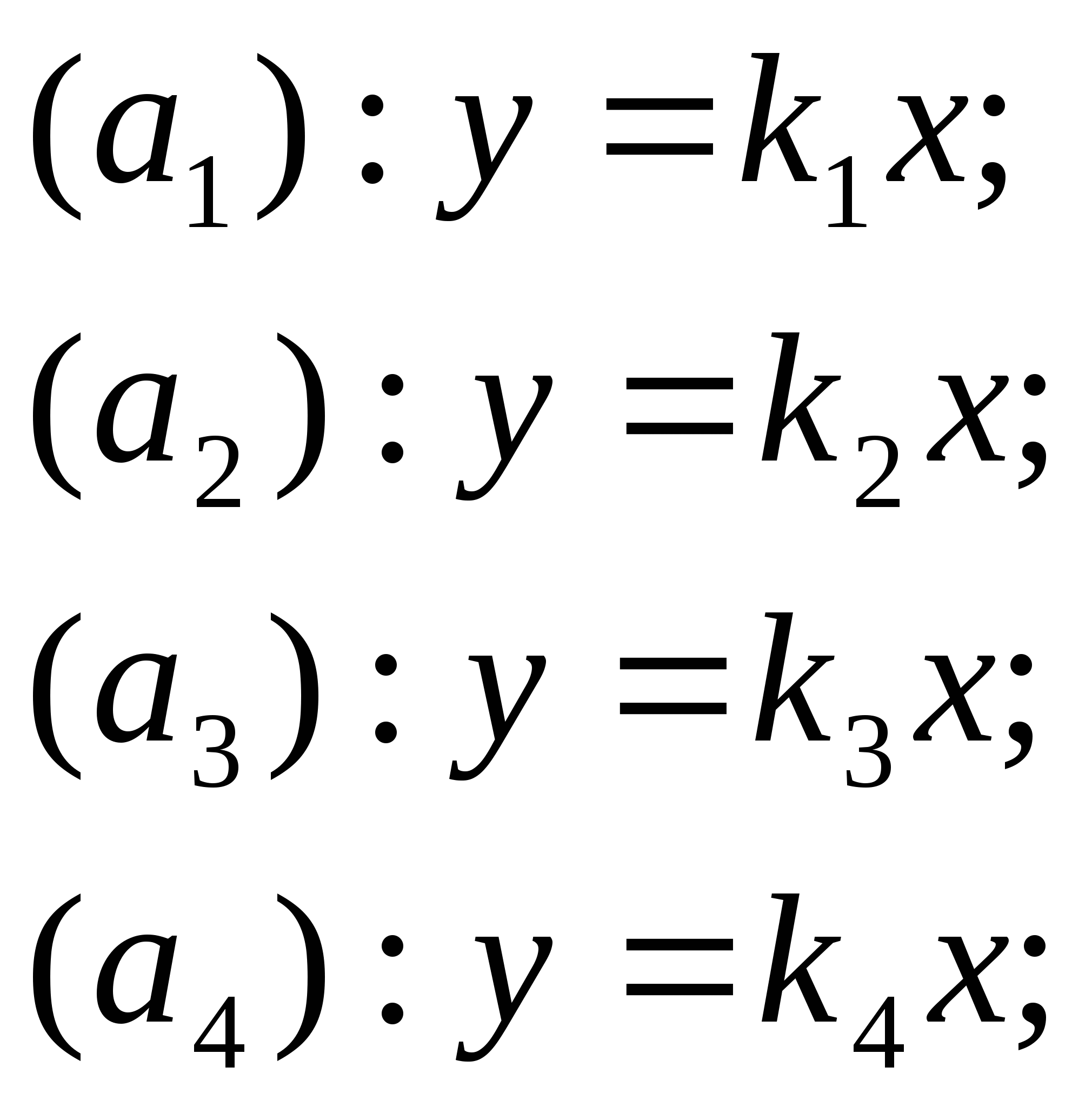. Прямая пересекает прямые пучка в точках Тогда Но Отсюда

(5).

Задача 17. Четыре прямые пучка заданы уравнениями:

Найти двойное отношение этих прямых.

Решение. Обозначим эти прямые Тогда угловые коэффициенты равны Двойное отношение находим

Задача 18. Даны три прямые своими уравнениями относительно декартовой системы координат. Найти уравнение четвертой прямой, гармонически сопряженной с прямой

Решение. Обозначим прямые : а искомую прямую через . По условию задачи Тогда, используя формулу (5), получим Отсюда и уравнение искомой прямой будет

1.4. Индивидуальные задания

КОНТРОЛЬНАЯ РАБОТА

ВАРИАНТ №1

1.Даны точки А(4), В(9), С(6),Д(-2). Найти (АВ,СД).

2.Даны три прямых пучка а, в, с с центром в точке S. Построить четвертую прямую d, гармонически сопряженную с в.

3.Проективное соответствие точек прямой в декартовых координатах задано формулой

Найти точку М, если

4.Даны три прямые пучка своими уравнениями y=2x, y=7x, y=x. Найти уравнение четвертой прямой гармонически сопряженной с прямой y=x.

5.Инволюция задана двумя парами точек Найти формулу инволюции.

ВАРИАНТ №2

1.Даны три точки А(7), В(-5), С(4). Найти точку Д такую, что (АВ,СД)=-2.

2.Построить четвертую гармоническую точку Д по трем данным А,В,С, если точка Д сопряжена с точкой С, а она не лежит на отрезке АВ.

3.Проективное соответствие на прямой в однородных координатах задано формулами

Найти , если А(3:4).

4.Четыре прямые заданы уравнениями y=5x, y=-3x, y=8x, y=x. Найти двойное отношение данных прямых.

5.Определить тип инволюции .

Комплексная контрольная работа по геометрии

Завдання №1

1. Гомотетія: поняття, різні її види, аналітичне подання (формули). Група гомотетій із спільним центром.

2. На підставі аналізу послідовних проектувань точок прямої та перетинань прямими пучків прямих зробити висновок.

3. Дано три вершини паралелограма А(3;-5); В(5;-3); С(-1;3). Визначити четверту вершину D, протилежну В.

4. На поверхні x²+y²+z²=9 знайти точку, для якої абсциса дорівнює 2, ордината дорівнює 5.

Завдання №2

1. Множина обертань площини із спільним центром є групою. Довести.

2. Дослідити взаємне розташування двох прямих, заданих канонічними рівняннями у тривимірному просторі.

3. Дано вершини трикутника А(1;4); В(3;-9); С(-5;2). Визначити довжину його медіани, проведеної з вершини В.

4. Скласти рівняння сфери, якщо вона проходить через початок координат і має центр С(4;-4;-2).

Завдання №3

1. Операції над векторами та їх властивості.

2. Як відшукати кут між площинами, заданими загальними рівняннями?

3. Дано вершини трикутника А(1;-3); В(3;-5); С(-5;2). Визначити точки перетину його медіан із сторонами.

4. Три колінеарні точки задані своїми афінними координатами: А(-3;1); В(2;11); С(1;9). Знайти на цій прямій точку D(x;y), щоб задовольнялась умова: (АВСD)=-2.

Завдання №4

1. Площина в прямокутній системі координат. Нормальне рівняння площини.

2. Дослідити симетричність правильних многогранників та встановити види вісей симетрії і їх кількість.

3. Пряма проходить через точки М₁(-12;-13); М₂(-2;-5). На цій прямій знайти точку, абциса якої дорівнює 3.

4. Визначити координати центра С та радіус r сфери, заданої рівнянням: x²+y²+z²-4x-2y+2z-19=0.

Завдання №5

1. Теорема про перетин трьох пар протилежних сторін повного чотиривершинника прямою (Друга теорема Дезарга).

2. Як визначаються координати лінійної комбінації векторів за координатами векторів складових?

3. Визначити площу паралелограма, якщо дано три його вершини: А(-2;3); В(4;-5); С(-3;1).

4. Знайти координати центра С та радіуса r сфери, заданої рівнянням:

x²+y²+z²+2x-6y+1=0.

Завдання №6

1. Ділення відрізка в даному відношенні (розглянути різні простори).

2. Дослідити можливості зведення загального рівняння прямої Ax+By+C=0 до окремих видів.

3. Знайти точку перетину прямої 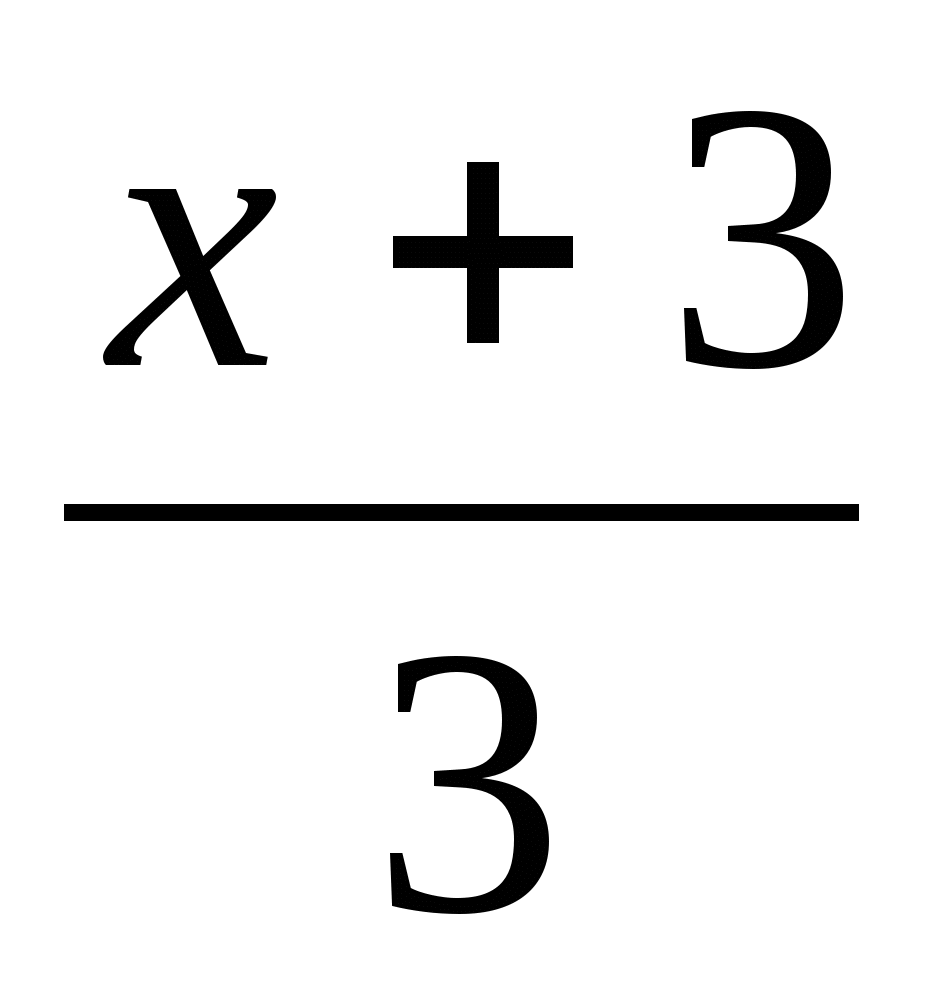==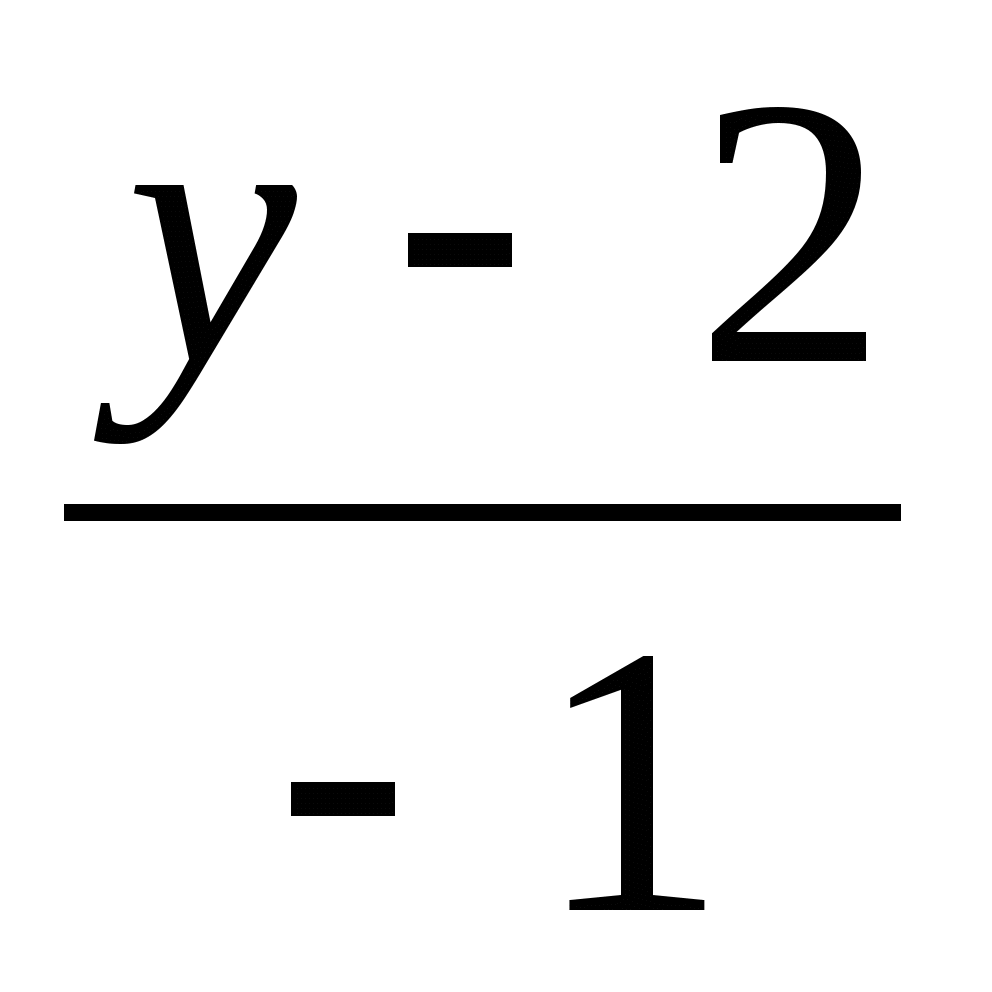 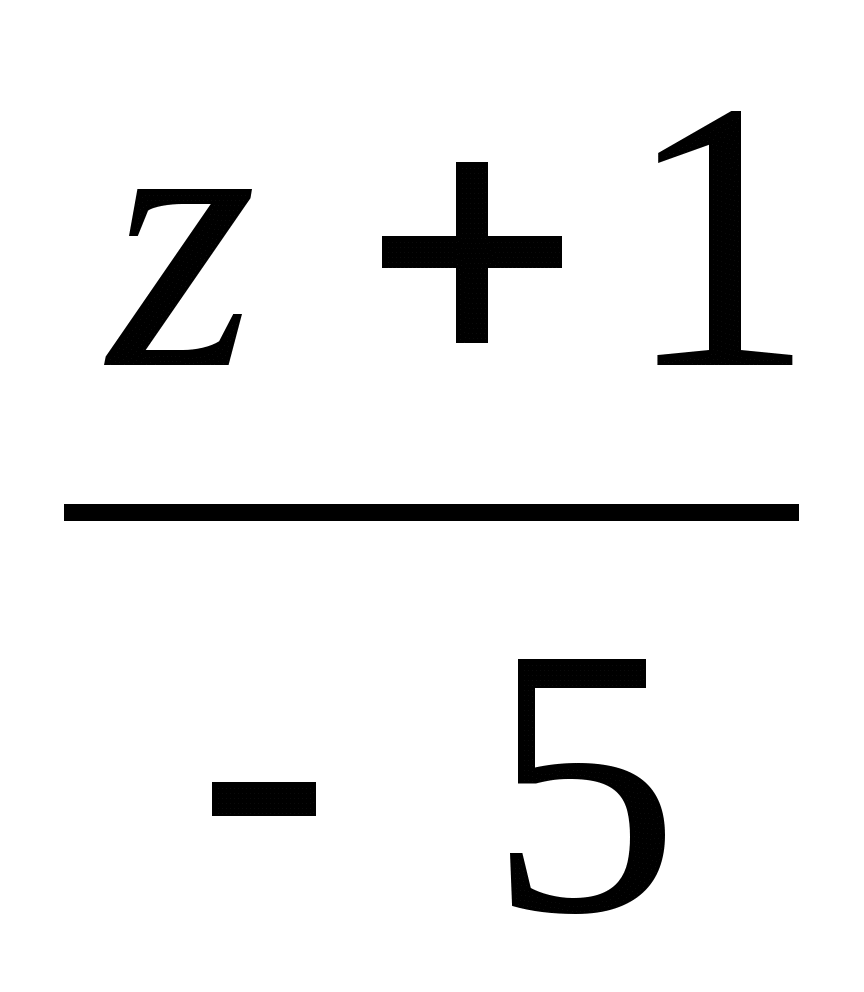та площини x-2y+z-15=0.

4. Дано чотири колінеарні точки своїми афінними координатами: А(2); В(3); С(4); D(5). Обчислити значення складних відношень цих точок, відповідних усім иожливим їх перестановкам.

Завдання №7

1. Пряма у n-мірному просторі, її рівняння тавластивості.

2. Дослідити взаємне розміщення прямої та площини за їх канонічними рівняннями.

3. Дан еліпс 9x²+25y²=225. Знайти його піввісі, фокуси та ексцентриситет.

4. Побудувати точку D, якщо задано три точки А, В, С, щоб виконувалась умова (АВСD)=-1, використовуючи властивість бісектрис кутів трикутника.

Завдання №8

1. Площина та її рівняння в аффінній системі координат.

2. Як знайти центр та радіус сфери за її загальним рівнянням?

3. Дано вершини трикутника: А(2;1); В(-1;-1); С(3;2). Скласти рівняння його медіан.

4. Дано: (а) x-y-3=0; (b) 2x-y-4=0; (c) 3x-y-5=0; (d) 5x-y-7=0. Обчислити: (abcd); (acbd).

Завдання №9

1. Центральна симетрія та її аналітичне представлення.

2. Дослідити розміщення площини в прямокутній системі координат в залежності від коефіціентів її загального рівняня.

3. Дано вершини трикутника: А(2;1); В(-1;-1); С(3;2). Скласти рівняння його висот.

4. Побудувати точку D за даними точками А, В, С, щоб виконувалась умова (АВСD)=-1, використовуючи властивість повного чотиривершинника.

Завдання №10

1. Пряма у тривимірному просторі та її рівняння.

2. Дослідити інваріанти рухів.

3. Дано еліпс 9x+5y=45. Знайти його піввісі, фокуси, ексцентриситет.

4. Три колінеарні точки задані своїми аффінними координатами: А(-5;2); В(2;6); С(4;8). Знайти на цій прямій точку D(x;y), щоб задовольнялась умова: (АВСD)=3.

2 НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

2.1. Общие сведения про изображения фигур

2.1.1. Центральное проецирование;

Пусть мы имеем некоторую пространственную фигуру , плоскость и точку , которая не принадлежит ни тетраэдру, ни плоскости (рис.1

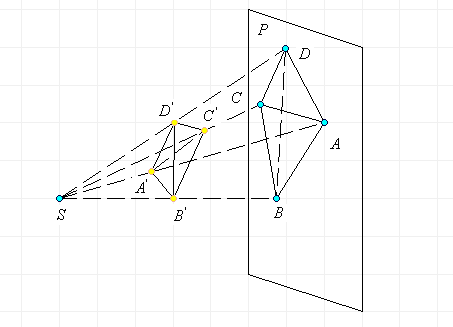
Проведем прямую до пересечения с плоскостью в точке . Точка называется центральной проекцией точки . Точка называется центром проецирования, прямая - проектирующей прямой, плоскость - плоскостью проекций.

Свойства центрального проецирования

1.Центральной проекцией точки есть точка;

2.Каждая непроктируемая прямая проектируется в прямую. Проектируемая прямая проектируется в точку;

3.Инциндентность точек и прямых центральным проецированием не нарушается;

4.Центральной проекцией непроектируемой плоскости есть плоскость, а проектируемой плоскости - прямая плоскости .

5.Каждая фигура , которая лежит в непроектируемой плоскости , параллельна плоскости проекций , проектируется в подобную ей фигуру

;

6.Двойное отношение четырех точек прямой есть инвариант центрального проецирования;

2.1.2. Параллельное проецирование.

Пусть дан тетраэдр а плоскости . Через каждую вершину тетраэдра проведем в определенном направлении параллельные прямые , которые пересекают плоскость в точках (рис.2).

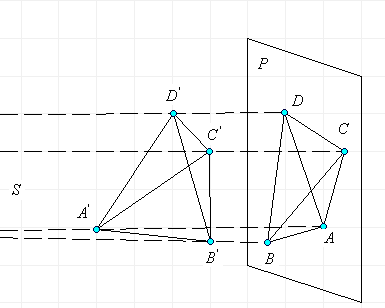
Соединяя полученные точки отрезками, получаем фигуру , которая называется параллельной проекцией тетраэдра на плоскость . Прямая называется проектирующей прямой, а плоскость - плоскостью проекций. Такой спрособ получения параллельной проекции фигуры называется параллельным проектированием в определенном направлении. И так, параллельное проектирование полностью задается направлением и плоскостью проекций.

Свойства параллельного проектирования

1.Параллельной проекцией точки есть точка;

2.Палаллельной проекцией прямой, непараллельной направлению проектирования, есть прямая, а параллельной направлению проектирования - точка;

3.Инциндентность точек и прямых при параллельном проектировании не нарушается;

4.Отношение отрезков прямой равно отношению их параллельных проекций;

5.Проекции параллельных прямых параллельны между собой;

6.Отношение отрезков двух параллельных прямых равно отношению параллельных проекций этих отрезков;

7.Длина отрезка прямой, параллельной плоскости проекций, равно длине его параллельной проекции;

8.При ортогональном проецировании длина проекции отрезка прямой равна произведению длины отрезка - оригинала на косинус угла его наклона к плоскости проекций.

Задача 1. Построить изображение прямоугольного треугольника с катетами , в котором из вершины прямого угла проведены медиана и высота (параллельное проецирование).

Решение.

Изображением данного прямоугольного треугольника будет произвольный треугольник. Медиана изображается медианой (рис.3).

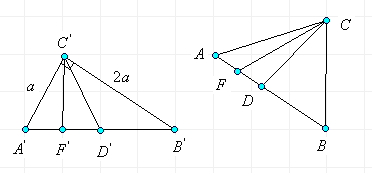
Для изображения высоты используем отношение, в котором делит основание высоты гипотенузу: .

Итак, на стороне надо построить точку , для которой .

2.2. Метод Монжа

2.2.1. Понятие про метод Монжа;

Определение. Изображение пространственной фигуры его двумя ортогональными проекциями на две взаимно перпендикулярные плоскости называют методом Монжа.

Этот метод впервые был научно обоснован французским геометром Гаспаром Монжом (1746 - 1818) в труде «Начертательная геометрия», опубликованном в 1799 году.

Метод Монжа на две плоскости рассмотрим на примере построения проекций точки.

Возьмем две взаимно перпендикулярных плоскости; одну назовем горизонтальной плоскостью проекций, обозначим , другую - вертикальной или фронтальной плоскостью проекций, обозначим .

Определение. Совокупность двух ортогональных проекций на две взаимно перпендикулярные плоскости , смещенные поворотом около оси на по часовой стрелке, называется эпюром (рис.4).

2.2.2. Система трех плоскостей проекций;

В инженерной практике для изображения сложных деталей машин двух проекций не достаточно. Поэтому систему двух плоскостей дополняют третьей плоскостью , профильная плоскость проекций (рис.5).

Задача 2. Построить эпюры точек: 1)

Решение.

1)Эпюр точки

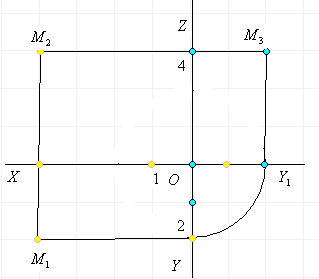
2)Эпюр точки

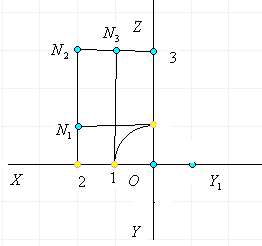
Задача 3. Построить на эпюре горизонтальную проекцию точки , если даны

Решение.

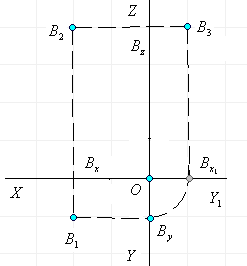
Через точку проведем прямую , перпендикулярно оси , на будет лежать искомая точка . Через точку проведем прямую, перпендикулярную оси до пересечения в точке . На оси отложим отрезок . Через точку проведем прямую, параллельную оси , до пересечения с прямой в искомой точке .

2.3. Метод аксонометрии

2.3.1. Основные понятия аксонометрии;

Термин «аксонометрия» образуется из двух слов древнегреческого языка: аксо - ось, метрео - измеряю. Суть метода заключается в том, что данная фигура вместе с осями пространственной декартовой системы координат проектируется на некоторую плоскость (рис.6).

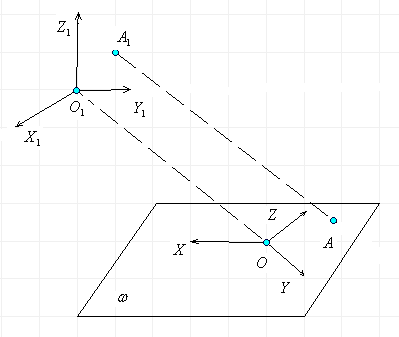
Определение. Отношение длин отрезков аксонометрической проекции к длине натурального отрезка называется коэффициентом искажения.

2.3.2. Основная теорема аксонометрии. Теорема Польке-Шварца.

Разным положениям осей в пространстве и разным направлениям проектирования соответствуют разные положения аксонометрических осей и разные длины аксонометрических единиц в плоскостях проекций, то есть разные коэффициенты искажения.

Возникает вопрос: В какой зависимости находятся направления аксонометрических осей и коэффициенты искажения от направления проектирования и положения натуральных осей координат в пространстве.

Этот вопрос полностью решил немецкий геометр К. Польке в 1853 году. Он доказал теорему, которую назвали основной теоремой аксонометрии.

Теорема (Польке) Любые три отрезка, которые выходят из одной точки на плоскости, можно принять за параллельные проекции трех равных и взаимно перпендикулярных отрезка в пространстве.

Доказательство этой теоремы было очень сложным, основывалось на фокальных свойствах поверхностей второго порядка.

В 1864 году немецкий ученый А. Шварц не только упростил доказательство Польке, но и обобщил его теорему.

Теорема (Польке - Шварца) Любой невырожденный четырехугольник вместе с его диагоналями можно считать параллельной проекцией тетраэдра, подобного наперед заданному.

Доказательство.

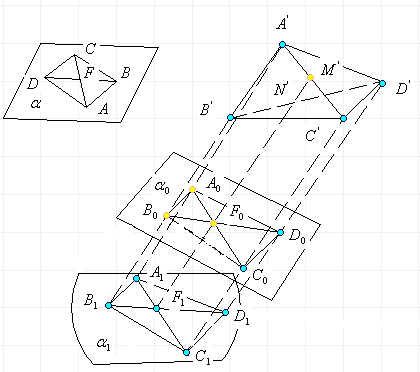
Пусть дан произвольный четырехугольник на плоскости , - точка пересечения его диагоналей. Дан произвольный тетраэдр в пространстве (рис. 7).

Покажем, что можно так выбрать направление проектирования, что тетраэдр проектируется в четырехугольник.

Поскольку при параллельном проецировании сохраняется инцидентность и простое отношение трех точек, то на противоположных ребрах и тетраэдра возьмем такие точки , что

.

Через точки проведем прямую, а через вершины тетраэдра прямые, параллельные прямой . Получим четырехугольную призму. Выполним сечение этой призмы плоскостью, перпендикулярно к боковым ребрам, в сечении получим четырехугольник , точка - пересечение его диагоналей.

Тогда , а учитывая равенство выше, получим Отсюда выходит, что существует аффинное преобразование плоскости в плоскость , при котором образом четырехугольника есть четырехугольник .

Любое аффинное преобразование плоскости в плоскость можно представить виде композиции подобного преобразования и ортогонального проектирования, поэтому четырехугольник можно рассматривать как ортогональную проекцию четырехугольника , подобного Так как ребра полученной четырехугольной призмы перпендикулярны плоскости четырехугольника , то на ребрах этой призмы можно разместить вершины четырехугольника, подобного четырехугольнику Итак, призму пересекаем такой плоскостью , что в сечении получим четырехугольник подобный четырехугольнику

Теорема доказана.

2.4. Метод основной плоскости

2.4.1. Основные понятия метода основной плоскости

С целью приближения методов изображения пространственных фигур к практическому использованию в учебном процессе российский геометр М.Ф. Четверухин разработал разновидность аксонометрического проецирования, который назвал методом основной плоскости. Суть этого метода состоит в том, что в пространстве фиксируется некоторая плоскость , которая называется основной плоскостью, и выбирается направление параллельного проецирования, по которому точки пространства проецируются на основную плоскость (рис.8).

2.4.2. Изображение пространственных фигур;

1.Изображение призмы

При построении изображения призмы за основную плоскость берут плоскость нижнего основания, а направление внутреннего проектирования - направление боковых ребер призмы. Построение начинают с построения нижнего основания, а затем через вершины многоугольника проводят вертикальные прямые и на каждой из них откладывают равные отрезки

(рис. 9).

2.Изображение пирамиды

Основной плоскостью при изображении пирамиды есть плоскость основания пирамиды, направление внутреннего проектирования - направление бокового ребра.

Для построения правильной пирамиды сначала изображают многоугольник, который лежит в основании пирамиды, потом точку О - центр основания. Через точку О проводят вертикальную прямую, выбирают на ней точку - изображение вершины пирамиды (рис.10).

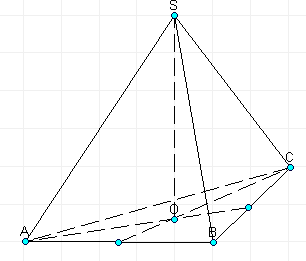
3.Изображение цилиндра

При построении кругового цилиндра основной плоскостью будет плоскость нижнего основания. Сначала строим эллипс, который изображает нижнее основание. Далее строят общие касательные к основаниям цилиндра (рис.11).

4.Построение конуса

Основной плоскостью при изображении конуса является плоскость основания. Сначала строят эллипс, который изображает основание конуса, Через центр основания строят вертикальную прямую и отмечают на ней точку , которая изображает вершину конуса. Точки выделяют видимую часть окружности основания. Отрезок не является большой осью конуса (рис.12).

5.Изображение шара

Изображение шара начинают строить , изображая его абрис, осевое сечение, окружность. Затем изображают сечение горизонтальной плоскостью - экватор, эллипс (рис.13).

2.4.3. Сечение многогранников плоскостью.

Метод следов

Пример1.

На ребрах АА' и В'С' призмы АВСА'В'С' зададим соответственно точку P и Q. Построим сечение призмы плоскостью (PQR), точку R которой зададим в одной из следующих граней:

а) ВССВ'С';

б) А'В'С';

в) АВС

Решение.

а) 1) Так как точки Q и R лежат в плоскости (ВСС'), то в этой плоскости лежит прямая QR. Проведем ее. Это след плоскости (PQR) на плоскость(ВСС'). (рис.1)

2) Находим точки В'' и С', в которых прямая QR пересекает соответственно прямые ВВ' и СС'. Точки В' и С' - это следы плоскости (PQR) соответственно на прямых ВВ' и СС'.

3) Так как точки В'' и Р лежат в плоскости (АВВ'), то прямая В''Р лежит в этой плоскости. Проведем ее. Отрезок В**Р - след плоскости (PQR) на грани АВВ'А'.

4) Так как точки Р и С лежат в плоскости (АСС'), то прямая РС'' лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АСС').

5) Находим точку V, в которой прямая РС'' пересекает ребро А'С'. Это след плоскости (PQR) на ребре А'С'.

6) Така как точки Q и V лежат в плоскости (А'В'С'), то прямая QV лежит в этой плоскости. Проведем прямую QV. Отрезок QV - след плоскости (PQR) на грани АВС. Итак, мы получили многоугольник QB''PV - искомое сечение.

б) 1) Так как точки Q и R лежат в плоскости (А'В'С'), то в этой плоскости лежит прямая QR. Проведем ее. Это след плоскости (PQR) на плоскости (А'В'С').(рис.2)

2) Находим точки D' и Е', в которых прямая QR пересекает соответственно прямые А'В' и B'С'. Так как точка D' лежит на ребре А'В', отрезок QD' - след плоскости (PQR) на грани А'В'С'.

3) Так как точки D' и P лежат в плоскости (АВВ'), то прямая D'P лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АВВ'), а отрезок D'P - след плоскости (PQR) на грани АВВ'А'.

4) Так как точки Р и Е' лежат в плоскости (АСС'), то в этой плоскости лежит прямая РЕ'. Проведем ее. Это след плоскости (PQR) на плоскости (АСС').

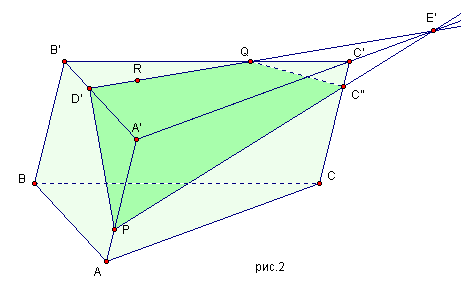
5) Находим точку С''=PE''CC'. Так как точка С'' лежит на ребре СС', то отрезок РС'' - это след плоскости (PQR) на грани АСС'А'.

6) Так как точки Q и С'' лежат в плоскости (ВСС'), то прямая QC'' лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (ВСС'), а отрезок QC''- след плоскости (PQR) на грани ВСС'В'. Итак, мы получили многоугольник QD'РС'' - это и есть искомое сечение.

в) 1) Из трех заданных точек Р, Q и R никакие две не лежат в какой-нибудь одной из плоскостей граней призмы, поэтому найдем основной след плоскости (PQR) (т. е. линию пересечения плоскости (PQR) с плоскостью (АВС), выбранной в качестве основной). Для этого сначала найдем проекции точек Р, Q и R на плоскость (АВС) в направлении, параллельном боковому ребру призмы. Так как точка Р лежит на ребре АА', то точка Р' совпадает с точкой А. Так как точка Q лежит в плоскости (ВСС'), то в этой плоскости через точку Q проведем прямую, параллельную прямой ВВ', и найдем точку Q', в которой проведенная прямая пересекает прямую ВС. Так как точка R по условию лежит в плоскости, выбранной в качестве основной, то точка R' совпадает с точкой R.(Рис.3)

2) Параллельными прямыми РР' и QQ' определяется плоскость. Проведем в этой плоскости прямые PQ и Р'Q' и найдем точку S=PQ пересекает P'Q'. Так как точка S' лежит на прямой PQ, то она лежит в плоскости (PQR), и так как точка S' лежит на прямой Р'Q', то она лежит в плоскости (АВС). Таким образом, точка S' является общей точкой плоскостей (PQR) и (АВС). Это значит, что плоскости (PQR) и (АВС) пересекаются по прямой, проходящей через точку S'.

3) Так как точка R совпадает с точкой R', то точка R - это еще одна общая точка плоскостей (PQR) и (АВС). Таким образом, прямая S'R - основной след плоскости (PQR). Проведем эту прямую. Как видим нз рисунка, прямая S'R пересекает ребра АВ и ВС основания призмы соответственно в точках S''и S'''.

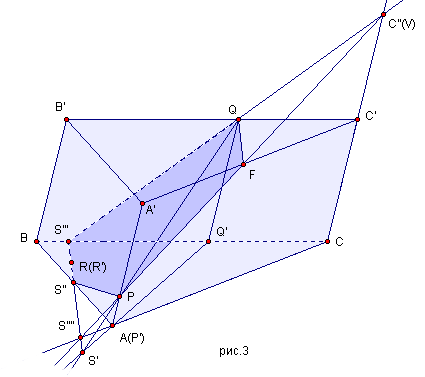
4) Так как точки S''' и Q лежат в плоскости (ВСС'), то прямая S''' Q лежит в этой плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (ВСС'). А отрезок S''' Q, - след плоскости (PQR) на грани ВСС'В'.

5) Аналогично находим отрезок S'' Р - след плоскости (PQR) на грани АВВ'А'.

6) Находим далее точку С,= S''' Q СС'. Так как точки С'' и Р лежат в плоскости (АСС'), то прямая С''Р лежит в плоскости (АСС'). Проведем эту прямую, являющуюся следом плоскости (PQR) на плоскости (АСС').

7) Находим точку F=PC'' пересекает A'С' и получаем затем отрезок PF - след плоскости (PQR) на грани АСС'А'.

8) Точки Q и F лежат в плоскости А'В'C', поэтому прямая QF лежит в плоскости (А'В'C'). Проведем прямую QF, получим отрезок QF - след плоскости (PQR) на грани А'В'C'. Итак, мы получили многоугольник QS'''S''PF- искомое сечение.

3 а м е ч а н и е. Покажем другой путь нахождения точки С'', при котором не находим точку пересечения прямой S''' Q с прямой С'С''. Будем рассуждать следующим образом. Если следом плоскости (PQR) на прямой СС' является некоторая точка V, то ее проекция на плоскость (АВС) совпадает с точкой С. Тогда точка S''''= V'P'пересекает VP лежит на основном следе S'R плоскости (PQR). Строим эту точку S'''' как точку пересечения прямых V'P' (это прямая СА) и S'R. А далее проводим прямую S''''Р. Она пересекает прямую СС' в точке V.

Пример 2.

На ребре МВ пирамиды МАВСD зададим точку Р, на ее грани MCD зададим точку Q. Построим сечение пирамиды плоскостью (PQR), точку R которой зададим:

а) на ребре МС;

б) на грани МАD;

в) в плоскости (МАС), вне пирамиды.

Решение.

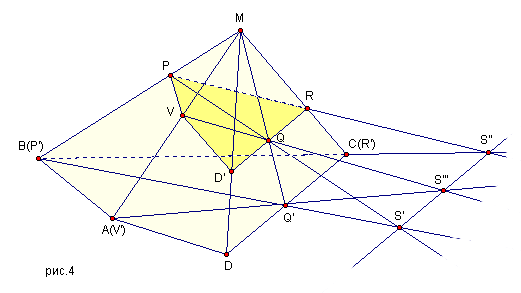
a) Cледом плоскости (PQR) на грани МВС является отрезок РR, а ее следом на грани MCD является отрезок RD', где точка D' - это точка пересечения прямой RQ с ребром МD. Ясно, что плоскость (PQR) имеет следы на гранях MAD и МАВ (так как с этими гранями плоскость (PQR) имеет общие точки). Найдем след плоскости (PQR) на прямой МА. Сделаем это следующим образом:

1) Построим точки Р', Q' и R' - проекции точек Р, Q и R из центра М на плоскость (АВС), принимаемую, таким образом, за основную плоскость. (Рис. 4)

2) Далее построим точки S'= РQ пересекает Р'Q' и S'' = PR пересекает P'R' и проведем прямую S' S'' - основной след плоскости (PQR).

3) Если плоскость (PQR) пересекает прямую МА в некоторой точке V, то точка V' совпадает с точкой А и точка S'''= VQ пересекает V'Q' лежит на прямой S' S''. Другими словами, в точке S''' пересекаются три прямые: VQ,, V'Q'' и S' S''. Две последние прямые из этих трех на чертеже уже есть. Поэтому точку S''' мы построим как точку пересечения прямых V'Q' и SS''.

4) Проведем прямую QS''' (она совпадает с прямой VQ, так как прямая VQ должна проходить через точку S''', т. е. точки V, Q и S''' лежат на одной прямой).

5) Находим точку V, в которой прямая QS'''пересекает прямую МА, Точка V - это след плоскости (PQR) на ребре МА. Далее ясно, что отрезки PV и VD' - следы плоскости (PQR)

соответственно на гранях МАВ и MAD. Таким образом, многоугольник PRD'V - искомое сечение.

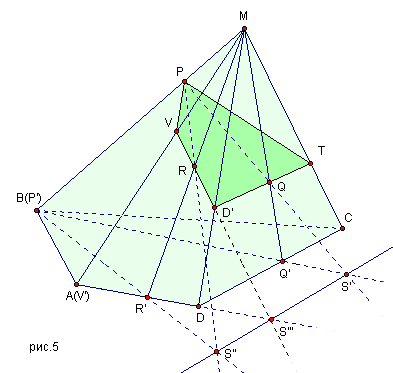
б) 1) Принимаем плоскость (АВС) за основную плоскость и строим точки P', Q' и R' - проекции соответственно точек Р, Q и R на плоскость (АВС). Центром этого внутреннего проектирования является точка М.(Рис.5.)

2) Строим прямую S'S'' - основной след плоскости (PQR).

3) Если плоскость (PQR) пересекает прямую МА в точке V, то точка V' - проекция точки V на плоскость (АВС) из центра М- совпадает с точкой А, а прямые S'S'', V'R' и прямая VR, точка V которой пока нами не построена, пересекаются в точке S'''. Находим эту точку S'''=V'R' пересекается S'S'' .

4) Проводим прямую RS''', и находим точку V=RS''' пересекается MA. Дальнейшее построение ясно. Искомым сечением является многоугольник PVD'Т.

в) Пусть точка R расположена в плоскости (МАС) так, как это показано на рисунке 6.

1) Принимаем плоскость (АВС) за основную плоскость и строим точки P', Q' и R' - проекции соответственно точек P, Q и R на плоскость (ABC). (центром проектирования является точка М.)

2) Строим прямую S'S'', - основной след плоскости (PQR).

3) Находим точку V - след плоскости (PQR) на прямой МА. Точка V' - проекция точки V на плоскость (АВС) из центра М- совпадает в этом случае с точкой А.

4) Находим точку S'''= P'V' пересекается S'S'', а затем и точку V =PS''' пересекается МА.

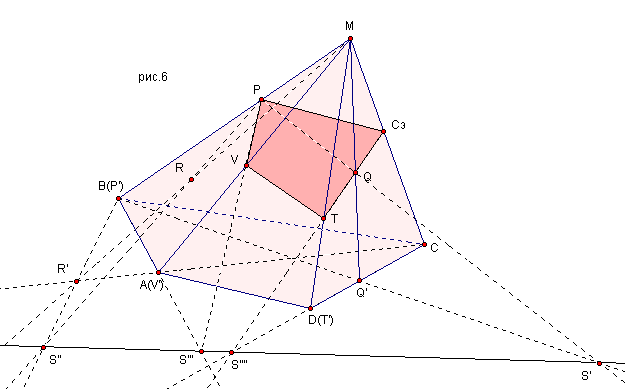
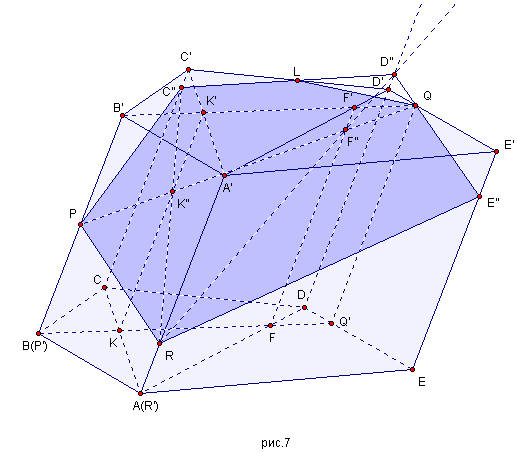
5) Получаем след РV плоскости (PQR) на плоскости (МАВ).

6) Находим точку T - след плоскости (PQR) на прямой МО. Ясно, что точка Т' в этом случае совпадает с точкой D. Для построения точки T строим точку S''''=Q'T' пересекается S'S'', а затем точку T=QS''''пересекается MT'.

7) Совокупность следов PV, VT, ТС', и С'P, т. е. многоугольник PVTC' - искомое сечение.

2.5.Индивидуальные задания

Сечения.

Задача №1.

В пространстве даны две параллельные плоскости и две сферы, причем первая сфера касается первой плоскости в точке А, вторая сфера касается второй плоскости в точке В и сферы касаются друг друга в точке С. Докажите, что точки А, В и С лежат на одной прямой.

Задача №2.

Около шара описан усеченный конус, основания которого являются большими кругами двух других шаров. Определите площадь полной поверхности усеченного конуса, если сумма площадей поверхностей трех шаров равна 8.

Задача №3.

Два противоположных ребра тетраэдра перпендикулярны, а их длины равны а и b расстояние -между ними равно с. В тетраэдр вписан куб, четыре ребра которого перпендикулярны этим двум ребрам тетраэдра, а на каждой грани тетраэдра лежат ровно две вершины куба. Найдите ребро куба.

Задача №4.

Какие правильные многоугольники могут получиться при пересечении куба плоскостью?

Задача №5.

Все сечения некоторого тела плоскостями являются кругами. Докажите, что это тело - шар.

Задача №6.

Через вершину А прямого кругового конуса проведено сечение максимальной площади. Его площадь и два раза больше площади сечения, проходящего через ось конуса. Найдите угол при вершине осевого сечения конуса.

Задача №7.

Плоскость делит медианы граней АВС, АСD и АDВ тетраэдра АВСD, выходящие из вершины Л, в отношениях 2:1, 1:2 и 4:1, считая от вершины. Пусть Р, Q и R. - точки пересечения этой плоскости с прямыми АВ, АС и АD. Найдите отношения АР : РВ, АQ: QС и АR : RD.

Задача №8.

В правильной шестиугольной пирамиде SАВСDЕF (с вершиной S} на диагонали АD взяты три точки, делящие ее на 4 равные части. Через эти точки проведены сечения, параллельные плоскости SАВ. Найдите отношения площадей полученных сечений.

Задача №9.

Сечение правильной четырехугольной пирамиды является правильным пятиугольником. Докажите, что боковые грани этой пирамиды - правильные треугольники.

ОТВЕТЫ

Задача №1.

По всяком случае, точки А, В и С лежат в одной плоскости, и поэтому можно рассмотреть сечение плоскостью, содержащей эти точки. Так как плоскость сечепня проходит через точку касания сфер (сферы п плоскости), и сечении получаются касающиеся окружности (окружность и прямая). Пусть О' и 0'' - центры первой и второй окружностей. Так как О'А || 0''В и точки O', С и 0'' лежат па одной прямой, уголАО'С = углуВО''С. Поэтому угол АСО' = углу ВСО'', т. е. точки А, В и С лежат на одной прямой.

Задача №2.

Осевое сечение данного усеченного конуса является описанной трапецией АВСD с основаниями АD = 2R и ВС = = 2r. Пусть Р - точка касания вписанной окружности со стороной АВ, О - центр вписанной окружности. В треугольнике АВО сумма углов при вершинах А и В равна 90°, поэтому он прямоугольный. Следовательно, АР : РО - РО : ВР, т. е. РО'2 = АР*ВР. Ясно также, что АР = R и ВР = r. Поэтому радиус РО вписанной в конус сферы равен квадратному корню из произведения R и r, а значит, S = 4п(R2 + Rr+ r2). Выражая объем данного усеченного конуса по формулам, получаем, что площадь его полной поверхности равна 2п(R2 + Rr+ r2) = S/2 (нужно учесть, что высота усеченного конуса равна удвоенному радиусу сферы, около которой он описан).

Задача №3.

Общий перпендикуляр к данным ребрам делится параллельными им плоскостями граней куба на отрезки длиной у, х и г (х - длина ребра куба; отрезок длиной у прилегает к ребру а). Плоскости граней куба, параллельные данным ребрам, пересекают тетраэдр по двум прямоугольникам. Меньшие стороны этих прямоугольников равны ребру куба х. Так как стороны этих прямоугольников легко вычисляются, получаем х = bу/с и х = az/с. Следовательно, с=х+у+г=х+сх/b + еx/а, т. е. х=аЬс/(аb + bс + сa).

Задача №4.

Каждая сторона полученного многоугольника принадлежит одной из граней куба, поэтому число его сторон не превосходит 6. Кроме того, стороны, принадлежащие противоположным граням куба, параллельны, так как линии пересечения плоскости с двумя параллельными плоскостями параллельны. Следовательно, сечение куба не может быть правильным пятиугольником, так как у того нет параллельных сторон. Легко проверить, что правильный треугольник, квадрат и правильный шестиугольник могут быть сечениями куба.

Задача №5.

Рассмотрим некоторый круг, являющийся сечением данного тела, и проведем через его центр прямую l, перпендикулярную его плоскости. Эта прямая пересекает данное тело по некоторому отрезку АВ. Все сечения, проходящие через прямую l являются кругами с диаметром АВ.

Задача №6.

Рассмотрим произвольное сечение, проходящее через вершину А. Это сечение является треугольником АВС, причем его стороны АВ и АС являются образующими конуса, т. с. имеют постоянную длину. Поэтому площадь сечения пропорциональна синусу угла ВАС. Угол ВАС изменяется от 0° до ф,

Проекции и сечения правильных многогранников.

Задача №1.

Докажите, что проекции додекаэдра и икосаэдра на плоскости, параллельные их граням, являются правильными многоугольниками.

Задача №2.

Докажите, что проекция додекаэдра на плоскость, перпендикулярную прямой, проходящей через его центр и середину ребра, является шестиугольником (а не десятиугольником).

Задача №3.

а) Докажите, что проекция икосаэдра на плоскость. перпендикулярную прямой, проходящей через его центр и вершину , является правильным 10-угольником. б). Докажите, что проекция додекаэдра на плоскость , перпендикулярную прямой, проходящей через его центр и вершину, является неправильным 12- угольником.

Задача №4.

Существует ли сечение куба, являющееся правильным т шетиугольником?

Задача №5.

Существует ли сечение октаэдра, являющееся правильным шестиугольником?

Задача №6.

Существует ли сечение додекаэдра, являющееся правильным шестиугольником?

Задача №7.

Две грани АВС и АВD икосаэдра имеют общее ребро АВ. Через вершину D проводится плоскость, параллельная плоскости АВС. Верно ли, что сечение икосаэдра этой плоскостью является правильным шестиугольником?

ОТВЕТЫ

Задача №1.

Для доказательства достаточно заметить, что эти многогранники переходят в себя при повороте, совмещающем проекцию верхней грани с проекцией нижней грани. Таким образом, проекция додекаэдра является 10-угольником, переходящим в себя при повороте па 36° (рис. 69, а), а проекция икосаэдра является шестиугольником, переходящим в себя при повороте на 60° (рис. 69, б).

Задача №2.

Рассмотрим куб, вершины которого расположены в вершинах додекаэдра. В нашей задаче речь идет о проекции на плоскость, параллельную грани этого куба. Теперь легко убедиться, что проекцией додекаэдра действительно является шестиугольник (рис. 70).

Задача №3.

а) Рассматриваемая проекция икосаэдра переходит в себя при повороте на З6° (при этом проекции верхних граней переходят в проекции нижних граней). Следовательно, она является правильным 10-угольнлком (рис. 71, а).

б) Рассматриваемая проекция додекаэдра является 12-угольником, переходящим в себя при повороте на 60° (рис. 71. б). Половина его сторон является проекциями ребер, параллельных плоскости проекции, а другая половина сторон - проекциями ребер, не параллельных плоскости проекции. Следовательно, этот 12-угольник неправильный.

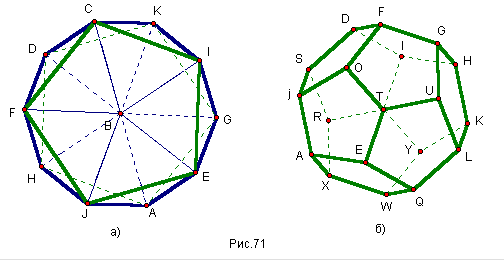
Задача №4.

Существует. Середины указанных на рис. 72 ребер куба являются вершинами правильного шестиугольника. Это следует из того, что стороны этого шестиугольника параллельны сторонам правильного треугольника PQR, а их длины вдвое меньше длин сторон этого треугольника.

Задача №5.

Существует. Проведем плоскость, параллельную двум противоположным граням октаэдра и равноудаленную от них. Легко проверить, что сечение этой плоскостью будет правильным шестиугольником (на рис. 73 изображена проекция на секущую плоскость).

Задача №6.

Существует. Возьмем три пятиугольные грани о общей вершиной А и рассмотрим сечение плоскостью, пересекающей эти грани и параллельной плоскости, в которой лежат три попарно общие вершины рассматриваемых граней (рис. 74). Это сечение является шестиугольником с попарно параллельными противоположными сторонами. При повороте на 120° относительно оси, проходящей через вершину А и перпендикулярной секущей плоскости, додекаэдр и секущая плоскость переходят в себя. Поэтому сечение является выпуклым шестиугольником с углами 120°, длины сторон которого, чередуясь, принимают два значения. Для того чтобы этот шестиугольник был правильный, достаточно, чтобы эти два значения были равны. Когда секущая плоскость движется от одного своего крайнего положения до другого, удаляясь от вершины А, первое из этих значений возрастает от 0 до d, а второе убывает от d до а, где а - длина ребра додекаэдра. (d - длина диагонали грани (d больше а). Поэтому в некоторый момент эти значения равны, т.е. сечение является правильным шестиугольником.

Задача №7.

Нет, не верно. Рассмотрим проекцию икосаэдра на плоскость АВС. Она является правильным шестиугольником (см. рис.69). Поэтому рассматриваемое сечение было бы правильным шестиугольником, лишь если бы все 6 вершин, соединенных ребрами с точками А, В и С (и отличных от А, В и С), лежали в одной плоскости. Но, как легко убедиться, это неверно (иначе получилось бы, что все вершины икосаэдра расположены на трех параллельных плоскостях).

3 ПРИЛОЖЕНИЯ

3.1.Образец выполнения контрольной работы

Задача 1

Постройте четырёхугольник по четырём сторонам и отрезку, соединяющему середины диагоналей.

Решение

Предположим, что четырёхугольник ABCD построен. Пусть M и N - середины его диагоналей AC и BD , MN=m , а P , Q , R и S - середины данных сторон AB=a , BC=b , CD=c , DA=d соответственно. Поскольку MP - средняя линия треугольника ABC , то MP = BC и MP || BC . Аналогично NP = AD и NP || AD , NR = BC и NR || BC , MQ = AB и MQ || AB . Отсюда вытекает следующее построение. Строим треугольник MPN по трём сторонам MN=m , MP= , NP= , затем аналогично строим треугольники MNR и MNQ . На сторонах MP и MQ gостроим параллелограмм PMQB . Его четвёртая вершина B есть вершина искомого четырёхугольника. На продолжении отрезка BQ за точку Q откладываем отрезок QC , равный BQ , на продолжении отрезка BP за точку P откладываем отрезок PA , равный BP , на продолжении отрезка CR за точку R откладываем отрезок RD , равный CR . У построенного таким образом четырёхугольника ABCD точка M - середина AC , т.к. по построению Q - середина BC и QM || BP . Поскольку PMRN - параллелограмм, то RN || PM || BC , поэтому N - середина диагонали BD . Наконец, AD=2PN = d , AB=2MQ=a , BC=2BQ=2PM=b , CD=2CR = 2QN=c и MN=m .

Задача 2

Пусть M - середина стороны BC треугольника ABC . Постройте прямую l , удовлетворяющую следующим условиям: l || BC ; l пересекает треугольник ABC ; отрезок прямой l , заключённый внутри треугольника, виден из точки M под прямым углом.

Решение

Предположим, что задача решена. Пусть прямая l , параллельная стороне BC треугольника ABC , пересекает его стороны AB и AC в точках D и E соответственно. Тогда точка P пересечения медианы AM с отрезком DE - середина DE , поэтому MP - медиана прямоугольного треугольника DME , проведённая из вершины прямого угла. Значит,

MP=PD=PE, BMD = PDM= PMD.

Следовательно, MD - биссектриса угла AMB . Отсюда вытекает следующее построение. Строим биссектрису MD треугольника AMB . Через точку D проводим прямую, параллельную стороне BC . Эта прямая пересекает сторону AC в точке E . Докажем, что DE - искомая прямая. В самом деле, пусть прямые DE и AM пересекаются в точке P . Тогда P - середина DE и

PDM = EDM = BMD = AMD = PMD.

Поэтому треугольник PMD - равнобедренный и EP=PD =PM , т.е. медиана MP треугольника DME равна половине стороны, к которой она проведена. Следовательно, DME = 90o .

Задача 11

В данную окружность впишите прямоугольный треугольник, катеты которого проходили бы через две данные точки внутри окружности.

(Пусть A и B - данные точки. На отрезке AB как на диаметре постройте окружность)

Решение

Если окружность, построенная на отрезке с концами в данных точках как на диаметре, пересекает данную окружность, то каждая точка пересечения - вершина искомого треугольника.

3.2.Темы рефератов

1.Исторические сведения о возникновении и развитии геометрии;

2.Центральное проецирование в евклидовом пространстве;

3.Построение проективного пространства;

4.Аксиомы евклидовой геометрии;

5.Аксиомы проективной геометрии;

6.Аксиомы принадлежности проективной геометрии;

7.Аксиомы порядка проективной геометрии;

8.Аксиома непрерывности проективной геометрии;

9.Отношение порядка точек проективной прямой;

10.Основные геометрические формы;

11.Принцип двойственности проективной геометрии;

12.Теорема Дезарга;

13.Двойное отношение четырех точек прямой;

14.Двойное отношение четырех прямых пучка;

15.Координаты точек на проективной прямой;

16.Гармонизм точек ряда;

17.Гармонизм прямых пучка;

18.Построение четвертой гармонической точки по трем данным;

19.Полный четырехвершинник;

20.Проективные ряды с общим носителем;

21.Проективные пучки с общим носителем;

22.Инволюция;

23.Проективное отображение двух рядов точек в координатах;

24.Инволюция в координатах;

25.Основные требования к чертежу, метод Монжа;

26.Изображение пространственных фигур;

27.Теорема Польке - Шварца.

3.3.Вопросы на экзамен

1.Исторические сведения о возникновении и развитии геометрии;

2.Центральное проецирование в евклидовом пространстве;

3.Построение проективного пространства;

4.Аксиомы евклидовой геометрии;

5.Аксиомы проективной геометрии;

6.Аксиомы принадлежности проективной геометрии;

7.Аксиомы порядка проективной геометрии;

8.Аксиома непрерывности проективной геометрии;

9.Отношение порядка точек проективной прямой;

10.Основные геометрические формы;

11.Принцип двойственности проективной геометрии;

12.Теорема Дезарга;

13.Двойное отношение четырех точек прямой;

14.Двойное отношение четырех прямых пучка;

15.Координаты точек на проективной прямой;

16.Гармонизм точек ряда;

17.Гармонизм прямых пучка;

18.Построение четвертой гармонической точки по трем данным;

19.Полный четырехвершинник;

20.Проективные ряды с общим носителем;

21.Проективные пучки с общим носителем;

22.Инволюция;

23.Проективное отображение двух рядов точек в координатах;

24.Инволюция в координатах;

25.Основные требования к чертежу, метод Монжа;

26.Изображение пространственных фигур;

27.Теорема Польке - Шварца.

</ ЛИТЕРАТУРА

1. Анатасян Л.С., Базылев В.Т. Геометрия. Ч. 1. -М.: Просвещение, 1986

2. Анатасян Л.С. Геометрия. Ч. 1. -М.: Просвещение, 1973.

3. Базылев В.Т. и др. Геометрия. 4.1. - М.: Просвещение, 1974,

4. Погорелов А.В. Геометрия.М.: Наука, 1983.

5. Погорелов А.В. Геометрия. 6 - 10. - К.: Рад. школа, 1989.

6. Анатасян Л.С. и др. Сборник задач по геометрии 4.1. - М.:Просвещение, 1973.

7. Клетеник А.В. Сборник задач по аналитической геометри. - М.: Наука, 1973.

8. Цубербиллер О.. Н. Задачи и упражнения по аналитической геометри. М.: Наука, 1968.

9. Игнатенко Н..Я. Практические занятия по высшей математике: в Зч - К.: Пед Пресса, 2000 - 530с.: 4л.

10. Яковець В.П., Боровик В.Н., Ваврикович Л.В. Аналітична геометрія: Навчальний посібник. - Суми: ВТД «Університетська книга», 2004. - 296с.

11. Яковець В.П., Боровик В.Н., Ваврикович Л.В. Аналітична геометрія в просторі. - Ніжин: НДПУ, 2002.

12. Боровик В.Н., Яковец В.П. «Курс высшей геометрии», г.Сумы, Университетская книга,2004 г.