Коррекционный материал по теме Неравенства и и их системы технология полного усвоения (9 класс)

Коррекционный материал по теме «Неравенства и их системы», 9 класс (технология полного усвоения)

Тема: Система нелинейных неравенств с одной переменной.

Определение: Система нескольких неравенств с одной переменной, в которой хотя бы одно неравенство нелинейно, называется системой нелинейных неравенств с одной переменной.

Чтобы решить неравенство, нужно найти все значения переменных, входящих в его сосстав, при которых данное неравенство истинно. Значения переменных, удовлетворяющие данному неравенству, называют его решением.

Примеры: х² - 2х + 3 >х³ - 1, , (а, b - заданные числа)

являются неравенствами, зависящими от одной переменной х. Число х = 1 является решением неравенства В этом можно убедиться непосредственной проверкой:

Вообще, при решении неравенств используюся свойства неравенств, рассмотренные ранее:

1. Если к обеим частям неравенства прибавить (отнять) одно и то же число (выражение), то получится равносильное ему равенство.

2. Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.

3. Если обе счасти неравенства умножить или разделить на одно и то же положительное число (выражение), то получится равносильное ему неравенство.

4. Если обе части неравенства умножить или разделить на одно и то же отрицательное число (выражение), изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

Рассмотрим решение квадратных неравенств с одной переменной.

Чтобы решить систему неравенств, сначала решают каждое неравенство этой системы и в качестве ответа берут пересечение полученных решений.

Пример. 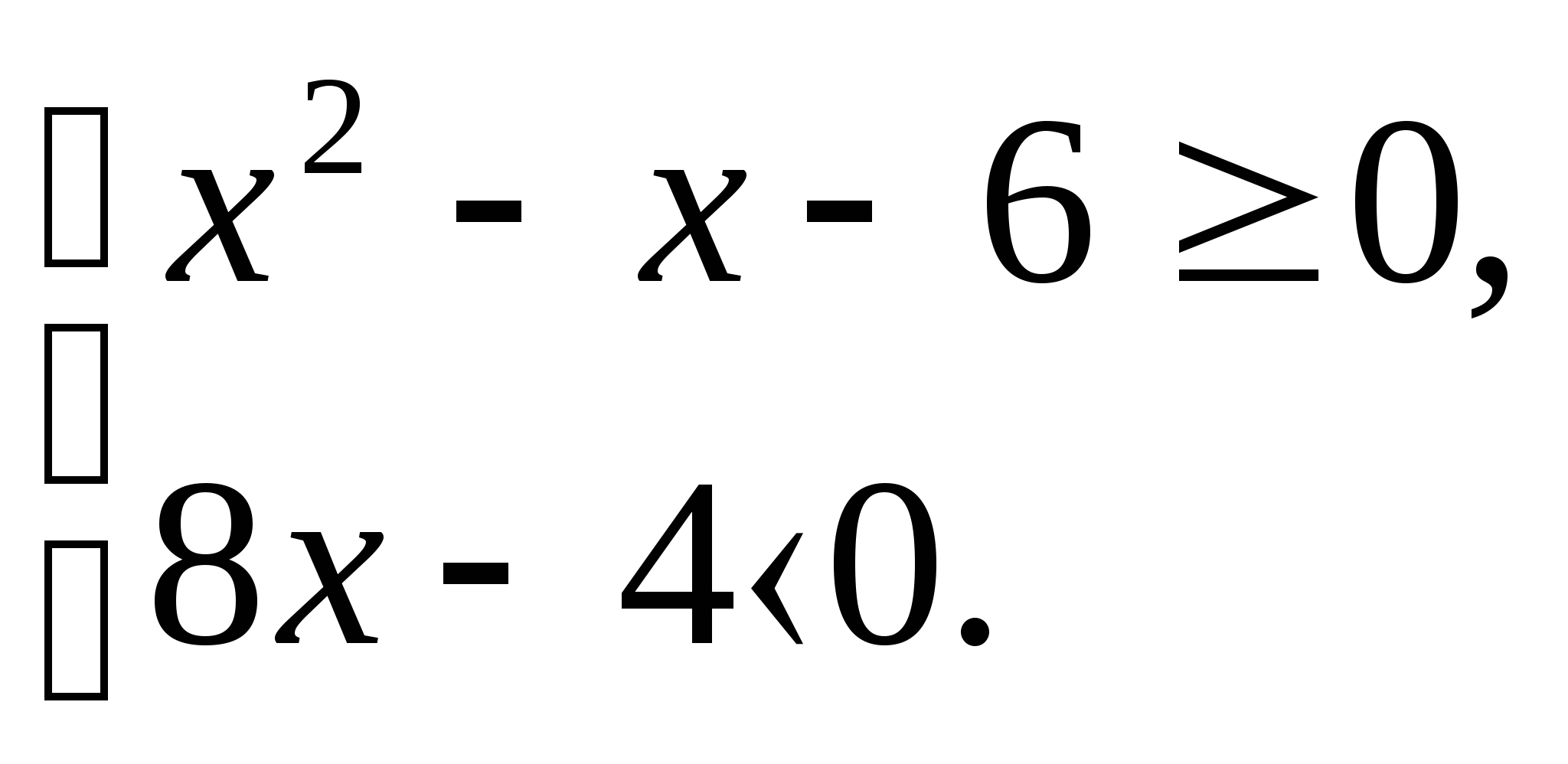Решение:1) находим корни квадратного трехчлена

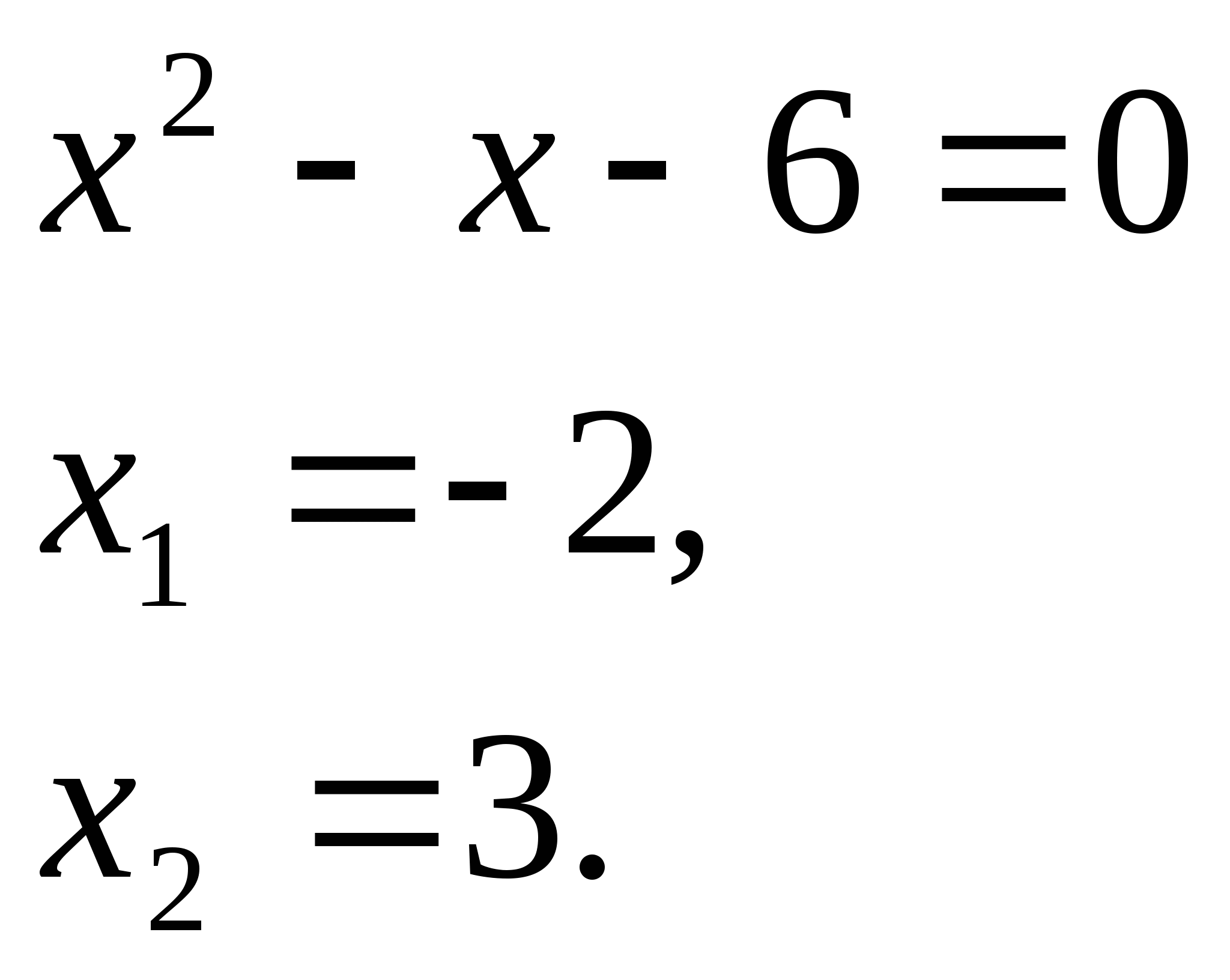
2)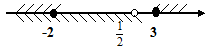

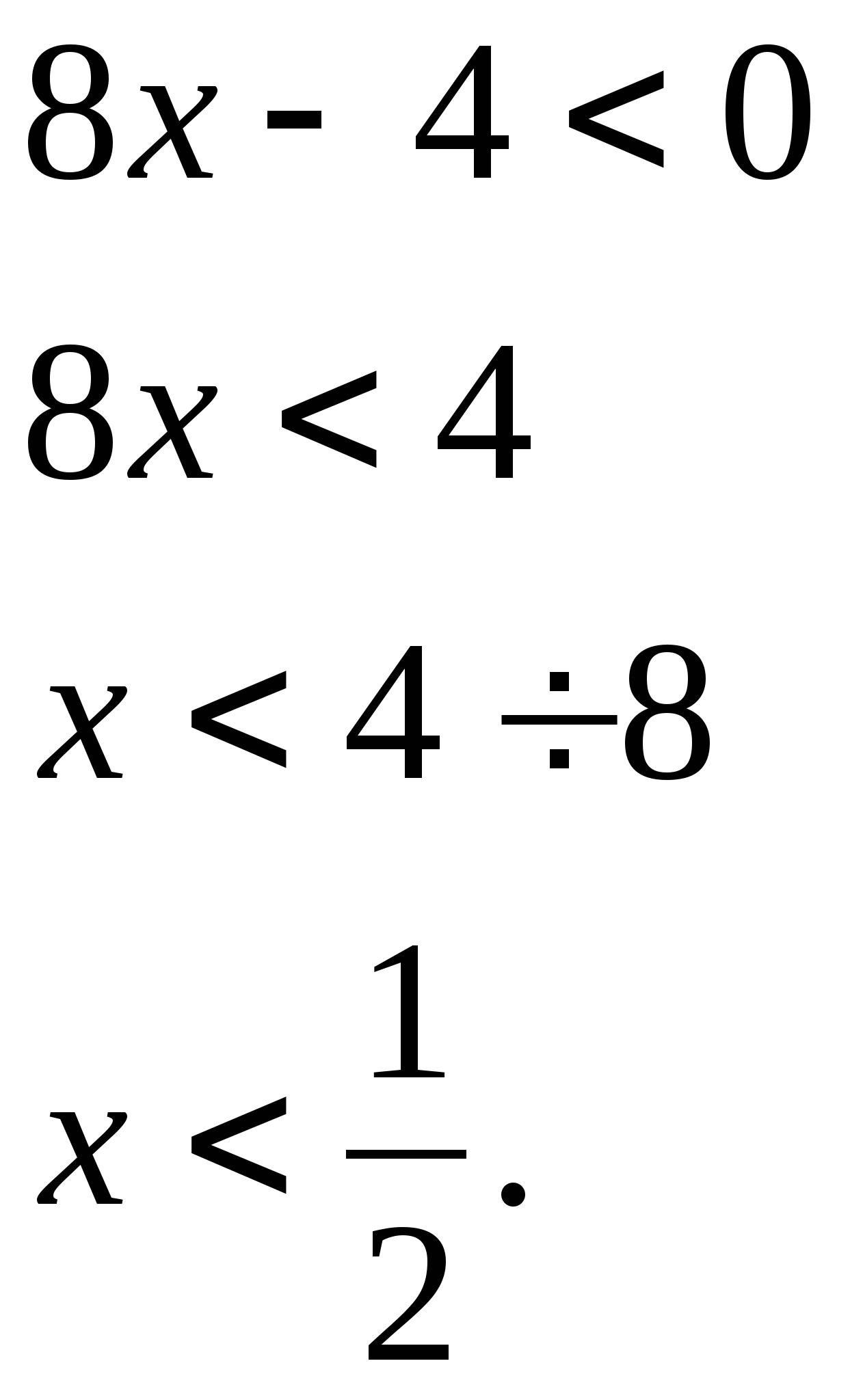
Ответ:

Тема: Неравенства с двумя переменными.

Определение: Неравенство, содержащее две переменные, называется неравенством с двумя переменными.

Например: 3х+7y>9; -2y+5x≤0; x²-6y≥0 являются неравенствами с двумя переменными.

Решить неравенство с двумя переменными - это значит найти множество пар чисел, обращающих данное неравенство в верное числовое неравенство, или доказать, что данное неравенство не имеет решений.

Используется следующий алгоритм:

1. Определить вид уравнения или функции, которые соответствуют данному неравенству;

2. Построить график этой функции или уравнения на координатной плоскости, т.е. разделить плоскость на части;

3. Определить, какая часть плоскости является множеством решений данного неравенства, для чего необходимо взять любую точку из одной части плоскости и проверить выполнимость неравенства; в качестве решения неравенства с двумя переменными нужно взять ту часть плоскости, где данное неравенство является верным и график самой функции при нестрогом знаке (≥ или ≤) неравенства.

Пример 1. Изобразим на координатной плоскости множество решений неравенства 2у+3х≤6.

Решение.

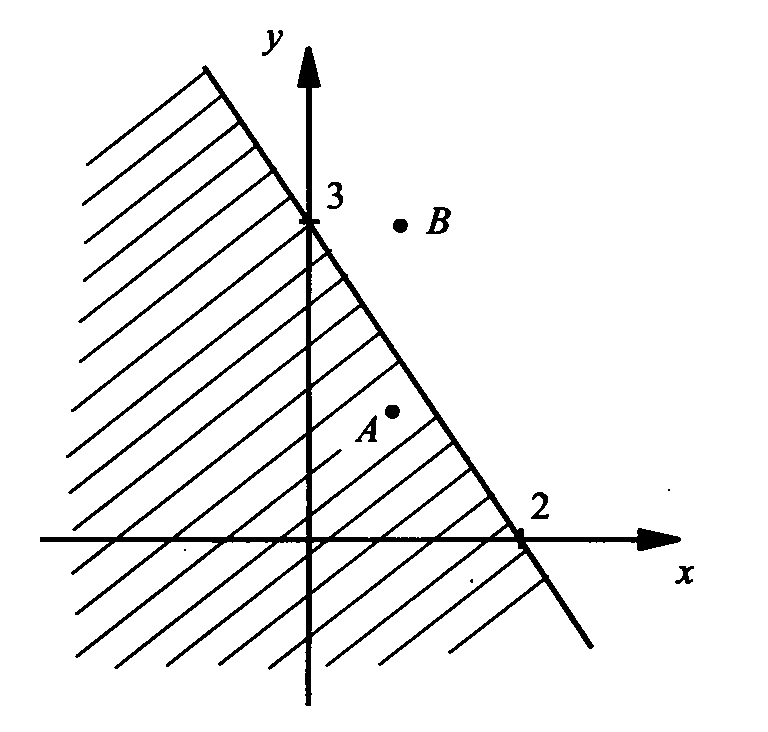
Строим прямую 2у+3х=6, у=3-1,5х, находим точки (0;3), (2;0).

Прямая разбивает множество всех точек координатной плоскости на точки, расположенные ниже ее, и точки, расположенные выше ее. Возьмем из каждой области по контрольной точке: А(1;1), В(1;3).

Координаты точки А удовлетворяют данному неравенству 2у+3х≤6, 2·1+3·1≤6, 5≤6

Координаты точки В не удовлетворяют данному неравенству 2у+3х≤6, 2·3+3·1≤6.

Данное неравенство может изменить знак на прямой 2у+3х=6, то неравенству удовлетворяет множество точек той области, где расположена точка А. Заштрихуем эту область. Мы изобразили множество решений неравенства 2у+3х≤6.

Тема: Система нелинейных неравенств с двумя переменными.

Определение: Решением системы неравенств с двумя переменными называется значения переменных, при которых верно каждое неравенство системы.

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений входящих в неё неравенств. На координатной плоскости множество решений системы неравенств изображается множеством точек, представляющих собой общую часть множеств, задаваемых неравенствами, входящих в систему.

Рассмотрим примеры.

П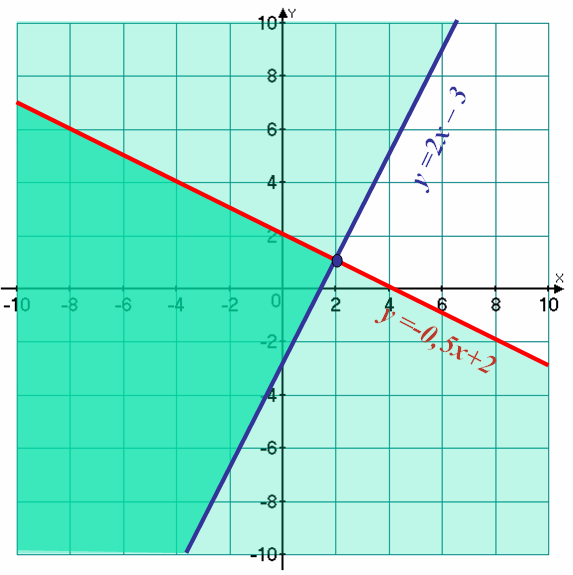ример 1. Решим систему неравенств:

Первое неравенство задает открытую полуплоскость, расположенную выше прямой y=2x-3. Второе неравенство задает открытую полуплоскость, расположенную ниже прямой y=-0,5x+2. Пересечением этих множеств является угол - множество решений данной системы неравенств.

П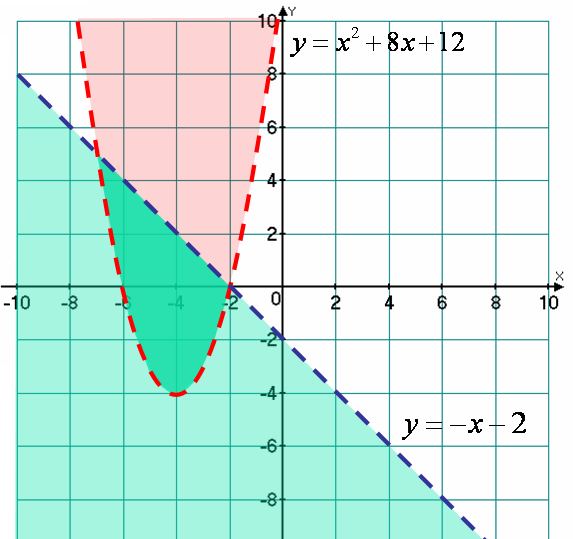ример 2. Решим систему неравенств: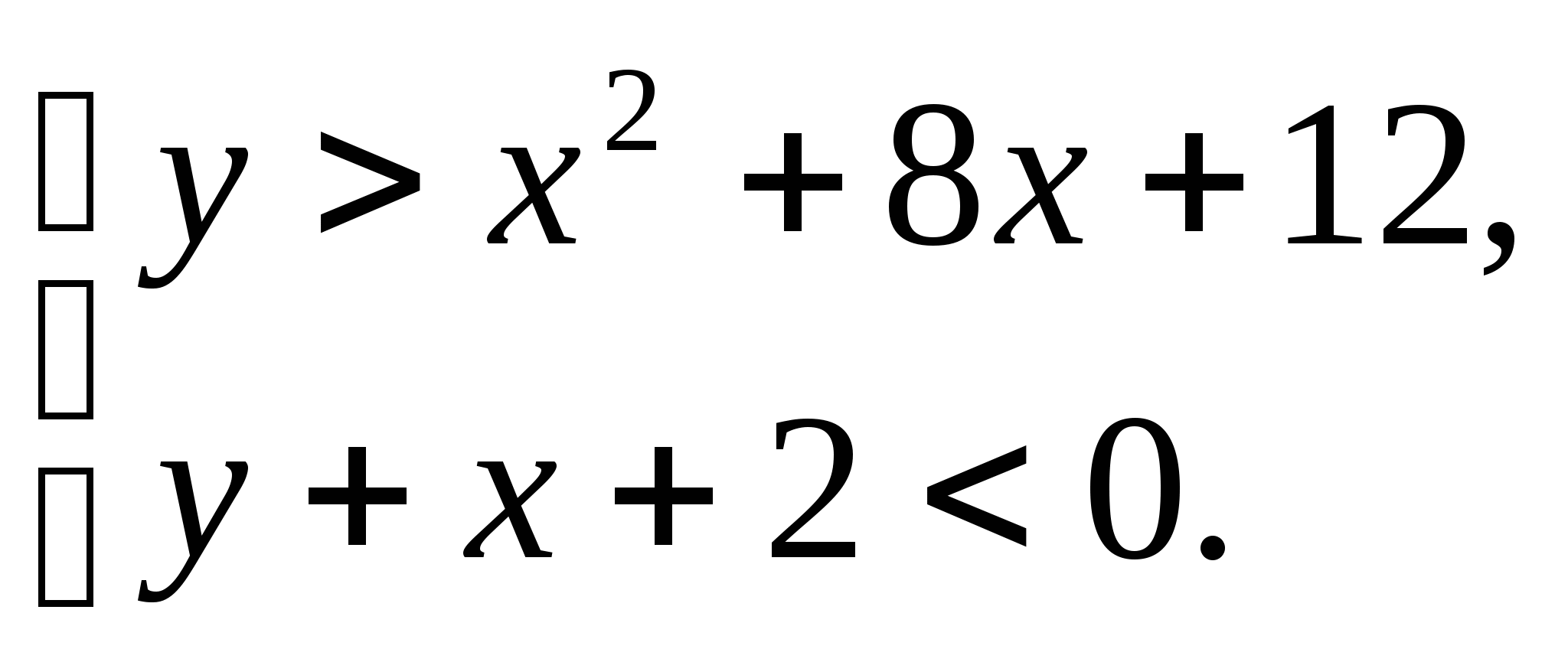

Запишем систему неравенств в виде: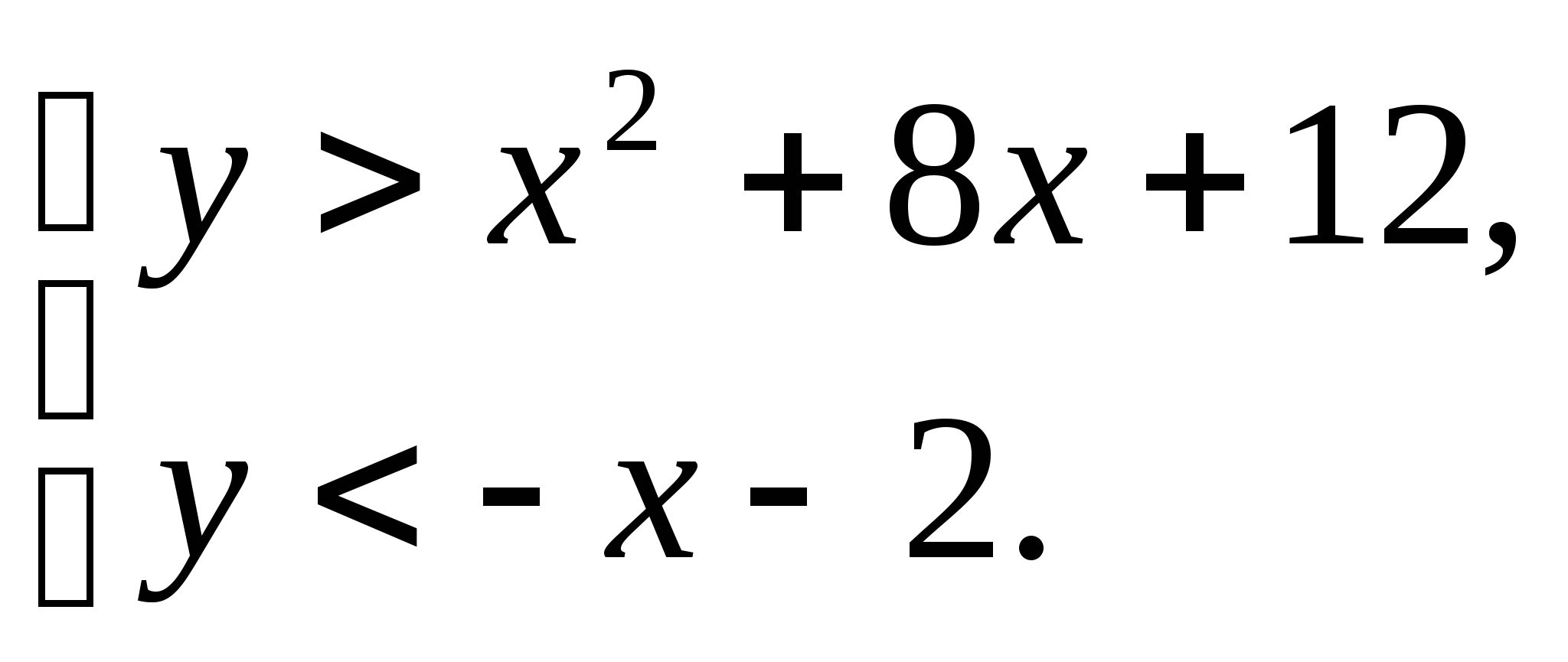

Изобразим множества точек решений каждого неравенства: y>x²+8x+12 и y<-x-2

Данная система неравенств задает ту из образовавшихся областей, которая расположена выше параболы и ниже прямой.