Урок по алгебре 'Преобразование графиков функций' (9 класс)

Приложение 6

Конспект интегрированного урока по информатике и математике

Тема УРОКА: ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ

Алгебра. 9 класс

Цели урока:

Образовательная: Обобщить и систематизировать теоретические знания учащихся о функции, ее свойствах и графиках; развивать умения выделять базовую функцию для представления общего вида графика; научить использовать программу GRAN1 для построения графиков функций.

Развивающая: Развитие логического мышления, развитие устной речи; формирование умения анализировать и делать выводы.

Воспитательная: Воспитание интереса к математике и информатике, внимания, организованности, уважительного отношения к учителю и друг к другу.

Продолжительность урока: 1 час (45 минут).

Тип урока: обобщение и систематизация знаний, умений и навыков.

Оборудование: раздаточный справочный и дидактический материал, компьютер..

Средства обучения: презентация Microsoft PowerPoint, программа GRAN1.

План урока:

1. Организационный этап. Сообщение темы и цели урока. (2 мин)

2. Мотивация учебной деятельности. (2 мин)

3. Актуализация опорных знаний. (3 мин)

4. Обобщение и систематизация основных теоретических положений. (20 мин)

5. Закрепление знаний и умений в процессе выполнения практических заданий.

(15 мин)

6. Подведение итогов урока. (2 мин)

7. Домашнее задание. (1 мин)

Ход урока

1. Организационный этап. Сообщение темы и цели урока

Учитель приветствует детей.

- Курс математики в школе строится так, что каждое понятие получает свое развитие в следующих классах. С понятием «функция» мы познакомились в 8 классе, встретились в 9-ом и обязательно вернемся к нему в 10-м и 11-м. Четыре урока мы изучали свойства функций, строили различные графики и преобразовывали их. Сегодня нам надо обобщить и систематизировать все полученные ранее знания.

II. Мотивация учебной деятельности

- Сегодня у нас с вами необычный урок алгебры. Мы пришли в кабинет информатики и, очевидно будем использовать компьютер. Зачем? А можно ли было обойтись без него? Станет ли урок интереснее от того, что мы будем использовать новые технологии? Больше ли материала мы сможем повторить и больше ли задач успеем решить? На все эти вопросы вы ответите мне в конце урока.

III. Актуализация опорных знаний

Форма работы - фронтальная.

- Чтобы вспомнить термины и определения, которые мы прошли за это время, я предлагаю вам заполнить кроссворд. (Каждому учащемуся дается карточка с кроссвордом).

1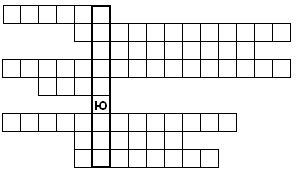. Как называется множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции? (график)

2. Как называется функция, если в некотором промежутке большему значению аргумента соответствует большее значение функции? (возрастающая)

3. Все значения, которые принимает зависимая переменная образуют … значений функции. (множество)

4. Как называются числовые промежутки, на которых функция сохраняет свой знак? (знакопостоянства)

5. Значения аргумента, при котором функция обращается в …, называются нулями функции. (нуль)

6. Как называется способ задания функции, если она задается с помощью математической формулы? (аналитический)

7. Как называется функция, если для любых х и -х из области определения выполняется равенство: f(-x) = f(x)? (четная)

8. Как по-другому называют независимую переменную? (аргумент)

- Какое слово в кроссворде получилось выделенным? (Компьютер) Для обобщения и систематизации теоретического материала мы будем использовать компьютер.

IV. Обобщение и систематизация основных теоретических положений.

Форма работы - в парах за компьютером.

- На Рабочем столе найдите пиктограмму Презентация ГРАФИКИ, вызовите контекстное меню правой кнопкой мыши, выберите команду Показать. Передвигаемся по презентации при помощи клавиши Enter.

Просмотр слайдов с параллельным обсуждением.

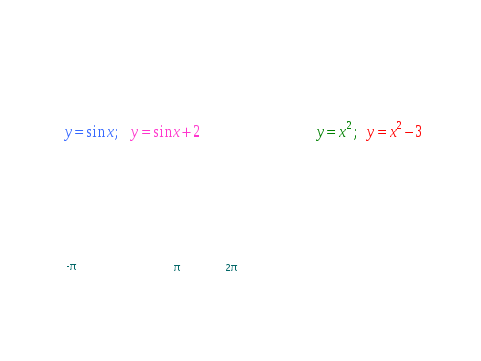
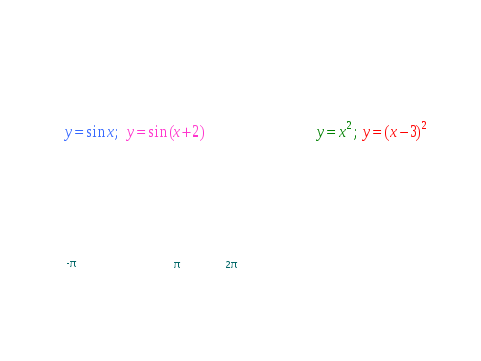
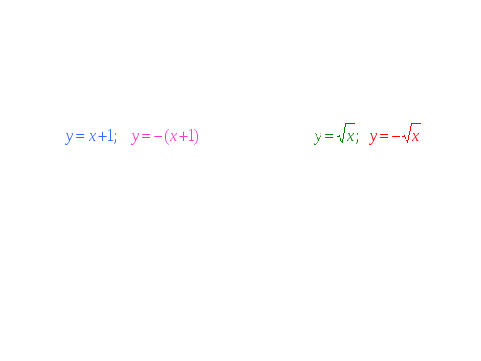
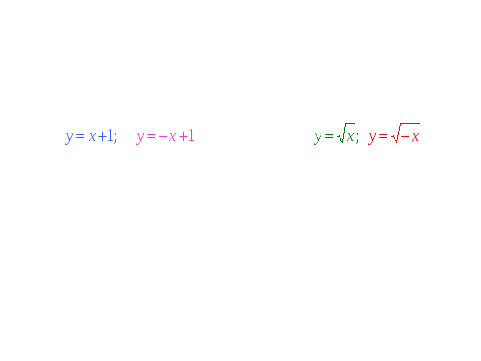
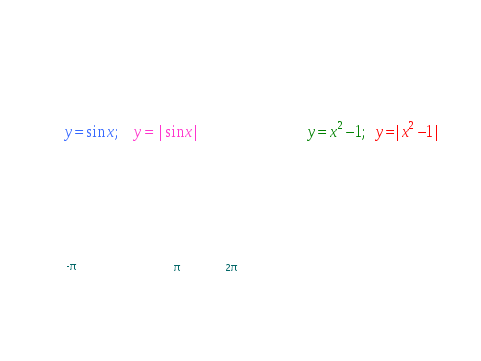
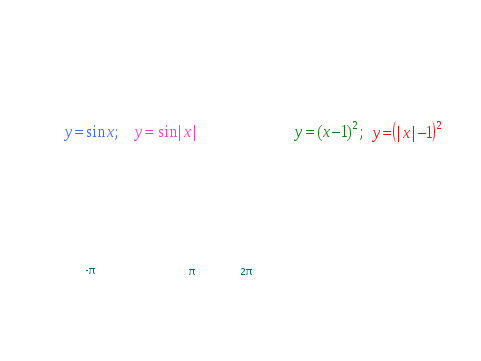
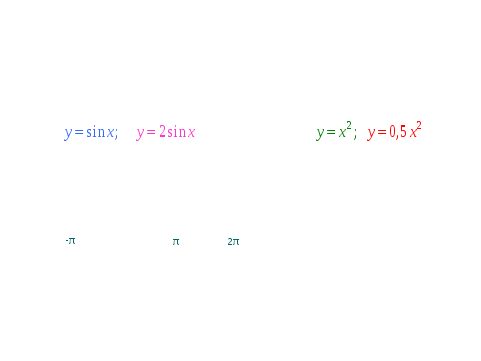
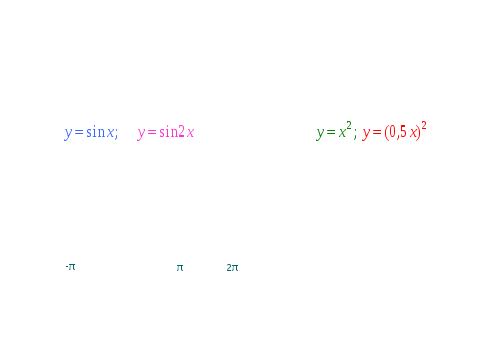
V. Закрепление знаний и умений в процессе выполнения практических заданий.

Форма работы - фронтальная.

- Чтобы говорить о преобразовании графика функции, надо четко знать, что является графиком данной функции и уметь выделять базовую функцию в выражении.

- Какая функция является базовой в предложенных примерах, и что является графиком этой функции?

- Какие надо выполнить преобразования базового графика?

- Научимся строить графики функций при помощи математической программы GRAN1. Запускаем программу при помощи ярлыка на Рабочем столе. (Знакомимся с интерфейсом программы. У каждого ученика на парте инструктивная карта).

Чтобы построить график функции, надо:

1. Выбрать в пункте меню Объект команду Новая функция (нажать на первую кнопку на панели инструментов или функциональную клавишу F4).

2. В открывшееся окно ввести с помощью мыши функцию и её аргумент (не забудьте аргумент взять в скобки).
   

3. Нажать три раза кнопку Ввод, если не требует изменения отрезок задания (в противном случае ввести изменения параметров А и В).

4. Выбрать в пункте меню График команду Построить (или нажать F5).

Чтобы удалить график, надо:

в поле Выбор щелкнуть по нужной функции, затем в меню Объект выбрать Удалить (или нажать F8).

1. у = х

у = |х|

у = |х - 3|

у = | |х| - 3|

2. у = (х  2)²

у = (|х| - 2)² - 3

у = (|х| - 2)² - 3

у = |(|х| - 2)² - 3|

у = − (|х| + 2)²

По ходу построения идет обсуждение типа преобразований и видов графиков.

VI. Подведение итогов урока.

- Сегодня мы систематизировали материал по преобразованию графиков функций. Ответьте на вопросы, которые я задала в начале урока:

- Стал ли урок интереснее от того, что мы использовать новые технологии?

- Больше ли материала мы смогли повторить?

- Больше ли упражнений успели сделать?

- В каких других областях кроме «чистой» математики вы встречали изображения графиков?

- Вы никогда не задумывались как создается картинка на экране монитора? (Показываю картинку, созданную в графическом редакторе Word'а). Программа хранит изображение в виде набора математического описания линий.

Отмечаю учащихся активно работавших на уроке.

V. Домашнее задание.

Сделать шаблоны парабол у = 2х², у = 1/2х². А.Г.Мерзляк, стр.20, № 82.