Урок в 9 классе Решение иррациональных уравнений

Урок по алгебре в 9 классе (с углубленным изучением математики) по теме "Решение иррациональных уравнений"

Соловьева Н.А., учитель

математики МБОУ СОШ №6

Цели:

1) Обобщение и углубление знаний учащихся о способах решения иррациональных уравнений.

2) Отработка навыков и умения решения иррациональных уравнений. Наблюдение за применением алгоритмов, оформлением решений иррациональных уравнений и записью ответов.

3) Повышение мыслительной деятельности учащихся; развитее логического мышления; навыков исследования; воспитания настойчивости и усердия.

Ход урока

I. Актуализация опорных знаний.

1. Решите уравнения с помощью математических рассуждений (устно).

а) + = -3;

б) 5 + = 1;

в) + = 0;

г) + = 6; (применить свойство монотонности функции)

д) = 8 - х; (оценить область определений)

2. Самостоятельная работа (с поверкой в классе)

Решите уравнения:

Вариант 1.

1) = 3; ()

2) = х - 2; (5)

3) - = 1; (4)

4) + 6 = х - 3; (12)

5) х + 2х + = 12. (-4; 2)

Вариант 2.

1) = 1; ()

2) = 6 - х; (3)

3) - = 2; (7)

4) х - 5 = 30 - ; (30)

5) х+ = х + 3. (0 ;1)

Работа выполняется под копирку. Один экземпляр учащиеся сдают учителю, по второму - проверяют работу (ответы записаны заранее на отворотах доски) исправляют ошибки, ставят себе оценки. В ходе работы учащиеся повторяют основные способы решения иррациональных уравнений.

II. Формирование умений и навыков.

1. Разбор уравнений из индивидуального домашнего задания. (Учитель дает отдельным учащимся решить дома два уравнения, намеренно выбирает решения с ошибками и просит учащихся записать эти решения на доске (заранее)).

а) - = 5 - х

1) х = 5 - корень уравнения (с помощью проверки)

2) 5 - х 0, т.е. х 5

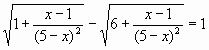
Нет решений

Ответ: 5

Потеря корня! Проводится стихийная пресс-конференция. Учащиеся находят, где допущена ошибка (рассмотрен случай >0).

Рассматривают случай <0; записывают верный ответ:

Верный ответ: 5; .

б)

нет решений

Ответ: -1.

Потеря корня! Почему и где?

Учащиеся выясняют, что произошло сужение ОДЗ уравнения. Записывают верное решение.

Верный ответ: -2; -1.

Примечание: домой учитель задает решить аналогичные уравнения.

2. Решите уравнения.

1) (введение новой переменной)

2) (возведение обеих частей в четную степень. Обратить внимание на ОДЗ)

3)

ОДЗ: R

Учащиеся повторяют: а) ;

б) Решение уравнений с модулями.

1 2

1)

2)

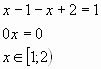
3)

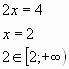
Ответ: .

Обратить внимание учащихся, что решением уравнения является числовой промежуток.

4)

Учащиеся решают самостоятельно

Ответ: -6; 5.

5)

t 0

Т.к. t 0, то

,

5t = 15

t = 3

х = 2

Проверка

4 = 4

Ответ: 2

6)

ОДЗ:

,

, т. е

Обратить внимание учащихся на обратную замену.

, т.е.

7)

Рациональнее возводить обе части уравнения в квадрат. Почему? Проанализировать ход решения.

Решение начать с нахождения ОДЗ, т.к. проверку сделать сложно.

ОДЗ: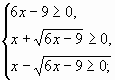

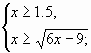
Т.к. , то , т.е.

ОДЗ:

Ответ:

III. Итог урока

Домашнее задание

№1. Решить уравнение:

а) ;

б) .

№ 11.132(в), 11.136(в), 11.137(в). 11.139(в) - Сборник задач по алгебре для 8-9 классов: учебное пособие для учащихся школ и классов с углубленным изучением курса математики/М.Л. Галицкий и др. - М.: "Просвещение", 2004 г.