- Учителю
- Разработка урока по теме Сумма двух векторов. Законы сложения векторов. Правило треугольника и параллелограмма.
Разработка урока по теме Сумма двух векторов. Законы сложения векторов. Правило треугольника и параллелограмма.
Г - 9 класс Урок № 3
Сам по себе научный метод никуда нас не приводит;
он и не появился бы без страстного стремления к познанию.
А. Эйнштейн.
Тема урока: «Сумма двух векторов. Законы сложения векторов. Правило параллелограмма».
Цели урока:
-
Дидактическая: ввести понятие суммы двух векторов, рассмотреть законы сложения векторов; сформировать умение находить сумму двух векторов по правилу треугольника и параллелограмма.
-
Развивающая: развивать воображение - репродуктивное, творческое, образное; абстрактное и логическое мышление, умение обобщать.
-
Воспитательная: нравственное воздействие, воспитание культуры умственного труда, культуры общения.
Оборудование: проектор, презентация MS POWERPOINT.
Ход урока.
-
Организация начала занятия.
Сообщение темы и целей урока.
-
Мотивация познавательной деятельности.
Учебный материал, изучаемый на данном занятии, служит основой для изучения и правильного понимания многих вопросов математики, физики и их приложений.
-
Проверка выполнения домашнего задания. Разбор нерешенных заданий.
-
Устно № 752.
Верно ли утверждение:
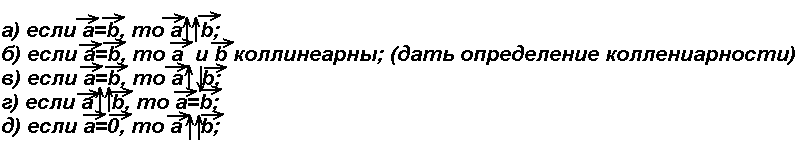
-
Изучение нового материала.
Рассмотрим движение, совершаемое в течение некоторого промежутка
времени, например, в течение одного часа, затем рассмотрим
расстояния, пройденные за этот промежуток времени. Задача сложения
движений сведется к простой задаче сложения пройденных расстояний.
Совпадают ли здесь правила сложения с правилами с правилом сложения
в арифметике, когда складывая 2 и 3, мы получаем 5? 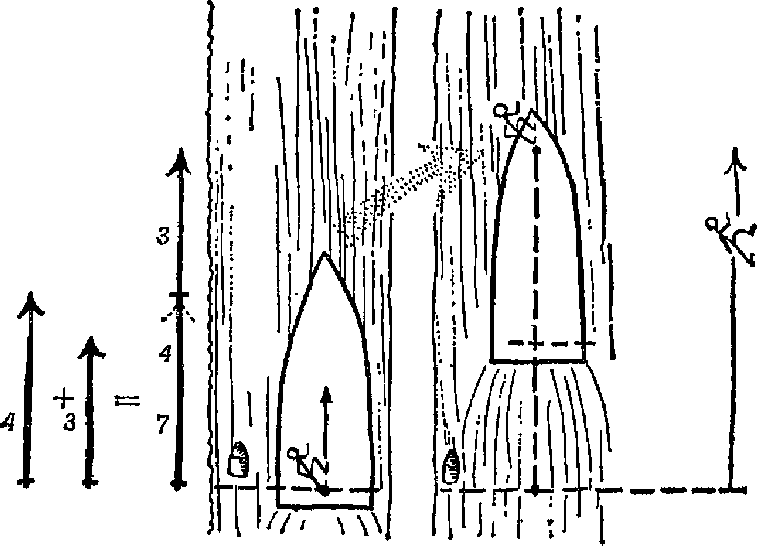 Эксперимент вскоре убеждает нас в том, что это правило действует
лишь в том случае, если отдельные складываемые перемещения
происходят по прямой линии в одном и том же направлении. Тогда
перемещение на 4 м в направлении на север на 3 м в направлении на
север дают суммарное перемещение в направлении на север равное 7 м;
Эксперимент вскоре убеждает нас в том, что это правило действует
лишь в том случае, если отдельные складываемые перемещения
происходят по прямой линии в одном и том же направлении. Тогда
перемещение на 4 м в направлении на север на 3 м в направлении на
север дают суммарное перемещение в направлении на север равное 7 м;
Е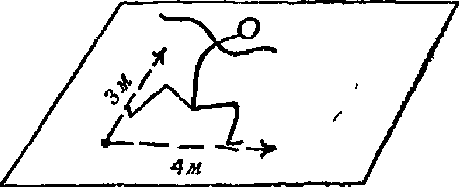 сли
же направления движения оказываются различными, то простая
арифметика бессильна. Если к перемещению на 3 м в северном
направлении прибавить перемещение на 4 м в восточном направлении,
то мы не получим перемещения на 7 м.
сли
же направления движения оказываются различными, то простая
арифметика бессильна. Если к перемещению на 3 м в северном
направлении прибавить перемещение на 4 м в восточном направлении,
то мы не получим перемещения на 7 м.
Чтобы действовать в соответствии с наблюдаемыми в жизни фактами, мы должны пользоваться другим типом сложения.
Ввести понятие двух векторов.

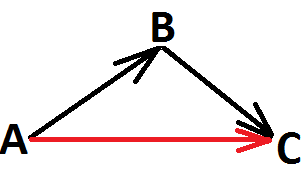
Отметим точку А, отложим от этой точки вектор ![]() , затем от точки В отложим вектор
, затем от точки В отложим вектор ![]() . Вектор
. Вектор ![]() называется суммой векторов
называется суммой векторов ![]() и
и ![]() . Это правило сложения векторов называется суммой векторов
. Это правило сложения векторов называется суммой векторов
![]() и
и![]() .
(или правило треугольника).
.
(или правило треугольника).
Сумма векторов ![]() и
и![]() обозначается
обозначается
![]() +
+![]() ;
;
Для любого вектора ![]() справедлива равенство
справедлива равенство ![]() ;
;
Практическое задание № 753
Турист прошел 20 км на восток из города А в город В, а потом 30
км на восток в город С. Выбрав подходящий масштаб начертите векторы
![]() и
и ![]() . Равны ли векторы
. Равны ли векторы ![]() +
+![]() и
и ![]() ?
?
Рассмотрим законы сложения веторов.
Теорема.
Для любых векторов ![]() ,
,![]() и
и
![]() справедливы равенства:
справедливы равенства:
-
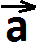 +
+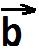 =
=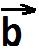 +
+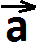 (переместительный закон)
(переместительный закон)
-
(
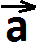 +
+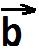 )+
)+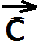 =
=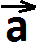 +(
+(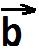 +
+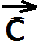 )
(сочетательный закон)
)
(сочетательный закон)
Доказательство
-
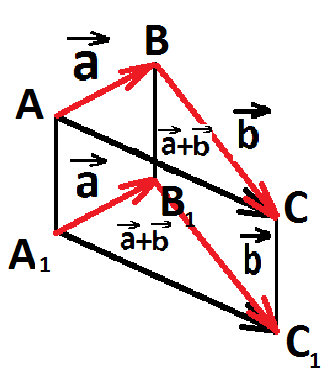
Рассмотрим случай, когда векторы
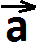 и
и 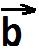 не коллинеарны. От произвольной точки А отложим векторы
не коллинеарны. От произвольной точки А отложим векторы
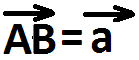 и
и 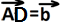 и на этих векторах построим параллелограмм АВСD.
и на этих векторах построим параллелограмм АВСD.
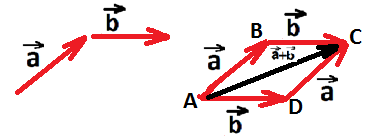
По правилу треугольника ![]() =
=![]()
Аналогично ![]()
Отсюда следует, что ![]()
При доказательстве свойства мы использовали правило параллелограмма. Это правило используется в физике при сложении двух сил.
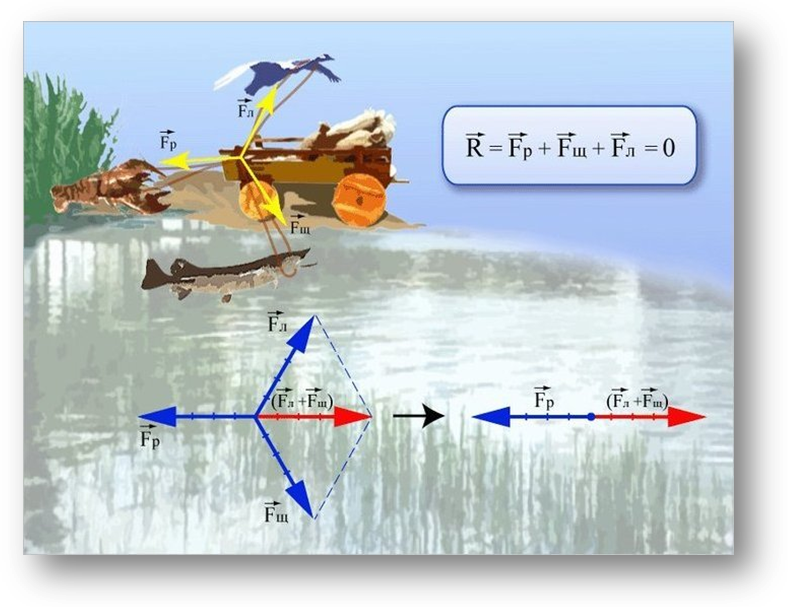
Задача о лебеде, раке и щуке.
История о том, как «лебедь, рак да щука везти с поклажей воз взялись», известна всем. Но едва ли кто пробовал рассматривать эту басню с точки зрения механики. Результат получается вовсе не похожий на вывод баснописца Крылова.
Перед нами механическая задача на сложение нескольких сил, действующих под углом одна к другой. Направление сил определено в басне так:
… Лебедь рвется в облака,
Рак пятится назад, а щука тянет в воду.
Это значит что одна сила, тяга лебедя, направлена вверх; другая, тяга щуки (0B), - вбок; третья, тяга рака (0C), - назад. Не забудем, что существует еще четвертая сила - вес воза, которая направлена отвесно вниз. Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех приложенных к возу сил равна нулю.
Так ли это? Посмотрим. Лебедь, рвущийся к облакам, не мешает работе рака и щуки, даже помогает им: тяга лебедя, направленная против силы тяжести, уменьшает трение колес о землю и об оси, облегчая тем вес воза, а может быть, даже вполне уравновешивая его, - ведь груз невелик («поклажа бы для них казалась и легка»). Допустив для простоты последний случай, мы видим, что остаются только две силы: тяга рака и тяга щуки. О направлении этих сил говорится, что «рак пятится назад, а щука тянет в воду». Само собой разумеется, что вода находилась не впереди воза, а где-нибудь сбоку (не потопить же воз собрались Крыловские труженики!). Значит, силы рака и щуки направлены под углом одна к другой. Если приложенные силы не лежат на одной прямой, то равнодействующая их никак не может равняться нулю.
Задача о крыловских лебеде, раке и щуке, решенная по правилам механики. Равнодействующая (0D) должна увлекать воз в реку.
Поступая по правилам механики, строим на обеих силах 0B и 0C параллелограмм, диагональ его 0D дает направление и величину равнодействующей. Ясно, что эта равнодействующая сила должна сдвинуть воз с места, тем более, что вес его полностью или частично уравновешивается тягой лебедя. Другой вопрос - в какую сторону сдвинется воз: вперед, назад или вбок? Это зависит уже от соотношения сил и от величины угла между ними.
Читатели, имеющие некоторую практику в сложении и разложении сил, легко разберутся и в том случае, когда сила лебедя не уравновешивает веса воза; они убедятся, что воз и тогда не может оставаться неподвижным. При одном только условии воз может не сдвинуться под действием этих трех сил: если трение у его осей и о полотно дороги больше, чем приложенные усилия. Но это не согласуется с утверждением, что «поклажа бы для них казалась и легка».
Во всяком случае, Крылов не мог с уверенностью утверждать, что «возу все нет ходу», что «воз и ныне там». Это, впрочем, не меняет смысла басни.
-
Первичная проверка понимания.
-
Начертите попарно неколлинерные векторы
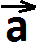 ,
,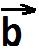 ,
,
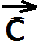 ; Постройте векторы
; Постройте векторы 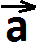 +
+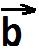 ;
;
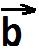 +
+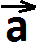 ;
;
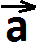 +
+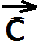 ;
(
;
(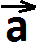 +
+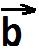 )+
)+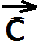 ;
;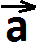 +(
+(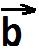 +
+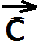 );(
);(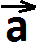 +
+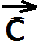 )+
)+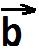 ;
Какие из построенных векторов равны друг другу? (Работа в
парах)
;
Какие из построенных векторов равны друг другу? (Работа в
парах)
Ответ на экране.
-
№ 759 (а) решить без чертежа. Докажите, что
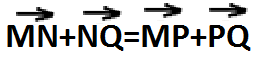
Доказательство:
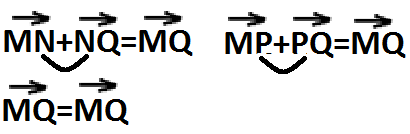
Равенство верно.
-
Упростить выражение.
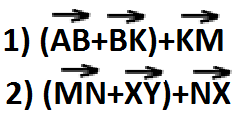
Решение.
Используем законы сложения
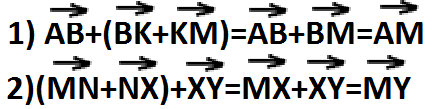
ПОДУМАЙ!!!
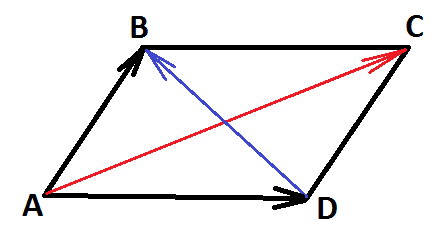
В случае параллелограмма, построенного на данных векторах, одна
из его диагоналей АС является суммой векторов ![]() и
и ![]() , а диагональ BD?
, а диагональ BD?
Самостоятельная работа по готовым чертежам. Балаян Э.Н. (задачи по готовым чертежам для подготовки в ГИА) стр. 135; № 4 и 5.
П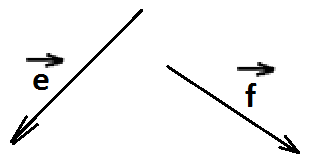 остроить
вектор
остроить
вектор ![]() двумя способами
двумя способами
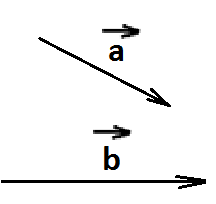
Построить вектор ![]() двумя способами
двумя способами
-
Подведение итогов работы.
1. Что узнали нового?
2. Какое практическое применение имеет данный материал?
3. В чем возникли затруднения?
4. Как вы оченили свою работу?
-
Домашнее задание: прочитать п. 79, 80 ; вопросы 7-10 стр 204; выполнить № 754, 759 (б) без чертежа, 763 (б).
8