Урок по теме Метод мини-максов при решении уравнений

МАОУ «Гимназия № 14»

Урок-лекция

Тема: Метод минимаксов

при решении уравнений.

Подготовила учитель математики гимназии № 14

Лунёва Людмила Юрьевна

Метод минимаксов при решении уравнений

(метод сравнения, метод мажоранта, использование ограниченности функций).

Цель урока: - систематизировать понятия области определения и области значений, в том числе D(f) и E(f) основных элементарных функций;

- познакомить учащихся с методом минимаксов, показать, в каких случаях его применяют.

Тип урока: урок-лекция.

Ход урока:

Сегодня мы вспомним понятия области определения (множество допустимых значений аргумента) и области значений (область изменения функции) функций - это пригодится при рассмотрении темы, кроме того, задания, связанные с данными понятиями, ежегодно встречаются в текстах ЕГЭ.

Далее мы рассмотрим один из нестандартных методов решения уравнений - метод мини-максов (метод сравнения, метод мажоранта, использование ограниченности функций) - его нет в некоторых учебниках 10-11 классов (например, в учебнике Колмогорова), т.е. по программе общеобразовательных классов эта тема не изучается. Но, например, в учебнике Никольского (для 11 класса) эта тема в какой-то степени представлена.

И одной из причин, по которой я рассматриваю сегодня эту тему, является та, что уравнения, решаемые данным методом, встречались в экзаменационных заданиях и, в частности, в заданиях ЕГЭ. Причём мы увидим, что встречаются уравнения, которые без знания этого метода решить невозможно или затруднительно.

Вспомним, что такое D(f) и E(f).

Найти D(f) и E(f) следующих функций:

Обращаю ваше внимание на то, оценить значения квадратичной функции вида f(х)= можно с помощью выделения полного квадрата, либо через координаты вершины параболы: E(f)= при и E(f)= при .

ПР-1. Решим уравнение .

Решение: Данное уравнение равносильно системе 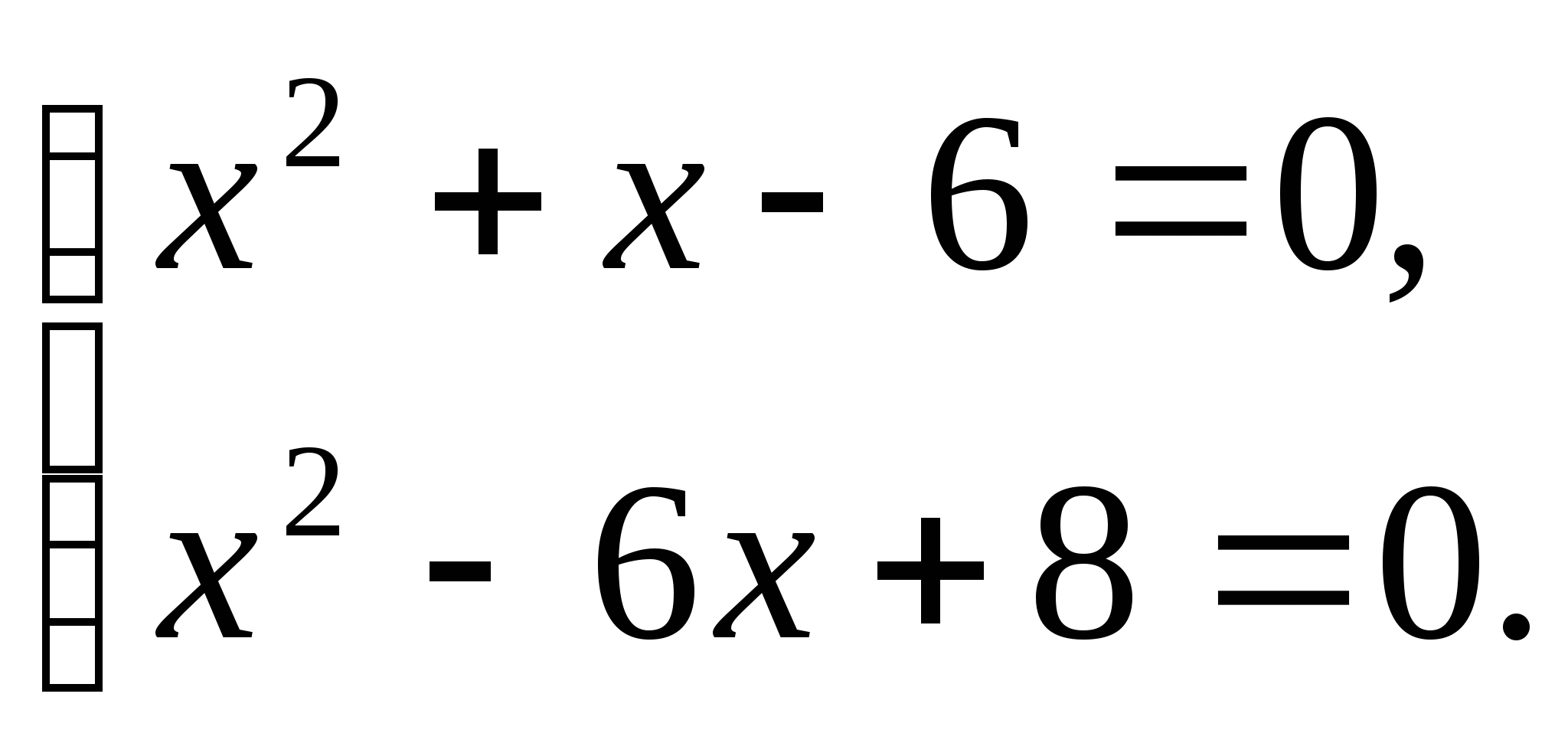Получаем 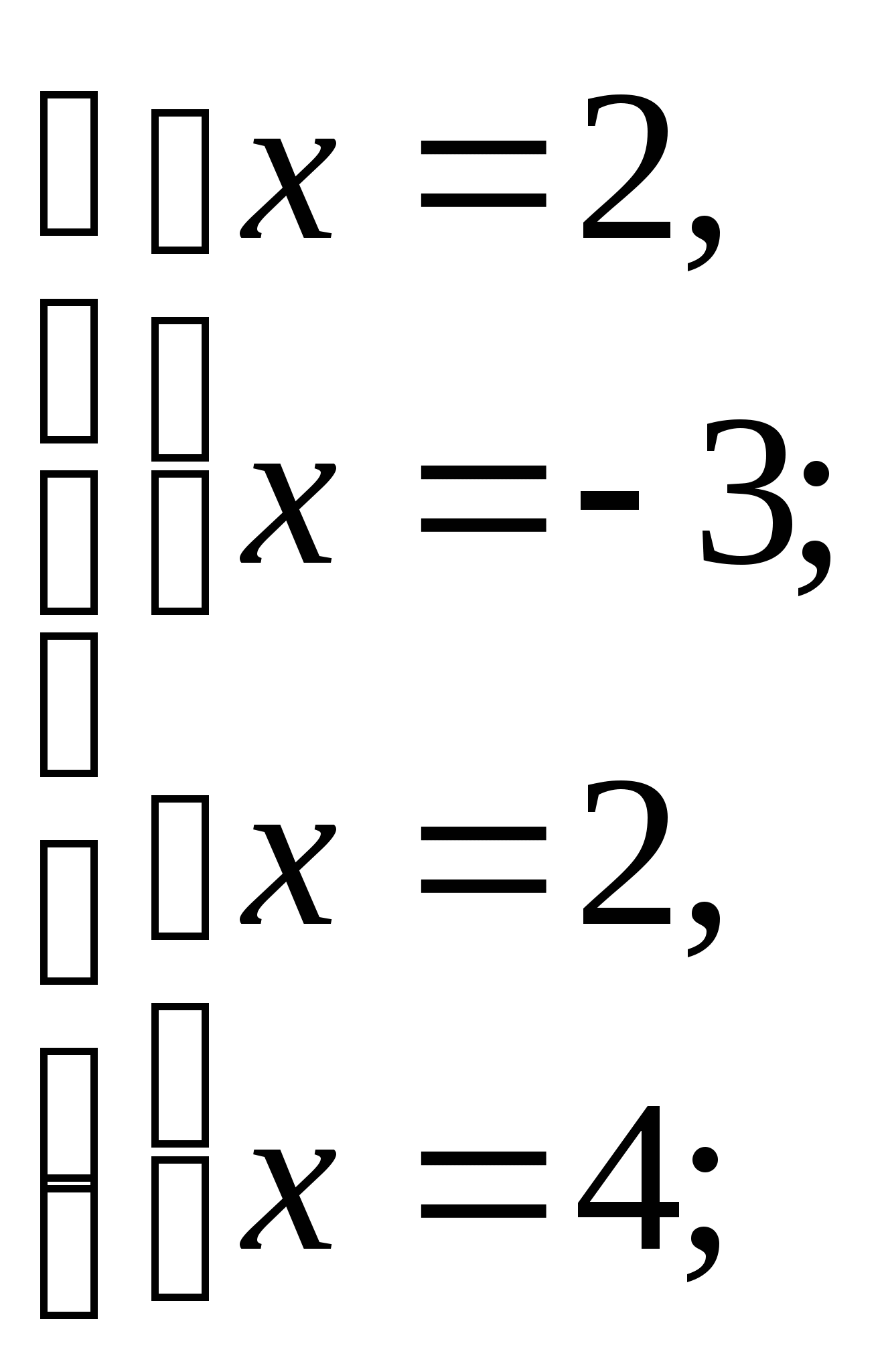(учащиеся находят корни уравнений самостоятельно). Значит х=2. Ответ: х=2.

Причём в данном уравнении показатели степени могли быть любыми чётными числами.

ПР-2. Решить уравнение .

Решение: данное уравнение можно решить, применяя формулу суммы косинусов (желающие могут выполнить это дома самостоятельно).

Областью допустимых значений (ОДЗ) аргумента является множество действительных чисел R. Но можно заметить, что

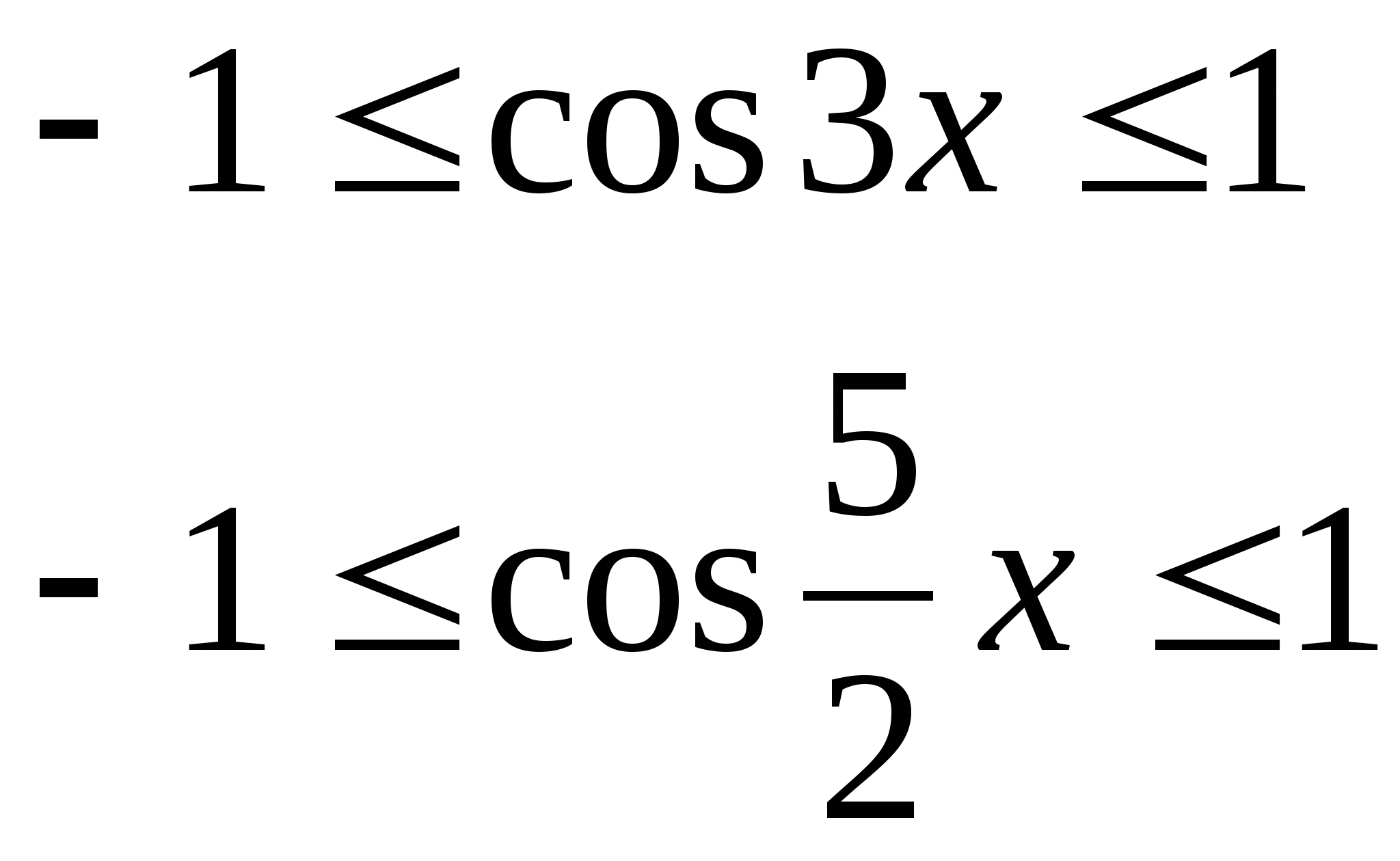значит . Причём равенство двум (согласно условию уравнения) достигается при одновременном равенстве слагаемых единице, т.е. получаем систему:

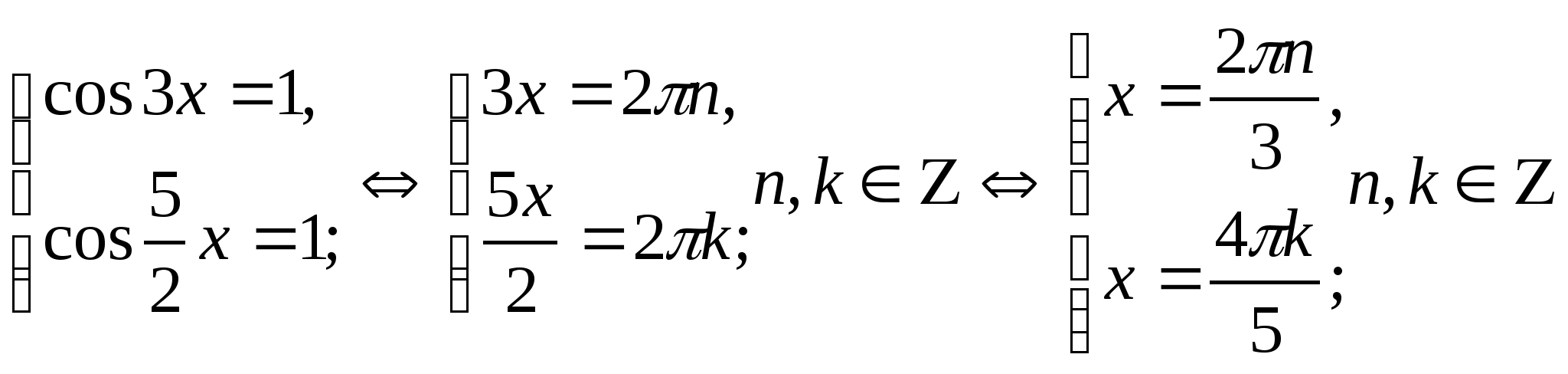
Найдём, при каких n и k значения х совпадут, т.е. система будет иметь решение - для этого выразим одну переменную через другую:

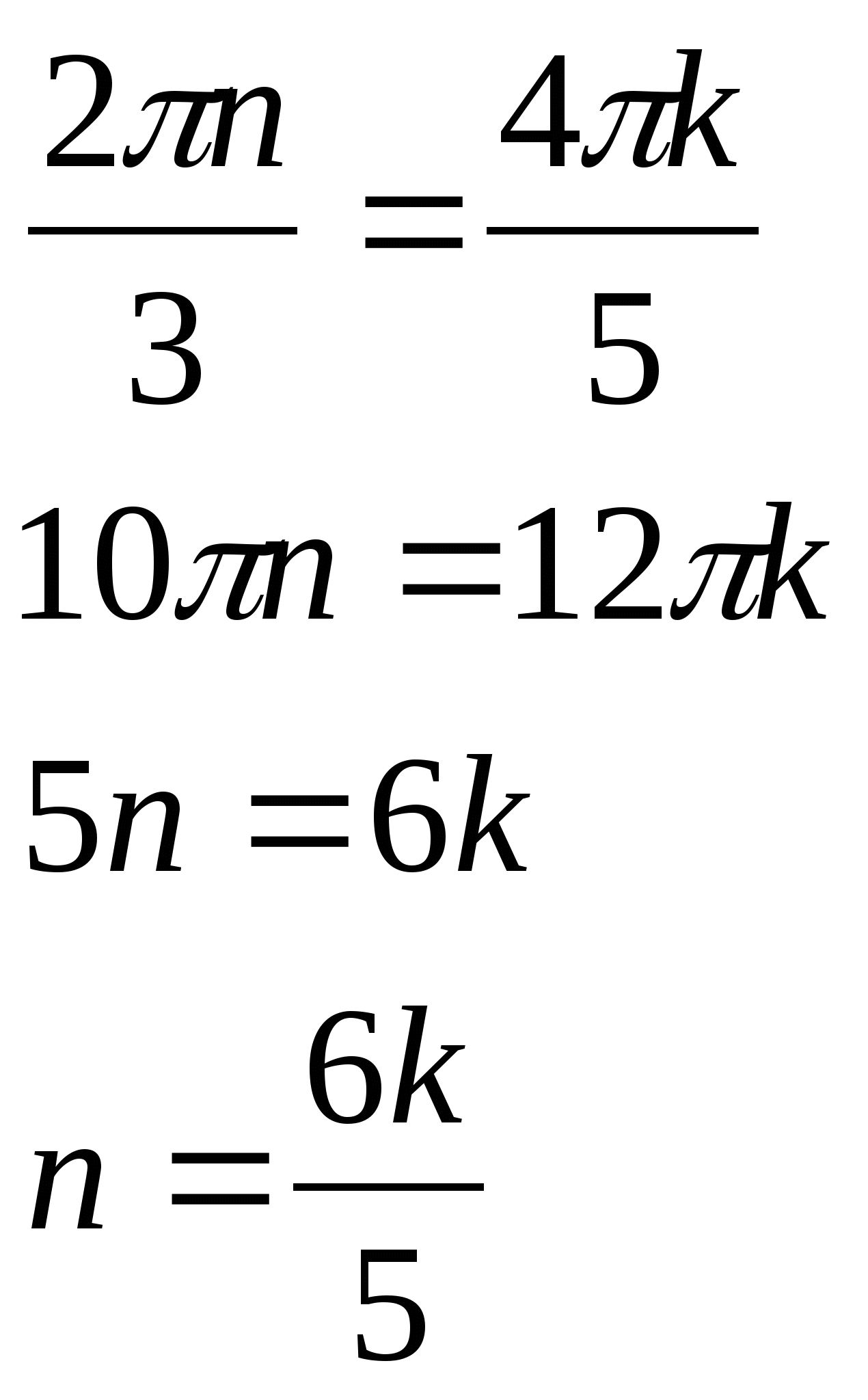
А т.к. , то получаем, что кратно 5, т.е.

. Ответ: х=.

При данном способе решения некоторые трудности могут возникнуть при отборе корней.

ПР-3. Решить уравнение .

Решение: В чём отличие этого уравнения от предыдущих?

Отличие состоит в том, что в предыдущих уравнениях их компоненты были выражениями одного типа, причём уравнения 1 и 2 можно было решать, не опираясь на область изменения значений входящих в них выражений, а в данном уравнении выражения разных типов: многочлен и тригонометрическое выражение.

При выполнении 1-го задания мы выяснили, что данные выражения имеют смысл при любых значениях переменных и что , а . Т.к. по условию уравнения значения данных выражений равны, то получаем, что это возможно только в случае, когда каждое из них равно 3, т.е. получаем, что данное уравнение равносильно системе: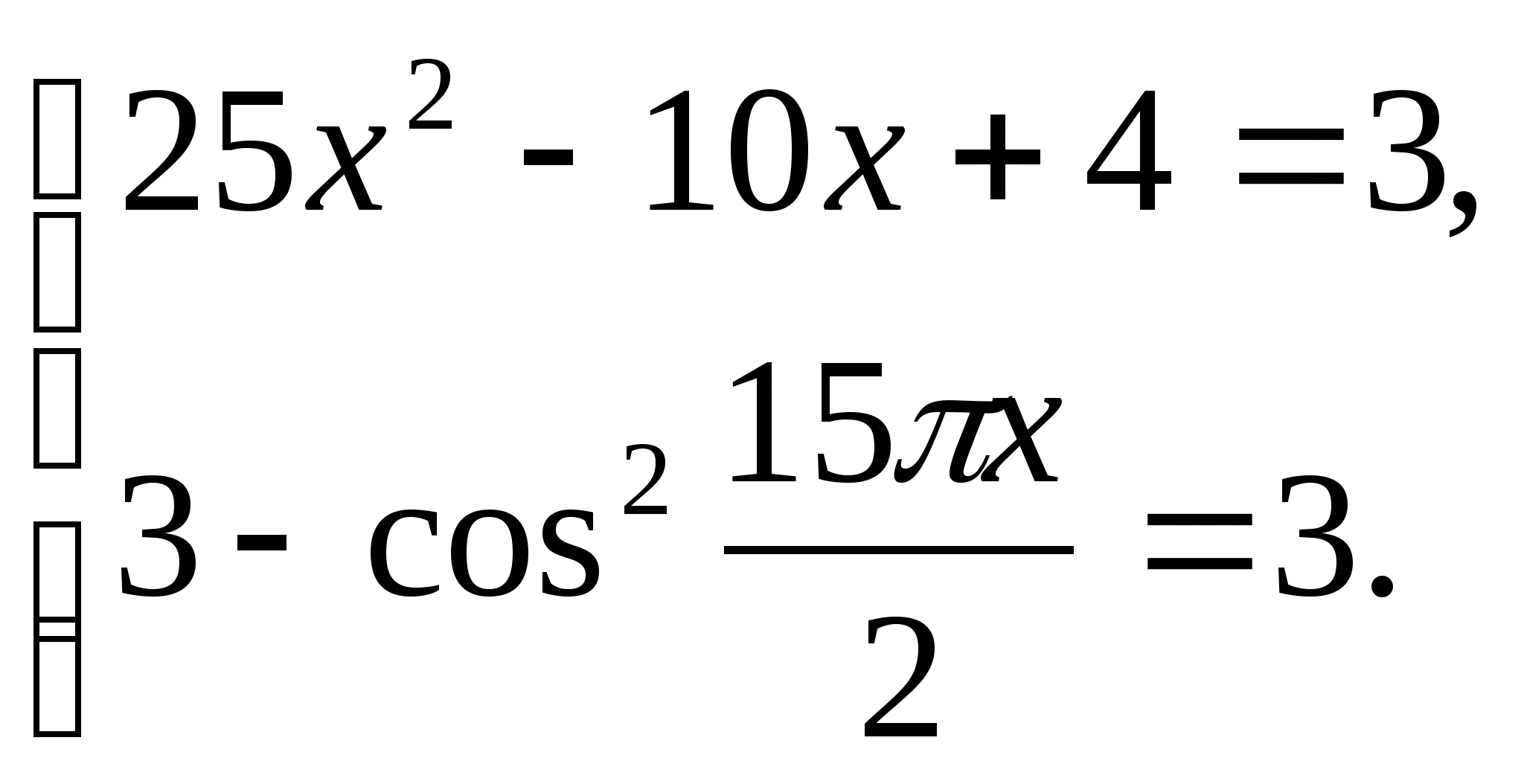

В данном случае проще всего решить первое уравнение системы и проверить, будут ли полученные числа корнями второго уравнения.

Корнем первого уравнения системы является х= (можно решить это уравнение через дискриминант, через выделение полного квадрата или по теореме Виета), проверка показывает, что при данном значении аргумента второе уравнение обращается в верное равенство (т.к.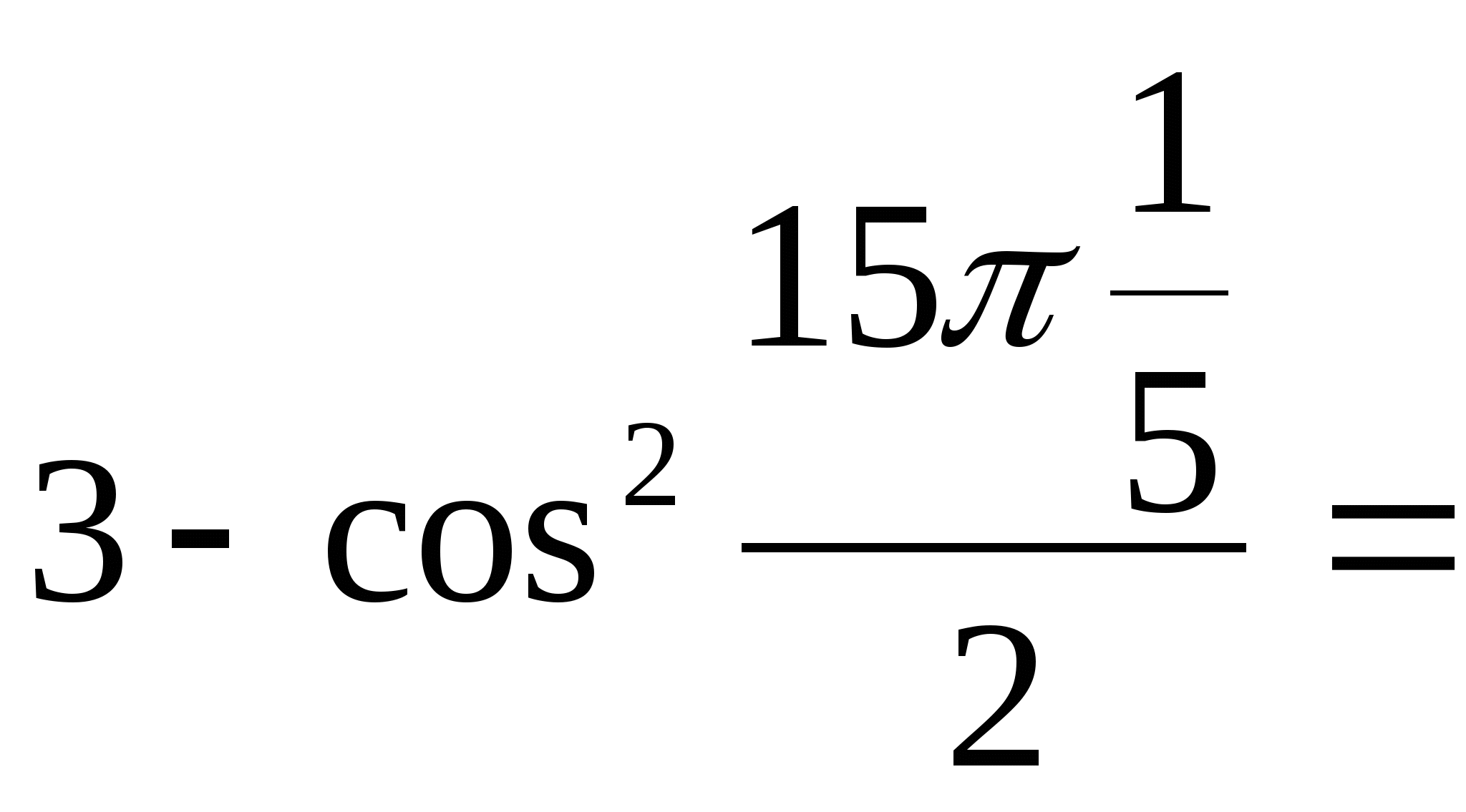). Ответ: х=0,2.

(Задание предлагалось в текстах ЕГЭ в 2006 году)

При решении данного уравнения (также как и предыдущих) мы воспользовались ограниченностью входящих в него выражений. Встречались ли вы с таким приёмом ранее?

Этот приём получил название метода минимаксов (метода сравнения, метода мажоранта, использование ограниченности функций). Можете ли вы объяснить, в чём его суть?

Если требуется решить уравнение вида f(х)=g(x) (1) и на общей области определения Е функций f(х) и g(x) выполняются неравенства f(х), g(x) (или f(х) , g(x) ), то уравнение (1) равносильно системе:

Число А и называют мажорантой функций.

При применении данного метода можно использовать некоторые базовые неравенства (см. далее): например, неравенство Коши (1), оценка двух взаимно обратных чисел (4), оценка однородного линейного тригонометрического выражения (6) и др.

Базовые неравенства, часто используемые для оценки при применении метода минимаксов:

1. Неравенство Коши (неравенство между средним арифметическим и средним геометрическим двух неотрицательных чисел):

Причём равенство достигается при . Если же , то .

(данное неравенство можно получить из неравенства ).

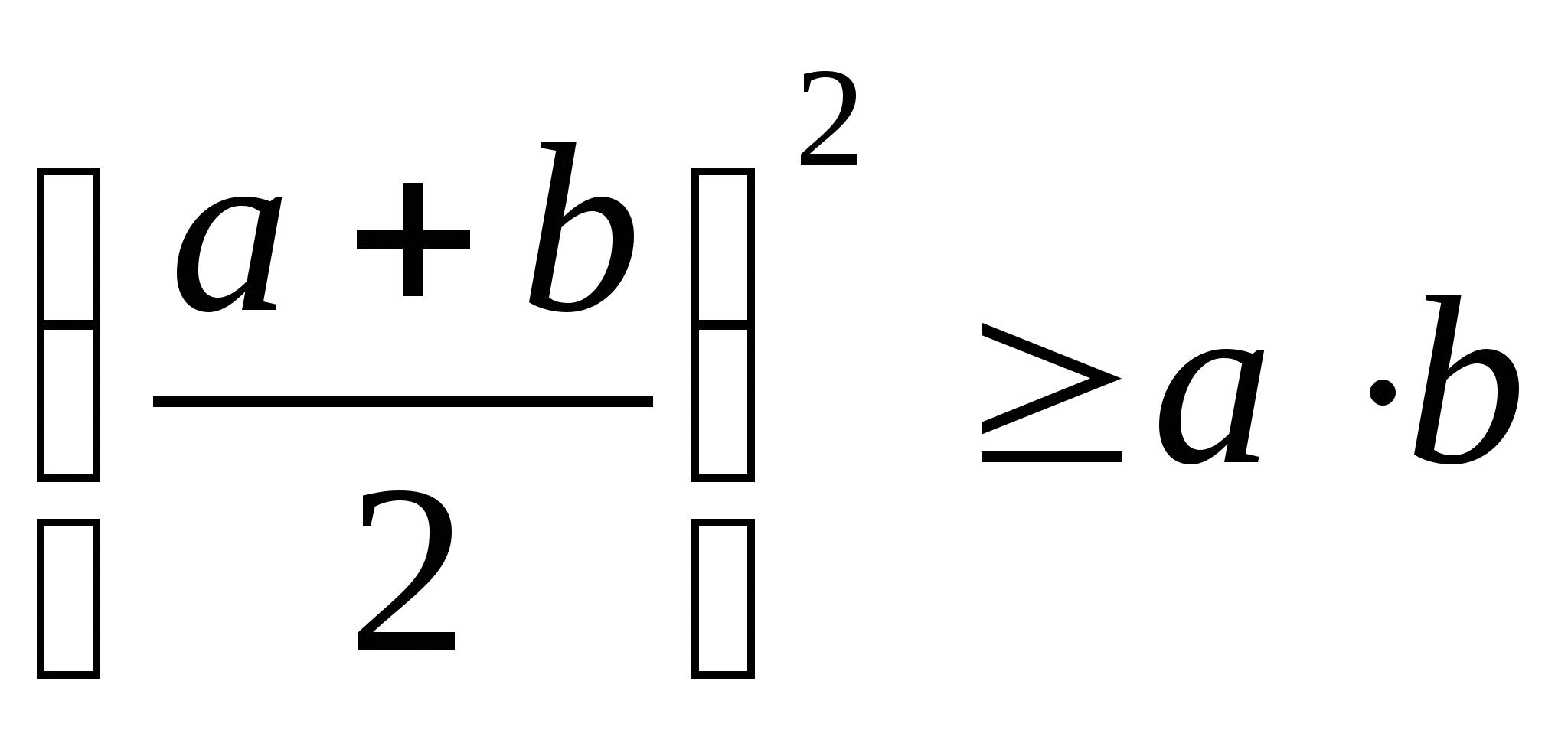2. , где 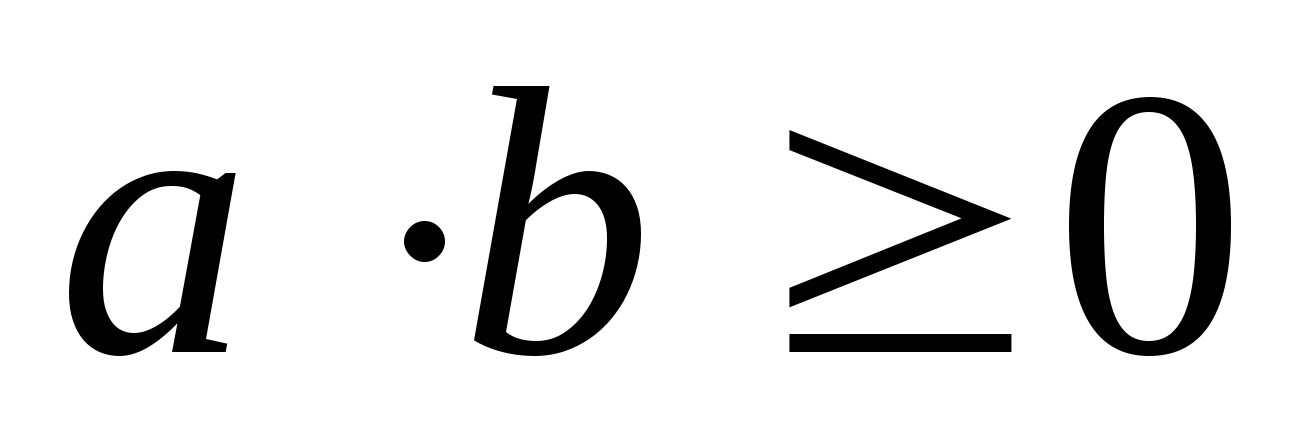; при условии 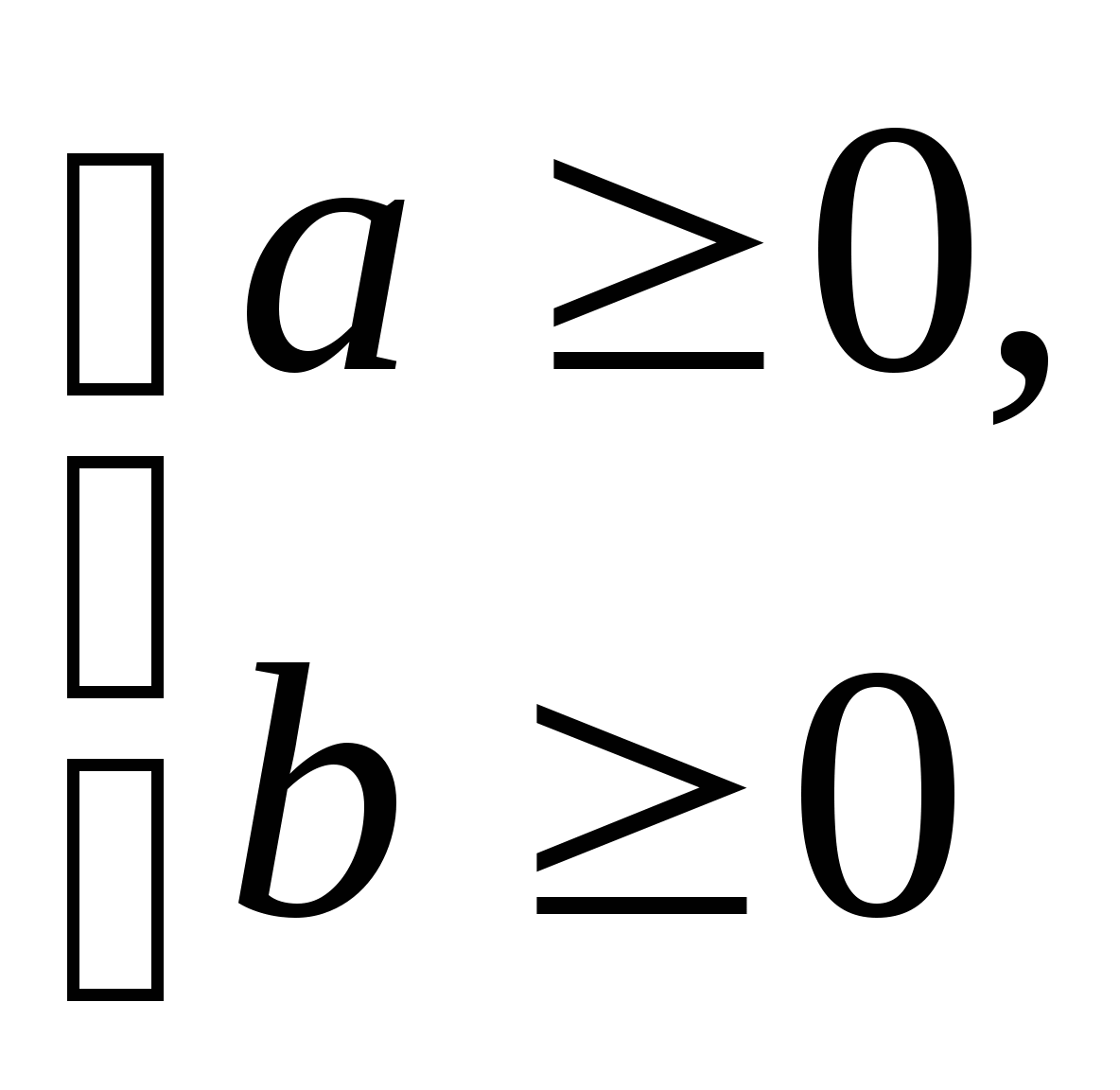данное неравенство равносильно неравенству Коши.

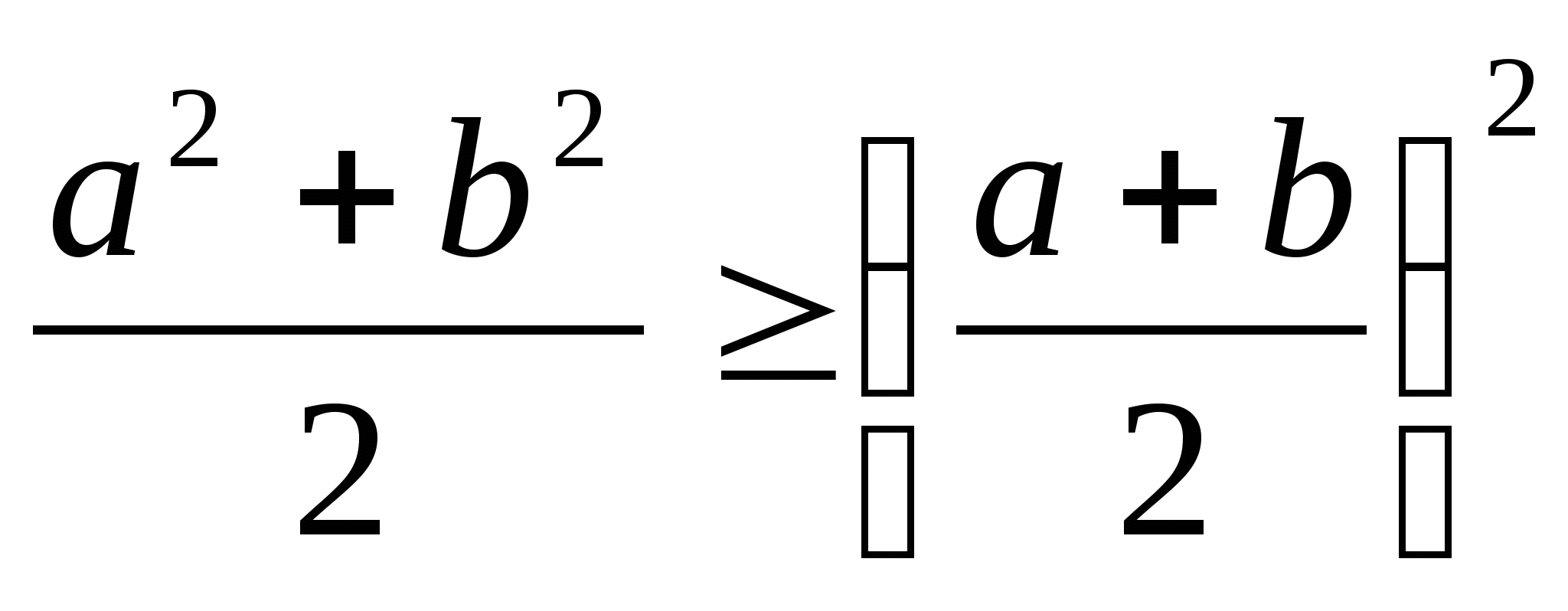3. , равенство достигается при 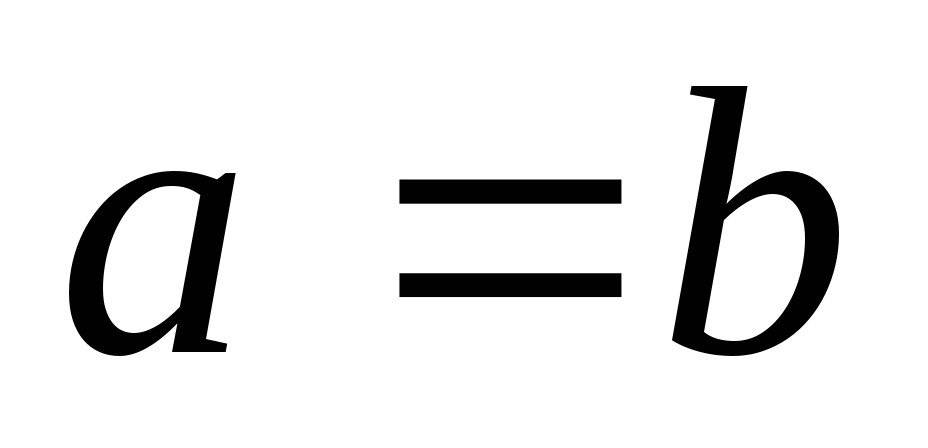(данное неравенство можно получить из неравенства ).

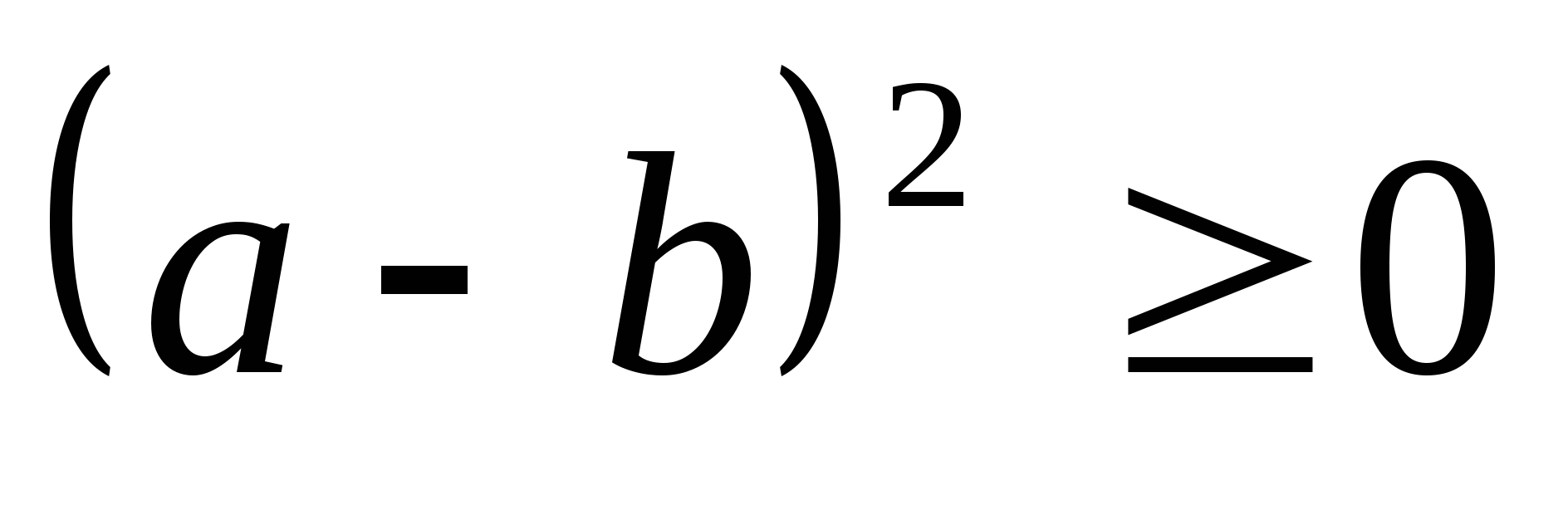4. Оценка суммы двух взаимно обратных чисел: 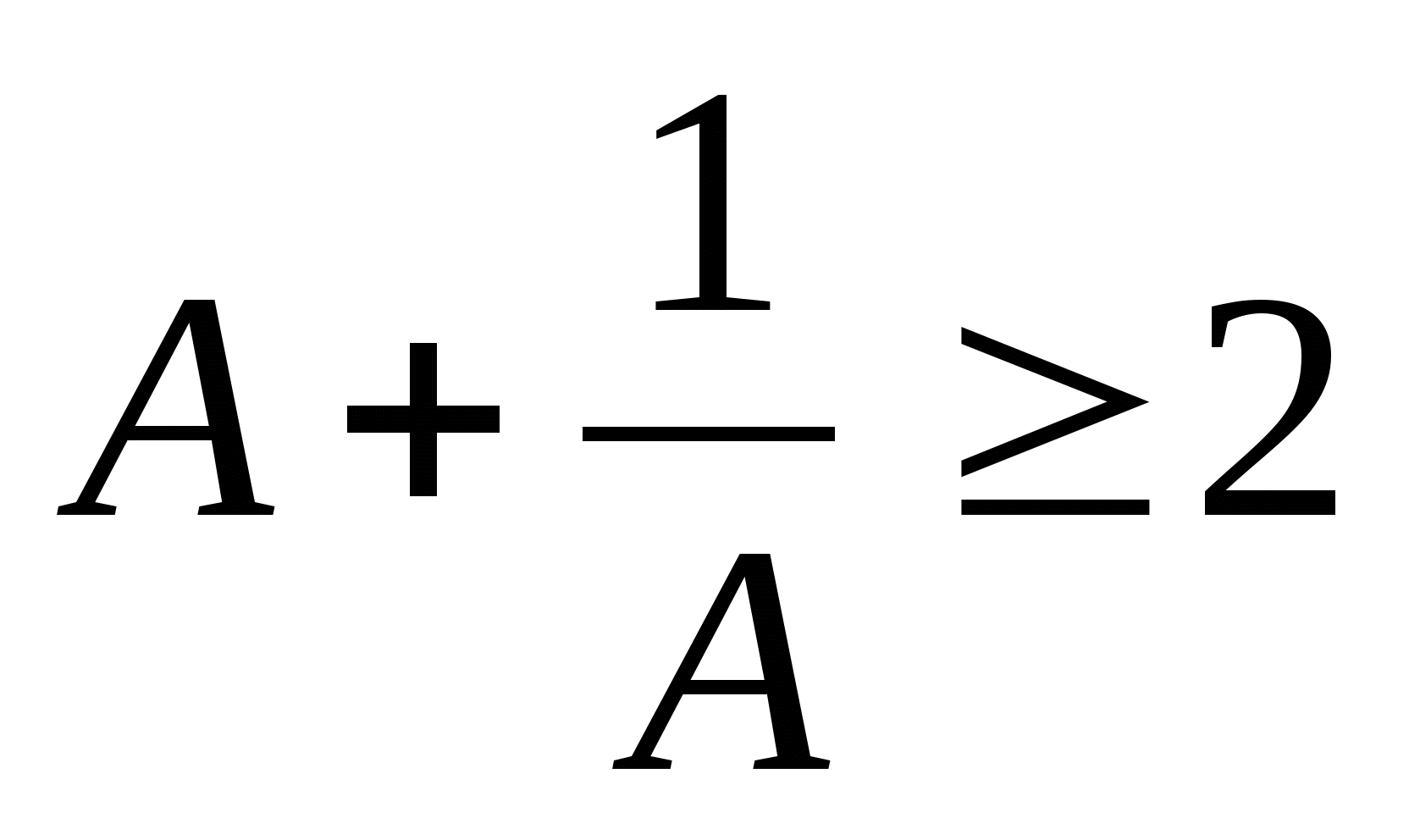, если 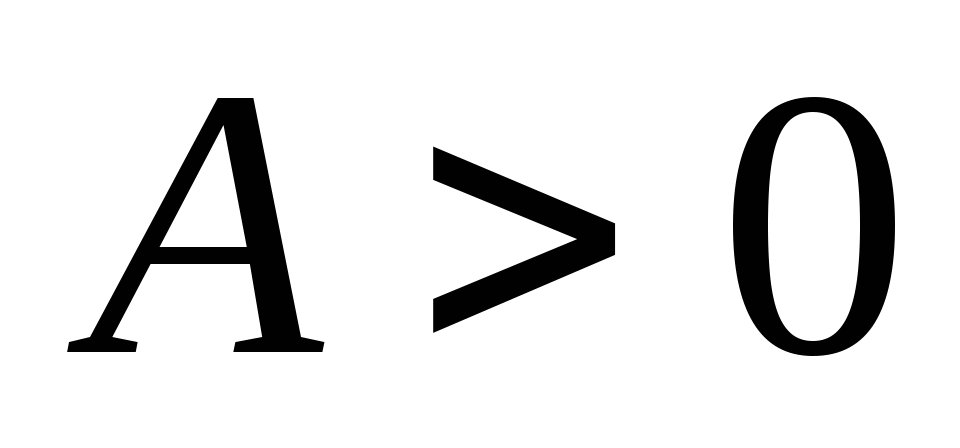; причём равенство достигается только при 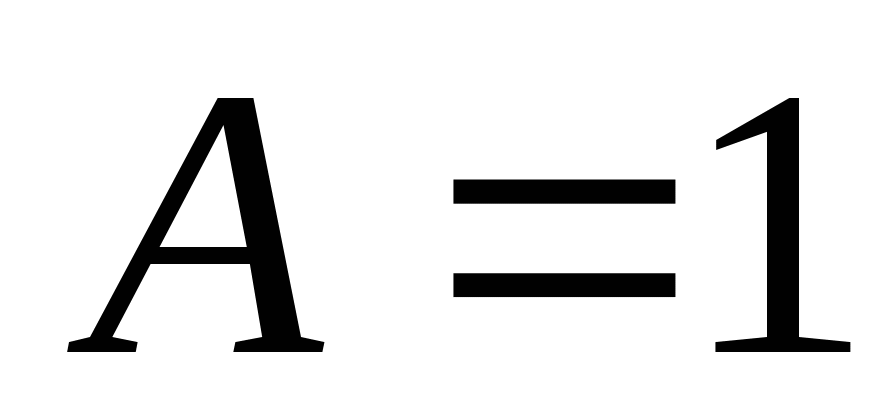. Если 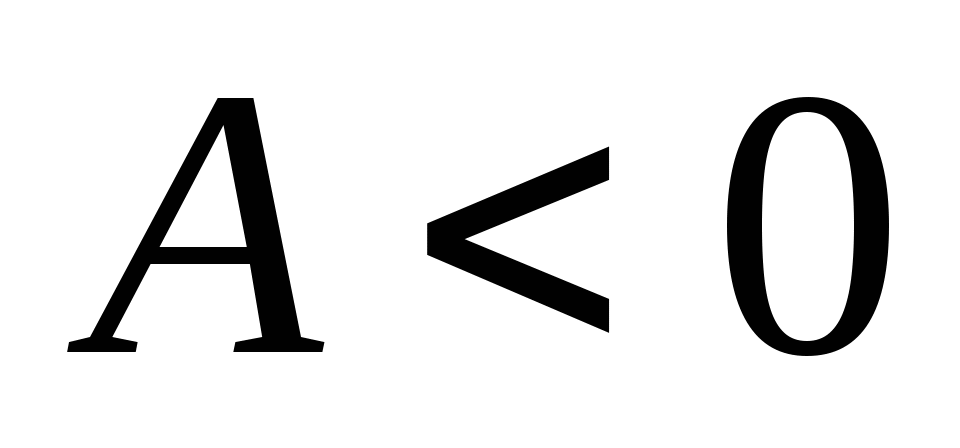, то .

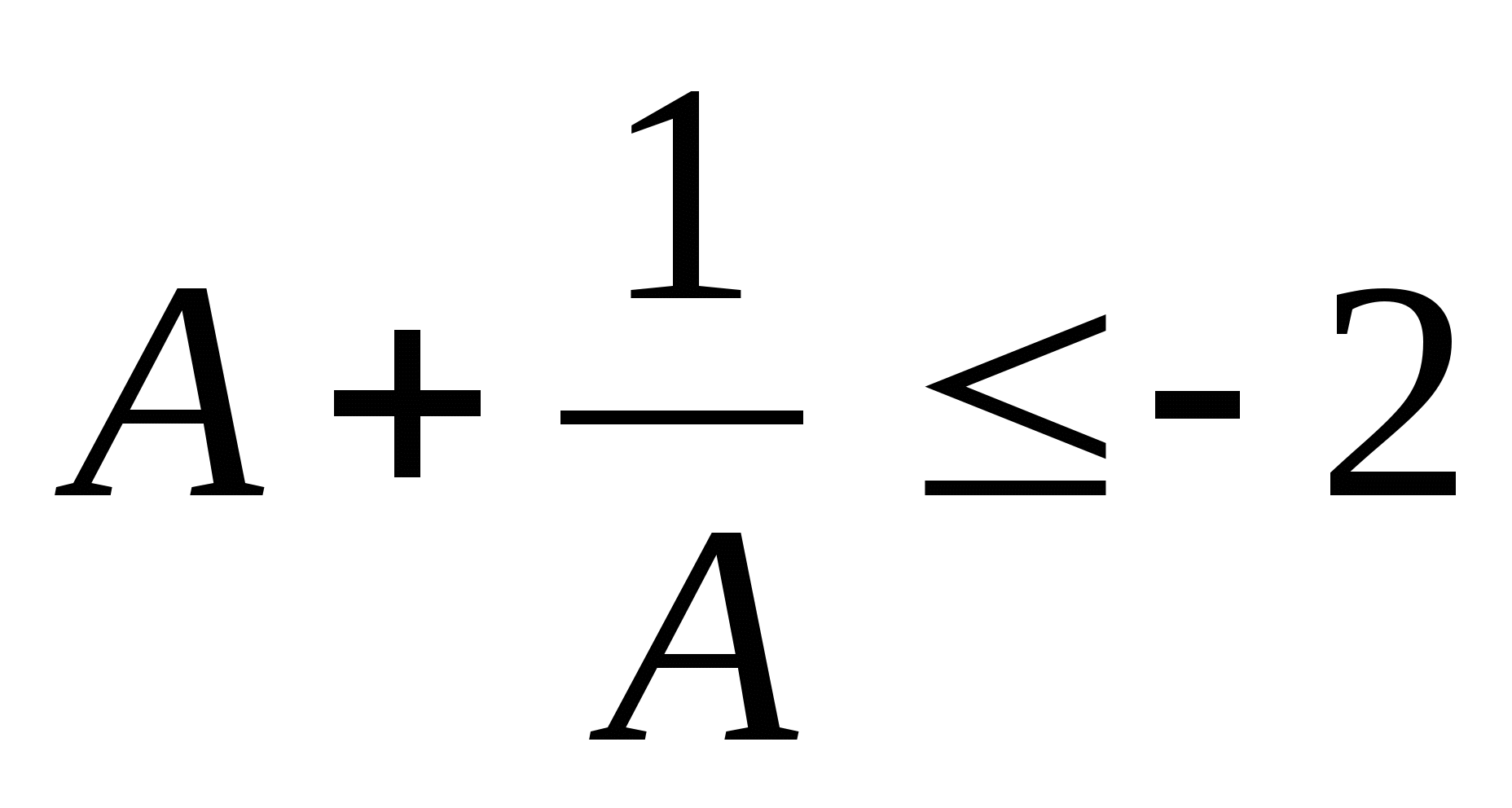5. Неравенство Коши для п переменных: 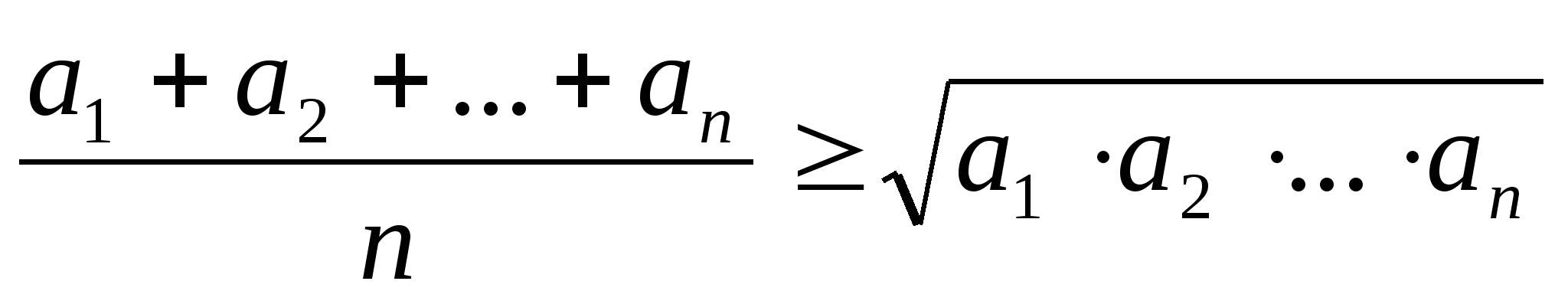, где 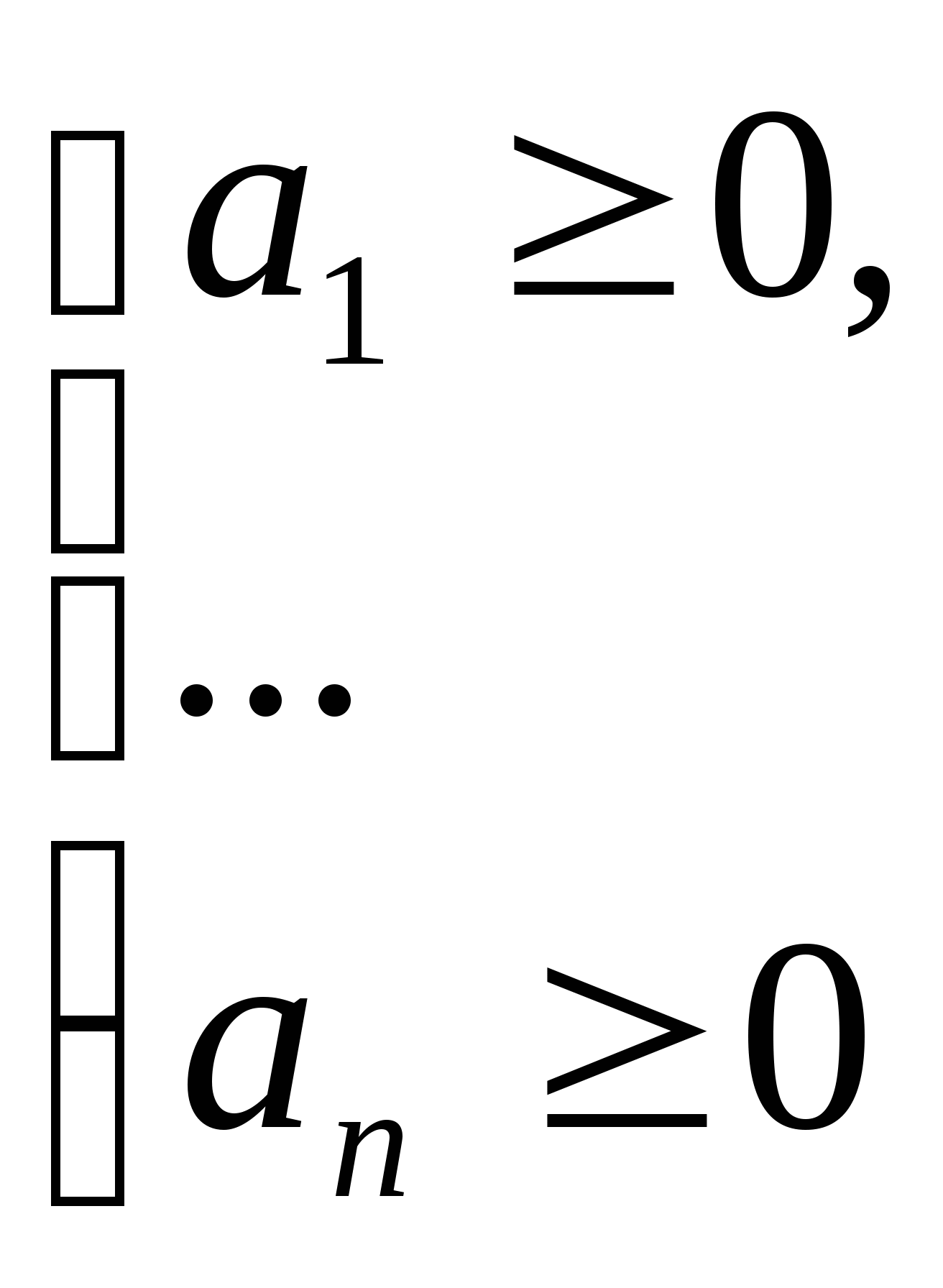. Равенство выполняется только при .

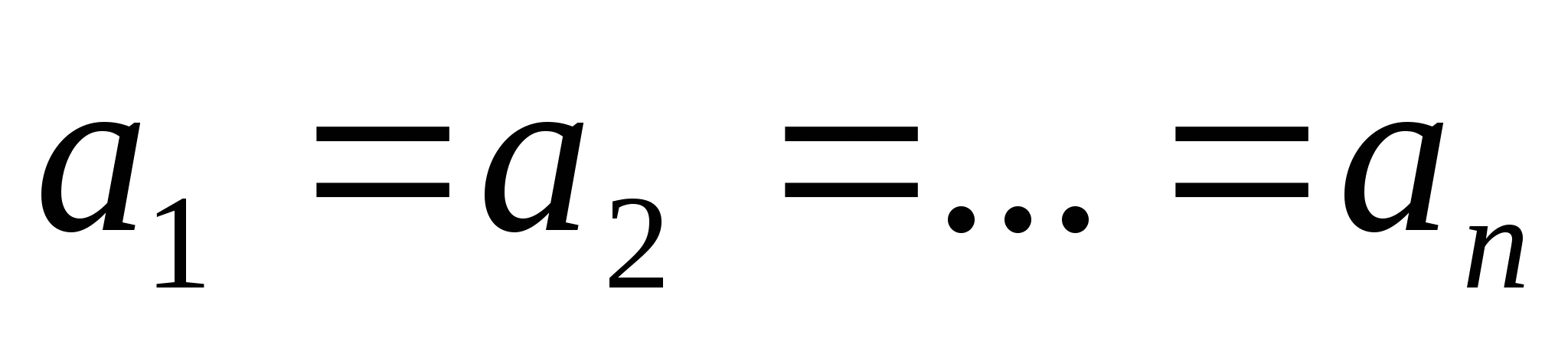6. Оценка однородного линейного тригонометрического многочлена:

(для доказательства данного неравенства используется метод вспомогательного аргумента).

7. Оценка квадратного трёхчлена:

если , то ; равенство достигается при ;

если , то ; равенство достигается при .

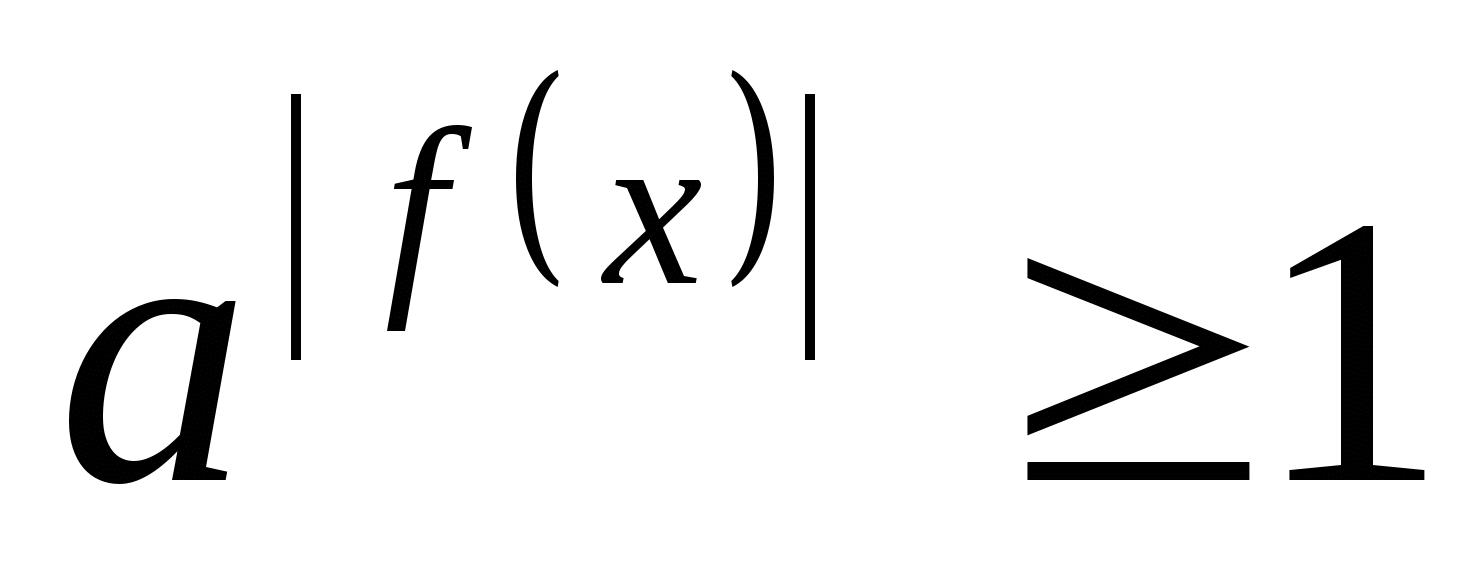8. , если 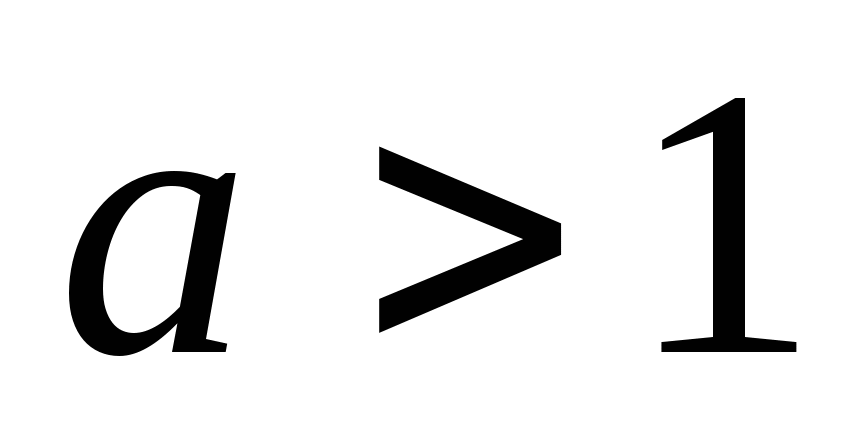; 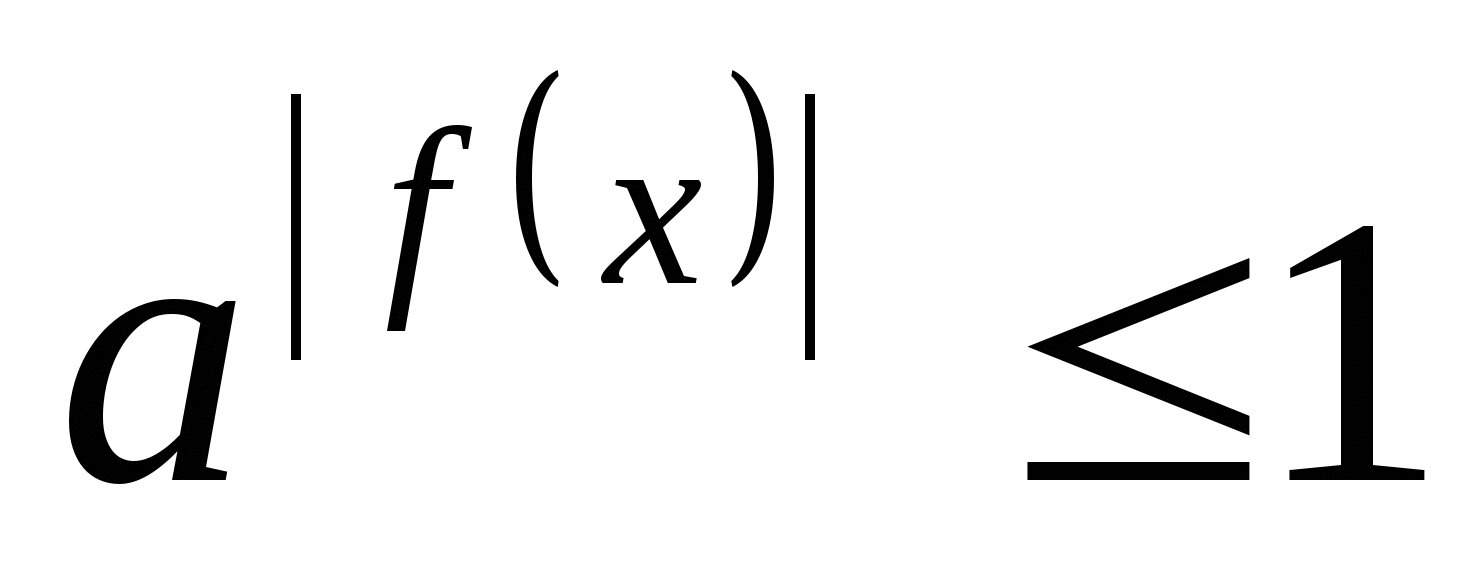, если .

9. .

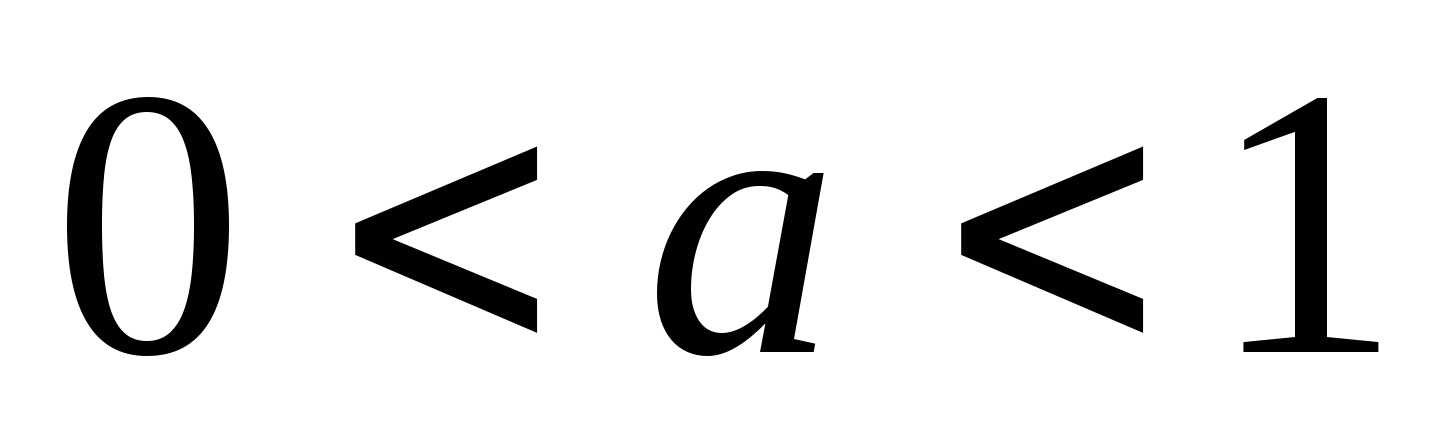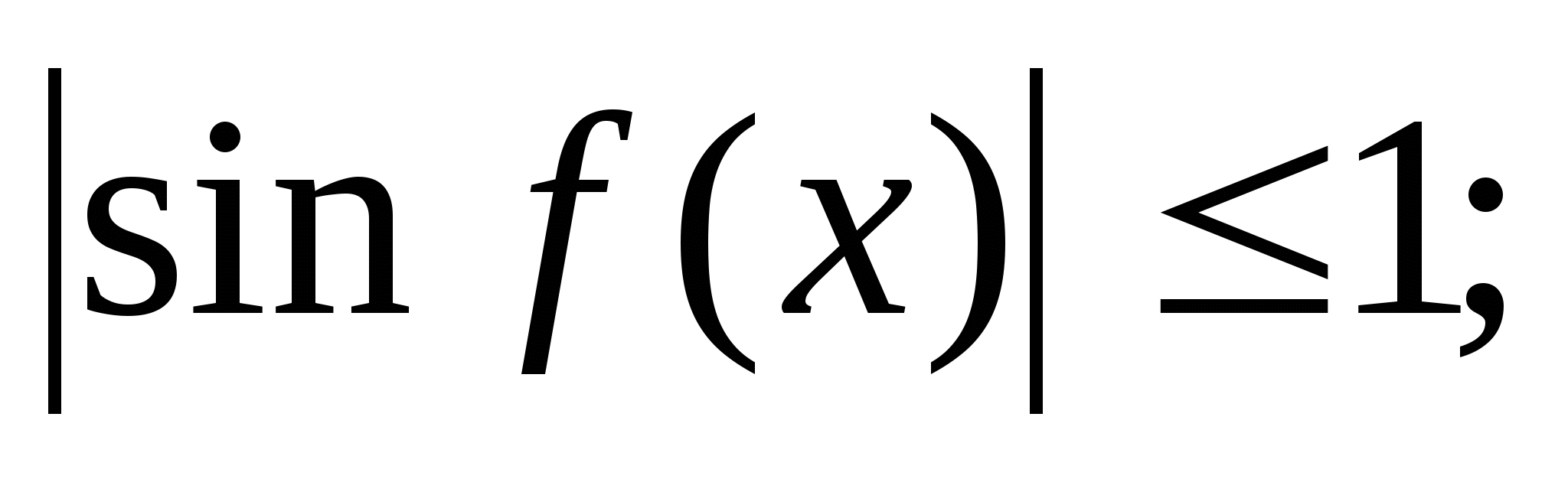
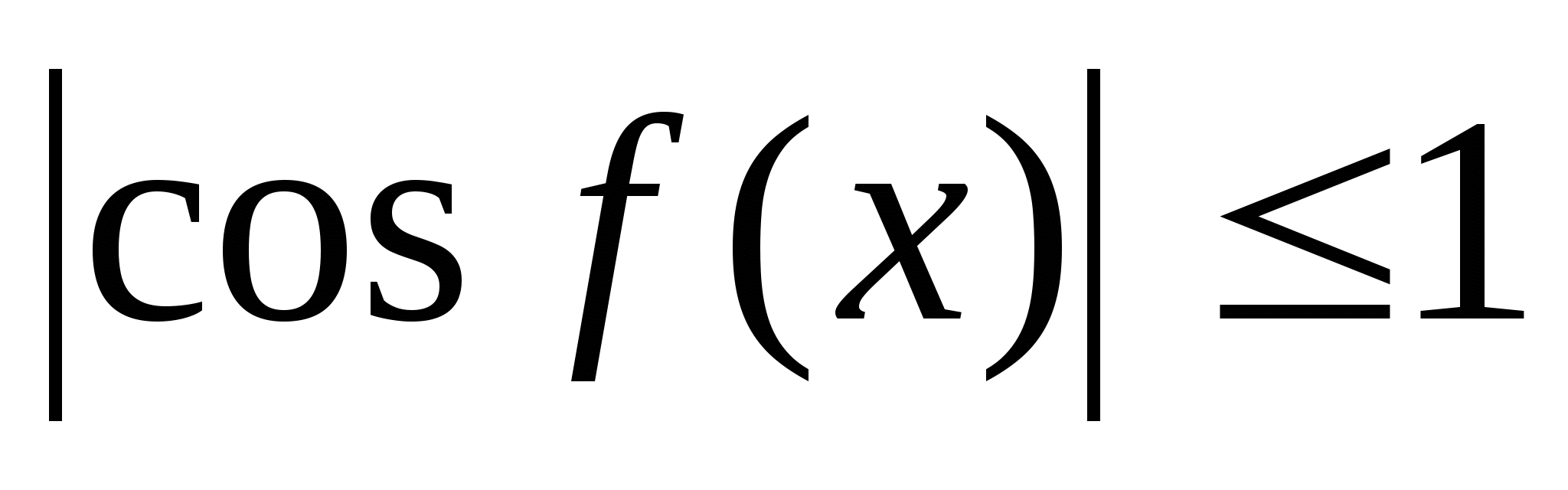При использовании метода минимаксов могут использоваться и другие, более специальные неравенства.

Можно ли по внешнему виду уравнения определить, что нужно применять метод минимаксов?

Применение данного метода часто можно определить по внешнему виду уравнения: если в уравнении присутствуют функции различного типа (алгебраические (записанные в виде многочлена), иррациональные, тригонометрические, показательные или логарифмические), то можно в первую очередь попробовать применить данный метод решения, т.к. применение стандартных способов решения часто бывает затруднительным или невозможным. Мы сегодня также рассматривали уравнения, содержащие функции одного типа, но их тоже было удобнее решать этим способом.

Как понятно из выше сказанного, данный метод применим в случае, если выражения, входящие в уравнение, во-первых, ограничены, и, во-вторых, верхняя граница одного выражения совпадает с нижней границей другого. Если же в некоторых случаях оценку одной части выполнить затруднительно, то можно дать оценку другой части и затем попробовать получить противоположную оценку первой части.

Предлагаю вам дома решить этим методом следующие уравнения

ПР-4.

ПР-5. .

ПР-6. (ЕГЭ 2006).

Желаю вам удачи не только при выполнении этих заданий, но и в дальнейшей работе. Буду очень рада, если этот метод когда-нибудь пригодится вам в затруднительной ситуации и может быть поможет решить задания на ЕГЭ тем, кто будет его сдавать.