Отчет по педагогической практике 7-го класса

Федеральное государственное автономное образовательное учреждение высшего образования

«Казанский (Приволжский) Федеральный Университет»

Приволжский межрегиональный центр повышения квалификации и профессиональной переподготовки работников образования

ОТЧЕТ

по педагогической практике

по направлению «Педагогика и образование» с правом преподавания предмета «Математика»

Период прохождения практики__17.02.2016 по 17.03.2016_________________

Практикант: учитель_______Гильфанов Ринат Газизьянович_______________

Место прохождения практики_______ МБОУ школа № 167________________

Руководитель пед. практики________Хасбиева Роза Петровна_____________

Казань 2016г.

Содержание:

Утверждаю

Директор МБОУ «Школа № 167»

Хасбиева Р. П.

Индивидуальный план прохождения практики

Гильфанова Рината Газизьяновича

Содержание работы

Срок выполнения

Посещение школы, консультация с руководителем учреждения, составление индивидуального графика прохождения практики, знакомство с методическим и дидактическим оснащением. Беседа с классным руководителем 7 «А» класса Ивановой Клавдией Петровной

17 февраля 2016 г

Посещение занятий учителя Ивановой К. П. по математике в 7, 8 классах и учителя Николаева Э. Н. с целью знакомства с программами учреждения, методиками обучения учащихся

18 февраля 2016 г

Посещение уроков 7 класса (анг. яз., обществознания, физики, информатики и технологи) с целью ознакомления с классом, получение информации о поведения учащихся на разных уроках

19 февраля 2016 г

Воспитательная работа с 7 классом. Подготовка к мероприятию посвященного 23 февраля и 8 марта

20 февраля по 4 марта 2016 г

Подготовка и проведение уроков алгебры и геометрии в 7 классе

С 17 февраля по 17 марта 2016 г

Подготовка и проведение открытого урока по алгебре 7 «А» класса на тему «Использование метода алгебраического сложения для решения систем уравнений»

25 февраля 2016 г

Подготовка и проведение открытого урока по геометрии 7 «А» класса на тему «Решение задач на применение признаков равенства треугольников»

3 марта 2016 г

Подготовка и проведение классного часа 7 «А» класса Игра на тему «Мой режим дня»

10 марта 2016 г

Подготовка и проведение внеклассного мероприятия 7 «А» класса Игра на тему «Самый умный математик»

14 марта 2016 г

Подведение итогов педагогической практики, оформление документации

14-17 марта 2016 г

Сведения о МБОУ «Средняя общеобразовательная школа №167 с углубленным изучением отдельных предметов» Советского района г. Казани

420100, г. Казань, ул. Академика Сахарова, д. 9

Телефон:

+7(843)-263-86-40;+7(843)-263-87-27

E-Mail:

wkola167@mail.ru

Министерство:

Министерство образования и науки Республики Татарстан

Короткое название:

МБОУ "Школа № 167"

Руководитель:

Хасбиева Роза Петровна

Год основания учреждения:

1999

Кол-во учеников

1200

Кол-во учителей

74

Расписание звонков и уроков

Список 7 «А» класса

Психолого-педагогическая характеристика класса

В 7 «А» классе обучается 30 ученика: 11 мальчиков и 19 девочек. Возраст 14 лет 2002 г. р. В коллективе 1 ученик из многодетной семьи, 1 - из неполной семьи.

В классе средняя успеваемость по всем предметам. На уроках учащиеся внимательны, добросовестно относятся к выполнению домашних заданий. Учатся на «отлично» - 4 человека, на «4» и «5» - 10 человек, на «3» и «4»- 10 человека и на на «3» - 6 человек. Таким образом, качество знаний по классу составило - 77 %.

Результаты ежегодного медицинского обследования свидетельствуют о том, что здоровье детей находится в пределах допустимых норм: основную группу здоровья имеют 95% семиклассников.

В коллективе имеются лидеры - это Минзянова Диана Фаридовна, Сташевски Эмиль Зенонович. Они самостоятельны, активны, способны повести за собой класс. Кроме этого есть группа ребят, которые обладают организаторскими способностями (Вафина Сабина Рустемовна, Нигматуллин Айрат Марселевич).

Ребята проявляют активность и творчество в проведении классных и школьных мероприятий, готовят отличные представления на праздники школы. Инициативность, активность, живой оклик на новые дела, творческие начинания - вот основные черты классного коллектива.

Некоторые дети занимаются в учреждениях дополнительного образования, как спортивного, так и эстетического направления.

У ребят привито бережное отношение к труду. Они понимают ценность труда, добросовестно относятся к самообслуживанию, бережливы в сохранности учебников и школьной мебели, проявляют огромный интерес к общественным делам.

Для выявления наиболее существенных свойств коллектива, межличностных отношений и взаимодействия, а также уровня развития таких общих характеристик, как направленность, организованность, интеллектуальная коммуникативность, психологический климат, было проведено обследование обучающихся 7 «А» класса.

Направление активности

Класс активен, полон творческой энергии. Ребята в своих делах ставят перед собой общественно полезные цели, положительные духовные запросы. Их объединяет общая цель деятельности, а не просто сходные цели каждого ученика в отдельности. Семиклассники стремятся постоянно общаться и сотрудничать друг с другом. Их отличают устойчивые интересы.

Организованность

В коллективе справедливо относятся ко всем одноклассникам, стремятся поддержать слабых (Ахмадеев Алмаз Ильхамович, Низамиева Алия Ирековна) в общей деятельности; разумно, доброжелательно решаются вопросы взаимопомощи. Трудные условия, ситуация опасности, неожиданные сильные воздействия еще более сплачивают класс.

Ребята с высокой результативностью согласует свои действия. Класс имеет хороших, способных организаторов Минзянова Диана Фаридовна, Сташевски Эмиль Зенонович), являющихся его авторитетными и полномочными представителями.

Интеллектуальная коммуникативность

Большинство ребят класса прислушиваются к мнению своих товарищей и приходят к единодушному суждению, легко находят общий язык, взаимопонимание при решении групповых задач. Критические замечания со стороны членов класса принимаются доброжелательно и способствуют созданию единого группового мнения.

Психологический климат

В классе преобладает добрый общий тон, доброжелательность во взаимоотношениях. Успехи или неудачи товарищей вызывают переживание, искреннее участие других членов класса, здесь имеют место одобрение, поддержка, а упреки и критика делаются с доброжелательных позиций. Ребятам нравится бывать вместе, им хочется чаще находиться в классе, участвовать совместной деятельности.

Введение

Содержание образования в современном мире является приоритетной сферой, от которой зависит развитие человека, способного самостоятельно и сознательно строить свою жизнь в духе общечеловеческих ценностей, с учётом традиций своего народа. Особый интерес в этом плане представляет дошкольное детство, как первая ступень системы непрерывного образования.

Учебная работа

План-конспект открытого урока по алгебре

Использование метода алгебраического сложения

для решения систем уравнений

Цель урока: способствовать деятельности учащихся по самостоятельному осваиванию еще одного способа решения систем уравнений - способ сложения; продолжать работу по развитию творческих способностей учащихся; продолжить работу по формированию ответственности учащихся за свою деятельность на уроке

Далее. Повторение и закрепление пройденного материала

Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

Контроль усвоения материала (самостоятельная работа).

Вариант 1 Способом подстановки решите систему уравнений:

3х + 5у = 11

5х - 2у = 8

2х + 7у = 9а - 5

3х - 5у = 2 - 2а

Вариант 2 Способом подстановки решите систему уравнений:

4х - 3у = 5

3х + 4у = 10

3х + 2у = 7а + 6

4х - 3у = 8 - 2а

Изучение нового материала

Рассмотрим еще один способ решения систем линейных уравнений - способ сложения. При таком способе решения данная система уравнений заменяется равносильной системой, в которой одно из уравнений содержит только одну переменную.

Пример 1

3х + 2у = 8

4х - 2у = 6 (1)

Заметим, что в уравнениях системы коэффициенты при переменной у являются противоположными числами. Сложим почленно уравнения системы: 3х + 2у + 4х - 2у = 8 + 6. Получим линейное уравнение с одной переменной х, а именно 7х = 14. Заменим одно из уравнений системы (1), например первое, полученным уравнением 7х = 14. Имеем равносильную систему:

7х = 14

4х - 2у = 6 (2)

Решим систему (2). Из первого уравнения находим х = 2.

Подставим это значение х во второе уравнение системы. Имеем линейное уравнение с переменной у: 4-2 - 2у = 6, или 8 - 2у = 6, или -2у = -2, откуда у = 1. Пара чисел (2; 1) - решение системы (2), а следовательно, и равносильной системы (1).

Из разобранного примера видно, что при сложении уравнений системы получилось уравнение только с одной переменной. В качестве второго уравнения системы можно выбрать любое из уравнений данной системы. В результате таких преобразований была получена система, равносильная данной. В этом состоит суть метода сложения.

Пример 2

3х - 5у = 9

2х - 7у = 17

В отличие от предыдущего примера в этом случае коэффициенты при у (а также и при х) не являются противоположными числами. Поэтому сложение уравнений не позволит получить уравнение с одной переменной. Следовательно, необходимо добиться того, чтобы в уравнениях коэффициенты при любой переменной, например при у, стали противоположными числами.

Коэффициенты при у являются простыми числами 5 и 7. Поэтому умножим все члены первого уравнения на число 7, второе уравнение - на число (-5). При этом уравнения будут равносильными и система также равносильна данной:

21х - 35у = 63

-10х + 35у = -85

В такой системе коэффициенты при у - противоположные числа. Поэтому сложим уравнения системы и получим линейное уравнение с одной переменной: 21х -35у - 10х + 35у = 63 - 85 или 11х = -22.

Запишем систему, равносильную данной. В качестве первого уравнения выберем полученное уравнение, в качестве второго уравнения, например, первое уравнение данной системы. Имеем:

11х = -22

3х - 5у = 9

Из первого уравнения найдем х = -2 и подставим это значение во второе уравнение. Получаем линейное уравнение с одной переменной: 3 (-2) - 5у = 9, или -6 -5у = 9, или -5у = 15, откуда у = -3. Итак, данная система уравнений имеет единственное решение (-2; -3).

Пример 3

6х + 5у = 7

4х - 3у = 11

Избавимся теперь от переменной х. Коэффициенты при х в уравнениях - числа 6 и 4 - уже не являются простыми числами (составные числа). Найдем их наименьшее общее кратное НОК (6; 4) = 12. Так как 12 : 6 = 2 и 12 : 4 = 3, то умножим все члены первого уравнения на число 2, второго уравнения - на число (-3). Получаем равносильную систему уравнении

12х + 10у = 14

-12х + 9у = -33

Сложим уравнения этой системы и получим линейное уравнение с переменной у: 12х + 10у - 12х + 9у =14-33 или 19у = -19.

Запишем равносильную систему уравнений. В качестве первого уравнения выберем полученное уравнение, в качестве второго уравнения - второе уравнение данной системы. Имеем:

19у = -19

-12х + 9у = -33

первого уравнения найдем у = -1 и подставим это значение во второе уравнение. Получаем линейное уравнение с одной переменной: 4.х - 3 (-1 ) = 11 или 4х = 8, откуда х = 2. Итак, данная система уравнений имеет единственное решение (2; -1).

Из рассмотренных примеров следует, что при решении систем линейных уравнений методом сложения:

1) умножают уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) складывают почленно левые и правые части уравнений системы;

3) решают полученное уравнение с одной переменной;

4) находят соответствующее значение второй переменной.

Отметим, что если в уравнениях системы коэффициенты при одной из переменных являются противоположными числами, то при решении пункт 1 пропускают и начинают сразу с пункта 2.

Способ сложения можно использовать и при решении систем уравнений с параметрами.

Контрольные вопросы

Основная цель при решении систем уравнений методом сложения.

Как решить систему уравнений методом сложения? Объясните на примере.

Задание на уроке № 13.2(a); 13.5 (в); 13.9 (а, г); 13.12 (а); 13.13 (г); 13.15 (б); 13.16 (а); 13.17(6); 13.18(a).

Задание на дом

№ 13.2 (б); 13.5 (а); 13.9 (б, в); 13.12 (б); 13.13 (в); 13.15 (г); 13.16 (б); 13.17(a); 13.18(6).

</

Творческие задания

Решите задания 1 и 2 из творческих заданий предыдущего урока методом сложения.

Самоанализ на открытый урок по алгебре

класса 7 «А» школы № 167

Целью урока было способствование деятельности учащихся по самостоятельному осваиванию еще одного способа решения систем уравнений - способ сложения. Данная цель была направлена на обозначение существования еще одного способа решения систем уравнений, которая позволяет решать систему уравнений за менее короткий срок. кроме того, овладение данного способа решения систем уравнений в дальнейшем сказывается на увеличенном объеме решаемых упражнений. Доведенный до автоматизма алгоритм решения стимулирует продолжению работы по развитию творческих способностей учащихся и продолжению работы по формированию ответственности учащихся за свою деятельность на уроке.

Тема урока «Использование метода алгебраического сложения для решения систем уравнений» следует после темы «Системы двух линейных уравнений» и «Использование метода подстановки для решения систем уравнений».

После введения систем двух линейных уравнений ученики учились подставлять вместо одной неизвестной переменной другое, и в результате получалось уравнение с одним неизвестным, что и способствовало решению уравнения (на уровне учеников).

После изучения «Систем уравнений» и методов решения систем уравнений» учащиеся способны пробовать самостоятельно решать текстовые задачи с помощью систем уравнений с двумя неизвестными. До изучения систем уравнений ученики могли решать задачи с одной неизвестной, но в задачах с двумя и более переменными решаются системами уравнений. По этому, предшествующие темы по введению систем уравнений и пройденной теме развили у учащихся инструментарий по решению текстовых задач с двумя неизвестными. Как раз следующая тема сопоставить использование знаний в решение систем уравнений с составлением таких систем при решении текстовых задачах.

При подготовке урока была произведена синхронизация с требованиями ФГОС, в урок были заложены развивающие способности учеников, такие как:

знание еще одного метода решения систем уравнений,

умение пользоваться методом сложения

и закреплены навыки по применению метода сложения уравнений при решении упражнений.

Специфика проведенного урока в осознание существования разных методов решения упражнений, включая системы уравнений. Это толкает ученика на изучение научной литературы в поисках еще одного метода решения систем уравнений и методов решения других упражнений.

Данный тип проведенного урока «Урок закрепления знаний и изучение нового материала» была проведена без интерактивной доски, без макетов, только фронтальная работа учителя с учениками. Для изучения методов решения уравнений, систем уравнений макеты не бывают. Интерактивная доска не применялась из-за отсутствия необходимости. Доска и мел позволяют в достаточной степени изображать свои мысли при изучении тяжелых тем и реагировать на уровень восприятия слушателей.

Главная задача при изучении «Использования метода алгебраического сложения для решения систем уравнений» была указана на существование другого метода решения. Были привиты навыки подбора общего коэффициента переменной и сложения уравнений. Были выработаны навыки решения систем уравнений двумя способами.

Структура проведенного урока выражена решением множества примеров, указывающих на суть новой темы и возможные ошибки по ходу решения задач.

Темп проведенного урока - средний. Быстрый темп урока выбирается при закреплении пройденного материала, а медленный темп при изучении объемных тем с использованием многих новых формул. Средний темп урока позволил держать ученика в тонусе урока, ученик не мог отвлекаться на игры во время урока и концентрируя внимание на учителя впитал необходимый (задуманный) объем информации.

Фронтальная работа учителя с учениками позволяла выявлять пробелы в прошлых и нынешних знаниях. Пробелы освежались и заполнялись знаниями. В ходе урока была проведена коррекция знаний учеников, упорядочиванием определений и формул.

Содержание изученного урока было сформировано на основании учебной программы. Данный метод изучения пройденной темы был выбран на основании сложившейся методике усвоения информации в данном классе. Использованное средство обучение было выбрано с учетом возможности изменения хода урока.

Перед началом урока был проветрен класс-кабинет, подготовлена классная доска, мел, тряпка, был составлен план-конспект урока.

В ходе проведения урока произошло отступление от плана урока. Ученикам понравился метод решения систем уравнений и во время решения упражнений они решили больше заданий, чем планировалось.

В ходе урока удалось достичь поставленной задачи, запланированный материал был изложен, материал был усвоен; и получить соответствующие результаты обучения в виде решенных упражнений.

В ходе урока удалось избежать перегрузки и переутомления учащихся с помощью диалога учителя с учеником во время устранения возможных ошибок при решении систем уравнений.

Во время решения примеров систем уравнений обозначались причины возникновения решаемых уравнений. Это мотивировало учеников плодотворно впитывать информацию.

Успех проведенного урока заключается в освоение пройденной темы, а контролем усвоения является срез знаний, и обязательно письменный, т. е самостоятельный. Недостатком проведенного урока является отсутствие возможности быстрого проведения среза знания, например, с использованием интерактивной доски с пультами управления.

В ходе урока не была выведена общая формула сложения двух уравнений из системы уравнений.

План-конспект открытого урока по геометрии

Решение задач на применение признаков равенства треугольников

Цель урока: закрепить и совершенствовать навыки решения задач на применение признаков равенства треугольников; продолжить выработку навыков решения задач на построение с помощью циркуля и линейки.

Далее.

Проверка домашнего задания. Повторение

Проверить решение дополнительных домашних задач.

(К доске вызвать учащихся, справившихся с решением задач.)

Решение задач по готовым чертежам (устно) рисунки подготовить на доске или на планшетах заранее.

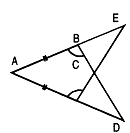
Рис. 2.174.

а) Дано: AB = AC, угол ACE = угол ABD.

Доказать: треуг АСЕ= треуг ABD.

б) Дано: АЕ = 15 см, ЕС= 10 см, АС= 1 см.

Найти: стороны треуг ABD.

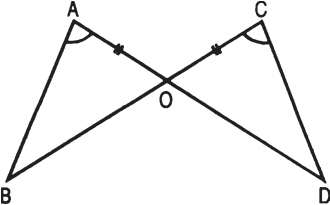
Рис. 2.175.

Дано: АО = ОС, треуг ВАО = треуг DCO.

Доказать: AB = CD.

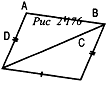
Рис. 2.176.

Дано: AB = DC, AD = ВС, = 15 см, Р_ABCD = 20 см.

Найти: АС.

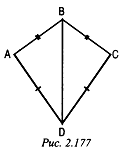
Рис. 2.177.

Дано: AB = ВС, AD = DC, угол ABD = 63°, ZADB = = 37°.

Найти: Z CBD, Z CDB.

3. Решение задач N 158, 165 (письменно в тетрадях и у доски).

Задача № 158

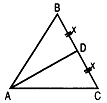
рис. 2.178

Дано: треуг ABC - равнобедренный (см. рис. 2.178), АС - основание, АС = 8 см. AD - медиана. P_ABD больше P_ADC на 2 см или наоборот.

Найти: боковую сторону треуг ABC.

Решение: Пусть BD = х см, тогда DC = х см, АВ=2х см. Пусть AD = у см.

Рассмотрим два случая:

1 )если P_ABD больше P_ADC на2см,то(АВ+ BD + AD)-(AD + DC + AC) = 2, то есть (2х + х+ у) - (у + х + 8) = 2.

Откуда х = 5, то есть BD= 5 см, АВ= 10 см.

2) если P_ADC больше P_ABD на 2 см, то (у + х + 8) - (2х + х + у) = 2, откуда х = 3, то есть BD= 3 см, AB =6 см. ( Ответ: 10 см или 6 см.)

Наводящие вопросы:

1 ) Что вы можете сказать о длинах отрезков AB, BD и DC? Чему равны AB и DC, если BD = x см?

2) По условию задачи сказано, что периметр одного треугольника больше периметра другого. Периметр, какого треугольника больше? Сколько решений имеет задача?

Задача № 165 (а)

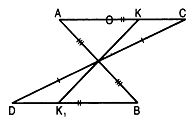
Решение (см. рис. 2.179):

1. треуг АОС = треуг BOD по двум сторонам и углу между ними (АО = ВО_, СО = DO, так как О - середина AB и CD; угол АОС = углу BOD как вертикальные). Следовательно, угол CAO = угол DBO.

2. треуг АКО = треуг ВК₁О по двум сторонам и углу между ними (АК = ВК_1, АО = ВО; угол КАО = угол К₁ВО, так как угол АОС = угол BOD). Отсюда следует, что ОК= ОК₁

Наводящие вопросы:

1) Чтобы ОК= ОК₁ нужно равенство треугольников, содержащих в себе отрезки ОК и ОК₁ в качестве своих сторон. Какие это треугольники?

2) Равны ли углы OAK и углы ОВК₁? Из равенства каких треугольников следует равенство углов OAK и ОВК₁?

Задача № 165 (б)

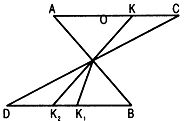
Решение (см. рис. 2.180):

Начертим луч ОК₂ так, что точка О лежит на отрезке КК₂ тогда угол AOK= углу ВОК₂ как вертикальные. Но по доказанному выше треуг АКО = треуг ВК₁О, следовательно, угол AOK= угол ВОК₁

Так как угол AOK= угол BOК₂ угол AOK= угол BOK₁ то угол BOK₂ = угол BOK₁ следовательно, луч OK₂ совпадает с лучом ОК₁ то есть точки О, K, К₁ лежат на одной прямой.

Наводящий вопрос:

1) Предположим, что точка О не лежит на прямой КК_Р а лежит на прямой КК_Т Что можно сказать в этом случае об углах АОК_п BOK_t и ВОК?

III. Самостоятельное решение задач

Iуровень: решить задачи № 157, 159, 162.

Задача № 157

Решение: Пусть треуг ABC - равнобедренный (AB = ВС), тогда АС = AB + 2 см, и АС = AB + ВС - 3 см. Но AB = ВС, поэтому можно составить равенство: AB+ 2 см = 2АВ-3 см, откуда AB = 5 см.

Тогда ВС -5 см, АС= 7 см. (Ответ: 5 см, 5 см, 7 см.)

Задача № 162 (а)

Доказательство (рис. 2.181):

1) треуг ADE - равнобедренный с основанием DE, следовательно, угол D = угол E как углы при основании равнобедренного треугольника.

2) треуг ADB = треуг АЕС по двум сторонам и углу между ними (AD = АЕ, DB= CE, ZD = ZE), следовательно, АВ = АС, угол DAB = угол ЕАС.

3) угол CAD= угол CAB + угол DAB, угол BAE= угол EAC+ угол CAB, но угол DAB = угол ЕАС, поэтому угол CAD = угол BAE.

Задача № 162 (6)

Доказательство (рис. 2.182):

1) треуг ADE- равнобедренный с основанием DE, следовательно, угол D = угол E

2) угол DAC= угол EAB, но угол DAC= угол DAB + угол ВАС, угол EAB= угол EAC + угол ВАС, следовательно, угол DAB = угол EAC.

3) угол DAB = угол EAC по стороне и прилежащим к ней углам (AD = АЕ, угол DAB = угол EAC, угол D= угол E), отсюда AB = AС, DB= CE.

IIуровень: решить задачи № 157, 160, 162, 163.

Задача № 160

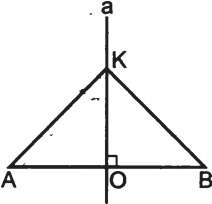
Доказательство (рис. 2.183):

а) Пусть К- произвольная точка прямой а. треуг АКВ - равнобедренный, так как СО - медиана и высота, значит, AB = ВС.

б) Пусть К- произвольная точка плоскости, такая, что АК = КВ. Тогда КО - медиана, проведенная к основанию, а значит, и высота. Получаем, что СО лежит на прямой а, т.е. С принадлежит а.

Задача № 163

Доказательство (рис. 2.184):

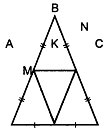
3) треуг ABC- равнобедренный с основанием АС, значит, Z угол A = угол С.

треуг АМК= треуг СNK по двум сторонам и углу между ними (AM = CN, так как М и N- середины боковых сторон равнобедренного треугольника; АК = СК, так как К- середина AC; угол A = угол Q

3) Так как треуг АМК - треуг CNK, то МК= NK, т.е. в треугольнике MNR две стороны равны, следовательно, треуг MNK- равнобедренный.

Домашнее задание

Решить задачи № 156, 161, 164.

Дополнительная задача Nq 166.

Задача № 156

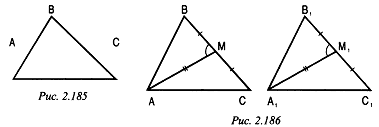
Решение (рис. 2.185):

Пусть ЛВ = х см, тогда ВС = (х + 2) см, С = (х + + 1) см. = 15 см, поэтому х + (jc + 2) + (х + 1) = 15, откуда х = 4.

Значит, 4 см, BС=6см,ЛС= 5 см. (Ответ: 4 см, ВС =6 см, ЛС= 5 см.)

Задаче № 161

Доказательство (рис. 2.186):

1) ВС= B₁С₁ M и M₁, - середины ВСи В₁С₁ следовательно, BM = МС = В₁М₁= M_lC₁

2) по двум сторонам и углу между ними (AM = =A_lM_ì, МВ= M_tB_l9

угол AMB= угол A₁M₁B₁), следовательно, AB = A₁B₁, угол B = угол B,.

3) треуг ABC = треуг А₁В₁С, по двум сторонам и углу между ними (AB = A₁B₁, BC=B₁C_l, угол B= угол B,).

Задача № 164

Доказательство: 1) Так как треуг ABC - равносторонний, и ЕВ = FC = DA, то АЕ= BF= CD, г угол A= угол B= угол С.

2) Л AED= A BFE= A CDF по двум сторонам и углу между ними (AD = = BE = FC, АЕ - BF= CD; ZA= ZB= ZQ

Следовательно, МК = MN = NK, то есть треугольник MNK - равносторонний.

Задача № 166

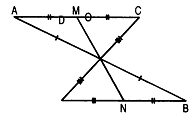
Доказательство (рис. 2.187):

1) треуг АОС = треуг BOD (АО = ВО, ОС = OD, угол AOC = угол BOD). Отсюда угол A = угол В, AC = BD

2) Так как AC = BD, М и N - середины AC и BD, то AM = BN.

3) треуг AMO = треуг BNO (AM = BN, АО = ВО, ZA = Z В). Отсюда МО = N0.

4) Докажем теперь, что точки М, N, О лежат на одной прямой. Предположим, что это не так. Но в этом случае найдется луч OL, являющийся продолжением луча ОМ. Тогда угол AOM = угол BOL как вертикальные. Но угол AOM= угол BON из равенства треугольников АОМ и В ON.

Так как угол AOM = угол BON и угол AOM= угол BOL, то угол BON= угол BOL. Следовательно, лучи ON и OL совпадают.

Значит, точки М, N, О лежат на одной прямой, а так как МО = N0, то О - середина отрезка MN.

Урок окончен

Самоанализ на открытый урок по геометрии

класса 7 «А» школы № 167

Целью урока было закрепление и совершенствование навыков решения задач на применение признаков равенства треугольников; продолжение выработки навыков решения задач на построение с помощью циркуля и линейки.

Я считаю, что урок цели достиг. Содержание, формы и методы отобраны в соответствии с целями урока.

Формы работы: индивидуальная, дифференцированный подход.

Методы: познавательный, частично-поисковый.

Все этапы урока работали на главный - обобщение материала. Урок начался с устной работы. Актуализация опорных знаний началась с устного опроса по теории. Ответы по теоретическому материалу ученики давали математически грамотные и полные. Углубление материала продолжилось других этапах урока (решение задач устно по готовым чертежам, а так же решение задач письменно и с использованием доски на применение признаков равенства треугольников).

Проверка знаний учащихся проходила в форме устных ответов - фронтальная работа и у доски.

Время на каждый этап урока распределено рационально. Использованы различные виды оценки: самооценка, взаимооценка, прогностическая оценка.

При работе в парах у учащихся формировался навык взаимоконтроля; при проверке заданий - самоконтроль и самооценка; со стороны учителя - мягкий контроль.

Считаю, что урок - адаптивный, так как все дети смогли реализовать свои образовательные потребности, возможности и способности. Ситуация успеха каждого ребёнка формировалась как на протяжении всего урока, так и на отдельных его этапах. В частности при выполнении упражнений.

Психологический настрой, движение во время проверки заданий, способствовало расслаблению детей, сохранности их здоровья.

Воспитательная работа

Отчет по воспитательной работе

1. Общие сведения.

Количество обучающихся в классе: мальчики - 11 чел., девочки - 19чел.

2. Цели и задачи воспитания в учебном году.

Цель: Создание условий для саморазвития и самореализации личности обучающегося

Задачи:

1. Формирование и развитие коллектива класса.

2. Организация системной работы с обучающимися в классе.

3. Создание благоприятных психолого-педагогических условий для развития и нравственного формирования личности каждого ребёнка, его самоутверждения, сохранения неповторимости и раскрытия его потенциальных способностей.

4. Организация системы отношений детей через разнообразные формы воспитывающей деятельности коллектива класса.

5. Защита прав и интересов обучающихся.

6. Гуманизация отношений между обучающимися, обучающимися и педагогическими работниками.

7. Формирование здорового образа жизни.

8. Формирование нравственных смыслов и духовных ориентиров детей.

9. Организация социально-значимой творческой деятельности обучающихся.

3. Результаты проведенной работы.

Во время педагогической практики были проведены 2 классных часа

1. Мой режим дня. Ученики составляли схему занятости, давали рекомендации по правильному режиму дня.

2. Как правильно учить уроки? Обсуждались алгоритмы организации деятельности при самоподготовке к урокам, необходимости успешной учёбы.

3. Формула здоровья. Обсуждались преимущества здорового образа жизни,

7 «А» принимал участие в творческих делах, с остальными классами участвовали в концерте, посвященного 8 марта.

Посещение уроков учениками предмета «Математика» составляет 80 %.

Классный час «Мой режим дня»

Цель классного часа заключалось в нахождение усредненной схема - таблицы режимы дня учащихся 7 «А» класса.

На доске для учащихся были представлены режимные составляющие, а учащиеся на отдельных листочках вписывали временные интервалы соответствующим режимам.

После письменной работы были собраны листочки и проведен анализ, который представлен в таблице.

Схема примерного построения режима школьника 7 класса

Правильная организация режима дня предполагает обязательное пребывание школьников всех возрастов на свежем воздухе в течение 1,5-2 ч. Это могут быть прогулки, активные спортивные игры и другие физические упражнения. Их следует проводить после занятий в школе, чтобы восстановить работоспособность - умственную активность для выполнения домашних заданий.

Активный отдых может продолжаться в пределах 1,5 ч. При превышении этого времени и интенсивной нагрузке работоспособность организма падает. Поэтому продолжительные спортивные игры не снимают переутомления и выполнении домашнего задания потребует от учащегося больших усилий. Время после ужина должно проходить в спокойной обстановке и использоваться в соответствии с индивидуальными интересами учащихся. Это может быть просмотр кинофильмов, но без сцен ужасов, чтение художественной литературы или непродолжительные прогулки 20-30 мин перед сном. Смена деятельности может выражаться и в активной помощи по дому, уборке своей комнаты, мытье посуды и т.п. Она приносит не только физическое, но и моральное удовлетворение.

Рекомендуется приучать детей и подростков вставать и ложиться в одно и то же время. Ужинать необходимо за 1,5-2 ч до сна. Перед сном следует исключить усиленную умственную работу или возбуждающие игры, проветрить помещение для сна. Обязательно совершать весь комплекс процедур вечернего и утреннего туалета (чистка зубов, умывание, уход за волосами).

Питание должно быть сбалансированным и рациональным по составу и осуществляться в строго определенное время в соответствии с возрастными особенностями учащихся - 3-4 раза в день.

Учебные занятия в школе и дома должны сопровождаться динамическими паузами - выполнением физических упражнений, играми. Смена видов деятельности снимает усталость и восстанавливает работоспособность.

Расписание уроков должно составляться с учетом сложности учебных предметов. Предметы естественного цикла должны чередоваться с гуманитарными, урок физической культуры следует проводить после третьего урока, чтобы снять утомление после активной умственной работы.

Анализ классного часа

26 февраля 2016 года в школе №167 города Казань я участвовал на классном часе в 7 «А» классе. Классный час проводился классным руководителем Ивановой Клавдией Петровной. Шестым уроком было проведен классный час и на нем присутствовали 26 учеников. Тема классного часа: «Мой режим дня».

Образовательно-воспитательные задачи: познакомить учащихся с большим многообразием режимов дня учащихся и определить благоприятный режим для учебы.

Классный руководитель актуально и своевременно организовал данное мероприятие и так, чтобы дети сами озвучили и вписали свои интервалы режимов дня.

Классный руководитель в начале классного часа создал положительное настроение, поднял интерес к происходящему. Затем передал слово подготовленным заранее ученикам. Надо отметить, что представленный материал отличался оригинальностью и разнообразием. Дети обсудили и ситуации неправильных режимов дня. В их размышлениях чувствовалось понимание темы разговора, а иногда они произносили очень серьёзные и обдуманные фразы.

В заключении классного часа классный руководитель подвел итоги беседы и поздравил детей с понимаем ответственности за соблюдением благоприятного режима дня.

При подготовке и проведении были решены все задачи классного часа. Было интересно послушать разнообразие режимов дня, а также их рассуждения. Такие воспитательные дела нужны, чтобы дети с раннего возраста уважали себя и своих близких.

Внеклассная работа по математике

Внеклассное мероприятие Игра «Самый умный математик»

Цели: - способствовать проявлению индивидуальных творческих способностей учащихся, активизации их познавательной деятельности.

- в увлекательной игровой форме углубить знания по алгебре и математике, способствовать развитию находчивости, смекалки у учащихся;

- развитие интуиции, эрудиции, логического мышления, расширение кругозора знаний учащихся, побудить познавательный интерес к изучению предмета;

- воспитание культуры общения, математического мышления и математической

Форма проведения: Урок-соревнование с использованием интерактивной доски.

Условия игры

Игра состоит из разминки и пяти туров. В игре участвуют 8 участников. Перед первым туром проводится разминка. Участникам будет задано 16 вопросов плюс три ребуса. Время на обдумывание вопроса не более 5 секунд. Участник, который первым правильно ответит на вопрос, получает 1 балл.

Игру начинает тот участник, который наберет большее количество баллов по итогам разминки, и далее по количеству баллов у каждого из участников. В первом туре участникам задается 5 тестовых вопросов. Время на решение данных тестовых заданий - 3 минуты. Участники получают баллы по количеству правильно решенных заданий. Два участника, которые наберут наименьшее количество очков,

Во втором туре в течение 2 минут игроки должны постараться разгадать кроссворд.

Учитывается время на отгадывание, а также количество правильно отгаданных слов.

За каждый правильный ответ игрок получает 1 балл. Участник, который в сумме двух туров наберет наименьшее количество очков, покидает игру.

В третьем туре в течение 1 минуты участники должны ответить правильно на заданные вопросы и набрать максимальное количество баллов. За каждый правильный ответ участник получает 1 балл. Участник, который в сумме трех туров наберет наименьшее количество очков, покидает игру.

В четвертом туре участникам необходимо будет отгадать загадки и перевести слово-отгадку на три языка: казахский, английский и русский. За отгаданное слово участник получает 1 балл, за перевод на двух языках - 3 балла, а за перевод на трех языках - 5 баллов. Участник, который в сумме четырех туров наберет наименьшее количество баллов, покидает игру.

В пятом финальном туре участникам предлагается игровое поле, которое состоит из 36 ячеек. В ячейках находятся по 10 вопросов по темам «Алгебра», «Геометрия», «Казахстанские олимпийцы», и «Общие вопросы» (6 вопросов) отмеченные красным, зеленым, синим и желтым цветами соответственно (рисунок 1). В течение 10 секунд игроки должны запомнить свои ячейки, затем после закрытия табло (рисунок 2), они должны постараться ответить на вопросы выбранной темы, за которые они получат по 2 балла. За ответы на вопросы соперника дается по 3 балла, за общие вопросы - 1 балл. Победителем турнира становиться участник, набравший наибольшее количество баллов по всем пяти турам.

Ход игры

Вступительное слово учителя: - Уважаемые гости! Уважаемые участники игры! Сегодня мы с вами собрались на математическую игру-турнир «Самый умный математик» с одной целью - узнать, кто же из наших участников завоюет титул самого умного математика.

Нас всех привела сюда общая любовь к математике. Математика многозначна и неисчерпаема. Одних покоряет ее логическая стройность, других - ее точность, а третьих - красота. Ведь не зря Жуковский Н.Е. говорил: «В математике есть своя красота, как в живописи». Так давайте, друзья, мы тоже посмотрим на красоту математики, порадуемся стройности, точности, логичности математики. А поможет нам в этом компетентное жюри. Поприветствуем их!

А теперь предоставим слово нашим участникам (Участники представляются).

Пожелаем удачи и успехов в игре!

Разминка

- Участникам будет задано 16 вопросов. Время на обдумывание вопросов не более 5 секунд. Участник, который первым правильно ответит на вопрос, получает 1 балл.

1. Сколько килограммов в половине тонны?(500 кг)

2. Отрезок, соединяющий центр окружности с точкой на окружности? (Радиус)

3. Что есть у каждого слова, растения и уравнения? (Корень)

4. На какой угол поворачивается солдат по команде «кругом»? (180°)

5. Какая цифра в переводе с латинского означает "ничего"? (0)

6. Чему равна тысячная доля килограмма. (Грамм)

7. Шесть штук картофелин сварятся за 30 минут.

За сколько минут сварится 1 картофелина? (30 минут)

8. Многогранник из Египта. (Пирамида)

9. Без чего не могут обойтись охотники, барабанщики и математики? (Без дробей)

10. Единица скорости на море. (Узел)

11. Отрезок, соединяющий противоположные вершины прямоугольника?

12. Назовите фигуру, не имеющую углов? (Окружность)

13. Единица с шестью нулями? (Миллион)

14. Расшифруйте НОД. (Наибольший общий делитель)

15. Число в обыкновенной дроби под чертой? (Знаменатель)

16. Эмблемой какого автомобиля являются 4 кольца? (Ауди)

- Подведем итоги разминки, пожалуйста, жюри объявите нам результат, скажите же, кто у нас в игре вырвался вперед и занял лидирующую позицию.

- В первом туре нашим участникам задается 5 тестовых вопросов. Участники получают баллы по количеству правильно решенных заданий. Два участника, которые наберут наименьшее количество очков, покидают игру. Время на решение данных тестовых заданий - 3 минуты.

- Уважаемое жюри, назовите нам, пожалуйста, победителя сегодняшней игры.

(Далее проходит награждение победителя грамотой и поощрительным призом, а также памятными призами участников игры в виде дополнительных пятерок)

Заключение

За время прохождения практики я познакомился с профилем учебного заведения, его деятельностью, а также его руководителями и педагогическим коллективом. Изучил основные цели и задачи организации учебно- воспитательной деятельности. Ознакомился с основными положениями Устава ИГПК, познакомился с видами локальных актов образовательного учреждения. Изучил основные приемы организации образовательного процесса. Исследовал уровень развития учебного коллектива, изучил особенности ученического коллектива. За время практики мне удалось разработать 4 и провести 24 урока и дать анализ на 2 урока.

За время практики я приобрёл много знаний и полезной информации, которая в дальнейшем, безусловно, мне очень пригодится.

В данной работе были достигнуты все поставленные задачи, а именно:

Получение практических навыков планирование учебно-воспитательной работы в группе учащихся;

Приобретение опыта профессиональной деятельности педагога по подготовке к циклу уроков теоретического обучения;

Получение начальных навыков проведения уроков по избранному предмету в группе учащихся;

Изучение педагогического опыта квалифицированных преподавателей учебного заведения.

Я считаю, что я справился со своими задачами и с уверенностью могу сказать, начинающим педагогам нужно равняться на старших коллег.

24