Конспект урока по геометрии на тему Примеры задач на построение (7 класс)

Геометрия 7

УРОК № 22 Глава 2. Треугольники (17 часов)

Тема урока. Примеры задач на построение.

Цель урока: Дать представление о задачах на построение; рассмотреть наиболее простые задачи на построение.

Тип урока: комбинированный.

Ход урока.

1. Организационный момент.

2. Проверка домашнего задания.

3. Объяснение нового материала.

Задачи на построение - это такие задачи, при решении которых нужно построить геометрическую фигуру, удовлетворяющим условиям задачи, с помощью циркуля и линейки без деления.

- Видеоурок «Задачи на построения» (от 2 мин 10 сек до 7 мин 14 сек)

Работа с учебником п.22,23.

1. На данном луче от его начала отложить отрезок, равный данному.

На данном луче от его начала отложить отрезок, равный данному.

Построим отрезок АВ и луч ОС.

Решение.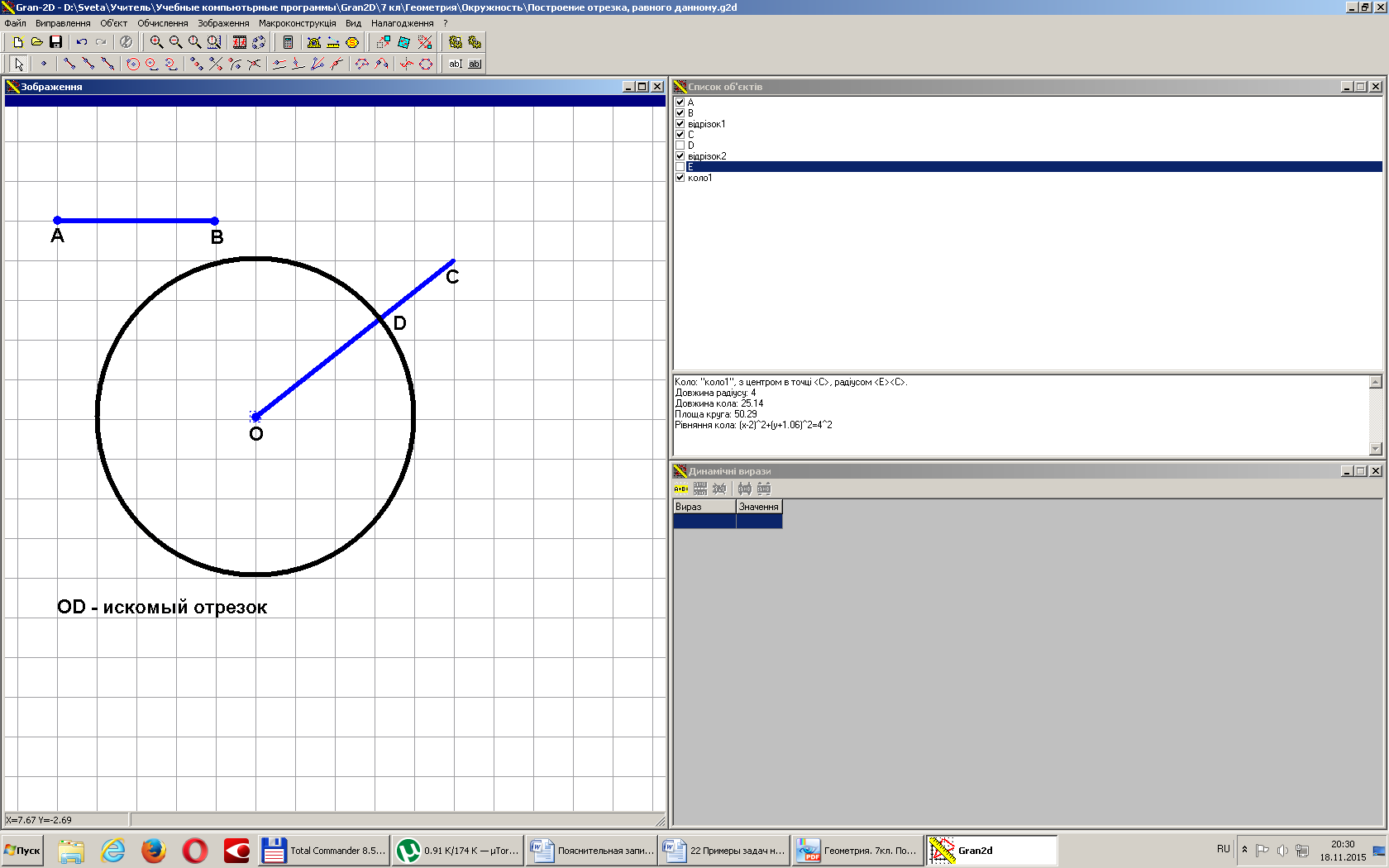

1) Строим Окр.(О, АВ).

2) OD - искомый отрезок.

2. Построение угла, равного данному. Отложить от данного луча угол, равный данному.

Построим и луч ОМ.

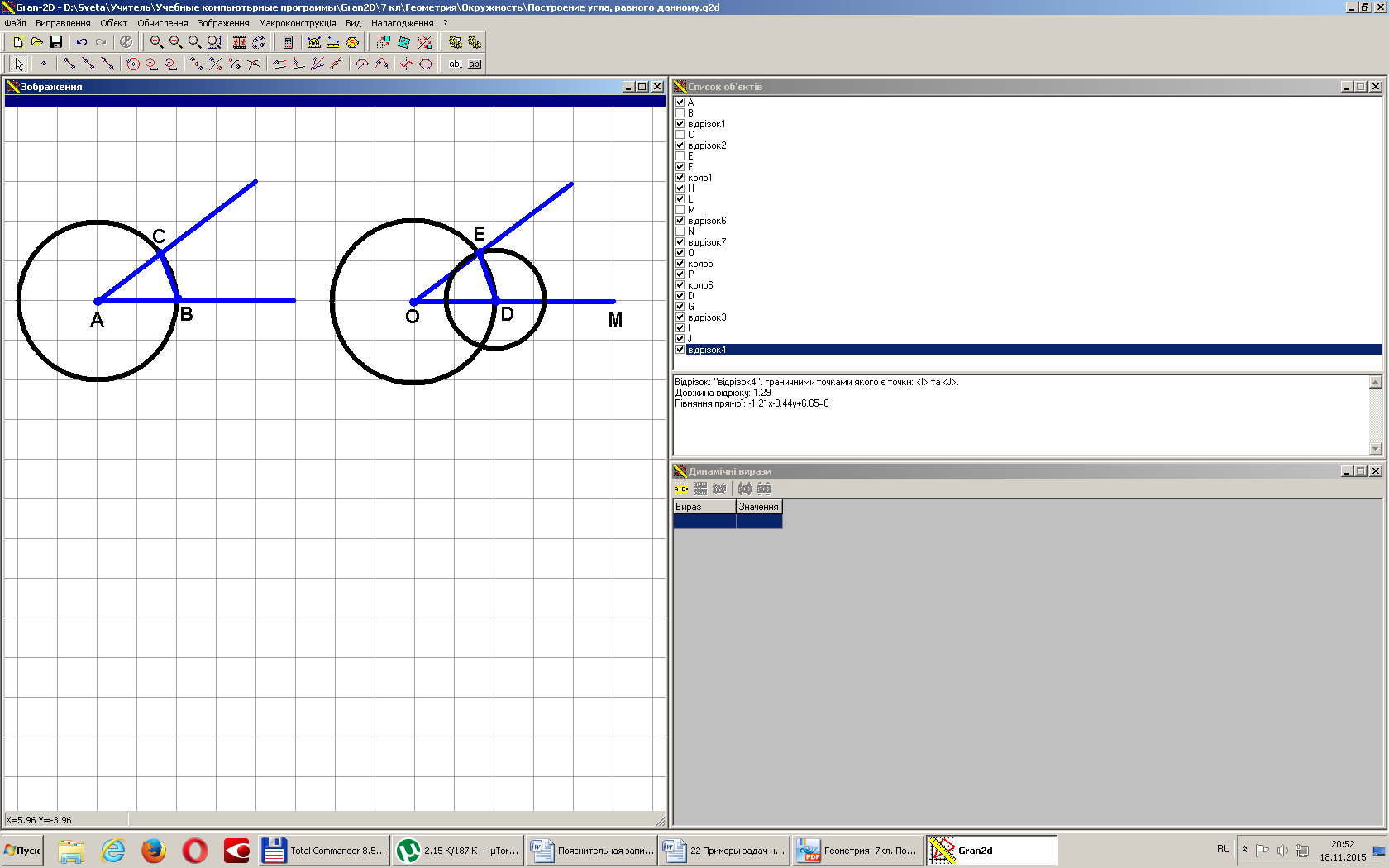
Решение.

1. Строим Окр.(А, r). Пересекает стороны угла в точках В и С.

2. Строим Окр.(О, r). Пересекает луч в точке D.

3. Строим Окр.(D, ВС). Пересекает Окр.(О, r) в точке Е. Проводим луч ОЕ.

4. .

Докажем это.

Рассмотрим ΔАВС и ΔODE. У них:

1. АВ = OD (как радиусы);

2. АС = OE (как радиусы);

3. ВС = DE (по построению).

Значит, ΔАВС = ΔODE (по трем сторонам).

То (как соответствующие углы равных треугольников).

Т.е. построенный .

3. Построение биссектрисы угла. Построить биссектрису данного угла.

Построим угол А.

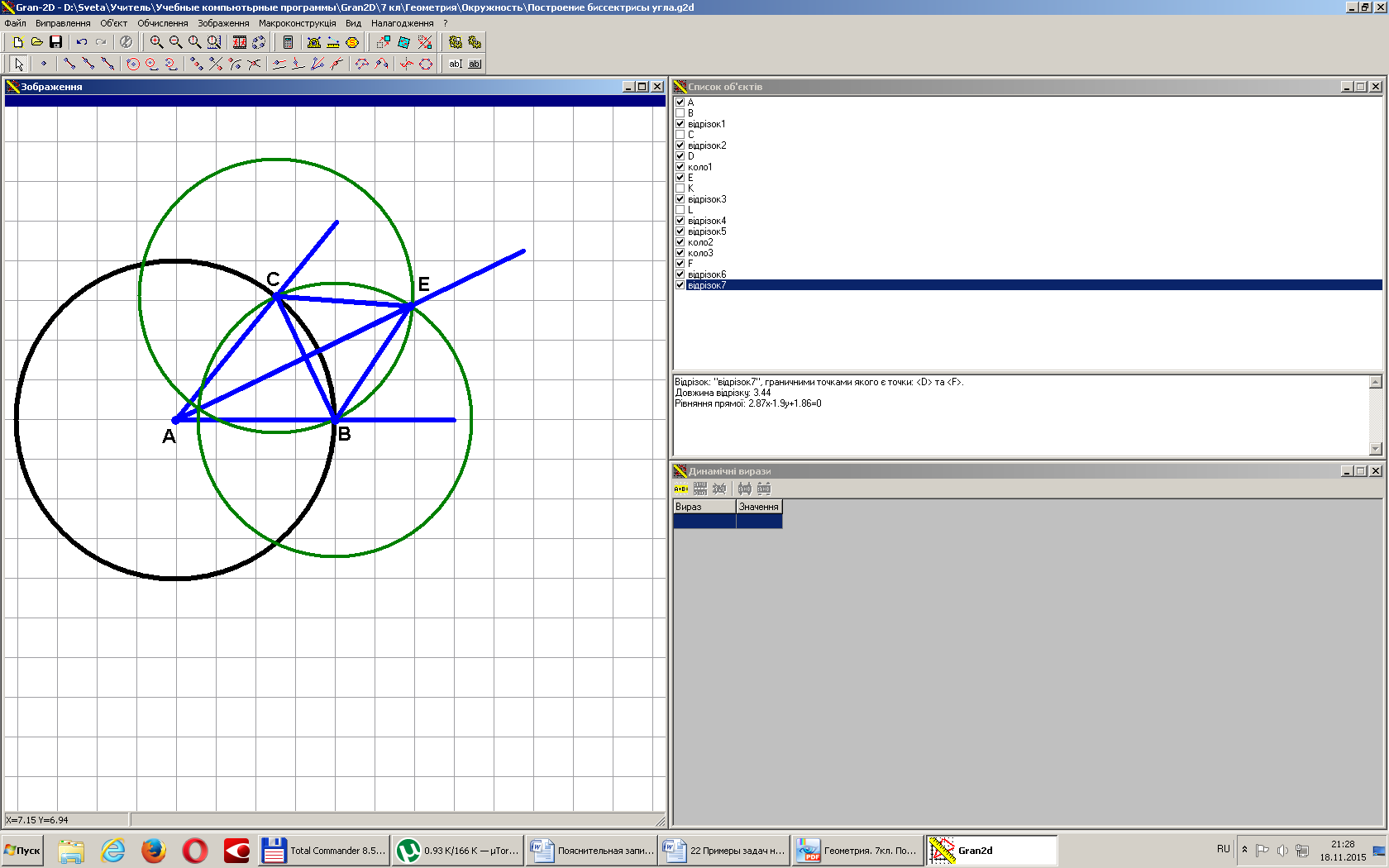
Решение.

1. Строим Окр.(А, r). Пересекает стороны угла в точках В и С.

2. Строим Окр.(В, ВС).

3. Строим Окр.(С, ВС).

4. Через А и точку пересечения окружностей проводим луч АЕ.

5. АЕ - биссектриса угла А.

Докажем это.

Рассмотрим ΔАСЕ и ΔАВE. У них:

1. АС = АВ (как радиусы);

2. АE - общая;

3. СЕ = ВE (по построению).

Значит, ΔАСЕ = ΔАВE (по трем сторонам).

То (как соответствующие углы равных треугольников).

Т.е. АЕ - биссектриса угла А.

4. Построение перпендикулярных прямых. Даны прямая и точка на ней. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой.

Построим прямую а и точку М, .

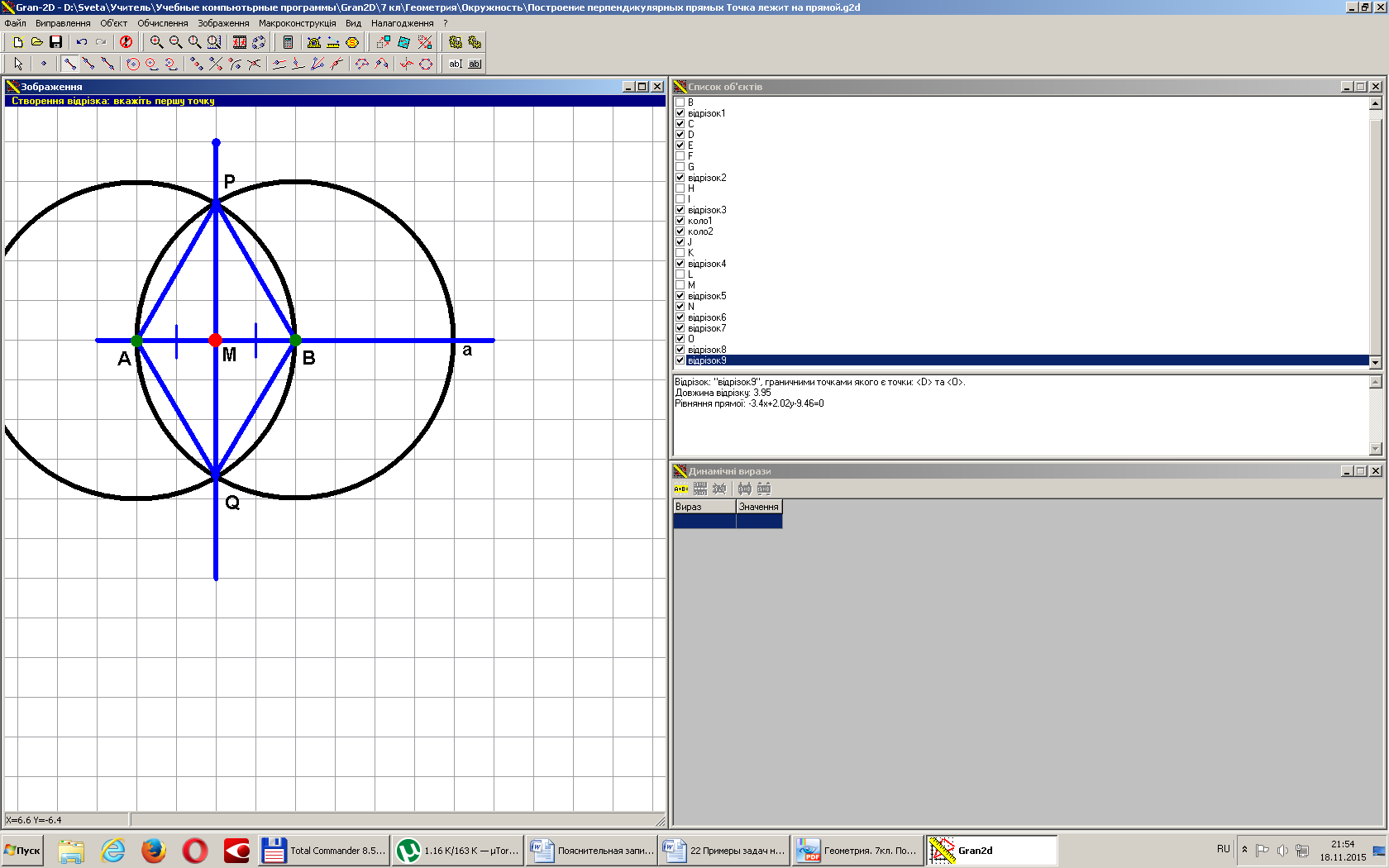
Решение.

1. Строим МА = МВ.

2. Строим Окр.(А, АВ).

3. Строим Окр.(В, АВ).

4. Через точки пересечения окружностей проводим прямую МP.

5. .

Докажем это.

Рассмотрим ΔАРВ, АР = РВ (как радиусы).

МР - медиана (т.к. АМ = МВ по построению).

Значит, (т.к. медиана в равнобедренном треугольнике является высотой).

5. Построение середины отрезка. Построить середину данного отрезка.

Пусть дан отрезок АВ.

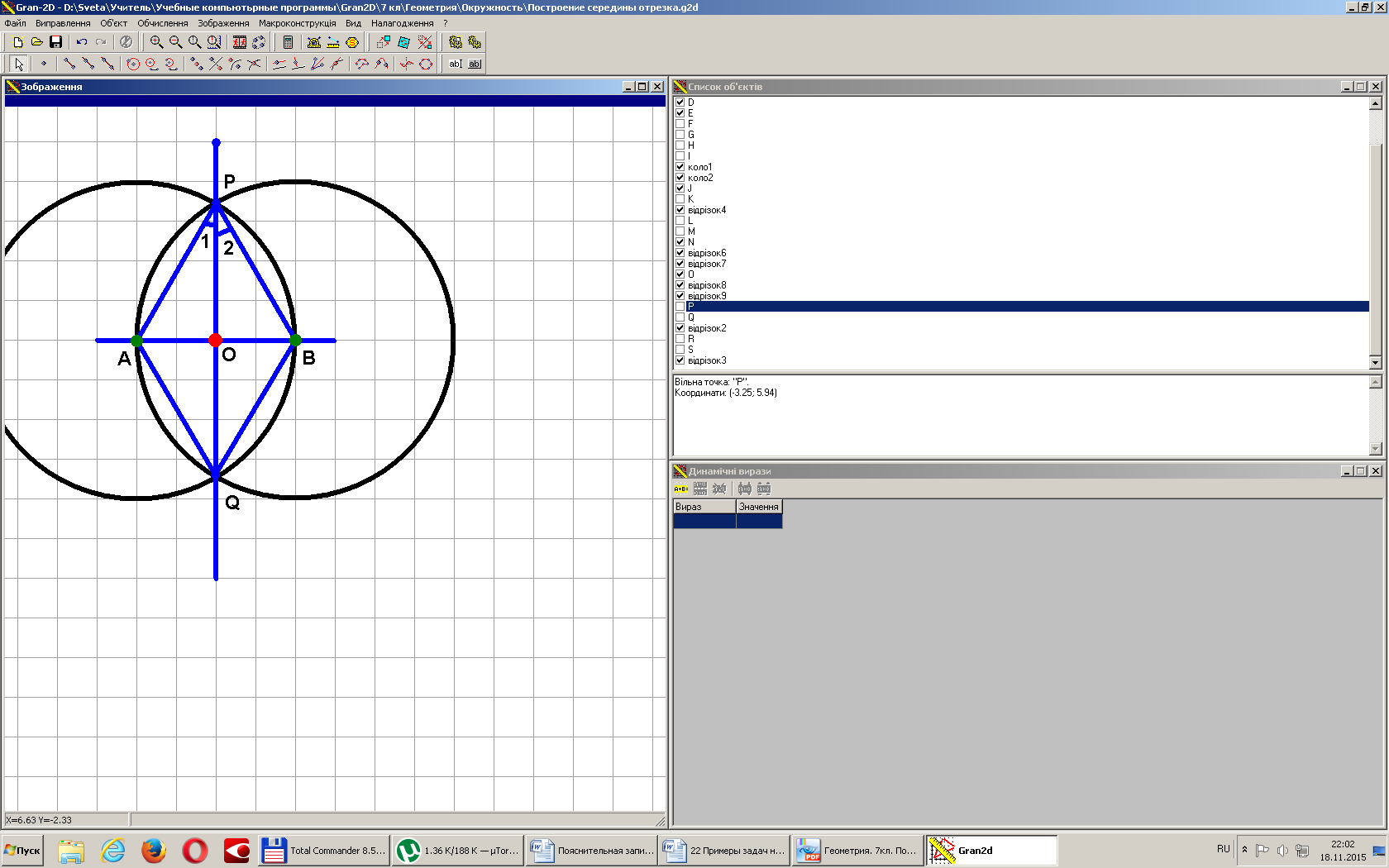
Решение.

1. Строим Окр.(А, АВ).

2. Строим Окр.(В, АВ).

3. Через точки пересечения окружностей проводим прямую PQ.

4. . O - середина АВ.

Докажем это.

Рассмотрим ΔАPQ и ΔВPQ. У них:

1. АP = ВP (как радиусы);

2. АQ = BQ (как радиусы);

3. PQ - общая.

Значит, ΔАСЕ = ΔАВE (по трем сторонам).

То (как соответствующие углы равных треугольников).

Поэтому PO - биссектриса равнобедренного ΔАРВ, а значит, и медиана .

Т.е. O - середина АВ.

4. Подведение итогов урока.

5. Домашнее задание. п.22,23 (выучить наизусть теорию). №153.