Урок по алгебре на тему Простейшие преобразования графиков функций

Урок № _____________

дата

Простейшие преобразования графиков функций

Цель: - формирование навыков выполнять преобразование графиков функций и

Оборудование: - компьютер, мультимедийный проектор, экран, шаблоны параболы для построения на доске и в тетрадях

Ход урока.

1. Организационный момент

2. Актуализация опорных знаний

- На предыдущем уроке вы повторяли уже изученные в 7, 8 классах свойства функций и выучили новые: нули функции, промежутки знакопостоянства и промежутки возрастания и убывания функции. Давайте перечислим свойства для знакомых вам функций

демонстрация графиков на экране с помощью программы Динамическая геометрия

Титульный интерфейс

Начнем с линейной функции. Перечислите свойства:

• формула

• область определения

• область значений

• график

• нули функции

• промежутки знакопостоянства

• промежутки возрастания и убывания

При перечислении свойств происходит работа с графиками функций:

при нажатии на кнопку линейная:

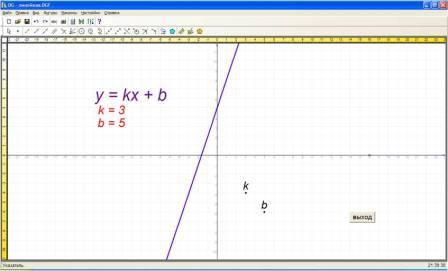
при изменении значений коэффициентов k и b меняется положение графика, уточняется вид угла наклона прямой и положительным направлением оси абсцисс

при нажатии на кнопку обратная пропорциональность:

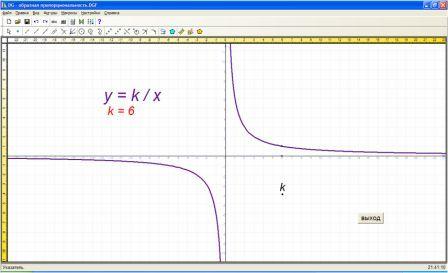
возможно изменение значения коэффициента k, при этом уточняется положение ветвей гиперболы и соответствующие свойства данной функции

при нажатии на кнопку квадратичная:

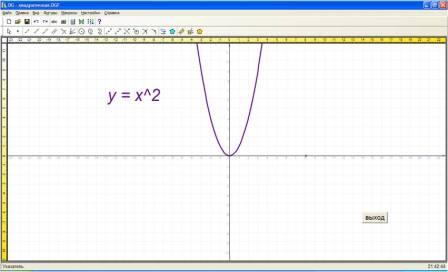
при нажатии на кнопку квадратный корень:

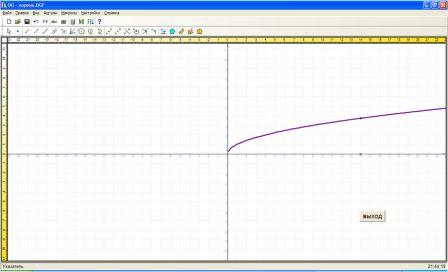
Вывод: зная положение графика функции легко охарактеризовать свойства рассматриваемой функции. Так что очень важно иметь представление о том, как выглядит график функции.

3. Постановка проблемы

- Мы с вами рассмотрели знакомые вам функции. А теперь посмотрите на доску:

на доске 1) 6)

2) 7)

3) 8)

4) 9)

5) 10)

- Нам необходимо построить графики записанных функций. Как это можно сделать? Как вы выполняли это задание в 7, 8 классах?

построить таблицу значений

- Но пользоваться таблицей значений функций не всегда удобно и быстро. Наверняка существуют более простые способы выполнения этого задания. Давайте познакомимся с мудрым высказыванием Леонардо да Винчи:

на экране слайд презентации Power Point:

- Так вот, следуя этой мудрой мысли, давайте на этом уроке вооружимся «рулем и компасом», т.е. разберёмся с тем, как всё-таки можно легко и просто выполнить построения графиков практически всех записанных функций.

4. Оглашение темы урока

- Запишем в тетрадях дату и тему урока: «Простейшие преобразования графиков функций»

5. Объяснение нового материала

- Начнём с первой, записанной на доске функции 1) . Какую знакомую вам функцию она напоминает? А чем отличается?

, прибавляется 3

- Так давайте построим в прямоугольной системе координат параболу . Это можно сделать, построив 5 опорных точек. Но сегодня с целью экономии времени для построения мы воспользуемся шаблонами. Для доски - свой, а на ваших партах лежат маленькие шаблоны. Определяем координаты вершины параболы, прикладываем шаблон и аккуратно обводим.

построение параболы

- Выделим на графике опорные точки. А теперь подумаем, как будут располагаться точки нового графика? Что происходит со значениями новой функции по сравнению с первоначальной?

увеличиваются на 3

- Построим эти точки. Плавной линией соединим их. Нетрудно сделать вывод, что вид параболы сохраняется. Но как поменял вид график функции по сравнению с графиком ?

сдвинулся вверх на 3 единичных отрезка

- Но ведь можно было рассмотреть и какую-нибудь другую функцию с похожим преобразованием. Запишем вывод в тетрадях в виде опорного конспекта:

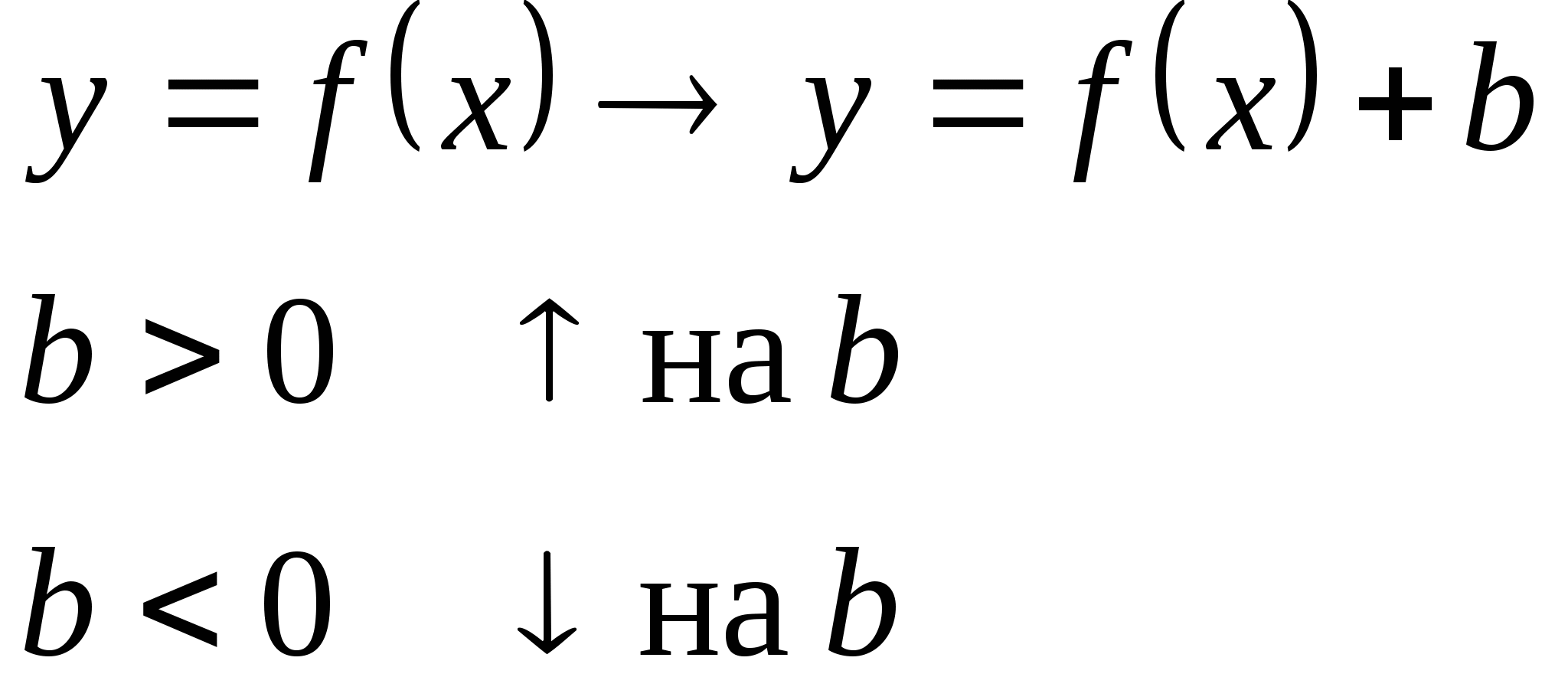
- Какие из представленных на доске функций подходят под это преобразование?

4) построение графика с помощью шаблона

7) устные рассуждения о построении

по мере построения графиков записанные функции вытираются с доски

- Теперь давайте разберёмся, как построить график функции 2) . И опять обратим внимание, на какую известную функцию похожа данная.

- Построим с помощью шаблона график . А теперь найдите для преобразованной функции для каких значениях аргумента значение функции будет равно 0?

- Отметим эту точку графика . А при каких значениях аргумента ?

- Отмечаем и эти точки, . Для какого значения y легко найти целые значения х и какие это значения?

,

- Получили ещё две точки графика и . В целом - пять опорных точек. Строим параболу.

построение параболы

- Как изменилось положение нового графика?

сдвинулся вправо на 2 единицы

- Обратите внимание на вид функции. Преобразование происходит над аргументом. Присутствующий знак «-» казалось бы «говорит» о том, что надо сдвинуть график влево, но на самом деле сдвиг происходит в обратную сторону. Запомните эту «коварность» преобразования вдоль оси абсцисс Ох! Запишем в тетради вывод для общего случая:

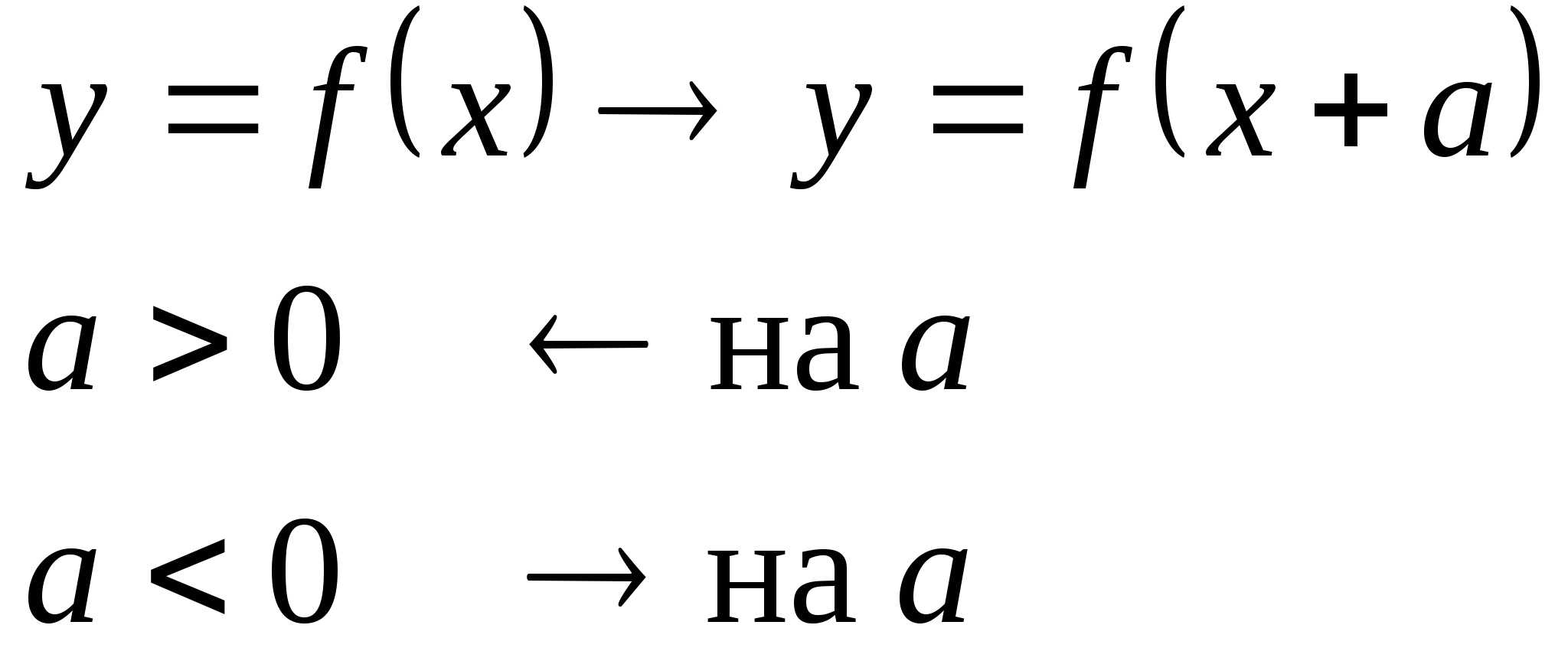
- И снова обратимся к списку функций. Какие из представленных функций подходят под это преобразование?

5) построение графика

9) устные рассуждения

6. Решение упражнений

а) устно

- Задания:

Как построить график функции:

с помощью программы Динамическая геометрия меняются значения а и b, при этом меняется расположение графика и проверяются ответы учащихся

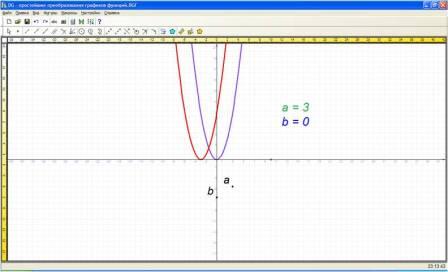
- Графики каких из приведенных функций вы ещё сможете построить?

3) и 8)

построение графиков функций учащимися на доске

7. Самостоятельная работа

- А сейчас проверим, как вы разобрались с темой урока.

Каждый ученик получил перед началом урока лист формата А5 с заданиями самостоятельной работы.

По окончании выполнения проверка с помощью компьютера.

8. Итоги урока

- Подводя итоги урока, давайте снова обратимся к высказыванию Леонардо да Винчи. Достигли ли мы поставленной цели?

- Припоминаете, как вы растерялись при виде записанных на доске функций? А оказывается так всё просто, когда вы «вооружены» теорией! Осталось только две функции и . А с особенностями построения графиков этих и подобных функций вы познакомитесь на следующих уроках.

9. Домашнее задание

п. 10, № 311, 314, 315

5