Урок на тему Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Дюртюлинский филиал

Федерального государственного образовательного учреждения

среднего профессионального образования

«Октябрьский нефтяной колледж им. С. И. Кувыкина»

Методическая разработка

открытого урока

по дисциплине «Математика».

Тема урока:

«Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами»

для специальности:

151031 «Монтаж и техническая эксплуатация

промышленного оборудования (по отраслям)».

Преподаватель

естественнонаучных дисциплин

Хаматова Ф.М.

Дюртюли -2013г.

Дата проведения: 26.10.2013 года

Группа: 2МД-10

Урок №14

Тема: «Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами».

Цели урока:

Образовательные:

• формирование учебно-познавательной компетенции;

• сформулировать определение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами;

• научить составлять характеристическое уравнение;

• показать, что общее решение дифференциального уравнения строится в зависимости от характера корней характеристического уравнения;

• закрепить решением примеров три случая нахождения общего решения дифференциального уравнения;

Развивающие:

• формирование компетенции личного самосовершенствования;

• развивать способности самостоятельно очерчивать учебную проблему, формулировать алгоритм ее решения, контролировать процесс и оценивать полученный результат.

• способствовать развитию памяти, пространственного воображения;

• развивать познавательные интересы через применение информационных технологий.

• развивать наблюдательность, самостоятельность, мышление студентов посредством логических учебных действий.

Воспитательные:

• воспитывать волю и настойчивость для достижения конечных результатов;

• воспитывать адаптивность к современным условиям обучения.

Тип урока: урок изучения нового материала.

Комплексно-методическое обеспечение: мультимедийный проектор с экраном, ноутбук, штатив, листы контроля, раздаточный материал,

презентация проекта в Power Point.

Методы обучения:

• словесные;

• наглядные;

• практические.

Использование инновационных технологий:

• технология дифференцированного обучения;

• проблемное обучение;

• личностно-ориентированное обучение;

• информационные технологии;

• блочно-модульное обучение.

Ход урока.

I.Организационный момент

Цель: обеспечить благоприятную внешнюю обстановку для работы на уроке, создать атмосферу делового общения, обеспечить психологическую подготовку студентов к работе.

Проверка подготовленности студентов и кабинета к уроку, выявление отсутствующих, организация внимания студентов.

(На доске и в тетрадях запись даты и темы)

II. Постановка целей. Мотивация учащихся.

1.Сформулировать определение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами; научить составлять характеристическое уравнение;

показать, что общее решение дифференциального уравнения строится в зависимости от характера корней характеристического уравнения;

закрепить решением примеров три случая нахождения общего решения дифференциального уравнения.

2. Способствовать развитию памяти, пространственного воображения, алгоритмической культуры; развивать познавательные интересы через применение информационных технологий; развивать наблюдательность, самостоятельность, мышление студентов посредством логических учебных действий.

3.Воспитывать волю и настойчивость для достижения конечных результатов; воспитывать адаптивность к современным условиям обучения.

А сейчас предлагаю определиться с вашими целями.

Перед каждым из вас на партах разложены листы контроля.

Лист самоконтроля.

Ф.И. студента

Задания

Количество баллов,

которые возможно набрать(0-36)

Мое участие на уроке

1

Вспомним определения

0-5

2

Тестирование

0-5

3

Изучение нового материала

0-7

4

Решение ключевых примеров

0-7

5

Закрепление

0-5

6

Задание« Найди и исправь ошибку»

0-2

7

Самостоятельное решение примеров

0-1

8

Рефлексия учебной деятельности

0-4

Общее количество баллов, набранных за урок

Напишите, пожалуйста, фамилию и имя. Наш урок состоит из нескольких этапов. После прохождения каждого этапа вы будете получать определенное количество баллов. Суммируя их, при подведении итогов сегодняшнего занятия, вы можете получить следующие отметки:

«5»:24-36 баллов.

«4»:18-23баллов.

«3»:9-17баллов.

Итак, ребята в добрый путь!

III. Актуализация опорных знаний.

• Вспомним определения:

1. Какое уравнение называется дифференциальным? (на экране).

Ответ: Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и ее производные или дифференциалы (на экране).

2. Что называется порядком дифференциального уравнения? (на экране).

Ответ: Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.

3. Что называется решением дифференциального уравнения? (на экране)

Ответ: Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.

4. Какое решение называется общим решением дифференциального уравнения? (на экране)

Ответ: Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения.

5. Какое решение называется частным решением? (на экране)

Ответ: Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных.

• Тест

1.Термин «дифференциальное уравнение» ввел: (на экране)

А) Г. Лейбниц(17 век);

Б) Ж.Лагранж(18 век);

В) П.Лаплас(18 век);

Г) Л.Эйлер(18век).

2. Определите порядок дифференциального уравнения: (на экране)

А) первого порядка;

Б) второго порядка;

В) третьего порядка;

Г) четвертого поря

3. К какому типу относятся дифференциальные уравнения? (на экране)

А) линейное дифференциальное уравнение первого порядка;

Б) уравнение Бернулли;

В) первого порядка с разделяющимися переменными

Г) неполное уравнение второго порядка.

4.Вычислите производную функции: . (на экране)

А)

Б)

В)

Г)

5.В каком из двух дифференциальных уравнении можно найти

частное решение: (на экране)

1. при х=-2;

2.

А) в первом и во втором;

Б) в первом;

В) во втором;

Г) нет правильного ответа.

Обменяйтесь тетрадями. Сверьтесь с правильными ответами на экране. Отметьте в тетрадях соседа верно выполненные задания теста знаком «+», а неверно выполненные задания со знаком «-»

IV. Изучение нового материала.

Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

Эпиграф (на экране) Числа не управляют миром, но они

показывают, как управляется мир.

И.Гете.

Не будем спорить - будем вычислять.

Г.Лейбниц.

(Студентам рассказываю сферу применения дифференциальных уравнений, тем самым, разъясняя выбор эпиграфов урока).

Прежде чем дать определение нового вида дифференциального уравнения, раскроем подробно его название(с привлечением студентов):

1)дифференциальное уравнение (по определению) обязательно содержит производные или дифференциалы искомой функции;

2)уравнение второго порядка содержит производную, наивысший порядок которой равен 2;

3)это- уравнение линейное относительно искомой функции, ее производных, т. е. содержит их в первой степени;

4) это- уравнение с постоянными коэффициентами; значит, коэффициенты при функции, ее производных являются постоянными величинами.

Учитывая все это, можно сказать, что рассматриваемое уравнение содержит в первой степени и коэффициенты при них - постоянные величины.

Определение: (на экране)

Линейным однородным дифференциальным уравнением второго порядка с

постоянными коэффициентами называется уравнение вида

где - постоянные величины.

Формула (А) может быть записана и так:

(B)

Для отыскания общего решения данного уравнения составляется характеристическое уравнение:

Это уравнение получается из первоначального уравнения путем замены производных искомой функции, соответствующими степенями и сама функция заменяется единицей. Тогда общее решение дифференциального уравнения строится в зависимости от характера корней:

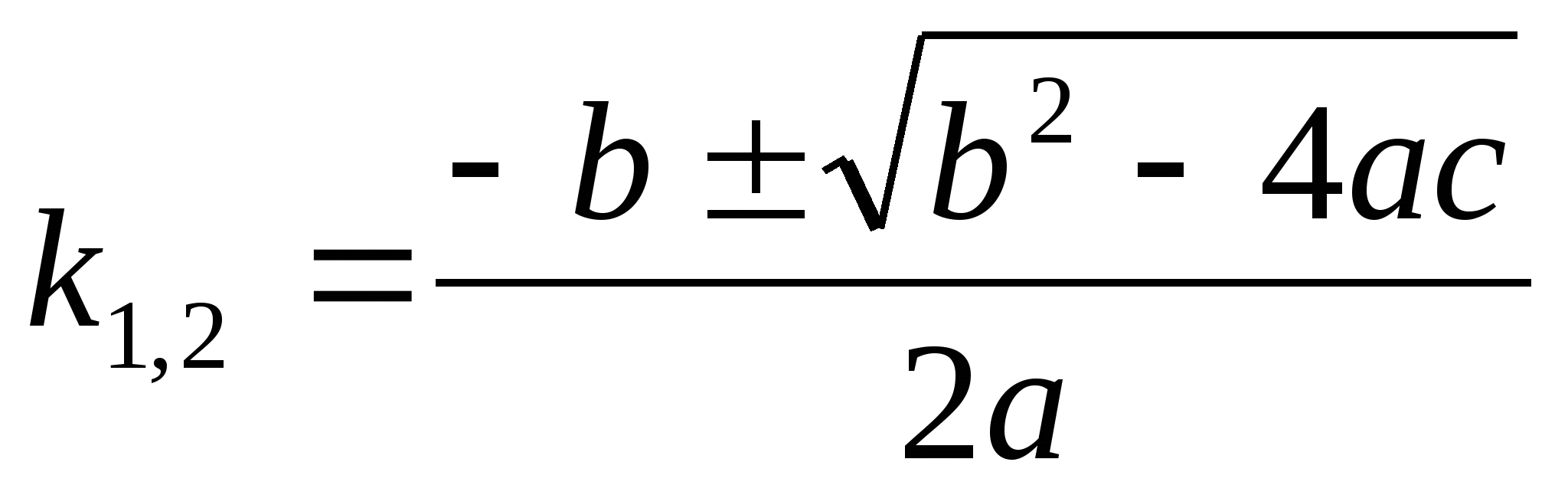
Возможны три случая: (на экране)

I случай: и - действительные корни и различные, тогда общее решение примет вид:

(1)

II случай:-действительные и равные, тогда общее решение

примет вид:

(2)

III случай: и - комплексные числа, а именно тогда общее решение имеет вид:

(3)

V.Решение ключевых задач.

Найти общее решение следующих дифференциальных уравнений.

Пример 1.

(Решаю и объясняю, потом на экране высвечивается полное оформление)

Решение:

Составим характеристическое уравнение:

Общее решение данного дифференциального уравнения, согласно формуле(1), имеет вид:

Ответ:

Пример 2.

(Студент вычисляет корни характеристического уравнения, сообща приходим к общему решению)

Решение:

Составим характеристическое уравнение:

Общее решение данного дифференциального уравнения, согласно формуле(2), имеет вид:

Ответ:

Пример 3. .

(Решаю и объясняю,)

Решение:

Составим характеристическое уравнение:

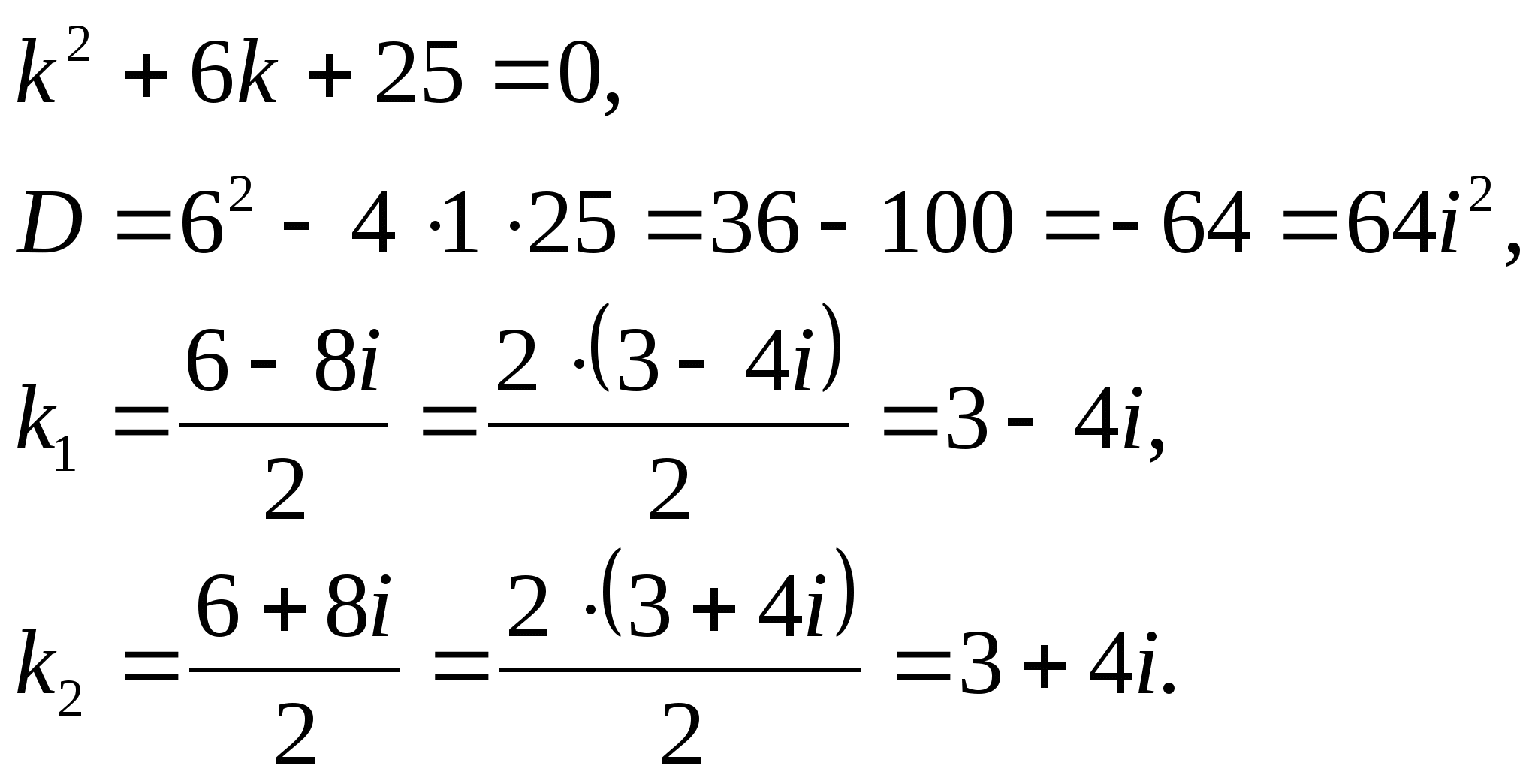
Общее решение данного дифференциального уравнения, согласно формуле(3), имеет вид:

Ответ:

Пример 4 .

(Решаю и объясняю)

Решение:

Составим характеристическое уравнение:

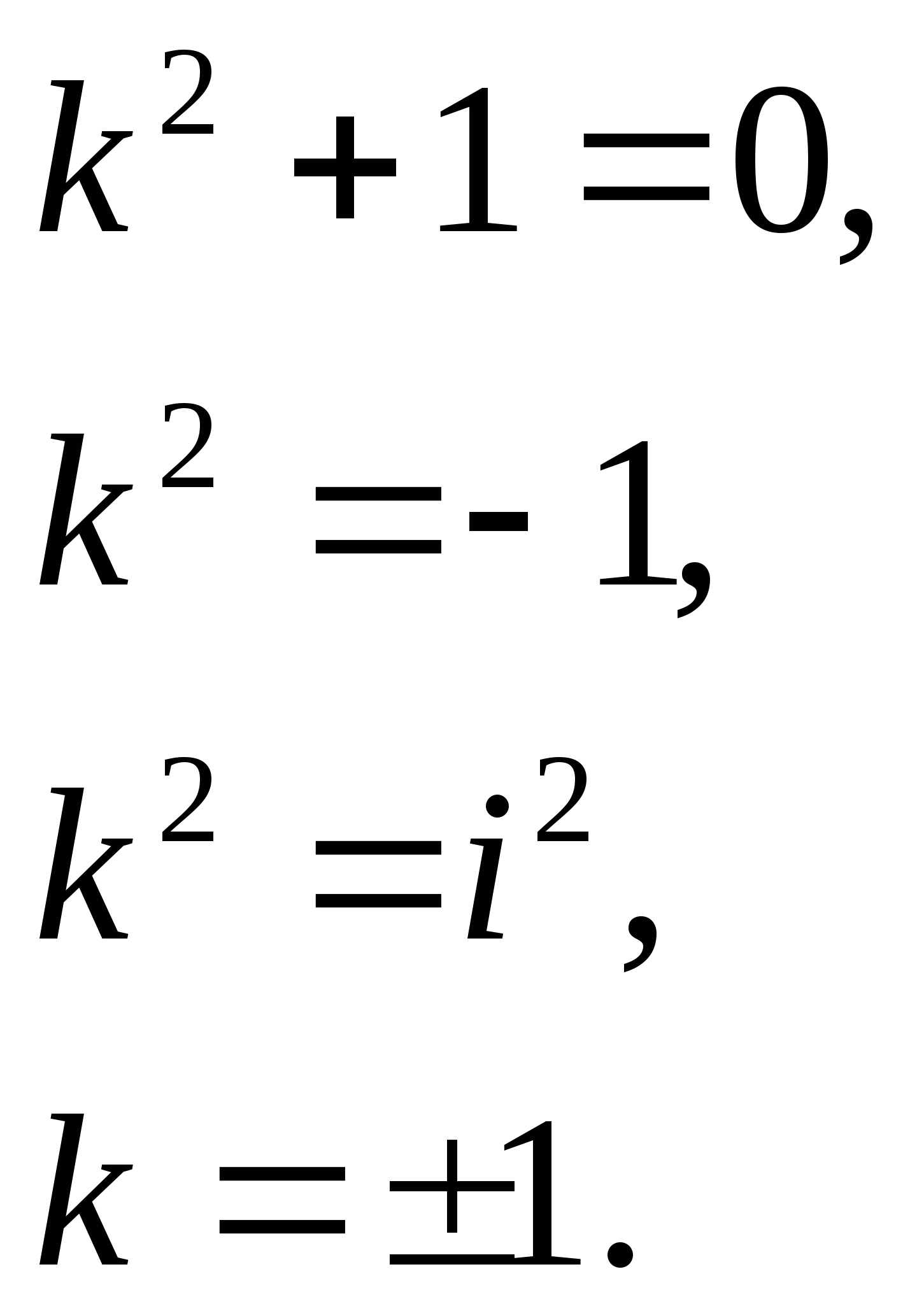
Это третий случай, где

Общее решение данного дифференциального уравнения, согласно формуле(3), имеет вид:

Ответ:

Пример5.Найти частное решение дифференциального уравнения , если у(0)=1 и .

(Решаю и объясняю с привлечением студентов)

Решение:

Составим характеристическое уравнение:

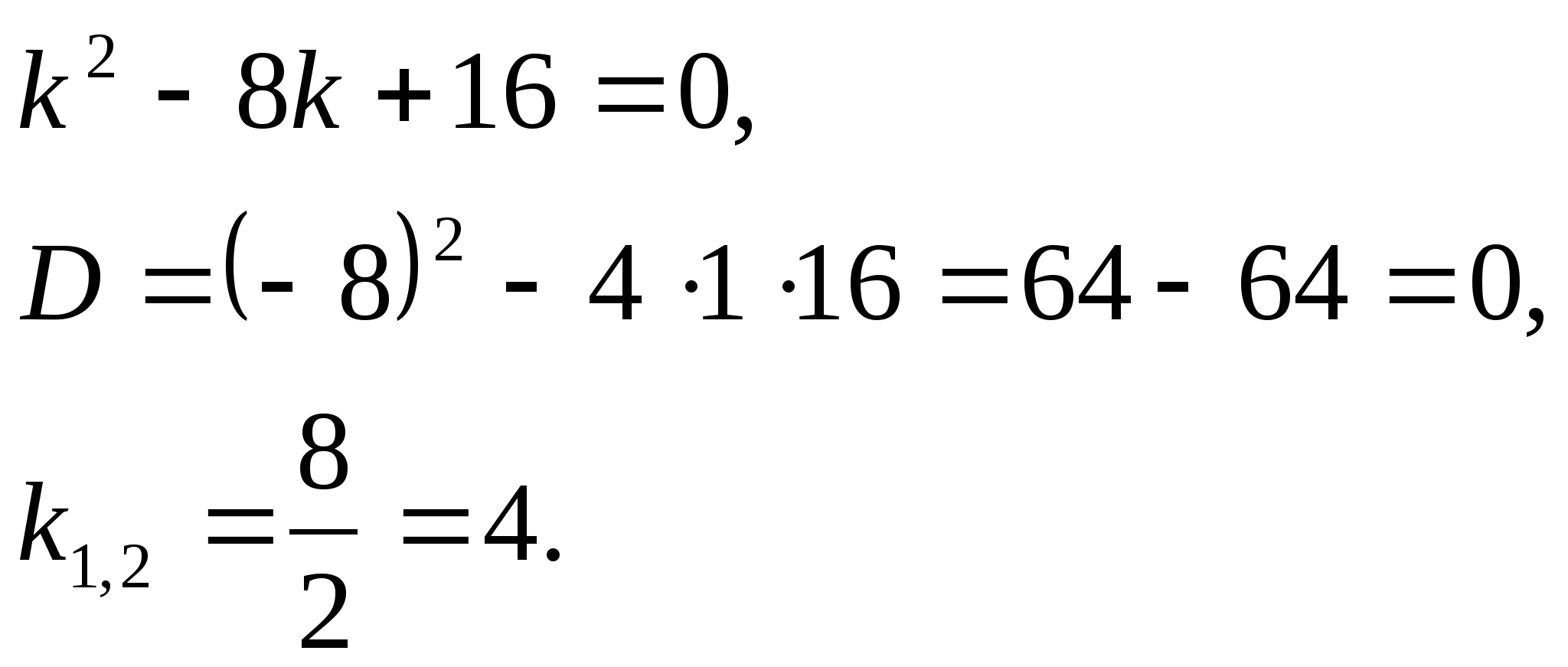
Общее решение данного дифференциального уравнения, согласно формуле(2), имеет вид:

Так как заданы начальные условия, то:

Чтобы найти значение , дифференцируем общее решение.

Таким образом, искомое частное решение имеет вид

Ответ:

VI. Закрепление изученной темы.

Решите уравнение:

№50(1) (студент решает у доски)

1)

Решение:

Составим характеристическое уравнение:

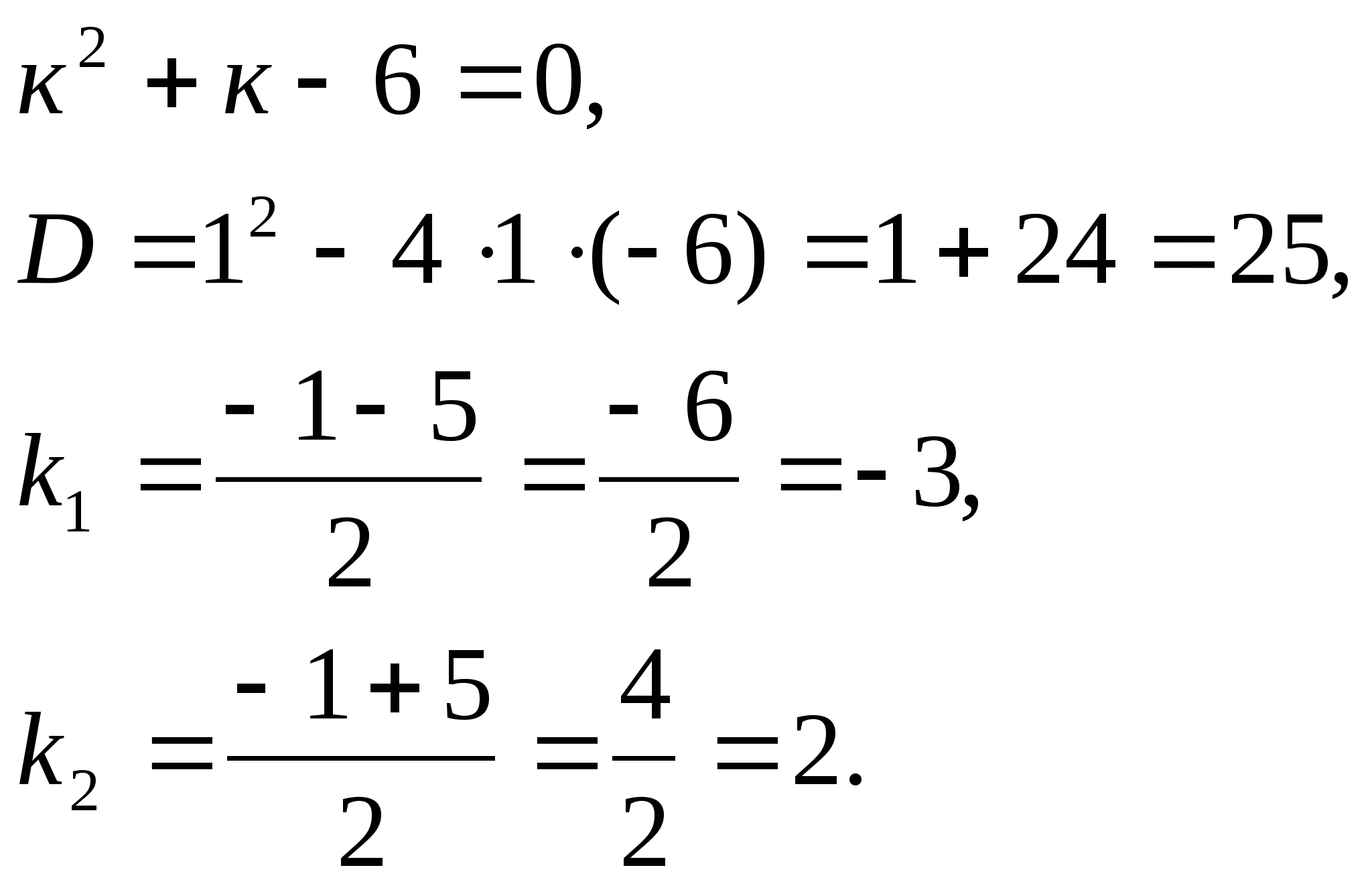
Общее решение данного дифференциального уравнения, согласно формуле(1), имеет вид:

Ответ:

№51(2) -студент решает у доски

2)

Решение:

Составим характеристическое уравнение:

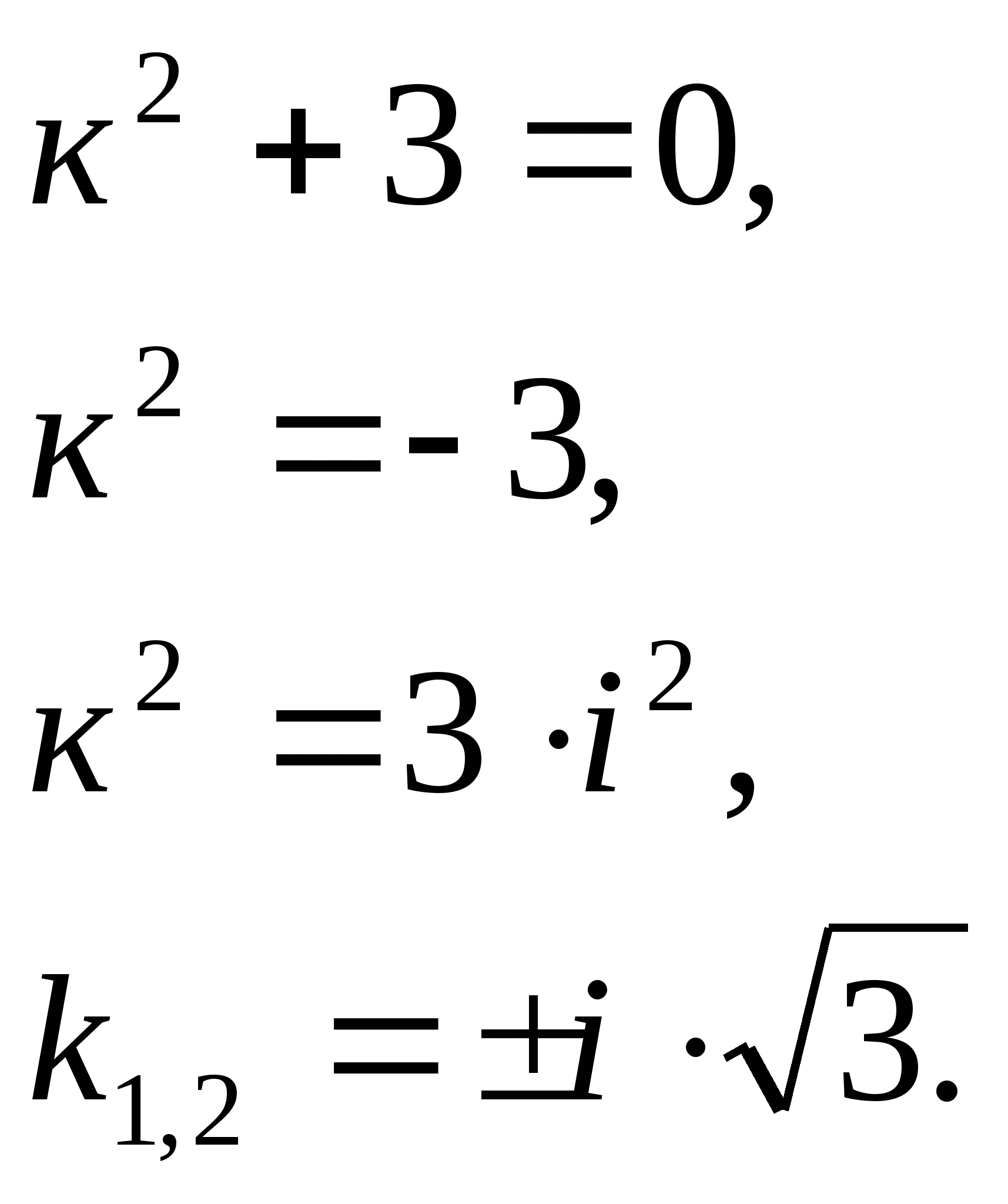
Это третий случай, где

Общее решение данного дифференциального уравнения, согласно формуле(3), имеет вид:

Ответ:

VII. Задание «Найди и исправь ошибку»:

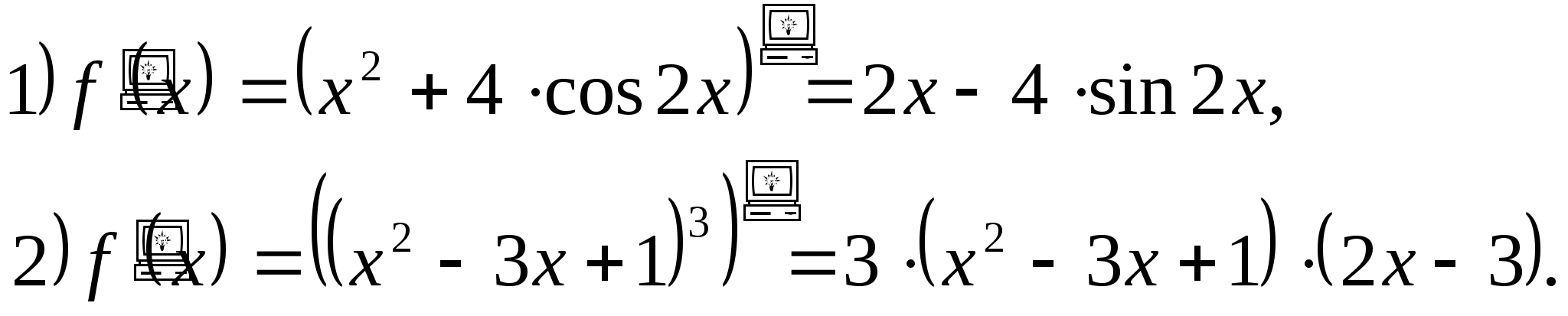
VIII.Примеры для самостоятельного решения

Все решают №54(1),нескольким студентам - индивидуальные задания.

№54(1)

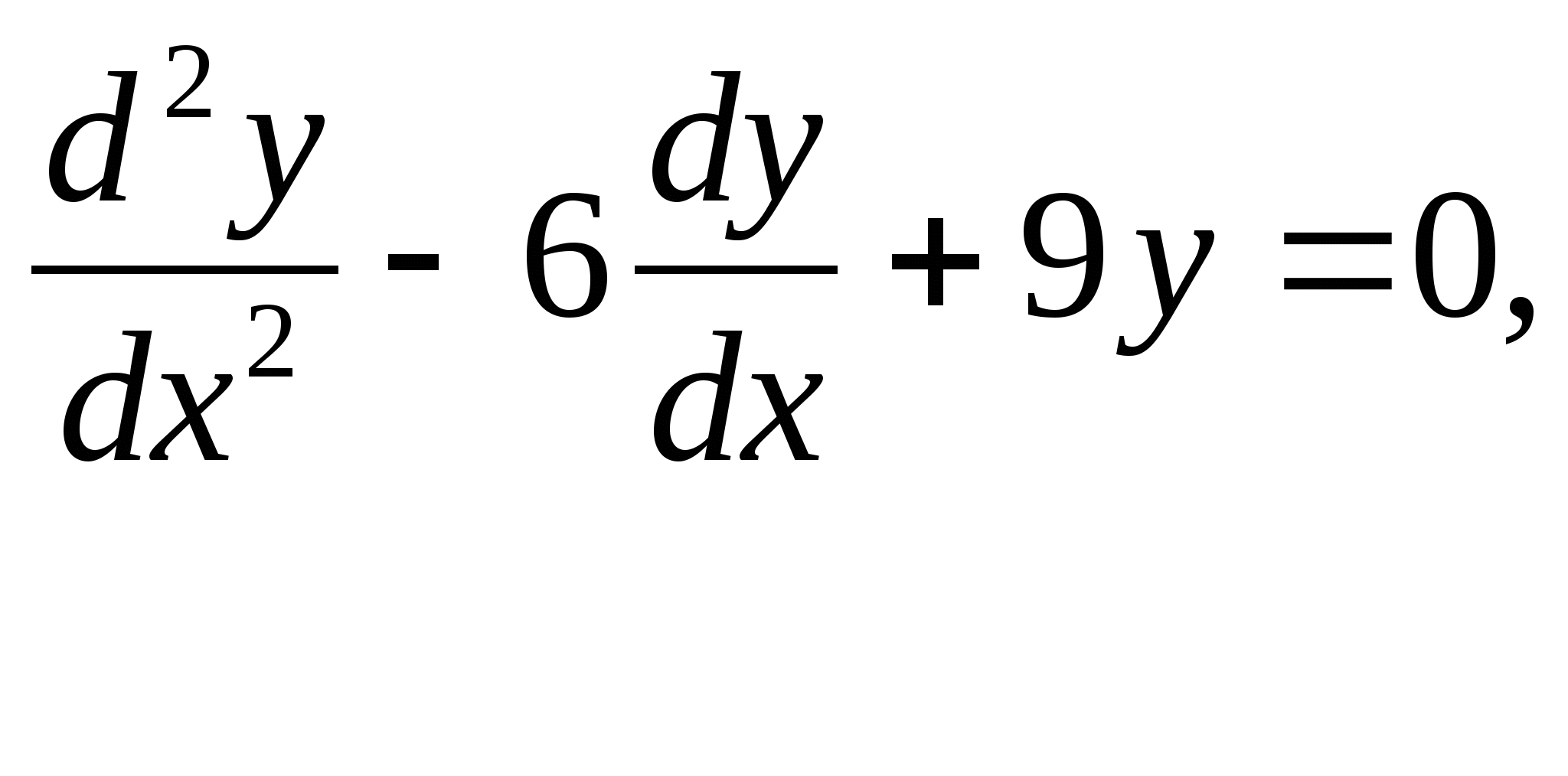
Решение:

Составим характеристическое уравнение:

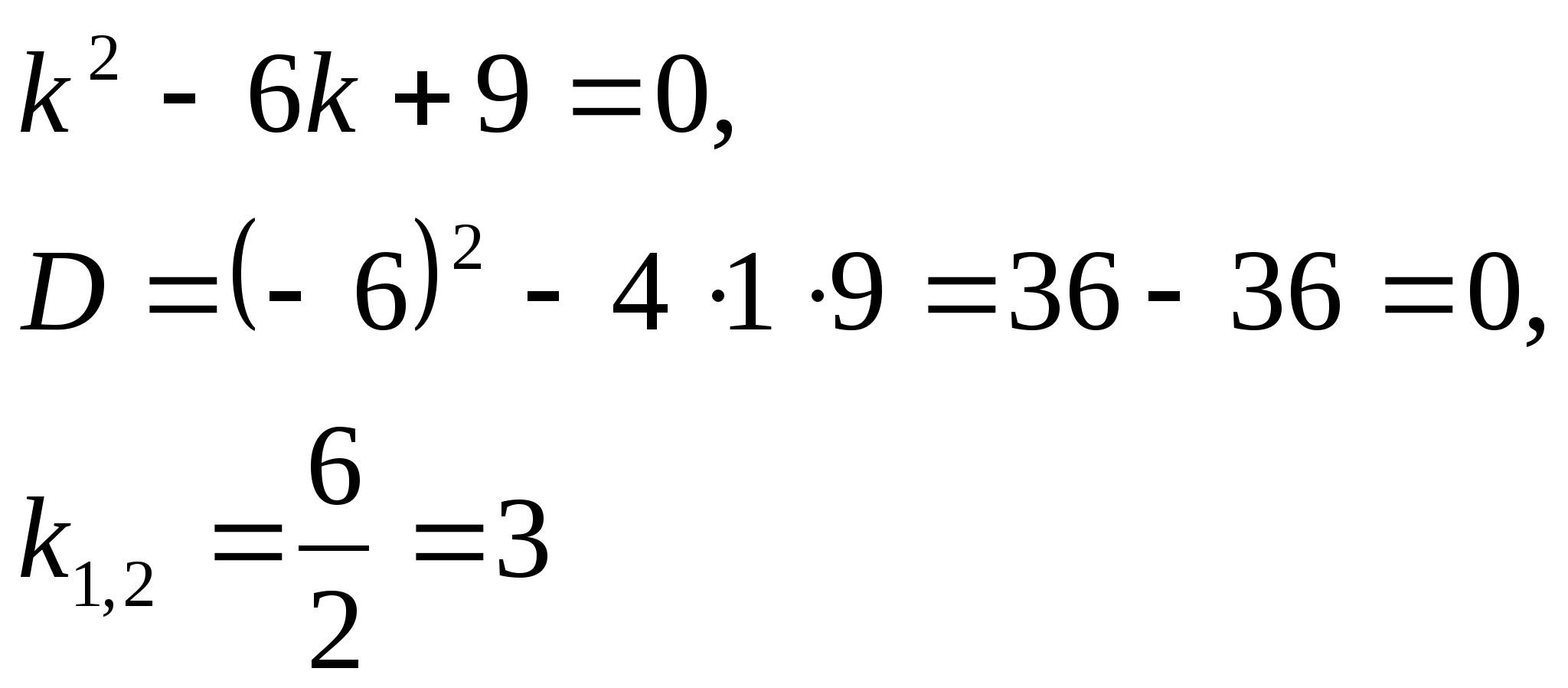
Общее решение данного дифференциального уравнения, согласно формуле(2), имеет вид:

Ответ:

IX. Рефлексия учебной деятельности.

1. Дать определение линейного однородного дифференциального уравнения

с постоянными коэффициентами.

2. Как решается данный вид уравнения?

3. Сколько корней может иметь характеристическое уравнение?

4.Сколько случаев нахождения общего решения дифференциального уравнения вы знаете?

X. Домашнее задание и актуализация темы следующего урока.

Цель: обеспечить понимание способов выполнения домашнего задания и актуальности следующей темы.

10.1. На следующем уроке будет практическое занятия по теме «Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами ».

10.2 Задание на дом: § 5 по учебнику Н.В.Богомолова; № 50 (2,3);

51 (1,3);изучить решение ключевого примера №5

XI. Подведение итогов урока по листам контроля.

Сводная таблица для выставления баллов заготовлена на оборотной стороне доски.

Все слайды находятся в презентации.