- Учителю
- Анализ урока математики(5 класс)
Анализ урока математики(5 класс)
Анализ урока математики
Анализ урока математики в 5 классе.
Тема: «Сложение и вычитание чисел с переходом через разряд в пределах 1000».
1. Общая организация урока.
1.1.Последовательность и распределение этапов по времени.
Это был урок закрепления пройденного. В соответствии с типом и целями урока была определена его структура, состоящая из 6 этапов:
- организационное начало урока;
- подготовка к основному этапу;
- основной этап, закрепление пройденного;
- первичная проверка ;
- вторичная проверка понимания;
- подведение итогов.
Цель организационного этапа - подготовить учащихся к работе на уроке. Включением в работу послужило предложение сесть тем детям, кто услышит трёхзначное число. Это заняло 1 мин.
Цель подготовки к основному этапу урока - организация мотивации и постановка цели учебной деятельности. Дети припомнили текущее время года, дополнили числа до круглого десятка (с учётом групп обучаемости по В.В.Воронковой). Продолжительность этапа -9 мин.
Цель основного этапа - обеспечение восприятия, осмысления, первичное закрепление изучаемого. Продолжительность этапа - 15 мин.
Цель этапа первичной проверки понимания - проверка правильности и осознанности усвоения нового материала, выявление пробелов, их коррекция. Продолжительность этапа - 10 мин.
Цель этапа вторичной проверки - использование полученных знаний при выполнении различных заданий. Продолжительность этапа - 8 мин.
На подведение итогов было отведено 2 мин.
Структура урока соответствовала его целям и типу. Соблюдалась логическая последовательность и взаимосвязь этапов. Распределение времени по этапам было рациональным.
1.2.Организация познавательной деятельности на уроке.
Для организации познавательной деятельности были использованы следующие формы: фронтальная, индивидуальная (работа по карточкам, составление задач, работа у доски).
1.3.Соблюдение охранительного режима.
Кабинет был готов к занятию. Помещение проветрено, освещено. Во время опроса дети вставали, выходили к доске, делали динамическую паузу. Предъявляемые учителем таблицы для чтения учащимися были напечатаны крупным шрифтом.
1.4.Подведение итогов урока.
Намеченный план был выполнен. Цели урока достигнуты. Дети сделали верные выводы по уроку.
2. Содержание урока.
2.1.Воспитательная и коррекционно-развивающая направленность урока.
Воспитательная цель урока - формировать у учащихся правильные представления о заботах людей в осеннее время.
Образовательная цель - закрепить знания учащихся о решении
примеровна сложение и вычитание с переходом через разряд, упражнять
в решении примеров данного вида.
Коррекционно-развивающая цель урока - учить устанавливать
причинно-следственные связи при решении составной задачи,
добиваться правильного конструирования предложений с использованием
математических терминов.
Для реализации данной цели были использованы следующие приёмы:
- составление задач;
- дополнение до круглого десятка;
- задание на внимание;
- рассуждение над задачами;
- рассматривание геометрической фигуры в рисунке;
- работа по образцу;
- вопросы на установление причинно-следственных связей;
- организация внимательного прослушивания ответов учащегося с целью взаимной оценки;
2.2.Правильность подбора материала на уроке.
Формирование навыка правильного решения примеров на сложение и вычитание с переходом через десяток осуществлялось(учебник по математике для 5 класса специальных (коррекционных) учреждений VIII вида), на основе государственной программы под редакцией Воронковой В.В., определяющая объём знаний с учётом развития познавательных интересов детей, расширение их кругозора, воспитания нравственных качеств.
2.3.Связь теории с практикой.
С целью преодоления недостатков личностных качеств учащихся, содержание урока сопрягалось с жизненным и субъективным опытом детей, которые высказывали своё представление о том, где и какие делают лопаты, подсчитали какой класс может сделать больше. Связь жизни людей с сезонными изменениями.
2.4.Организация повторения на уроке, его содержания. Связь повторенного с новым материалом.
Для целостного представления по теме было проведено предварительное узнавание и называние овощей, которые растут в огороде. Рассмотрены рисунки сорной травы.
2.5.Уровень знаний, умений, навыков.
Учащиеся класса умеют отвечать на вопросы учителя, составлять простые предложения знают некоторые обобщённые понятия, по вопросам учителя делают выводы, решают примеры с единичными ошибками, умеют осуществлять самопроверку.
3. Методическая сторона урока.
3.1.Методы и приёмы обучения. Были адекватны задачам урока и уровню развития познавательных возможностей детей. Использовались репродуктивный и частично-поисковый методы. При репродуктивном методе учитель давал образец выполнения задания и требовал выполнения задания в соответствии с образцом. При частично-поисковом методе, учащиеся частично участвовали в поиске решения поставленной задачи.
3.2.Оборудование урока и его использование.
В качестве средств обучения использовались:
- рисунок тучки с каплями;
- плакаты с краткой записью задач;
- 2 рисунка лопат;
- задание на внимание;
- индивидуальные карточки;
- таблица со схемой примеров в два действия.
3.3.Методы опроса. Правильность ответов учащихся.
Были организованы:
-фронтальная устная проверка, когда правильность ответов оценивал учитель;
- самопроверка;
-опрос, при котором ученики следили за правильностью ответа товарища, оценивали его.
4.Общие моменты урока, влияющие на его качество.
4.1.Поведение учителя.
Внешний вид учителя соответствовал требованиям. Видна собранность, организованность, продуманность каждого действия и жеста, речь небыстрая по темпу, в меру эмоциональная.
4.2.Отношение учащихся к работе.
Учащиеся работали достаточно активно, заинтересованно. Смена заданий поддерживала работоспособность учащихся на разных этапах урока. Дисциплина в классе была хорошая. Учащиеся показали умение слушать друг друга, работать по печатным таблицам, карточкам, поддерживать порядок на рабочих местах.
5.Выводы по уроку.
5.1.Реализация образовательных коррекционно-развивающих, воспитательных задач урока.
Урок достиг своих целей. Были созданы условия для восприятия и первичного осознания учащимися нового материала. Развивалось произвольное внимание детей, мышление, речь учащихся, коммуникативные умения. Проведённый урок был направлен на формирование вычислительного навыка, обогащение личностного опыта учащихся.
6. Предложения и методические рекомендации по совершенствованию урока.
- организации работы в парах, группах;
- в реализации рефлексивного алгоритма.
Самоанализ урока математики в 9 - а классе.
Характеристика класса.
В классе, в котором проводился урок - 12 учащихся. Они делятся на три группы по возможностям обучения. Учащиеся первой группы быстро решают, умеют мыслить, анализировать и искать пути решения. У ребят второй группы хорошие вычислительные навыки, но им требуется больше времени на выполнение задания. В третьей группе находится 1учащийся, нуждающийся в постоянной помощи со стороны учителя. - Никитченко А.
Тема: «Решение примеров и задач» (тридцатый урок по плану).
Тип урока: систематизация и обобщение знаний и способов деятельности.
Метод урока: проблемно - поисковый.
Цели урока:
Содержание урока:
1. Урок соответствует программе целям и задачам урока.
2. Проведена устная работа по актуализации тем необходимых для продолжения и обобщения темы урока.
3. Урок способствует формированию знаний умений и навыков использование математических формул в бытовой жизни.
4. Сложный материал урока делается доступным к восприятию учащихся данного класса путем наличия ярких примеров, аналогий и сравнений.
5. Урок способствовал развитию творческих сил и способностей каждого ученика.
6. Во время урока совершенствовались умения выполнять совместные действия десятичных и обыкновенных дробей.
7. На уроке осуществлялась межпредметная связь с уроком СБО
8. Урок способствовал развитию интереса к учению.
Тип, структура урока
I. Орг. момент.
II. Устная работа.
III. Проверку домашнего задания
IV. Актуализация имеющихся знаний
V. Создание проблемной ситуации.
VI. Домашнее задание
VII. Подведение итогов урока.
Таким образом, урок был проведен с комбинированной структурой, была построена логическая цепь последовательно соединенных этапов урока. Наблюдалась целостность и завершенность урока.
Методы обучения:
1. По источникам знаний: словесные и наглядные
2. По степени воздействия учителя и учащихся самостоятельная работа.
Организация учебной работы на уроке:
При проектировании урока были учтены индивидуальные особенности учащихся, темп работы, степень обученности и уровень обучаемости, что позволило добиться дифференцированного подхода к каждому конкретному учащемуся. В течение всего урока оценивалось интеллектуальное и эмоциональное состояние учащихся. Для этого использовались такие приёмы, как психо - эмоциональный настрой как в начале урока, так и в течение всего урока, смена видов деятельности.
Проведение организационного момента обеспечило психологический настрой на деятельность, а также валеологическую поддержку, что позволило создать все условия для дальнейшей работы.
Одной из основных и первоначальных задач при обучении математики является совершенствование навыков устного вычисления. Поэтому вторым этапом урока стала «Устная работа». Работа на устный счет обеспечила закреплений знаний «Сложение и вычитание обыкновенных дробей с одинаковыми и разными знаменателями» и включение учащихся в совместную деятельность на выявление знаний фактического материала и воспроизведение имеющихся знаний по изучаемой теме.
Этап проверки домашнего задания был проведен в форме устной фронтальной работы. Учащиеся показали достаточный уровень активности и подготовленности. Итогом данного этапа стало формулирование темы и цели урока.
Для обобщения и систематизации знаний были использованы различные приёмы и формы работы:
1. Работа с учебником - решение примера на совместные действия десятичных и обыкновенных дробей - у доски - по цепочке
2. Дифференцированная работа по карточкам. Привитие элементарной экономической грамотности является одним из факторов обеспечения, улучшения и ускорения социальной адаптации учащихся и их интеграции в общество.
При проведении закрепления материала перед учащимися поставлена проблемная ситуация через выполнение практического упражнения социально - адаптированного к жизненной ситуации. Учебно-познавательная деятельность была организована через фронтальную работу, индивидуальную, дифференцированную, а также работу в парах. Такая организация позволила включить каждого учащегося в активную деятельность по достижению цели. Учащиеся сотрудничали друг с другом, оказывая взаимопомощь. При выполнении практической работы осуществлялся самоконтроль, взаимоконтроль партнёра.
Применение методов проблемного обучения позволило активизировать мыслительную деятельность учащихся в процессе обучения, научить мыслить логически, научно, творчески, формировать такие чувства, как удовлетворённость от учебной работы, положительное отношение к математике.
Домашнее задание дано дифференцировано.
Система работы учащихся:
1. Учащиеся были организованы и активны во время урока
2. Учащиеся очень хорошо относятся к предмету.
3. Усвоили основные понятия, умело и творчески использовали полученные знания
Общие результаты урока:
1. План урока выполнен.
2. На уроке реализовывались общеобразовательные, воспитывающие развивающие задачи урока.
3. Урок был эффективный.
4. Атмосфера на уроке была дружеская, творческая;
5. Цель урока достигнута.тема
лекция
семинар
самообразование
всего
Введение. Предмет методики преподавания математики и информатики.
2
2
Общая методика .Формы мышления в процессе преподавании математики и информатики.
2
2
индукция, дедукция и аналогия
2
2
Принципы методики преподавания математики и информатики.
2
2
Урок математики и информатики , типы уроков.
2
2
Анализ урока
1
2
Конспект урока.
1
2
Место и роль задач в преподавания математики и информатики
2
2
Частная методика.Методика преподавания тем о числах.
2
2
Математические выражения и методика преподавания их.
2
2
Цели урока:
Образовательные:
· повторить правила умножения на двузначные и трехзначные числа;
· провести ряд упражнений в умножении чисел;
· совершенствовать вычислительные навыки и умение решать задачи.
Воспитательные:
· воспитывать интерес к предмету;
· воспитывать бережное отношение к тетради, учебнику.
Развивающие:
· развивать логическое мышление, внимание, память.
ХОД УРОКА
1. Орг. момент. Сегодня на уроке мы с вами будем упражняться в умножении многозначных чисел. Вы знаете, что путешествуя мы знакомимся с новым, вспоминаем старое, узнаем много интересного. Сегодня на уроке мы отправляемся в путешествие на поезде, но чтобы отправиться в путь, нам надо сформировать поезд, а для этого надо выполнить определенные задания.
2. I вагон "Математический экспресс" (устный счет). Наш поезд будет называться "Математический экспресс", а что обозначает слово "экспресс"? (быстрый). Давайте быстро устно посчитаем.
а) Как называются компоненты при сложении?
- Как называются компоненты при вычитании?
- Как называются компоненты при умножении?
- Как называются компоненты при делении?
б) Расположите карточки так, чтобы произведения, записанные на них, возрастали. Если вы их расположите правильно, то сможете прочитать слово.
в) Итак, мы отправляемся в путешествие по нашей Родине. А чтобы наш поезд отправился в путь давайте, выполним еще одно задание. Игра "Молчанка"
- прочитайте выражение по-разному и найдите значение выражения:
- На какие две группы можно разделить выражения? (на умножение и деление, на произведение и частное).
г) А теперь начинаем движение в парах ограниченной сменности. Вам надо будет устно решить уравнения, для этого давайте вспомним, как найти неизвестный множитель? Как найти делимое? Как найти делитель?
Работа в П. О. С. (карточки см. приложение)
3. II вагон "Исторический". Давайте пройдем во 2 вагон. Он называется "Исторический". Числа миллион и миллиард - великаны. Считать подряд от 1 до миллиона и миллиарда нам не приходилось. Это займет много времени, но в жизни добычу полезных ископаемых, выплавку стали, изготовление различных машин исчисляют в миллионах и миллиардах. Давайте в тетради и на доске попробуем записать числа - великаны. На доске записаны числа, давайте их увеличим в 100, в 1000 и в 10 раз. Для этого вспоминаем правила умножения на 10, 100 и 1000.
На доске:
540 878 х 10 =
600 849 х 100 =
17 937 х 1 000 =
А теперь запишите число 2 428 600 327
- Прочитайте самое большое число
- Прочитайте самое маленькое число
- Какие арифметические действия мы с вами используем для решения задач и примеров?
- А какие знаки арифметических действий вы знаете?
Эти знаки появились 300-400 лет назад и до сиз пор помогают нам производить действия над числами.
4. III вагон "Сообразительный". Наш третий вагон называется "Сообразитель-ный". Здесь мы будем решать задачи.
# Автобус двигался со скоростью 50 км/ч. Какое расстояние он прошел за 2 часа?
Полную информацию смотрите в файле.
Цели урока:
Уметь проводить тождественные преобразования выражений, содержащих квадратные корни, а именно: разложение на множители и вынесение множителя из под знака корня и внесение множителя под знак корня; преобразовать иррациональную дробь в дробь, не содержащую в знаменателе квадратных корней;
Развивать вариативное мышление, развивать навыки самоконтроля;
Ход урока
Проверка домашнего задания.
№ 495 (б), (г), № 496 (а), № 489 (б).
Задания написаны учителем на доске (решенные). Учащиеся должны проверить правильность выполнения своих домашних работ и если есть ошибки, то исправить.
Устно.
Вынесите множитель из под знака корня
4. Задайте формулой график
5. При каких значениях переменной верно равенство.
В это время за крыльями доски двое учащихся работают по карточкам (задания у обоих одинаковые)
Карточка
Выполните действия
2. Сократить дроби
3. Упростите
Закрепление.
Докажите, что значение выражения есть число натуральное.
За крыльями доски работает два ученика
Карточка № 1 (для слабого учащегося)
Освободится от иррациональности в знаменателе
IV. Итог урока
V. На дом: № 503 (б); № 496 (б;в)

Весь материал - смотрите документ.
Тип урока: урок обобщения и систематизации знаний
Оборудование: урок сопровождается презентацией Microsoft Power Point, экран, проектор, компьютер, раздаточный материал.
Цели урока:
Образовательные: обеспечить повторение, обобщение и систематизацию материала темы; создать условия контроля (самоконтроля) усвоения знаний и умений.
Развивающие: способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного, переноса знаний в новую ситуацию, развития математического кругозора, мышления и речи, внимания и памяти.
Воспитательные: содействовать воспитанию интереса к математике, активности, целеустремлённости, организованности, умения общаться.
Ход урока
-
Организационный момент. (Слайд 1)
Ребята, сегодня на уроке вы услышите сказку, но чтобы рассказать её до конца потребуется ваша помощь. С помощью сказки мы с вами постараемся повторить, обобщить весь материал по теме: «Одночлены и многочлены». Девиз нашего занятия: «Дорогу осилит идущий, а математику мыслящий».
Ваша задача: показать свои познания по теории и практике. Подвести итоги урока поможет оценочный лист. Самые активные обучащиеся получат оценки сразу на уроке.
И так я начинаю рассказывать сказку…(Слайд 2)
-
( Устно) «Вычислительная пауза»
В некотором царстве, в некотором государстве жил - был Иван - царевич. И было у него три сестры. Отец с матерью у них умерли. Отдал Иван - царевич своих сестёр замуж и остался один. Целый год жил он один в своём королевстве, наскучила ему такая жизнь, и решил он, отправится в путешествие в соседнее королевство, а заодно и проведать своих сестёр. Соседнее королевство называлось «Королевство премудростей» и правила им Василиса Премудрая.
У Василисы Премудрой не было отбоя от женихов. Да только замуж она ни за кого не шла, т. к. все женихи не могли ответить на три её премудрых вопроса. Решил Иван - царевич попытать счастья и постараться ответить на её вопросы, уж очень ему понравилась царевна. Василиса Премудрая была современной девушкой и очень она любила смотреть передачу « Что? Где? Когда?» Особенно она любила, когда знатокам выпадал «Блиц - вопрос». Василиса Премудрая решила задать первый вопрос Ивану - царевичу.
1 вопрос: Какого происхождение слова « блиц»? (Слайд 3)
Ребята, давайте поможем ответить Ивану - царевичу на этот вопрос. Чтобы ответить на этот вопрос, нужно узнать из какого языка пришло к нам это слово. Для этого вычислите пример и найдите ответ в таблице.
Смотрите документ.
В оценочном листе ставится знак «+», если задание выполнено правильно.
Молодцы, ребята, помогли определить, из какого языка пришло это слово!
-
Тестирование.
Сказка продолжается…
Иван - царевич ответил, что слово «блиц» пришло к нам из немецкого языка. Василиса Премудрая похвалила Ивана - царевича и решила задать ему следующий вопрос.
2 вопрос: Что означает слово «блиц» в переводе на русский язык?
Каждый обучающийся в классе получает тест из 6 заданий и таблицу для внесения ответов (приложение). Обучающиеся должны постараться тест выполнить устно. После сдачи таблицы с ответами, тест проверяется. (Слайд 4 и 5). В оценочном листе каждый сам выставляет себе оценку.
Курс математики в средней школе и методика преподавания
Предмет методики преподавания математики (содержание, цели, задачи ).
Три фундаментальные комплексные проблемы методики преподавания математики. Проблема содержания школьного курса математики. Проблема структуры этого курса. Проблема методов обучения математике в средней школе. Движение за реформу математического образования. Цели обучения математике в средней общеобразовательной школе. Значение школьного курса математике в общей системе образования. Формирование научного мировоззрения, воспитание учащихся в процессе изучения математики. Связь обучения математике с жизнью.
Составные части методики преподавания математики
Цели обучения математике
Взаимосвязь целей, содержания, форм и методов обучения математике
Движение за реформу математического образования
Предмет математики, роль математики, роль практики в возникновении и развитии математики, математические абстракции
Математическая деятельность, её составные части
Практические приложения математики
Связь математики с другими учебными дисциплинами (мировоззренческий аспект)
Составные части методики преподавания математики
Методика преподавания математики - дисциплина, которая занимается разработкой целей, содержания, средств, форм и методов обучения математике в учебных заведениях различных типов.
Учебный курс методики преподавания математики состоит из двух разделов: общая методика и частные методики (методики изучения отдельных учебных предметов).
Цели обучения математике
1. Ведущие цели обучения математике в школе. Три крупные группы целей:
а) прогностические (обучающие);
б) мировоззренческие, направленные на воспитание математической культуры (воспитательные и развивающие);
в) личностно-ориентированные (воспитательные в более узком смысле).
2. Требования к целям:
а) прогностические цели должны обладать - конкретностью, конструктивностью, проверяемостью, участием ученика в процессе учения;
б) мировоззренческие должны пронизывать весь учебный процесс, выражать стремление к аргументации и четким логическим схемам рассуждения, к четкому расчленению рассуждения и т.п.;
в) личностно-ориентированные должны учитывать формирование возможных в том или ином возрасте качеств личности средствами предмета.
3. Этапы формирования действия целеполагания у учащихся:
а) первый этап - учитель раскрывает структуру действия постановки (полагания) цели;
б) второй этап - учитель привлекает детей к постановке цели и критическому осмыслению полученных результатов при достижении цели;
в) третий этап - учащиеся под руководством учителя конструируют цель изучения конкретного учебного материала;
г) четвертый этап - учащиеся самостоятельно ставят цели, а классный коллектив критически анализирует процедуру постановки цели и достижения результата.
Цели обучения математике отражают общедидактические цели и вместе с тем учитывают специфику данного учебного предмета. Разработка целей обучения является непростым делом. В дидактике и частных методиках в этом направлении сделаны определенные шаги. Цели обучения математике подразделяются на несколько групп: образовательные (в том числе-практические), воспитательные, развивающие.
Образовательные цели обучения во многом зависят от принятой формы дифференциации обучения. Основным документом, в котором фиксируются цели обучения математике, является программа по математике. Необходимо различать два уровня описания целей обучения: общая характеристика целей обучения и конкретное их представление. Общая характеристика целей обучения дается в объяснительной записке к программе по математике. Существуют различные способы конкретного представления целей обучения. Образовательные цели, например, формулируются в виде требований к уровню математической подготовки учащихся. В программе по математике для этого выделяется специальный раздел "Требования к математической подготовке учащихся". Другой раздел программы "Содержание обучения" представляет образовательные цели в еще более конкретной форме. Дальнейшей конкретизацией образовательных целей служит учебник. Предельно конкретный уровень представления образовательных целей имеет место в экзаменационных билетах для учащихся, контрольных работах, предлагаемых Министерством общего и профессионального образования. В методических пособиях часто формулируются цели обучения для отдельных тем, уроков. Образовательные цели призваны разграничить основной и второстепенный материал и в соответствии с этим помочь учителю рационально распределить учебное время.
Умение правильно формулировать цели уроков приходит к начинающему учителю не сразу. В период педагогической практики студенты нередко испытывают затруднения в постановке целей урока. При формулировании ими образовательной цели урока не всегда хватает четкости, конкретности (особенно в дифференциации целей "соседних" уроков). Иногда образовательная цель повторяет (или почти повторяет) название темы урока. Например, цель урока на тему "Первый признак равенства треугольников" чаще всего формулируется так: "Изучить первый признак равенства треугольников". Аналогично формулируются цели и в других случаях: "Изучить теорему Виета", "Изучить определение производной функции" и т.д. Во всех этих формулировках имеется общий недостаток: в них не уточняется, на каком уровне должен быть изучен данный элемент учебного материала. Необходимо указывать, когда ставится цель только ознакомить учащихся с тем или иным элементом учебного материала, когда - добиться хорошего воспроизведения учебного материала учащимся, а когда - заложить первоначальные умения и навыки и т. д. Еще большие затруднения начинающий учитель испытывает при постановке воспитательных и развивающих целей урока.
В некоторых методических руководствах имеются непосредственные указания, на каком уровне должен быть изучен тот или иной теоретический материал, в решении каких задач должны быть сформированы умения и навыки. Эти указания помогут начинающему учителю точнее формулировать цели урока.
Первым практическим навыком, которым должен овладеть студент, является навык безошибочной дифференциации целей обучения по трем группам (образовательные, воспитательные и развивающие). В изучении данного вопроса, приобретении соответствующих умений помогут следующие задания.
Несколько слов о постановке воспитательных целей. Они должны быть тесно связаны с содержанием урока. Это могут быть цели по формированию мировоззрения, сознательного отношения к учебе, развитию" познавательной и общественной активности, культуры учебного труда, воспитанию сознательности, расширению политехнического кругозора, подготовке к сознательному выбору профессии и т. д.
Развивающие цели должны находиться также в тесной связи с содержанием урока. Приведем примеры постановки развивающих целей:
развитие у учащихся навыков применения анализа, синтеза, сравнения, аналогии, индукции, дедукции, обобщения, конкретизации, моделирования классификации;
развитие у учащихся геометрической, алгебраической и числовой интуиции, пространственного представления и воображения, сообразительности, наблюдательности, памяти и т. д.
Взаимосвязь целей, содержания, форм и методов обучения математике
Цели, содержание и методы обучения взаимно связаны и обусловливают друг друга (при сохранении ведущей роли целей обучения). Из различных целей обучения наиболее подвижны и изменчивы образовательные цели. Следующие задания помогут подтвердить это положение и проиллюстрировать механизм взаимодействия целей, содержания и методов обучения.
Отдельно отметим воспитательные возможности исторического материала. Исторические экскурсы позволяют в доступной для учащихся форме раскрыть основу происхождения математических понятий и фактов. Они положительно сказываются на эмоциональном отношении учащихся к учебному материалу, на воспитании их моральных качеств и развитии интеллекта. Незаменимым средством при этом являются также старинные задачи, задачи с занимательным сюжетом, математические игры и т. п.
Остановимся на функциях компьютеризации обучения, являющейся одним из требований реформы школы. Первый шаг в осуществлении компьютеризации обучения заключается в использовании в школе микрокалькуляторов. В чем состоят образовательные, воспитательные и развивающие цели применения микрокалькуляторов на уроках математики? Прежде всего, очевидна практическая значимость применения микрокалькуляторов (коль скоро вычислительной техникой оснащается наука и производство).
Микрокалькулятор удобно использовать при введении, например, понятий длины окружности и площади круга. Вычислив 8-9 членов последовательности периметра (площадей) правильных вписанных n-угольников, учащиеся наглядно убеждаются в сходимости этих последовательностей. С помощью микрокалькулятора удобно организовать машинный эксперимент по обнаружению некоторых теорем (например, при изучении теоремы Виета, теоремы Пифагора, теоремы косинусов, теоремы синусов и т. д.).
Список литературы
Для подготовки данной работы были
Роль задач в обучении математике
-
Зайцева Галина Геннадиевна, учитель математики
Разделы: Преподавание математики
Введение (Актуальность темы)
Математика, как и другие науки, изучает действительный мир и, в своих понятиях и законах, отражает закономерности этого мира. Специфика математики как особой науки состоит в том, что она специально выделяет количественные отношения и пространственные формы, которые присущи всем без исключения предметам и явлениям действительности, и делает их объектами своего исследования. Период современной математики обычно относят к середине ХIХ века. К этому времени математика стала настолько абстрактной наукой, что перемахнула за пределы той концепции, которая рассматривала в качестве предмета только число и геометрическую фигуру. Качественные изменения произошли в этот период и в алгебре: значительно расширилось понятие исчисления, различные операции начали производиться не только над числами, но и над векторами, матрицами, логическими высказываниями. В этот период характерно стремление к содержанию единства в многообразии математических фактов и методов, весьма далеких друг от друга. Это выразилось в создании разветвленной теории групп, знаменовавшей собой успехи аксиоматического метода, в дальнейшем развитие теории множеств, общие понятия и методы которой позволили охватить с единой точки зрения области математики, которые ранее казались сильно удаленными друг от друга.
Между математической наукой и математикой учебным предметом существует глубокое внутреннее единство, которое в целом определяется логикой самой науки. Однако это не исключает, а предполагает различие между ними. Наиболее существенное различие между ними заключается, во-первых, в том, что если цель науки - открытие новых закономерностей, то учебная дисциплина преследует педагогические цели обучения и воспитания. Во-вторых, математическая наука способна развиваться неограниченно, в то время как для предмета обучения должны быть указаны "пределы" его предложения в том или ином курсе. И, наконец, если структура науки определяется внутренней логикой ее предмета, то при построении математики как учебного предмета теории и разделы выстраиваются вряд, удобный для лучшего усвоения курса.
Важнейшая задача школы - давать подрастающему поколению глубокие и прочные знания основ наук, вырабатывать навыки и умения, применять их на практике. Одной из основных и главных задач школы является формирование у детей прочных знаний по математике.
Обучение математике должно обеспечить надежную основу, как в отношении знаний и умений учащихся, так и в отношении их развития для дальнейшего изучения математики в 5-11-х классах.
Переход учащихся из начальной школы в среднюю часто сопровождается трудностями адаптации к новым условиям обучения даже в случае, когда начальная и средняя школа работают в рамках единой дидактической темы. Важное значение имеет соотношение между программами по математике в начальной системе и в основном звене. За последние годы произошло значительное обновление содержания математики как в начальной школе, так и в 5-11-х классах. Современное содержание математического образования направлено, главным образом, на интеллектуальное развитие школьников, формирование культуры и самостоятельности их мышления. Существенное усиление алгебраической и геометрической пропедевтики, включение системы содержательно-логических заданий, игр, вопросов направлены на развитие познавательных процессов у детей.
Таким образом, происходящие изменения в структуре и содержании математического образования вызвали ряд проблем, одной из которых является проблема преемственности преподавания математики в школе и ВУЗах и техникумах.
Актуальность данной проблемы заключается в том, что изучение математики невозможно без опоры на знания, полученные в младших классах. Особенно это актуально в связи с вариативным обучением математике. Так, например, учащиеся нашего лицея занимаются по следующим направлениям: гуманитарное, химико-биологическое, знакомятся с элементами комбинаторики, логики, статистики и теории вероятностей.
Исходя из проведенной проблематики и актуальности исследования цель моей работы:
1. Показать влияние решения задач на развитие логического мышления на уроках математики.
Для этого необходимо решить следующие задачи:
1. Разработать и создать сборник задач по математике для развития логического мышления учащихся.
2. Разработать рекомендации для учителей математики по организации обучения математике.
Объектом исследования является процесс обучения математике школьников.
Предметом исследования - решение задач, направленных на развитие логического мышления учащихся.
Глава I. Роль задач в обучении математики.
В связи с развернувшейся в настоящее время во многих странах мира реформой математического образования проблема постановки задач в школьном курсе математики стала одной из самых важных и животрепещущих проблем в развитии преподавания.
Если понятие математической задачи тактируется достаточно широко (в частности, если всякую теорему считать задачей), то решение задач является единственной возможностью для математической деятельности учащихся. Умения решать математические задачи является наиболее яркой характеристикой состояния математического образования.
Как же обстоит дело с обучением учащихся математической деятельности? И, прежде всего, как понимает учащийся (и учитель!) цель постановки задач в школьном курсе математики?
Почти все учащиеся средней школы считают, что если предложенная им математическая задача решена верно, если полученный ответ совпадает с ответом, данным в учебнике, или одобрен учителем, то работа их окончена, о решенной задаче можно и нужно забыть.
Таким образом, учащиеся (а также многие учителя) забывают об обучающем характере каждой задачи, решаемой в процессе обучения, о том, что всякая решаемая ими задача должна учить их умению ориентироваться в различных проблемных ситуациях, обогащать их знания и опыт, учить их математической деятельности.
Проявляя (в традиционной методике обучения решению задач) значительную заботу о применения математических знаний при решении задач и не обращая внимания на процесс актуализации этих знаний, мы нарушаем единство процесса математического мышления и поэтому не можем обеспечить его должного развития у учащихся.
Английский кибернетик Д.М.Маккей установил четыре основные черты, отличающие "интеллект от простой способности вычислять":
-
способность успешно перерабатывать и объединять информацию в зависимости;
-
способность совершать пробные действия, поиск и переходы, не вытекающие из наличной информации (т.е. совершать "скачок через разрыв, существующих данных");
-
способность управлять поисковым и исследовательским процессом, руководствуясь "чувством близости решения";
-
способность рассматривать ограниченный, но достаточно большой ряд положений и заключений, совместных с данным положением.
Традиционная система школьных математических задач этим целям пока не отвечает.
Подавляющее большинство задач традиционного школьного курса математики были шаблонными упражнениями тренировочного характера, которые по существу не имеют права на название "задача".
Но даже эти шаблонные задачи не приведены, как правило, в определенную методическую
Роль задач в обучении математике
-
Зайцева Галина Геннадиевна, учитель математики
Разделы: Преподавание математики
Введение (Актуальность темы)
Математика, как и другие науки, изучает действительный мир и, в своих понятиях и законах, отражает закономерности этого мира. Специфика математики как особой науки состоит в том, что она специально выделяет количественные отношения и пространственные формы, которые присущи всем без исключения предметам и явлениям действительности, и делает их объектами своего исследования. Период современной математики обычно относят к середине ХIХ века. К этому времени математика стала настолько абстрактной наукой, что перемахнула за пределы той концепции, которая рассматривала в качестве предмета только число и геометрическую фигуру. Качественные изменения произошли в этот период и в алгебре: значительно расширилось понятие исчисления, различные операции начали производиться не только над числами, но и над векторами, матрицами, логическими высказываниями. В этот период характерно стремление к содержанию единства в многообразии математических фактов и методов, весьма далеких друг от друга. Это выразилось в создании разветвленной теории групп, знаменовавшей собой успехи аксиоматического метода, в дальнейшем развитие теории множеств, общие понятия и методы которой позволили охватить с единой точки зрения области математики, которые ранее казались сильно удаленными друг от друга.
Между математической наукой и математикой учебным предметом существует глубокое внутреннее единство, которое в целом определяется логикой самой науки. Однако это не исключает, а предполагает различие между ними. Наиболее существенное различие между ними заключается, во-первых, в том, что если цель науки - открытие новых закономерностей, то учебная дисциплина преследует педагогические цели обучения и воспитания. Во-вторых, математическая наука способна развиваться неограниченно, в то время как для предмета обучения должны быть указаны "пределы" его предложения в том или ином курсе. И, наконец, если структура науки определяется внутренней логикой ее предмета, то при построении математики как учебного предмета теории и разделы выстраиваются вряд, удобный для лучшего усвоения курса.
Важнейшая задача школы - давать подрастающему поколению глубокие и прочные знания основ наук, вырабатывать навыки и умения, применять их на практике. Одной из основных и главных задач школы является формирование у детей прочных знаний по математике.
Обучение математике должно обеспечить надежную основу, как в отношении знаний и умений учащихся, так и в отношении их развития для дальнейшего изучения математики в 5-11-х классах.
Переход учащихся из начальной школы в среднюю часто сопровождается трудностями адаптации к новым условиям обучения даже в случае, когда начальная и средняя школа работают в рамках единой дидактической темы. Важное значение имеет соотношение между программами по математике в начальной системе и в основном звене. За последние годы произошло значительное обновление содержания математики как в начальной школе, так и в 5-11-х классах. Современное содержание математического образования направлено, главным образом, на интеллектуальное развитие школьников, формирование культуры и самостоятельности их мышления. Существенное усиление алгебраической и геометрической пропедевтики, включение системы содержательно-логических заданий, игр, вопросов направлены на развитие познавательных процессов у детей.
Таким образом, происходящие изменения в структуре и содержании математического образования вызвали ряд проблем, одной из которых является проблема преемственности преподавания математики в школе и ВУЗах и техникумах.
Актуальность данной проблемы заключается в том, что изучение математики невозможно без опоры на знания, полученные в младших классах. Особенно это актуально в связи с вариативным обучением математике. Так, например, учащиеся нашего лицея занимаются по следующим направлениям: гуманитарное, химико-биологическое, знакомятся с элементами комбинаторики, логики, статистики и теории вероятностей.
Исходя из проведенной проблематики и актуальности исследования цель моей работы:
1. Показать влияние решения задач на развитие логического мышления на уроках математики.
Для этого необходимо решить следующие задачи:
1. Разработать и создать сборник задач по математике для развития логического мышления учащихся.
2. Разработать рекомендации для учителей математики по организации обучения математике.
Объектом исследования является процесс обучения математике школьников.
Предметом исследования - решение задач, направленных на развитие логического мышления учащихся.
Глава I. Роль задач в обучении математики.
В связи с развернувшейся в настоящее время во многих странах мира реформой математического образования проблема постановки задач в школьном курсе математики стала одной из самых важных и животрепещущих проблем в развитии преподавания.
Если понятие математической задачи тактируется достаточно широко (в частности, если всякую теорему считать задачей), то решение задач является единственной возможностью для математической деятельности учащихся. Умения решать математические задачи является наиболее яркой характеристикой состояния математического образования.
Как же обстоит дело с обучением учащихся математической деятельности? И, прежде всего, как понимает учащийся (и учитель!) цель постановки задач в школьном курсе математики?
Почти все учащиеся средней школы считают, что если предложенная им математическая задача решена верно, если полученный ответ совпадает с ответом, данным в учебнике, или одобрен учителем, то работа их окончена, о решенной задаче можно и нужно забыть.
Таким образом, учащиеся (а также многие учителя) забывают об обучающем характере каждой задачи, решаемой в процессе обучения, о том, что всякая решаемая ими задача должна учить их умению ориентироваться в различных проблемных ситуациях, обогащать их знания и опыт, учить их математической деятельности.
Проявляя (в традиционной методике обучения решению задач) значительную заботу о применения математических знаний при решении задач и не обращая внимания на процесс актуализации этих знаний, мы нарушаем единство процесса математического мышления и поэтому не можем обеспечить его должного развития у учащихся.
Английский кибернетик Д.М.Маккей установил четыре основные черты, отличающие "интеллект от простой способности вычислять":
-
способность успешно перерабатывать и объединять информацию в зависимости;
-
способность совершать пробные действия, поиск и переходы, не вытекающие из наличной информации (т.е. совершать "скачок через разрыв, существующих данных");
-
способность управлять поисковым и исследовательским процессом, руководствуясь "чувством близости решения";
-
способность рассматривать ограниченный, но достаточно большой ряд положений и заключений, совместных с данным положением.
Традиционная система школьных математических задач этим целям пока не отвечает.
Подавляющее большинство задач традиционного школьного курса математики были шаблонными упражнениями тренировочного характера, которые по существу не имеют права на название "задача".
Но даже эти шаблонные задачи не приведены, как правило, в определенную методическую систему. В этом следует искать ещё одну причину слабого развития способностей к математической деятельности у учащихся средней школы.
К числу недостатков в постановке задач, характерных для традиционного обучения математике, можно отнести, например, следующие:
-
излишняя стандартизация содержания и методов решения задач в традиционном обучении;
-
увеличение числа решаемых школьниками стандартных задач в ущерб их обучающему качеству;
-
излишне узкое понимание роли и целевого назначения математической задачи в процессе обучения;
-
несовершенство методики обучения через задачи;
-
несоответствие постановки задач и их решений в школе закономерностям развивающего мышления;
-
увлечение обучением решению таких задач или таких упражнений, которые в дальнейшем почти не находят приложений ни в процессе изучения основ наук, ни в практике;
-
обучение школьников через задачи таким умением и навыком, которые в современной практической деятельности почти не применяются, а в деятельности недалёкого будущего будут переданы автоматическим устройствам;
-
отсутствие в школьном курсе математики задач, решение которых могло бы подготовить школьника к деятельности, характерной для современного производства: наладке, управлению, рационализации и т.п.;
-
отсутствие чётких критериев учебной значимости каждой задачи, поставленной в процессе обучения, критерия, способного установить необходимое число задач какого-либо типа для достижения реализуемой через них цели обучения, и т.д.
Таким образом, налицо различных аспекты проблемы постановки задач в процессе обучения математике: методический, психологический и даже кибернетический.
Как правило, традиционные школьные математические задачи таковы, что требуют для своего решения определенных знаний, умений или навыков по узкому вопросу программного материала. Поэтому роль и значение их исчерпывается в течение того непродолжительного вопроса программы.
При этом вспомогательная роль таких задач в процессе обучения не является секретарём ни для учащихся, ни для учителя: проиллюстрировать изучаемый теоретический вопрос, разъяснить его смысл, помочь усвоить изучаемый факт через простейшие упражнения, выполняемые по образцу, продиктованному теорией, и только.
Плохо то, что, несмотря на значительные затраты учебного труда и времени на решение таких задач в школе, мы не достигаем ожидаемых результатов для значительного числа выпускников средней школы.
Основным становится формирование у школьника умения ориентироваться в новых задачных ситуациях, накапливать информацию, полезную для решения других задач или изучения новых разделов математики, обучение учащихся разнообразным математическим методам познание реальной действительности и т.д.
Именно этот аспект обучения математике отражён в следующем перечне целей обучения через задачи:
-
заинтересовать или мотивировать;
-
приводить и практиковать "технику решения задач";
-
формировать понятие математической модели.
Говоря о роли математических задач в развитии у школьников способностей к самостоятельной познавательной деятельности творческого характера, отметим полезность постановки в школьном обучении математических задач проблемного характера.
Правильная постановка задач и упражнений в обучении математике во многом определяет современную методику преподавания, так как решение задач служит различным конкретным целям обучения. Так, например, задачи могут использоваться при введении в изучение новой темы, для самостоятельного установления школьниками какого-либо математического факта, подлежащего изучению или иллюстрации этого факта, с целью глубокого усвоения теоретического материала или выработке необходимых умений и навыков, для контроля знаний и самоконтроля, возбуждения и развития интереса к математике и, наконец, приобщения учащихся к деятельности математического характера- поисковой и творческой, развития у школьников логического математического мышления.
Решение каждой математической задачи осуществляется по четырем основным этапом:
-
понимание условия и требования задачи; ясное усвоение и осмысливание отдельных элементов условия;
-
составление плана решения;
-
практическая реализация плана во всех его деталях;
-
окончательное рассмотрение задачи и её решения с целью усвоения тех моментов, которые могут стать полезными для дальнейшего решения задач.
Для выработки правильного понимания школьниками поставленной задачи можно рекомендовать соблюдение следующих требований:
-
начинайте изучение условия задачи с аккуратно выполненных схем. Помните, что правильное графическое представление условия задачи означают по существу четкое, ясное и конкретное представление о всей задачной ситуации в целом;
-
представьте ясно и детально все основное, связанное с данной задачей. Обстоятельно выясните, что дано, что надо найти; выделите при этом главное в тексте условия задачи и сконцентрируйте на нем своё внимание. Выделите на чертеже данные и искомые величины различными яркими цветами;
-
проверьте тщательно каждое выдвигаемое в процессе решения задачи положение контрольными вопросами вида: что это означает, какие имеются основание для данного утверждения, какую пользу можно извлечь из данного факта?
-
проверьте, однозначно ли сформулирована задача. Нет ли в условии задачи избыточных или недостающих данных?
-
Говоря о первой из этих требований, отметим, что оно особенно важно при решении геометрических задач, где наглядный и четкий чертеж позволяет иной раз с первого же взгляда обнаружить возможные пути решения.
Немаловажную роль в успешном решении задач играет целенаправленность поиска решения, т.е. сознательное ограничение числа проб и ошибок, характерных для начальной его стадии.
Иногда учащийся не в состоянии самостоятельно проанализировать задачу и решить ее без помощи учителя. Однако в этом случае не следует сообщать ему готовое решение, а тем более заставлять школьника заучить данный в готовом виде способ действия.
При создании оптимальных условий, которые бы активизировали мыслительную деятельность учащихся при решении задач, весьма часто применяется особый дидактический прием, называемый системой подсказок. Система подсказок, состоящая из вспомогательных задач, вопросов и т.д., не подменяя мышление школьника, придает ему нужное направление, т.е. делает поиск решения целенаправленным.
Полезность упорядочения поисковой деятельности в процессе решения задач школьникам следует продемонстрировать на эффективно подобранной задаче и ее решении.
Например, представьте себе, говорит учитель, что ваш друг задумал некоторое натуральное число в промежутке от 1 до 1024. Чтобы угадать задуманное число, вы будете отвечать на вопросы "да" и "нет". Может показаться невероятным, но достаточно всего лишь десяти вопросов, чтобы наверняка отгадать любое такое число.
Пусть задуманное число 1.
Спрашиваем:
-
Задуманное больше 512 (половину промежутка 1024)? - Нет.
-
Оно больше 256? - Нет.
-
Оно больше 128 (половину того промежутка, в каком оно может быть)? - Нет.
-
Оно больше 64? - Нет.
-
Оно больше 32? - Нет.
-
Оно больше 16? - Нет.
-
Оно больше 8? - Нет.
-
Оно больше 4? - Нет.
-
Оно больше 2? - Нет.
-
Это число 1? - Да.
Итак, постепенно уменьшая область поисков, мы решили задачу. Попробуйте сами решить эту задачу в предположении, что ваш друг задумал число 720; пусть ваш сосед по парте задумает число - угадайте его!
Решение задач требует наличие у школьников так называемых комбинационных способностей, под которыми понимают умение сделать подходящий выбор в условиях избытка активных и пассивных знаний. Понятно, что поиск и отбор полезной для решения данной задачи информации также должен быть целенаправленным. Нередко этот выбор может быть легко осуществлен при обращении к подходящей аналогии.
Отыскание подходящих аналогий активизируется вопросами: "Где мы раньше встречали что - либо подобное, видели что - либо родственное, встречали одинаковые характерные свойства?"
Для простоты отыскания аналогии полезно применять сравнительные чертежи, вспомогательные формулировки.
Применяя аналогию при решении задач, часто бывает полезным изменять формулировку задачи.
Например, пусть в условии некоторой задачи говорится о том, что треугольники АВС делится прямой MN, параллельной основанию на две части (Треугольник и трапецию), площади которых относятся как 2:3.
Еще не начиная решения этой задачи, школьники вспомнят известную им аналогичную по содержанию теорему об отношении площадей подобных треугольников. Но наличие в условии отношения площадей треугольника и трапеции может затормозить стремление использовать эту теорему при решении задачи.
Для этого достаточно сказать, что треугольник АВС делится прямой MN на два треугольника, отношение площадей которых легко установить.
Наконец, аналогия может оказаться полезной на начальном этапе решения задачи. Если уже на этом этапе удается сравнить данную задачу с задачами, решенными ранее, то сходство условий, требований, способа решения и т.д., часто сразу "наталкивает" учащихся на плодотворные идеи при планировании решения.
Очевидно, что решение многих математических задач сводится к решению некоторых частных задач, а последние, в свою очередь, расчленяются на простые задачи, решение которых или постулируется (например, в задачах на построение), или же находится из определений и аксиом.
Учителю необходимо научить ребят видеть составные задачи в ходе решения основной, научить составлять их, так как только благодаря такой работе возможен успешный поиск решения задач.
До недавнего времени в школьном обучении математике мало уделялось внимания такому важному виду математической деятельности учащихся, каким является самостоятельное составление тех или иных математических задач. Умение школьников составлять свои задачи по заранее известным условиям, по аналогии с данной задачей и т.д. является весьма ценным.
Например, дано уравнение: 8х - 3 = 5х +6. Составить задачу, решение которой приводит к решению этого уравнения.
Показ учителем способа составления некоторой задачи превращает аналогичное задание не только в доступное для всех, но даже - в стандартное. Помощь учителя должна быть и в этом случае дидактически разумной.
Рассмотрим пример того, как решение готового уравнения сопровождается самостоятельным составлением аналогичных уравнений:

Такая форма "параллельных" записей облегчает учебную деятельность школьников по составлению задач.
Значительно оживляют уроки математики и дидактические весьма полезны различные занимательные задачи, нешаблонные вопросы и "задачи на смекалку".
Задачи - шутки и вопросы на сообразительность (для устного решения).
-
На дереве сидело 10 птиц. Охотник выстрелил и подстрелил одну птицу. Сколько птиц осталось на дереве?
-
Как из трех спичек, не ломая их, образовать четыре?
В такого рода задачах необходимо увидеть и преодолеть психологический барьер.
Задачи типа "Внимателен ли ты?" Такие вопросы и задачи развивают внимание и наблюдательность школьников.
-
Сколько углов на чертеже?
-
Сколько кубиков на чертеже?
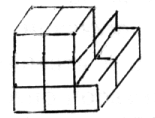
Очень интересными, своеобразными задачами являются так называемые дудлы, которые обычно вызывают у ребят большое желание самим придумывать и задавать их друг другу.
Что это такое?
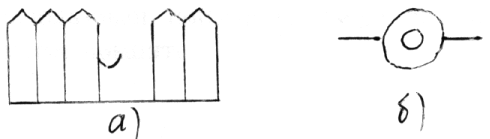
Возможны ответы: на рисунке а - проходящий вдоль забора солдат с собакой; на рисунке б - человек в сомбреро, едущий на велосипеде, т.д.
Полезными и нужными являются задачи на отыскание всевозможных закономерностей. Такие задачи формируют навыки математического мышления: умение анализировать, обобщать, находить закономерности.
Какое слово надо выкинуть как "из ряда вон выходящее": кортик, падеж, стакан, книга, паркет?
Учителю полезно использовать подобного рода задачи не только на внеклассных занятиях по математике, но и на обычных уроках.
Чем же должен руководствоваться учитель при подборе учебных задач?
Рассмотрим памятку для анализа педагогической ценности задачи:
-
Какую учебную цель преследует данная задача?
-
Какие элементы математического образования имеются в виду?
-
Необходима ли именно эта задача?
-
Почему такие, а не другие.
-
Почему выбрана такая фабула задачи?
-
Почему взяты такие, а не другие числовые данные?
-
Отвечают ли числовые данные реальной обстановке, в которой могла бы возникнуть аналогичная задача?
-
Интересна ли задача для учащихся, увлекательна, естественная ли постановка вопроса, вызывает ли она у учащихся интерес к ответу или способу решения, чем именно?
-
Сможет ли учащийся самостоятельно решить данную задачу? Что он для этого должен знать, уметь, помнить, представлять себе? Если учащийся не сможет этого сделать, о чем будет свидетельствовать этот факт?
-
Чем и в какой мере ему может и должен помочь учитель?
-
Как эта задача связана с предшествующий и последующей учебной работой учащегося? И т.д.
Давая такую оценку каждой учебной задаче, учитель сумеет при минимальной затрате учебного времени добиться хороших результатов как в обучении, так и в развитии математического мышления школьников.
Но учиться не только должен сам уметь оценивать задачу, выявляя все ее полезные учебные качества, он должен научиться этому и учащихся.
Даже очень хорошие учащиеся, получив ответ на вопрос задачи и тщательно изложив ход ее решения, закрывают тетрадь, пологая работу законченной. Учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам. всегда остается что - нибудь, над чем можно и нужно поразмышлять; всегда можно усовершенствовать любое решение, глубже его осмыслить, выявить полезную и новую для учащихся информацию. Поэтому после решения каждой задачи следует еще раз оглянуться назад, обратить внимание на метод, который был использован, попытаться найти другие пути решения, выявить то, что необходимо помнить.
Решение одной задачи несколькими способами часто бывает более полезным, чем решение одним способом нескольких задач, так как при оценке способов решения задачи активно работают такие умственные операции, как анализ, сравнения, обобщения и другие. А это, несомненно, оказывает свое положительное влияние на развитие математического мышления школьников.
Прежде чем говорить о том, какие математические задачи следует рассматривать в школьном курсе математики и как обучать школьников решению задач, нужно уточнить, что следует понимать под термином "задача".
Например, уравнение 11423*х = 616842 представляет проблемную ситуацию для любого человека. Но проблемную ситуацию является понятием относительным. Например, ситуация, выраженная уравнением х+9=10, является проблемной для начинающего школьника и не является таковой для учащихся старших классов.
Числовое равенство 123+2*х=197 становится задачей, если оно сопровождается целевым заданием "решить уравнение".
Решить задачу - значит преобразовать данную проблемную ситуацию или установить, что такое преобразование в данных условиях (или в данной среде) невозможно.
Естественно определить процесс решения задачи как целенаправленную мыслительную или практическую деятельность человека, осуществляющего решение задачи.
Глава II. Формирование интеллектуальных умений
Создание учебных проблемных ситуаций на уроке математики - оправдавшей себя на практике дидактический прием, посредством которого учитель держит в постоянном напряжении одну из внутренних пружин процесса обучения - детская любознательность.
Справедливо указывает академик АН УССР Б.В.Чиденко: "Потеря интереса к обучению, на каком - то этапе рождает безразличие и апатию, безразличие рождает лень, а лень - безделье и потерю способностей. Вот почему важно продумать курс математики так, чтобы его изучение было интересно; содержание было совершенно, будило мысль и развивало способности, а также открывало пути, как в научную, так и в практическую деятельность".
Учебные проблемы, которые ставятся перед учеником, могут решаться на протяжении как одного, так и нескольких уроков; они могут выступать и форме обычных вопросов к учащимся, таких, например, как:
-
Почему треугольник назван треугольником? Можно ли дать ему другое название, также связанное с его свойствами?
-
Как можно объяснить название "развернутый угол"?
-
Как бы вы назвали треугольник, у которого один угол прямой? (Вопрос задается до ознакомления с этим термином.)
Учебную проблемную ситуацию можно создать при решении любой задачи. Рассмотрим одну из задач: решить квадратное уравнение: х2 -5х+6=0.
Что известно о решении квадратного уравнения? О его свойствах?
а) х1 х2=-p/2 ![]()
б) теорема Виета: х + х = - р; х * х = q;
в) если х - корень уравнения, то х21 + 5х2 + 6 =0 - верное равенство.
Необходимо подвести учащихся к тому, чтобы они сами поставили перед собой вопросы: что можно извлечь из этих знаний? Что можно и интересно было бы узнать? Какие задачи можно составить, отправлять от этого уравнения? Например:
-
Пусть х1 и х2 - корни уравнения; нельзя ли иначе, чем в учебнике получить теорему Виета?
-
Нельзя ли распространить теорему Виета на уравнения х3+рх2+qх+е=0? (Проблема!)
-
Как можно еще решить квадратное уравнение? (Не зная формулы его решения.)
-
Нельзя ли решение уравнения х3+рх2+qх+е=0 свести к решению системы трех уравнений с тремя неизвестными? (Проблема!)
-
Какими интересными свойствами обладает квадратный трехчлен f(х)=х2-5х+6?
-
Как установить, при каких значениях х f(х)=х2-5х+6 имеет наименьшее значение?
-
Нельзя ли решить геометрически квадратное уравнение х2 -5х+6 = 0?
Проблемные ситуации в обучении математике возникают также в случае необходимости проверить умозаключение, сделанное на основе интуиции, на основе аналогии или попытке общения. Примеры таких проблем:
-
Между углами и сторонами треугольника имеются определенные зависимости. Сохраняются ли они для четырехугольника?
-
Средняя линяя треугольника параллельна основаниям. А у ромба? У параллелограмма? У любого четырехугольника?
-
Равнобедренный треугольник имеет определенные свойства. А равнобедренная трапеция? Сохраняются ли для нее аналогичные свойства?
Очень часто проблемность достигает выполнением какого-то практического упражнения или решением соответствующей задачи. Например: Какие углы может иметь равнобедренная трапеция, если она разбивается диагонально на два равнобедренных треугольника?
Проблемность этой задачи заключается в умении увидеть все случаи, исчерпать все возможное в этой задаче.
1.Ответ:углы ВАД=СДА=720, углыАВС=ДСВ=1080
2.Ответ:углы А=В=С=Д=900(частный случай трапеции)
3.Ответ:углы А=С=1200, В=Д=600 и т.д.
Интересными задачами-проблемами являются задачи, ведущие к открытию новой теории.
Своеобразие нестандартных задач заключается в том, что почти каждая из них - это маленькая проблема. Решение маленьких математических проблем опирается не столько на специальные знание, сколько на сообразительность и изобретательность. Эти качества ума и необходимо активно развивать у школьников.
В процессе решения учебных математических задач следует уделять особое внимание актуализации знаний учащихся. С этой точки зрения весьма полезны специально подобранные серии задач, составленные так, чтобы научить школьников умело пользоваться прошлым опытом при поиске решения новой задачи.
Прежде чем предложить трудную нестандартную задачу, учащимся было предложена довольно простоя задача:
1.Дан прямоугольный треугольник со сторонами 3см. и 4см. Найти длину медианы, проведенной к гипотенузе.
Школьники предложили два способа решения:
1 - й способ. | АВ | = ![]() =5 (см). Достроим прямоугольный
треугольник до прямоугольника. А в прямоугольнике диагонали
конгруэнтны и в точке переcеxxeия делятся пополам: | СМ | = 2,5 см.
=5 (см). Достроим прямоугольный
треугольник до прямоугольника. А в прямоугольнике диагонали
конгруэнтны и в точке переcеxxeия делятся пополам: | СМ | = 2,5 см.
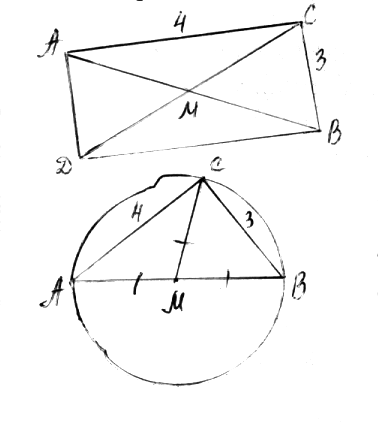
2- й способ. | АВ | =5 см - египетских треугольник. Точка М является центром описанной окружности, тогда | СМ | = 1/2*|АВ| = 2,5, так как СМ - радиус этой окружности, а АВ - ее диаметр.
Вместе со школьниками учитель сравнивает оба способа решения. Установили, что по сложности они равноценны, но второй способ более интересен, так как он необычен: надо уметь пользоваться свойствами описанной окружности.
Учитель ставит вопрос: как обобщить задачу, ведь в этой конкретные данные? Школьники сами сформулировали условие более общей задачи.
2.Доказать, что медиана, проведенная из вершины прямого угла треугольника, равна половине гипотенузы.
Тем самым было установлено свойство медианы прямоугольного треугольника, проведенной из вершины прямого угла на гипотенузу. (Этим определяется учебная полезность задачи - расширения теоретической базы).
Затем учитель предложил следующую задачу:
3.Доказать, что в прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, проведенными к гипотенузе.
Школьники справились с задачей самостоятельно и почти у каждого - свой способ решения.
Учащиеся сравнили все эти способы и подвели итог:
-
нужно смелее пользоваться дополнительными построениями;
-
активнее применять соответствующие разделы теории;
-
полезно с разных сторон "подходить" к рисунку - чертенку, находить в нем важную особенность и суметь воспользоваться ею.
Была составлена и обратная задача: если медиана и высота, проведенная из одной вершины треугольника, делят величину его угла на три равные части, то этот треугольник прямоугольный.
Эту задачу школьники решили также разными способами. Далее учитель провел обобщение, указав на взаимосвязь высоты, медианы и биссектрисы в прямоугольном треугольнике. В равнобедренном прямоугольном треугольнике высота, биссектриса и медиана совпадают.
При движении точки С окружности высота и биссектриса "отходят" от медианы. Биссектриса делит угол между ними пополам. Когда угол В=600- второй частный случай, обладающей тем свойством, что углы, образованные катетами, медианой и высотой, конгруэнтны. При дальнейшем перемещении точки С угол между медианой и высотой увеличиваются, а свойство биссектрисы остается.
В процессе решения этих задач учащиеся использовали для связи элементов треугольника описанную окружность.
Эта серия задач оказалась весьма полезной для учащихся, так как она способствовала развитию у них умения нешаблонно, с интересом подойти к решению задач, побудило их к составлению новых задач, систематизировала известные знания и опыт, т.е. содействовала всестороннему развитию их математического мышления.
При решении этих задач у учащихся развивалась способность и потребность к актуализации (упорядочению знай и опыта и умению применить его в новой ситуации). Тем самым мне удалось в какой - то мере реализовать то, что следует называть обучением решению задач.
2.1. Рекомендации по организации обучения математики
Сравнительный анализ результатов выполнения базовых заданий одинаковой тематики в 2002-2005 гг. по алгебре и началам анализа показывает, что из года в год повторяются типичные ошибки. Авторам учебников и разработчикам методических пособий следует обратить внимание на формирование базовых умений. Очевидны и проблемы, связанные с организацией обучения математике в средней школе. Одна из основных проблем состоит в том, что из года в год значительный процент выпускников не овладевает даже минимумом содержания, предусмотренным программой по математике: школьники делают ошибки при прямом применении изучаемых фактов и свойств, стандартных методов решения уравнений и неравенств, на распознавание и применение свойств функций. Так, например:
при делении степеней с одинаковыми основаниями "теряется" основание степени;
- в качестве правильного школьники выбирают тот ответ, где разность логарифмов представлена как логарифм разности;
- при решении иррациональных уравнений большинство
выпускников правильно находят корни уравнения-следствия, но не выясняют, какие из них являются корнями исходного уравнения;
- при решении логарифмических неравенств выпускники часто не учитывают область определения логарифмической функций, не меняют знак неравенства при переходе к линейному неравенству в том случае, когда основание логарифма меньше 1; не представляют число, стоящее в правой части неравенства, как значение логарифма;
- путают понятия "множество значений" и "область определения" функции при описании её свойств.
Подобные ошибки свидетельствуют о том, что в процессе обучения не было уделено должного внимания отработке базовых умений. В этой связи учителя справедливо отмечают, что в базисном учебном плане старшей школы отводится недостаточно времени на математику: это, по их мнению, приводит к тому, что многим ученикам не хватает учебного времени на прочное усвоение изучаемых тем.
В педагогической и методической литературе много говорится об индивидуализации обучения, об учёте готовности ученика к восприятию материала, о дозировании заданий с, учётом потребностей и возможностей школьника, но традиционно урок готовится в расчёте на некоего усреднённого. Ученика, что и приводит к столь невысоким результатам обучения. Поэтому и возникают сомнения в том, что могут быть рекомендации, пригодные для всех. Ведь каждый ученик личность, и в каждом классе есть ребята, которые схватывают всё на лету, и такие, которым всё надо подробнейшим образом несколько раз пояснить; увлечённые математикой и не любящие её; готовые много заниматься математикой дома и не притрагивающиеся к учебнику.
И тем не менее, несмотря на все индивидуальные отличия школьников, существует нечто в организации учебного процесса по математике при классноурочной системе обучения, определяющее успешность или неуспешность усвоения материала: объективные закономерности усвоения. Ясно, что понимание этих закономерностей и следование им в реальном педагогическом процессе - важнейший резерв повышения эффективности обучения только формулировки теорем и следствий и них и вовсе не рассматриваются их обоснования; при этом, как правило, не систематизируются имеющиеся и не обобщаются новые и ранее полученные знания. Даже при систематизации материала не всегда расставляются акценты - какой учебный материал важнее для решения конкретных задач по теме (а значит, и приоритеты в изучении). Действительно, в каждом из рассмотренных случаев не обеспечивается прочное усвоение большинством учеников класса ни программного, ни дополнительного материала, поскольку мы изначально недостаточно чётко определили цель изучения того или иного материала, а, следовательно, некачественно организовали деятельность всех учеников класса.
Следствием этого становится несформированность у старшеклассников умения самостоятельно добиваться знания и использовать их в несколько изменённой ситуации.
Как известно, наиболее трудна и для слабых, и для сильных школьников
"Тригонометрия": слишком много формул и недостаточно времени на их отработку. В варианты КИМ был включён справочный материал, в котором содержались формулы по тригонометрии (косинус(синус)суммы (разности), из которых самыми элементарными способами получались следствия (формулы приведения, двойного угла). Результаты выполнения заданий на применение формул приведения и нахождение синуса (косинуса) двойного угла позволяют сделать вывод о том, что для многих учащихся справочный материал бесполезен, поскольку они не умеют им пользоваться.
Итак, правильный отбор изучаемого материала, ориентированный на минимум содержания и требования стандарта, создаст предпосылки для продуктивного изучения, но не обеспечит его без следования основам теории поэтапного формирования умственных действий.
Л.С Выгодский утверждал, что знания усваиваются только в процессе собственной работы обучаемого с этими знаниями. Из чего можно сделать важный практический вывод: главная задача преподавателя на уроке - организовать собственную самостоятельную работу каждого ученика с материалом, который нужно усвоить.
Если учитель это понимает, он сведёт свои пояснения и разъяснения к "оптимальному минимуму", посвятив всё остальное время урока управлению той работой, которую выполняет на уроке с изучаемым материалом каждый из учеников. Очевидно, что чем меньше учитель говорит сам, чем больше он направляет и контролирует работу каждого из учеников класса, тем эффективнее обучение.
В соответствии с этой теорией преподаватель должен не только объяснить новый материал так, чтобы каждый ученик понял, что же именно ему надо усвоить и как работать с этим материалом, но и фиксировать основное содержание материала, которое позволяет приступить к работе без всякого предварительного заучивания.
Рассмотрим вторую проблему преподавания: закрепление базовых умений на уроках математики.
Объясняя материал и кратко его записывая на этапе ориентировки, учитель должен расчленить его на отдельные порции. Работа с каждой порцией - самостоятельный шаг ученика, отдельная операция. Необходимо организовать первоначальное закрепление материала так, чтобы учитель имел возможность проконтролировать ход и результаты выполнения каждой операции. Именно поэтому нельзя допустить, чтобы на этом этапе работа велась в уме. Итак, схема организации усвоения нового материала, в соответствии с теорией поэтапного формирования умственных действий, имеет следующий вид:
-фиксирование основного содержания подлежащего усвоению материала и способов работы с ним в краткой схематичной форме, удобной для использования при решении задач;
-организация самостоятельной работы, позволяющей проконтролировать ход работы и её результаты;
-постепенный переход от пошагового контроля со стороны преподавателя к самоконтролю обучающихся.
Может показаться, что при столь серьёзной и продолжительной организации процесса объяснения и первоначального закрепления с учётом малого количества часов, отводимого на изучение математики базисным учебным планом старшей школы, не хватит времени на закрепление с применением варьирования: при знакомстве с новыми объектами придётся ограничиться лишь стандартными ситуациями, что, с одной стороны, несомненно, приведёт к ошибкам, а с другой стороны, будет препятствовать развитию сильных учащихся. Однако по результатам многолетних экспериментов, проведённых в школах под руководством Н.Ф. Талызиной, сделан вывод о том, что если учить плохо; если в результате обучения определение не становится для ученика руководством к действию; если, выполняя распознавание, ученик (сильный или слабый) руководствуется сложившимся в сознании эталоном, и только им; если его не научили опираться при распознавании на определение, то варьирование несущественных признаков единственное, что может помочь сформировать обобщённый, освобождённый от случайных, несущественных свойств зрительный образ. А если та кой образ не сформирован неоткуда взяться правильному решению.
Но если учить хорошо, если обеспечить подлинное усвоение определения - значение варьирования оказывается неизмеримо более скромным.
Открытость требований к проведению ЕГЭ, возможность познакомиться с планом экзаменационной работы на текущий учебный год и демонстрационным вариантом, поучаствовать в пробном экзамене по этому предмету важные, но недостаточные условия успеха. Умение анализировать ситуацию и делать выводы на основании имеющихся теоретических знаний безусловно, одна из самых важных составляющих успеха на экзамене по математике. Достаточно популярно такое закрепление, как решение множества однотипных упражнении для того, чтобы "набить руку". Выделил и "новый" приём работы в выпускных классах в конце учебного года - постепенное (в некоторых школах, еженедельное) выполнение работ, составленных по типу ЕГЭ. Большинство учителей не имеют и тени сомнения в том, что выполнение множества однотипных заданий совершенно необходимое условие успешного усвоения и залог успеха. Правда, они же вынуждены констатировать, что однотипные задачи сильным ученикам скучны и неинтересны.
Изучив итоги пятилетней работы по введению Единого Государственного Экзамена по математике, можно утверждать: механизм проведения итоговой аттестации в форме ЕГЭ позволяет констатировать, что значительная часть выпускников российских школ выполняет большинство требований стандарта. Вместе с тем очевидны серьезные пробелы в работе педагогов с теми школьниками, которые не овладевают этими требованиями.
Среди нереализованных педагогами возможностей повышения качества математического образования главная - совершенствование подготовки и проведения урока математики на основе:
- более активного внедрения в практику работы школы принципов индивидуализации и дифференциации обучения;
использования активных форм организации деятельности школьников (а не собственной деятельности педагога);
- организации самостоятельной работы учащихся по усвоению изучаемого материала;
- внедрения проверенных и признанных на практике достижений в области педагогической психологии.
Итоговая аттестация в форме ЕГЭ не требует от педагогов изменения методики преподавания математики, а потому проблемы, возникающие в подготовке как слабых так и сильных учеников можно рассматривать как следствие недостаточной реализации потенциала современного урока.
Один из потенциалов - это использование информационных технологий на уроках математики. Оно делает обучение более содержательным, зрелищным, способствует развитию самостоятельности и творческих способностей обучаемого, существенно повышает уровень индивидуализации обучения. Ученикам, обладающим высокими учебными возможностями, они создают условия за то же самое время получить углубленные или расширенные знания, что значительно экономит время ребенка и учителя. Причем ребенок сам выбирает и уровень учебного материала, который может усвоить. Полностью решается проблема пропущенного материала. Необходимо также отметить интерес ребенка к использованию компьютера на уроках математики.
Для проверки усвоения знаний учащихся можно использовать компьютерные тесты. Особенность их в том, что ученик в случае ошибки может видеть образец правильного ответа. Компьютерные тесты хорошо использовать не только для контроля знаний, но и для самоконтроля, как при подготовке к контрольным работам, так и для повторения ранее изученного материала, знание которого потребуется при изучении новой темы. Учащимися старших классов можно использовать эти тесты для повторения материала перед экзаменом. Особенно примечательным является тот факт, что те ученики, которые психологически не справляются на письменных контрольных работах, очень успешны при сдаче и выполнении работ с помощью тестов.
Важную роль играют при изучении математики уроки-презентации. На таких уроках реализуются принципы доступности, наглядности. Уроки эффетивны своей эстетической привлекательностью, также между учителем и учеником существует посредник - компьютер, что способствует часто эффективному взаимодействию. Урок-презентация также обеспечивает большой объем информации и заданий за короткий период. Всегда можно вернуться к предыдущему слайду.
Важным положительным эффектом применения компьютерной техники на уроке является повышение мотивации учения. При этом особенно ярко видно влияние новых компьютерных средств преподавания на "слабых" учащихся; для многих из них работа с компьютером оказывается той единственной ступенькой к возрождению интереса к учебе, возможностью добиться успеха. Учащиеся охотно создают презентации, используя дополнительный материал, возможности Интернета, собственные знания по информатике и математике.
Применение информационных технологий при изучении различных предметов в первую очередь требует высокой подготовки учителя, который знаком с этими программами и умеет с ними работать. Во-вторых, уроки с применением компьютера позволяют выполнить больший объем заданий, операций, действий и при этом качественно. Возможности программного обеспечения растут с каждым днем, компьютер все больше и больше внедряется во все сферы общества. Поэтому каждому учителю необходимо научиться использовать информационные технологии в образовании.
Заключение
Урок был и остается основной формой организации учебно-воспитательного процесса. Сущность урока составляет организация учителем разнообразной работы учащихся по усвоению новых знаний, умений, навыков, в ходе которой осуществляется их воспитание и развитие. Современный урок-это урок, на котором учитель умело использует все возможные формы организации познавательной деятельности учащихся.
При решении задач у учащихся развивалась способность и потребность к актуализации (упорядочению знаний и опыты и умению применять его в новой ситуации). В работе даны основные подходы к решению творческих задач, требующих использования логических способностей. Предложена целенаправленная подборка развивающих задач на применение элементарных и сложных логических операций, связанных с поиском закономерностей, связей, отношений, причин, следствий. Выполнение предложенных заданий является еще одним переходным шагом к развитию логического, комбинационного, версионного, метафорического мышления как основных характеристик творческих способностей.
Тем самым мне удалось в какой-то мере реализовать то, что следует называть обучением решению задач и, разработать рекомендации для учителей математики по организации обучения математики.
Литература
-
Колягин Ю.М. и др. Общая методика преподавания математики в средней школе. М., "Просвещение", 1975, 1977.
-
Колягин Ю.М., и др. Частные методики. М., "Просвещение", 1978.
-
Леонтьев А.Н. Теоретические проблемы психического развития ребенка. - Советская педагогика, 1957.
-
Платов К.К. Занимательная психология. СПБ: Питер Пресс, 1997.
-
Занимательная математика.5-11 классы/Гаврилова Т.Д.-Волгоград:Учитель,2004
-
Занимательная математика для всех./Быльцов С.Ф.-СПб.:Питер,2005
-
Задачи Санкт-Петербургской олимпиады школьников по математике 2003 года./Кохась К.П. и др.-СПб.:Невский Диалект;БХВ-Петербург,2003
-
Математические олимпиады в школе.5-11 классы./Фарков А.В.-М.:Айрис-пресс,2006
-
Предметные недели в школе. Математика/Гончарова Л.В.-Волгоград:Учитель,2004
Приложение
1. На трех жестяных банках с печеньем перепутаны этикетки "Овсяное печенье", "Шоколадное печенье" и "Миндальное печенье". Все этикетки расположены неправильно. Банки закрыты, внутрь заглянуть нельзя. Вы можете открыть только одну банку, после чего правильно расположить этикетки.
2. Маше 16 лет и она на 5 см выше Эрика. Дима, Машин брат, ростом ниже Маши. Эрик - единственный ребенок в семье". Какое из следующих утверждений наиболее точно?
1. Дима выше Эрика. 2. Дима ниже Эрика. 3. Дима такого же роста, как Эрик; 4. Нельзя точно сказать, кто выше - Дима или Эрик. Зачем здесь возраст?
3. Бегуны прошли дистанцию и на табло загорелась надпись: Рустам не был вторым Эдуард отстал от Рустама на 2 места Яков не был первым Галина не была ни первой, ни последней Карина финишировала сразу после Якова Каково распределение бегунов на финише?
Подзадача 1: Кто был первым?
4. Фрэнк Стокман. Принцесса или тигр ? (сказка)
Узник должен угадать, в какой из двух комнат находится принцесса, а в какой тигр. Если он угадает комнату принцессы, то женится на ней, если ошибется, его растерзает тигр.
В первый день были проведены три испытания, При этом король объявил узнику, что в ходе всех грех испытаний в какой - то из комнат будет находиться либо принцесса, либо игр, причем может оказаться, что в какой комнате будет по тигру или там окажутся одни принцессы.
На комнатах висят таблички. На первой: "В этой комнате находится принцесса, а в другой сидит тигр". На второй:
В одной из комнат находится принцесса, кроме того, в одной из этих комнат сидит тигр.
В какой комнате находится принцесса, если на одной табличке написана правда, на другой - ложь?
5. Из двух братьев-близнецов один всегда лжет, другой всегда говорит правду. Как можно узнать, кто из них лжец, задав только один вопрос?
6. Одного из этих близнецов зовут Джон. Как узнать, которого, если можно задать ему только 1 вопрос из 3-х слов?
7. Борис выше Маши, которая, в свою очередь, выше Степы. Рома, Машин брат, такого же роста, как и Дима, который на З см ниже Бориса. Какое из следующих утверждений является верным?
а) Борис и Степа одного роста.
б) Дима и Рома - братья.
в) Борис - второй по росту в этой компании.
г) Ни одно из этих утверждений не является правильным.
(Правильный ответ - "г")
8. Логическое рассуждение: Если З дня назад был день, предшествующий понедельнику, то какой день будет послезавтра?
9. Утомившись от споров и летнего зноя, 3 греческих мудреца уснули под деревом. Пока они спали, шутники испачкали углем их лбы. Проснувшись и взглянув друг на друга, все 3 пришли в веселое настроение и начали смеяться. Но это никого не тревожило, так как каждому казалось естественным, что двое других смеются друг над другом.
Внезапно один из мудрецов перестал смеяться , так как сообразил, что его лоб также испачкан. С чего эго он взял?
10. Вот тебе сковорода, - сказал Король. - Испечешь мне наконец кренделей или нет?
- Без рецепта? - спросила Королева.
- Воспользуйся своим обычным рецептом, - закричал нетерпеливо Король. - В прошлый раз крендели у тебя удались на славу!
- Не могу, - ответила Королева. - В прошлый раз я испекла крендели по рецепту из моей поваренной книги, а её-то и украли!
Наибольшие подозрения пали на кухарку Герцогини. Поваренную книгу действительно нашли на кухне у Герцогини. Похитить её могли только кухарка, Герцогиня и Чеширский Кот.
- Поваренную книгу украл Чеширский Кот! - сказала Герцогиня на суде.
- О да, поваренную книгу украл я! - согласился Чеширский Кот.
- Я не крала поваренную книгу! - утверждала кухарка. Выяснилось, что лгал тот, кто украл поваренную книгу, и что по крайней мере один из остальных говорил правду.
Кто украл поваренную книгу?
11. После того, как поваренную книгу была возвращена Королеве, её украли во второй раз. И опять подозрение пало на Герцогилю, кухарку и Чеширского Кота. На суде все трое дали те же показания, что и в прошлый раз. Но теперь тот, кто похитил поваренную книгу, солгал, а двое других сказали правду.
Кто украл поваренную книгу на этот раз?
12. - Вот тебе твоя поваренная книга, - сказал Ко-
- Теперь и рецепт у тебя есть. Испеки мне кренделей!
- Без молока, без масла, без яиц?
- Горе мне! - вскричал Король. - Это уж слишком!
- Но теперь я точно знаю, кто украл мои припасы! Это сделали Мартовский Заяц, Болванщик и Соня, - закричала Королева, топая ногами от ярости.
Когда я вошла в кухню, то видела, как они вылезали из окна. И каждый нес с собой что-нибудь из припасов, только я не разглядела, что у кого было.
- Это мы скоро выясним, - грозно пообещал Король. Все припасы были найдены в домике, где жили Мартовский Заяц, Болванщик и Соня. Все трое были взяты под стражу и дали на суде следующие показания:
Мартовский Заяц. Масло украл Болванщик.
Болванщик. Яйца украла Соня.
Соня. Я украла молоко.
В ходе судебного разбирательства выяснилось, что тот, кто украл масло, говорил правду, а тот, кто украл яйца, лгал.
Кто что украл?
-
Информация
о современных образовательных технологиях и/или методиках,
используемых аттестуемым педагогическим работником в практической профессиональной деятельности
(заполняется педагогом)№
п/п
Современные образовательные технологии и/или методики
(Название, автор/авторы)
Цель использования технологии/методики
Описание порядка использования (применения)
технологии/методики в практической профессиональной деятельности
Результат использования технологии/методики
1.
Здоровьесберегающие
технологии
(В.И.Ковалько)
Обеспечить школьнику
возможности сохранения здоровья за период обучения в школе, формировать у него необходимые знания, умения и навыки по здоровому образу жизни и научить применять полученные
знания в повседневной
жизни.
Создание условий для здорового
развития учащихся ( соблюдение организационно-педагогических условий проведения урока :плотность, чередование видов учебной деятельности, проведение физкультминуток, упражнений для зрения и т.п.)
создание благоприятного психологического климата в классе;
соблюдение правил техники безопасности
и санитарно-гигиенических требований,
направленных на предупреждение
травматизма и сохранение здоровья учащихся.
Сформированы аспекты здорового образа жизни.
Наблюдается снижение
утомляемости детей на уроках, повышается уровень концентрации внимания .
Урок приносит радость и удовлетворение
2.
Технология
«Портфолио»
(М.Чошанов, С.Дж.Пейн)
Систематизация накапливаемого опыта, знаний.
Четкое определение направления своего развития.
Систематическое использование знаний видов портфолио для применения в дальнейшей деятельности.
Умение показать разнообразие и уровень своей деятельности.
Развитие навыков самооценки и рефлексии.
Умение анализировать достигнутые результаты.
Систематическая работа по оформления и сбору материала.
3.
Технология
проектного обучения
(Н.Г.Чернилова, И.С.Павлова
Карл Фрей,)
Создать условия для
самостоятельного и охотного приобретения недостающих знаний из разных источников,
развитие исследовательских умений, развитие системного мышления
Использование окружающей жизни как лаборатории, в которой происходит процесс познания.
Создание системы действий педагога и учащихся по разработке проекта.
Развитие ощущений эффективности выполненной работы.
Сбалансированное развитие основных физиологических и психических функций ученика, глубокое осознанное усвоение базовых знаний.
4.
Информационные
(Апатова Н.В.,Талызина Н.Ф.)
Информационные
технологии помогают сделать общение с
учащимися интересным,
увлекательным, эмоциональным. Они формируют новое мышление, связанное с тем информационным пространством, в котором ученик познает окружающую жизнь, активно
действует. Благодаря
им можно разнообразить
формы работы на уроке, активизировать внимание, повысить творческий потенциал личности
Для своей подготовки к урокам использую
возможности Интернета. Даю детям
опережающие задания с целью
поиска интересной, необходимой
информации по теме, которой нет в учебнике (групповые и индивидуальные). Делаю это с учетом дифференцированного
подхода. Активно использую в практике работы слайд-презентации как совместные, так и выполненные детьми самостоятельно..
Высокий темп урока.
- Приобретение опыта публичного выступления
- умений пользоваться интернет-ресурсами.
- умение поиска и обработки информации.
5.
Технология
педагогического общение
(В.А.Сластеник, И.Ф.Исаев, Е.Н. Шиянов).
Моделирование предстоящего общения в процессе подготовки к уроку или управление общением.
Планирование коммуникативной структуры взаимодействия, адекватной педагогическим задачам.
Управление общением, создание эмоциональной атмосферы.
Создание стадии обратной связи в общении существует. Учащиеся на уроке чувствуют себя комфортно.
Владение коррекционным педагогическим взаимодействием, что помогает учащимся ориентироваться в предмете,легко адаптироваться в 5 классе, полюбить предмет
В настоящее время ведутся поиски совершенствования различных компонентов методической системы, особенно содержания и методов обучения математике для всех звеньев её изучения в школе. Усовершенствование методики направлено на максимальную активизацию познавательной деятельности учащихся в процессе обучения. Одним из важных средств повышения эффективности обучения математике, повышения активности школьников в учении является рациональная организация работы по обучению младших школьников решению текстовых задач.
Переход школ на новое содержание обучения обуславливает существенное изменение структуры задач, методов их решения и методики обучения их решению. Однако для повышения роли обучения решению текстовых задач в совершенствовании математического образования младших школьников использованы далеко не все возможности.
Система текстовых задач начального курса математики в целом в настоящее время претерпела существенные изменения, направленные на повышение эффективности задач как одного из средств обучения. Сейчас ставится цель осознанного усвоения знаний, обеспечивающего возможность их применения в самых разнообразных, во многом новых для учащихся условиях. Это исключает возможность выработки вредных штампов в
решении задач; дети с самого начала будут поставлены перед необходимостью каждый раз производить основательный анализ задачи, прежде чем выбрать то или иное действие для её решения.
Но в программе указывается и на значение математических задач в деле развития у детей мышления, памяти, внимания, творческого воображения, наблюдательности, строгой последовательности рассуждения и его доказательности, для развития логического мышления учеников, для обучения их искусству кратко, точно, ясно и правильно излагать свои мысли. Все эти предпосылки должны быть возможно полнее использованы при обучении детей математике.
Но подавляющее большинство задач выполняют преимущественно обучающие и тренировочные функции, что способствует формированию лишь репродуктивного мышления школьника. И лишь немногие задачи предусматривают в различной степени конструирование нового способа решения, позволяют формировать различные уровни продуктивного мышления.
Усиление роли развивающего обучения, необходимость формирования у учащихся навыков упорядоченного анализа, синтеза и элементарного исследования обусловили появление в учебниках математики 1-4 классов некоторых задач, значительно отличающихся от обычных по содержанию, форме и методам решения. Такие задачи в методике математики принято называть нестандартными. Нестандартность этих задач заключается не в сложности, а в непривычности для учащихся. Появление нестандартных задач свидетельствует об эволюции содержания и структуры текстовых задач в зависимости от других компонентов методической системы, об изменении их роли и места в обучении, то есть является вполне закономерным, обоснованным процессом.
В период, когда на протяжении десятков лет содержание математического образования младших школьников не изменялось, задачи повышенной трудности применялись лишь в качестве занимательного материала с целью повышения интереса к математике у наиболее способных учащихся. Основной формой использования этих задач являлись различные виды внеурочной работы.
Теперь же наметилась тенденция использования задач повышенного уровня трудности, как необходимого компонента обучения младших школьников математике. Задачи повышенного уровня трудности необходимы в обучении математике. Объясняется это, прежде всего, возрастающими требованиями, направленными на усиление воспитывающих и развивающих функций обучения. Эти задачи:
- учат детей не только использовать готовые алгоритмы, но и самостоятельно определять оригинальные способы решения задач;
- препятствуют выработке вредных штампов при решении задач, разрушают неправильные ассоциации в знаниях и умениях учащихся и тем самым оказывают положительное влияние на формирование навыков решения типовых задач;
- предполагают развитие у учащихся способности к обнаружению новых связей в знаниях, к переносу знаний в новые условия, к овладению разнообразными приемами умственной деятельности;
- создают благоприятные условия для повышения прочности и глубины знании учащихся, обеспечивают более сознательное овладение основным содержанием курса математики
Усовершенствование школьного образования привело к изменению содержания и функций текстовых задач в начальном обучении. Текстовые задачи стали служить не только целью, а и важным средством обучения. Наряду с дидактическими функциями большое число задач начального курса математики призвано нести познавательные и развивающие функции.
Для решения большинства нестандартных задач не требуется знания учащимися каких-либо правил; часто учащиеся вынуждены «изобретать» новый приём решения. Нестандартные задачи могут являться важным средством формирования навыка самостоятельного построения учениками новых алгоритмов решения задач.
Решение задач имеет большое образовательное и воспитательное значение. Н.А. Мечинская и М.И. Моро отмечают, что решение задач всегда рассматривалось как такая учебная деятельность, которая преследует двоякую цель: во-первых, решение задач является средством, способствующим усвоению математических понятий и законов, а во-вторых, оно имеет самостоятельную ценность, поскольку служит для развития творческого мышления учащихся.
Совершенствование содержания и методов обучения младших школьников математике в современных условиях, вызванное изменением целей обучения, обусловило не только изменение роли текстовых задач в обучении математике, но и объективное
появление нестандартных задач, значение которых в связи с новыми задачами начального обучения стало очень большим. Авторы учебников подчёркивают, что наряду с обычными (и необходимыми!) для начальной школы тренировочными упражнениями,
направленными на автоматизацию приобретённых навыков, в учебниках широко представлены упражнения нового типа - развивающего характера. Это задания, выполняя которые, ученики должны провести те или иные наблюдения, сопоставить
наблюдаемые факты, сделать самостоятельные выводы, наметить различные пути решения выдвинутой задачи, проблемы, обосновать свои действия, проверить правильность выдвинутых предложений, подметить ту или иную зависимость,
закономерность и другие.
Эти задачи, включенные в учебники, дают возможность не только разнообразить систему задач, но и познакомить учащихся с вопросами, не сформулированными
непосредственно в программе, но имеющими значение для общего развития. Каждая из таких задач, может быть, и не даст непосредственного результата, но он проявится позже как итог общего подхода к обучению детей умению решать разнообразные задачи. Решение учащимися нестандартных задач предполагает развитие у учащихся не столько способности к овладению фиксированными операциями и приёмами, сколько (и это очень важно!) к обнаружению новых связей, к переносу знаний в новые условия, к овладению новыми приёмами умственной деятельности, к деятельности творческого характера.
Решение этих задач, с одной стороны, повышает общую и математическую культуру школьников, способствует развитию их математического мышления, а с другой стороны, вызывает у них стремление к открытию нового, ранее неизученного.
Главное при решении нестандартных задач - это научить учащихся думать над задачей, рассуждать, догадываться, делать правильные умозаключения. По результатам выполнения заданий учитель имеет возможность сформированность различные способы умственной деятельности: умение производить анализ, синтез, делать сравнения, сопоставления, обобщения, классифицировать предметы и явления, формулировать выводы. А эти умения носят обобщенный, межпредметный характер. Выполнение этих заданий воспитывает такие качества знаний, как глубина и полнота, осознанность и оперативность.
В повседневной жизни, трудовой и научной деятельности чаще всего приходится иметь дело с нестандартными задачами, стереотипные же задачи, способ решения которых найден и хорошо известен, занимают более скромное место. Следовательно,
нестандартные задачи нельзя игнорировать и с точки зрения подготовки учащихся к практической деятельности, так как такие задачи стимулируют учащихся к творчеству.
Младших школьников нужно подготовить к тому, чтобы в будущем они умели решать самые разнообразные задачи. Формирование методов мышления в процессе решения нестандартных задач - это один из возможных каналов, по которому должно осуществляться общее развитие учащихся, в частности, воспитание их умственных способностей.
Творческий подход к решению нестандартных задач не рождается сам по себе. Для этого нужно создать определённые условия. Наибольший эффект нестандартные задачи развивающего характера могут дать лишь при условии, если учитель умело организует поисковую деятельность детей, правильно направляет мысль учащихся. Важно на разнообразных нестандартных задачах и упражнениях формировать общие приёмы решения любых доступных возрасту учащихся задач.
Следует особо подчеркнуть большое общеобразовательное значение специального обучения младших школьников решению нестандартных задач. Каждая нестандартная задача - это маленькая проблема, которая требует от учеников умственной активности и находчивости в поисках непроторенных путей решения, способствует развитию логико-математического продуктивного, эвристического мышления учащихся, активизации мыслительных операций, их самостоятельности, отточенности; вырабатывает ценные умственные качества: последовательность мысли, логичность, сообразительность, смекалку, то есть улучшает и повышает качество математической подготовки учащихся.
Эффективность обучения младших школьников решению нестандартных задач зависит от нескольких условий:
1. Задачи следует вводить в процесс обучения в определенной системе с постепенным нарастанием сложности, так как непосильная задача мало повлияет на развитие учащихся.
2. Необходимо предоставлять ученикам максимальную самостоятельность в поиске решения задач, давать возможность пройти до конца по неверному пути, убедиться в ошибке, вернуться к началу и искать другой, верный путь решения.
3. Нужно помочь учащимся осознать некоторые способы, приемы, общие подходы к решению нестандартных арифметических задач.
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Процессы обновления, происходящие в нашем обществе, не могут не вызывать серьезных изменений системы народного образования. Перспективные пути экономического развития страны в первую очередь требуют совершенствования обучения учащихся с целью повышения качества их знаний и усиления практической направленности преподавания школьных дисциплин. Развитие при этом умений школьников владеть современными методами анализа и исследования и способностей эффективного использования полученных знаний способствует воспитанию человека активной жизненной позиции, готового к трудовой деятельности в условиях демократизации и нарастания ускорения научно-технического прогресса.
Совершенствование организации обучения математике в соответствии с указанными направлениями обуславливает необходимость развития мышления, познавательных способностей и практических навыков учащихся. Поэтому для преподавания алгебры, геометрии и начал математического анализа усиливается актуальность вопросов о месте и повышении роли задач - материала, служащего для школьников показателем действенности получаемых ими знаний.
Принципы постановки и выявление значения математических задач в процессе обучения традиционно являются объектами пристального внимания ученых (исследования Н.Г. Алексеева, Л.Л. Гуровой, В.А. Гусева, Ю.М. Колягина, В.М. Монахова, Г.И. Саранцева, И.Ф. Тесленко, Л.М. Фридмана и других) и практических работников советской школы. Однако, обобщение опыта работы учителей и анализ знаний учащихся позволяют сделать вывод о том, что проблема совершенствования методики использования задач не исчерпана и остается актуальной. В частности, особого внимания в процессе преподавания математики требуют сюжетные задачи, выступающие носителем специфической функции выделения явлений, описанных в условиях с определенной точностью, из реальной окружение и учащихся действительности. Важность изучения отмеченной проблемы на материале этих задач усиливается возможностью применения для ее реализации математического моделирования. Достижение при этом сочетания высокой степени абстракции с практическим применением математической теории, эффективно влияя на содержательное усвоение материала учащимися, способствует повышению качества их знаний.
Наиболее полно специфика сюжетных задач проявляется в райках системы обучения, когда, одновременно с местом и значением задачного материала определяется во взаимосвязи комплекс его основных функцицй, проводится типология и устанавливаются обязательные уровни усвоения в знаниях учащихся.
В плане рассмотрения дидактических функций сюжетных задач следует отметить, что на протяжении всего школьного курса обучения они не являются постоянными. Анализ теоретических исследовали Н.А. Каллаура, В.А. Ланкова, К. И. Пешкова, А.Д. Семушина, А.П. Сманцера, В.П. Радченко и других и практический опыт учителей показывают, что определенные функции задач в процессе обучения могут быть усилены или же включены элементами в комплексы различных систем организации знаний и умений. При этом лишь некоторые ИЗ НИХ сохраняют ведущее значение на всех этапах образования и позволяют организовать на своей основе реализацию дополнительных направлений.
В практике работы учителя решение вопросов о целевом выборе функций с общих позиций требует существенных дополнений, раскрывающих место сюжетных задач в построении всей системы знаний школьного курса математики с учетом глубины их взаимосвязей с различными заданиями и связей с другими дисциплинами, направленных на повышение качества усвоения учащимися теоретического материала, применении при обучении дифференцированной методики.
Указанные факторы обусловили выбор в качестве объекта исследования совокупность сюжетных задач и процесс реализации их образовательных функций в школьном курсе математики.
Работы Е.И. Лященко, М.Р. Леонтьевой, С.Б.Суворовой, посвященные поиску приемов, форм и методов эффективного использования отдельно взятой задачи в процессе обучения, выделяют требования, связанные с формированием у учащихся умений и навыков их решения. При наличии достаточно широкого спектра исследований в этом плане (работы М.Б. Балка, В.Г. Болтянского, А.Б. Василевского, Н.Я. Виленкина, В.И. Крупича и других) естественно, что не все вопросы разработаны в равной мере. Дальнейшего изучения требуют выбор эффективных путей включения рассматриваемого материала в логическую структуру математического образования, направления использования сюжетных задач учителем для установления обратной связи при закреплении теоретического материала, исследование мыслительной деятельности и развития творческих способностей учащихся при индивидуализации обучения поиску сюжетных задач.
Сказанное определяет актуальность исследования и позволяет сформулировать проблему, состоящую в выявлении условий, влияющих на развитие математического мышления и выработку у школьников умений исследования реальной ситуации на различных уровнях ее формализации при организации работы с сюжетными задачами.
Цель исследования состоит в решении поставленной проблемы.
Предметом исследования являются методы и средства реализации специфических и функций сюжетных задач в процессе преподавания школьного курса алгебры и начал математического анализа.
Теоретический анализ проблемы исследования показал недостаточную направленность действующей методики обучения учащихся поиску решения задач на содержательное развитие идеи применения математического моделирования. При этом, поиск конструктивных основ предмета исследования позволил выделить принцип, объективно обладаюший системообразующим свойством на совокупности сюжетных задач школьного курса алгебры и начал математического анализа. Этот принцип, отражающий математическую структуру "основного отношения" (термин В.И. Крупича) процесса, описанного в сюжете позволяет в рамках классификации на основе соглашений (например, по "сюжетам" или "темам") охарактеризовать сюжетные задачи через отношения, которыми определяются функции каждой из них в системе формирования умений моделирования и выделить приемы, организовать работу по выработке стратегии поиска их решения.
Для осуществления цели исследования в условиях принятия сформулированного принципа была выдвинута следующая гипотеза: рациональная постановка сюжетных задач в школьном курсе алгебры и начал математического анализа при формировании представлений школьников о моделировании процессов реальной действительности обеспечивает осознанность и развитие мыслительных умений учащихся при поиске решения практических задач и способствует качественному усвоению теоретического материала на различных уровнях его изложения.
Необходимость достижения обязательных результатов обучения требует творческую деятельность школьников при поиске решения задачи подчинить исходящей из фабулы сюжета «внутренней мотивации». Сюжетная интерпретация элементов, отвечающих за такую мотивацию, определяется ролью задачи в процессе обучения, а их выделение проводится по признаку места каждой задачи в разработанной иерархии и основывается на анализе функционально-семантической структуры текста сюжета или условий течения процесса, описанного фабулой.
Для достижения поставленной цели научной достоверности гипотезы потребовалось решить следующие частные задачи:
1) раскрыть особенности сюжетных задач как учебного материала, рассмотреть их место и роль в процессе обучения, выделить специфические функции этих задач для развития математического мышления и творческих способностей учащихся;
2) разработать принцип организации совокупности сюжетных задач в целях усиления их роли в процессе изучения теоретического материала, осуществления внутрипредметных и межпредметных связей, развития практических умений учащихся;
3) проанализировать механизм мыслительной деятельности учащихся при решении задач и установить факторы, влияющие на успешность осуществления поиска модели и интерпретации ответа в процессе развития умений школьников обосновывать приемы и выбор рациональных суждений при моделировании ситуаций, приближенных к реальной действительности;
4) выявить причины характерных ошибок и затруднений при решении сюжетных задач и разработать методику организации профилактической работы по их предупреждению.
Решение поставленных задач обусловило выбор следующих методов исследования:
1) изучение работ по теории познания как методологической основы исследования, психолого-методической и математической литературы, анализ школьных учебников и учебных пособий;
2) теоретическое исследование проблемы;
3) обобщение опыта работы учителей, преподавателей и педагогических институтов, анализ знаний учащихся, абитуриентов и студентов;
4) проведение педагогического эксперимента;
5) психолого-педагогическое доказательство целесообразности разработанной методики работы с сюжетными задачами;
6) наблюдение за ходом внедрения дидактических материалов в практику и обобщение полученных результатов.
Новизна проведенного исследования состоит:
- в выявлении специфической роли сюжетных задач в развитии творческого мышления учащихся и их места в формировании у школьников умений моделирования на основе реализации внутрипредметных и межпредметных связей;
- в разработке дидактической организации совокупности сюжетных задач курса алгебры и начал математического анализа на основе принципа, позволяющего внешне субъективную последовательность их расположения подчинить динамике представлений у учащихся о моделировании процессов реальной действительности и установить обязательные уровни умений при решении задач на процессы с определенным характером изменения;
- В разработке рекомендаций по предупреждению характерных ошибок и затруднений учащихся при решении сюжетных задач на этапе моделирования.
Теоретическая значимость работы состоит в обосновании приемов рационального использования сюжетных задач в процессе обучения учащихся математике, формирования у них общих и развитии частных умений моделирования процессов реальной действительности.
Практическую значимость работы определяют рекомендации по использованию:
- дифференцированной методики обучения решению сюжетных задач, позволяющей на практике работы учителя максимально использовать возможности исследуемого материала для предупреждения формализма в знаниях учащихся и повышения качества их практических умений;
- целевой направленности при подготовке будущих учителей математики в педагогических институтах на занятиях по методике преподавания математики и практикуму по решению задач при дидактическом анализе путей организации поиска модели сюжетных задач;
- преемственности и установке перспективных путей развития творческих знаний для школьников.
На защиту выносятся следующие положения:
1) специфика роли и места сюжетных задач в системе общего математического образования и творческого развития школьников с целью повышения качества их знаний;
2) иерархическая структура сюжетных задач курса алгебры и начал математического анализа на основе выделения определяющей зависимости процесса, описанного в сюжетеучащихся на применение научных методов исследования к ситуациям, приближенным к реальной действительности;
3) содержание и структура учебного материала для изучения дифференциальных уравнений в курсе математического анализа средней школы;
4) методика решения сюжетных задач на основе выделения определяющей зависимости в рамках дифференциального подхода к развитию мыслительной операции учащихся по переносу знаний и приемы организации работы по предупреждению характерных ошибок и затруднений школьников на этапе моделирования.
СОДЕРЖАНИЕ ДИССЕРТАЦИИ
Структура: диссертация состоит из введения, двух глав, заключения, списка используемой и цитируемой литературы, содержащего 197 наименований, и приложения.
Во введении обоснован выбор темы, раскрыта ее актуальность, сформулированы объект, предмет, цель и гипотеза, показаны научная новизна, теоретическая и практическая и практическая значимость, методика исследования.
Глава 1 «Психолого-педагогические основы обучения учащихся решению сюжетных задач'' посвящена изучению общих вопросов, обеспечивающих достижение поставленной цели исследования.
Трактовка понятия «сюжетная задача» проводится в диссертации в соответствии с точкой зрения Л.Л. Гуровой, Ю.М. Колягина, П.М. Эрдниева в рамках выделенных Г.А. Баллом подходов к обозначению «задачи». В силу специфики школьного образования в выбранное определение наряду с поставленной целью нами включаются также условия, в которых эта цель должна быть достигнута.Творческий характер деятельности при решении сюжетных задач определяет проекция выбранных зависимостей в фабулу ситуаций различных видов человеческой деятельности всякий раз в новых, неповторяющихся условиях. Сюжет задачи рассматривается в работе как внешне ее содержание, форма выражения внутреннего содержания математической конструкции модели, задающей основу описываемых отношений. При этом считается, что каждое действие по решению задачи направлено на нахождение неизвестного внутренней конструкции на основе использования его связей с известным.
Принимаемое определение сюжетных задач, содержащее в основе их существенную особенность - наличие фабулы, позволяет объединить эти задачи в отдельный класс внутри совокупности текстовых математических задач.
Выделение роли сюжетных задач в формировании знаний при изучении школьного курса математики нами проводится согласно следующей схеме для структуры деятельности, являющейся отражением структуры мышления учащихся. (схема 1)
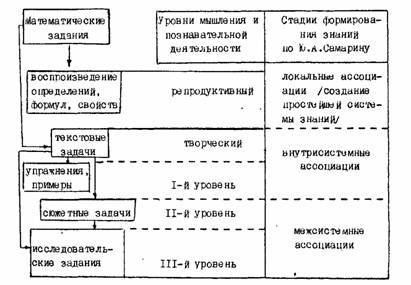
Выделение значимости формирования отношений теории и практики в стадии развития межсистемных ассоциаций при требовании гуманизации знаний усиливает необходимость ознакомления учащихся с общей идеей и принципами математического моделирования. Поэтому в качестве схемы решения сюжетной задачи мы рассматриваем модификацию традиционного плана исследования явлений реальной действительности. Схема 2.Сюжет → условия
МОДЕЛЬ
ОТВЕТ
Внутримодельное решение
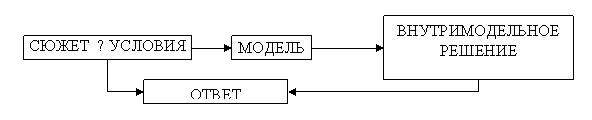
Схема 2.
Для характеристики сюжета в работе введено понятие предметной линии, которая задается принадлежностью терминологического языка фабулы к некоторой области знаний (деятельности). Установлено, что наличие схемы 2 специфического блока СЮЖЕТ, являющегося по существу интерпретацией через предметные линии определенной математической конструкции, определяет функцию сюжета рассматриваемого вида задач. Эта функция является основой реализации практической направленности обучения. Ее существенное обогащение в плане «эмоционально-ценностной» (термин Г.И. Щукиной) ориентации достигается проведением исторической и краеведческой обусловленности в рамках экономической, бытовой, алгебраической и геометрической предметных линий. Условие обусловленности позволяет описать такие задачи внутри класса сюжетных задач и принять в работе строгую терминологию сюжетных типов: «историческая задача», «задача с краеведческой направленностью».
Психолого-дидактический анализ механизма перехода на этапе сюжет → модель, являющегося с одной стороны завершением познания сущности сюжета, с другой - составляя основу познания конкретных значений его явления (для реализации следующих блоков и связей), в концепции «решения сюжетной задачи» позволил выделить еще одну ее функцию - функцию поиска. Как метод познания моделирование на рассматриваемом этапе является гиперонимом, т.е. определителем для способов моделирования (составления уравнений, построение графиков, схем, таблиц, графов).
Сочетание функций сюжета и поиска в процессе решения задачи позволяет учащимся устанавливать обратные связи с теоретическим материалом как результат самостоятельного обобщения своего практического опыта, что активно влияет на развитие интереса к изучению математики и убежденность школьников в действенности получаемых ими знаний.
В рамках углубления межсистемных ассоциаций (по "Схеме I") при построении модели экспериментально подтверждена целесообразность разделения дидактических функций задачи с определенной предметной линией сюжета и подобной ей задачей, решаемой, например, на уроках физики или химии. В первом случае моделирование выступает тем содержанием, которым школьники учатся владеть, тогда как во втором - моделирование есть учебное действие обеспечивающее
полноценность и успешность обучения. Теоретический анализ полученного результата и исследование механизма его достижения позволили выделить необходимость формирования на уроках математики при решении задач логических и репродуктивных ассоциаций в двух направлениях: сюжет → модель и модель → сюжет.
Развивая идеи М.В. Крутихиной о типе ассоциаций, этапы мыслительной деятельности школьников в первом направлении мы рассматриваем в следующем коде : предметные термины → сущность понятий, обозначенных терминами, → характеристические свойства понятий в принимаемом законе связи этих свойств с реальным течением процесса → символическое обозначение → конструкции закона связи → модель.
Устанавливая единство существа причинно-следственной связи между объектами сюжета и определенной математической конструкцией (моделью), учащиеся практически осуществляют мыслительную деятельность но переносу знаний из некоторой области (по предметной линии) в область математики. Успешность осуществления такого переноса зависит в первую очередь от создания в смысле К.А. Славской '"внутренних условий переноса", определяющихся, по нашему мнению, развитием умений выделения общего.
Проведенный анализ школьных задач показал, что их "общность" следует рассматривать в двух аспектах: модельном - при единстве сущности связи понятий, их характеристических свойств в принимаемом законе соответствия реальности, но различной терминологии сюжета и сюжетном - при единстве предметной линии, но различии в законах связей между понятиями.
Общность модельная объединяет обширный гласе задач курса алгебру
"на движение", "переливание", "работу", "покупку" при условии
равномерности С одинаковости) скорости, производительности,
стоимости. В основе внутренней конструкции таких задач -
возможность линейного выражения связи основных предметных
компонентов: ![]() ;
; ![]() , где А - работа, р -
производительность;
, где А - работа, р -
производительность; ![]() , где Z - стоимость, С - цена
единицы товара, а - количество единиц товара.
, где Z - стоимость, С - цена
единицы товара, а - количество единиц товара.
Содержательную иллюстрацию предметной общности возможно провести
внутри физической предметной линии на основе сравнения и
качественной оценки исследовании решения задачных ситуаций при
условиях равномерного движения, когда ![]() и
и ![]() ; его равнопеременности,
когда
; его равнопеременности,
когда ![]() и
и
![]() т.е.
т.е.
![]() и при
определенном свойстве изменения ускорения, когда, например,
и при
определенном свойстве изменения ускорения, когда, например,
![]() В контексте
проведенных в реферируемой работе исследований развития у
школьников умений моделировать в рамках общности в первом и втором
аспектах специальное внимание уделено вопросу организации
совокупности сюжетных задач, которая в плане формирования
соответствующих знаний обладает свойством системности.
В контексте
проведенных в реферируемой работе исследований развития у
школьников умений моделировать в рамках общности в первом и втором
аспектах специальное внимание уделено вопросу организации
совокупности сюжетных задач, которая в плане формирования
соответствующих знаний обладает свойством системности.
В основу иерархической организации задач положено понятие "характер изменения определяющей зависимости". Оно определяется конструкцией закона связи характеристических компонент предметной ситуации и выделено нами, исходя из онтологической статус - функции этих задач, выражающейся, с одной стороны, в правильном понимании и осознании школьниками законов изменения, с другой - в принципах построения математических моделей.
Ситуацию обучения учащихся решению задач предложенный иерархический подход дополняет важнейшим элементом учебной цели: научить исследовать процессы реальной действительности с необходимой, достаточной или максимально возможной (на определенном уровне знаний) точностью. Например, для решения задачи "Два тела имеют температуру в 100°. Они вынесены на воздух (его температура 0°) . Через 10 минут температура одного тела стала 80°, а другого - 64? Через сколько минут после начала остывания разность их температур будет 25°?" В указанном аспекте можно построить две качественно разные модели. Первую - на основе предположения о равномерном изменении определяющей зависимости - скорости остывания, другую - при условии учета пропорционального изменения скорости остывания разности температур остывающего тела и среды (экспоненциальном характере изменения). Наблюдений за работой учащихся показали, что раскрытие возможности обоснованного выбора той или другой модели для поиска решения ставит их в ситуацию необходимости неформального понимания материала даже на общеобразовательном (по классификации Г.И. Глейзера) уровне. При этом, в частности, реализуется мотивационная компонента изучения более сложных уравнений по сравнению с линейными.
Проведение в рамках разработанном организации задач содержательного анализа сюжетов по признаку модельного общего требует от учащихся усвоения приемов выделении (или самостоятельного предположения) характера определяющей зависимости и установления адекватности внутреннего содержания задачи определенной ступени иерархической системы по общности модельной конструкции: для равномерных процессов - линейные уравнения, равнопеременных - квадратные, для неравнопеременных - дифференциальные уравнения.
Результаты экспериментального исследования показали, что формированию и закреплению умений выделения модельного общего каждой ступени при решении сюжетной задачи как единицы построенной организации наряду с применением элементов метода ослабленной аналогии М.Н. Скаткина способствует установление "операции" (по критерию Ж. Пиаже) мышления при переносе. Основой развития мыслительной "операции" служит переход модель → сюжет.
Дополнительным эффективным фактором развития мыслительной деятельности учащихся является интерпретация ответа. В частности установлено, что для формирования "операции" существенное значение имеет выработка у школьников умений интерпретировать ответ на двух последовательных уровнях: операции - при сравнении результатов внутримодельного решения с предметным смыслом сюжета и действия, когда выделяется механизм управления процессом сюжета.
Обеспечение уровня действия определяет выход в исследовательское задание (по схеме 1) и достигается согласованием задачи с теоретическими знаниями учащихся по следующим установленным компонентам: I) узнавание явления по внешним признакам; 2) установление или выделение условий течения процесса сюжета; 3) воспроизведение связи характеристик явления; 4) понимание механизма течении явления и учет его использования на практике.
Анализ материалов теоретическою исследования позволил установить пути практического осуществления развития математического мышления учащихся при поиске решения сюжетных задач и влияние этих задач на уровень знаний обучаемых. В числе факторов успешной реализации первого направления нами выделены: проведение анализа условия, решения и выбора ответа; выполнение требования плановости, четкости выражения мыслей при решении; постановка и решение проблемных ситуации; самостоятельное составление задач; рассказ (обсуждение) решения учениками. В плане реализации второго направления - мера включения сюжетных задач на уроке для возможности применения теоретического материала при их решении; проведение систематизации, обобщения, ограничения, сравнения; установление места аналогии, дополнение теоретического материала иллюстрациями и приложениями; организации самостоятельной работы; необходимые уровни достижения обязательных результатов обучения при решении задач с определенным характером изменения.
Во второй главе "Методика решения сюжетных задач в курсе математики средней школы" разработаны практические рекомендации по организации поиска решении задач, а также проведено педагогическое исследование и доказательство эффективности их применения в работе с учащимися и студентами.
Исходя из анализа выявленных причин ошибок и затруднений на этапе моделирования в ситуации ученик-задача, центральным направлением профилактической работы выбрана методика развития мыслительной деятельности учащихся по осознанию существа процесса и правильному выделению и математическому выражению зависимостей между величинами сюжета.
Разработанные приемы поиска модели на основе выделения определяющая зависимости, позволяют преодолеть формальный подход учащихся к связям условия и предполагаемой модели, когда, при отсутствии видения процесса в делом, построение уравнения (неравенства) представляет собой лишь непосредственную фиксацию частных зависимостей сюжета, "выхваченных" из остальных условий вне определяющей его линии.
Для понимания сущности процесса и развития умений учащихся его фиксации в некоторой символической форме, обладавшей направленной информацией, в рамках этапа построения математической модели нами выделены следующие требования к анализу сюжета, предшествующие введению и обозначению неизвестного: I) выделение из фабулы исследуемых величин и установление моделируемой ситуации; 2) определение по условию или в дополнительном предположении характера процесса; 3) выделение (словесное или символическое) определяющей зависимости моделируемой ситуации.
Задавая ориентировку на конструкцию внутреннего содержания задачи, выделение определяющей зависимости позволяет корректировать логику аналитического поиска при сравнении рациональности разрешения моделей, построенных относительно разных, входящих в определяющую зависимость, компонент. Кроме того, проведение анализа образования наименования определяющей зависимости способствует разъяснению и предупреждению характерной ошибки учащихся, состоящей в подмене связи в частях уравнения (неравенства) однородных величин формальной связью данных условия.
Исследования по раскрытию ''слов-признаков" магматического смысла в сюжетах задач определенных классов построенной иерархи позволяют наметить дополнительные пути дифференцированного обучения учащихся с различным уровнем математического мышления поиску их решения. Основу варьирования методики при организации работы с сюжетными задачами курса алгебры и начал математического анализа (на дифференциальные уравнения) составляют изменения в сочетании уровня ориентировки учащихся в данных сюжета ( по классификации В.П.Беспалько) и установления формируемого этапа моделирования. Так, для задач на основные отношения, выделенные В.И. Крупичем, при целевой установке обязательного овладения методом как компонентой моделирования в целом, нами установлена последовательность формирования ассоциативно - обобщающей деятельности для школьников, испытывающих затруднения при выделении общего в модельном аспекте, представшая следующей схемой:
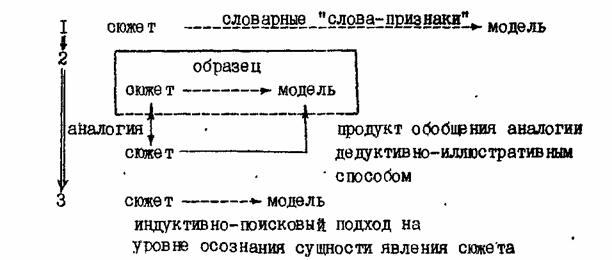
Схема 3.
На основе углубления связей знаний учащихся о структуре математической модели алгебраической задачи и отысканием действия для ее решения в качестве пути введения дифференциальных уравнений в школьном курсе начал математического анализа установлен принцип отрицания (отрицание равномерности и равнопеременности) для более точного описания реальных процессов. Для мотивационного этапа моделирования разработана, методика решения задач, связанных с экспоненциальным и гармоническим характером изменения.
Представленный в приложении материал содержит иллюстрацию установленных в исследовании методических приемов для решения различных по конструкции математических моделей задач. Разработанные фрагменты рекомендуются для организации обобщающего повторения с учащимися старших классов на уроках и факультативе.
Педагогический эксперимент, направленный на проверку результативности разработанной концепции использования сюжетных задач в школьном курсе математики, проходил в период с 1987 по I990 годы и содержал 4 основных этапа.
Выделяя особенности экспериментального исследования, отметим, что 1-й и 2-й его этапы носили поисковый и конструктирующий характер. Проведенная в этот период работа с учащимися 4-х и 9-10-х классов 4-х школ г. Свердловска и области была направлена на поиск общих приемов обучения решению сюжетных задач и в большей степени применялась к слабоуспевающим и мало интересующимся математикой школьникам.
III-й этап был связан с разработкой критериев диагностики эффективности методики, направленной на выработку у школьников внутренней мотивации при поиске модельной конструкции сюжетной задачи. Среди учащихся 9-I0-x классов на этом этапе была выделена группа школьников, не испытывающих затруднений в работе даже при решении задач повышенной трудности. С ними был проведен дополнительный эксперимент по организации индивидуальной работы, показавший возможности и пути использования рассматриваемого материала на углубленном уровне на уроке и при проведении внеклассных мероприятий.
В результате прогнозирующего этапа эксперимента были обобщены полученные выводы и проведена корректировка итогов 1-го и 2-го этапов, формулировки гипотезы и задач исследования.
Учебная задача 4-го этапа состояла в проверке системы действий и операций, направленной на поиск решения задач с различным характером определяющей зависимости. Исследования проводились среди слушателей очно-заочных подготовительных курсов СвГПИ на математическом, физическом и ПиМНО факультетах, учащихся 4-х школ г. Свердловска и области, CПТУ №214 г. Выборга.
При установлении уровня овладения школьниками умениями решения сюжетных задач по стадиям развития 3-х компонентов: мотивационной, вычислительной, реализационной, более подробно по цели исследования рассматривалась первая. Анализ и статистическая обработка материалов по критерию Вилкоксока-Манна-Уинти показали, что в экспериментальных группах, методика работы в которых была основана на реализации разработанных подходов и рекомендаций, отмечается белое высокий, по сравнению с контрольными, процент учащихся строящих свою деятельность по типу продуктивно - преобразующей (анализ оценок знаний по среднему арифметическому - 8,27, против 6,4 в контрольных группах). При такой деятельности мышлению свойственен индуктивно- поисковый подход при решении задачи на уровне осознания ее сущности. При включении новых связей их обогащение происходит с позиции развития отлей идеи моделирования. Знания действия отличает правильная трактовка предметных понятий, содержательное истолкование внутри - и межпредметных связей.
Итоги экспериментального исследования позволяют утверждать, что предлагаемые методические приемы при работе над сюжетной задачей на этапе моделирования оказывают существенное влияние на качество овладения учащимися математических знаний и развитие уровня их мышления. Показателем результативности разработанной методики является эффективность организации на ее основе дифференцированной работы с учащимися при поиске решения задачи, обладающими различными математическими способностями, а также профилактики неуспеваемости.,
В процессе исследования подтверждена научная гипотеза и получены следующие основные результаты:
1) выделение сюжетных задач как носителей специфических функций сюжета и поиска из совокупности текстовых математических заданий определяют их роль как важной логической компоненты в математическом образовании школьников и позволяет повысить эффективность проведения внутрипредметных и межпредметных связей.
2) Построение иерархической структуры сюжетных задач на основе выделения «характера определяющей зависимости» дает возможность определить в качестве генеральной идеи при организации работы по поиску их решения направленность на развитие у учащихся умений моделирования реальных процессов при последовательном приближении к более точному их описанию и разработать методику использования сюжетных задач для изучения дифференциальных уравнений в курсе начал математического анализа школы;
3) На основе изучения дидактических условий мыслительной деятельности по выработке стратегии поиска модели выделены методические приемы обучения решению сюжетных задач учащихся с различными математическими способностями. В качестве фактора успешности перехода в ориентировке данных при анализе сюжета задачи от иллюстративного к содержательному уровню обоснована способность мыслительной деятельности школьников по переносу знаний. Развитие этой способности тесно связано с глубиной понимания учащимися применения методов аналогии, сравнения, ограничения, обобщения;
4) рациональное включение сюжетных задач в процесс изучения те еретического материала способствует профилактике неуспеваемости учащихся на основе установления и развития обратной связи при обобщении их фактического опыта.
Апробация работы:
с сообщениями по теме исследования автор выступала на Зональной конференции (г. Свердловск), Герценовских чтениях в ЛГПИ им. А.И. Герцена, на конференциях и секциях учителей математики г. Свердловска и г. Березовского Свердловской обл. в соответствии с планом работы по программе "Педвуз-школа" в 1988/89 и 1989/90 учебных годах.
Основные положения диссертации отражены в публикациях:
1. Сюжетные задачи на дифференциальные уравнения в курсе математики средней школы /Метод. рек: Свердловск, 1987 12 с.
2. Соотношение формальных и неформальных этапов при решении сюжетных задач на дифференциальные уравнения в средней школе //Математический анализ. Вопросы теории, истории и методики преподавания. Сб. научи. тр: ЛГПИ, Л., 1988., 4с.
3. Решение сюжетных задач в 7-м классе /Метод, рек: Свердл. пед. ин-т, Свердловск, 1988, 15с.
4. Роль сюжетных задач школьного курса математики в формировании метода моделирования у учащихся средней школы //Актуальные вопросы истории и методики преподавания математического анализа/ Сб. научи, тр: ЛГПИ, Л., 1988 - Деп. в НИИВШ 16.02.89 М 36952 4с.
5. Проблема развития познавательной активности учащихся в историческом аспекте //Развитие познавательной деятельности учащихся при изучении математики /Уч. пос: .Свердл. пед. ин-т, Свердловск, 1988 (в соавторстве) 24 с.
В заключении автор выражает глубокую признательность заведующей кафедрой методики преподавания математики Свердловского пединститута кандидату педагогических наук, доценту Н.А. Шмаковой за серьезное внимание к исследованию и научные консультации, оказавшие неоценимую помощь в процессе выполнения работы.
Цели обучения математике
1. Ведущие цели обучения математике в школе. Три крупные группы
целей:
а) прогностические (обучающие);
б) мировоззренческие, направленные на воспитание математической
культуры (воспитательные и развивающие);
в) личностно-ориентированные (воспитательные в более узком смысле).
2. Требования к целям:
а) прогностические цели должны обладать - конкретностью,
конструктивностью, проверяемостью, участием ученика в процессе
учения;
б) мировоззренческие должны пронизывать весь учебный процесс,
выражать стремление к аргументации и четким логическим схемам
рассуждения, к четкому расчленению рассуждения и т.п.;
в) личностно-ориентированные должны учитывать формирование
возможных в том или ином возрасте качеств личности средствами
предмета.
3. Этапы формирования действия целеполагания у учащихся:
а) первый этап - учитель раскрывает структуру действия постановки
(полагания) цели;
б) второй этап - учитель привлекает детей к постановке цели и
критическому осмыслению полученных результатов при достижении
цели;
в) третий этап - учащиеся под руководством учителя конструируют
цель изучения конкретного учебного материала;
г) четвертый этап - учащиеся самостоятельно ставят цели, а классный
коллектив критически анализирует процедуру постановки цели и
достижения результата.
Цели обучения математике отражают общедидактические цели и
вместе с тем учитывают специфику данного учебного предмета.
Разработка целей обучения является непростым делом. В дидактике и
частных методиках в этом направлении сделаны определенные шаги.
Цели обучения математике подразделяются на несколько групп:
образовательные (в том числе-практические),
воспитательные, развивающие.
Образовательные цели обучения во многом зависят от принятой формы
дифференциации обучения. Основным документом, в котором
фиксируются цели обучения математике, является программа по
математике. Необходимо различать два уровня описания целей
обучения: общая характеристика целей обучения и
конкретное их представление. Общая характеристика целей
обучения дается в объяснительной записке к программе по математике.
Существуют различные способы конкретного представления целей
обучения. Образовательные цели, например, формулируются в виде
требований к уровню математической подготовки учащихся. В программе
по математике для этого выделяется специальный раздел "Требования к
математической подготовке учащихся". Другой раздел программы
"Содержание обучения" представляет образовательные цели в еще более
конкретной форме. Дальнейшей конкретизацией образовательных целей
служит учебник. Предельно конкретный уровень представления
образовательных целей имеет место в экзаменационных билетах для
учащихся, контрольных работах, предлагаемых Министерством общего и
профессионального образования. В методических пособиях часто
формулируются цели обучения для отдельных тем, уроков.
Образовательные цели призваны разграничить основной и
второстепенный материал и в соответствии с этим помочь учителю
рационально распределить учебное время.
Умение правильно формулировать цели уроков приходит к начинающему учителю не сразу. В период педагогической практики студенты нередко испытывают затруднения в постановке целей урока. При формулировании ими образовательной цели урока не всегда хватает четкости, конкретности (особенно в дифференциации целей "соседних" уроков). Иногда образовательная цель повторяет (или почти повторяет) название темы урока. Например, цель урока на тему "Первый признак равенства треугольников" чаще всего формулируется так: "Изучить первый признак равенства треугольников". Аналогично формулируются цели и в других случаях: "Изучить теорему Виета", "Изучить определение производной функции" и т.д. Во всех этих формулировках имеется общий недостаток: в них не уточняется, на каком уровне должен быть изучен данный элемент учебного материала. Необходимо указывать, когда ставится цель только ознакомить учащихся с тем или иным элементом учебного материала, когда - добиться хорошего воспроизведения учебного материала учащимся, а когда - заложить первоначальные умения и навыки и т. д. Еще большие затруднения начинающий учитель испытывает при постановке воспитательных и развивающих целей урока.
В некоторых методических руководствах имеются непосредственные указания, на каком уровне должен быть изучен тот или иной теоретический материал, в решении каких задач должны быть сформированы умения и навыки. Эти указания помогут начинающему учителю точнее формулировать цели урока.
Первым практическим навыком, которым должен овладеть студент, является навык безошибочной дифференциации целей обучения по трем группам (образовательные, воспитательные и развивающие). В изучении данного вопроса, приобретении соответствующих умений помогут следующие задания.
Несколько слов о постановке воспитательных целей. Они должны быть тесно связаны с содержанием урока. Это могут быть цели по формированию мировоззрения, сознательного отношения к учебе, развитию" познавательной и общественной активности, культуры учебного труда, воспитанию сознательности, расширению политехнического кругозора, подготовке к сознательному выбору профессии и т. д.
Развивающие цели должны находиться также в тесной связи с содержанием урока. Приведем примеры постановки развивающих целей:
развитие у учащихся навыков применения анализа, синтеза, сравнения, аналогии, индукции, дедукции, обобщения, конкретизации, моделирования классификации;
развитие у учащихся геометрической, алгебраической и числовой интуиции, пространственного представления и воображения, сообразительности, наблюдательности, памяти и т. д.
Назад к оглавлению | К началу главы
Взаимосвязь целей, содержания, форм и методов обучения математике
Цели, содержание и методы обучения взаимно связаны и обусловливают друг друга (при сохранении ведущей роли целей обучения). Из различных целей обучения наиболее подвижны и изменчивы образовательные цели. Следующие задания помогут подтвердить это положение и проиллюстрировать механизм взаимодействия целей, содержания и методов обучения.
Отдельно отметим воспитательные возможности исторического материала. Исторические экскурсы позволяют в доступной для учащихся форме раскрыть основу происхождения математических понятий и фактов. Они положительно сказываются на эмоциональном отношении учащихся к учебному материалу, на воспитании их моральных качеств и развитии интеллекта. Незаменимым средством при этом являются также старинные задачи, задачи с занимательным сюжетом, математические игры и т. п.
Остановимся на функциях компьютеризации обучения, являющейся одним из требований реформы школы. Первый шаг в осуществлении компьютеризации обучения заключается в использовании в школе микрокалькуляторов. В чем состоят образовательные, воспитательные и развивающие цели применения микрокалькуляторов на уроках математики? Прежде всего, очевидна практическая значимость применения микрокалькуляторов (коль скоро вычислительной техникой оснащается наука и производство).
Микрокалькулятор удобно использовать при введении, например, понятий длины окружности и площади круга. Вычислив 8-9 членов последовательности периметра (площадей) правильных вписанных n-угольников, учащиеся наглядно убеждаются в сходимости этих последовательностей. С помощью микрокалькулятора удобно организовать машинный эксперимент по обнаружению некоторых теорем (например, при изучении теоремы Виета, теоремы Пифагора, теоремы косинусов, теоремы синусов и т. д.).
Назад к оглавлению | К началу главы | Далее
Глава 3
Принципы дидактики в преподавании математики
Принципы обучения как категории дидактики. Принцип воспитания. Принцип направленности обучения на взаимосвязанное решение задач образования, воспитания и развития учащихся. Принцип научности. Принцип усиления прикладной направленности обучения. Принцип систематичности и последовательности. Принцип доступности. Принцип сознательности, активности, самостоятельности и прочности усвоения. Принцип наглядности. Принцип индивидуального подхода к учащимся. Принцип прочности знаний. Сущность каждого принципа, возможности его реализации. Конкретные примеры
-
Реализация дидактических принципов в обучении математике
-
Принципы обучения как категории дидактики
-
Принцип воспитания
-
Принцип направленности обучения на взаимосвязанное решение задач образования, воспитания и развития учащихся
-
Принцип научности
-
Принцип усиления прикладной направленности обучения
-
Принцип систематичности и последовательности
-
Принцип доступности
-
Принцип сознательности, активности, самостоятельности и прочности усвоения
-
Принцип наглядности
-
Принцип индивидуального подхода к учащимся
-
Принцип прочности знаний
Реализация дидактических принципов в обучении математике
Обучение математике, как и любому учебному предмету, может стать эффективным средством формирования личности, достичь непосредственной цели - прочного и сознательного усвоения ее содержания - лишь в случае, если в основу обучения будут положены определенные положения, вытекающие из основных закономерностей дидактики, подтвержденные опытом преподавания. Система таких положений, специально ориентированная на особенности математики как учебного предмета, и составляет основное содержание этой главы. В ней описываются наиболее важные принципы, характеризующие подход к обучению математике в школе, - принцип воспитания, принцип научности, принцип сознательности обучения, принцип систематичности и др. Владение этими принципами необходимо будущему учителю для того, чтобы правильно организовать свой труд, грамотно, квалифицированно анализировать различные учебные пособия, которыми ему придется пользоваться в своей работе.
Назад к оглавлению | К началу главы
Принципы обучения как категории дидактики
Процесс обучения, являясь составной частью целостного педагогического процесса, в советской школе направлен на формирование всесторонне и гармонически развитой личности.
Обобщенный опыт обучения школьников основам науки показывает, что для обеспечения единого подхода к учащимся, к выбору средств и методов учебной работы учитель должен придерживаться положений, носящих в определенном смысле универсальный характер.
В связи с этим в советской дидактике разработаны принципы, которые рассматриваются как важнейшие требования к организации процесса обучения, его содержанию, формам и методам. Эти единые требования .получили название дидактических принципов или принципов обучения. Организация процесса обучения в соответствии с дидактическими принципами позволяет построить его на научной основе.
Вместе с тем следует иметь в виду, что дидактические принципы, выражая определенные закономерности обучения и передовой опыт учебновоспитательной деятельности школы, не являются раз и навсегда установленными. Они постоянно углубляются и видоизменяются в соответствии с теми задачами, которые ставит перед школой общество.
Таким образом, дидактические принципы - это основные направляющие положения, возникающие в результате анализа научнопедагогических закономерностей и практического педагогического опыта. Они являются главным ориентиром в педагогической работе учителя.
Известные советские дидакты М. А. Данилов, И. Я. Лернер, М. Н. Скаткин в своих исследованиях показали, что принципы обучения, являясь категориями дидактики, характеризуют способы использования законов и закономерностей обучения в соответствии с целями воспитания и образования.
Дидактические принципы - это принципы деятельности, представляющие собой наиболее общее нормативное знание о том, как надо строить, осуществлять и совершенствовать обучение и воспитание. Закономерности этой деятельности являются теоретической основой для выработки норм учебно-воспитательной работы учителя. Однако сами по себе они не содержат конкретных указаний для такой деятельности. Эти указания дают принципы. Таким образом, принципы обучения взаимообусловлены его закономерностями. Например, принцип проблемности в обучении вытекает из закономерности, установленной С. Л. Рубинштейном, состоящей в том, что мышление возникает из проблемной ситуации и направлено на ее разрешение.
Однако, кроме законов и закономерностей обучения в становлении принципов, учитываются и другие факторы, а именно: 1) цели, которые ставит общество перед обучением и воспитанием; 2) конкретные условия, в которых осуществляется учебный процесс; 3) психологические характеристики процесса учения; 4) существующие способы конструирования учебных и воспитательных ситуаций.
Здесь следует заметить, что если речь идет не о дидактическом, а о методическом принципе, то в этом случае должна учитываться специфика конкретного учебного предмета и его функции в общем образовании.
Например, А. А. Столяр предлагает систему дидактических
принципов дополнить двумя принципами, характерными для обучения
математике:
1) школьный курс математики должен отражать фундаментальные идеи и
логику современной математики (в соответствии с уровнем
мыслительной деятельности учащихся);
2) процесс обучения математике должен строиться подобно процессу
исследования в математике, он должен имитировать процесс
творческого поиска в математике (в определенной мере, в какой это
допускает уровень мыслительной деятельности учащихся).
Первый принцип относится к построению содержания обучения математике и в определенной степени конкретизирует дидактический принцип научности. Второй принцип относится к построению процесса обучения и конкретизирует дидактический принцип проблемности обучения.
В методической литературе по математике общепризнанной является
следующая система дидактических принципов:
1. Принцип воспитания в обучении математике.
2. Принцип научности в обучении математике.
3. Принцип сознательности, активности и самостоятельности в
обучении математике.
4. Принцип систематичности и последовательности в обучении
математике.
5. Принцип доступности в обучении математике.
6. Принцип наглядности в обучении математике.
7. Принцип индивидуального подхода к учащимся в обучении
математике.
8. Принцип прочности знаний в обучении математике.
Назад к оглавлению | К началу главы
Принцип воспитания
Общей целью воспитания в школе является подготовка всесторонне развитых людей, способных построить и защитить общество. Всестороннее развитие личности предполагает умственное и нравственное развитие, политехническое образование и профессиональную подготовку, богатую духовную жизнь, физическое и эстетическое развитие. Реализация общей цели воспитания требует поэтому решения более частных задач, которые рассматриваются в качестве составных частей или сторон воспитания. Составными частями воспитания являются трудовое, нравственное, умственное, эстетическое и физическое воспитание.
Выделение составных частей воспитания опирается на объективные требования общества в развитии определенных свойств (качеств) личности. Так как свойства личности формируются не изолированно друг от друга, то и стороны воспитания, находясь во всеобщей взаимосвязи, способствуют формированию целостной личности. Поэтому такие качества целостной личности, как знание, умение, убеждение, поведение и др., могут быть составной частью каждой из указанных выше сторон воспитания.
Но воспитание в процессе обучения вообще и математике в частности как принцип обучения имеет и свою содержательную направленность. Содержательная направленность всех сторон воспитания в обучении определяется формированием коммунистического мировоззрения и морали. Формирование мировоззрения и морали - центральная задача воспитания. Под мировоззрением понимается система философских, научных, политических, нравственных и эстетических представлений и убеждений человека, которая отражает понимание человеком окружающей его природной и социальной среды, его отношение к ней и определяет общую направленность всей его деятельности.
Мораль - это совокупность норм, принципов и правил, регулирующих поведение людей во всех сферах общественной жизни. Воспитание мировоззрения и морали способствует формированию характера каждого школьника. Чтобы учащийся мог действовать в соответствии с принципами мировоззрения и морали, он должен сформировать у себя такие черты характера, как принципиальность, сила воли, скромность, честность по отношению к самому себе и другим людям.
Мировоззрение, базирующееся на научном знании и практическом жизненном опыте, связывает в единое целое эти свойства личности. Отсюда вытекают возможность и необходимость передачи всем людям знаний о закономерностях развития природы, общества и человеческого мышления, чтобы они могли сознательно осуществлять деятельность, направленную на построение общества.
Итак, принцип воспитания подрастающего поколения имеет своей целью воспитание в процессе обучения всесторонне развитой личности на основе формирования мировоззрения и морали.
Следовательно, в формировании убеждений возрастает роль процесса усвоения знаний. В связи с этим в преподавании математики (как и каждого учебного предмета) необходимо повышать активность учащихся и возбуждать у них интерес к вопросам, имеющим мировоззренческое значение. Важную роль в этом приобретает освещение в преподавании математики (также других предметов) новых идей современной науки.
Чтобы в обучении (в частности, математике) реализовывался принцип воспитания, учителю необходимо руководствоваться принципами научности, сознательности, активности и самостоятельности, стимулирования и мотивации положительного отношения школьников к учению и т. п.
Назад к оглавлению | К началу главы
Принцип направленности обучения на взаимосвязанное решение задач образования, воспитания и развития учащихся
При планировании содержания, средств, методов и форм обучения учитель призван обеспечить решение всего комплекса образовательных, воспитательных и развивающих задач
Назад к оглавлению | К началу главы
Принцип научности
Требование научности содержания образования было выдвинуто в советской педагогической литературе еще в работах Н. К. Крупской (см.: "О работе над новым учебником для новой программы").
Статус дидактического принципа требование научности в обучении приобрело с 1950 г., когда оно было сформулировано и обосновано М. Н. Скаткиным. Было показано, что воспитание человека коммунистического общества непосредственно связано с требованием научности содержания школьного образования.
В дальнейшем Л. Я- Зорина показала, что под научностью
содержания образования следует понимать такую его качественную
характеристику, которая удовлетворяет трем признакам:
а) соответствие содержания образования уровню современной
науки;
б) создание у учащихся верных представлений об общих методах
научного познания;
в) показ важнейших закономерностей процесса познания. Эти условия
взаимосвязаны между собой, ибо реализация каждого из последующих
обусловлена выполнением предыдущих. Каждое предыдущее условие
является необходимой базой для реализации последующего.
Первое условие говорит о том, что в соответствии с принципом научности образовательный материал, составляющий содержание школьного обучения, должен в определенной мере соответствовать уровню современной науки. Это требование принципа научности было с достаточной полнотой реализовано в процессе проведенной в последние годы модернизации обучения математике в школе.
Второе условие говорит о том, что принцип научности требует также знания общих методов научного познания. Но это лишь необходимое условие научности знаний. Оно недостаточно для создания у учащихся представлений о процессе познания. Одним из наиболее эффективных методов научного познания действительности в математике является построение математических моделей изучаемых явлений. Метод моделирования широко применяется сейчас в самых разнообразных областях знаний. Поэтому второе требование принципа научности естественным образом выдвигает на первый план обучение школьников доступным для них способам математического моделирования.
Третье условие указывает на то, что принцип научности требует формирования у учащихся представлении о процессе познания и его закономерностях.
В обучении математике у учителя имеется много возможностей показать учащимся закономерности процесса познания. Эти вопросы будут предметом специального рассмотрения в последующих главах. Именно поэтому в процессе обучения основам наук в школе шире должны внедряться проблемное обучение и разнообразные исследовательские приемы. В процессе реализации принципа научности учитель должен соблюдать также принцип доступности, чтобы содержание, формы и методы обучения учитывали реальные возможности учащихся. При этом необходимо учитывать и то, что принцип доступности предполагает обучение на достаточно высоком уровне трудности. Однако это можно достигнуть лишь при наилучшем сочетании индивидуальных и коллективных форм познавательной деятельности школьников в обучении.
Можно выделить три аспекта реализации принципа научности в обучении: 1) реализация его в учебнике (соответствие содержания учебника современному уровню науки); 2) обеспечение высокого научного уровня изложения учебного материала учителем на уроке; 3) выработка у учащихся учебно-исследовательских навыков и умений.
Принцип усиления прикладной направленности обучения
Изучение основ науки должно осуществляться в тесной связи с раскрытием важнейших их применений в промышленности, сельском хозяйстве и общественной жизни. При этом основы науки не должны подменяться ее приложениями.
Использование в обучении математических моделей реальных ситуаций, отбор содержания обучения, отвечающего поставленной цели, представляют собой основные средства реализации принципа связи обучения с жизнью. Важной составной частью этих средств являются задачи и примеры прикладного характера.
Назад к оглавлению | К началу главы
Принцип систематичности и последовательности
Нельзя овладеть наукой, не изучая ее в определенной системе. В такой же мере нельзя успешно развивать познавательные и творческие способности учащихся без строго продуманной системы их обучения и воспитания.
"Принцип систематичности и последовательности в обучении обусловливается и логикой самих наук, изучаемых в школе, и особенностями познавательной и практической деятельности учащихся. протекающей в соответствии с закономерностями их умственного и физического развития. Принцип систематичности и последовательности в обучении лежит в основе построения учебных программ, определяет систему работы учителя и деятельность учащихся в процессе обучения"
Принцип систематичности и последовательности в обучении проводится во всей системе учебной работы. Излагать знания систематически - это значит при изучении нового опираться на ранее пройденное, выделять в нем главное, вскрывать общую идею, формировать у учащихся умение анализировать, систематизировать и обобщать изучаемые явления и факты.
Важное значение принцип систематичности и последовательности приобретает в выработке у учащихся умений и навыков самостоятельной работы с книгой, в воспитании у них навыков организованности и последовательности в приобретении знаний.
Систематичность в обучении математике предполагает соблюдение определенной последовательности в изучении учебного материала н постепенное овладение основными понятиями школьного курса математики.
Принцип систематичности ориентирует учителя на достижение системности знаний в сознании учащихся путем установления теснейшей связи между элементами изучаемого материала, раскрытия единства элемента и структуры, части и целого. Следовательно, смысл принципа систематичности заключается в том, что учащиеся осознают приобретенные знания как элементы целостной, единой системы.
Сказанное позволяет утверждать, что научность обучения немыслима без систематичности, а с систематичностью тесно связан вопрос о преемственности в обучении. Ее характеризует опора на пройденное, дальнейшее развитие имеющихся у учащихся знаний, умений н навыков, установление связей между немыми и ранее приобретенными знаниями. В результате этого знания становятся прочными и глубокими.
Систематичность имеет место и в организационных приемах работы учителя - в системе его требований к учащимся. Систематичность должна быть также в учебной деятельности учащихся, в системе методов работы над каждым учебным предметом, в последовательности выполнения домашних заданий и т. п.
Последовательность в обучении математике означает, что обучение осуществляется в соответствии с правилами обучения: а) от простого к сложному; б) от легкого к трудному; в) от известного к неизвестному; г) от представлений к понятиям; д) от знания к умению, а от него к навыку.
Учитель реализует этот принцип, если обучение математике представляет собой цепочку последовательных шагов, каждый из которых последовательно дополняет известные учащимся знания, умения и навыки разумной дозой новых знаний, умений и навыков.
В заключение отметим, что успешная реализация принципа систематичности и последовательности в обучении во многом зависит от того, какое значение придается учителем межпредметным связям в обучении, как скоординированы требования к учащимся между преподавателями различных учебных предметов, соблюдается ли преемственность в изучении отдельных тем и учебных предметов. При этом важное значение приобретает преемственность обучения в младших, средних и старших классах.
Систематические знания характеризуются как знания о научных основах учебного предмета. Они формируются на основе усвоения понятий и фактов в определенной логической последовательности. Наиболее полное свое выражение этот принцип находит в систематических курсах математики. Можно выделить три вида систематизации учебного материала: целевая, логическая и психологическая. В качестве методов систематизации широко применяются индуктивные и дедуктивные методы, аналогия, обобщение, конкретизация и др. Встречаются попытки "ревизии" принципа систематичности, которые выражаются в отказе от изложения в среднем звене обучения основ науки. (Такая идея высказана, например, М. М. Постниковым.) В отдельных странах (например, в Англии, Швеции, Финляндии), по существу, отказались от систематического курса геометрии. Это обстоятельство не замедлило отрицательно сказаться на уровне логического развития учащихся, на их возможностях в усвоении курса математики.
Различают еще системные знания. Они характеризуются, прежде всего, как методологические знания основ научной теории. Одним из средств формирования системных знаний является включение в учебник сведений о математической теории и способах ее построения.
Назад к оглавлению | К началу главы
Принцип доступности
Принцип доступности в обучении вытекает из требований учета возрастных особенностей учащихся. Он лежит в основе составления учебных планов и программ.
Принцип доступности требует, чтобы объем и содержание учебного материала были по силам учащимся, соответствовали уровню их умственного развития и имеющемуся запасу знаний, умений и навыков.
Доступность не следует понимать как учение без трудностей. Она не исключает приучение учащихся к преодолению трудностей в учебной деятельности. Это понятно, так как учебная работа требует определенных усилий учащихся в достижении поставленных целей. Суть вопроса заключается не в том, чтобы обходить трудности, а в том, чтобы эти трудности не подрывали, а развивали силы ученика и способствовали повышению результатов учебных занятий.
Реализация принципа доступности предполагает выполнение следующих условий - дидактических правил: а) следовать в обучении от простого к сложному; б) от легкого к трудному; в) от известного к неизвестному.
Отсюда следует, что строгое соблюдение в обучении принципа систематичности и последовательности предопределяет успешную реализацию принципа доступности.
Следовать в обучении от простого к сложному означает, что изучение учащимися фактов, явлений, закономерностей, понятий и т. п. должно начинаться с наиболее простых, с тем чтобы подготовить их к пониманию более сложных. Это положение касается как теоретического, так и практического учебного материала.
Принцип доступности в обучении привлекает к себе особое внимание также в связи с проблемой индивидуального подхода к учащимся и условиях массового обучения.
Принцип доступности требует, чтобы обучение строилось на основе учета возрастных возможностей учащихся. С его помощью регулируется уровень сложности учебного материала, определяется выбор методических подходов изложения его на уроке, правильная дозировка домашних заданий. Слишком упрощенное содержание обучения снижает его развивающие и воспитательные возможности. Поэтому рекомендуется (по Л. В. Занкову), чтобы содержание заданий для учащихся находилось в "зоне их ближайшего развития".
Принцип сознательности, активности, самостоятельности и прочности усвоения
Данный принцип заключается в целенаправленном активном восприятии изучаемых явлений, их осмыслении, творческой переработке и применении. Он вытекает из целей и задач средней школы, призванной готовить активных и самостоятельных членов общества, а также из особенностей процесса обучения, требующего осмысленного и творческого подхода к изучаемому материалу.
Реализация принципа сознательности, активности и
самостоятельности в обучении предполагает выполнение следующих
условий:
а) соответствие познавательной деятельности учащихся
закономерностям процесса учения;
б) познавательная активность учащихся в процессе учения;
в) осознание школьниками процесса учения;
г) владение учащимися методами умственной работы в процессе
познания "нового".
Остановимся кратко на сущности этой совокупности условий. Учебное познание есть учение, т. е. деятельность учащихся по усвоению новых знаний и способов деятельности. Следовательно, говоря об усвоении, мы имеем в виду познавательную деятельность учащихся (процесс учения), но всегда в единстве с руководящей, обучающей ролью учителя и содержанием учебного материала с учетом его структуры.
Отсюда следует, что сущность процесса обучения в целом и его составной части - учения (усвоения) заключается в том, что этот процесс вытекает из общего хода процесса познания и его закономерностей. В соответствии с ним дидактика выделяет в процессе усвоения диалектически взаимосвязанные этапы познавательной деятельности учащихся: восприятие - осмысление - закрепление - применение.
Если в процессе познания нового учащиеся будут совершать умственные и практические действия в соответствии с выделенными этапами процесса учения, включающими в себя действия по восприятию изучаемого материала, его осмыслению (пониманию), закреплению и применению, то можно утверждать, что в обучении созданы условия для активизации познавательной деятельности учащихся и осознания ими процесса учения.
Здесь следует обратить внимание на три обстоятельства. Во-первых, процесс познавательной деятельности в каждом отдельном случае не обязательно проходит по всем этапам учебного познания и в указанной последовательности. Например, при дедуктивном рассуждении учащимся нет необходимости проходить этап восприятия изучаемых явлений и формирования соответствующих представлений. Так, при усвоении нового знания о том, что всякое сечение шара плоскостью есть круг, учащимся предлагается конкретный факт - данная плоскость пересекает шар - и общее правило относительно всех плоскостей, пересекающих шар, - всякое сечение шара плоскостью есть круг.. Применив это общее правило к конкретному факту, учащиеся приходят к одному и тому же выводу: "Следовательно, данное сечение есть круг". Во-вторых, выделенные выше четыре условия реализации принципа сознательности, активности и самостоятельности не являются независимыми. Выполнение первого условия означает выполнение остальных. Однако выделение такой совокупности условий раскрывает дидактический механизм действия самого принципа, что важно и необходимо знать учителю. В-третьих, чтобы в обучении было установлено соответствие познавательной деятельности учащихся закономерностям процесса учения (первое условие), необходима целенаправленная деятельность учителя по формированию у учащихся ответственного отношения к приобретению и усвоению знаний, их осмысливанию и практическому применению. Только в результате такой управляющей деятельности учителя можно говорить о реализации принципа сознательности, активности и самостоятельности учащихся в обучении.
Сознательность понимается в дидактике как овладение учащимися данными науки, учебным материалом, глубокое осмысление его, умение пользоваться знаниями на практике в новых условиях, превращение знаний в убеждения, в руководство к действию.
В процессе сознательного усвоения знаний формируется творческое отношение к изучению и применению знаний, логическое мышление учащихся и их мировоззрение. Сознательное усвоение знаний исключает догматическое, при котором учащиеся принимают на веру преподносимые учителем знания. Результатом догматического усвоения является формализм знаний. Основными признаками формализма знаний являются отсутствие конкретных представлений об изучаемых явлениях; запоминание без понимания, без умения творчески применять знания на практике; безынициативность; отсутствие высоких общественных идеалов, глубоких убеждений и готовности бороться за них.
Конкретно в обучении математике формализм в знаниях особенно часто проявляется в том, что учащиеся безошибочно дают формулировку определения того или иного понятия, но не могут им воспользоваться при решении задач, доказательстве теорем.
В теории обучения выявлены признаки осознанности знаний,
которыми может руководствоваться учитель в процессе обучения. К ним
относится следующая совокупность признаков:
а) понимание учащимися характера связей между знаниями
(рядоположности и соподчиненности, степени их существенности);
б) понимание механизма становления и проявления связей;
в) умение обосновывать знания;
г) понимание способов получения знаний и сферы их применения.
Сознательное обучение обязательно предполагает активную
деятельность учащихся в этом процессе.
Активность есть деятельное состояние учащегося, которое характеризуется стремлением к учению, умственным напряжением и проявлением волевых усилий в процессе овладения знаниями. Такую активность учащихся в обучении называют познавательной активностью.
В учебном процессе активность учащихся получает свое выражение не только в работе мысли, но и в практической деятельности, в общественной работе, в волевом напряжении и в эмоциональных переживаниях.
Умственная активность учащихся в процессе обучения математике имеет особо важное значение при формировании понятий. Поэтому учителю необходимо владеть методическими приемами, возбуждающими мыслительную активность учащихся в этом процессе.
Активность учащихся в обучении проявляется в их инициативности и высокой степени самостоятельности (или познавательной самостоятельности).
Познавательная самостоятельность является высшей формой активности и сознательности учащихся в процессе учения. Поэтому осуществление в обучении сознательного и активного процесса учения неизбежно формирует такое важное качество личности, как познавательная самостоятельность, которая является важнейшей характеристикой деятельности школьника в учебном процессе.
В теории обучения выделены признаки познавательной самостоятельности учащихся. К ним относятся стремление и умение самостоятельно мыслить; способность ориентироваться в новой ситуации, найти свой подход к решению новой задачи; желание понять не только усваиваемые знания, но и способы их добывания; критический подход к суждению других; независимость собственных суждений. Большое значение в плане формирования познавательной активности и самостоятельности учащихся имеют самостоятельные работы. Самостоятельные работы являются формой совместной единой деятельности учителя и учащихся. Выполняя самостоятельную работу, учащиеся активно оперируют приобретенными знаниями, умениями и навыками, совершают поисковую деятельность. Поэтому в этой самостоятельной деятельности учащегося укрепляются и взаимообусловливаются его познавательная активность и самостоятельность, а такая деятельность отличается высоким уровнем сознательности.
Если в результате обучения учащиеся приобрели такое качество личности, как познавательная самостоятельность, то можно утверждать, что на всех этапах учебного познания реализовывался дидактический принцип сознательности, активности и самостоятельности в обучении.
Сознательное усвоение характеризуется: пониманием изученного, осознанием путей получения нового знания, умением применять знания.
Применение знаний связано с "переносом" их в те или иные ситуации. Возможность осуществления учащимися переноса более высокого уровня (на более отдаленную, необычную, существенно отличающуюся от первоначальной новую ситуацию) свидетельствует о высокой степени сознательности усвоения.
Сознательное усвоение помогает избежать формализма в знаниях. Различаются два вида формализма (по Я. С. Дубнову):
1) ученик не видит связи математических понятий и фактов с реальным миром - формализм первого вида;
2) ученик воспроизводит определение, но не понимает его смысла (например, формулирует определение логарифма, но не может найти log100) - формализм второго вида.
Прочность усвоения может быть обеспечена четким выделением главного в учебном материале, выявлением внутренних и внешних связей изучаемого материала (например, с помощью логико-структурных схем), продуманной системой повторения и применения знаний, дифференцированным подходом к объяснению наиболее сложных мест учебного материала.
Назад к оглавлению | Назад | Далее
Принцип наглядности
Теоретическое обоснование принципу наглядности впервые было дано чешским педагогом Я.А. Коменским, который выдвинул требование учить людей познавать самые вещи, а не только чужие свидетельства о них.
Русский педагог К.Д. Ушинский указывал, что наглядность отвечает психологическим особенностям детей, мыслящих "формами, звуками, красками, ощущениями". Наглядное обучение, по словам К. Д. Ушинского, "строится не на отвлеченных представлениях и словах, а на конкретных образах, непосредственно воспринятых ребенком". Наглядность обогащает круг представлений ребенка, делает обучение более доступным, конкретным и интересным, развивает наблюдательность и мышление.
Принцип наглядности вытекает из сущности процесса восприятия, осмысления и обобщения учащимися изучаемого материала. Он означает, что в обучении необходимо, следуя логике процесса усвоения знаний, на каждом этапе обучения найти его исходное начало в фактах и наблюдениях единичного или в аксиомах, научных понятиях. и теориях, после чего определить закономерный переход от восприятия единичного, конкретного предмета к общему, абстрактному или, наоборот, от общего, абстрактного к единичному, конкретному. Таким образом, советская дидактика исходит из единства чувственного и логического, считает, что наглядность обеспечивает связь между конкретным и абстрактным, содействует развитию абстрактного мышления, во многих случаях служит его опорой. Однако характер и степень использования наглядности различны на разных этапах обучения. Излишнее увлечение наглядностью в обучении может привести к нежелательным результатам. Конкретная наглядность (например, рассмотрение моделей геометрических тел) должна постепенно уступать место абстрактной наглядности (рассмотрению плоских чертежей).
Говоря о значении принципа наглядности и о его роли в процессе учебного познания, дидактика утверждает, что наглядность является исходным моментом обучения главным образом в младших классах. По мере движения учащихся к старшим классам учитель постепенно должен находить в обучении историко-индуктивный путь пополнения знаний: постановка проблемы, история ее решения и современное состояние, затем практические или лабораторные работы. Здесь наглядность получает свою реализацию дважды: как иллюстрация истории открытия и как способ раскрытия современного решения проблемы.
Однако исторический подход занимает много времени и не всегда необходим. Поэтому исходным началом могут быть теоретические положения, аксиомы, системы понятий, усвоенные учащимися на предшествующих этапах обучения. В этом случае наглядность используется лишь для иллюстрации усвоенных учащимися знаний в процессе их применения к решению задач. По характеру отражения окружающей действительности различают следующие виды наглядности:
натуральная (естественная) наглядность, представляющая собой реальные предметы или процессы (объекты и явления, раздаточный материал и др.);
изобразительная наглядность (фотографии, художественные картины, рисунки, учебные картины и др.) применяется, когда показ натурального предмета затруднен, а созерцание конкретного образа необходимо;
символическая наглядность (чертежи, графики, схемы, таблицы, диаграммы) по существу является своеобразным языком, а потому должна специально изучаться, чтобы стать понятной. Например, при изучении свойств функций (возрастание, убывание, максимум, минимум и др.) целесообразно их аналитическую запись переводить на язык графиков и на этой основе тренировать учащихся "читать" графики функций.
Различные виды наглядности выполняют различные функции. Одни содействуют оживлению представлений (картины, предметы жизни), другие являются опорой для отвлеченного мышления.
Наглядность применяется и как средство познания нового, и для иллюстрации мысли, и для развития наблюдательности, и для лучшего запоминания материала. Средства наглядности используются на всех этапах процесса обучения: при объяснении нового материала учителем, при закреплении знаний, формировании умений и навыков, при выполнении домашних заданий, при контроле усвоения учебного материала.
Применение наглядных пособий в обучении подчинено ряду правил: ориентировать учащихся на всестороннее восприятие предмета с помощью разных органов чувств;
обращать внимание учащихся на самые важные, существенные признаки предмета;
показать предмет (по возможности) в его развитии; предоставить учащимся возможность проявлять максимум активности и самостоятельности при рассмотрении наглядных пособий;
использовать средств наглядности ровно столько, сколько это нужно, не допускать перегрузки обучения наглядными пособиями, не превращать наглядность в самоцель.
Следовательно, умелое применение средств наглядности в обучении всецело находится в руках учителя. Учитель в каждом отдельном случае должен самостоятельно решать, когда и в какой мере надо применять наглядность в процессе обучения, ибо от этого в определенной степени зависит качество знаний учащихся.
Принцип наглядности, по выражению Я. А. Коменского, является "золотым правилом дидактики". Он требует сочетания наглядности и мысленных действий, наглядности и слова. Вредным является как недостаточное, так и избыточное применение средств наглядности. Их недостаток приводит к формальным знаниям, а избыток может затормозить развитие логического мышления, пространственного представления и воображения. Встречаются примеры нетрадиционного применения принципа наглядности.
Назад к оглавлению | К началу главы
Принцип индивидуального подхода к учащимся
Повышение эффективности обучения непосредственно связано с тем, насколько полно учитываются особенности каждого учащегося. Важной индивидуальной особенностью учащихся является их способность к усвоению знаний, т. е. обучаемость. Под влиянием возрастающих требований жизни увеличивается объем и усложняется содержание знаний, подлежащих усвоению в школе. Чем глубже развивается этот процесс, тем более четко выступают индивидуальные различия в обучаемости школьников.
Как показали многочисленные психолого-дидактические исследования, если уровнять многие факторы, влияющие на уровень усвоения новых знаний, а именно: обеспечить одинаковый исходный минимум знаний у всех учащихся, положительное отношение их к уроку, желание как можно лучше усвоить материал, тщательно разработать методику введения нового материала, то, несмотря на равенство этих условий, новые знания будут усвоены поразному. Одни школьники достаточно полно усвоят новое и могут применить его в новых, но сходных с учебной обстановкой условиях, требующих самостоятельного развития новых знаний (высший уровень усвоения). Другие усвоят существенные стороны нового понятия или закономерности и сумеют применить их к решению задач, близких к тем, которые разбирались в процессе объяснения нового материала (средний уровень усвоения). Наконец, будут и такие, кто вынес лишь отдельные, нередко несущественные стороны нового понятия или закономерности и не может применить их к решению даже простых задач (низший уровень усвоения). При этом потребуется различное количество упражнений и различная мера помощи со стороны учителя тем учащимся, которых предстоит довести до высшего уровня усвоения.
В психологии обучения выявлено несколько характеристик индивидуальных различий учащихся, связанных с понятием обучаемости. К ним относятся: а) темп усвоения или продвижения в обучении как наиболее устойчивая характеристика; б) полнота и точность анализа и синтеза и неразрывно связанных с ними обобщения и абстрагирования; в) устойчивая предрасположенность школьников к тому или иному виду анализа, особенно при первичной работе над материалом; г) уровень формируемых у школьника обобщений; д) уровень выделения и обобщения школьниками способов оперирования знаниями; е) экономичность мышления и др.
Следует заметить, что предпоследняя (указанная здесь) сторона мыслительной деятельности позволила психологам сделать предположение о том, что не всякое усвоение знаний означает сдвиг в умственном развитии учащегося. Этот сдвиг происходит тогда, когда обучение обеспечивает овладение не только содержанием знаний, но и методами, способами их приобретения, благодаря чему учащиеся могут самостоятельно приобретать новые знания.
Отмеченные выше явления, имеющие место в обучении школьников, показали невозможность создать в обучении систему, равно оптимальную для каждого учащегося. Это обстоятельство привело к необходимости реализации в обучении принципа индивидуального подхода к учащимся. Сущность принципа индивидуального подхода по существу состоит в адаптации (приспособлении) обучения либо к содержанию и уровню знаний, умений и навыков каждого учащегося, либо также к характерным для него особенностям процесса усвоения, либо даже к некоторым устойчивым особенностям его личности. Основным средством реализации принципа индивидуального подхода являются индивидуальные самостоятельные работы, предназначенные для учащихся. Они выступают в качестве специфического дидактического средства организации и управления самостоятельной деятельностью учащихся на всех этапах обучения.
Назад к оглавлению | К началу главы
Принцип прочности знаний
Принцип прочности знаний обусловливается как задачами школы, так и закономерностями процесса обучения. Опираться на приобретенные знания, умения и навыки можно лишь в том случае, когда они усвоены твердо и длительное время удерживаются в памяти.
Прочные знания, умения и навыки необходимы как для успешного продолжения образования, так и для формирования у учащихся научного мировоззрения, развития их способностей, подготовки к практической деятельности.
В дидактике сформулированы условия прочности знаний. К ним относятся:
активное приобретение знаний с целью сознательного их усвоения; научность обучения;
создание в обучении условий для запоминания учебного материала.
Содержание и сущность принципов научности и сознательности в обучении было раскрыто выше. Поэтому рассмотрим некоторые основы механизма запоминания в процессе обучения.
Запоминание есть процесс памяти, в результате которого происходит закрепление нового путем связывания его с ранее приобретенным. Запоминание всегда избирательно: в памяти сохраняется не все, что оказывает воздействие на органы чувств индивида. От чего это зависит? Запоминание является закономерным продуктом действия субъекта с объектом, т. е. запоминается то, с чем человек действует. При этом успешность запоминания учебного материала определяется мотивами, целями и способами деятельности личности. Назовем основные условия запоминания материала в обучении: учебный материал запоминается учащимися лучше, если он входит в содержание основной цели деятельности. Например, если целью действий учащихся является выявление свойств той или иной геометрической фигуры, то их запоминание будет лучшим, нежели в том случае, когда свойства фигуры сообщаются непосредственно учителем; учебный материал запоминается лучше, если он вызывает активную умственную работу над ним. Поэтому материал более трудный запоминается лучше, чем легкий, так как связи между элементами трудного текста являются более содержательными.
Глава 4
Методы обучения математике
Сущность и роль проблемы методов в современном обучении математике. Понятие метода обучения. Методы преподавания и методы обучения. Условия успешного применения различных методов обучения
-
Методы обучения, выделяемые по источнику знаний
-
Словесные методы обучения
-
Наглядные методы обучения
-
Практические методы обучения
-
-
Методы обучения, определяемые уровнем познавательной деятельности учащихся
К методам этой группы относятся репродуктивные, проблемно-поисковые и самостоятельная работа учащихся.
В практике многих учителей широко используется самостоятельная работа учащихся. Она проводится почти на каждом уроке в пределах 7-15 мин. Первые самостоятельные работы по теме носят в основном обучающий и корректирующий характер. С их помощью осуществляется оперативная обратная связь в обучении: учитель видит все недостатки в знаниях учащихся и своевременно устраняет их. От занесения в классный журнал оценок "2" и "3" можно пока воздержаться (выставляя их в тетради или дневнике учащегося). Если самостоятельная работа носит контролирующий характер, то в журнал выставляются все оценки. Такая система оценивания является достаточно гуманной, хорошо мобилизует учащихся, помогает им лучше осмысливать свои затруднения и преодолевать их, способствует повышению качества знаний. Учащиеся оказываются лучше подготовленными к контрольной работе, у них исчезает страх перед такой работой, боязнь получить двойку. Количество неудовлетворительных оценок, как правило, резко сокращается. У учащихся вырабатывается положительное отношение к деловой, ритмичной работе, рациональному использованию времени урока.
О сочетании методов обучения
-
Проблемное обучение математике.
Общая характеристика проблемного обучения. Проблемное изучение нового материала. Проблемы обучения при решении задач. Виды учебной работы школьников в условиях проблемного обучения. Контроль и оценка поисковой деятельности учащихся в условиях проблемного обучения, роль отметки
-
Методы проблемного обучения
-
Исследовательский метод
-
Метод проблемного изложения
Эвристический метод обучения математике
Сущность эвристики. Роль эвристической деятельности в науке и практике обучения математике. Эвристическая беседа. Достоинства и недостатки эвристического метода обучения математике
Эвристика - молодая научная дисциплина, возникшая на стыке таких наук, как философия, кибернетика, психология и педагогика. Специалисты каждой из этих наук рассматривают эвристику со своих позиций, придают своеобразное толкование ее основным понятиям и положениям.
Так, кибернетики считают, что эвристика - методы и способы, связанные с улучшением эффективности системы (человека или машины), решающей задачи. Психологи считают эвристику разделом психологии, изучающим творческое мышление. Педагоги считают эвристикой науку о средствах и методах решения задач. Философы термин "эвристический" приписывают таким правилам или утверждениям, которые способствуют открытию нового.
В последние годы к эвристике относят и те исследования представителей кибернетики, которые пытаются моделировать высшие проявления интеллекта. Уже и сейчас проблемы эвристики разрабатываются инженерами и математиками, психологами и физиологами, педагогами и организаторами производства. Все же основой эвристики является психология, особенно тот ее раздел, который получил название психологии творческого, или продуктивного, мышления.
Эвристическая деятельность или эвристические процессы, хотя и включают в себя умственные операции в качестве важного своего компонента, вместе с тем обладают некоторой спецификой. Именно поэтому эвристическую деятельность следует рассматривать как такую разновидность человеческого мышления, которая создает новую систему действий или открывает неизвестные ранее закономерности окружающих человека объектов (или объектов изучаемой науки).
Попытки проникнуть в механизм этого процесса, раскрыть его закономерности предпринимали и предпринимают многие исследователи в различных отраслях науки.
В эвристике, как молодой, развивающейся науке, не все понятия достаточно четко определены. Это прежде всего относится к понятию "эвристический метод". Многие исследователи понимают под ним определенный эффективный, но недостаточно надежный способ решения задач. Он позволяет ограничивать перебор вариантов решения, т. е. сокращать число вариантов, изучаемых перед тем, как выбрать окончательное решение. Понятно, что это определение понятия "эвристический метод" не может быть признано удовлетворительным, так как в нем представлена лишь внешняя характеристика явления, но не раскрыты существенные его черты.
Чтобы раскрыть существо этого понятия, необходимо иметь в виду, что сам термин "эвристический" применим к явлениям двоякого рода. Во-первых, можно рассмотреть как эвристическую такую деятельность человека, которая приводит к решению сложной, нестандартной задачи, во-вторых, эвристическими можно считать и специфические приемы, которые человек сформировал у себя в ходе решения одних задач и более или менее сознательно переносит на решение других задач.
Эвристические приемы как готовые схемы действия составляют объект эвристической логики, а реальный процесс эвристической деятельности - объект психологии. Но если эвристические приемы могут быть представлены в виде определенной логической схемы, т. е. могут быть описаны математическим языком, то эвристическая деятельность на современном этапе развития науки не имеет своего математического выражения.
Начало применения эвристического метода как метода обучения - математике можно найти еще в книге известного французского педагога - математика Лезана "Развитие математической инициативы". В этой книге эвристический метод не имеет еще современного названия и выступает в виде советов учителю. Вот некоторые из них:
Основной принцип преподавания - "сохранять видимость игры, уважать свободу ребенка, поддерживая иллюзию (если есть таковая) его собственного открытия истины"; "избегать в первоначальном воспитании ребенка опасного искуса злоупотреблением упражнениями памяти", ибо это убивает его врожденные качества; обучать, опираясь на интерес к изучаемому.
Лезан приводит множество примеров, наглядно показывая, как сделать обучение математике более эффективным, опираясь на явную заинтересованность учащихся процессом обучения.
Эвристический метод обучения рассматривался в русской школе с начала XIX в. Многие русские педагоги-математики того времени не раз пересматривали традиционные методы обучения, представлявшиеся им устаревшими, не отвечающими основным задачам математического образования.
На необходимость пересмотра традиционной программы обучения в русской школе указывал, в частности, известный педагог-математик С. И. Шохор-Троцкий. В книге "Геометрия на задачах" он писал, что нельзя излагать учащихся данный раздел математики в совершенно готовом виде. Поступать так - значит идти вразрез с основными принципами обучения и воспитания. В частности, он указывал, что "занятия геометрией могут быть для ученика занимательны только тогда, когда они требуют от него посильного и планомерного труда... требуют умственной работы, а не заучивания слов на память".
Большое значение эвристическому методу обучения в школе придавал другой русский педагог-математик Н. А. Извольский. В книге "Комбинационная работа" он писал, что "главной задачей обучения является развитие творческих способностей".
Известный методист-математик В. М. Брадис определяет эвристический метод следующим образом: "Эвристическим называется такой метод обучения, когда руководитель не сообщает учащимся готовых, подлежащих усвоению сведений, а подводит учащихся к самостоятельному переоткрытию соответствующих предложений и правил"
Определение эвристического метода преподавания дается также В. В. Репьевым. Только название метода здесь звучит несколько иначе - эвристическая беседа. "... Этот метод состоит в том, что учитель ставит перед классом проблему (теорему, задачу), а затем путем целесообразных вопросов приводит учащихся к решению проблемы".
Но суть этих определений одна - самостоятельный, планируемый лишь в общих чертах поиск решения поставленной проблемы.
Роль эвристической деятельности в науке и в практике обучения математике подробно освещается в книгах американского математика Д. Пойа. В книге "Как решать задачу". Д. Пойа пытается охарактеризовать эвристику как специальную отрасль знания. Цель эвристики - исследовать правила и методы, ведущие к открытиям и изобретениям. Интересно, что основным методом, с помощью которого можно изучить структуру творческого мыслительного процесса, является, по его мнению, исследование личного опыта в решении задач и наблюдение за тем, как решают задачи другие. Автор пытается вывести некоторые правила, следуя которым можно прийти к открытиям, не анализируя той психической деятельности, в отношении которой предлагаются эти правила. "Первое правило - надо иметь способности, а наряду с ними удачу. Второе правило - стойко держаться и не отступать, пока не появится счастливая идея". Интересна приводимая в конце книги схема решения задач. Схема указывает, в какой последовательности нужно совершать действия, чтобы добиться успеха. Она включает четыре этапа:
1. Понимание постановки задачи.
2. Составление плана решения.
3. Осуществление плана.
4. Взгляд назад (изучение полученного решения).
В ходе выполнения этих этапов решающий задачу должен ответить на следующие вопросы: Что неизвестно? Что дано? В чем состоит условие? Не встречалась ли мне раньше эта задача, хотя бы в несколько другой форме? Есть ли какая-нибудь родственная данной задача? Нельзя ли воспользоваться ею?
Нетрудно видеть, что эта схема подчеркивает главным образом один принцип эвристической деятельности: использование в том или ином виде прошлого опыта. Но этот принцип не может считаться единственным в структуре творческой мыслительной деятельности. Понятно, что многие весьма важные компоненты продуктивного мышления в работах Д. Пойа и не могут выступить с должной отчетливостью, так как речь у него идет об учебных, а не о чисто творческих задачах.
Близка точке зрения Д. Пойа та характеристика эвристической деятельности, которая дается известным американским психологом Д. Брунером в его книге "Процесс обучения". Эвристические приемы характеризуются Д. Брунером как некоторые не вполне точные способы решения задач, с помощью которых можно прийти, а можно и не прийти к нужному результату. У Брунера понятие "эвристический" служит для характеристики лишь приемов, помогающих решать задачу, как и у Д. Пойа. Д. Брунер не исследует эвристическую деятельность человека как процесс, приводящий к формированию приемов или схемы действий. Между тем обучение деятельности - это значительно более сложная и вместе с тем гораздо более важная проблема, чем обучение готовым, сложившимся приемам решения задач.
Весьма интересна с точки зрения применения эвристического метода в школе книга американского педагога У. Сойера "Прелюдия к математике".
"Для всех математиков, - пишет Сойер, - характерна дерзость ума. Математик не любит, когда ему о чем-нибудь рассказывают, он сам хочет дойти до всего"
Эта "дерзость ума", по словам Сойера, особенно сильно проявляется у детей.
"Если вы, например, преподаете геометрию 9-10-летним ребятам, - говорит Сойер, - и рассказываете, что никто еще не смог разделить угол на три равные части при помощи линейки и циркуля, вы непременно увидите, что один-два мальчика останутся после уроков и будут пытаться найти решение. То обстоятельство, что в течение 2000 лет никто не решил эту задачу, не помешает им надеяться, что они смогут это сделать в течение часового перерыва на обед. Это, конечно, не очень скромно, но и не свидетельствует об их самонадеянности. Они просто готовы принять любой вызов. А ведь в действительности уже доказано, что невозможно разделить угол на три равные части при помощи линейки и циркуля. Их попытка найти решение - того же рода, что попытка представить "корень из двух" в виде рациональной дроби p/q
Хороший ученик всегда старается забежать вперед. Если вы ему объясните, как решать квадратное уравнение дополнением до полного квадрата, он непременно захочет узнать, можно ли решить кубическое уравнение дополнением до полного куба. Вот это желание исследовать является отличительной чертой математика. Это одна из сил, содействующих росту математика. Математик получает удовольствие от знаний, которыми он уже овладел, и всегда стремится к новым знаниям".
Другим необходимым качеством математика является интерес к закономерностям. Закономерность - это наиболее стабильная характеристика постоянно меняющегося мира. Сегодняшний день не может быть похожим на вчерашний. Нельзя увидеть дважды одно и то же лицо под одним и тем же углом зрения. Закономерности встречаются уже в самом начале арифметики. В таблице умножения имеется немало элементарных примеров закономерностей. Вот один из них. Обычно дети любят умножать на 2 и на 5, потому что последние цифры ответа легко запомнить: при умножении на 2 всегда получаются четные цифры, а при умножении на 5, еще проще, всегда 0 или 5. Но даже в умножении на 7 есть свои закономерности. Если мы посмотрим последние цифры произведений 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, т.е. на 7, 4, 1, 8, 5, 2, 9, 6, 3, 0, то увидим, что разность между последующей и предыдущей цифрами составляет:-3; +7;-3;-3; +7; -3; -3, -3. В этом ряду чувствуется совершенно определенный ритм.
Если прочесть конечные цифры ответов при умножении на 7 в обратном порядке, то мы получаем конечные цифры от умножения на 3. Даже в начальной школе можно развить навык наблюдения за математическими закономерностями.
В книге "Прелюдия к математике" Сойер приводит много примеров наблюдений закономерностей и в арифметике, и в алгебре, и в геометрии. Итак. одним из основных методов, который позволяет учащимся проявить творческую активность в процессе обучения математике, является эвристический метод. Грубо говоря, этот метод состоит в том, что учитель ставит перед классом некоторую учебную проблему, а затем путем после-довательно поставленных заданий "наводит" учащихся на самостоятельное обнаружение того или иного математического факта. Учащиеся постепенно, шаг за шагом, преодолевают трудности в решении поставленной проблемы и "открывают" сами ее решение.
Известно, что в процессе изучения математики школьники часто сталкиваются с различными трудностями. Однако в обучении, построенном эвристически, эти трудности часто становятся своеобразным стимулом для изучения. Так, например, если у школьников обнаруживается недостаточный запас знаний для решения какой-либо задачи или доказательства теоремы, то они сами стремятся восполнить этот пробел, самостоятельно "открывая" то или иное свойство и тем самым сразу обнаруживая полезность его изучения. В этом случае роль учителя сводится к тому, чтобы организовать и направить работу ученика, чтобы трудности, которые ученик преодолевает, были ему по силам. Нередко эвристический метод выступает в практике обучения в форме так называемой эвристической беседы. Опыт многих учителей, широко применяющих эвристический метод, показал, что он влияет на отношение учащихся к учебной деятельности. Приобретя "вкус" к эвристике, учащиеся начинают расценивать работу по "готовым указаниям", как работу неинтересную и скучную. Наиболее значимыми моментами их учебной деятельности на уроке и в домашних условиях становятся самостоятельные "открытия" того или иного способа решения задачи. Явно возрастает интерес учащихся к тем видам работ, в которых находят применение эвристические методы и приемы.
Современные экспериментальные исследования, проведенные в советской и зарубежной школах, свидетельствуют о полезности широкого использования эвристического метода при изучении математики учащимися средней школы, начиная уже с начального школьного возраста. Естественно, что в таком случае перед учащимися можно поставить только те учебные проблемы, которые могут быть поняты и разрешены учащимися на данном этапе обучения.
К сожалению, на частое применение эвристического метода в процессе обучения поставленных учебных проблем требуется гораздо больше учебного времени, чем на изучение этого же вопроса методом сообщения учителем готового решения (доказательства, результата). Поэтому учитель не может использовать эвристический метод преподавания на каждом уроке. К тому же длительное использование только одного (даже весьма эффективного метода) противопоказано в обучении. Однако следует отметить, что "время, затраченное на фундаментальные вопросы, проработанные с личным участием учащихся,-не потерянное время: новые знания приобретаются почти без затраты усилий благодаря ранее полученному глубокому мыслительному опыту".
-
Метод программированного обучения в преподавании математики
Характерные черты программированного обучения. Линейный и разветвленный способы программирования учебного материала. Методика проведения занятий с применением программированных материалов
Особенности программированного обучения
-
Методы информатики в обучении математике
Логико-алгоритмический метод, программированное обучение, компьютеризация обучения математике. Технологический подход к построению обучения математике
Методы информатики в обучении математике
-
Методы научного познания в обучении математике
Общая характеристика методов научного исследования. Наблюдение, опыт и измерение, анализ и синтез, сравнение и аналогия, обобщение, абстрагирование и конкретизация, математическое моделирование в процессе обучения математике. / Характеристика каждого метода, его достоинства и недостатки, примеры
-
Эмпирические методы познания
-
Логические методы познания
-
Математические методы познания
Назад к оглавлению | К следующей главе
Глава 4
Методы обучения математике
Сущность и роль проблемы методов в современном обучении математике. Понятие метода обучения. Методы преподавания и методы обучения. Условия успешного применения различных методов обучения
-
Методы обучения, выделяемые по источнику знаний
-
Словесные методы обучения
-
Наглядные методы обучения
-
Практические методы обучения
-
-
Методы обучения, определяемые уровнем познавательной деятельности учащихся
К методам этой группы относятся репродуктивные, проблемно-поисковые и самостоятельная работа учащихся.
В практике многих учителей широко используется самостоятельная работа учащихся. Она проводится почти на каждом уроке в пределах 7-15 мин. Первые самостоятельные работы по теме носят в основном обучающий и корректирующий характер. С их помощью осуществляется оперативная обратная связь в обучении: учитель видит все недостатки в знаниях учащихся и своевременно устраняет их. От занесения в классный журнал оценок "2" и "3" можно пока воздержаться (выставляя их в тетради или дневнике учащегося). Если самостоятельная работа носит контролирующий характер, то в журнал выставляются все оценки. Такая система оценивания является достаточно гуманной, хорошо мобилизует учащихся, помогает им лучше осмысливать свои затруднения и преодолевать их, способствует повышению качества знаний. Учащиеся оказываются лучше подготовленными к контрольной работе, у них исчезает страх перед такой работой, боязнь получить двойку. Количество неудовлетворительных оценок, как правило, резко сокращается. У учащихся вырабатывается положительное отношение к деловой, ритмичной работе, рациональному использованию времени урока.
О сочетании методов обучения
-
Проблемное обучение математике.
Общая характеристика проблемного обучения. Проблемное изучение нового материала. Проблемы обучения при решении задач. Виды учебной работы школьников в условиях проблемного обучения. Контроль и оценка поисковой деятельности учащихся в условиях проблемного обучения, роль отметки
-
Методы проблемного обучения
-
Исследовательский метод
-
Метод проблемного изложения
Эвристический метод обучения математике
Сущность эвристики. Роль эвристической деятельности в науке и практике обучения математике. Эвристическая беседа. Достоинства и недостатки эвристического метода обучения математике
Эвристика - молодая научная дисциплина, возникшая на стыке таких наук, как философия, кибернетика, психология и педагогика. Специалисты каждой из этих наук рассматривают эвристику со своих позиций, придают своеобразное толкование ее основным понятиям и положениям.
Так, кибернетики считают, что эвристика - методы и способы, связанные с улучшением эффективности системы (человека или машины), решающей задачи. Психологи считают эвристику разделом психологии, изучающим творческое мышление. Педагоги считают эвристикой науку о средствах и методах решения задач. Философы термин "эвристический" приписывают таким правилам или утверждениям, которые способствуют открытию нового.
В последние годы к эвристике относят и те исследования представителей кибернетики, которые пытаются моделировать высшие проявления интеллекта. Уже и сейчас проблемы эвристики разрабатываются инженерами и математиками, психологами и физиологами, педагогами и организаторами производства. Все же основой эвристики является психология, особенно тот ее раздел, который получил название психологии творческого, или продуктивного, мышления.
Эвристическая деятельность или эвристические процессы, хотя и включают в себя умственные операции в качестве важного своего компонента, вместе с тем обладают некоторой спецификой. Именно поэтому эвристическую деятельность следует рассматривать как такую разновидность человеческого мышления, которая создает новую систему действий или открывает неизвестные ранее закономерности окружающих человека объектов (или объектов изучаемой науки).
Попытки проникнуть в механизм этого процесса, раскрыть его закономерности предпринимали и предпринимают многие исследователи в различных отраслях науки.
В эвристике, как молодой, развивающейся науке, не все понятия достаточно четко определены. Это прежде всего относится к понятию "эвристический метод". Многие исследователи понимают под ним определенный эффективный, но недостаточно надежный способ решения задач. Он позволяет ограничивать перебор вариантов решения, т. е. сокращать число вариантов, изучаемых перед тем, как выбрать окончательное решение. Понятно, что это определение понятия "эвристический метод" не может быть признано удовлетворительным, так как в нем представлена лишь внешняя характеристика явления, но не раскрыты существенные его черты.
Чтобы раскрыть существо этого понятия, необходимо иметь в виду, что сам термин "эвристический" применим к явлениям двоякого рода. Во-первых, можно рассмотреть как эвристическую такую деятельность человека, которая приводит к решению сложной, нестандартной задачи, во-вторых, эвристическими можно считать и специфические приемы, которые человек сформировал у себя в ходе решения одних задач и более или менее сознательно переносит на решение других задач.
Эвристические приемы как готовые схемы действия составляют объект эвристической логики, а реальный процесс эвристической деятельности - объект психологии. Но если эвристические приемы могут быть представлены в виде определенной логической схемы, т. е. могут быть описаны математическим языком, то эвристическая деятельность на современном этапе развития науки не имеет своего математического выражения.
Начало применения эвристического метода как метода обучения - математике можно найти еще в книге известного французского педагога - математика Лезана "Развитие математической инициативы". В этой книге эвристический метод не имеет еще современного названия и выступает в виде советов учителю. Вот некоторые из них:
Основной принцип преподавания - "сохранять видимость игры, уважать свободу ребенка, поддерживая иллюзию (если есть таковая) его собственного открытия истины"; "избегать в первоначальном воспитании ребенка опасного искуса злоупотреблением упражнениями памяти", ибо это убивает его врожденные качества; обучать, опираясь на интерес к изучаемому.
Лезан приводит множество примеров, наглядно показывая, как сделать обучение математике более эффективным, опираясь на явную заинтересованность учащихся процессом обучения.
Эвристический метод обучения рассматривался в русской школе с начала XIX в. Многие русские педагоги-математики того времени не раз пересматривали традиционные методы обучения, представлявшиеся им устаревшими, не отвечающими основным задачам математического образования.
На необходимость пересмотра традиционной программы обучения в русской школе указывал, в частности, известный педагог-математик С. И. Шохор-Троцкий. В книге "Геометрия на задачах" он писал, что нельзя излагать учащихся данный раздел математики в совершенно готовом виде. Поступать так - значит идти вразрез с основными принципами обучения и воспитания. В частности, он указывал, что "занятия геометрией могут быть для ученика занимательны только тогда, когда они требуют от него посильного и планомерного труда... требуют умственной работы, а не заучивания слов на память".
Большое значение эвристическому методу обучения в школе придавал другой русский педагог-математик Н. А. Извольский. В книге "Комбинационная работа" он писал, что "главной задачей обучения является развитие творческих способностей".
Известный методист-математик В. М. Брадис определяет эвристический метод следующим образом: "Эвристическим называется такой метод обучения, когда руководитель не сообщает учащимся готовых, подлежащих усвоению сведений, а подводит учащихся к самостоятельному переоткрытию соответствующих предложений и правил"
Определение эвристического метода преподавания дается также В. В. Репьевым. Только название метода здесь звучит несколько иначе - эвристическая беседа. "... Этот метод состоит в том, что учитель ставит перед классом проблему (теорему, задачу), а затем путем целесообразных вопросов приводит учащихся к решению проблемы".
Но суть этих определений одна - самостоятельный, планируемый лишь в общих чертах поиск решения поставленной проблемы.
Роль эвристической деятельности в науке и в практике обучения математике подробно освещается в книгах американского математика Д. Пойа. В книге "Как решать задачу". Д. Пойа пытается охарактеризовать эвристику как специальную отрасль знания. Цель эвристики - исследовать правила и методы, ведущие к открытиям и изобретениям. Интересно, что основным методом, с помощью которого можно изучить структуру творческого мыслительного процесса, является, по его мнению, исследование личного опыта в решении задач и наблюдение за тем, как решают задачи другие. Автор пытается вывести некоторые правила, следуя которым можно прийти к открытиям, не анализируя той психической деятельности, в отношении которой предлагаются эти правила. "Первое правило - надо иметь способности, а наряду с ними удачу. Второе правило - стойко держаться и не отступать, пока не появится счастливая идея". Интересна приводимая в конце книги схема решения задач. Схема указывает, в какой последовательности нужно совершать действия, чтобы добиться успеха. Она включает четыре этапа:
1. Понимание постановки задачи.
2. Составление плана решения.
3. Осуществление плана.
4. Взгляд назад (изучение полученного решения).
В ходе выполнения этих этапов решающий задачу должен ответить на следующие вопросы: Что неизвестно? Что дано? В чем состоит условие? Не встречалась ли мне раньше эта задача, хотя бы в несколько другой форме? Есть ли какая-нибудь родственная данной задача? Нельзя ли воспользоваться ею?
Нетрудно видеть, что эта схема подчеркивает главным образом один принцип эвристической деятельности: использование в том или ином виде прошлого опыта. Но этот принцип не может считаться единственным в структуре творческой мыслительной деятельности. Понятно, что многие весьма важные компоненты продуктивного мышления в работах Д. Пойа и не могут выступить с должной отчетливостью, так как речь у него идет об учебных, а не о чисто творческих задачах.
Близка точке зрения Д. Пойа та характеристика эвристической деятельности, которая дается известным американским психологом Д. Брунером в его книге "Процесс обучения". Эвристические приемы характеризуются Д. Брунером как некоторые не вполне точные способы решения задач, с помощью которых можно прийти, а можно и не прийти к нужному результату. У Брунера понятие "эвристический" служит для характеристики лишь приемов, помогающих решать задачу, как и у Д. Пойа. Д. Брунер не исследует эвристическую деятельность человека как процесс, приводящий к формированию приемов или схемы действий. Между тем обучение деятельности - это значительно более сложная и вместе с тем гораздо более важная проблема, чем обучение готовым, сложившимся приемам решения задач.
Весьма интересна с точки зрения применения эвристического метода в школе книга американского педагога У. Сойера "Прелюдия к математике".
"Для всех математиков, - пишет Сойер, - характерна дерзость ума. Математик не любит, когда ему о чем-нибудь рассказывают, он сам хочет дойти до всего"
Эта "дерзость ума", по словам Сойера, особенно сильно проявляется у детей.
"Если вы, например, преподаете геометрию 9-10-летним ребятам, - говорит Сойер, - и рассказываете, что никто еще не смог разделить угол на три равные части при помощи линейки и циркуля, вы непременно увидите, что один-два мальчика останутся после уроков и будут пытаться найти решение. То обстоятельство, что в течение 2000 лет никто не решил эту задачу, не помешает им надеяться, что они смогут это сделать в течение часового перерыва на обед. Это, конечно, не очень скромно, но и не свидетельствует об их самонадеянности. Они просто готовы принять любой вызов. А ведь в действительности уже доказано, что невозможно разделить угол на три равные части при помощи линейки и циркуля. Их попытка найти решение - того же рода, что попытка представить "корень из двух" в виде рациональной дроби p/q
Хороший ученик всегда старается забежать вперед. Если вы ему объясните, как решать квадратное уравнение дополнением до полного квадрата, он непременно захочет узнать, можно ли решить кубическое уравнение дополнением до полного куба. Вот это желание исследовать является отличительной чертой математика. Это одна из сил, содействующих росту математика. Математик получает удовольствие от знаний, которыми он уже овладел, и всегда стремится к новым знаниям".
Другим необходимым качеством математика является интерес к закономерностям. Закономерность - это наиболее стабильная характеристика постоянно меняющегося мира. Сегодняшний день не может быть похожим на вчерашний. Нельзя увидеть дважды одно и то же лицо под одним и тем же углом зрения. Закономерности встречаются уже в самом начале арифметики. В таблице умножения имеется немало элементарных примеров закономерностей. Вот один из них. Обычно дети любят умножать на 2 и на 5, потому что последние цифры ответа легко запомнить: при умножении на 2 всегда получаются четные цифры, а при умножении на 5, еще проще, всегда 0 или 5. Но даже в умножении на 7 есть свои закономерности. Если мы посмотрим последние цифры произведений 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, т.е. на 7, 4, 1, 8, 5, 2, 9, 6, 3, 0, то увидим, что разность между последующей и предыдущей цифрами составляет:-3; +7;-3;-3; +7; -3; -3, -3. В этом ряду чувствуется совершенно определенный ритм.
Если прочесть конечные цифры ответов при умножении на 7 в обратном порядке, то мы получаем конечные цифры от умножения на 3. Даже в начальной школе можно развить навык наблюдения за математическими закономерностями.
В книге "Прелюдия к математике" Сойер приводит много примеров наблюдений закономерностей и в арифметике, и в алгебре, и в геометрии. Итак. одним из основных методов, который позволяет учащимся проявить творческую активность в процессе обучения математике, является эвристический метод. Грубо говоря, этот метод состоит в том, что учитель ставит перед классом некоторую учебную проблему, а затем путем после-довательно поставленных заданий "наводит" учащихся на самостоятельное обнаружение того или иного математического факта. Учащиеся постепенно, шаг за шагом, преодолевают трудности в решении поставленной проблемы и "открывают" сами ее решение.
Известно, что в процессе изучения математики школьники часто сталкиваются с различными трудностями. Однако в обучении, построенном эвристически, эти трудности часто становятся своеобразным стимулом для изучения. Так, например, если у школьников обнаруживается недостаточный запас знаний для решения какой-либо задачи или доказательства теоремы, то они сами стремятся восполнить этот пробел, самостоятельно "открывая" то или иное свойство и тем самым сразу обнаруживая полезность его изучения. В этом случае роль учителя сводится к тому, чтобы организовать и направить работу ученика, чтобы трудности, которые ученик преодолевает, были ему по силам. Нередко эвристический метод выступает в практике обучения в форме так называемой эвристической беседы. Опыт многих учителей, широко применяющих эвристический метод, показал, что он влияет на отношение учащихся к учебной деятельности. Приобретя "вкус" к эвристике, учащиеся начинают расценивать работу по "готовым указаниям", как работу неинтересную и скучную. Наиболее значимыми моментами их учебной деятельности на уроке и в домашних условиях становятся самостоятельные "открытия" того или иного способа решения задачи. Явно возрастает интерес учащихся к тем видам работ, в которых находят применение эвристические методы и приемы.
Современные экспериментальные исследования, проведенные в советской и зарубежной школах, свидетельствуют о полезности широкого использования эвристического метода при изучении математики учащимися средней школы, начиная уже с начального школьного возраста. Естественно, что в таком случае перед учащимися можно поставить только те учебные проблемы, которые могут быть поняты и разрешены учащимися на данном этапе обучения.
К сожалению, на частое применение эвристического метода в процессе обучения поставленных учебных проблем требуется гораздо больше учебного времени, чем на изучение этого же вопроса методом сообщения учителем готового решения (доказательства, результата). Поэтому учитель не может использовать эвристический метод преподавания на каждом уроке. К тому же длительное использование только одного (даже весьма эффективного метода) противопоказано в обучении. Однако следует отметить, что "время, затраченное на фундаментальные вопросы, проработанные с личным участием учащихся,-не потерянное время: новые знания приобретаются почти без затраты усилий благодаря ранее полученному глубокому мыслительному опыту".
-
Метод программированного обучения в преподавании математики
Характерные черты программированного обучения. Линейный и разветвленный способы программирования учебного материала. Методика проведения занятий с применением программированных материалов
Особенности программированного обучения
-
Методы информатики в обучении математике
Логико-алгоритмический метод, программированное обучение, компьютеризация обучения математике. Технологический подход к построению обучения математике
Методы информатики в обучении математике
-
Методы научного познания в обучении математике
Общая характеристика методов научного исследования. Наблюдение, опыт и измерение, анализ и синтез, сравнение и аналогия, обобщение, абстрагирование и конкретизация, математическое моделирование в процессе обучения математике. / Характеристика каждого метода, его достоинства и недостатки, примеры
-
Эмпирические методы познания
-
Логические методы познания
-
Математические методы познания
Применение индукции и дедукции в преподавании математики
Два основных вида умозаключений: дедукция и индукция. Различные формы проявления индукции. Неполная и полная индукция. Исследовательская /экспериментальная индукция/. Метод математической индукции. Дедукция.
-
Индукция
-
Математическая индукция
-
Дедукция
Глава 6
Методика введения математических понятий в школьном курсе математики
Понятия, суждения, умозаключения. Процесс формирования математических понятий . Обобщения через понятия. Содержание и объем понятия. Понятия и термины. Определения понятия. Требования, предъявляемые к формированию определений. Классификация понятий . Введение понятий конкретно-индуктивным и абстрактно-дедуктивным способом. Контроль за степенью усвоения математических понятий. Понятие о математическом суждении и умозаключении
-
Математические понятия
-
Математические понятия, предложения и доказательства
-
Математические суждения и умозаключения
-
Основные виды математического суждения
Назад к оглавлению | К следующей главеГлава 8
Методика обучения решению задач
Роль задач в процессе развития математического мышления учащихся. Виды задач. Общие методы обучения решению задач. Анализ и синтез в поиске решения задач . Работа учителя с условием задачи . Классификация геометрических задач и методы их решения. Задача практического содержания и их роль в профессиональной ориентации школьников
-
Роль задач в обучении математике. Обучение общим методам решения задач
-
Значение учебных математических задач
-
Роль задач в процессе обучения математике
-
Обучение математике через задачи
-
Общие методы обучения решению математических задач
-
Организация обучения решению математических задач
Роль задач в обучении математике. Обучение общим методам решения задач
В процессе обучения математике задачи выполняют разнообразные функции. Учебные математические задачи являются очень эффективным и часто незаменимым средством усвоения учащимися понятий и методов школьного курса математики, вообще математических теорий. Велика роль задач в развитии мышления и в математическом воспитании учащихся, в формировании у них умений и навыков в практических применениях математики. Решение задач хорошо служит достижению всех тех целей, которые ставятся перед обучением математике. Именно поэтому для решения задач используется половина учебного времени уроков математики (700-800 академических часов в IV-Х классах). Правильная методика обучения решению математических задач играет существенную роль в формировании высокого уровня математических знаний, умений и навыков учащихся.
В этой главе рассматриваются общие и наиболее важные аспекты использования задач в обучении математике, общие методы, применяемые при решении задач, и т. д. Значительное внимание уделяется вопросам организации обучения решению задач на уроках, приводятся практические рекомендации, которые могут быть использованы в процессе учебной работы над задачей.
Назад к оглавлению | К началу главы
Значение учебных математических задач
При обучении математике задачи имеют большое и многостороннее значение.
Образовательное значение математических задач. Решая математическую задачу, человек познает много нового: знакомится с новой ситуацией, описанной в задаче, с применением математической теории к ее решению, познает новый метод решения или новые теоретические разделы математики, необходимые для решения задачи, и т. д. Иными словами, при решении математических задач человек приобретает математические знания, повышает свое математическое образование. При овладении методом решения некоторого класса задач у человека формируется умение решать такие задачи, а при достаточной тренировке - и навык, что тоже повышает уровень математического образования.
Практическое значение математических задач. При решении математических задач ученик обучается применять математические знания к практическим нуждам, готовится к практической деятельности в будущем, к решению задач, выдвигаемых практикой, повседневной жизнью. Почти во всех конструкторских расчетах приходится решать математические задачи, исходя из запросов практики. Исследование и описание процессов и их свойств невозможно без привлечения математического аппарата, т. е. без решения математических задач. Математические задачи решаются в физике, химии, биологии, сопротивлении материалов, электро- и радиотехнике, особенно в их теоретических основах, и др.
Это означает, что при обучении математике учащимся следует предлагать задачи, связанные со смежными дисциплинами (физикой, химией, географией и др.), а также задачи с техническим и практическим, жизненным содержанием.
Значение математических задач в развитии мышления. Решение математических задач приучает выделять посылки и заключения, данные и искомые, находить общее, и особенно в данных, сопоставлять и противопоставлять факты. При решении математических задач, как указывал А. Я' Хинчин [24], воспитывается правильное мышление, и прежде всего учащиеся приучаются к полноценной аргументации. Решение задачи должно быть полностью аргументированным, т. е. не допускаются незаконные обобщения, необоснованные аналогии, предъявляется требование полноты дизъюнкции (рассмотрение всех случаев данной в задаче ситуации), соблюдаются полнота и выдержанность классификации. При решении математических задач у учащихся формируется особый стиль мышления: соблюдение формальнологической схемы рассуждений, лаконичное выражение мыслей, четкая расчлененность хода мышления, точность символики.
Воспитательное значение математических задач. Прежде всего задача воспитывает своей фабулой, текстовым содержанием. Поэтому фабула многих математических задач существенно изменяется в различные периоды развития общества. Так, в русских дореволюционных задачниках и в задачах, которые решают современные школьники капиталистических стран, сюжетное содержание многих математических задач связано с вопросами получения выгоды при купле и перепродаже товара, расчетов выигрышапроигрыша в азартной игре и т. п. Совсем иное сюжетное содержание у задач, помещенных в современных советских учебниках, учебниках по математике социалистических стран: в них сюжет направлен на воспитание у у учащихся высоких моральных качеств, научного мировоззрения, интернационализма, коллективизма, гордости за свою социалистическую Родину, на ознакомление с достижениями народного хозяйства.
Воспитывает не только фабула задачи, воспитывает весь процесс обучения решению математических задач. Правильно поставленное обучение решению математических задач воспитывает у учеников честность и правдивость, настойчивость в преодолении трудностей, уважение к труду своих товарищей. С введением в школу элементов математического анализа выявились более широкие возможности воспитания у учеников в процессе решения задач диалектико-материалистического мировоззрения.
Назад к оглавлению | К началу главы
Роль задач в процессе обучения математике
Каждая конкретная учебная математическая задача предназначается для достижения чаще всего не одной, а нескольких педагогических, дидактических, учебных целей. И эти цели характеризуются как содержанием Задачи, так и назначением, которое придает задаче учитель. Дидактические цели, которые ставит перед той или иной задачей учитель, определяют роль задач в обучении математике. В зависимости от содержания задачи и дидактических целей ее применения из всех ролей, которые отводятся конкретной задаче, можно выделить ее ведущую роль.
Обучающая роль математических задач. Обучающую роль математические задачи выполняют при формировании у учащихся системы знаний, умений и навыков по математике и ее конкретным дисциплинам. Следует выделить несколько видов задач по их обучающей роли.
1) Задачи для усвоения математических понятий. Известно, что формирование математических понятий хорошо проходит при условии тщательной и кропотливой работы над понятиями, их определениями и свойствами. Чтобы овладеть понятием, недостаточно выучить его определение, необходимо разобраться в смысле каждого слова в определении, четко знать свойства изучаемого понятия. Такое знание достигается прежде всего при решении задач и выполнении упражнений.
2) Задачи для овладения математической символикой. Одной из целей обучения математике является овладение математическим языком и, следовательно, математической символикой. Простейшая символика вводится еще в начальной школе и в IV-V классах (знаки действий, равенства и неравенства, скобки, знаки угла и его величины, параллельности и т. д.). Правильному употреблению изучаемых символов надо обучать, раскрывая при решении задач их роль и назначение.
3) Задачи для обучения доказательствам. Обучение доказательствам - одна из важнейших целей обучения математике.
Простейшими задачами, с решения которых практически начинается обучение доказательствам, являются задачи-вопросы и элементарные задачи на исследование. Решение таких задач заключается в отыскании ответа на вопрос и доказательстве его истинности.
Задачи-вопросы обычно требуют для своего решения (доказательства истинности ответа) установления одной импликации, одного логического шага от данных к доказываемому. Доказательство же при решении более сложной задачи или доказательство теоремы представляет собой цепочку шагов-импликаций.
Целью решения задач-вопросов является и осознание, уточнение и конкретизация изучаемых понятий и связей между ними. Задачи-вопросы необходимы также для усвоения учащимися вводимой символики и используемого языка.
Существенную роль в обучении доказательствам играют упражнения в заполнении пропущенных слов, символов и их сочетаний в тексте готового доказательства. Аналогичные упражнения довольно часто применяются при изучении русского языка, на уроках же математики они встречаются редко, в учебниках и задачниках их нет вовсе. Начинать надо с достаточно простых задач.
4) Задачи для формирования математических умений и навыков (см. далее).
5) Обучающую роль играют и задачи, предваряющие изучение новых математических фактов, концентрирующие внимание учащихся на вновь изучаемых идеях, понятиях и методах математики, задачи, с помощью которых вводятся новые понятия и методы, задачи, создающие проблемную ситуацию с целью приобретения учащимися новых знаний. Здесь же следует рассмотреть и задачи, с помощью которых подготавливается сложное для учащихся доказательство теоремы.
Созданию проблемной ситуации для введения и изучения способов решения квадратных уравнений послужит задача, приводящая к такому уравнению.
Полезно вспомнить, что решение конкретных задач (например, о мгновенной скорости, о касательной, о плотности стержня) приводит к понятию производной, а задачи о площади криволинейной трапеции, о работе переменной силы, действующей вдоль прямой, - к понятию интеграла.
Для подготовки к изучению более или менее сложных теорем, играющих серьезную роль в курсе математики, могут быть предложены задачи, приводящие к формулировке теоремы, задачи на доказательство одного из промежуточных фактов в доказательстве теоремы и т. д.
Развитие мышления учащихся при решении математических задач.
1) Мыслительные умения, восприятие и память при решении задач. Решение математических задач требует применения многочисленных мыслительных умений: анализировать заданную ситуацию, сопоставлять данные и искомые, решаемую задачу с решенными ранее, выявляя скрытые свойства заданной
ситуации; конструировать простейшие математические модели, осуществляя мысленный эксперимент; синтезировать, отбирая полезную для решения задачи информацию, систематизируя ее; кратко и четко, в виде текста, символически, графически и т. д. оформлять свои мысли; объективно оценивать полученные при решении задачи результаты, обобщать или специализировать результаты решения задачи, исследовать особые проявления заданной ситуации. Сказанное говорит о необходимости учитывать при обучении решению математических задач современные достижения психологической науки.
Исследованиями советских психологов установлено, что уже восприятие задачи различно у различных учащихся данного класса. Способный к математике ученик воспринимает и единичные элементы задачи, и комплексы ее взаимосвязанных элементов, и роль каждого элемента в комплексе. Средний ученик воспринимает лишь отдельные элементы задачи. Поэтому при обучении решению задач необходимо специально анализировать с учащимися связь и отношения элементов задачи. Так облегчится выбор приемов переработки условия задачи. При решении задач часто приходится обращаться к памяти. Индивидуальная память способного к математике ученика сохраняет не всю информацию, а преимущественно "обобщенные и свернутые структуры". Сохранение такой информации не загружает мозг избыточной информацией, а запоминаемую позволяет дольше хранить и легче использовать. Обучение обобщениям при решении задач развивает, таким образом, не только мышление, но и память, формирует "обобщенные ассоциации". При непосредственном решении математических задач и обучении их решению необходимо все это учитывать.
2) Обучение мышлению. Эффективность математических задач и упражнений в значительной мере зависит от степени творческой активности учеников при их решении.
Собственно, одно из основных назначений задач и упражнений и заключается в том, чтобы активизировать мыслительную деятельность учеников на уроке.
Математические задачи должны прежде всего будить мысль учеников, заставлять ее работать, развиваться, совершенствоваться. Говоря об активизации мышления учеников, нельзя забывать, что при решении математических задач учащиеся не только выполняют построения, преобразования и запоминают формулировки, но и обучаются четкому мышлению, умению рассуждать, сопоставлять и противопоставлять факты, находить в них общее и различное, делать правильные умозаключения.
Правильно организованное обучение решению задач приучает к полноценной аргументации со ссылкой в соответствующих случаях на аксиомы, введенные определения и ранее доказанные теоремы. С целью приучения к достаточно полной и точной аргументации полезно время от времени предлагать учащимся записывать решение ^ задач в два столбца: слева - утверждения, выкладки, вычисления, справа - аргументы, т. е. предложения, подтверждающие правильность высказанных утверждений, выполняемых выкладок и вычислений.
3) Задачи, активизирующие мыслительную деятельность учащихся. Эффективность учебной деятельности по развитию мышления во многом зависит от степени творческой активности учащихся при решении математических задач. Следовательно, необходимы математические задачи и упражнения, которые бы активизировали мыслительную деятельность школьников. А. Ф. Эсаулов подразделяет задачи на следующие виды: задачи, рассчитанные на воспроизведение (при их решении опираются на память и внимание); задачи, решение которых приводит к новой, неизвестной до этого мысли, идее; творческие задачи. Активизирует и развивает мышление учащихся решение задач двух последних видов. Рассмотрим некоторые из них.
а) Задачи и упражнения, включающие элементы исследования. Простейшие исследования при решении задач следует предлагать уже с первых уроков алгебры и геометрии и даже на уроках математики в IV-V классах.
В последующих классах следует предлагать не только задачи с элементами исследований, но и задачи, включающие исследование в качестве обязательной составной части. Такие исследования необходимо включаются в решение многих геометрических задач на построение (как в планиметрии, так и в стереометрии), уравнений и неравенств (особенно тригонометрических, показательных и логарифмических с параметрами) и др. Задачи и упражнения с выполнением некоторых исследований могут найти свое место во всех разделах школьного курса математики, например -при изучении действительных чисел в IX классе.
б) Задачи на доказательство доказывают существенное влияние на развитие мышления учащихся. Именно при выполнении доказательств оттачивается логическое мышление учеников, разрабатываются логические схемы решения задач, возникает потребность учащихся в обосновании математических фактов.
в) Задачи и упражнения в отыскании ошибок также играют значительную роль в развитии математического мышления учащихся. Такие задачи приучают обращать внимание на особо тонкие места в логических рассуждениях, помогают различать во многом сходные понятия, приучают к точности суждений и математической строгости и т. д. Первые упражнения в отыскании ошибок должны быть несложными.
Психологи установили, что решение одной задачи несколькими способами приносит больше пользы, чем решение подряд нескольких стереотипных задач. Рассмотрение учеником различных вариантов решения, умение выбрать из них наиболее рациональные, простые, изящные свидетельствуют об умении ученика мыслить, рассуждать, проводить правильные умозаключения. Различные варианты решения одной задачи дают возможность ученику применять весь арсенал его математических знаний. Таким образом, рассмотрение различных вариантов решения задачи воспитывает у учащихся гибкость мышления. Поиск рационального варианта решения лишь на первых порах требует дополнительных затрат времени на решение задачи. В дальнейшем эти затраты с лихвой окупаются.
Надо отметить, что рациональные приемы решения не появляются сами, по одному только желанию. Рациональным способам решений надо обучать. Один из путей обучения и есть решение задач несколькими способами, выбор лучшего из них.
Вообще же полезно хотя бы знакомить учащихся с различными подходами к решению наиболее распространенных задач. Приведем пример.
Один из заключительных уроков геометрии в VIII классе учитель начал с простейшей задачи: разделить данный отрезок пополам. К огорчению учителя и учеников, обнаружилось, что полный набор чертежных инструментов имеют только 6 человек, а у некоторых учеников вообще не оказалось никакого инструмента. Тогда учитель предложил каждому решить задачу, применяя тот инструмент, который у него имеется, а тем, у кого не было инструмента, использовать прямой угол из плотной бумаги (тетрадный лист сложили по осям симметрии в 4 слоя) или его половину - угол в 45°.
В результате на уроке были рассмотрены 8 вариантов решения с помощью: а) циркуля и линейки; б) прямого угла; в) двусторонней линейки; г) чертежных угольников; д) угла величиной 45°; е) угла в 30°; ж) острого угла и односторонней линейки; з) транспортира и односторонней линейки. Польза такого обсуждения задачи несомненна. е) Составление задач учащимися. Сознательное изучение математики и развитие мышления учащихся стимулируется самостоятельным составлением (конструированием) математических задач. При этом, во-первых, воспитывается самостоятельность (школьники оперируют изученными и изучаемыми объектами и фактами математики, т. е. рассматривают и оценивают свойства, различия и характерные особенности этих объектов); во-вторых, развивается творческая мыслительная активность учеников.
Конструирование задач учениками заставляет их использовать больший объем информации, применять рассуждения, обратные применяемым при обычном решении задач. Следовательно, при составлении задачи ученик применяет логические средства, отличные от тех, с помощью которых решаются обычные задачи, открывает новые связи между математическими объектами. Это развивает их мышление. При изучении первых понятий алгебры (например, действий с рациональными числами) следует предлагать учащимся составлять вычислительные упражнения, в которых бы для упрощения вычислений применялись законы действий, особенно Дистрибутивный. Учащиеся должны свободно оперировать законами действий.
Очень полезны упражнения в составлении уравнений по заданным их корням, систем уравнений по данным решениям, задач по заданным уравнениям или их системам.
Составление задач по заданным уравнениям полезно хотя бы потому, что задачи эти бывают разнообразны по фабуле, а это убеждает в общности математических методов.
Следует предостеречь учителя от чрезмерного увлечения конструированием задач. Нет необходимости доводить конструирование задач до навыка, поэтому не нужно предлагать ученикам трафареты для составления математических объектов и задач. Всякий трафарет, шаблон в конструировании губит главное, ради чего эти упражнения вводятся: творческую мысль ученика.
Воспитательная роль математических задач. Процесс обучения теснейшим образом связан с воспитанием учащихся. В школе обучение не мыслится в отрыве от воспитания. Обучая решению математических задач, учитель математики в то же время воспитывает учащихся, формирует у них качества, присущие советскому общественному строю.
Назад к оглавлению | К началу главы | Далее
Обучение математике через задачи
Примерно половина уроков математики в средней школе, как уже указывалось, отводится решению математических задач и выполнению упражнений. Таким образом, обучение математике осуществляется и при решении задач. Уже рассмотрена обучающая роль учебных математических задач: при решении математических задач учащиеся усваивают многие математические понятия, овладевают математической символикой, обучаются проведению доказательств и т. д., т.е. обучаются математике. Но этим не ограничивается обучение математике через задачи. Осуществляя такой путь обучения математике, учитель ставит перед той или иной конкретной задачей дидактические цели, при достижении которых и осуществляется обучение через задачи. Какие же дидактические цели могут быть поставлены перед математическими задачами?
Математические задачи могут иметь своей дидактической целью подготовку к изучению теоретических вопросов математики (новых понятий, методов, теорем). Такая же цель ставится перед решением задач, с помощью которых перед изучением новых теоретических вопросов в памяти и сознании учащихся восстанавливаются те сведения, знание которых необходимо для изучения новых математических фактов. Эти задачи не должны быть сложными и могут решаться устно. Примеры:
1. Перед изучением свойств степеней с рациональными показателями полезны будут упражнения в применении свойств степеней с целыми показателями.
2. Изучению распределительного закона умножения (по отношению к сложению) для рациональных чисел могут предшествовать задачи, при решении которых напоминается применение этого закона для целых чисел. Именно так ученики обучаются верному применению аналогии.
Решение некоторых задач в IV-VI классах может быть проведено с таким расчетом, что после серии задач (упражнений) учитель может сформулировать новое предложение (определение, алгоритм и т. д.).
3. Введению определения умножения положительных и отрицательных чисел могут предшествовать упражнения в вычислениях с такими числами, выполняемые с помощью модели термометра. Четкое выделение характеристик (знака и модуля) произведения, сравнение их с соответствующими характеристиками множителей позволяют заметить закономерности выполнения умножения и сформулировать определение (правило).
Дидактической целью учебных математических задач может быть закрепление только что приобретенных теоретических знаний. Это могут быть задачи для усвоения математических понятий и их определений, для формирования умений, для закрепления формулировок, аксиом и теорем, для закрепления методов доказательств и т. д. Такие задачи следуют за изучением теоретических сведений. Примеры:
4. Два угла имеют общую вершину. Могут ли они быть несмежными и невертикальными?
Эта задача предназначена для закрепления у учащихся понятий о смежных и вертикальных углах.
5. Для закрепления формулировки теоремы Виета полезно решать задачи, подобные следующей. В уравнении х+рх+35 = 0 один из корней равен - 7. Вычислите Другой корень и значение коэффициента р.
Иллюстрация приложений изученного также может быть дидактической целью математических задач. С такой целью предлагаются учащимся практические задачи, иллюстрирующие приложения математики в технике, быту, смежных школьных предметах
Такое же назначение имеют задачи на применение тождественных преобразований к упрощению вычислений.
Пример: Докажите, что сумма двух диагоналей выпуклого четырехугольника меньше его периметра, но больше полупериметра. При решении этой задачи применяются свойство расстояний (так называемая "аксиома треугольника") и свойства неравенств.
Задачи на приложения могут быть предложены после изучения теории, при формировании умений и навыков, а могут и предшествовать изучению теории с целью создания проблемной ситуации.
Дидактической целью задач и упражнений может быть формирование умений и навыков.
1) Цель формирования умений обычно ставится при решении первых задач, выполнении первых упражнений по овладению новым приемом, алгоритмом, методом решения некоторого класса задач, а также задач, показывающих практическую ценность изучаемых способа, приема, метода. Это должны быть задачи, при решении .которых учащиеся приучаются оперировать вновь изученным, применять общий способ, алгоритм, метод в конкретной ситуации. Такие задачи не должны быть сложными, в них. должно отчетливо проявляться вновь изучаемое, лишь постепенно в задачи могут вводиться усложнения, так чтобы вновь формируемое умение включалось в уже имеющуюся систему математических умений и навыков учащихся. Первые такие задачи следует решать с подробным объяснением со стороны учащихся всех новых деталей решения, с подробными записями на доске. Это помогает осмысленному формированию умений, осмысленные же умения формируются быстрей и дольше сохраняются.
2) Формирование математических навыков может быть дидактической целью не отдельной задачи, а системы задач и упражнений. Умение оперировать многими приемами, способами и методами решения математических задач должно быть автоматизировано, доведено до навыка, чтобы при решении задач техническая сторона не отвлекала мышление решающего задачу, а помогала решению. Учащиеся должны владеть прочными и стойкими навыками вычислений, тождественных преобразований, решения у равнений, неравенств и их систем, геометрических построений и др.
Навыки формируются на основе осмысленных знаний и умений путем многократног" повторения операций, действий, приемов, алгоритмов, составляющих предмет изучения. Поэтому для формирования навыков нужна тщательно продуманная система упражнений и задач. В такой системе должна быть правильно установлена последовательность упражнений с учетом индивидуальных особенностей и возможностей учащихся и принципа "от простого к сложному". Следует соблюдать разумное разнообразие упражнений и задач в системе. При этом знания учащихся по математике должны совершенствоваться с решением каждой новой задачи. Следует добиваться, чтобы осознанные умения и навыки ученики получали при наименьших затратах времени.
Прочные, стойкие и гибкие навыки формируются тогда, когда они применяются совместно с ранее сформированными умениями и навыками в выполнении других действий. Именно таким образом вновь формируемые навыки включаются в систему знаний человека. К тому же решение задач, требующих применения и ранее полученных навыков, существенно помогает подкреплению очень важного умения применять полученные знания, умения и навыки в различных ситуациях.
Дидактической целью математических задач является и повторение ранее изученного. При решении большинства задач учащиеся применяют ранее полученные знания, умения, навыки. Такова особенность математики, заключающаяся в тесной взаимосвязи и взаимообусловленности ее разделов. Таким образом, независимо от целей, поставленных учителем перед решением конкретной задачи, при ее решении происходит повторение изученного ранее. Но повторение изученного может быть и специальным назначением задач, предложенных учителем. Например, решение задач на завершающих уроках по той или иной теме имеет своей дидактической целью повторение, систематизацию и уточнение знаний, полученных при изучении этой темы, и закрепление сформированных умений и навыков, что также требует повторения. Таково же назначение задач, решаемых при повторении математики в конце учебных четвертей года.
Контроль за усвоением математических знаний - одна из дидактических целей математических задач и упражнений. Каждая задача практически имеет своим назначением текущий контроль или самоконтроль. Задачи, решаемые фронтально с воспроизведением решения учащимися на доске, предназначаются и для выяснения затруднений учащихся, пробелов в их знаниях, степени усвоения новых теоретических знаний, изучаемых методов решения задач, прочности, стойкости и гибкости ранее приобретенных знаний, умений и навыков. Такое же предназначение имеется и у самостоятельно решаемых задач.
В проверочных и контрольных работах главным назначением решаемых задач является итоговый контроль за тем, насколько верно учитель учил, а ученики обучались по тем или иным разделам математики.
Назад
Общие методы обучения решению математических задач
Анализ и синтез при решении задач. Анализ и синтез находят широкое применение при решении математических задач. Напомним, что анализ - это метод рассуждений от искомых к данным. Синтез - метод рассуждений, ведущий от данных к искомым. Оба эти метода обычно применяются во взаимосвязи.
Анализ и синтез находят применение практически при решении каждого вида задач, каждой задачи.
1) Анализ и синтез при решении задач на доказательство.
2) Анализ и синтез при решении текстовых задач. Текстовыми задачами здесь названы математические задачи, в которых входная информация содержит не только математические данные, но еще и некоторый сюжет (фабулу задачи).
При решении текстовых задач с помощью аппарата арифметики роль анализа сводится к составлению плана решения, задача же чаще всего решается синтетическим методом.
3) Анализ и синтез при решении задач на построение в геометрии. Анализ и синтез применяются и при решении задач на построение в геометрии, иначе, конструктивных задач геометрии. Как известно, решение этих задач выполняется по следующему плану: анализ, построение, доказательство, исследование. Название первой части - анализ говорит само за себя: это действительно метод анализа, ведущий от искомых ("предположим, что искомая фигура построена") к данным, точнее, к их использованию в построении. При анализе намечается план построения, которое выполняется синтетическим путем. При доказательстве возможно использование как анализа, так и синтеза, но чаще применяется последний. Исследование предполагает преимущественное применение метода анализа.
Другие общие методы решения задач.
Рассмотренные в предыдущих пунктах анализ и синтез являются самыми общими методами решения задач. Ниже излагаются также общие методы решения задач, которые имеют более ограниченное применение.
Один из них - метод исчерпывающих проб, основой которого является выявление всех логических возможностей и отбор из них таких, которые удовлетворяют условию задачи. Если логических возможностей, соответствующих условию задачи, - конечное число, то может оказаться возможным перебрать все их и в ходе этого перебора выделить вполне удовлетворяющие условию. С помощью этого приема решаются, в частности, некоторые элементарные задачи теоретико-числового содержания. Методом исчерпывающих проб с большим успехом можно пользоваться и для решения многих логических задач. Развитием указанного приема служат некоторые методы решения в целых или рациональных числах неопределенных уравнений, и в частности хорошо .известный метод рассеивания.
Второй метод - это метод сведения. Суть его состоит в том, что .данные задачи подвергаются последовательным преобразованиям. Концом получающейся таким образом цепочки преобразований может быть состояние, простое рассмотрение которого дает требуемый 'результат. Если, например, нужно решить уравнение, то обычно составляют такую конечную последовательность уравнений, эквивалентных данному, последним звеном которой является уравнение с 'очевидным решением. Точно так же поступают при решении систем уравнений, неравенств, систем уравнений и неравенств. Решение задач на доказательство очень часто представляет собой цепочки тождественных преобразований, тянущиеся от левой части доказываемых тождеств к правой, или наоборот, или от левой и правой частей к одному и тому же выражению. Конечно, указанное сведение нужно понимать и как выведение, как конечную последовательность, ведущую от искомых к данным. Этот метод наиболее часто применяется в тех случаях, в которых заданное отношение обладает свойством транзитивности. Таковы отношения эквивалентности (равенства, уравнения, тождества, логическая равносильность, параллельность) м порядка (строгие и нестрогие неравенства, включение множеств, логическое следование). Прием "сведения" лежит в основе решения геометрических задач на построение. В каждой задаче этого вида содержится требование: исходя из данных фигур (или данных их элементов), с помощью указанных конструктивных элементов построить фигуру, удовлетворяющую определенным условиям. Это означает, что требуемое построение должно быть сведено к так называемым элементарным построениям, выполняемым реальными инструментами.
Метод сведения находит постоянные применения при решении текстовых задач арифметическими способами. Суть дела здесь состоит в том, что данная задача сводится к простым задачам.
Решение задач на доказательство теорем в своей основе имеет также сведение: доказываемое утверждение сводится к ранее доказанным теоремам и ранее введенным аксиомам и определениям данной научной области. Доказать - это значит свести новую теорему (задачу) в конечном счете к аксиомам.
Третий метод решения задач имеет своей основой моделирование (математическое и предметное). Для моделирования привлекаются различные математические объекты: числовые формулы, числовые таблицы, буквенные формулы, функции, уравнения алгебраические или дифференциальные и их системы, неравенства, системы неравенств (а также неравенств и уравнений), ряды, геометрические фигуры, разнообразные графосхемы, диаграммы Венна, графы и т. д.
Математическое моделирование находит применение при решении ' многих текстовых (сюжетных) задач. Уже уравнение, составленное по условию текстовой задачи, является ее алгебраической (аналитической) моделью. Чертеж фигуры, заданной в геометрической задаче, с обозначенными на ней данными и искомыми тоже является геометрической моделью задачи. Но нередко решению задачи помогает и предметная ее модель (например, объемная геометрическая фигура, модель с использованием или изображением предметов и объектов, заданных в задаче, и др.).
Большое практическое значение имеют методы нахождения приближенных значений искомых величин.
Все графические приемы решения задач на вычисление дают приближенные решения. Но приближенные решения могут получаться и с помощью численных методов (например, при решении квадратных уравнений по формулам их корней).
В геометрии используются приближенные методы построения. Примерами их служат спрямление окружности, построение квадрата, равновеликого данному кругу, деление угла на равные части и т. д.
Таковы основные приемы решения задач по курсу математики средней школы. Остается подчеркнуть, что в практике решения задач они часто комбинируются.
Одна из основных целей решения задач в школьном курсе математики и состоит в том, чтобы обеспечить действенное усвоение каждым учеником основных методов и приемов решения учебных математических задач.
Общие советы учителя ученику при решении задач. Для того чтобы научиться решать задачи, надо приобрести опыт их решения. Редкие ученики самостоятельно приобретают такой опыт. Долг учителя - помочь учащимся приобрести опыт решения задач, научить их решать задачи. Однако помощь учителя не должна быть чрезмерной. Если учитель много будет помогать ученику, на долю последнего ничего не останется или останется слишком мало работы по приобретению опыта решения задач. Так ученик не научится решать задачи. Если же помощь учителя будет мала, ученик также .может не научиться решать задача. Учитель должен помогать ученику путем советов, как решать задачу, или вопросов, отвечая на которые ученик успешнее решит задачу. Иногда учитель разыгрывает решение задачи, сам задавая вопросы и сам же отвечая на них. Ученики подражают ему в этом, постепенно приучаясь решать задачи. Но такой вариант обучения требует большей затраты времени и не всегда приводит к хорошим результатам. Можно сказать, что механическое подражание не метод обучения решению задач. Нужны вопросы и советы учителя ученику, вызывающие развивающие мыслительную деятельность школьников, помогающие развивать творческий подход к решению задач.
Такие вопросы и советы должны обладать общностью для различных задач, иначе ученики не научатся решать многие задачи, а будут учиться решать каждую конкретную задачу в отдельности. В то же время вопросы и советы должны быть естественны и просты, должны иметь своим источником простой здравый смысл. Они должны оказывать ученику действенную, но не назойливую помощь.
Но одних вопросов и советов учителя ученику недостаточно для обучения решению задач. Нельзя забывать, что "умение решать задачи есть искусство, приобретаемое практикой" .
Вопросы и советы ученику условно можно подразделить на четыре группы. Это подразделение вопросов, вообще говоря, не является категоричным. Может оказаться, что вопросы, рекомендуемые для первого этапа, окажут помощь и на втором этапе, а рекомендуемые для второго этапа - на третьем и т. п. Дело в том, что этапы решения задачи не могут быть строго изолированы один от другого, между ними существует определенная связь, в их единстве заключается процесс решения задачи.
Далее формулируются и поясняются вопросы и советы учителя ученику, предлагаемые на каждом этапе решения задачи.
1) Вопросы и советы для усвоения содержания задачи (1-й этап). Нельзя приступать к решению задачи, не уяснив четко, в чем заключается задание, т. е. не установив, каковы данные и искомые или посылки и заключения. Первый совет учителя: не спешить начинать решать задачу. Этот совет не означает, что задачу надо решать как можно медленней. Он означает, что решению задачи должна предшествовать подготовка, заключающаяся в следующем: а) сначала следует ознакомиться с задачей, внимательно прочитав ее содержание. При этом схватывается общая ситуация, описанная в задаче; б) ознакомившись с задачей, необходимо вникнуть в ее содержание. При этом нужно следовать такому совету: выделить в задаче данные и искомые, а в задаче на доказательство -посылки и заключения.
в) Если задача геометрическая или связана с геометрическими фигурами, полезно сделать чертеж к задаче и обозначить на чертеже данные и искомые (это тоже совет, которому должен следовать ученик).
г) В том случае, когда данные (или искомые) в задаче не обозначены, надо ввести подходящие обозначения. При решении текстовых задач алгебры и начал анализа вводят обозначения искомых или других переменных, принятых за искомые.
д) Уже на первой стадии решения задачи, стадии понимания задания, полезно попытаться ответить на вопрос: "Возможно ли удовлетворить условию?" Не всегда сразу удается ответить на этот вопрос, но иногда это можно сделать.
Отвечая на вопрос: "Возможно ли удовлетворить условию?", полезно выяснить, однозначно ли сформулирована задача, не содержит ли она избыточных или противоречивых данных. Одновременно выясняется, достаточно ли данных для решения задачи.
2) Составление плана решения задачи (2-й этап). Составление плана решения задачи, пожалуй, является главным шагом на пути ее решения. Правильно составленный план решения задачи почти гарантирует правильное ее решение. Но составление плана может оказаться сложным и длительным процессом. Поэтому крайне необходимо предлагать ученику ненавязчивые вопросы, советы, помогающие ему лучше и быстрее составить план решения задачи, "открыть" идею ее решения:
а) Известна ли решающему какая-либо родственная задача? Аналогичная задача? Если такая или родственная задача известна, то составление плана решения задачи не будет затруднительным. Но далеко не всегда известна задача, родственная решаемой. В этом случае может помочь в составлении плана решения совет.
б) Подумайте, известна ли вам задача, к которой можно свести решаемую. Если такая задача известна решающему, то путь составления плана решения данной задачи очевиден: свести решаемую задачу к решенной ранее. Может оказаться, что родственная задача неизвестна решающему и он не может свести данную задачу к какой-либо известной. План же сразу составить не удается.
Стоит воспользоваться советом: "Попытайтесь сформулировать задачу иначе". Иными словами, попытайтесь перефразировать задачу, не меняя ее математического содержания.
При переформулировании задачи пользуются либо определениями данных в ней математических понятий (заменяют термины их определениями), либо их признаками (точнее сказать, достаточными условиями). Надо отметить, что способность учащегося переформулировать текст задачи является показателем понимания математического содержания задачи.
Некоторые авторы относят к переформулировке задачи и перевод ее на язык математики, т. е. язык алгебры, геометрии или анализа. Это, скорее, формализация задачи, "математизация" ее. К такому приему и приходится часто прибегать при решении многих текстовых задач.
г) Составляя план решения задачи, всегда следует задавать себе (или решающему задачу ученику) вопрос: "Все ли данные задачи использованы?" Выявление неучтенных данных задачи облегчает составление плана ее решения.
д) При составлении плана задачи иногда бывает полезно следовать совету: "Попытайтесь преобразовать искомые или данные". Часто преобразование искомых или данных способствует более быстрому составлению плана решения. При этом искомые преобразуют так, чтобы они приблизились к данным, а данные - так, чтобы они приблизились к искомым. Так, при каждом случае тождественных преобразований данные преобразуются, постепенно приближаясь к результату (искомому). Аналогично уравнение, систему уравнений, неравенство или систему неравенств преобразуют в равносильные, чтобы найти их корни или множество решений.
е) Нередко случается так, что, следуя указанным выше советам, решающий задачу все же не может составить план ее решения. Тогда может помочь еще один совет: "Попробуйте решить лишь часть задачи", т. е. попробуйте сначала удовлетворить лишь части условий, с тем чтобы далее искать способ удовлетворить оставшимся условиям задачи.
ж) Нередко в составлении плана решения задачи помогает ответ на вопрос: "Для какого частного случая возможно достаточно быстро решить эту задачу?" Обнаружив такой частный случай, решающий ставит перед собой новую цель - воспользоваться решением задачи в найденном частном случае для более общего (но, может быть, не самого общего) случая. Так можно поступить, постепенно обобщая задачу до исходной, решаемой задачи. Предполагаемый вариант рассуждений - явное применение полной индукции. Итак, совет: "Рассмотрите частные случаи задачной ситуации, решите задачу для какого-нибудь частного случая, примените индуктивные рассуждения".
3) Реализация плана решения задачи (3-й этап). План указывает лишь общий контур решения задачи. При реализации плана решающий задачу рассматривает все детали, которые вписываются в этот контур. Эти детали надо рассматривать тщательно и терпеливо. Но при этом ученику (решающему задачу) полезно следовать некоторым советам:
а) Проверяйте каждый свой шаг, убеждайтесь, что он совершен правильно. Иными словами, нужно доказывать правильность каждого шага ссылками на соответствующие, известные ранее математические факты, предложения.
б) При реализации плана поможет и совет: "Замените термины и символы их определениями". Так, термин "параллелограмм" заменяется его определением: "Четырехугольник, у которого противоположные стороны попарно параллельны", термин "предел числовой последовательности" для доказательства, например, того предложения, что предел суммы двух последовательностей, имеющих пределы, равен сумме пределов этих последовательностей, можно заменить, и вполне успешно, его определением.
в) При решении некоторых задач помогает совет: "Воспользуйтесь свойствами данных в условии объектов".
4) Анализ и проверка правильности решения задачи (4-й этап). Даже очень хорошие ученики, получив ответ и тщательно изложив ход решения, считают задачу решенной. А ведь получение результата не означает еще, что задача решена правильно. Тем более не означает, что для решения выбран лучший, наиболее удачный, изящный, если можно так выразиться, вариант. По В. М. Брадису, задачу можно считать решенной, если найденное решение: 1) безошибочно, 2) обоснованно, 3) имеет исчерпывающий характер. Поэтому анализ решения задачи, проверка решения и достоверности результата должны быть этапом решения задачи. Итак, два совета: "Проверьте результат", "Проверьте ход решения". Проверка результата может производиться различными способами. Проверяя правильность хода решения, мы тем самым убеждаемся и в правильности результата. Значит, надо выполнить совет: "Проверьте все узловые пункты решения", еще раз убедитесь в истинности проведенных рассуждений.
Второй способ проверки результата заключается в получении того же результата применением другого метода решения задачи, поэтому полезно всегда задавать решающему вопрос: "Нельзя ли тот же результат получить иначе?" Иными словами, стоит последовать совету: "Решите задачу другим способом". Если при решении задачи другим способом получен тот же результат, что и в первом случае, задачу можно считать решенной правильно. К тому же получение различных вариантов решения одной и той же задачи имеет важное обучающее значение.
Изложенные выше советы для решения задач позволяют решать многие задачи, но, разумеется, не могут служить рецептом для решения любой задачи. Эти советы, многие из которых сформулировал Д. Пойа, правильно ориентируют решающего задачи на поиск решения, сокращают время решения многих задач, повышают вероятность отыскания верного и рационального способа решения задач. Единого же рецепта для решения любых задач попросту не существует.
5) От общих советов к частным. Начинать надо с общих вопросов, с общих советов, т. е. именно с тех, которые были приведены выше. Может оказаться, что общие вопросы не окажут помощи какому-то ученику. Тогда надо обратиться к дополнительным, более частным вопросам, так чтобы дойти до вопросов, соответствующих уровню развития и математической подготовке ученика. Переходить к частным, конкретным вопросам надо постепенно, чтобы на долю ученика досталась наибольшая часть работы по решению задачи.
Задавая более частные, дополнительные вопросы, нужно учитывать следующее: вопросы должны быть такими, чтобы они направляли мысль ученика в нужную сторону, заставляя его активно мыслить над решением задачи. Разумеется, предлагая вопросы ученикам, надо предоставить время на обдумывание ответов на эти вопросы.
Ясно, что систематизирующие рассмотрения не только ценны для повторения теории и решения задач, но и имеют еще и явно выраженный исследовательский характер, содержат элементы творчества. Существенно, наконец, что они являются верным средством установления связей между различными математическими вопросами.
Организация обучения решению математических задач
Фронтальное решение задач. Под фронтальным решением задач обычно понимают решение одной и той же задачи всеми учениками класса в одно и то же время. Организация фронтального решения задач может быть различной.
1) Устное фронтальное решение задач наиболее распространено в IV-VII классах, несколько реже, хотя и находит применение, в старших классах средней школы. Это прежде всего выполняемые устно упражнения в вычислениях или тождественных преобразованиях и задачи-вопросы, истинность ответов на которые подтверждается устными доказательствами. В настоящее время учителя математики IV-VII классов почти на каждом уроке проводят "пятиминутки" устных упражнений. К сожалению, часто этим и ограничивается выполнение устных упражнений. А надо отметить, что одной из задач обучения математике является обучение быстрым устным вычислениям. Решения этой задачи надо добиваться на всех этапах обучения, поэтому там, где это возможно (а не только на "пятиминутках" устного счета), вычисления следует выполнять устно. Если ученики научатся устно выполнять вычисления и несложные преобразования, то на уроках математики, физики, химии освободится значительная часть времени, которое сейчас расходуется на нерациональное выполнение вычислений и выкладок.
При организации устных фронтальных упражнений следует учесть, что использование табличек, таблиц, кодоскопа и других средств представления учащимся устной задачи значительно экономит врем; устных упражнений и оживляет уроки математики.
Таблички изготавливает обычно учитель или отдельные ученик) по его заданию. На рисунке 44 приводятся примеры табличек с заданиями для устных вычислений при изучении умножения дробны) и целых чисел (удобные размеры табличек 300 х 150мм).
Таблицы для устных упражнений могут иметь различную форм и применяются неоднократно с различными заданиями.
Как таблички, так и таблицы могут быть изображены на пленке и спроецированы на экран или доску через кодоскоп. Изготовление табличек и таблиц - более трудоемкое дело, чем транспарантов (кодопозитивов), а результаты использования практически равноценны.
2) Письменное решение задач с записью на классной доске. В практике обучения немало таких ситуаций, в которых удобнее, чтобы одну и ту же задачу решали все ученики класса одновременно с решением этой же задачи на доске. При этом задачу на доске может решать либо учитель, либо ученик по указанию учителя. Наиболее часто такую организацию решения задач на уроках математики применяют: а) при решении первых после показа учителем задач по ознакомлению с новыми понятиями и методами; б) при решении задач, самостоятельно с которыми могут справиться не все ученики класса; в) при рассмотрении различных вариантов решения одной и той же задачи - для сравнения и выбора лучшего варианта; г) при разборе ошибок, допущенных несколькими учениками класса при самостоятельном решении задачи и т.д. Во всех этих случаях бывает полезно и коллективное решение (или коллективный разбор решения задач).
Рассмотрим подробнее, как можно провести сравнение различных вариантов решения задачи. Учитель может при фронтальном устном анализе условия задачи наметить вместе с учениками несколько вариантов решения задачи. Некоторые из них как нерациональные могут быть сразу отвергнуты. Другие же неотвергнутые варианты для лучшего рассмотрения, оценки и сравнения стоит записать на доске. В этих целях можно сразу вызвать двухтрех учеников к доске для одновременного решения задачи разными способами (если позволяют размеры доски). Надо только учесть, что руководство решением задачи в этом случае требует некоторого мастерства от учителя: необходимо правильно распределить свое внимание между учащимися, решающими задачу у доски, и остальными учениками класса. Нужно также предусмотреть, чтобы внимание учащихся класса, решающих задачу, не рассеивалось действиями учеников у доски. Можно варианты решения воспроизводить на доске поочередно, но это займет больше времени. Для ускорения работы учитель может сам быстро выполнить на доске необходимые записи некоторых вариантов решения. Возможно также использовать кодоскоп, с помощью которого можно воспроизводить заготовленные заранее записи других решений задачи.
3) Письменное самостоятельное решение задач. Наиболее эффективной является такая организация решения математических задач, при которой ученики обучаются творчески думать, самостоятельно разбираться в различных вопросах теории и приложений математики. Самостоятельное решение учащимися задач на уроках математики имеет многие преимущества.
Во-первых, оно значительно повышает учебную активность учащихся, возбуждает их интерес к решению задач, стимулирует творческую инициативу. Таким образом, повышается эффективность урока. Самостоятельное решение задач развивает мыслительную деятельность учащихся, а в этом заключается одно из основных назначений задач и упражнений на уроках математики. Во-вторых, не имея возможности копировать решение задачи с доски, ученик вынужден сам разбираться в решении задачи, а потому и лучше готовиться к урокам математики. В-третьих, самостоятельное решение математических задач часто сокращает время, необходимое для опроса учащихся на уроках математики, так как оценивать успехи учащихся в некоторых случаях можно и по итогам самостоятельного решения задач. В-четвертых, учитель получает возможность направлять индивидуальную работу учеников по решению задачи, предотвращать ошибки, указывать пути их исправления.
Допустимы различные формы организации самостоятельного решения задач учащимися.
Некоторые учителя так организуют самостоятельные работы по решению задач на уроках математики: учитель подбирает задачи; в процессе работы учитель помогает некоторым ученикам советом, как лучше их решить, другим он советует обратиться к учебнику, третьи справляются с работой без помощи учителя. Учитель все время наблюдает за работой учеников, отмечая, кому из учеников и в чем он помог. Затем самостоятельная работа проверяется и оценивается с учетом степени самостоятельности ученика. При такой организации самостоятельной работы осуществляется и обучение, и контроль знаний по изучаемому разделу математики. Чаще всего учитель заранее предопределяет цели самостоятельных работ по решению задач. Такие работы могут быть обучающими новым знаниям, умениям и навыкам, могут быть предназначены для закрепления изученного и тренировки в применении теоретических сведений, могут быть предложены с целью проверки подготовленности учащихся по изученным вопросам. На обучающих самостоятельных работах по решению математических задач учитель может оказывать помощь отдельным учащимся, а может предложить самостоятельное решение задачи после предварительного ее анализа и составления плана решения.
Существуют и такие формы самостоятельных обучающих работ по математике, при выполнении которых учащиеся самостоятельно изучают небольшой теоретический материал, разбирают образцы решения задач, предложенные учителем, самостоятельно решают аналогичные задачи.
Для лучшего проведения самостоятельных работ учащихся по решению математических задач полезно перед началом такой работы проводить инструктаж, в котором четко указать, что должны выполнить учащиеся в такой работе, каков порядок ее выполнения, сроки и пр. Желательно после проверки правильности самостоятельных решений проанализировать с учащимися результаты такой работы. Это возможно на следующих уроках или на консультациях.
4) Комментирование решения математических задач. Комментирование решения задач заключается в следующем: все ученики самостоятельно решают одну и ту же задачу, а один из них последовательно поясняет (комментирует) решение. Некоторые учителя превращают комментирование в запись под диктовку: один ученик воспроизводит голосом все, что он записывает в тетрадь (без каких-либо пояснений), а все остальные поспешно записывают сказанное им. Ясно, что такое применение комментирования не приносит должной пользы.
Комментирование обозначает объяснение, толкование чего-нибудь. Именно так и следует понимать комментирование при решении математических задач. Ученик-комментатор объясняет, на каком основании он выполняет то или иное преобразование, проводит то или иное рассуждение, построение. При этом каждый шаг в решении задачи должен быть оправдан ссылкой на известные математические предложения. Вот пример комментирования:
"4. Доказать, что сумма трех последовательных натуральных чисел не может быть простым числом.
Обозначим первое из этих чисел буквой n. Тогда два следующих за ним числа запишутся n+1,n+2, так как второе на 1, а третье на 2 больше первого числа. Запишем сумму этих трех чисел и преобразуем ее. Сначала раскрываем скобки, применяя сочетательный закон сложения. Затем приводим подобные члены. Вынося общий множитель (по распределительному закону), получаем результат.
Полученное выражение есть произведение двух множителей 3 и n +1, а потому оно не может быть простым числом ни при каких натуральных значениях n." Такое комментирование приносит явную пользу при решении задач. Учащиеся, даже недостаточно подготовленные по математике, услышав объяснение следующего этапа в задаче, постараются выполнить его самостоятельно. Правда, такое объяснение требует от учеников не только формального решения задачи, но, что очень важно, и понимания существа выполняемого преобразования, активной работы мысли. Но ведь этого и следует добиваться при решении задач.
Индивидуальное решение задач.
1) Необходимость индивидуального подхода при организации обучения решению задач. Фронтальное решение учебных математических задач не всегда приводит к желаемым результатам в обучении математике. При фронтальной работе все ученики класса решают одну и ту же задачу. Для одних учащихся эта задача может оказаться очень легкой, и они при решении такой задачи практически не почерпнут ничего нового. У других, наоборот, задача может вызвать серьезное затруднение. Поэтому необходим учет индивидуальных особенностей учащихся и в связи с этим индивидуальный подбор задач. Задачи следует подбирать и систематизировать так, чтобы, с одной стороны, учитывались возможности и способности ученика, с другой стороны, его способности развивались бы.
Задача учителя заключается, следовательно, в том, чтобы выяснить подготовку, возможности и способности к изучению математики каждого ученика класса и в соответствии с этим организовать решение математических задач. Стоит подчеркнуть эту мысль. Мысль об индивидуализации учебных математических задач по силам и возможностям учащихся. Это позволяет овладеть необходимыми умениями и навыками слабым ученикам и в значительной степени совершенствоваться более сильным.
2) Индивидуализация самостоятельных работ учащихся по решению задач. В условиях, когда все ученики самостоятельно решают одну и ту же задачу, учитель может учитывать индивидуальные особенности учащихся лишь при оказании им помощи в решении задачи, при проверке выполненной работы. При этом не полностью учитываются возможности учащихся. Для более полного учета способностей и математической подготовки учащихся, использования их возможностей необходимо предлагать для самостоятельного решения учащихся не одинаковые, а различные задачи с учетом индивидуальных особенностей ученика. Но поскольку в классе есть примерно равные по успехам в математике ученики, то можно подбирать задачи не для каждого ученика в отдельности (это было бы затруднительно для учителя), а для отдельных групп школьников класса. В этих целях полезно использовать издающиеся теперь "Дидактические материалы по алгебре", "Дидактические материалы по геометрии" для различных классов. При такой постановке обучения слабые ученики, справившись самостоятельно или при помощи учителя с простейшими задачами, обретают веру в свои силы. Сильные же учащиеся имеют возможность совершенствовать свои способности и познания в математике. Разумеется, подбор индивидуальных заданий преследует цель для каждой выбранной учителем группы учащихся составить систему задач. Желательно, чтобы учащиеся не знали о том, кого из них в какую группу определил учитель. Эти группы не должны иметь постоянного состава: по мере овладения необходимыми знаниями учащиеся "переводятся" из группы для менее подготовленных в другую - для более подготовленных.
3) Индивидуализация самостоятельных работ учащихся по устранению пробелов в знаниях математики. Исключительное значение приобретают самостоятельные работы учеников по устранению пробелов в знаниях математики. Такие пробелы могут быть выявлены с помощью проверочных и контрольных работ, а также при решении задач на уроке или дома. Ученикам, работающим над устранением пробелов в своих знаниях по математике, надо указать в тетради допущенные ошибки. При этом сильным ученикам достаточно подчеркнуть неверный результат, а ошибку такой ученик найдет сам. Одним ученикам полезно подчеркнуть допущенные ошибки, а некоторым, наиболее слабо подготовленным, исправить. В тетрадях указываются разделы учебника, которые ученик обязан восстановить в своей памяти, и выписываются .задачи (можно указать номера задач из задачников или учебников), которые надлежит ученику решить, чтобы восполнить имеющийся пробел в знаниях и умениях. Конечно, задачи подбираются с учетом причин, вызвавших ошибку. Дело в том, что одна и та же ошибка может быть допущена по различным причинам и устранять надо не ошибку, а причину, ее породившую. Такая организация решения задач по ликвидации пробелов в знаниях школьников приносит большую пользу, чем фронтальные работы над ошибками. При этом учитываются как индивидуальные особенности учащихся, так и характер изучаемого материала.
4) Домашнее решение задач учащимися. Содержание задач и упражнений, предлагаемых для домашней работы учащихся, должно быть подготовлено предшествующей работой на уроке. Это не означает, что для домашнего решения должны предлагаться лишь задачи, аналогичные решенным в классе. Такие домашние задания мало помогают усвоению математики. Решая домашние задачи "как в классе", ученики в лучшем случае прибегают к аналогии, а одной аналогии для обучения решению задач недостаточно. При такой работе ученики, как правило, сначала решают задачи (выполняют письменное задание), а затем читают учебник по математике. Порядок же должен быть иной: сначала повторение по учебнику теоретических сведений, затем решение задач.
Домашнее задание имеет целью не только повторение изученного на уроке, но и дальнейшее совершенствование математических знаний, умений и навыков. С учетом этого оно и должно быть составлено. Учитель дает необходимые указания по решению домашних задач, однако не устраняет всех трудностей, которые должны преодолеть учащиеся в процессе решения домашних задач. Ученики, решая задачи самостоятельно дома, обязаны проявлять свою инициативу, смекалку и настойчивость, мобилизовать для решения задач свои знания. Домашние задания по решению задач целесообразно связывать с углублением и уточнением изученного, с открытием каких-то новых его сторон.
Поскольку ученики обычно имеют индивидуальные особенности, различную подготовку по математике, следует индивидуализировать домашние задания по решению математических задач. При этом надо учитывать многие факторы: ученики при решении домашних задач должны устранить пробелы в знаниях (у кого они имеются), закрепить приобретенные на уроке знания, совершенствовать их. Через индивидуальные домашние задания (параллельно с работой на уроке) можно выявить наклонности отдельных учащихся, воспитывать у них увлечение математикой. Посильные же задания для слабых и отстающих учащихся помогут им преодолеть многие трудности в обучении решению задач. Надо заметить, что ученики с особым желанием решают задачи, предложенные им в индивидуальном порядке. Такие задания можно заготовить на специальных карточках.
Заключительный этап в решении учебной математической задачи. Для учебных задач особое значение имеет не получение ответа, а процесс нахождения его, процесс переработки входной информации в выходную. Ответ особенно существен для задач, которые человеку приходится решать в практической деятельности, для учебной же задачи на первом месте стоят поиски решения, осуществление его и познавательные выводы из проделанной работы. Поэтому необходим заключительный этап работы над учебной задачей.
Основным содержанием его должно быть осмысление выполненного решения, формулирование и решение других задач (если оказывается возможным), явно связанных с первой, порождаемых ею, и извлечение из всей проделанной работы выводов о том, как находятся и выполняются решения.
1) Необходимость обсуждения задачи и ее решения вытекает из основного назначения учебных математических задач. При обсуждении решения задачи нужно остановиться на следующих вопросах:
а) Более полное использование условия задачи. При решении многих задач следует стремиться к достаточно полному использованию содержащейся в них входной информации. Практически это означает, что по одному и тому же условию полезно решать не одну, а несколько задач, целью которых является получение различных результатов. Значит, многие задачи должны явно содержать несколько вопросов. В противном случае целесообразно задавать и дополнительный вопрос: "Что еще можно узнать из условия задачи?"
Можно сделать вывод, что в методическом отношении гораздо полезней многовопросные задачи. Действительно, многовопросность развивает основательность мышления. Она приучает школьников к установлению многосторонних связей в рассматриваемых ситуациях. Многовопросные задачи позволяют более экономно использовать время, отведенное для решения задач на уроках математики, так как на усвоение содержания задачи при этом расходуется гораздо меньше времени, чем при решении нескольких различных по условию одновопросных задач.
б) Обсуждение работы по поиску решения. Основная трудность при решении математической задачи состоит в нахождении решения, а не в осуществлении его. Поэтому оказывается необходимым выявление идеи (главной мысли), положенной в основу решения (как эта идея возникла? .Что помогло найти решение?), иначе говоря, нуждается в обсуждении подход к решению задачи, поиск решения.
Приступая к решению задачи, ищут прежде всего ведущую идею (принцип), из которой следует исходить. Если такая идея найдена, то дальнейшее решение представляет собой ее конкретизацию, воплощение. Но может случиться так, что найденная идея не обеспечивает достижения цели. Тогда ищут иные идеи, подходящие для данной задачи, и испытывают их. Вот эти поиски и отбор идей, из которых можно исходить при решении задач, наверное, и составляют основную трудность решения. Поэтому важно учесть и использовать факторы, помогающие этим поискам, и преодолеть факторы, мешающие им.
Чтобы иметь возможность выбрать идею решения задачи, нужно располагать достаточным запасом таких идей. Этот запас и создается в практике решения задач (при обсуждении решений). Успешные действия при решении подкрепляются, и добытая ценная информация фиксируется в долговременной памяти. Так накапливается хороший опыт решения задач.
Нужно учить школьников пользоваться запасом ведущих идей для решения разнообразных задач, учить выбирать и применять нужную идею. Многие из таких идей были высказаны в качестве советов и вопросов решающему задачу. После решения задачи полезно еще раз обратить внимание учащихся на такие идеи, приводящие к удачному решению задачи.
в) Выявление связей с ранее решенными задачами. При решении математических задач часто используются методы и результаты решения предшествующих задач. Именно поэтому полезно выявление связей рассматриваемой задачи с решенными ранее. Но не только поэтому. Сравнивая задачу с решенными ранее сходными задачами, ученики выявляют их общие и различные черты, лучше усваивают идею решения данной задачи, глубже познают метод решения класса сходных задач и таким образом готовятся к решению следующих задач.
2) Вторая часть заключительного этапа в решении задачи - поиски и осуществление новых способов ее решения, их сравнение и выбор лучшего варианта решения..
Стоит только отметить, что более эффективного пути для воспитания гибкости математического мышления и находчивости, чем путь поисков различных решений задач, пожалуй, нет.
3) Третья составная часть заключительного этапа работы с задачей - формулирование и решение некоторых других задач, "порожденных" разобранной. Мы имеем здесь в виду обобщения и специализации исходной задачи, а также получение других задач из данной в результате частичного изменения ее условия.
Это могут быть задачи, в которых часть данных исходной задачи принимается за искомое, а некоторые искомые считаются данными; задачи, полученные заменой одних объектов другими (без изменения искомых) и т. д. Так возникают задачи, обратные данным, суперпозиции задач, серии задач с различными данными, приводящими к одному результату, и т. п. Эту часть заключительного этапа можно назвать развитием темы задачи. Трудно переоценить значение развития темы задачи для воспитания математического мышления учащихся, развития познавательных способностей, формирования личности ученика. Очень полезно развитие темы задачи и в практическом отношении, так как изменения, обобщения и специализации задач воспитывают творческое отношение к тем задачам, которые ставит перед нами жизнь, делают наше мышление инициативным и более оперативным. В методическом отношении развитие темы задачи особенно ценно тем, что приучает учащихся к переконструированию задач, а это, как известно, основной прием поиска решений. Приведем примеры развития темы задачи.
Пример. Не изменяя основания, преобразуйте данный параллелограмм в равновеликий ему параллелограмм.
Эту у можно специализировать, например, так: а) Дан параллелограмм. Постройте ромб, равновеликий данному параллелограмму и имеющий своей стороной основание этого параллелограмма, б) Постройте прямоугольник, равновеликий данному параллелограмму и имеющий то же самое основание.
Пример. Периметр прямоугольника 2 р. Каким должен быть этот прямоугольник, чтобы площадь его была наибольшей? Обращенной задачей по отношению к данной будет такая:
Площадь прямоугольника 5. Каким должен быть этот прямоугольник, чтобы периметр его был наименьшим?
Пример 4. Задача: "Восстановите равнобедренный треугольник по одной из его вершин и основаниям двух высот" - допускает следующие изменения: а) восстановите равнобедренный треугольник по двум его вершинам и основанию одной из высот, б) восстановите равнобедренный треугольник по основаниям двух высот, лежащим на его боковых сторонах, и двум отличным от вершин точкам основания треугольника, в) восстановите равнобедренный треугольник по основаниям трех его высот, г) восстановите треугольник по основаниям трех его высот. Изменения этой задачи ведут к обобщению как задачи, так и метода ее решения. а
Развитие темы задачи в качестве заключительного этапа работы с ней особенно ценно при творческом подходе учителя к обучению решению задач.
4) По отношению к некоторым задачам с ярко выраженными особенностями (по содержанию и приемам решения) следует говорить и о четвертой части заключительного этапа. Мы имеем в виду прежде всего поучительные выводы (фиксации) из проделанной работы о том, как в подобных случаях находится и осуществляется решение, а также какие особенности задач подсказывают прием решения.
К этой части следует отнести и систематизацию различных возможных подходов к задачам определенного содержания. В ходе работы по решению серии связанных между собой задач наступает момент, когда оказывается очень полезным подвести итоги проделанной работы, систематизировать приемы решений, полнее выявить возможности для осуществления решений задач рассматриваемого вида и сходных с ними.
Ясно, что систематизирующие рассмотрения не только ценны для повторения теории и решения задач, но и имеют еще и явно выраженный исследовательский характер, содержат элементы творчества. Существенно, наконец, что они являются верным средством установления связей между различными математическими вопросами.
Глава 9
Урок математики
Урок как основная форма организации обучения в школе. Специфика уроков математики. Типы урока. Подготовка учителя к урокам
-
Организация обучения математике
-
Урок, его структура. Основные требования к уроку. Типы уроков
Организация обучения математике
Помимо анализа содержания курса школьной математики, в задачи методики математики входит исследование и описание значительного количества вопросов, связанных с обучением математике. В числе этих вопросов одно из самых существенных мест занимает вопрос об организации обучения математике, рассмотрение которого с различных сторон является основной темой данной главы. Наибольшее внимание в ней отводится описанию наиболее распространенной организационной формы обучения - уроку. Рассматриваются различные виды уроков, выясняются основные их функции в процессе обучения математике, анализируются возможности использования различных методов обучения при проведении уроков каждого типа. В соответствии с базисной установкой педагогики на формирование интереса к учению рассматриваются организационные приемы активизации процесса обучения и повышения заинтересованности в нем учеников. С этих позиций описаны вопросы организации домашней работы учеников и различных видов контроля. В данной главе кратко описываются также особенности организации процесса обучения математике в вечерних (сменных) средних общеобразовательных школах и средних профтехучилищах.
Назад
Урок, его структура. Основные требования к уроку. Типы уроков
Сущность урока математики. Основной формой организации учебно-воспитательной работы с учащимися в советской средней шко-ле является урок. Сущность его раскрывается в дидактике.
Понятие "урок" имеет характерные черты (основные характери-стики): цель, содержание, средства и методы обучения, организация учебной деятельности.
Главную роль среди основных характеристик играют цели урока: образовательные, воспитательные и развивающие. К образовательным целям относится формирование математических знаний, умений и навыков. Но формировать надо не только математические, но и общеучебные знания, умения и навыки, позволяющие более рационально организовать обучение математике. В единстве с обучением осуществляются цели воспитания и развития личности школьника.
Учебные программы по математике предусматривают решение определенных воспитательных задач. Для усиления воспитывающего влияния обучения учитель обязан тщательно анализировать воспитательные возможности математики и выделять воспитательную цель каждого урока.
В соответствии с целью урока отбирается содержание обучения, и прежде всего содержание урока. Поставить цель урока, рационально отобрать учебный материал учителю помогают учебные программы, учебники, методические пособия, дидактические материалы и др. Специфика учебного предмета "математика" такова, что изложение математического материала на уроке строится с сохранением логики раскрытия этой темы в школьном учебнике.
Выбор оптимальных методов обучения - одна из трудных методических задач. В педагогической литературе имеются рекомендации по выбору оптимальных методов обучения. Вот одна из таких рекомендаций:
"Выбор метода не будет оптимальным, если избранный метод не удовлетворяет хотя бы одному из условий, от которых он зависит:
1) цель урока (обучающая, воспитывающая и развивающая);
2) особенности содержания изучаемого материала (сложность, новизна, характер);
3) особенности учащихся класса (уровень развития мышления. уровень знаний, умений, сформированность навыков учебного труда уровень воспитанности учащихся и др.);
4) оснащенность кабинета дидактическими материалами, техническими средствами обучения;
5) эргономические условия (время проведения урока по расписанию, наполняемость класса и т. д.);
6) индивидуальные особенности учителя (черты характера, уровень овладения тем или другим методом, его отношения с классом)".
Учебный процесс предполагает органическое единство средств методов и приемов работы с организационными формами обучения Каждому методу, приему обучения соответствует своя организационная форма, определяющаяся отношениями между учителем и учащимися и учащихся между собой.
Учитель управляет всей учебной деятельностью на уроке, используя при этом общие (работа со всем классом), групповые (звено, брига да и т. д.) и индивидуальные формы ее. Указанные выше формы организации учебной деятельности выступают на уроке в различных сочетаниях и последовательностях.
В современных условиях обучения достаточно четко ставится вопрос о применении таких организационных форм работы на уроке которые обеспечивали бы эффективное приобретение не только знаний, умений и навыков, но и ценного опыта нравственных и коллективистских отношений.
Огромная роль здесь принадлежит коллективным формам работы которые позволяют уплотнять время урока, создают ситуации взаимообучения учащихся и существенно влияют на развитие личности.
О структуре урока. Рассматривая урок с точки зрения логики процесса обучения, мы придем к понятию "структура урока". В дидактике исследуется понятие "общая дидактическая структура", сущность и компоненты которой усматриваются из схемы:
-

Формирование новых знаний и способов действий

Применение - формирование умений и навыков
Число компонентов общей структуры неизменно - их всегда три. Будем говорить теперь о структуре конкретного урока математики. По сути своей она остается той же, но форма ее может быть изменена в силу многих причин. Одна из таких причин - это необходимость детализации компонентов общей структуры.
Каждый из компонентов общей структуры слишком широк по содержанию и объему. Например, под актуализацией прежних знаний и способов действий понимается не только воспроизведение ранее изученных знаний и способов действий, но и их применение в новых ситуациях, стимулирование познавательной активности учащихся, проверка учителем уровня усвоения знаний и т. д. Столь же широки два других компонента общей структуры урока. Разукрупняя компоненты общей дидактической структуры, мы фактически получаем более конкретные шаги (этапы) процесса обучения на уроке, которые могут выступать в различных последовательностях и взаимосвязях.
Используя понятие "структура урока математики", важно выделить из множества возможных основные этапы урока :
1. Постановка цели урока перед учащимися.
2. Ознакомление с новым материалом.
3. Закрепление нового материала: а) на уровне воспроизведения информации и способов деятельности, б) на уровне творческого применения и добывания знаний.
4. Проверка знаний, умений и навыков.
5. Систематизация и обобщение изученного материала (по теме, разделу и т.п.).
Для каждого урока обязательным является первый этап - постановка цели, выбор остальных обусловлен целью урока.
Опираясь на мотивы учения, необходимо привлечь учащихся к предстоящей на уроке работе, вызвать потребность в познании, в самоконтроле и самооценке своей деятельности и т. д. В течение всего урока учитель изучает реакцию учащихся на все происходящее на уроке.
Мы знаем, что отдельный урок - это только одно звено в цепи других уроков по данной теме или разделу школьного курса. Но, с другой стороны, урок и даже каждый его этап - это нечто целое, законченное.
Основные требования к уроку математики. Анализ структуры урока показывает, что ведущую роль в ней играет цель урока: именно цель урока определяет его структуру, задает отношение между этапами урока, соподчиняет их и объединяет в единое целое.
Итак, одно из главных требований к уроку - его целенаправленность.
В литературе по методике преподавания математики можно найти конкретные рекомендации по постановке общей цели урока, суть которой сводится к следующему: вначале выделяется основная дидактическая (учебная) цель, исходя из которой выявляются возможности для установления целей воспитания и развития учащихся на уроке математики через его математическое содержание.
Целенаправленно и планомерно должно осуществляться не только обучение математике, но и воспитание на уроках математики.
Для практики обучения очень важно, чтобы цель урока, поставленная учителем, была понята учеником. Осознанные учеником цель, учебная познавательная задача помогают ему действовать активно и ускоряют процесс получения результата своих действий.
Очевидно, что одна структура урока может обеспечить более интересную и активную деятельность учащихся, чем другая. И надо стремиться к тому, чтобы урок оптимально обеспечивал активную познавательную деятельность учащихся.
Общая цель урока (единство обучения, воспитания и развития) порождает новые по содержанию и структуре уроки математики. Кратко опишем структуру двух уроков, проводимых с целью "учить учиться".
Пример 1. Учитель X. в системе уроков, проводимых в младших классах с целью "учить учиться", предусматривает специальные уроки: "Как я учу уроки по математике".
В один день недели у пятиклассников было запланировано провести два урока математики. На первом уроке вводилось новое для учащихся правило сложения рациональных чисел с разными знаками и делались первые шаги по выработке умений применять полученное правило на практике. В конце первого урока пятиклассники получили задание на дом: проработать текст учебника, выполнить упражнения. Учащиеся выполняли его не дома, а на следующем уроке математики.
Учитель дает целевую установку: "Ребята, сейчас мы будем вместе выполнять домашнее задание".
Договорились о последовательности его выполнения: прежде всего необходимо проработать текст из учебного пособия, затем выучить правило сложения, но не путем многократного повторения его, а в процессе выполнения упражнений, проговаривая правило вначале вслух, а потом про себя.
Учащиеся с IV класса учатся читать учебную книгу по специальному образцу, подробное описание которого можно найти в книге Н. И. Борисова.
Каждый ученик имеет в учебнике закладки - чистые полоски бумаги, длины которых совпадают с длиной страницы, а ширина - с шириной ее поля. Одна такая полоска совмещается с полем читаемой страницы. Чтение текста ведется с карандашом в руках. При первом чтении на пронумерованной полоске делаются разметки прочитанного: главная мысль, например, отмечается круглыми скобками, особо важные места - восклицательным знаком или двумя вертикальными чертами и т. п. При повторном чтении ученик стремится разобрать трудные места в тексте, перечитать главные мысли, сформулировать основные вопросы и записать ответы на них в рабочей тетради и т. д.
В работе над текстом прошлого урока учащиеся отметили самое главное - правило сложения и образцы выполнения действия. Затем в соответствии с образцами, проговаривая шаги, указанные в правиле, они выполняют сложение.
Так постепенно учащиеся приобретают умения "учить уроки".
Пример 2. В старших классах возможно, исходя из допущения, что ученики умеют извлекать новые знания из математической книги, построить урок так, что на первый план выступает обсуждение нового материала, который изучался учениками самостоятельно дома. Учащиеся вначале задают вопросы по самостоятельно проработанному новому материалу, показывают, как они выделяли главное, делали выводы и т. д.
Второе важное требование к уроку математики - это рациональное построение его содержания. Бесспорно, что на уроке математики главным является его математическое содержание, которое должно глубоко отражать логику данного учебного предмета и быть определяющим во всем, что делается на уроке. Именно на базе математического содержания урока формируются у учащихся три вида умений и навыков: математические, общеинтеллектуальные (приемы умственной деятельности), умения и навыки учебной деятельности.
Важно обучать учащихся не столько математическим фактам самим по себе, а приобщать учащихся к методам математики, развивать у них мышление.
Если, например, планируется познакомить учащихся на уроке с новой теоремой и ее доказательством, то на все содержание урока надо посмотреть с точки зрения обучения дедуктивным умозаключениям, общим методам доказательства и т. п. Это же математическое содержание учитель анализирует и с точки зрения возможностей продвижения учащихся в овладении учебными действиями, например действиями "получение следствий" и "подведение под понятие".
Обучение всем видам содержания, умений и навыков должно вестись планомерно, в определенной системе.
В каждом уроке важно выделить стержневую идею его математического содержания и вокруг нее сгруппировать все остальное. Третье требование к уроку - это оптимальный выбор средств, методов и приемов обучения и воспитания на уроке.
Большая роль в отборе средств, методов и приемов работы на уроке отводится учителю. Успех дела зависит здесь во многом от того, насколько глубоко проникает учитель в специфику учебного материала, насколько умело ставит учебные познавательные задачи, учитывая при этом уровень общей и математической подготовки учащихся, их личностные качества и прогнозируя результаты использования того или иного средства, метода или приема.
Выбирая средства, методы и приемы обучения, необходимо помнить, что нельзя их универсализировать. Ни одно из средств, ни один из методов, взятых изолированно, не смогут обеспечить достижения целей обучения.
Специфика самого предмета "математика" такова, что основным в обучении являются наглядно-вербальные средства в различных сочетаниях. Урок математики характеризуется комплексным применением наглядных и технических средств обучения.
Насущные задачи самообразования усилили роль печатных средств на уроках математики. В частности, усилено внимание к работе с учебной книгой непосредственно на уроке. Об этом уже шла речь выше.
Абстрактный характер математических понятий затрудняет восприятие их учащимися. Одним из средств преодоления затруднений такого рода является моделирование.
В школьном курсе математики для раскрытия сущности понятий и отношений между ними используются модели различного вида: предметные, графические, знаковые и др. Среди разнообразия их важно уметь выделять главные, основные. К таким можно отнести координатную прямую, координатную плоскость и др.
В методической литературе нередко встречается термин "опора", который трактуется как вспомогательное средство обучения. Так, вышеупомянутые модели по сути своей есть также своеобразные опоры. В каждой теме школьного курса математики можно выделить различного рода опоры (наглядно-образные, условно-символические и др.), назначения которых весьма разнообразны. На уроках математики каждый раз, когда встает проблема рассказать просто о сложном, используются наглядно-образные опоры (рисунки, чертежи, подчеркивающие самое главное, характерное для данного явления или понятия).
Опоры различного рода могут строить сами учащиеся. Например, они могут дать схему доказательства теоремы или решения задач какого-то вида.
Урок математики характеризуется разнообразием форм организации учебной деятельности учащихся.
Задачи самообразования, самоконтроля и самооценки своего труда требуют развития индивидуальных форм организации учебной деятельности.
Берутся на вооружение и групповые формы работы учащихся на уроках. Правильно организовать работу учащихся в группах - серьезная oметодическая проблема. Недопустимо, чтобы активными в неоднородных группах были только более сильные учащиеся, чтобы они навязывали другим членам группы свои мнения, решения проблем, давали списывать готовые решения задач и т. п. Непродуманная групповая работа может нанести большой вред обучению и воспитанию. Хорошо, если сильные направляют работу более слабых учащихся данной группы, помогают им продвигаться вперед, следят за успехами других.
В зависимости от поставленной цели группы могут формироваться весьма различными способами.
Типы уроков. В современной дидактической и методической литературе чаще всего применяется классификация по основной дидактической цели урока.
Пусть основная дидактическая цель урока - это ознакомление учащихся с новым материалом. В соответствии с этой целью центральным этапом урока является ознакомление с новым материалом. Остальные этапы могут либо отсутствовать, либо быть менее значимыми по сравнению с основным.
Если основная дидактическая цель урока - закрепление изученного материала, то урок естественно отнести к виду уроков по закреплению знаний и т. д. Идя таким путем, мы получим четыре основных типа уроков математики:
1. Урок по ознакомлению с новым материалом.
2. Урок по закреплению изученного.
3. Урок проверки знаний, умений и навыков.
4. Урок по систематизации и обобщению изученного материала. Заметим сразу, что рассматриваемая классификация исключает уроки комбинированного типа.
Возможны разновидности указанных выше основных типов уроков. Например, урок по закреплению знаний делится на два подтипа: урок тренировочного характера и урок творческого применения знаний. Такое подразделение связано с репродуктивным и продуктивным уровнями применения знаний. Но это не означает, что урок тренировочного характера не содержит продуктивных методов, а на уроке творческого применения знаний исключаются репродуктивные методы.
При обучении математике закрепление знаний проходит в основном через решение задач, поэтому уроки закрепления знаний называют уроками по решению задач.
В практике обучения довольно часто выделяют и говорят как о самостоятельных видах об урокахлекциях, уроках самостоятельной работы учащихся, уроках общественного смотра знаний и др.
Рассматривая эти уроки с точки зрения их основной дидактической цели, мы видим, что все они являются лишь разновидностями одного из четырех указанных выше основных типов. Урок-лекция - это урок по ознакомлению с новым материалом, а урок общественного смотра знаний - урок проверки знаний, умений и навыков и т. д. Рассмотренная классификация уроков по их основной дидактической цели не лишена недостатков. Например, названия основных типов уроков в этой классификации ничего не говорят .ни о внутренней организации учебного процесса, ни о способах проведения урока, Вот почему для характеристики уроков используются различные классификации и даже их совокупности.
На практике, кроме выше рассмотренной, получила распространение еще классификация уроков по способам их проведения.
Здесь выделяются, например, урок повторения, урок-беседа, урок - контрольная работа, комбинированный урок и т. д.
Чаще всего, характеризуя какой-либо конкретный урок, исходят из двух классификаций - по основной его дидактической цели и по способам проведения. Например, в самом названии "урок-лекция" усматривается и его основная цель, и способ его проведения.
Бесспорно, что ни одна из классификаций не может всесторонне и исчерпывающе охарактеризовать урок.
Глава 10
Средства обучения математике. Кабинет математики
-
Наглядные пособия и технические средства информации прямой связи в преподавании математики
-
Технические средства обратной связи в обучении математике
Наглядные пособия и технические средства информации прямой связи в преподавании математики
Наглядность в преподавании математики. Модели и таблицы. Технические средства прямой связи для статической демонстрации (эпи- и диапроекторы, кодоскопы) и дидактические материалы к ним. Кино и телевидение в преподавании математики
Облегчение восприятия и усвоения учащимися математических знаний может быть достигнуто разумным использованием различных средств и пособий наглядности - моделей, таблиц, чертежей и рисунков, предназначенных для показа с помощью разнообразных проекционных устройств, демонстрацией специальных кинофильмов и т. д.
Однако чрезмерно частое использование средств наглядности может привести к задержке развития у школьников абстрактного мышления, затруднениям при решении задач, требующих развитого пространственного представления, и т. д.
Естественно, невозможно дать универсальные рецепты "соблюдения меры" в использовании тех или иных средств наглядности. В каждом отдельном случае эта мера определяется практически. Пусть, например, решается некоторая стереометрическая задача в классе. Сначала учащиеся должны самостоятельно вычертить чертеж по условию задачи. Некоторые справляются с этим заданием, другие затрудняются. Используя пространственные представления учащихся, учитель пытается добиться выполнения этого задания, проводя дополнительное объяснение. Для тех, кто все еще не понимает задачу, выполняется чертеж на доске, демонстрируется кадр диафильма или диапозитив или же показывается модель.
В другом случае, когда, например, ученики впервые знакомятся с тем или иным понятием, например геометрическими фигурами, целесообразно провести демонстрацию этих понятий по модели на более раннем этапе изложения. Но учителю не следует стараться любой вопрос, любую задачу подкреплять соответствующей наглядностью в той или иной форме.
В распоряжении учителя математики в настоящее время имеются различные средства наглядности, выпускаемые промышленностью. В этих условиях необходимость в изготовлении самодельных наглядных пособий понемногу уменьшается, но вряд ли отпадет совершенно.
Во-первых, изготовление некоторых средств наглядности может быть легко связано с решением ряда вычислительных и геометрических задач и проводиться лабораторно. В этом случае нельзя пренебрегать обучающей функцией этой работы. Мы имеем в виду прежде всего изготовление разнообразных многогранников, тел вращения и особенно их разверток. Важность умения практически рассчитать развертку совершенно очевидна.
Во-вторых, "номенклатура" наглядных пособий, которые могут быть легко изготовлены на месте, всегда шире, чем фабричных, и в значительной мере зависит от вкусов, взглядов умений самого учителя. В преподавании математики можно выделить следующие средства наглядности: а) модели и макеты; б) (настенные) таблицы; в) диапозитивы (слайды), кодограммы и дидактические материалы для эпипроектирования; г) диафильмы; д) кинокольцовки, кинофрагменты и кинофильмы. Средствами наглядности могут служить также разнообразные геометрические, вычислительные и измерительные приборы, которые мы специально рассматривать не будем. Хотя различные средства наглядности обладают большим сходством дидактических функций, можно заметить и некоторые особенности в практическом использовании каждого из них.
Плоские и объемные модели хорошо известны каждому преподавателю математики. Они представляют собой натуральные объекты для наблюдения и непосредственного изучения и применяются во всех классах. Эффективность применения моделей становится особенно ясной, если вспомнить такие образцы, как шарнирные параллелограмм и ромб, равносоставленные фигуры, треугольник, основание которого сохраняется постоянным, а вершина перемещается параллельно основанию (стороны его образуются резиновой нитью или шнуром) - в планиметрии, динамические модели тел вращения, модели многогранников, различные стереометрические наборы, прозрачные и полупрозрачные модели сечений, вписанных и описанных тел и т. д.-в стереометрии, модель термометра - для демонстрации свойств целых чисел и т. д.
Настенные таблицы по математике используются для решения различных дидактических задач, но основная их особенность - возможность размещения на стенах классной комнаты на длительное время. Многократное их использование обеспечивает более глубокое запоминание содержащегося в них материала, с одной стороны, и дает возможность быстро навести необходимую справку - с другой.
В настоящее время практически каждая школа располагает разнообразными техническими средствами прямой связи, в частности диа- и эпипроекторами, а в самое последнее - время на вооружение школ стало поступать новое мощное проекционное устройство - кодоскоп.
Между диапозитивами и диафильмами много общего. Диафильм, разрезанный на отдельные кадры (слайды), представляет собой основу диапозитива. Но если диапозитивы можно демонстрировать в любой последовательности, которая часто определяется самим ходом учебного процесса, то последовательность демонстрации кадров диафильма является значительно более жесткой. В соответствии с этим диафильмы целесообразнее использовать при изложении материала, требующего определенной логической последовательности, в частности при изложении различных теоретических положений, а также при решении постепенно усложняющихся и тесно между собой связанных задач практического характера. Диапозитивы используются в тех случаях, когда последовательность их применения определяется в ходе работы - например, при решении некоторой задачи обнаружилось незнание учащимися некоторых свойств, которые легко усматриваются с помощью диапроектирования. Тут же извлекается соответствующий диапозитив и демонстрируется. Если намечалось решить несколько тесно связанных между собой задач, но в ходе работы оказалось, что ученики усвоили метод их решения раньше, чем предполагалось, то соответствующие слайды пропускаются. Число диафильмов и наборов диапозитивов, выпускаемых промышленностью, неуклонно увеличивается. Сведения о новых диапозитивах и диафильмах регулярно публикуются в журнале "Математика в школе". Учитель математики должен регулярно пополнять школьную фильмотеку через магазины наглядных пособий.
С помощью эпископов могут демонстрироваться непрозрачные чертежи, рисунки, записи и т. д. Слабая освещенность в этих проекционных устройствах требует специального затемнения помещения. Для демонстрации диапозитивов и диафильмов имеются такие проекционные устройства, как диапроекторы "ЛЭТИ" или "Свет" с мощными источниками освещения, которые можно применять почти без затемнения. В этом смысле применение новых проекционных устройств для демонстрации материалов на прозрачной подложке имеет значительные преимущества, хотя и не заменяет возможностей эпипроекционных устройств.
В последнее время появились новые проекционные устройства -o кодоскопы. Помимо значительно более яркого изображения, кодоскоп имеет ряд важных особенностей и преимуществ, резко отличающих его от проекционных устройств других типов.
Прежде всего, кодоскоп допускает демонстрацию разнообразнейших материалов на прозрачной подложке, в том числе текста и рисунков, заранее заготовленных или наносимых учителем на прозрачную карточку или ленту непосредственно на уроке, в процессе изложения, причем учитель при этом обращен лицом к классу, а изображение проектируется на переднюю стенку класса или непосредственно на классную доску (желательно, окрашенную в светлые тона).
Заранее заготовив изображение основных фрагментов некоторого чертежа и спроектировав его на доску, учитель может уже на доске дочертить недостающие его части, сечения, списанные фигуры и т. д., чем достигается важный педагогический эффект.
Промышленность уже выпускает наборы дидактических материалов для кодоскопов (назовем их кодограммами), кодограммы легко могут быть изготовлены и на месте. Важной особенностью кодоскопа является возможность наложения нескольких кодограмм друг на друга, чем достигается эффект присутствия при построении и создаются большие возможности для составления' условий задач на комбинации геометрических тел, на графическое решение уравнений и их систем, на построение сечений и т. д. Представляет интерес и возможность смещения кодограмм друг относительно друга при их совмещенном показе, например при изложении тем о геометрических преобразованиях.
Новые возможности достигаются при использовании кодоскопа в ходе, опроса учеников. Нескольким ученикам раздаются прозрачные карточки, на которых шариковыми ручками или специальными карандашами ученики записывают ответы. После этого записи учеников демонстрируются через кодоскоп перед всем классом. Если при этом окажется, что требуется внести исправления, ученик возвращается со своей кодограммой на место, где и устраняет недочеты.
Недостаточное количество кодоскопов может быть уже сейчас частично компенсировано довольно простой переделкой в кодоскоп школьного эпидиаскопа. Более подробно о дидактических возможностях кодоскопа говорится в статье "Применение кодоскопа па уроках математики"
Там, где нужно продемонстрировать некоторое математическое свойство в динамике, в процессе изменения некоторого объекта, незаменимой является кинокольцовка, кинофрагмент, кино-фильм. Число дидактических материалов, выпущенных для кино-проектирования, также довольно значительно. Некоторые неудобства причиняет необходимость затемнения помещения при кино-демонстрации. Оно устраняется частично применением "дневных экранов" и "дневных киноустановок", изготовляемых во многих школах. В дальнейшем положение улучшится в результате применения новых мощных источников света, осваиваемых в настоящее время предприятиями, изготовляющими школьное оборудование и киноустановки. Следует помнить общее правило: кинодемонстрация органически вписывается в урок, если она длится недолго. В этом смысле кинокольцовки и короткие кинофрагменты предпочтительнее кинофильмов. Желательно также наличие наиболее характерных кадров кинофрагментов в виде отдельных слайдов - для продолжительной демонстрации их с помощью статических проекторов. Сочетание статического и динамического показа во многих случаях обеспечивает более высокий уровень усвоения.
Некоторые перспективы в области преподавания математики имеет учебное телевидение. Так, телевидение возможно применять для организации серии учебных телепередач с участием наиболее квалифицированных преподавателей одновременно для ряда школ и классов. Отметим, что в течение самого последнего времени в школу начинают проникать замкнутые, т. е. не имеющие выхода в эфир, телевизионные системы. Эти устройства имеют большое будущее для распространения передового опыта, проведения педагогических исследований и т.д., а также в преподавании физики, химии и других дисциплин. Предполагается, что высшей формой организации использования разнообразных технических средств обучения со временем станет школьный технический центр, оборудованный замкнутой телевизионной системой. Из этого центра будет, в частности, удобйо организовать показ кинокольцовок, фрагментов и т. д. непосредственно на экранах телевизоров, расположенных в классных комнатах. В этом случае отпадает проблема затемнения и транспортировки из класса в класс кинопроекционных устройств.
Все возрастающая роль в обучении технических средств, наглядных пособий, вспомогательных дидактических материалов приводит к необходимости создания в каждой школе специализированного математического кабинета (см. [1.63], [1.16]).
Технические средства обратной связи в обучении математике
Роль и место обратной связи в процессе обучения. Способы ввода информации в обучающие устройства. Простейшие технические средства обратной связи. Автоматизированные классы
Проверка знаний и учет успеваемости всегда были важными компонентами процесса обучения на всех уровнях. Но важность этих компонентов становится особенно очевидной в свете кибернетического подхода к интерпретации учебного процесса. Как известно, кибернетика - наука об управлении и связях в сложных динамических системах и процессах, к которым относится и система "учитель - ученик". Под связями здесь подразумеваются прием, преобразование, хранение, использование и передача информации.
С кибернетической точки зрения система "учитель - ученик" в процессе обучения представляется так: объясняя новый учебный материал на основе некоторой развернутой программы своих действий, учитель передает учащимся новые знания, формирует у них необходимые умения и навыки, способность применять полученные знания в практической деятельности. Информационный канал, который при этом используется учителем, называется каналом прямой связи. О степени совпадения фактического состояния ученика, т. е. количества и качества усвоенных знаний, уровня сформированности умений и навыков, с некоторым заданным, эталонным состоянием можно судить на основе информации обратной связи, т.е. педагогического наблюдения и различных форм контроля. Сравнивая эталонное и фактическое состояние учебной деятельности управляемого им классного коллектива, учитель определяет степень их несоответствия (рассогласования). Если эта степень превышает некоторый допустимый предел, учитель вносит коррективы в применяемые им приемы, в форму изложения, рассматривает дополнительные примеры, применяет добавочную наглядность, вообще применяет методы и способы педагогического воздействия, направленные на уменьшение сигнала рассогласования, на активизацию умственной деятельности своих учеников, на мобилизацию их волевых усилий с целью добиться выполнения поставленных учебных и воспитательных задач.
Однако если канал прямой связи достаточно широк и к тому же в течение нескольких последних -десятилетий усиленно вооружается информационными техническими средствами: эпи-, диа-и кинопроекционными устройствами, звукозаписью, учебным телевидением и т. п., то канал обратной связи -от учеников к учителю - значительно уже и обладает заниженной пропускной способностью на самом выходе- у учителя, который не может в достаточно короткий срок воспринять и проанализировать сигналы обратной связи (ОС), поступающие сразу со всех рабочих мест. Это усложняет учителю задачу определения "степени рассогласования", что, в свою очередь, ухудшает его возможности в управлении процессом обучения. Расширение канала ОС на выходе, применение учителем специальных средств ОС, принимающих, сохраняющих и (хотя бы частично) перерабатывающих сигналы ОС от учащихся - важный резерв улучшения условий управления процессом обучения, повышения уровня успеваемости, повышения "коэффициента полезного действия" педагогического труда.
В настоящее время проблеме разработки, совершенствования и внедрения в учебный процесс различных технических средств обратной связи (ТСОС) уделяется весьма значительное внимание Некоторые из них выпускаются серийно и применяются в учебном процессе высшей и средней школы.
Дидактические функции различных ТСОС в значительной мере определяются их конструктивными особенностями, что позволяет нам в рамках, ограниченных данным параграфом, рассмотреть некоторые особенности использования различных ТСОС в преподавании математики, пользуясь следующей упрощенной их классификацией: а) простейшие технические средства ОС; б) электромеханические контролирующие устройства индивидуального пользования; в) автоматизированные классы и г) сложные обучающие комплексы на базе электронных вычислительных машин.
Общей для всех ТСОС является проблема ввода в них информации ОС, т. е. ответов учащихся на поставленные перед ними тем или иным способом вопросы по изучаемому материалу.
Возможности способов ввода информации в ТСОС определяются, вопервых, необходимостью обеспечить простоту сбора, хранения и переработки информации ОС, что вызывает стремление выделить в ответах учеников ту их часть, которая несет основную информационную нагрузку, с другой стороны, ограниченными техникоконструктивными возможностями самих ТСОС различных типов и образцов. В силу этого приходится проявлять подчас изощренность, граничащую с искусством, для того чтобы, пользуясь весьма упрощенным машинным языком, получить достаточно полную и надежную информацию ОС о состоянии знаний, умений и навыков учащихся. Наиболее распространенным в настоящее время является так называемый выборочный способ ввода, имеющий несколько разновидностей. Весьма важный в преподавании математики числовой способ ввода граничит, с одной стороны, с выборочным способом, а с другой - со способами ввода конструированных ответов, которые, в свою очередь, граничат со свободно формируемыми ответами учеников.
1. Общим для всех разновидностей выборочного способа ввода ответов является то, что правильные ответы выбираются учениками из некоторого предложенного им списка. Несмотря на некоторые ограничения, о которых речь будет ниже, в преподавании математики могут применяться разнообразные вопросы с множественным выбором. Применяются следующие разновидности выборочного способа ввода.
а) Ввод ответов на вопрос альтернативного типа (от лат. alterius - один из двух). Несмотря на высокую вероятность угадывания вопросы этого типа могут применяться особенно при фронтальном опросе, когда требуется получить информацию об усвоении нового материала в ходе изложения. Особенно перспективно использование таких вопросов в условиях применения на этом этапе урока контролирующих устройств коллективного пользования - автоматизированных классов. Вот несколько примеров.
Объяснив свойства параллелепипеда, учитель ставит перед классом несколько вопросов:
Является ли правильная четырехугольная призма параллелепипедом? (Ответ имеет вид "да" или "нет" или сводится к этому виду.) Является ли прямой параллелепипед правильной призмой? Может ли основанием прямоугольного параллелепипеда служить ромб? и т. п.
Если ответы на такие вопросы собраны с помощью оборудования автоматизированного класса, учитель может очень быстро сделать достаточно обоснованные выводы о степени понимания и усвоения учащимися того или иного учебного материала. Распределение правильных и неправильных ответов на несколько подобных вопросов позволит выяснить причины основных ошибок, а на этой основе более целенаправленно управлять учебным процессом в ходе изложения нового материала. Появляется также возможность выставления оценки каждому ученику в соответствии с проявленным им вниманием и прилежанием.
б) Богатые возможности представляются при применении вопросов выборочного типа. когда на каждый вопрос приводится или предполагается несколько ответов, из которых, как правило, только один верный.
Вот пример.
-
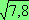 <="" td="">
<="" td="">
с точностью до 0,01.
Ваш ответ: 1) 0,279. 2) 2,793; 3) 0,28. 4) 2.79. Легко заметить, что в этом примере значащие части почти одинаковы, отличие их в точности и порядке. Ответ, который вводится в контролирующее устройство с помощью числового кода, представляющего собой номер правильного, по мнению ученика, ответа, должен выявить здесь умение ученика расположить движок в нужном для извлечения корня из 7,8 положений, определить порядок результата, указать ответ с заданной точностью. В этом случае против применения вопроса с множественным выбором не возникает возражений.
в) Против выборочных вопросов приведенного выше типа иногда выдвигаются возражения не очень, правда, обоснованные, что приводимые среди ответов для выбора ошибочные ответы могут приниматься учениками в качестве верных. Это опасение устраняется в перекрестновыборочных разновидностях этого способа ввода, когда в ходе решения приходится установить соответствие между элементами множества вопросов и множества ответов на них. Вот характерные примеры:
Пример 1. Установите соответствие между количеством граней многогранников, названных в левой колонке, и числами в правой колонке. (В качестве ответов последовательно введите коды чисел правой колонки.)
-
1. Четырехугольная пирамида
2. Октаэдр.
3. Икосаэдр.
4. Параллелограмм.
5. Додекаэдр.
20.
5.
12.
8.
6.
г) Остановимся еще на одной разновидности перекрестно-выборочиого способа ввода, которую назовем условно аддитивно-выборочной. Для того чтобы заставить ученика подвергнуть анализу совокупность нескольких вопросов, можно поступить так.
Среди приводимых ниже функций выбрать только четные. В качестве ответов ввести номера (коды) четных функций и их сумму.
-
у=5х2+cos x
-
у=2x2-5
-
y=(x-2)/(x+3)
-
у=tg x-sin x
-
y=(cos x +2)/(x2+4)
-
y=2+tg x
В качестве ответа на данный вопрос следует ввести числа 1, 2 5 или 1+2+5) = 8. Последнее число получится только после анализа всей совокупности вопросов. К сожалению, не во всех конструкциях ТСОС ввод этой разновидности выборочного способа осуществляется достаточно просто.
Весьма совершенным в условиях преподавания математики способом машинного ввода является так называемый числовой ввод когда ответом служит некоторое натуральное число, определяющееся в ходе решения. Числовой способ ввода можно рассматривать как расширение выборочного ввода: ответом служит одно из ограниченного множества чисел (первого десятка, сотни и т.д.). В случае, если в качестве ответов получаются дробные или иррациональные числа, можно применить число- кодированный ввод.
Вот несколько примеров.
(Ответ. Число 2 определяется решением. Это число и вводится в ТСОС.)
2. Решите уравнение х+lg(1+2x )=х lg 5+lg 6.
(Ответ. 1 - определяется и вводится в ТСОС.) Оба примера демонстрируют естественность применения числового ввода при решении уравнений.
3. Плоскость, проходящая через сторону основания правильной треугольной призмы и середину противолежащего угла, образует с основанием угол в 45°. Сторона основания 1 см. Определите площадь боковой поверхности.
Примечание. Перед вводом результат разделить на ![]() . Здесь полученный в
результате решения ответ 3
. Здесь полученный в
результате решения ответ 3![]() после деления на
после деления на ![]() определяется числом 3,
которое и вводится в машину. Это образец число-кодированного ввода.
определяется числом 3,
которое и вводится в машину. Это образец число-кодированного ввода.
Числовой и число-кодированный ввод, как уже упоминалось, граничит с одной стороны с выборочным вводом, а с другой - с так называемым конструируемым вводом, когда ответ составляется учащимися тем или иным способом из нескольких закодированных компонентов. В качестве примера рассмотрим применение одной из разновидностей конструируемого ответа результативной.
Выполните следующие упражнения на применение основных
соотношений между элементами треугольника. а) Вычислите площадь
ромба по его стороне а и острому углу ![]() . б) Определите высоту
дерева, если наблюдатель, удаленный на а метров от дерева,
видит его вершину под углом
. б) Определите высоту
дерева, если наблюдатель, удаленный на а метров от дерева,
видит его вершину под углом ![]() (ростом наблюдателя пренебречь).
в) Определите площадь параллелограмма, если известны его диагонали
а и b и угол между ними
(ростом наблюдателя пренебречь).
в) Определите площадь параллелограмма, если известны его диагонали
а и b и угол между ними ![]() .
.
Примечание. Ответ ввести в виде суммы кодов составных частей полученных выражений, воспользовавшись приведенной таблицей:
-
величина
Код
Действия
Код
а
b
a2
sin
1§а
21
2
3
4
5
6Умножить
Разделить
7
8
Ответы будут иметь такой вид и код:a2*sin

3+7+4=14
б) а*tg

1+7+5=13
в) (аb*sin
 )/2
)/2
1+7+2+7+4+8+6 = 35
В связи с громоздкостью и сравнительно сложным машинным языком, таящим опасности неоднозначного выражения ответа, этот способ ввода применяется сравнительно редко, хотя некоторые ТСОС специально рассчитаны на его применение.
К простейшим ТСОС следует отнести, прежде всего, различные устройства типа перфопакетов и перфокассет. В простейшем случае перфопакет представляет собой конверт из плотной бумаги или картона, в котором имеется некоторое количество рядов отверстий диаметром 6-8 мм. Каждый ряд и столбик пронумерованы: ряды, например, индийскими цифрами 1, 2, 3, 4, ..., а столбики-римскими I, II, III, IV....
При использовании выборочного способа ввода ответов в каждом столбике можно ограничиться 4-5 отверстиями. В случае, если, кроме выборочного метода ввода, предусматривается также применение числового и число-кодированного ввода, число отверстий в каждом столбике доводится до 10. Количество столбиков может быть разным- обычно 10.
Для фиксации ответов в пакеты вкладываются чистые листы бумаги (контрольные листы); задания предъявляются фронтально всему классу, или, что лучше, на отдельных карточках каждому ученику. Работая над своим заданием, ученик вводит найденные им ответы пометками на контрольном листе в соответствующих отверстиях.
Например, необходимо установить, какие из чисел нижеприведенного списка делятся на 7: 1) 864913; 2) 53832:3) 76131; 4) 376922; 5) 137831. Найдя в этом случае, что соответствующие числа имеют номера 1 и 4, ученик перечеркивает контрольный лист в отверстиях 1 и 4 первого столбика.
Следующий пример характеризует применение числовой формы введения ответов (в перфопакете с 10 отверстиями в каждом столбике).
Найти наибольший общий делитель чисел: 1) 2310; 2) 15015; 3) 3927.
Ответ ввести в 1-III столбики.
Правильный ответ 231 вводится учеником поразрядно в три столбика. После окончания работы учитель собирает перфопакеты и проверяет правильность ответов. Проверка ускоряется тем, что в ответах выделяется только то, что несет основную информационную нагрузку. Естественно, что в сомнительных случаях требуется полная проверка, которая ускоряется применением шаблонов, дешифровочных перфокарт (с заранее нанесенными правильными ответами).
Недостатком описанных перфопакетов является отсутствие внутренней обратной связи (ученик не может получить немедленно после введения своего ответа подтверждения его правильности) и отсутствие внешней оперативной обратной связи (информация о выполненной работе поступает к учителю после окончания работы учеников). С помощью таких устройств удобно проводить короткие самостоятельные работы на закрепление проработанного материала в конце урока.
Для обеспечения внутренней обратной связи применяются перфопакеты. Здесь верные ответы нанесены на дополнительный лист, отделенный от контрольного дополнительной перфокартой. Ученик, разрывая контрольный лист в отверстиях, соответствующих, по его мнению, правильному ответу, убеждается в его правильности. Чтобы ученик не смог подсмотреть правильные ответы на кодировочном листе, перфопакеты предварительно "пломбируют", например прошивают ниткой определенного цвета.
Значительное распространение в высшей и отчасти средней школе получили электромеханические контролирующие устройства различных конструкций. Наиболее известны в нашей стране "Ласточки", "КИСИ-5" и "Альфы" (на рис. 1 изображена машина К-53 "Ласточка").
-
1. Кнопки ввода кода ответов.
2. Кнопка сброса до оценки.
3. Билетные поля 1-5 билетов.
4. Билетные поля 6-10 билетов.
8. Крышка билетных полей.
6. Кнопка сброса после оценки
7. Оперативный ключ.
8. Кнопка вызова оценки.
9. Лампа готовности оценки.
10 Индикаторы последовательности
Большинство контролирующих устройств электромеханического типа слишком дороги, обеспечивают лишь выборочный способ ввода ответов и плохо приспособлены для помощи учителю в управлении процессом обучения, они предназначены скорее для индивидуализированной самостоятельной работы вне аудитории и для заключительного контроля. Значительно более приспособлены для классно-урочной работы комплекты устройств оперативной обратной связи коллективного пользования - автоматизированные классы (АК), не совсем верно называемые иногда классами программированного обучения. Хотя в некоторых конструкциях этих классов и осуществляется контролируемое обучение по программированным материалам, основное их назначение - активизация умственной деятельности учащихся в процессе изучения нового материала, организация фронтальной работы по проверке домашнего задания и по закреплению проработанного материала, а также организация управления индивидуализированной самостоятельной работой учащихся.
Существуют -различные конструкции АК, обеспечивающие выполнение разного набора дидактических функций. Некоторые из них уже начали выпускаться серийно (например, "Львов-2"), другие без больших затрат могут быть изготовлены в школьных мастерских, например "Николаев-10"
Среди различных режимов проведения занятий в А К особое внимание привлекает самостоятельная работа над индивидуализированными заданиями учебно-тренировочного характера, в том числе над разветвленными программированными материалами.
В АК эта работа проводится так: перед началом самостоятельной работы учитель сообщает всем учащимся сведения, необходимые для ее выполнения. (Часть этих сведений, впрочем, может быть включена в текст заданий.) Затем каждый получает свой вариант задания. Число вариантов таких заданий в АК описываемой конструкции может быть любым, обычно ограничиваются шестью вариантами. Так как рабочие места можно закрепить за определенными учениками, задания могут быть дифференцированы в соответствии с индивидуальными особенностями учеников по трудности и оформлению. Приступив к работе, ученики по мере выполнения упражнений вводят числовым кодом свои ответы в свои пульты, и уже через несколько минут на ЦП учителя возникает своеобразная световая столбчатая диаграмма выполнения задания коллективом всего класса в динамике. (Естественно, что каждый ученик работает в наиболее доступном ему темпе, причем оборудование обеспечивает поэтапную оперативную внутреннюю обратную связь.) Следя за индикацией, учитель видит, кто из учеников в каждый данный момент занятия нуждается более других в его педагогическом воздействии - совете, консультации, внушении и т. п. Вызывая с помощью специальной сигнализации ученика к себе или подойдя к нему непосредственно, учитель устраняет причины отставания данного ученика и переходит к помощи другому. Интенсивность работы как учеников, так и учителя значительно повышается, одновременно повышается и "коэффициент ее полезного действия". Сразу же в конце занятия учитель может подвести его итоги, выставить оценки, отставшим дать дополнительное задание домой и т. д. Более полная информация, которую можно использовать не только для текущей оценки успеваемости, но и для сбора количественной информации об экспериментальной работе, может быть получена просмотром контрольных листков учащихся на их индивидуальных пультах.
Аналогично организуется работа и в режиме проверки домашнего задания, когда ученики получают задания, цель которых проверить усвоение домашнего задания и степень подготовки к восприятию нового материала, и в течение 10-15 минут отвечают на него каждый самостоятельно, учитель же получает немедленно сведения об этой работе и учитывает их при изложении нового материала.
Глава 11
Проверка и оценка знаний учащихся
Цели и задачи проверки и оценки знаний учащихся по математике. Проверка домашних заданий. Устная проверка знаний учащихся. Письменные работы и их проверка. Тестовые формы проверки знаний, умений и навыков учащихся по математике
Проверка и оценка знаний учащихся по математике
Проверка знаний, умений и навыков учащихся в процессе обучения математике имеет важнейшее обучающее и воспитательное значение. Прежде всего, проверка знаний, умений и навыков позволяет выявить уровень успеваемости, т. е. степень усвоения учебного материала, полноту, глубину, сознательность и прочность знаний на разных этапах обучения, и обеспечивает таким образом накопление информации, необходимой для направленной деятельности по устранению несоответствия между заданным и истинным уровнем знаний, для управления процессом обучения. Проверка знаний, умений и навыков учащихся повышает их учебную дисциплину, побуждает к активизации умственной деятельности по усвоению материала, способствует выработке сознательного отношения к регулярному труду.
На разных этапах обучения проверка знаний может иметь разное целевое значение. Пожалуй., наиболее важной является систематическая текущая проверка состояния успеваемости, при рациональной организации которой учитель получает в свое распоряжение ценнейшие данные о наличии пробелов в знаниях учащихся и немедленно использует эти данные для устранения пробелов и недочетов. Важное значение имеет также проверка усвоения темы, раздела или проверка на заключительных этапах обучения - в конце четверти, в конце года и по окончании школы.
Результаты проверки успеваемости выражаются в условных баллах, а также в оценочных суждениях учителя. В советской школе принята пятибалльная шкала оценок. При выставлении оценок успеваемости руководствуются утвержденными органами народного образования нормами оценок.
Следует отметить, что существующие нормы оценок весьма условны: один и тот же ответ, одна и та же работа разными учителями оценивается поразному. С другой стороны, пятибалльная система оценок в некоторых случаях, особенно при проведении тонких дидактических экспериментов, при проверке новых пособий, новых методов и средств, оказывается недостаточно чувствительной.
Методы проверки домашних заданий различны. Это и устный опрос у доски или с места по домашнему заданию, и короткая письменная работа, но прежде всего это непосредственная проверка задания в тетрадях - беглая, фронтальная при обходе класса в начале урока и более основательная, выборочная во внеурочное время.
Сопутствующий проверке домашнего задания устный опрос не всегда достаточно экономен - некоторая часть учеников в это время отключается от участия в учебном процессе. Поэтому опытные учителя стараются сочетать устные и письменные формы проверки знаний учеников перед изложением нового материала так, чтобы загрузить в это время работой всех учеников в классе.
Положение облегчается, если применять специальные технические средства проверки знаний учащихся, с помощью которых сведения о проделанной работе могут быть быстро собраны.
Устная проверка знаний учащихся может применяться на разных этапах урока, в том числе и при проверке усвоения домашнего задания, о чем уже шла речь выше. По организационным формам устная проверка может быть индивидуальной и фронтальной. При индивидуальной проверке в течение определенного времени опрашивается только один ученик. Во время опроса могут быть проверены основательно знания данного ученика со всех точек зрения: полноты, глубины, сознательности и прочности, умения и правильности выразить их в устной речи и т. д. Весьма важно в ходе индивидуального опроса не допустить бездействия других учеников - их загружают в это время другими видами работы.
Фронтальная устная проверка знаний учеников может также применяться на разных этапах урока, но лучше всего ее применять для активизации познавательной деятельности учеников, мобилизации умственных и волевых усилий их на овладение учебным материалом в процессе его изложения. Характерным для фронтальной устной проверки знаний является то, что вопросы, как правило, ставятся всему классу. В обычных условиях отвечает на эти вопросы кто-нибудь один, но применение оборудования автоматизированных классов позволяет учителю воспринять и ответы всех учеников одно временно.
О роли частной и оперативной проверки знаний в процессе обучения уже говорилось. Одним из средств такой проверки являются кратковременные письменные работы. Применение этого вида проверки позволяет загрузить самостоятельной работой сразу всех учеников, а в результате его выполнения получить значительную информацию об успеваемости учеников в данный момент времени. Кратковременные письменные работы могут быть совмещены с устным индивидуальным опросом. Такие работы лучше проводить по нескольким вариантам, заимствуя их из дидактических материалов или составленные заранее учителем (обычно 4-6), варианты раздаются всем ученикам в классе. Такие работы могут проводиться в начале урока - для мобилизации внимания и привлечения знаний учащихся к восприятию нового материала, но лучше проводить их в конце урока - на закреплении проработанного материала.
Особый вид письменной работы представляют собой так называемые математические диктанты, целью которых является научить учащихся использованию математической символики, сознательному переходу от устного оформления математических выражений к письменному, к буквенной символике, закрепить в сознании учащихся порядок действий и конструкцию наиболее распространенных алгебраических выражений. Сущность этого вида работы в том, что учитель читает словесный текст, а ученики записывают его с помощью известной им математической символики.
Время от времени в процессе обучения математике практикуется проведение более длительных контрольных работ, на которые отводится один, а иногда и два смежных урока. В ходе таких работ может быть проверен относительно большой комплекс знаний по целой теме или разделу. Такие работы практикуются также в конце четверти или учебного года по совокупности всего материала, проработанного за данный период времени. Можно выделить несколько видов таких работ: а) работы на решение задач и упражнений; б) выполнение чертежей и графиков; в) работы по теоретическому материалу (вывод формул, доказательство теорем, ответы на другие вопросы теоретического характера); г) комбинированные письменные работы с (или без) подробным объяснением.
В связи с тем что эффективность процесса обучения зависит от частоты и оперативности, с которой учителем контролируется ход и степень усвоения учащимися учебного материала, в настоящее время большое внимание уделяется совершенствованию средств и методов контроля.
В частности, исследуется возможность применения в преподавании математики тестовых форм контроля знания. Слово "тест" (англ. test - проба, проверка, испытание) в нашей литературе обычно употребляется в следующем смысле: "тест - это кратковременное, технически просто обставленное испытание, проводимое в равных для всех испытуемых условиях и имеющее вид такого задания, решение которого поддается количественному учету и служит показателем степени развития к данному моменту известной функции у данного испытуемого"
Проведение предварительно проверенных тщательно составленных тестов исключает влияние преподавателя, проводящего тесты, на оценку успеваемости учащегося. Результаты тестирования лучше поддаются статистической обработке, чем балльные оценки; качество самих тестов также может быть проверено математико-статистическими методами.
Каждый тест состоит из вопросов и ответов, подобранных и построенных в соответствии с определенными принципами. Характер вопросов в значительной степени определяется спецификой и логикой того учебного предмета, для проверки которого данный тест предназначается.
Вопросы тестов можно свести к двум основным типам: основанные на узнавании и основанные на припоминании и дополнении.
Наибольшее распространение получили тесты с вопросами первого типа, часто называемые избирательными тестами. К каждому вопросу предлагается несколько ответов на выбор, ученик должен найти среди них правильный.
Среди избирательных тестов, в свою очередь, можно выделить альтернативные тесты, тесты множественного выбора и тесты перекрестного выбора.
Альтернативные тесты сводятся к тому, что ученик должен ответить на предложенный вопрос "да" или "нет". Примеры вопросов альтернативного теста:
1. Является ли правильная четырехугольная призма параллелепипедом? Да, нет (верное подчеркнуть).
2. Делится 3521 на 9?
3. Является ли единица простым числом? и т. д.
Альтернативные тесты применяются реже других разновидностей избирательных тестов. Их применение имеет, однако, определенные перспективы при проведении фронтального устного опроса, особенно при использовании при этом оборудования автоматизированных классов, о чем уже шла речь выше.
Тесты множественного выбора обычно предполагают выбор одного ответа из числа нескольких предложенных. Распространение тестов в последнее время объясняется прежде всего удобством их использования для ввода ответов учеников в различные контролирующие устройства.
Одной из разновидностей избирательных тестов являются тесты перекрестного выбора, или тесты на сопоставление, предназначенные для установления ответов к ним, записанных в произвольном порядке.
Пример. Установите соответствие между количеством граней многогранников, названных в левой колонке, с числом в правой колонке.
-
1. Четырехугольная пирамида
2. Октаэдр.
3. Икосаэдр.
5. Додекаэдр.
4. Параллелепипед.
1) 20.
2) 5.
3) 12.
4)4.
5) 6
Ваш ответ: 1-2-3-4-5-. 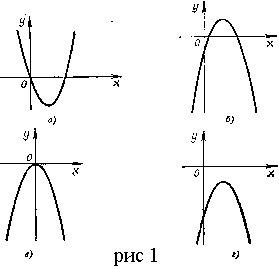
К тестам на сопоставление можно отнести также тесты идентификации, когда вместо словесных или числовых ответов приводятся схемы, графики, диаграммы, чертежи и т. п. Ученик должен распознать изображения и пронумеровать их в соответствии с условием. Пример:
Установите, существует ли соответствие между графиками функции у = ах2 + bх + с (рис. 1) и соотношениями:
а) а < О, ![]() = 0;
= 0;
б) а < О, ![]() > 0;
> 0;
в) а > О, ![]() > 0;
> 0;
г) а > О, ![]() = 0 (где
= 0 (где ![]() - дискриминант).
- дискриминант).
Сюда же можно отнести и тесты на систематизацию, используемые для определения знания учащимися алгоритмов различных процессов, умения упорядочить те или иные понятия по определенному признаку и т. д. Получили известное распространение и технические средства для их реализации, называемые тренажерами.
Пример. Расположите номера нижеследующих многогранников в порядке возрастания числа их вершин.
1. Параллелепипед.
2. Шестиугольная пирамида.
3. Тетраэдр.
4. Октаэдр.
5. Пятиугольная усеченная пирамида.
Тесты на припоминание и дополнение, т. е. тесты второго типа строятся обычно так: ученику предлагается связный текст, в котором пропущены отдельные числа, слова, формулы или выражения, он должен заполнить пропуски.
Такие тесты используются, в частности, в тетрадях с печатной основой, подобное оформление ответов применяется также в линейных программированных материалах. При машинной проверке знаний ответы к вопросам тестов этого типа вводятся с помощью числового, число - кодированного и результативного способов ввода ответов.
Несколько примеров позволят составить представление об особенностях тестов этого типа.
1. Сторона треугольника, лежащая против прямого угла, называется ............ Это характерный пример из линейного программированного пособия. Ученик должен припомнить и вписать название соответствующей стороны.
2. Дана функция у = х2 - 10х + 2.
Область определения этой функции - интервал ......... График этой функции - кривая, называемая ............ пересекает ось Ох в точке .......... и ось Оу в точке ...... Так как знак коэффициента при старшем члене ............ ветви кривой направлены. .............. . Координаты вершины кривой .......... . Функция принимает положительные значения в интервалах, ..........и отрицательные в ..... . Функция возрастает в................ и убывает в ......
Такой тест характерен для заданий в тетрадях с печатной основой. Вместо оформления полного ответа ученик ограничивается здесь только вписыванием выражений, несущих основную информационную нагрузку, чем достигается экономия времени и учеников и учителя. Изменяя исходные данные, можно пустить в оборот любое количество разных индивидуальных заданий.
Глава 13
Повышенная математическая подготовка учащихся
Краткая характеристика работы ЮМШ, ВМШ, ЗМШ. О работе школ с математической специализацией. О преподавании математики в школах и классах с углубленным изучением предмета
Школы и классы с углубленным изучением математики и специфика их работы
Бурное развитие математики и физики не могло не наложить определенного отпечатка на уровень развития и направление интересов учащейся молодежи. Интерес молодежи к технике, физике и математике стал приобретать массовый характер. Для особо любознательных учащихся, интересующихся математикой, хотя и открылись общедоступные источники информации (через литературу и телевидение), но разобраться в этой информации самим школьникам, без "направляющей руки", было бы очень трудно.
Так как кружковые занятия проводятся в школе обычно лишь два раза в месяц, то естественно, что этот весьма незначительный объем интересной для учащихся работы не может удовлетворить многих из них.
Кроме того, круг вопросов, выходящих за рамки школьной программы, которыми интересуются учащиеся и которыми учитель владеет в совершенстве, обычно не слишком велик; это, конечно, создает большую трудность в проведении занятий математического кружка всегда на таком научнометодическом уровне, который мог бы удовлетворить и учителя, и учащихся.
С другой стороны, в современных условиях математизации науки и техники возникла необходимость непрерывного притока в различные отрасли народного хозяйства молодежи, хорошо подготовленной к математике, обладающей определенными способностями к творческой деятельности. Это сделало актуальной задачу "организованного поиска" и воспитания талантливой молодежи.
Таким образом, движение за создание новых, более эффективных форм внеклассной работы с учащимися по математике явилось двусторонним движением: со стороны учащихся и со стороны общественности, и в первую очередь - вузов (заинтересованных в высокой подготовке в нужном направлении своих студентов).
Поэтому за последнее десятилетие возникли новые и весьма разнообразные формы внеклассной работы с учащимися по математике: публичные лекции для учащихся, юношеские математические школы, специальные школы (программистов-вычислителей), общематематические школы и классы, вечерние и заочные математические школы, школыинтернаты, летние и зимние математические школы.
Возникновение юношеских математических школ (ЮМШ) было обусловлено несоответствием возросших интересов молодежи к математике, потребностями общества в математических кадрах и теми средствами, которыми располагала массовая школа для достижения этих целей.
Первые ЮМШ были организованы в 1959/60 учебном году при Ивановском и Кишиневском пединститутах, а в 1960/61 учебном году при Тамбовском и Московском областном педагогическом институте им. Н. К. Крупской.
В организационном плане ЮМШ многое переняли от обычной школы: определенный и постоянный состав учащихся и преподавателей, определенная фиксированная программа, жесткое расписание занятий. Однако, так как учащиеся этих школ являются еще и учащимися общеобразовательных школ или студентами техникумов, рабочими или служащими, занятия в ЮМШ, как правило, проходят 1-2 раза в неделю.
ЮМШ по существу представляют собой своеобразный сплав школьного кружка и лектория. Хотя основной задачей этих школ является повышение общего математического уровня слушателей, обучение в них отвечает и целям профессиональной ориентации учащихся, помогая им в выборе для себя будущей профессии.
Единой программы работы ЮМШ нет. Это и понятно, так как, во-первых, программы находятся еще в стадии разработки и творческого поиска, а, во-вторых, они, естественно, изменяются и будут изменяться (ведь, как правило, вопросы школьного курса математики здесь не дублируются, а расширяются и дополняются).
Нередко программа в определенной степени учитывает и интересы преподавателей ЮМШ или возможности организаторов этих школ (вуза, отдела народного образования, школы).
Как правило, основная работа в этих школах ведется высококвалифицированными и обладающими большим опытом работы преподавателями. Для усиления индивидуализации занятий с учащимися привлекаются аспиранты и студенты вузов. Эти школы работают на общественных началах.
В ЮМШ принимаются учащиеся, имеющие 8-летнее образование; в некоторых случаях к обучению в ЮМШ допускаются и учащиеся седьмых классов (таким образом, срок обучения в ЮМШ составляет два года).
Как правило, все учащиеся, интересующиеся математикой, первоначально имеют доступ для посещения занятий ЮМШ. Однако через некоторое время с ними проводится собеседование, выясняющее примерный уровень подготовки поступающих в ЮМШ и круг тех вопросов математики, которыми бы учащиеся желали заниматься в процессе обучения.
Кроме ЮМШ, весьма традиционными формами внеклассной работы вузов со школьниками по математике являются различные лектории, кружки и секции для учащихся.
В частности, при МГУ в течение более 30 лет функционировала целая система таких кружков, на основе которой в 1963 г. была организована первая вечерняя математическая школа (ВМШ) для учащихся VII-IX классов Москвы и Московской области, действующая и в настоящее время.
ВМШ при МГУ рассчитана на школьников, проявляющих склонность и способность к серьезным занятиям математикой. Основная задача этой школы состоит в том, чтобы оптимально способствовать общему математическому развитию школьников, привить им вкус и навыки исследовательской математической деятельности.
Для учащихся VIII и IX-Х классов раз в неделю профессорами и преподавателями МГУ и других институтов читаются лекции или циклы лекций. После каждого цикла лекций учащиеся сдают зачеты.
Важная роль отводится в ВМШ групповым занятиям, которыми руководят аспиранты и студенты МГУ (к руководству группами VII и VIII классов иногда привлекаются и наиболее сильные старшеклассники специализированных математических школ).
На групповых занятиях учащиеся занимаются решением разнообразных нестандартных задач. Некоторые из этих задач могут быть связаны с материалом лекций, однако большинство задач не привязано к какой-либо определенной теме.
Среди учащихся 2-3 раза в год проводится конкурс по решению задач. Наиболее интересные решения задач, предлагаемые школьниками на конкурс, печатаются в специальных сборниках "Математическая школа".
Школьники, приходящие в ВМШ, являются вначале своеобразными ее гостями; и лишь те, кто успешно справляется с решением задач, вносятся затем в официальные списки учащихся ВМШ; им выдаются зачетные книжки, в которых отмечаются сданные учащимися зачеты и результаты участия в конкурсах по решению задач.
По примеру Москвы ВМШ были организованы и в других городах. Эти школы ставят своей целью более раннее выявлены математически талантливой молодежи, а также популяризацию математики, развитие интереса к ней у возможно большего числа учащихся.
Организация таких школ в городах, крупных поселках стала весьма .обычным явлением. Однако сельская молодежь, часто обладающая не меньшими врожденными математическими способностями (реже - ярко выраженными, а чаще скрытыми), при такой постановке дела не имеет по существу тех широких возможностей, какие имеет городская молодежь.
Выход из этого положения подсказали сами учащиеся средней -школы: "Хотим учиться в вашем институте, но готовиться трудно- нет литературы, нет руководителя в постоянной четкой работе. Помогите!"
Первыми на этот призыв откликнулись сотрудники мехмата МГУ. Было продумано, как организовать действенную помощь сельским учащимся. Параллельно с вечерней математической школой в 1964 г. была организована Заочная математическая школа (ЗМШ)
Авторитет ЗМШ рос, число желающих обучаться в этой школе возрастало и вскоре уже стало невозможным обеспечить всех учащихся ЗМШ соответствующими учебными материалами и контролем. Тогда по предложению МГУ на базах различных институтов, по различным областям страны были организованы филиалы ЗМШ.
Год спустя (1965) Новосибирский государственный университет организовал такую же ЗМШ для учащихся, живущих в восточной части страны и имеющую также свои филиалы.
Появилась и закрепилась еще одна новая форма работы с учащимися - организация, называемая "Коллективный ученик". Эта форма внеклассной работы с учащимися по математике явилась связующим звеном между ЗМШ, имеющей руководящий центр, и школьным математическим кружком. Особенно полезным было то, что в работу учащихся был активно включен школьный учитель; работа стала носить организованный (официальный) характер. Такая форма работы лучше отвечает целям углубленной математической подготовки учащихся, развитию у них устойчивого интереса к математике, сообразительности, математических способностей, наклонности к творческой деятельности, качеств, так необходимых каждому человеку. Да и учитель школы, проводящий такую работу, получил возможность обратиться за помощью и советом в соответствующий центр.
Итак, основными задачами, которые ставят перед собой различные математические школы (ЮМШ, ВМШ, ЗМШ и др.), являются:
1) популяризация математики среди учащейся молодежи;
2) выявление и развитие интереса к математике у учащихся;
3) развитие математического мышления и математических способностей учащихся;
4) привитие учащимся вкуса и навыка к исследовательской деятельности;
5) расширение круга знакомств учащихся с доступными им приложениями математики;
6) расширение и углубление знаний учащихся по программе школьной математики;
7) оказание положительного влияния на коллектив класса обычной школы, в которой учатся эти школьники.
Рост алгоритмизации производственных процессов, появление в производстве различного вида электронных и счетно-решающих устройств привели к постановке новой проблемы - подготовке кадров специалистов-математиков. Появилась новая массовая профессия - вычислитель-программист. И одновременно с ЮМШ (которые возникли в общемто по желанию учащихся) стали возникать экспериментальные классы (школы) со специальной профессиональной ориентацией - вычислитель-программист.
Первый эксперимент в этом направлении был проведен в школе № 444 (425) Первомайского района Москвы в 1959 - 1960 гг. Поначалу организация работы в этой школе была сопряжена с большими трудностями - родители учащихся не верили в успех эксперимента и поэтому набор в эти классы шел с большим трудом. В то же время и сама мысль о допуске учащихся к работе на вычислительных машинах казалась дерзкой и неосуществимой.
Как показал опыт, непосредственную работу на математических машинах и на различных программирующих устройствах могут успешно выполнять лица со специальным средним образованием. Однако такое профессиональное обучение, хотя и связано со специальной теоретической подготовкой и определенными навыками труда, опирается на значительные общематематические знания и математическое развитие
Однако основные трудности остались позади, и сейчас уже в нашей стране создано достаточно много школ и классов с углубленным изучением математики и, что отрадно отметить, работают они вполне успешно.
Изучение расширенного курса математики, курса программирования и вычислительной математики в классах и школах с углубленным изучением математики имеет своей целью дать учащимся повышенную математическую подготовку, вооружить элементами знаний и навыков по программированию и вычислительной математике.
На основе такой подготовки учащиеся смогут выявить свои интересы и наклонности к математике и ее применениям, получить прочную базу для успешного продолжения обучения в высших учебных заведениях физико-математического профиля или работы на предприятиях. Выпускники школ, которые сразу после школы поступят на работу, смогут за короткое время работы на предприятии или вычислительном центре освоить специальности средней квалификации, требующие математической подготовки и умения использовать ЭВМ для решения конкретных народно-хозяйственных задач.
Математическая специализация начинается с IX класса. Организация таких классов проводится преимущественно в тех школах, которые имеют возможность использования вычислительной техники. При наличии благоприятных условий (вычислительный центр для проведения практики, высококвалифицированные преподаватели значительное машинное время и др.) школа может совместно с шефствующим вычислительным центром доводить знания и навыки учащихся до уровня, допускающего присвоения выпускникам квалификации "Программист-вычислитель".
Программа "Общего курса математики" этих школ включает в себя программу массовой школы и содержит некоторые дополнительные вопросы из математического анализа, алгебры и других разделов математики. Это имеет важное общеобразовательное значение, должно способствовать более высокому уровню усвоения учащимися математики и призвано служить основой для специальной подготовки.
Общий курс математики школ с математической специализацией состоит из трех учебных предметов: математического анализа, алгебры и геометрии.
Курс "Математический анализ" ближе других предметов примыкает к специальным вопросам. Этим объясняется его больший по сравнению с другими (вопросами) предметами объем и значение в специальной и. общеобразовательной подготовке.
В соответствии с профессиональной ориентацией в курсе алгебры обращается особое внимание на выработку у школьников высокой техники тождественных преобразований алгебраических выражений, решения алгебраических уравнений и систем уравнений, решения и доказательства неравенств и др.
Профилирующим предметом в данных классах является и курс физики, хотя на его изучение отводится дополнительно лишь 1 час в неделю в Х классе.
В качестве основного прикладного учебного предмета выступает курс "Программирование и вычислительная математика".
Заметим, что программа курса предполагает параллельное изучение теории и практических занятий. Учебные практические занятия проводятся одновременно с изучением теории (без отрыва от других классных занятий). Эти занятия непосредственно связаны с изучением теории по программированию и вычислительной математике с использованием электронных вычислительных машин.
Подготовка вычислителей-программистов не является единственной формой математической специализации на уровне средней школы. В настоящее время уже действуют школы и классы, осуществляющие подготовку лаборантов-техников по обслуживанию ЭВМ, специалистов по применению математических методов в экономике предприятий и т. д.
Отметим также, что ведутся экспериментальные исследования возможности и целесообразности введения начальной математической специализации в VII -VIII классах.
Уже в настоящее время в различных учреждениях работает свыше 700 тысяч научных работников с вспомогательным персоналом более 3 млн. человек. Поэтому резко возросла важность проблемы подготовки научных кадров. Опыт показал, что поиски отбор способной к научной работе молодежи должен вестись в школе. И в первую очередь этот вопрос касается подготовки молодежи по математике, так как большинство способных к изучению математики школьников часто совсем не подозревают об этом и нередко выбирают профессию, не соответствующую их склонностям и способностям. Известно, что математические способность молодых людей в своем развитии достигают максимума в 20 - 30-летнем возрасте; поэтому важно как можно более раннее выявление этих способностей у учащихся и создание оптимальных условий для их развития.
Эта цель стала основной при организации в 1963 г. школы-интерната № 18 при МГУ, явившейся первой экспериментальной школой с общематематическим уклоном В школу-интернат стали принимать, в первую очередь, способных учащихся из сельской местности или небольших городов, т. е. тех учащихся, которые без этой школы (в силу отдаленности от культурных центров) не смогли бы получить хорошего математического или физического образования. Опыт работы этой школы быстро распространился по всей стране. В настоящее время такие школы-интернаты организованы почти при всех университетах страны.
Наряду с созданием школ-интернатов математического профиля в отдельных обычных школах стали создаваться специальные классы с общематематическим уклоном.
Обучение в этих классах не преследовало цели дать школьникам ту или иную узкую математическую специальность (например, программиста), а дать наиболее способным и интересующимся математикой учащимся общую ' углубленную подготовку по математике, дающую им возможность в дальнейшем успешно работать в любой области науки и техники, тесно связанной с математикой.
Опыт показал, что создание классов с общематематическим уклоном является не только хорошим дополнением к школам общематематического профиля, но и является наиболее гибкой и экономичной формой углубленной математической подготовки школьников, так как эта форма работы имеет целый ряд преимуществ по сравнению со специальными школами общематемати-ческого профиля. Так, например, если для создания целой математической школы необходим весьма большой преподавательский персонал, имеющий достаточно высокий квалифицированный уровень (что практически очень трудно осуществить в небольшом городе), то для создания класса с математическим уклоном бывает достаточно иметь одного высококвалифицированного учителя. Другое преимущество в создании отдельных классов с общематематическим уклоном (а не школ), заключается в относительной легкости набора учащихся в один-два класса, а также в возможности почти в каждой школе "вырастить" будущих учащихся для такого математического 8-9 класса из состава учащихся 4-7 классов той же школы с помощью кружков, факультативных занятий и т.п.
Охарактеризуем преподавание в классах с математическим уклоном, опираясь на опыт работы авторов пособия в IX-Х классах школы №352 Москвы.
Опыт показал, что программу курса математики 9 - 10 классов с математическим уклоном и преподавание в этих классах целесообразно построить в соответствии со следующими основными принципами.
1. Изучение математики в классах соответствующего профиля должно давать учащимся глубокие математические знания и широкое математическое развитие на базе основного курса математики; при этом должны обеспечиваться такие условия, чтобы вопросы действующей программы и полезные традиции преподавания математики органически переплетались между собой и рассматривались с современной точки зрения.
2. Учащиеся - выпускники математических классов - должны обладать такими знаниями и умениями, которые полностью отвечали бы требованиям, предъявляемым к математической подготовке учащихся обычных школ и вместе с тем были бы более глубокими и прочными. При этом, получаемое в процессе изучения математическое развитие учащихся математического класса должно давать им возможность осуществлять творческий подход к процессу изучения математики. Учащиеся должны научиться работать самостоятельно с учебной математической литературой и обладать к концу обучения устойчивым интересом к предметам естественно-математического цикла.
3. Возможное расширение программы должно быть органически связано с основным курсом и соответствовать имеющимся (или возникающим в процессе изучения) интересам учащихся и их познавательным возможностям. Поэтому большинство разделов математики, составляющих содержание факультативных занятий в общеобразовательной школе, было включено в содержание основного программного материала и составляло органическое целое с основным курсом.
Так, например, изучение факультативной темы "Элементы теории множеств и математической логики" в начале IX класса дает возможность более прочного, а также более быстрого (благодаря применению символики и более высокой логической культуре) усвоения учащимися многих последующих разделов курса и также возможность более современного и научного толкования важнейших математических понятий (числа, функции, уравнения, фигуры и т. п.).
Для особого факультативного изучения полезно отнести: а) решение нестандартных математических задач; б) элементы программирования и принцип работы электрон" новычислительных машин;
в) творческие индивидуальные работы учащихся над избранными ими самими вопросами элементарной математики.
4. В процессе преподавания математики в этих классах перед учителем открываются большие возможности в осуществлении оптимальной индивидуализации обучения, в использовании школьниками эвристического метода изучения и проблемной формы обучения, т. е. широкая возможность оптимальной активизации обучения.
Организуя набор в такие классы, целесообразно (учитывая оценки по предметам естественно-математического цикла) проводить общую для всех контрольную работу с последующим собеседованием с каждым из учащихся для выявления уровня их развития и степени интереса к математике (чтению научно-популярной литературы, склонности к другим предметам, увлечения).
Каждую четверть учащиеся оцениваются по трем предметам математического цикла и сдают зачет по практикуму "Решение задач".
Решение задач теоретического и прикладного характера в соответствии с разделами программы ведется в течение всего года. Широко используется решение задач не стандартных, конкурсных, предлагаемых на вступительных экзаменах в вузы и проблемных задач.
Сделаем некоторые методические замечания о реализации данной программы в процессе преподавания математики в IX-Х классах с математическим уклоном.
1. В процессе преподавания курса "Алгебра и начала анализа" следует уделить особое внимание функциональной направленности этого курса. Так, вопросы исследования функций (позднее с помощью производной) в той или иной форме следует ставить в течение всего времени обучения, подчеркивая при этом единство таких понятий, как функция, уравнение, неравенство. Например, от учащихся нужно требовать ясного понимания того, что решение уравнения f(х) = 0 и неравенства f(х ) > 0 являются частным случаями задачи исследования функции у = f(х) (корни функции и промежутки знакопостоянства). Понятие функции полезно трактовать с теоретико-множественных позиций; это дает возможность более четкого определения многих математических понятий, более тесно свяжет изучаемые математические свойства объектов с жизненной практикой.
2. Первую неделю учебного года в IX классе полезно полностью посвятить "Тригонометрии треугольника". Благодаря этому возникает возможность не только провести повторение основных вопросов геометрии восьмилетней школы, но и выявить уровень знаний и математического развития учащихся. Основным содержанием этих уроков является решение комбинированных задач, более сложных, чем традиционные.
3. Включая в программу IX класса факультативный курс "Элементы векторного исчисления", учитель имеет возможность провести построение всего курса геометрии на векторной основе. Однако можно пойти и по другому пути: дать учащимся возможность с иной точки зрения взглянуть на уже изученное, использовать новые методы при решении задач и доказательстве теорем. В частности, в процессе изучения геометрии учащимся полезно разрешать приводить "векторные" доказательства различных теорем, разрешать не вычерчивать чертежей, если доказываемую теорему можно легко представить "в воображении", поощрять использование плоского чертежа какого-либо сечения тела, достаточного для решения поставленной задачи. То есть, вообще говоря, полезно предоставить учащимся свободу в выборе наиболее рациональных средств для решения поставленной перед ними математической проблемы.
4. При изучении объемов многогранников и тел вращения в основном целесообразно использовать формулу Симпсона; однако это не исключает использования для этой цели понятия интеграла или принципа Кавальери или, наконец, традиционного "метода пределов"; следует обратить внимание учащихся на необходимость доказательства формул объема призмы и цилиндра "методом пределов" ввиду того, что вывод формулы Симпсона опирается на эти соотношения.
Многие вопросы курса можно предложить учащимся для самостоятельного изучения; например, основные понятия и определения, относящиеся к какомулибо классу фигур (круглые тела, многогранники и т. п.), учащиеся вполне могут изучить самостоятельно.
5. При изучении темы "Элементы интегрального исчисления" можно отправляться от понятия определенного интеграла и только после его введения и моделирования в виде различных физических величин (или их значений) перейти к понятию неопределенного интеграла. Такой путь оправдывает себя, так как находится в определенном единстве со схемой изучения производной:
а1 задачи реального содержания, приводящие к этому понятию, и метод решения их;
б) некоторый предел и разнообразие его реальных моделей; в) вычисление этого предела по его определению и неудобства этого способа вычисления;
г) изучение свойств данного предела, выявление удобных правил его вычисления и составление таблиц; . д) различные приложения при решении задач.
Не следует уделять особое внимание отработке навыка в исчислении производных и интегралов; важно, чтобы учащиеся сознательно овладели сущностью данных понятий.
6. При постановке темы "Элементы геометрии Лобачевского" имеется в виду прежде всего познакомить учащихся с методологическими основами построения геометрии, дать понятие об аксиоматическом методе, проиллюстрировать этот метод на геометрии Лобачевского, выявив ее отличие от геометрии Евклида.
Здесь же следует обратить внимание учащихся на логическую структуру математических понятий, суждений и умозаключений (неопределяемые понятия и отношения, определение понятий и отношений, аксиома, теорема, доказательство, опровержение, проблема существования математического объекта).
7. Постановка элементов математической логики в начале обучения в IX классе позволяет учащимся достаточно рано применять логико-математическую символику при записи доказательств теорем или решении задач.
8. При введении новой темы полезно использовать методический принцип: практика - теория - практика. В силу этого принципа изучение темы обычно начинается с так называемых "целесообразных" задач практического характера, решение которых приводит к необходимости (или, по крайней мере, к целесообразности) изучения соответствующего раздела теории.
Этот методический принцип можно применять и в другой форме: не по ступенькам (практика-теория-практика), а одновременно. Так, при изучении темы "Логарифмы и логарифмическая функция" полезно, чтобы учащиеся умели формулировать некоторые свойства на "трех языках" (языке функции, языке логарифмов, языке графика);
например:
а) логарифмическая функция f (х) = 1оga х непрерывна; б) малому изменению числа соответствует столь же малое изменение его логарифма; в) кривая графика - сплошная линия; г) свойство непрерывности дает практическую возможность ограничиться при вычислении четырехзначными таблицами логарифмов:
lg 6,42567695 ![]() lg 6,426.
lg 6,426.
9. Полезно применять в самых разнообразных формах эвристический метод обучения. Так, например, изучение темы "Последовательности и прогрессии" можно провести так.
Учащимся предлагается множество последовательностей, из которых нужно выбрать серии особенных последовательностей (у них легко определить следующий за последним написанным член). После классификации данных последовательностей по сериям естественно возникает вопрос о целесообразности их определения, поиска их характеристических свойств и формул общего члена.
Такой метод изучения данной темы способствует весьма успешному и эффективному ее усвоению, вызывая у учащихся значительный интерес.
Многие темы, подлежащие изучению, можно ввести, создав проблемную ситуацию. Так, например, теорему "Сложение круговых функций" можно представить сначала в виде следующих задач:
10. При проведении уроков повторения нужно обратить особое внимание на систематизацию знаний учащихся по основным ведущим идеям школьного курса математики ("Учение о числе", "Учение о функции", "Исчисление площадей и объемов" и т. п.). Повторение должно охватывать не только все основные вопросы теории, но и практики. Упражнения, которые при этом рассматриваются, должны быть достаточно сложными. Именно при повторении полезно решать задачи, составляющие содержание конкурсных экзаменов в МГУ, МФТИ и других институтах.
В заключение заметим, что, помимо основной задачи (отбор, обучение и воспитание молодежи, проявившей к изучению математики особый интерес и способности), школы и классы физико-математического профиля решают задачу поиска перспективного содержания, форм и методов обучения математике для массовой школы, т. е. являются по существу своеобразными школами-лабораториями, нацеленными в будущее.
Несомненно, процесс поиска новых форм внеклассной и внешкольной работы по математике с учащимися средней школы будет продолжаться и развиваться.
Назад к оглавлению | К следующей главе
Глава 14
Внеклассная работа с учащимися по математике и методика ее преподавания
Общая характеристика внеклассных занятий по математике. Занятия с отстающими. Основные цели внеклассной работы по математике. О содержании внеклассной работы по математике. Основные формы внеклассной работы по математике
-
Внекласная работа учащихся по математике и методика её проведения
-
Кружковые занятия по математике и методика их проведения
-
Работа учащихся с дополнительной литературой при обучении математике
-
Факультативные занятия по математике и методика их проведения
Внекласная работа учащихся по математике и методика её проведения
Требования, предъявляемые программой по математике, школьными учебниками и сложившейся методикой обучения, рассчитаны на так называемого "среднего" ученика. Однако уже с первых классов начинается резкое расслоение коллектива учащихся: на тех, кто легко и с интересом усваивают программный материал по математике, на тех, кто добивается при изучении математики лишь удовлетворительных результатов, и тех, кому успешное изучение математики дается с большим трудом.
Все это приводит к необходимости индивидуализации обучения математике, одной из форм которой является внеклассная работа.
Под внеклассной работой по математике понимаются необязательные систематические занятия учащихся с преподавателем во внеурочное время.
Следует различать два вида внеклассной работы по математике: работа с учащимися, отстающими от других в изучении программного материала (дополнительные внеклассные занятия);
работа с учащимися, проявляющими к изучению математики повышенный, по сравнению с другими, интерес и способности (собственно внеклассная работа в традиционном понимании смысла этого термина).
Говоря о первом направлении внеклассной работы, отметим следующее.
Этот вид внеклассной работы с учащимися по математике в настоящее время имеет место в каждой школе. Вместе с тем повышение эффективности обучения математике с необходимостью должно привести к снижению значения дополнительной учебной работы с отстающими. В идеальном случае первый вид внеклассной работы должен иметь ярко выраженный индивидуальный характер и проявляться лишь в исключительных случаях (например, в случае -продолжительной болезни учащегося, перехода из школы другого типа т. п.). Однако в настоящее время эта работа требует еще значительного внимания со стороны учителя математики.
Основной целью ее является своевременная ликвидация (и предупреждение) имеющихся у учащихся пробелов в знаниях и умениях по курсу математики.
Передовой опыт работы учителей математики свидетельствует об эффективности следующих положений, связанных с организацией и проведением внеклассной работы с отстающими.
1. Дополнительные (внеклассные) занятия по математике целесообразно проводить с небольшими группами отстающих (по 3-4 человека в каждой); эти группы учащихся должны быть достаточно однородны как с точки зрения имеющихся у школьников пробелов в знаниях, так и с точки зрения способностей к обучаемости.
2. Следует максимально индивидуализировать эти занятия (например, предлагая каждому из таких учащихся заранее подготовленное индивидуальное задание и оказывая в процессе его выполнения конкретную помощь каждому).
3. Занятия с отстающими в школе целесообразно проводить не чаще одного раза в неделю, сочетая эту форму занятий с домашней работой учащихся по индивидуальному плану.
4. После повторного изучения того или иного раздела математики на дополнительных занятиях необходимо провести итоговый контроль с выставлением оценки по теме.
5. Дополнительные занятия по математике, как правило, должны иметь обучающий характер; при проведении занятий полезно использовать соответствующие варианты самостоятельных или контрольных работ из "Дидактических материалов", а также учебные пособия (и задания) программированного типа.
6. Учителю математики необходимо постоянно анализировать причины отставания отдельных учащихся при изучении ими математики, изучать типичные ошибки, допускаемые учащимися при изучении той или иной темы. Это делает дополнительные занятия по математике более эффективными.
Второе из указанных выше направлений внеклассной работы по математике-занятия с учащимися, проявляющими к ее изучению повышенный интерес, отвечает следующим основным целям:
1. Пробуждение и развитие устойчивого интереса учащихся к математике и ее приложениям.
2. Расширение и углубление знаний учащихся по программному материалу.
3. Оптимальное развитие математических способностей у учащихся и привитие учащимся определенных навыков научно-исследовательского характера. :
4. Воспитание высокой культуры математического мышления.
5. Развитие у учащихся умения самостоятельно и творчески работать с учебной и научно-популярной литературой.
6. Расширение и углубление представлений учащихся о практическом значении математики в технике и практике социалистического строительства.
7. Расширение и углубление представлений учащихся о культурно-исторической ценности математики, о ведущей роли советской математической школы в мировой науке.
8. Воспитание учащихся чувства коллективизма и умения сочетать индивидуальную работу с коллективной.
9. Установление более тесных деловых контактов между учителем математики и учащимися и на этой основе более глубокое изучение познавательных интересов и запросов школьников.
10. Создание актива, способного оказать учителю математики помощь в организации эффективного обучения математике всего коллектива данного класса (помощь в изготовлении наглядных пособий, занятиях с отстающими, в пропаганде математических знаний среди других учащихся).
Предполагается, что реализация этих целей частично осуществляется на уроках. Однако в процессе классных занятий, ограниченных рамками учебного времени и программы, это не удается сделать с достаточной полнотой. Поэтому окончательная и полная реализация этих целей переносится на внеклассные занятия этого вида.
Вместе с тем "Между учебно-воспитательной работой, проводимой на уроках, и внеклассной работой существует тесная взаимосвязь: учебные занятия, развивая у учащихся интерес к знаниям, содействуют развертыванию внеклассной работы, и, наоборот, внеклассные занятия, позволяющие учащимся применить знания на практике, расширяющие и углубляющие эти знания, повышают успеваемость учащихся и их интерес к учению. Однако внеклассная работа не должна дублировать учебную работу, иначе она превратится в обычные дополнительные занятия.
Говоря о содержании внеклассной работы с учащимися, интересующимися математикой, отметим следующее.
Традиционная тематика внеклассных занятий ограничивалась обычно рассмотрением таких вопросов, которые хотя и выходили за рамки официальной программы, но имели много точек соприкосновения с рассматриваемыми в ней вопросами. Так, например, при изучении в 6 классе признаков делимости натуральных чисел на занятиях математического кружка рассматривались признаки делимости чисел, не предусмотренные программой (признак делимости на 7, на 11 и т. д.); при изучении геометрических задач на построение циркулем и линейкой на занятиях математического кружка рассматривались геометрические построения при помощи одной линейки и т. п. Также традиционным для рассмотрения на внеклассных занятиях по математике были исторические экскурсы по той или иной теме, математические софизмы, задачи повышенной трудности и т. д.
За последние десятилетия в математике возникли новые направления, имеющие не только большое практическое значение, но и большой познавательный интерес. Экспериментальные исследования, проведенные в ряде школ показали, что многие вопросы так называемой современной математики (в объеме своих начальных понятий) вполне доступны и весьма интересны для изучения их учащимися, даже начиная с 5 класса. На это справедливо указывал Н. Я. Виленкин, предлагая на внеклассных занятиях по математике знакомить учащихся с элементами вычислительной математики, производной и интегралом, основными понятиями математической логики, современной алгебры, комбинаторики, теории информации и т. д. Н. Я. Виленкин рекомендует обращать внимание и на практическую направленность внеклассных занятий и ее занимательность, которые можно реализовать рассмотрением соответствующих задач.
Отметим, что многие из этих вопросов уже нашли свое отражение в программе факультативных занятий по математике; вместе с тем некоторые из них могут быть интересными и доступными для учащихся IV-VI классов.
Происходящее сейчас обновление содержания основного курса математики привело к возникновению тенденции обновления содержания внеклассных занятий по математике, однако это не означает, что следует полностью отказаться от тех или иных традиционных вопросов, которые составляли до сих пор содержание внеклассных занятий и вызывают у учащихся неизменный интерес (например, функции и графики, математические парадоксы и софизмы, неопределенные уравнения, логические и исторические задачи и т. д.).
Можно рекомендовать следующие формы проведения внеклассной работы с учащимися, особо интересующимися математикой:
математические кружки;
математические викторины, конкурсы и олимпиады;
математические вечера; математические экскурсии;
внеклассное чтение математической литературы;
математические рефераты и сочинения; школьная математическая печать.
Говоря об олимпиаде, следует отметить, что до сих пор эта форма внеклассной работы с учащимися являлась своеобразным итогом проделанной работы (чаще всего кружковой). Олимпиада - соревнование, которое, несомненно, стимулирует рост учащихся в смысле их математического образования, воспитывает у них математическое мышление, интерес к математике, настойчивость - желание не отстать от тех, которые успешно справляются с олимпиадным заданием; часто именно участие в олимпиаде и подготовка к ней побуждает учащихся самостоятельной работе, вырабатывает умение работать с научно-популярной литературой и т. д.
Математические олимпиады проводятся на различных уровнях: школьные, районные, городские, областные, республиканские, общесоюзные и международные. В проведении областных и республиканских олимпиад активно участвуют педагогические институты и университеты; общесоюзная олимпиада проводится под эгидой Московского государственного университета им. М. В. Ломоносова.
Олимпиады также оказывают положительное влияние и на общий уровень преподавания математики, во многом позволяют выявить качество математических знаний учащихся и, кроме того, в какой-то степени ориентируют учителя, характеризуя уровень той математической подготовки, которая считается высокой.
Однако следует обратить внимание на то немаловажное обстоятельство, что олимпиады не являются серьезным источником новой, интересующей учащихся информации и потому не могут считаться основной формой углубленной математической подготовки молодежи.
В последнее время все большую популярность среди учащихся, проявляющих к изучению математики повышенный интерес и способности, завоевывают такие формы углубленной специальной математической подготовки, примыкающие к внеклассной работе, как юношеские математические школы (ЮМШ), заочные математические школы (ЗМШ), школы и классы с математическим уклоном специально для подготовки программистов-вычислителей.
Имея в виду, что каждая из выше перечисленных форм достаточно полно представлена в методической литературе мы ограничимся здесь лишь краткой характеристикой основных форм этого вида работы: математического кружка, внеклассного чтения математической литературы, школ и классов с математическим уклоном.
Кружковые занятия по математике и методика их проведения
Общая характеристика кружковых занятий по математике
Математический кружок-одна из наиболее действенных и эффективных форм внеклассных занятий. В основе кружковой работы лежит принцип строгой добровольности. Обычно кружковые занятия организуются для хорошо успевающих учащихся. Однако следует иметь в виду, что иногда и слабо успевающие учащиеся изъявляют желание участвовать в работе математического кружка и нередко весьма успешно занимаются там; учителю математики не следует этому препятствовать. Необходимо лишь более внимательно отнестись к таким учащимся, постараться укрепить имеющиеся у них ростки интереса к математике, проследить за тем, чтобы работа в математическом кружке оказалась для них посильной. Конечно, наличие слабо успевающих учащихся среди членов математического кружка затрудняет работу учителя, однако путем индивидуализации заданий, предлагаемых учителем кружковцам, можно в некоторой степени ослабить эти трудности. Главное - сохранить массовый характер кружковых занятий по математике, являющийся следствием доступности посещения кружковых занятий всеми желающими.
Уже при организации математического кружка необходимо заинтересовать учащихся, показать им, что работа в кружке не является дублированием классных занятии, четко сформулировать цели и раскрыть характер предстоящей работы (для этого целесообразно выделить часть времени на одном из уроков математики, с тем чтобы обратиться с сообщением об организации кружка ко всему классу).
На первом занятии кружка надо наметить основное содержание работы, выбрать старосту кружка, договориться с учащимися о правах и обязанностях члена кружка, составить план работы и распределить поручения за те или иные мероприятия (выпуск математической стенной газеты, ведение документации работы кружка и т. п.).
Занятия кружка целесообразно проводить один раз в неделю, выделяя на каждое занятие по одному часу. К организации работы математического кружка целесообразно привлекать самих учащихся (поручать им подготовку небольших сообщений по изучаемой теме, подбор задач и упражнений по конкретной теме, подготовку справок исторического характера, изготовление моделей и рисункЬв к данному занятию и т. д.). На занятиях математического кружка учитель должен создать "атмосферу" свободного обмена мнениями и активной дискуссии. Тематика кружковых занятий по математике в современной школе весьма разнообразна. В тематике кружковых занятий для 5-11 классов находят место вопросы, связанные с историей математики, жизнью и деятельностью российских и зарубежных известных математиков.
Работа учащихся с дополнительной литературой при обучении математике
Общая характеристика работы учащихся с дополнительной литературой по математике. Психологические основы эффективной работы школьников с математической литературой. Обучение школьников общим приемам работы с дополнительной литературой по математике
Перед школой стоят задачи повышения общего уровня развития учащихся, подготовки школьников к дальнейшему образованию и самообразованию и к практической творческой деятельности по любой специальности. Для решения этих задач учителю математики необходимо не только обеспечить определенный запас знаний у школьников, но и выработать умение добывать эти знания, развить в учениках стремление и способности к самостоятельному приобретению новых знаний.
Среди различных источников новых знаний по математике одно из первых мест занимает книга. Всю литературу, знакомящую школьников с основами математики и с их применением, можно разделить на учебную (стабильные учебники, дидактические материалы, сборники задач, справочники) и дополнительную (научно-популярные книги и статьи, сборники задач олимпиадного характера).
В процессе обучения математике учащиеся весьма широко используют основную учебную литературу; однако дополнительную литературу по математике все еще читают весьма немногие, причем это чтение не носит организованного характера. Между тем обучающее значение работы учащихся с дополнительной литературой по математике весьма велико, так как именно эта работа способствует не только повышению качества знаний учащихся, но и развитию у них устойчивого интереса к математике.
Немалое обучающее и развивающее значение имеют также умения и навыки работы с математической литературой.
Опыт, приобретаемый школьниками в процессе работы с учебной литературой, оказывается недостаточным для успешной работы с дополнительной литературой. Поэтому умения и навыки работы школьников с математической литературой необходимо целенаправленно развивать, причем развивать систематически. Этому, в частности, способствует:
1) возможно более полное соответствие изучаемой литературы направлениям познавательных интересов школьников;
2) систематическое использование учителем и учащимися дополнительной литературы в процессе обучения математике (на классных занятиях и в домашней работе учащихся);
3) целенаправленная деятельность учителя по обучению учащихся общим приемам работы с математической литературой;
4) постановка специальных заданий школьникам, требующих привлечения дополнительной литературы по математике и контроль за их выполнением;
5) постоянное использование дополнительной математической литературы на факультативных занятиях и т. д.
Эффективность самостоятельной работы учащихся с учебной или дополнительной литературой вообще (и математической в частности) зависит и от некоторых психологических факторов (установка, вдохновение, интерес, волевое усилие, самостоятельность, трудолюбие и т.п.).
Одним из важнейших условий успешной работы с книгой является наличие особого состояния умственной деятельности, называемого установкой.
Под установкой понимается готовность к действию в определенном направлении, т. е. своеобразное состояние психики, возникающее при единстве мотива деятельности (потребности в ней) и ситуации, которая ему соответствует.
Экспериментальные исследования, проведенные психологом Д. Н. Узнадзе и другими, показали, что наличие четкой установки к деятельности значительно повышает ее эффективность.
Применительно к работе с книгой такая установка способствует активизации внимания и памяти, способствует точности восприятия содержания, помогает выделять в тексте главную мысль, развивает способность творчески воспринимать получаемую информацию и т. д., т. е. способствует выработке умений и навыков самостоятельного приобретения новых знаний в процессе работы над литературой.
"Процесс формирования всякого навыка есть выработка и фиксация у субъекта установки на осуществление определенного действия.
Учение - определенная форма поведения, управление которым достигается установкой индивида. Установку следует считать опорой нормального функционирования механизма обратных связей в организме у каждого учащегося".
Поэтому целенаправленность работы учащихся с дополнительной (и учебной) литературой, наличие сильной мотивации (соответствия познавательных интересов и деятельности) во многом определяют эффективность этого важного вида учебной деятельности.
К числу основных компонентов, определяющих выработку умений и навыков эффективной самостоятельной работы учащихся с научной (математической) литературой, относятся:
1) умение логически (структурно) осмыслить текст;
2) умение читать с пониманием;
3) умение выделить и запомнить главное;
4) умение акцентировать свое внимание на той или иной основной мысли, выраженной в тексте;
5) умение творчески перерабатывать информацию (в том числе "читать между строк");
6) умение составить план, конспект на тему, сделать из него выписки;
7) самостоятельность и критичность восприятия;
8) усилие воли, чтобы заставить себя работать и в случае возникновения трудностей и неясностей (что особенно характерно для работы с математическим текстом);
9) настойчивость в преодолении трудностей.
В связи с последними из этих компонентов уместно привести следующее высказывание В. И. Ленина: "...сразу кое-кого, может быть, и отпугнет трудность изложения, - надо опять предупредить, что этим не следует смущаться, что непонятное на первый раз при чтении будет понятно при повторном чтении, или когда вы подойдете к вопросу впоследствии с, несколько иной стороны... "
В перечне этих условий заложена своеобразная программа обучающей деятельности учителя математики при организации самостоятельной работы учащихся с книгой.
Для формирования и развития рассмотренных выше умений и навыков полезно применять определенную систему специальных учебных заданий.
1. Задания, формулирующие и развивающие умение выборочного чтения дополнительной литературы по математике. Такие задания обычно выражены в форме вопросов, ответы на которые явно или скрыто содержатся в данной для изучения дополнительной литературе. Таковы, например, задания по наведению справок исторического характера, задания типа "Установить, какая фигура называется ромбоидом", "Найти в данной книге одно-два предложения, эквивалентных аксиоме параллельности Евклида" и т. д.
2. Задания, формулирующие способность сопоставления новых знаний, полученных при чтении дополнительной литературы, с уже усвоенными знаниями.
Так, например, после самостоятельного изучения учащимися преобразования инверсии по дополнительной литературе учащимся предлагаются задания: "Сравнить свойства инверсии со свойствами гомотетии" и т. п.
3. Задания, формирующие способность применения новых знаний, полученных при чтении дополнительной литературы. Так, например, при изучении какого-либо нового метода решения задач учащимся предлагается применить этот метод к решению уже известной задачи или самим подобрать (составить) задачи, решаемые этим методом.
4. Задания, формирующие умение свести прочитанное в определенную целостную систему. Таковы, например, задания: а) подготовить доклад по прочитанному; б) прореферировать данную книгу (главу книги); в) составить какую-либо таблицу (диаграмму, схему) по прочитанному и т. д.
Назад
Факультативные занятия по математике и методика их проведения
Общая характеристика факультативных занятий по математике. Основные формы и методы проведения факультативных занятий по математике. Об изучении факультативного курса для VIII-IX классов "Множества и операции над ними. Бесконечные множества"
Факультативные занятия по математике ведутся в школе с 8 класса со следующим числом недельных часов: 8 класс -1 час, 9 - 2 часа, 10 - 2 часа и 11-2 часа.
Главной целью факультативных занятий по математике является углубление и расширение знаний, развитие интереса учащихся к предмету, развитие их математических способностей, привитие школьникам интереса и вкуса к самостоятельным занятиям математикой, воспитание и развитие их инициативы и творчества.
Программа основного курса математики вместе с программой факультативных занятий по математике для средней школы составляют программу повышенного уровня по данному предмету для учащихся данного класса.
Программа факультативных занятий по математике составлена так, что все вопросы ее могут изучаться синхронно с изучением основного курса математики в школе. В тех случаях, когда в данном классе основной курс математики ведет один учитель, а факультативный - другой, изучение тем факультатива может проводиться независимо от основного курса программы (в этом случае изучение тем можно проводить с некоторым запозданием по отношению к основному курсу программы).
Для того чтобы факультативные занятия по математике были эффективными, необходимо их организовать там, где есть:
1) высококвалифицированные учителя или другие специалисты, способные вести занятия на высоком научно-методическом уровне;
2) не менее 15 учащихся, желающих изучать данный факультативный курс.
Если школа имеет классы с небольшой наполняемостью (что особенно характерно для некоторых сельских школ), то группы учащихся для факультативных занятий можно комплектовать по параллелям или из учащихся смежных классов (8-9 классы, 10-11 классы и т. п.).
Запись учащихся на факультативные занятия производится на добровольных началах в соответствий с их интересами. Не следует принуждать учащихся обязательно изучать факультативные предметы. Особенно внимательно следует относиться к тем учащимся, которые встречают трудности в изучении математики или совмещают обучение в школе с другими видами занятий (спорт, музыка и т. д.). По окончании факультативного курса учащиеся сдают зачет (с оценкой), о чем делается отметка в аттестате. Учитель математики несет полную ответственность за качество факультативных занятий; факультативные занятия вносятся в расписание и оплачиваются учителю.
Проведение факультативных занятий по математике не означает отказа от других форм внеклассной работы (математические кружки, вечера, олимпиады и т. д.). Они должны дополнять эти формы работы с учащимися, которые интересуются математикой.
Возможность 1-2 часа в неделю дополнительно работать со школьниками, проявляющими повышенный интерес и способности к математике, представляет собой одно из проявлений новой формы обучения математике - дифференцированного обучения.
По существу факультативные занятия являются наиболее динамичной разновидностью дифференциации обучения.
В какой бы форме и какими бы методами не проводились факультативные занятия по математике, они должны строиться так, чтобы быть для учащихся интересными, увлекательными, а подчас и занимательными. Необходимо использовать естественную любознательность школьника для формирования устойчивого интереса к своему предмету. Известный французский физик Луи де Бройль писал, что современная наука - "дочь удивления и любопытства, которые всегда являются ее скрытыми движущими силами, обеспечивающими ее непрерывное развитие".
Основными формами проведения факультативных занятий по математике являются в настоящее время изложение узловых вопросов данного факультативного курса учителем (лекционным методом), семинары, собеседования (дискуссии), решение задач, рефераты учащихся (как по теоретическим вопросам, так и по решению цикла задач), математические сочинения, доклады учащихся и т. д.
Однако учителю не следует отдавать предпочтение какой-либо одной форме или методу изложения. Вместе с тем, памятуя о том, что на факультативных занятиях по математике самостоятельная работа учащихся должна 'занять ведущее положение, следует все же чаще применять решение задач, рефераты, доклады, семинары-дискуссии, чтение учебной и научно-популярной литературы и т. п.
Одной из возможных форм ведения факультативных занятий по математике является разделение каждого занятия на две части. Первая часть посвящается изучению нового материала и самостоятельной работе учащихся по заданиям теоретического и практического характера. По окончании этой части занятия учащимся предлагается домашнее задание по изучению теории и ее приложений. Вторая часть каждого занятия посвящена решению задач повышенной трудности и обсуждению решений особенно трудных или интересных задач. Эта форма проведения факультативных занятий может способствовать успешному переходу от форм и методов обучения в школе к формам и методам обучения в высших учебных заведениях.
Естественно также при проведении факультативных занятий в основном использовать методы изучения (а не обучения) математики, а также проблемную форму обучения.
В частности, ее можно осуществить, если представить изучаемый факультативный курс в виде серии последовательно расположенных задач. "Решая последовательно все задачи самостоятельно или при незначительной помощи преподавателя, школьники постепенно изучают курс при большом личном участии, проявляя активность и самостоятельность, овладевая техникой математического мышления. Теоремы имеют вид задач. Если теорема, которую учащиеся должны доказать, является большой или трудной, то она разбивается на несколько задач так, что решение предыдущей помогает решить последующую. Определения либо включаются преподавателем в текст задачи, либо сообщаются особо. В необходимых случаях преподаватель проводит предварительную беседу или делает обобщения. Листочки с заданиями, размноженные на машинке, на каждое занятие выдаются всем ученикам"
Полезно также широко использовать задачи проблемного характера
В настоящее время факультативные занятия по математике проводятся по двум основным направлениям:
а) изучение курсов по программе "Дополнительные главы и вопросы курса математики"; б) изучение специальных математических курсов. Содержание программы "Дополнительные главы и вопросы" систематического курса математики позволяет решить и углубить изучение программного материала, ознакомить учащихся с некоторыми общими современными математическими идеями, раскрыть приложение математики в практике, готовит учителя к работе по новой программе".
В качестве конкретного примера постановки факультативного курса рассмотрим объединенную тему "Множества и операции над ними. Бесконечные множества". Содержание программы по этой факультативной теме явно ориентирует на то, чтобы общие понятия о множествах, элементах множества и операциях над множествами возникали из рассмотрения конкретных примеров множеств решений уравнений, неравенств и их систем.
Такая постановка вопроса не соответствует той роли, которую играет понятие множества вне рамок учения об уравнениях и неравенствах как в математике, так и за пределами этой науки. Поэтому не исключено, что после изучения этой темы учащиеся не заметят первоначального объективного источника возникновения понятия о множестве и не поймут фундаментального значения этого понятия для всей математики. Для того чтобы указанная тема наиболее полно способствовала углублению математических знаний учащихся, у них должно быть сформировано представление о понятии множества как о первоначальном понятии математики, из которого развивается наука-математика. Здесь не идет речь о строгом логическом обосновании математики. Достаточно показать на конкретных примерах, как проявляются понятия множества, отношения между множествами и операции над множествами в различных разделах математики - арифметике, алгебре, геометрии, в учениях о функциях, уравнениях и неравенствах. Вот эта линия и должна последовательно проводиться на факультативных занятиях.
Объем материала по теории множеств, изучаемого на факультативных занятиях в девятых классах, зависит от того, изучались или не изучались элементы теории множеств на факультативных занятиях в восьмых классах.
Если эта тема изучалась в 9 классе, то некоторые из входящих в нее вопросов рассматриваются лишь в порядке повторения (полезнее - при решении соответствующих задач); если же эта тема не ставилась ранее, то в целях сокращения материала некоторые из более элементарных задач или упражнений следует опустить. Рассмотрение универсального множества имеет важное значение в развитии функционального мышления учащихся. Раскрытию содержания этого понятия, его относительного характера должно быть уделено большое внимание. В 9 классе для обоснования свойств отношений между множествами и операций над множествами вполне достаточно применение кругов Эйлера. В 10 классе кругами .Эйлера целесообразно иллюстрировать результаты аналитических обоснований.
Если учитель дополнит алгебру множеств сведениями из математической логики (логические функции, область истинности предиката), то это без сомнения будет способствовать более углубленному и осознанному усвоению учащимися многих вопросов школьного курса математики, в частности вопросов теории уравнений, неравенств и их систем.
При изучении вопроса о бесконечных множествах даже на факультативных занятиях нет возможности основательно ознакомить учащихся с арифметикой трансфинитных чисел. Да в этом, на наш взгляд, и нет необходимости. Важно лишь, чтобы учащиеся осознали главные особенности конечных и бесконечных множеств, проявляющиеся в специфике арифметики натуральных и трансфинитных чисел.
Уже после первого занятия учащиеся систематически получают задания для самостоятельного изучения соответствующего материала.
На самих занятиях качество усвоения теории проверяется в процессе решения задач и примеров. Здесь совершенно недопустимы такие формы работы, которые сковывали бы инициативу учащихся. Занятие начинается с постановки упражнения для всех учащихся. За время, которое отводится на выполнение задачи или примера, учитель успевает проследить, кто и как справляется с заданием. Не следует торопить учащихся. Обычно, если не все, то некоторые из них выполняют задание в запланированное учителем время, а затем начинается разбор и теоретическое обоснование решений. Инициатива в оценке способов решения, в исправлении ошибок, в постановке вопросов представляется самим учащимся. В процессе этой работы достигается логическая точность в формулировках определений понятия или их свойств. В заключительном слове учитель дает мотивированную оценку знаний учащихся. Помимо указанной формы контроля знаний, целесообразно проводить кратковременные 15-20-минутные проверочные работы. Занятия по курсу 9 класса полезно завершить часовой контрольной работой.
На занятиях в 10 классе полезно практиковать постановку докладов учащихся. Темами докладов могут, например, быть: "Понятие об универсальном множестве", "Декартово произведение множеств", "Мощность и порядковый тип вполне упорядоченного множества".
При подготовке к докладам учащиеся используют различную дополнительную литературу, указанную учителем. Не следует увлекаться большим количеством докладов, в противном случае у учителя просто не хватит времени для хорошей подготовки докладчиков. Проверка и оценка знаний учащихся девятых классов осуществляется так же, как это делается в восьмых классах.
Назад к оглавлению | Список использованной литературы



 Список использованной
литературы
Список использованной
литературы
-
Епишева О.Б. Общая методика преподавания математики в средней школе / Тобольск, Изд-во ТГПИ им. Д.И. Менделеева, 1997 -191 стр.
-
Ермолаева Н.А. Маслова Г. Г. Новое в курсе математики средней школы / М:, Просвещение, 1978.
-
Журнал "Математика в школе ".
-
Ирошников Н.П. Организация обучения математике в 4-5 классах сельской школы : Пособие для учителей ,2-е издание переработано / М: Просвещение, 1982.
-
Колягин Ю.М., Луканкин Г.Л., Мокрушин Е.Л. и другие. Методика преподавания математики в средней школе. Частные методики / М., Просвещение, 1977.
-
Методика преподавания математики в средней школе : Общая методика; Учебное пособие для студентов физико-математического факультета педагогических институтов / В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский, -2-е издание переработано и дополнено / М., Просвещение ,1980.
-
Методические рекомендации по изучению курса методики преподавания математики / Сост. Петрова Е.С., Саратов, Изд-во "Полиграфист", 1983 - 67 стр.
-
Программы общеобразовательных учреждений / Москва, Просвещение, 1994.
-
Программы школьных факультативов по математике.
-
Понтрягин Л.С. О математике и качестве её преподавания - Коммунист, 1980.
-
Новосельцева З.И. Развернутые планы лекций и учебные задания для студентов по курсу "Теоретические основы обучения математике"/ С.-Петербург, Изд-во "Образование", РГПУ, 1997 -38стр.
-
Пичурин Л.Ф., Репьев В.В. Вопросы Общей методики преподавания математики / Москва Изд-во "Просвещение", 1979 - 80 стр.
-
Рогановский Н.М. Методика преподавания математики в средней школе / Минск, Изд-во "Высшая школа", 1990 - 270 стр.
-
Учебники для средней школы и соответствующие пособия для учителя.
-
Черкасов Р.С., Столяр А.А. Методика преподавания математики в средней школе / Москва, Изд-во "Просвещение", 1
-
Проблема формирования вычислительной культуры школьника почти равносильна проблеме подготовки молодого человека к вступлению в реальную жизнь. Без преувеличения можно сказать, что эта проблема «стара, как мир». В истории возникновения, становления и развития методической науки о преподавании математики не было сколько-нибудь продолжительного периода, в течение которого проблема формирования вычислительной культуры не звучала бы как актуальная. Однако, несмотря на столь пристальное внимание к данной проблеме, она не была до сих пор четко сформулирована. Часто в публикациях понятие «вычислительной культуры» подменяется понятием «вычислительные навыки». Так, например, в «Методике преподавания математики в средней школе» Ю.М. Калягина и др. [89, стр. 78], читаем: « Достаточно высокий уровень вычислительной культуры учащихся может быть охарактеризован следующей совокупностью признаков:
-
1) прочные и осознанные знания свойств и алгоритмов операций над числами;
-
2) умение по условию поставленной задачи, определить, являются ли исходные данные для вычислений точными или приближенными числами, прочные знания правил приближенных вычислений и навыки их выполнения;
-
3) умение правильно сочетать устные, письменные вычисления и вычисления с применением вспомогательных средств;
-
4) устойчивое применение рациональных приемов вычислений;
-
5) автоматизм навыков безошибочного выполнения вычислительных операций;
-
6) аккуратная и экономичная запись расчетов;
-
7) применение рациональных приемов контроля вычислений;
-
8) умение на определенном теоретическом уровне обосновать правила и приемы, применяемые в процессе вычислений».
-
То же положение наблюдается в пособии для учителя «Повышение вычислительной культуры учащихся» [146, стр. 80]. Приведем название разделов сборника статей «Повышение вычислительной культуры учащихся средней школы» [146, стр. 167-168]:
-
1. Некоторые вопросы повышения техники вычислений в средней школе.
-
2. Приближенные вычисления в школе.
-
3. Логарифмическая линейка. Номограммы.
-
Устойчивое внимание методистов к проблеме формирования вычислительной культуры связано с обстоятельством, на котором во все времена базировались школьные программы и учебники по математике, -школьник должен быть подготовлен к применению математики в практической деятельности, при изучении других наук, в процессе овладения профессией. А.Д.Александров, определяя цели изучения математики, выделял два аспекта: «первый - практическая польза предмета, те знания и навыки, которые понадобятся человеку в жизни; второй - место предмета в общем образовании. Практическое значение большинства разделов школьной математики очевидно: каждый, например, должен уметь считать и решать без затруднения хотя бы простейшие задачи» [9, стр. 420]. Данное обстоятельство не только не теряет своей актуальности, но с внедрением ЭВМ в нашу жизнь и быт превращается в требование массового овладения технической грамотностью. По мнению Н.Я.Виленкина: «Математизация всех областей науки и техники, бурное развитие вычислительной техники, внедрением ЭВМ и микропроцессоров во все сферы производства, экономики, управления и даже в обыденную жизнь делают необходимым всемерное улучшение математической подготовки учащихся, приближение школьного курса математики к требованиям современности . Задача обучить школьников умению применять математику становится центральной, мировоззренческой» [42, стр. 40]. И в этом смысле с понятием числа и вычислениями может конкурировать только понятие геометрической фигуры. Огромная значимость этих понятий бесспорна в вопросах приложений и использования математики. Это связано с тем, что оба этих понятия являются исторически первыми математическими понятиями, причем настолько древними, что сама история их возникновения прослеживается только на гипотетическом уровне. Об этом свидетельствует обширная историко-математическая литература, например [6, 13, 38, 54, 55, 80 и др.]. Интересно и то, что ни одна из практических вычислительных задач, насколько бы древней она ни была, не потеряла своего значения до сегодняшнего дня, начиная, вероятно, с первой задачи - задачи счета. Усложнение и увеличивающееся многообразие видов практической деятельности, возникновение и развитие наук и производства, совершенствование вычислительных средств, развитие соответствующих разделов математики только пополняют список вычислительных задач, делают вычисления все более значимыми. Число проникает порой в самые неожиданные отрасли знания о природе, обществе и человеке, и признается настоящим научным достижением, если удается измерить или вычислить то, что до той поры было невыразимо числом. Вместе с таким широким распространением числа, с развитием вычислительных средств, снимающих проблему трудоемкости вычислений, превращающих ранее невозможное и практически неосуществимое в легко и каждому доступное, обостряется проблема грамотного и корректного использования числа. Очень тонко и очень точно подметил замечательный русский поэт Н.Гумилев:
-
Все оттенки смысла умное число передает».
-
Действительно «все оттенки», но только «умное число». Даже искренне ищущий истину, но недостаточно подготовленный (с низким уровнем вычислительной культуры) исследователь или человек в обстоятельствах самой обычной жизненной ситуации может приписать смысл и большое значение числу, которое фактически ничего не выражает или имеет в точности противоположный смысл. С другой стороны, в руках и устах умелого манипулятора должным образом подобранное число, впечатляющие своим размахом и объемом вычисления, может быть всего лишь ловким приемом сокрытия истины, формирования неверных, выгодных кому-то представлений, определяющих общественное мнение, влияющих на принятие решений и т.п. Таким образом, число давно перестало быть объектом, с которым работают только специально обученные люди и в специфических областях деятельности. Высокий уровень вычислительной культуры без преувеличения нужен каждому человеку, даже если он встречается с числом только на страницах газет или в простейших жизненных обстоятельствах. Все вышесказанное вряд ли может вызвать возражения, в то же время это означает, что проблема воспитания вычислительной культуры - одна из важнейших задач школьного математического образования. Мы считаем весьма своевременным обратиться к выяснению места и значения числа и вычислений в методике обучения математике, так как результаты школьного обучения по одной из центральных линий курса очевидно неудовлетворительны. В этом нас убеждают многочисленные публикации. Например, в [89, стр. 79] читаем: «Обеспечение высокой культуры вычислений и тождественных преобразований представляет важную проблему обучения математике. Однако эта проблема решается далеко неудовлетворительно. Доказательство этому - статистические данные органов народного образования, в которых ежегодно констатируются ошибки и нерациональные приемы вычислений и преобразований, допускаемые учащимися различных классов при выполнении контрольных работ. Это подтверждается и отзывами высших учебных заведений о качестве математических знаний и навыков абитуриентов. Нельзя не согласиться с выводами органов управления образованием и ВУЗов о том, что недостаточно высокий уровень культуры вычислений. в средней школе является следствием формализма в знаниях учащихся, отрыва теории от практики».
-
Аналогичное положение наблюдается и в зарубежных странах. Рольф Хедрен, преподаватель математики в Фалун-Берленге, председатель комитета, занимающегося изучением влияния введения калькуляторов в старших классах начальной школы (что соответствует как раз возрасту учащихся пятых классов в России), пишет: «Уровень подготовленности учащихся к выполнению несложных упражнений на закрепление традиционных приемов счета невысок. Не удовлетворяют в настоящее время и навыки решения математических задач, то есть выполнение правильных математических действий в правильном контексте и в правильной последовательности.» [169, стр. 132]. К таким же выводам нас приводят данные, полученные в ходе констатирующего эксперимента, в частности результаты опросов учителей. Понятие вычислительной культуры постоянно находится в сфере внимания методистов. Различным формам проявления вычислительной культуры посвящены многие работы [9, 26, 27, 42, 50, 55, 60, 72, 76, 77, 78, 79, 81, 122, 146, 149, 150, 153, 171, 185]. Наше исследование базировалось на выводах и результатах, полученных И.Ф. Соколовским в его диссертации «Вычислительная культура как основа методики введения начал математического анализа в средней школе» [150]. Наиболее важным для нашего исследования являются следующие положения:
-
1 .Существующая методика, а вслед за ней и практика преподавания, одну из форм проявления вычислительной культуры - вычислительные знания, умения и навыки - воспринимает, как сущность вычислительной культуры, поэтому преподавание сводится к воспроизводству явления, а не к постижению его сущности.
-
2 .Сущность вычислительной культуры. состоит в правильном движении мысли от первоначальной качественной картины явления к его количественному описанию и от него - к сущности явления.
-
Нами используется понятие «сущность вычислительной культуры» в общефилософском понимании, в том смысле, что сущность и явление представляют собой общефилософские категории, отражающие необходимые стороны всех объектов и процессов в мире. Явления - это конкретные события, выражающие форму проявления сущности. Сущность - совокупность глубинных связей, отношений и внутренних законов, определяющих основные черты и тенденции развития материальной системы. Это означает, что одно и то же явление может быть рассмотрено как в буквальном смысле, так и в глубинном, сущностном.
-
Академик Б.М. Кедров отмечал, что « всякое число абстрактно, отвлечённо, оно отражает лишь одну внешнюю, количественную сторону изучаемого. Вместе с тем оно, взятое само по себе, единично, а потому случайно, отрывочно» [84,стр.3]. Только тогда, когда число приводится в связь с другими числами, оно обретает определённый качественный смысл. Всё это - результат мышления. «Мысль. ищет связь между отдельными числами, стремится раскрыть взаимозависимость количественной стороны изучаемого предмета с его качественной стороной, между внешней и внутренней его сторонами». Далее автор анализирует процесс открытий в различных областях науки и приходит к выводу о том, что: «Раскрытие качества является первичной предпосылкой и исходной основой для правильного познания количества (числа). Пока не раскрыта качественная сторона изучаемого предмета, его количественная (числовая) сторона не может быть измерена верно. Однако, после того, как качество предмета установлено, и на его основе развернулось количественное исследование, это, последнее, может способствовать более глубокому и расширенному изучению качества». [84,стр.6]
-
Сказанное выше означает, что определение сущности вычислительной культуры можно представить следующим образом:
-
Нельзя сформировать вычислительную культуру школьника, если основной акцент делать на решении чисто вычислительных задач (т. е., задач, в которых исходные числовые данные, погрешность и алгоритм заданы условиями, и не требуется качественного осмысления ответа) [148].
-
В процессе решения задачи каждый из выделенных шагов является необходимым. Пропуск любого из них приводит к возникновению тех явлений, которые свидетельствуют о наличии формализма в знаниях учащихся. Поэтому требование выполнения всех трёх шагов при решении задачи будем называть принципом единства .
-
Подход к формированию вычислительной культуры, при котором методическими средствами создаются условия для реализации принципа единства, будем называть сущностным подходом к формированию вычислительной культуры школьников.
-
На уровне теоретического осмысления имеющегося опыта преподавания математики в средней школе нами выдвинуто положение о том, что заниматься вопросом формирования вычислительной культуры следует постоянно и систематически в процессе изучения всего школьного курса математики. Проблема формирования вычислительной культуры не локализуется ни во времени, ни в пространстве школьного курса математики. Иначе говоря, нельзя однозначно определить момент, когда следует начинать и когда заканчивать формирование вычислительной культуры, как нельзя
-
Первонач& качественн явления
-
Количественное описание явленш. 2 определить отдельную тему школьного курса, внутри которой формирование вычислительной культуры может быть осуществлено в достаточной степени. Это следует из того, что постижение сущности вычислительной культуры требует не простого овладения вычислительными навыками, а их использование в качественно различных ситуациях, разнообразие которых, вообще говоря, безгранично.
-
Это положение будем называть принципом непрерывности формирования вычислительной культуры.
-
Мы считаем, что начинать с пятого класса средней школы ещё не поздно, т.к. начальная школа работает, преимущественно, с небольшими натуральными числами, доступными интуиции. Там требование абсолютной точности на уроках математики соответствует представлениям, сложившимся на основании опыта. Но уже при переходе к большим натуральным числам, а, тем более, рациональным, должно проявиться противоречие, которое академик А.Д. Александров выразил словами: «Либо абсолютная точность без связи с реальностью, либо связь с реальностью без абсолютной точности»[8,стр.278]. Настоящая практика преподавания, учебники, методики, пособия замалчивают, игнорируют это противоречие. Никто не утверждает, что в реальности есть абсолютная точность, но задачи с так называемым практическим содержанием решают как идеальные, т.е. абсолютно точные. Поэтому, если в пятом классе не начать соответствующую работу, то у ребёнка складывается неадекватная реальности картина мира: нужно начинать работу по формированию вычислительной культуры в этот школьный период. Отсутствие методики формирования вычислительной культуры пятиклассников и потребность в ней обуславливают актуальность исследования и определяют его цель.
-
Цель исследования: разработать методику формирования вычислительной культуры школьников пятых классов в её сущностном понимании.
-
Сказанное выше определило проблему нашего исследования.
-
Проблема исследования: выявить условия (элементы содержания курса, его идейную направленность и методику обучения), при которых возможна реализация сущностного подхода к формированию вычислительной культуры школьников пятых классов.
-
Мы предположили, что программный материал по математике в пятом классе позволит подойти к решению сформулированной проблемы.
-
Объект исследования: процесс изучения учащимися пятых классов материала по линии: «Числа и вычисления».
-
Принятое нами определение вычислительной культуры в её сущностном понимании не достаточно конкретно для того, чтобы непосредственно указывать на содержание материала и методику его преподавания в пятом классе. Это и определило задачи исследования.
-
Задачи исследования: •S построить и теоретически обосновать определение вычислительной культуры школьника пятого класса, достаточно конструктивно определяющее методику формирования вычислительной культуры учащихся;
-
S выявить средства формирования вычислительной культуры;
-
S подобрать качественные задачи, доступные ученикам пятого класса и приводящие к необходимости получить и осмыслить число;
-
S разработать методику использования таких задач в процессе изучения программы по математике в пятом классе;
-
S разработать методику неформального ознакомления учащихся пятых классов с правилами простейших приближённых вычислений; S выявить роль и место использования микрокалькулятора в процессе формирования вычислительной культуры;
-
S экспериментально проверить и уточнить методику формирования вычислительной культуры пятого класса.
-
Результаты теоретического анализа литературы и качественного анализа хода и результатов констатирующего эксперимента делают, по нашему мнению, обоснованным следующее определение:
-
Вычислительная культура школьника пятого класса характеризуется: способностью школьника отобрать и оценить те качественные стороны рассматриваемого явления, которые приводят к постановке вычислительной задачи и определению допустимой погрешности (в пределах имеющихся знаний и жизненного опыта); способностью школьника соотнести данное ему число с качественными особенностями знакомой ему ситуации, в которой это число возникло, и на этой основе отделить действительно реальную ситуацию от идеальной; хорошо развитыми навыками точных вычислений и освоенными на неформальной основе приемами простейших приближенных вычислений; способностью грамотно и по существу использовать микрокалькулятор.
-
Умения, характеризующие вычислительную культуру пятиклассников, будем считать необходимыми для реализации сущностного подхода, их наличие представляет собой основы вычислительной культуры в её сущностном понимании.
-
Необходимость выбора средств формирования вычислительной культуры пятиклассников определила предмет исследования. Средствами формирования вычислительной культуры школьника в соответствии с её определением могут быть такие задания, систематическое выполнение которых будет приучать ребёнка к правильному движению мысли от качественной картины явления к его количественному описанию и от него к сущности явления (новому качеству). Задачи, работа с которыми создаёт условия для осмысления связи качества и количества, будем называть качественными.
-
Под качественной задачей мы будем понимать задачу, отвечающую следующим требованиям:
-
• задача формулируется, как правило, в виде качественного вопроса;
-
• вопрос должен быть таким, как он обычно ставится на практике: хватит ли, успеем ли и т.д.;
-
• если заданы какие-то величины, их значения должны быть реальными, взятыми из жизни; если нет, то должно быть понятно, с помощью каких измерений, с какой точностью и какими инструментами можно получить необходимые числовые данные;
-
• ситуация, описываемая в задаче, должна быть абсолютно ясной, близкой, понятной и естественной для учащихся;
-
• полученный результат, выраженный с помощью числа, позволяет сделать вывод о целесообразности той или иной стратегии поведения в данной ситуации, т.е. человек, получивший число, может использовать его для определённых качественных выводов.
-
Задачи, соответствующие сформулированным требованиям, мы будем использовать, как средство формирования вычислительной культуры. Так как в качественных задачах данные представляют собой результаты измерений, то они в подавляющем числе случаев носят приближённый характер. Это означает, что ребёнок должен уметь работать с приближёнными числами. Мы считаем, что приближённые вычисления могут быть средством формирования вычислительной культуры, если в пятом классе познакомить учащихся со способами сложения, вычитания, умножения и деления приближённых чисел по данным, полученным из непосредственных измерений, с точностью, соответствующей точности исходных данных. И, что важно, простейшие приёмы приближённых вычислений осваиваются школьниками на неформальной основе.
-
Так как ключевым моментом формирования вычислительной культуры школьника мы считаем создание необходимости осмысления связи между числом и качеством, то работа на этапе решения чисто вычислительной задачи может быть организована с помощью вычислительной техники. Это означает, что грамотное, культурное использование микрокалькулятора также можно рассматривать как средство формирование вычислительной культуры.
-
Предмет исследования: средства формирования вычислительной культуры школьников пятых классов.
-
Исходя из проблемы, объекта и предмета исследования мы выдвигаем следующую гипотезу.
-
Гипотеза исследования: в процессе изучения курса математики пятого класса можно заложить основы вычислительной культуры в ее сущностном понимании через использование качественных задач, приближенных вычислений и микрокалькулятора.
-
Методы исследования:
-
S теоретический анализ методической, психолого-педагогической, математической литературы, а также программ и учебников по математике;
-
S наблюдение за деятельностью учащихся и учителей; •S организация и проведение констатирующего, поискового и обучающего экспериментов;
-
•S обработка и интерпретация данных, полученных в процессе проведения экспериментов.
-
База исследования. Изучение состояния проблемы и педагогические эксперименты проходили на базе средних школ №83 и № 518 Выборгского района Санкт-Петербурга, средней общеобразовательной школы при
-
Посольстве РФ в Израиле, математического факультета РГПУ им. А.И. Герцена, курсов повышения квалификации учителей математики на базе СПб ГУПМ.
-
Организация и этапы исследования.
-
Этап 1. (1994-1995г.г.) - анализ образовательной практики, направленной на повышение вычислительной культуры школьников, выявление основных проблем и поиск путей их разрешения. Анализ психолого-педагогической, методической, математической литературы, программ и учебников по математике. Теоретическое осмысление проблемы.
-
Этап 2. (1995-1997г.г.) Проведение констатирующего и поискового экспериментов.
-
Этап 3.(Т997-2003г.г.) Проведение обучающего эксперимента. Анализ и обобщение результатов опытно-экспериментальной работы. Оформление диссертации.
-
Научная новизна проведённого исследования заключается в том, что впервые в методике обучения математике рассмотрено понятие сущности вычислительной культуры. понятие сущности вычислительной культуры конкретизировано в виде трактовки определения вычислительной культуры пятиклассников. выявлены условия, при которых возможна реализация и реализован сущностный подход к формированию вычислительной культуры при разработке методики. предложено оригинальное обоснование места и значения жизненного опыта учащихся в реализации сущностного подхода к формированию вычислительной культуры.
-
Теоретическая значимость проведённого исследования состоит в том, что: сформулировано определение понятия вычислительной культуры школьника пятого класса; обоснован способ конструирования определения понятия «вычислительная культура школьника пятого класса», соответствующего сущности общего понятия «вычислительная культура»; выделены основные средства формирования вычислительной культуры пятиклассников: качественные задачи с реальным содержанием и, как следствие, приближённые вычисления.
-
Практическая значимость заключается в том, что: разработана методика формирования вычислительной культуры пятиклассников на основе использования качественных задач; разработана методика неформального освоения правил простейших приближённых вычислений; полученные результаты могут быть использованы учителем в практике преподавания математики; могут быть учтены при разработке программ, написании учебников и методических пособий; облегчают применение математики при изучении других предметов школьного курса; показывают способы реализации, практической и прикладной направленности математики в процессе её преподавания.
-
Апробация результатов исследования осуществлялась в виде:
-
• докладов на Герценовских чтениях (Санкт-Петербург, 1995,1997,1998,2004г.г.);
-
• докладов на семинаре аспирантов и преподавателей кафедры методики обучения математике РГПУ им. А.И.Герцена (1995,1997,1998,1999,2004г.г.);
-
• выступлений на «августовских» совещаниях руководителей заграншкол МИД РФ и региональных совещаниях администраций заграншкол (2000, 2001, 2002, 2003 г.г.).
-
На защиту выносятся:
-
1. Трактовка понятия вычислительной культуры пятиклассников является теоретической основой, на базе которой возможно построение методики, направленной на формирование вычислительной культуры.
-
2. В основе методики формирования вычислительной культуры лежат следующие принципы:
-
S принцип единства (необходимость выполнения трёх шагов в процессе решения задачи);
-
S принцип непрерывности (вычислительная культура формируется в процессе изучения всего школьного курса математики). Принципы реализуются через использование в процессе обучения качественных задач, приближённых вычислений и микрокалькулятора.
-
Основные положения диссертационного исследования отражены в следующих публикациях:
-
1. Казакова Т.Н. О построении множества действительных чисел в школе//Школьное математическое образование: вопросы содержания и методов. Тезисы докладов на Герценовских чтениях.//СПб.Образование.-1995 -0,1 п. л.
-
2. Казакова Т.Н. Использование знаний учащихся о числовых системах при ознакомлении школьников с основными понятиями школьной алгебры//Актуальные проблемы преподавания математики в школе и вузе. Материалы межвузовской конференции, посвященной 105-летию со дня рождения В.М.Брадиса.//Тверь.1995 - 0,13 п.л
-
3. Казакова Т.Н. О приближённых вычислениях в курсе математики 5 класса средней школы//Сочетание общекультурной и предметной составляющих в общем математическом образовании учащихся и в профессиональной подготовке будущих учителей математики.//Тезисы докладов на Герценовских чтениях. Пб.Образование-1997- 0,13 п.л.
-
4. Казакова Т.Н. Об использовании исторических сведений при формировании понятия числа//Сочетание общекультурной и предметной составляющих в общем математическом образовании учащихся и в профессиональной подготовке будущих учителей математики.// Тезисы докладов на Герценовских чтениях. Пб.1997 -.0,13 п.л.
-
5. Казакова Т.Н. Об использовании МК при знакомстве с приближёнными вычислениями в 5-6 классах//Личностно-ориентированный подход при обучении математике (содержательный и процессуальный аспекты).// Тезисы докладов 51 Герценовских чтений. СПб. 1998- 0,1 п.л.
-
6. Казакова Т.Н. Методика использования качественных задач и приближённых вычислений при изучении в 5 классе темы «Умножение и деление натуральных чисел»//Проблемы теории и практики обучения математике. СПб. 2004 - 0,4 п.л.
-
Заключение диссертации по теме "Теория и методика обучения и воспитания (по областям и уровням образования)", Казакова, Тамара Николаевна
-
ЗАКЛЮЧЕНИЕ.
-
Настоящая диссертационная работа, являясь законченным исследованием в смысле задач, которые были поставлены, не исчерпывает и не закрывает тему формирования вычислительной культуры школьника, но показывает возможность корректной постановки и решения этой проблемы уже на уровне пятого класса. Теоретически обосновано и экспериментально проверено, что формирование вычислительной культуры по предлагаемой методике закладывает основы правильных представлений об отношении математики к реальной действительности и специфических особенностях математического метода познания закономерностей окружающего мира.
-
Вместе с тем, результаты, представленные в настоящей работе, а также исследования, проводимые нами за ее пределами (работа со школьниками 611 классов, студентами и учителями), показывает, что основные положения методики формирования вычислительной культуры школьника пятого класса могут быть перенесены для продолжения решения этой же проблемы в следующие классы. Опыт, накопленный в ходе экспериментального преподавания, показывает, что главные трудности, связанные с формированием вычислительной культуры школьника, обусловлены идеологией традиционного курса математики и, как следствие, недостаточной подготовленностью учителей к реализации предлагаемой методики. Поэтому, по-настоящему, проблема формирования вычислительной культуры школьника может быть решена только на пути перестройки школьного курса математики. При этом мы имеем в виду не отрицание существующего курса, а его правильное дополнение или, как об этом говорится в данной работе, его методическое и дидактическое сопровождение, обеспечивающее решение проблемы формирования вычислительной культуры. Необходимо отметить, что вычислительная культура не относится к разряду отдельных тем курса математики. Это категория иного порядка. Правильный, сущностный подход к вычислительной культуре решает важнейшие методические и мировоззренческие задачи, в частности, помогает ученику понять отношение математики к реальной действительности, обеспечивает грамотное применение математики при решении практических задач в повседневной жизни, профессиональной деятельности, изучении других наук.
-
Список литературы диссертационного исследования кандидат педагогических наук Казакова, Тамара Николаевна, 2004 год
-
1. Абаляев Р.Н. Элементы политехнического образования в связи с изучением математики. // Начальная школа. - 1982. - № 3. - с. 51-55.
-
2. Абрамова Г. С. Возрастная психология. М. Академический проект, 2001.
-
3. Абрамович С.М. О воспитании графической культуры учащихся. // Математика в школе. 1989. - № 5. - с. 26.
-
4. Авраменко B.C. Квадратные уравнения и МК на математическом кружке. // Математика в школе. 1989. - № 5. - с. 84-85.
-
5. Автайкина А.К. Некоторые формы организации устного счета.// Математика в школе. -1991. № 3. - с. 21.
-
6. Александров А.Д. Математика, ее содержание, методы и значение. Том I. М.: Изд-во АН СССР, 1956.
-
7. Александров А. Д. О геометрии. // Математика в школе. 1980. -№ 3. - с. 56-59.
-
8. Александров А.Д. Основания геометрии. М.: Наука, 1987.
-
9. Александров А.Д. От дважды два до интеграла. // Проблемы науки и позиция ученого. JL: Наука, 1988. - 420-425 с.
-
10. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И. Алгебра 8. М.: Просвещение, 1991.
-
11. Аллабергенов С.А. Элементарные приближенные расчеты в среднем образовании: Автореферат диссертации к.п.н. М., 1975.
-
12. Ананьев Б.Г. Психология чувственного познания. М.: Наука, 1960.
-
13. Андронов И.Л. Трилогия предмета и метода математики. М.: Просвещение, 1974.f
-
14. Антипов И.Н., Боковнев О.А., Шамшурин B.JI. Обучение учащихся 7 класса работе на микрокалькуляторе МКШ-2. // Математика в школе. 1985. - № 3. - с. 33-35.
-
15. АнтиповИ.Н. Основные приемы вычислений на микрокалькуляторе "Электроника БЗ-18А". М.: Высшая школа, 1980.
-
16. Арутюнян Е.Б., Волович М.Б., Глазков Ю.А. Система устных заданий для 5 класса. // Математика в школе. 1983. - № 4. - с. 24.
-
17. Асылбеков Ш.Ж. Компьютер и наглядность. // Математика в школе. 1989. - № 5. - с. 90.
-
18. Атутов П.Р. Формирование у школьников политехнических знаний и умений в процессе обучения основам наук. М.: Просвещение, 1966. -48 с.
-
19. Балк М.Б., Полухин А. А. О некоторых особенностях решения уравнений с помощью микрокалькулятора. // Математика в школе. -1983.- №5.-с. 35-36.
-
20. Баранова И.В. Приближенные вычисления в курсе математики восьмилетней школы. Ученые записки ЛГПИ им. А.И.Герцена, т. 235. -Л., 1963.
-
21. Баранова И.В., Борчугова З.Г. Математика. Учебник для 5 класса средних общеобразовательных учреждений. СПб.: Специальная литература, 1997.
-
22. Бекаревич А.Н. Приближенные вычисления в средней школе. -Минск: Народная асвета, 1979.
-
23. Бекбоев И.К. К вопросу осуществления связи обучения математике с жизнью. Фрунзе: Мектеп, 1964. - 132 с.
-
24. Березанская Е.С. Методика арифметики. М.: Учпедгиз, 1955.
-
25. Березанская Е.С. Сборник задач и упражнений по арифметике для 5 и 6 классов семилетней и средней школы. М.: Учпедгиз, 1951.
-
26. Блох А.Я., Черкасов Р.С. О современных тенденциях в методике преподавания математики. // Математика в школе. 1989. - № 5.-с. 132-142.
-
27. Болтянский В.Г. Математическая культура и эстетика. // Математика в школе. 1982. - № 2. - с. 40-43.
-
28. Болтянский В.Г. Школа и микрокалькулятор. // Математика в школе. 1979. - № 2. - с. 46-49.
-
29. Болтянский В.Г., Григорян Э.В. Микрокалькулятор в начальных классах. // Математика в школе. 1983. - № 5. - с. 24-29.
-
30. Болтянский В.Г., Григорян Э.В., Пашкова JI.M., Шахбазян Г.Б. Использование микрокалькуляторов в обучении математике. М.: Просвещение, 1990.
-
31. Болтянский В.Г., Пашкова Л.М. Проблема политехнизации курса математики. // Математика в школе. 1985. - № 5. - с. 6-13.
-
32. Болтянский В.Г., Рубцов В.В. Проблема компьютеризации обучения. // Математика в школе. 1986. - №. 1 - с. 69.
-
33. Бородина В.Н. Устные вычисления в 4 классе. // Математика в школе. 1987.-№6.- с. 37.
-
34. Брадис В.М. Как надо вычислять. М.: Просвещение, 1965.
-
35. Брадис В.М. Методика преподавания математики в средней школе. М.: Учпедгиз, 1954.
-
36. Брадис В.М. Средства и способы элементарных вычислений. М.: АПН РСФСР, 1951.
-
37. Брадис В.М. Теория и практика вычислений. М.: Учпедгиз, 1935.
-
38. Бурбаки Н. Очерки по истории математики. М.: И.Л., 1963.
-
39. Васильев М.Г. О приближенных вычислениях в старших классах. // Математика в школе. 1953. - № 3.
-
40. Васильев-Куклин А.А. Формирование навыков использования микрокалькулятора "Электроника МКШ-2" при решениищматематических и физических задач в средней школе. Методические рекомендации. JI.:, 1987.
-
41. Венгер А. Л. Психологическое развитие ребёнка в процессе совместной деятельности.//Вопросы психологию-2001.-№3.-с.74.
-
42. Виленкин Н.Я., Мышкис. Научно-техническая революция и школьный курс математики. // Математика в школе. 1987. - № 3. - с. 40.
-
43. Виленкин Н.Я., Оксман В.М., Шварцбурд С.И. Микрокалькулятор школьнику.
-
44. Виленкин Н.Я., Чесноков А.С., Шварцбурд С.И.,
-
45. Жохов В. И. Математика 5. М.: Просвещение, 1992.
-
46. Возняк Г.М., Гусев В . А. Прикладные задачи на экстремумы в курсе математики в 4-8 классах: Пособие для учителя. М.: Просвещение, 1985. - 144 с.
-
47. Всестороннее и глубокое овладение электронно-вычислительной техникой важнейшая задача. Передовая статья // Математика в школе. - 1985.-№4.-с. 3-6.
-
48. Г а б ы ш е в а Л.Р. Вычислительные упражнения по теме «Десятичные дроби».// Математика в школе. -2000. -№6. -с.43.
-
49. Гайбуллаев Н.Р. Повышение эффективности практическойдеятельности учащихся при изучении математики. // Математика в школе. 1982. - № 6. - с. 22-23.
-
50. Гайбуллаев Н.Р. Совершенствование обучения математике в школе на основе повышения эффективности практической деятельности учащихся: диссертация в форме научного доклада д.п.н. -М., 1983.-47 с.
-
51. Гладкий А.В. Об уровне математической культуры выпускников средней школы. // Математика в школе. 1990. - № 4, - с. 7-9.
-
52. Глазков Ю.А. Электроника "МКШ-2". // Математика в школе. -1982.-№1. -обложка.
-
53. Глейзер Г. Д., Черкасов Р.С. Математика и педагогика две грани одного таланта. // Математика в школе. - 1996. - № 3. - с. 6.
-
54. Гнеденко Б.В. Политехнические аспекты преподавания математики в средней школе. // На путях обновления школьного курса математики. М., 1978. - 121-132 с.
-
55. Гнеденко Б.В. Формирование мировоззрения учащихся в процессе обучения математике. М.: Просвещение, 1982. - 144 с.
-
56. Гнеденко Б.В., Черкасов Р.С. О преподавании математики в предстоящем тысячелетии. // Математика в школе. 1996. - № 1. - с. 5254.
-
57. Гребенча М.К. Ляпин С.Е. Арифметика. Пособие для учительских институтов. М.: Учпедгиз, 1952.
-
58. Грибанов В.У. Приближенные вычисления в средней школе. М.: Учпедгиз, 1958.
-
59. Гусева И. Л. Два землекопа и две трети. // Математика в школе. -1999. -№5.-с.27.
-
60. Дорофеев Г.В., Петерсон Л.Г. Математика 5 класс ч. 1.// "Баллас", "С-Инфо", 1996.
-
61. Дорофеев Г.В. О принципах отбора содержания школьного математического образования. // Математика в школе. 1990. - № 6. - с. 2-5.
-
62. Дорф П.Я. Методика преподавания математики. Л.: ЛГУ, 1960. -124 с.
-
63. Дуглас А. Насколько важно изучать математику? // Перспективы. Вопросы образования. // 1982. № 1-2. - с. 41-47.
-
64. Дудницын Ю.П., Пашкова Л.М., Сытина Т.Д. Урок математики: наглядные пособия и технические средства обучения в СПТУ. М: Высшая школа, 1987.
-
65. Елгест Иос. Проблемный подход к преподаванию естественнонаучных дисциплин. // Перспективы. Вопросы образования. 1982. - № 4.
-
66. Ершов А.П. Компьютеризация школы и математическое образование. // Математика в школе. -1989. № 1. - с. 14.
-
67. Жак Я.Е. Несколько простых прикладных задач. // Математика в школе. 1980. - № 2. - с. 37-39.
-
68. Законников П.Н. О решении некоторых практических задач в связи с трудовой деятельностью учащихся. // Математика в школе. -1959.- №5.- с. 90-93.
-
69. Зеленская Т.Я. Об оптимальной модели микрокалькулятора для школы. // Математика в школе. 1984. - № 1. - с. 30.
-
70. Зимняя И.А. Педагогическая психология. М. Логос,1999.
-
71. Зубов В.Г. Политехническое образование в современных условиях. // Советская педагогика. 1975. - № 3. - с. 3-11.
-
72. Иванов А.И. Изменение величин и их измерений на уроках физики и математики в восьмилетней школе: Автореферат диссертации к.п.н. -М., 1981.
-
73. Икрамов ДЖ. Математическая культура школьника. Ташкент: "Укитувчи", 1981.
-
74. Ионов Г. Н. Микрокалькулятор как средство обучения и контроля. // Математика в школе. 1984. - № 3. - с. 51-52.
-
75. Ионов Г.Н. Электронный помощник учителя. // Математика в школе. 1983. - № 5. - с. 31-33.
-
76. Кадемия М.Е. Микрокалькуляторы как средство интенсификации учебного труда учащихся средних профтехучилищ. // Математика в школе.- 1983.-№ 1.-е. 30.
-
77. Казакова Т.Н. О построении множества действительных чисел в школе // Школьное математическое образование: вопросы содержания и методов. Тезисы докладов на Герценовских чтениях. СПб.: Образование, 1995.
-
78. Казакова Т.Н. Методика использования качественных задач и приближённых вычислений при изучении в 5 классе темы «Умножениеи деление натуральных чисел»//Проблемы теории и практики обучения математике. СПб. 2004.
-
79. Канин Е.С. К формированию умений и навыков в вычислениях и тождественных преобразованиях. // Математика в школе. 1984. - № 5.
-
80. Карп А.П. Образовательные стандарты петербургской школы. Математика. СПб.: Центр педагогической информации, 1997.
-
81. Киселев А.П. Арифметика. Учебник для 5 и 6 классов семилетней и средней школы. М.: Учпедгиз, 1950.
-
82. Ковалев М.П, Шварцбург С.И. Электроника помогает считать. -М.: Просвещение, 1983.
-
83. Коган Н.И. Чему учит физика.//Школьный психолог.-2000.-№11 .-с.28.
-
84. Колмогоров А.Н. Научные основы школьного курса математики. М.: Просвещение, 1973.
-
85. Колягин Ю.М. и др. Методика преподавания математики в средней школе. Частные методики. М.: Просвещение, 1977.
-
86. Король Я.А. Реализация политехнического принципа в обучении математике младших школьников: Автореферат диссертации к.п.н., М., 1982.- 16 с.
-
87. Крылов А.Н. Мои воспоминания. М.: изд-во АН СССР, 1945.
-
88. Крылов В.В. Установление содержательных взаимосвязей учебного материала на практикуме по решению математических задач посредством качественных заданий. Дисс. на соискание уч. ст. к.п.н.,СПб., 2000.
-
89. Кузнецов Е.Ю. Электроника МК-51. // Математика в школе. -1982.-№5.
-
90. Кузнецов Е.Ю., Минкин JI.K. Микрокалькулятор в школе, виды микрокалькуляторов. // Математика в школе. 1982. 135-136 с.
-
91. Кузнецова Jl.В., Бунимович Е.А., Пигарев Б.В., Суворова С.Б. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы. 9 класс. М.: Дрофа, 1996.
-
92. Кукушкин Б.Н., Купцов Л.П. Микрокалькулятор в школе.// Математика в школе. 1987. - № 1. - с. 52-53.
-
93. Кулагина И.Ю. Возрастная психология. М. УРАО, 1999.
-
94. Курант Р. Математика в современном мире. // Математика в современном мире. М.: Мир, 1967. - с. 5-28.
-
95. Леднев B.C., Никандров Н.Д. Учебные стандарты школ России. Математика. Естественнонаучные дисциплины. Книга 2. М.: Прометей, 1998.
-
96. Лиман М.М. Практические задачи по геометрии для 8-летней школы. М.: Учпедгиз, 1961. - 92 с.
-
97. Лиховецкая Т.П. Игра "Вычислительная машина". // Математика в школе. 1985. - № 3.
-
98. Локалова Н.П. Уроки психологического развития для младших подростков.//Вопросы психологии.-2003 .-№6.-с.36.
-
99. Леонтьев А. Н. Деятельность. Сознание. Личность. М.: Политиздат, 1977. - 304 с.
-
100. Мадбабаев М.М. Методика изучения приближенных вычислений в курсе математики восьмилетней школы на базе измерений: Автореферат к.п.н., МГПИ им.Ленина. М., 1987.
-
101. Макс Л.Белл Преподавание математики как инструмент решения задач. // Перспективы. Вопросы образования. 1982. - № 1-2. - с. 112120.
-
102. Маркушевич А.И. Об очередных задачах преподавания математики в школе. // Математика в школе. 1962. - № 2. - с. 3-14.
-
103. Маркушевич А.И. Алгебра7.-М.: Просвещение, 1980.
-
104. Мельникова Н.Б. Проблема прикладной экономической ориентации курса алгебры: Автореферат диссертации к.п.н. М., 1980. -20 с.
-
105. Меражов З.Ш. Формирование измерительных навыков при обучении математике: Автореферат диссертации к.п.н. МГПИ. М., 1986.
-
106. Минаева С.С. Начальные сведения о калькуляторе в 4 классе. // Математика в школе. 1987. 36-37 с.
-
107. Минаева С.С. О формировании навыков вычислений в уме. // Математика в школе. 1987. - № 5. - с. 35.
-
108. Минаева С.С. О формировании понятия приближения в школе. // Углубленное изучение математики и ее приложений. М., 1977. - с. 5659.
-
109. Минаева С.С. Повышение уровня вычислительных измерений учащихся старших классах. // Математика в школе. 1983. - № 5. - с. 1921.
-
110. Минаева С.С., Оксман В.М. Использование микрокалькулятора "Электроника БЗ-18" в обучении алгебре и началам анализа. М.: Высшая школа, 1980.
-
111. Мишин В.И. Методика преподавания математики в средней школе. Частная методика. М.: Просвещение, 1987.
-
112. Малкова Т.В., Гайбуллаев Н.Р., Мусаелян Р.А., Аллабергенов С.А. Методика обучения приближенным вычислениям в школе. Ташкент: Укитувчи, 1982. - с. 136.
-
113. Монахов В.М. Введение в школу приложений математики, связанных с ЭВМ: Автореферат диссертации к.п.н. М., 1973. - 59 с.
-
114. Монахов В.М. Реализация принципа политехнизма при обучении алгебре в восьмилетней школе. // Преподавание алгебры в 6-8 классах. -М., 1980. с. 46-62.
-
115. Моро М.И. Об усилении практической направленности в обучении математике. // Начальная школа. 1979. - № 8. - с. 16-21.
-
116. Мусаелян Р.А. Проблема усиления прикладной ориентации обучения приближенным вычислениям: Автореферат диссертации к.п.н. М., 1977. - 22 с .
-
117. Мышкис А.Д., Сатьянов П.Г. О формировании культуры построения и применения графиков функций. // Математика в школе. -1985.-№4.-с. 44-48.
-
118. Н е м о в Р.С. Психология образования, Кн.2.//Психология, в 3 кн.-М. -.Просвещение, 1995.
-
119. Нурк Э.Р., Тельгмаа А.Э. Математика 5. М.: Просвещение,1988.
-
120. Об использовании микрокалькуляторов в учебном процессе. Инструктивно-методическое письмо. // Математика в школе. 1982. - № 3. - с. 6-8.
-
121. Обухова Л.Ф. Детская возрастная психология. М. Педагогическое общество России, 1999.
-
122. Оксман В.М. Прикладные аспекты применения микрокалькуляторов. // Профобразование. 1981. - № 10.
-
123. Оксман В.М. Дидактические возможности программируемой игрушки. // Математика в школе. 1988. - № 5, обложка.
-
124. Оксман В.М. Компьютер при изучении показательной функции. // Математика в школе. 1988. - № 5. - обложка.
-
125. Оксман В.М. Компьютер строит график. // Математика в школе.1989. № 5. - обложка.
-
126. Оксман В.М. Микрокалькулятор в системе профессионально-технического образования. // Математика в школе. 1983. - № 5. - с. 3031.
-
127. Поллак Х.О. Как мы можем научить приложениям математики. -М., 1980. 42-62 с.
-
128. Панасенко М.З. Некоторые способы быстрых вычислений. // Математика в школе. 1992. - № 1. - с. 22.
-
129. Пашбалтаев М. Больше внимания проблеме компьютеризации. // Математика в школе. -1991. № 2. - с. 5-7.
-
130. Пашкова J1.M., Оксман В.М. Микрокалькуляторы в учебный процесс. // Профтехобразование. 1980. - № 5.
-
131. Петерсон Л.Г,. Дорофеев Г.В. Математика 5 класс. М.: Ассоциация "Школа - 2000", 1997.
-
132. Пойя Дж. Математическое открытие. -М.: Наука, 1970.
-
133. Политехническое обучение в советской школе. // Математика в школе. -1953.-№2.-с. 1.
-
134. Пономарев С.А. К вопросу о политехническом обучении в преподавании математики. // Математика в школе. 1953. - № 3.
-
135. Пономарев С.А., Стратилатов П.В., Сырнев Н.И. Арифметика для 5 и 6 классов средней школы. М.: Просвещение, 1966.
-
136. Пономарев С.Д., Сырнев Н.И. Сборник задач и упражнений по арифметике для 5-6 классов восьмилетней школы. М.: Просвещение, 1965.
-
137. Принцев Н.А., Ягодовский М.И. Арифметика. Учебник для 5-6 классов средней школы. М.: Просвещение, 1966.
-
138. Программы средней общеобразовательной школы. Математика. М.: Просвещение, 1991.
-
139. Прочухаев В.Г. Приближенные вычисления в школе. Учебное пособие. М., 1973.
-
140. Рейнгард И.А. Сборник задач по геометрии и тригонометрии с практическим содержанием. М.: Учпедгиз, 1960. - 116 с.
-
141. Ройтман П.Б. и др. Повышение вычислительной культуры учащихся. М: Просвещение, 1980. - 80 с.
-
142. Семушин А.Д. Политехническое содержание школьного курса математики. // Математика в школе. 1977. - № 4. - с. 20-26.
-
143. Скобелев Г.Н. Расчеты на МКШ-2 с многократным использованием второго компонента операций. // Математика в школе. 1986. - № 2. - с. 66-67.
-
144. Соколовский И.Ф. Вычислительная культура как основа методики введения начал математического анализа в средней школе. Автореферат диссертации к.п.н. JI, 1988.
-
145. Соколовский И.Ф. Вычислительная культура как основа методики введения начал математического анализа в средней школе: диссертация на соискание звания к.п.н. Л., 1988.
-
146. Спатару Н.К. Арифметика (учебник для 5 класса). Кишинев: Изд-во Лумина, 1970.
-
147. Столяр А.А. Педагогика математики. Минск: "Высшая школа", 1974.
-
148. Столяр А.А. Роль математики в гуманизации образования. // Математика в школе. 1990. - № 6. - с. 5-7.
-
149. Стратилатов П.В. Повышение вычислительной культуры учащихся средней школы. М.: Просвещение, 1965. - 168 с.
-
150. Теляковский С.А.и др. Алгебра 8.-М.: Просвещение, 1991.
-
151. Теляковский С.А.и др. Алгебра7. -М.: Просвещение, 1989.
-
152. Теплова Л.И. Диагностика развития умственного развития учащихся при переходе из начальной школы в среднюю. Автореферат диссертации к.п.н., М.,1998.
-
153. Тесленко И.Ф., Распопов В.Б. Задачи компьютеризации.// Математика в школе. 1985. - № 2. - с. 29-32.
-
154. Тихонов A.M., Костомаров Д.П. Вводные лекции по прикладной математике. М.: Наука, 1984.
-
155. Фахрутдинова Р.К. Курс наглядно-практической геометрии.// Математика в школе.-1999. -№4. -с.49.
-
156. Фельдштейн Д.И. Приоритетные направления развития психологических исследований в области образования и самообразования современного человека.// Вопросы психологии.-2003.-№6.-с.4.
-
157. Филичев С.В., Чекмарев Я.Ф. Сборник задач и упражнений по арифметике 5 и 6 классов неполной средней и средней школы. М.: Учпедгиз, 1949.
-
158. Фирсов В.В. Некоторые проблемы обучения теории вероятностей как прикладной дисциплины: Автореферат диссертации к.п.н. М., 1974. - 27 с.
-
159. Фирсов В.В. О прикладной ориентации курса математики. // Углубленное изучение алгебры и анализа. М., 1977. 215-239 с.
-
160. Фирсов В.В. Обязательный минимум содержания обучения. // Математика в школе. 1998. - № 3.
-
161. Фирсов В.В. Планирование обязательных результатов обучения математике. М.: Просвещение, 1989.
-
162. Фридман JI.M. Психолого-педагогические основы обучения математике. М. .Просвещение, 1983.
-
163. Фройденталь Ханс. Новая математика или новое образование. // Перспективы. Вопросы образования. 1982. - № 1-2. - с. 121-129.
-
164. Хедрен Рольф. Калькуляторы и математика в начальной школе. // Перспективы. Вопросы образования. 1982. - № 1-2. - с. 131-134.
-
165. Хемминг Р.В. Численные методы. М.: Наука, 1976.
-
166. Ц у к а р ь А.Я. О полезности интерпретации решения задач.// Математика в школе. 2000.-№7. -с.42.
-
167. Цукарь А.Я. Применение ЭВМ в обучении математике. // Математика в школе. -1991. № 2. - с. 26-27.
-
168. Цукарь А.Я. Схематизация и моделирование при решении текстовых задач.// Математика в школе. -1998. -№5.-с.27.
-
169. Чесноков А.С., Нешков К.И. Дидактические материалы по математике 5 класса. М.: Просвещение, 1990.
-
170. Чудовский А.Н., Сомова JI.A. Сборник заданий для проведения письменного экзамена по математике в девятых классах общеобразовательных школ РСФСР. М.: Просвещение, 1990.
-
171. Чуканцев С.М. О некоторых недостатках в школьных учебниках по арифметике. // Математика в школе. 1952. - № 2.
-
172. Ш а м о в а Т.Н., Давыденко Т.М. Управление образовательным процессом в адаптивной школе. М.: Педагогический поиск, 2001.
-
173. Шварцбурд С.И. О политехнической направленности школьного математического образования. // Советская педагогика. 1975. - № 3. -с. 42-47.
-
174. Шварцбурд С.И.О приближенных вычислениях. М., 1974.
-
175. Шеврин J1.H., Гейн А.Г., Коряков И.О., Волков М. В. Математика 5. Учебник-собеседник. М.: Просвещение, 1994.
-
176. Шевченко Г.С. Применение микрокалькулятора при изучении темы "Предел последовательности". // Математика в школе. 1984. - № З.-с. 54-56.
-
177. Шевченко И.Н. Методика преподавания арифметики в 5-6 классах. М.: изд-во АПН РСФСР, 1961.
-
178. Шевченко И.Н. Начальные сведения о приближенных вычислениях. М.: Изд-во АПН РСФСР, 1958.
-
179. Шихалиев Х.Ш. Больше внимания формированию математической культуры. // Математика в школе. 1994. - № 2. - с. 12-13.
-
180. Эльконин Д.Б. Обучение и умственное развитие в младшем школьном возрасте.//Эльконин Д.Б. Избранные психологические труды. М. :Педагогика, 1989.
-
181. Эсаулов А.Ф. Психология решения задач. М.: Высшая школа, 1972.
-
182. Якубов А. ЭВМ в средней школе. // Математика в школе. 1989. -№ 6. - с. 47.
-
Научная библиотека диссертаций и авторефератов disserCat www.dissercat.com/content/metodika-formirovaniya-vychislitelnoi-kultury-shkolnikov-pyatykh-klassov#ixzz3Jx6A9tAb
При определении целей обучения математике в средней школе исходят как из общих целей обучения, так и из места и роли математики в современной науке, технике, производстве, жизни современного общества, из специфики математики как науки. Обычно цели обучения условно разделяют на группы; чаще всего - это три группы целей (или три - единая дидактическая цель):
-
образовательные (обучающие),
-
развивающие,
-
воспитательные.
Иногда выделяется группа практических (или жизненно-практических) целей преподавания математики. Естественно, что все группы целей тесно переплетаются между собой, взаимосвязаны. Так, например, нельзя достичь необходимого развития ученика без приобретения им определенных знаний, но и развитие не является простым следствием усвоения определенной суммы знаний.
Раскроем содержание каждой группы целей.
Современное состояние математики характеризуется огромным расширением сферы ее приложений. Еще несколько десятков лет назад это были лишь механика, физика, астрономия, геодезия. Сейчас математика применяется с большим успехом почти в каждой области высокоорганизованной человеческой деятельности. В то же время потребности техники, экономики, военного дела и д. Вызвали к жизни совершенно новые математические дисциплины, такие как кибернетика, теория информации, теория линейного программирования, теория игр и т.д. Таким образом, профессий, где математика имеет непосредственное применение, очень много. Без знания определенной, твердо установленной суммы математических фактов, без наличия определенных, хорошо усвоенных математических навыков невозможно изучать и другие науки, учиться многим профессиям.
С другой стороны, новые экономические отношения, развитие новых общественных институтов, становление новых духовных ценностей диктует необходимость давать обучаемым такие знания и умения. Которые формировали бы новый взгляд на мир, общество и место человека в нем, помогали бы осваивать новые технологии интеллектуальной деятельности, повышали уровень общей культуры. Образование должно стать средством для достижения комфортного и безопасного существования личности в современном мире.
С этих позиций образовательные цели обучения математике можно сформулировать следующим образом:
-
передача учащимся определенной системы математических знаний, умений и навыков - основ математической науки, необходимых для общего образования, для его продолжения в высшей школе, для изучения других дисциплин и для практической деятельности в повседневной жизни;
-
помощь учащимся в овладении математическими идеями и методами познания реальной действительности, необходимых для продолжения изучения математики в любой системе непрерывного образования и будущей профессиональной деятельности;
-
знакомство учащихся с элементами гуманитарного знания, связанного с математикой.
В программе по математике для средней школы эти цели конкретизируются - после каждой темы раздела "Тематическое планирование" сформирована так называемая "основная цель", объединяющая образовательные цели 1) - 3) и требования к математической подготовке учащихся по теме.
Развитие общества, наук, в частности, самой математики, появление новых взглядов на проблемы обучения и воспитания, возникновения и развитие технологического подхода к обучению приводят к естественному пересмотру как содержания целей школьного образования, так и к их постановке. Так, с точки зрения технологического подхода к обучению необходимо осуществить переход от общего представления о результате обучения к конкретному эталону и критерию его достижения учеником. Общее требование к такому переходу - описать то, что ученик может сделать в результате обучения, т.е. признаки достижения целей. Например, из двух формулировок целей -1) ученик усваивает правило и 2) ученик применяет правило в знакомой (новой) ситуации - следует выбрать вторую как более определенную. Способ постановки целей, который предлагает педагогическая технология, отличается повышенной инструментальностью. Он состоит в том, что цели обучения формулируются через результаты обучения, выраженные в действиях учащихся, причем таких, которые учитель может надежно опознать.
Определение шаги в этом направлении сделаны в разработанном документе "Стандарт среднего математического образования". Под стандартом образования понимается система основных параметров, принимаемых в качестве государственной нормы образованности, отражающей общественный идеал и учитывающей возможности реальной личности и системы образования по достижению этого идеала. Одна из основных целей стандарта спланировать обязательные результаты обучения математике, которые реализуются через совокупность требований к математической подготовке учащихся. Эти требования фиксируются по ступеням обучения, внутри каждой ступени структурированы по содержа -тельным линиям и задаются на двух уровнях: уровень возможностей и уровне обязательной подготовкив виде типовых заданий и процедур оценивания их выполнения учащимися.
Второй уровень (обязательной подготовки) характеризует тот минимум, который должен получить все учащиеся, он определяет нижнюю допустимую границу результатов математического образования. Первый уровень (возможностей) характеризует результаты, которых должны достичь учащиеся, изучающие общеобразовательный курс, но с учетом их разных возможностей (фактически он выделяет, с одной стороны, самый низкий из возможных и, с другой - самый высокий).
Кроме того, стандарты должны дать возможность проверить результаты обучения на трех профильных уровнях - гуманитарных, общеобразовательных и математических классов. Таким образом, стандарт призван помимо критериально оценочной функции выполнять функции сохранения единства образовательного пространства страны, гуманизации образования и повышения его качества. Является целевым компонентом методической системы.
В самом общем плане основной целью обучения должно быть развитие ученика. Конечно, в процессе и в результате усвоения знаний происходит умственное развитие учащихся, а математику даже называют гимнастикой ума, но определенное развитие получается только в результате специально организованного. Ориентированного на достижение этого развития обучения. Перечислим развивающие цели обучения математике:
-
развитие мышления, необходимого образованному человеку для полноценного функционирования в современном обществе (в частности, эвристического и алгоритмического), а также абстрактного, специфического для математики;
-
развития элементов творческой деятельности как качеств мышления - интуиции, пространственного воображения, смекалки и др.;
-
развитие мировоззрения, понимания философской стороны математики как науки об определенных свойствах действительного мира и ее роли в освоении научной картины мира;
-
развитие устной и письменной речи(в том числе, математической), формирование языка и аппарата математики, выработка умения читать математическую, а, следовательно, и техническую литературу;
-
развитие знаний, умений и навыков учебной деятельности, того, что называют "умением учиться";
-
развитие памяти.
Остановимся подробнее на отдельных составляющих развивающих целей обучения математике.
Развитие мышления учащихся в процессе обучения математике в настоящее время выдвигается на первое место. Это диктуется: во-первых, все возрастающей математизацией наук и производства и вытекающей отсюда потребностью в собственно математиках; во-вторых, тем. Что нельзя овладеть основами науки с тем, чтобы научиться применять свои знания, без умения мыслить; в-третьих, изменившейся в наше время парадигмой образования, ставшей в центр его человека, становление новых духовных ценностей. Образование сейчас должно формировать, у обучаемых, новый взгляд на мир, общество и место человека в нем, учить основам жизненного самоопределения, повышать уровень общей культуры. Изучение всех предметов должно быть не целью, а средством изучения мира, давать возможность учащихся научиться проникать в сущность изучаемых проблем. Известный психолог Я.А.Пономарев говорил: "Мышление - необходимая предпосылка всякой другой деятельности, ибо любая деятельность в конечном счете есть его свернутый и переработанный итог".
Понятие "мышление человека" очень многогранно, и процесс мышления изучается разными науками, которые устанавливают его общие закономерности. Специфика содержания и методов математики накладывает на них некоторые особенности. Как правило, математика требует наиболее развитых отдельных компонентов мышления, и у человека, занимающего математикой, развитое мышление бывает выражено более ярко, чем у другого специалиста (известное изречение "математик это сделает лучше"). Разделим условно компоненты мышления на следующие группы, отметив их особенности в сфере математики.
1. Формы мышления (изучаемые логикой): понятия, служения (общие,частные, единичные), умозаключения (индукция, дедукция, аналогия). Мышление в форме понятий называется понятийным (абстрактным, отвлеченным, теоретическим) мышлением. Для математики характерно преобладание такого типа мышления над предметным (наглядно - образным) и практически- действенным мышлением. Последнее имеет место на самых низких уровнях и на первых этапах изучения математического материала. Образное мышление - это мышление, протекающее в форме наглядных образов, практически-действенное - мышление, основанное на личном практическом опыте человека. Но умственное развитие каждого человека проходит первоначальную школу такого мышления, познавательная деятельность учащихся возникает на его основе. Недостаток этих типов мышления - их долгая связь с образом, а математика отражает формы и отношения действительного мира, отвлеченные от их содержания. Поэтому в развитии математического мышления нельзя долго задерживаться на этом первом этапе.
Высшей формой понятийного мышления является категориальное или структурное мышление. Категориями называются мыслительные структуры, у которых закрепляются существующие отношения вещей и явлений. Такой тип мышления, которое отражает реальность в сеть категорий, очень характерен для современной математики, а для математической деятельности - тенденция к быстрому сокращению, "свертыванию" рассуждений, к мышлению сокращенными умозаключениями, "свернутыми" структурами.
Важнейшей особенностью математики, отличающий ее от всех наук, является дедуктивный характер ее умозаключений. Теорема (форма суждения) считается доказанной, если она дедуктивно выведена из других предложений; систематически применяемый при изложении математических дисциплин дедуктивный метод переходит в дедуктивную систему. Поэтому математику называют преимущественно дедуктивной наукой, а характерной особенностью мышления в сфере математических объектов - дедуктивное мышление. Последнее не исключает значимости для процесса обучения и развития мышления учащихся индивидуальных умозаключений, играющих эвристическую роль.
Мышление в форме понятий, суждений и умозаключений по правилам и законам логики называют логическим мышлением. Математике приписывают особую роль в развитии такого мышления, однако исследования психологов и педагогов показали, что одна тренировка в логических рассуждениях без понимания того, как рассуждаем, не приводит к требуемому уровню развития логики мышления; что логические понятия и действия, формируемые у ребенка стихийно, как правило, неполны и часто искажены; что логическим понятиям и действиям, приемам логического мышления нужно специально обучать.
2. Операции мышления (изучаемые психологией): анализ, синтез, сравнение, обобщение, абстрагирование, конкретизация, классификация, систематизация. Анализ как метод логического доказательства теорем, как средство поиска доказательства и решения других математических задач, его характерные формы, связанные со спецификой математики, - все это в большой степени присуще мыслительной деятельности в сфере математических объектов. Для человека, владеющего анализом, характерен так называемый аналитический стиль мышления: отдельные этапы его отчетливо выражены и думающий может рассказать о ней другому человеку. С другой стороны, изложение математического материала с древних времен осуществляется с помощью синтеза того, что получено при его анализе, оно переходит в математике в синтетическую систему.
Очень полезно в любой познавательной деятельности сравнить изучаемые объекты и явления. К Ушинский называл сравнение основой всякого понимания и всякого мышления.
Существенную роль в математике играет обобщение - понятий, связей и отношений между ними. Обобщение - путь расширения математических знаний, основываясь на результатах анализа, синтеза, сравнения, обобщение составляет основу абстрагирования, являющегося характерной особенностью математической деятельности. В.Давыдов указывал, что особенности процесса обобщения в единстве с процессами абстрагирования и образования понятий характеризуют тип всей мыслительной деятельности человека, и только усвоение школьниками теоретических обобщений может служить основой формирования у них теоретического мышления. Значение обобщения в математике хорошо иллюстрирует принцип, сформулированный У. Сойером: "Большая степень обобщения и большая простота неотделим друг от друга…после обобщения результат становится более полезным". Обобщение - предпосылка и результат понятийного и структурного мышления, оно составляет сущность математики. Поэтому математическое мышление - в высшей степени обобщенное мышление.
Операция абстрагирования тесно связана с предыдущими, с ее помощью осуществляется мышление в форме понятий. Абстракции математики отличаются от всех других своим содержанием, их суть - в глубоком отвлечении от качественной определенности предметов и явлений и в выделении их количественной стороны.
Характерные виды абстракции в математике:
а) Абстракция отождествления (образование абстрактного понятия путем отождествления предметов, связанных отношением типа равенства, например, возникновение понятия числа или геометрической фигуры). Этот вид абстракции может применяться повторно к результату предшествующей абстракции; в итоге возникают характерные для математики многоступенчатые абстракции, которые уже не имеют прямой связи с реальной действительностью (например, понятия многоугольника, п-мерного векторного пространства и т.п.)
б) Абстракция потенциальной осуществимости (отвлечение от реальных границ наших конструктивных возможностей, обусловленных ограниченностью нашей жизни в пространстве и во времени). Например, мы можем представить себе сколь угодно длинный ряд чисел как практически осуществимы, хотя эта осуществимость потенциальная: это было бы практически осуществимо, если бы наша жизнь длилась достаточно долго и мы имели бы достаточно места и материала для этого. Все операции с числами базируются на этой абстракции, с ее помощью образуются математические понятия (число, прямая, плоскость, бесконечное множество и т.п.).
в) Абстракция актуальной бесконечности (отвлечение от незавершенности и незавершимости процесса образования бесконечного множества, от невозможности задать такое множество путем полного перечисления его элементов). Этот вид абстракции позволяет, например. Рассматривать отрезок прямой как бесконечное множество точек, каждую из которых можно выделить и обозначить каким - нибудь действительным числом.
Таким образом, для математики характерна "крайняя абстрактность", "абстракция наибольшей силы". В математике процесс абстрагирования идет значительно дальше, чем вообще в естествознании, математическое мышление - в высшей степени абстрактное мышление. В этой самостоятельности математики, в том, что она формирует свои понятия исходя из уже готовых понятий, а не из предметов реального мира, заключается существенная особенность математики как науки, ее абстрактный характер.
Специфические приемы абстрагирования в математике:
а) идеализация - реальный объект заменяется в нашем сознании абстрактной моделью, наделяемой идеализированными свойствами (совершенно отсутствующими у реальных прообразов этих объектов или отражающих их в значительно измененном виде). Введение идеальных объектов позволяет выразить эмпирически найденные законы природы на языке математики, что имеет огромное значение для создания строгих научных теорий о сложных явлениях действительность.
б) Символизация -полученное в результате абстрагирования общее количество обычно обозначается каким -нибудь знаком - словом. Символом, графиком и т.д. Таким образом, оно превращается в самостоятельный и особый предмет последующих действий, с помощью которого структурные особенности объектов изучаются в "чистом виде".
Операция конкретизации (иллюстрации абстрактных понятий и их свойств) помогает научиться применять обобщенное, абстрактное, знание к отдельным частным случаям, и поэтому также важна в развитии абстрактного мышления, как и сама операция абстрагирования.
Операция классификации и систематизации помогают "переварить" поток информации в сознании учащегося в полноценные знания, учат находить в нем связи и закономерности. "Только система…дает нам власть над нашими знаниями, - писал К.Ушинский, - голова, наполненная отрывочными, бессвязными знаниями, похожа на кладовую, в которой все в беспорядке и где сам хозяин ничего не сыщет".
"Принцип системности" вообще играет огромную роль в современной науке, изучающей сложные социальные и технические системы. Данный объект называется системой, если каким - либо определенным способом его можно расчленить на составные части - подсистемы, а эти подсистемы - на элементы.
Мышление с помощью явно выраженных и осознанных операций мышления называют операционным мышлением. Такая характеристика мышления, по словам С.Рубинштейна, не исключает, а предполагает многообразие мыслительных операций со своими специфическими особенностями, связанными с особенностями содержания. Для математики это, например, счетные, графические, алгебраические и т.д. операции.
Качества мышления: (изучаемые психологией):
Убедительность (доказанность),
Критичность и объективность,
Гибкость, лаконизм и ясность,
Самостоятельность и активность,
Глубина и широта,
Любознательность и пытливость,
Интуиция,
Готовность памяти,
Вкус к исследованию и поиску закономерностей.
Эти качества мышления, называемые еще качествами ума, создают предпосылки для успешного учения и развития творческой деятельности.
Убедительность - это умение выделить существенные признаки явлений и объяснить себе и другим причины и приемы использования тех или иных умственных действий, стремлений к обоснованию каждого шага решения проблемы.
Критичность и объективность - обязательное присутствие этапа проверки и оценки предположений перед ответом на поставленный вопрос с точки зрения их достоверности и значимости, в противовес оперированию готовыми, заученными фразами, подсказанными памятью, без участия их творческой переработки.
Гибкость- умение изменять намеченный план решения задач, привлекать к решению вопроса имеющегося знания, легко образовывать новые сочетания знакомых элементов знания, целесообразно варьировать способы решения познавательных проблем, выходить за границы привычного способа действий. Антиподом гибкости мышления является его косность, шаблонность или психологическая инерция, предрасположение к какому-либо конкретному методу мышления. Высший уровень нешаблонного мышления - его оригинальность, которая чаще всего есть следствие глубины мышления.
Лаконизм и ясность - сознательное стремление всегда находить кратчайший, ведущий к цели логический путь, стремление не допустить ничего лишнего, скупость и строгость мысли.
Самостоятельность и активность - умение увидеть и поставить новый вопрос (проблему) и затем решить его своими силами; постоянство усилий, направленных на решение проблемы, определяется одновременным проявлением прежде всего гибкости и критичности. Сочетание творческой активности и критичности создает инициативность мышления, которая в сочетании с быстротой определяет сообразительность.
Глубина и широта - умение поставить вопросы "почему?", "отчего" и т.д. и вскрыть суть явления, отделить главное от второстепенного, охватить вопрос целиком, не упуская существенных деталей и возможных частных случаев, обобщить проблему и способы ее решения. Антиподом глубины мышления является его поверхность, антиподом широты- узость мышления.
Любознательность и пытливость - стремление узнать новое, его источники и условия, причины наблюдаемых явлений и т.д. своеобразным антиподом этого качества является простое любопытство.
Интуиция -"схватывание" значения, важности ситуации или явления, или структуры задачи без опоры на развернутые аналитические рассуждения, при отсутствии четко определенных этапов мышления.
Готовность и организованность памяти - качество, понятое из названия, способность к быстрой актуализации нужных знаний для решения новых проблем; организованность памяти означает способность к запоминанию, долговременному сохранению, быстрому и правильному воспроизведению учебной информации. Антипод этого качества - неорганизованность памяти - запоминание несущественного, забывание нужного.
Целенаправленность мышления - стремление осуществлятьразумный выбор действий при решении проблемы, постоянно ориентируясь на поставленную цель, а также стремление отыскать кратчайшие пути ее достижения. Целенаправленность мышления способствует проявлению такого качества, как рациональность мышления, характеризуемого склонностью к экономии времени и средств для решения поставленной проблемы, стремлением отыскать оптимально простое ее решение. Антиподом целенаправленности является бесцельность мышления.
Вкус к исследованию и поиску закономерностей, по выражениюУ.У. Сойера, - одно из характерных качеств, содействующих росту математика.
Таким образом, творческое мышление выражается в его а) легкости (легко приходят на ум идеи, устанавливаются связи, выражаются свои соображения в словах), б) подвижности (способность найти различные варианты действий, видеть их последствия и поступать в соответствии с этим), в) оригинальности (нестандартности решения предложенных задач), г) в присутствии периода бессознательной переработки информации- свернутом восприятии проблемы сразу, свернутом характере процесса рассуждений.
Умение действовать в пространстве, оперируя геометрическими знаниями и навыками, характеризует пространственное или геометрическое мышление. Оно складывается из овладения приемами пространственного мышления как общими, так и специальными, геометрической интуицией, пространственным воображением.
По каким же законам развивается математика? Обратимся к основным положениям диалектики - науки о наиболее общих законах развития природы, общества и мышления:
Природа - единое связное целое, ее явления зависимы и взаимно обусловлены.
Все в природе изменяется, развивается, движется.
В математике эти положения в большей степени выражены в понятии функции и ее производной. Проф. А. Хинчин называл понятие не только "одним из важнейших понятий школьного курса математики, но и тем стержнем, проходящим от элементарной арифметики до высших разделов алгебры, геометрии и тригонометрии, вокруг которого группируется все математическое преподавание… Поэтому, во-вторых, что ни одно из других понятий не отражает явлений реальной действительности с такой непосредственностью и с такой конкретностью, как понятие функциональной зависимости, в котором воплощены и подвижность, динамичность реального мира, и взаимная обусловленность реальных величин. Поэтому, во-вторых, что это понятие, как ни одно другое, воплощает в себе дидактические черты современного математического мышления"
Изучение математики, таким образом, способствует развитию функционального мышления, являющегося специфической формой диалектического мышления.
Источники, причины, движущие силы развития отражены в законах дидактики: единства и борьбы противоположностей, перехода количества в качество, отрицания . Математика и история ее развития содержат немало примеров проявления этих законов. Так, часть и целое, простое и составное, тождество и различие, положительное неотрицательное, прямые и обратные явления (операция), случайность и необходимость, дискретное и непрерывное и другие противоположности в математике на каждом шагу.
В чем же критерий истинности математических теорий? На этот вопрос отвечают следующие положения теории познания:
а) источник возникновения знаний - практическая деятельность людей;
б) правильность знаний о природе проверяется практикой;
в) не только потребности практики являются движущей силой развития науки, но и достижения науки преобразуют практику.
Одним из основных признаков мышления является его связь с речью. В речи ставится задача, речью пользуются для пояснения способов ее решения; теоретическое мышление, в отличие от практически-действенного, осуществляется только словесным путем. Каждое понятие выражается в слове, свойства понятий - в предложениях разных видов, различные виды и формы речи строятся по законам.
Таким образом, общая задача развития речи учащихся в процессе обучения математике складывается из задач овладения ими
а) математической терминологией,
б) приемами построения определений понятий и оперирования ими,
в) приемами формулировки различных видов теорем,
г) приемами письменного и устного изложения доказательства теоремы или решения задачи,
д) приемами работы с учебником математики,
е) приемами конспектирования и составления плана устного рассказа по определенной теме,
ж) приемами ведения тетради по математики,
з) умением задавать вопросы,
и) умением говорить красиво, грамотно, четко и в нужном темпе,
к) умением слушать речь других, понимать и оценивать ее, так же, как и свою собственную.
Ю. Бабанским разработана классификация основных умений и навыков учебной деятельности школьников:
Учебно-организационные умения: принимать и намечать задачи деятельности, создавать благоприятные условия для деятельности -режим дня, гигиена рабочего места, закаливание и др.
Учебно-информационные умения: осуществлять библиографический поиск, работать с книгой и справочниками, работать с техническими источниками информации, осуществлять наблюдения.
Учебно-интеллектуальные умения: мотивировать свою деятельность, внимательно воспринимать информацию,рационально запомнить, логически осмысливать учебный материал, самостоятельно выполнять упражнения, осуществлять самоконтроль в учебно-познавательной деятельности.
Владение совокупностью общеучебных умений называют "умением учиться" Специфика математики накладывает на них некоторые особенности, например, мы отличаем умения работать с учебником математики и математическими таблицами, ведения тетради по математике и т.д., и их совокупность образует "умение учиться математике"
Для изучения математики нужно иметь хорошую память, в то же время занятия математикой способствуют развитию памяти. Память - это запоминание, сохранение и воспроизведение всего того, что было в нашем опыте, в восприятии и действии.
Чтобы развивать память учащихся, нужно обучать их приемам такого запоминания, например, располагать материал группами и блоками, выделять смысловые опорные пункты, составлять алгоритмы и словесные формулировки и т.т.
Таким образом, формирование определенной системы приемов учебной деятельности учащихся в процессе обучения математике является целью исредством их обучения и развития в учебном процессе.
Важнейшим фактором успеха в обучении является интерес учеников к предмету. Следовательно, и учебник, и урок должны быть увлекательными. Интерес школьника к учению надо рассматривать как один из самых мощных факторов обучения. Но игровое обучение - это не уступка ленивому ученику, чтобы позабавить его и тем самым заставить учиться. Обучение должно вызывать удовольствие. Математику надо рассматривать не как систему истин, которые надо заучивать, а как систему рассуждений, требующую творческого мышления.
Умение заинтересовать математикой - дело непростое, и в этом смысле личного мастерства учителя или автора учебника нельзя недооценивать. Многое зависит от того, как поставить даже очевидный вопрос, и от того, как вовлечь всех учащихся в обсуждение сложившейся ситуации. Творческая активность учащихся, успех урока целиком зависят от методических приемов, которые выбирает учитель.
Элементы игры, включенные в урок, оказывают заметное влияние на деятельность учащихся. Игровой мотив является для них действенным подкреплением познавательному мотиву, способствует активности мыслительной деятельности, повышает концентрацию внимания, настойчивость, работоспособность, создает дополнительные условия для появления радости, удовлетворенности, чувства коллективизма.
Игровые занятия разрабатываются таким образом, чтобы к учащимся были предъявлены определенные требования.
Чтобы играть, нужно знать суть игры - вот первое требование, которое придает игре познавательный характер.
Правила игр, игровые ситуации должны быть действенными, то есть такими, чтобы у учащихся появилось желание участвовать в игре. Поэтому игровые занятия должны составляться с учетом возраста учащихся.
Правила и организация дидактических игр должны составляться и разрабатываться с учетом индивидуальных особенностей учащихся, то есть с учетом различных групп (с высоким и низким математическими возможностями, активных и пассивных и т.д.)
По возможности, игра должна носить обучающий характер.
Игра называется обучающей, если учащиеся, участвуя в ней, приобретают новые навыки и знания.
Для учащихся с низкими способностями нужно предусматривать ослабленные варианты игры, чтобы искусственно создать возможность успеха, и наоборот, трудные варианты - для способных учащихся.
Игры можно использовать на различных этапах урока: при опросе или проверке домашнего задания, при самостоятельном изучении нового материала, при закреплении его.
Таким образом, игровые моменты на уроках необходимы для воспитания личности, для развития интереса к предмету. Если ученик видит перед собой примеры творческого подхода к делу своих наставников, то у него самого возникает потребность творчества.
Работая учителем математики в школе, я провела много разнообразных игр, и убедилась, что с помощью игр можно обучать учащихся практически всем видам деятельности. Кроме этого, игру можно применять на уроках различных типов и использовать при этом различные формы учебной деятельности.
В 5-6 -х классах можно проводить игры - путешествия, которые, с моей точки зрения, очень эффективны на уроках повторения и систематизации знаний, контроля.
После изучения крупного блока "Обыкновенные дроби" обычно проводится игра- путешествие и внеклассное мероприятие. И эта необычная атмосфера игры развивает актерские способности учащихся, умение общаться, помогает проявить себя, раскрыть свои таланты. Игра каждой команды обязательно оценивается положительно.
Разнообразие творческих заданий по форме, содержанию и степени сложности способствует развитию у школьников мышления, смекалки, находчивости, сообразительности, чувства юмора. Участие в игре оказывает сильное эмоциональное воздействие на учеников, которое не сопоставимо с воздействием других форм обучения, что положительно влияет на их отношение к учебе, предмету, одноклассникам, учителю.
Можно сделать вывод, что игра дает учителю возможность увидеть творческий потенциал ученика, раскрыть и развивать его творческие способности. Опыт убедил меня, что только во время игры создаются такие условия, в которых ученик развивает свои творческие способности.
Среди множества задач школьного математического образования основная - развитие мыслительной деятельности учащихся. Поэтому я объединила учащихся в математический кружок. Планируя занятия, наполняя их определенным содержанием, я взяла на вооружение положение, установленное Л.С. Выготским, о том, что ориентироваться нужно не на уже достигнутый ребенком уровень развития, а немного забегать вперед, предъявляя к его мышлению требования, несколько превышающие его возможности, то есть не на уровень актуального, а на зону ближайшего развития. Всюду, где только возможно, будила мысль ученика, развивала активное, самостоятельное и - как высший уровень- творческое мышление.
Работа кружка, на мой взгляд, имеет возможность не только развивать и поддерживать интерес к математике, а следовательно, желание заниматься ею и приобретать новые знания по этому предмету, но и способствует развитию личности, ее мыслительной деятельности: умению выделять главное в проблеме: формированию высокого уровня элементарных мыслительных операций (анализа и синтеза, сравнения, аналогии, классификации), высокого уровня активности мышления, переходящего в творческое, когда учащийся способен осознавать собственные способы мышления, действовать в нестандартной обстановке.
Существуют разные формы развития творческих способностей на уроках математики: конкурсы, викторины, игры, соревнования, которые позволяют ученикам проявить свою смекалку, выдумку, находчивость. Такие уроки можно проводить во всех классах, но наиболее заинтересованные и увлекающиеся - это младшие школьники. Но мне хотелось бы рассказать о творческих домашних заданиях, ведь работать дома можно неограниченное количество времени и использовать дополнительные источники информации.
Домашние работы имеют большое значение в развитии творчества учащихся. Начиная с 5-ого класса я предлагаю ученикам выполнять домашние задания в виде ярких листовок, плакатов, на которых изображены самостоятельно составленные задачи с иллюстрациями, кроссворды, и т.д. Удачные и интересные работы затем используются для работы в классе, во время проведения математической недели. И т.д. Такое внимание "авторам" очень приятно.
Готовиться к неделе математики мы начинаем заранее. Классы получают задание составить кроссворд, придумать и проиллюстрировать задачу на смекалку и т.д. Проходит конкурс на лучший "Математический листок". Оценивается красочность исполнения, занимательность содержания, простота и доступность изложения.
Подведу итог всего вышесказанного:
-
Творческие домашние задания должны быть регулярными;
-
Задания должны быть и индивидуальными, и коллективными, состав групп желательно менять от задания к заданию с целью сплочения коллектива и выработки умения распределять обязанности внутри группы;
-
Творческие домашние задания должны использоваться на уроках либо при проведении внеклассных мероприятий (при этом обязательно упоминается автор работы);
-
Задания должны оцениваться, а исполнители поощряться оценкой, или заметкой в стенгазете, или награждением на линейке и т.д.
Литература:
-
Стандарты в образовании: Проблемы и перспективы. // Математика. Еженедельное приложение к газете "Первое сентября", 1995,№48.
-
Стандарт среднего математического образования.//Математика в школе, 1993,№4.
-
В.В.Давыдов. Проблемы развивающего обучения. М., Педагогика, 1986.
-
В.В. Давыдов. Виды обобщения в обучении . Педагогика,1972.
-
У.У. Сойер. Прелюдия к математике. М.,Просвещение, 1972.
-
С.Л. Рубинштейню. О мышлении и путях его исследования. М., 1958.
-
А.Я. Хинчин. Педагогические статьи. М., 1963.
-
А.Д. Александров. Математика и диалектика.//Математика в школе. 1992. № 1-2.//
-
Б.В. Гнейденко. Формирование мировоззрения учащихся в процессе обучения математике. М., Просвещение,1982.
-
И.А. Гибш. Развитие речи в процессе изучения школьного курса математики.//Математика в школе,1995, №6.//
-
Ю.К. Бабанский. Оптимизация учебно-познавательного процесса. М., Просвещение,1982.
-
В.А. Кулько, Т.Д.Цехместрова. Формирование у учащихся умения учиться: Пособие для учителей. М.,Просвещение,1983.
-
О.Б. Епишева. Учить школьников учиться математике. Кн.для учителя. М., Просвещение.1990.
-
Е.Н. Кабанова - Меллер. Учебная деятельность и развивающее обучение. М., Знание.1981.
Поделиться…
![]()
Неравенства и их системы играют важную роль в современной математике.
Это объясняется тем, что неровностям отводится центральное место в отдельных областях современной математики - линейное и нелинейное программирование, теория игр, исследование операций и т. д.
Проблема дифференциации обучения на сегодня является весьма актуальной. Из данной темы проводится большая экспериментальная работа, накоплен уже определенный опыт.
Однако, несмотря на большое количество работ о дифференциации обучения, эта актуальная проблема остается мало разработанной.
Проведенный анализ показал необходимость создания не только методик, которые бы учли четырехуровневую систему обучения, но и соответствующие дидактические материалы к ним: системы задач и проверочные работы для уровневого обучения.
Исходя из выше сказанного, ученые разработали дидактические материалы, тематические уровню проверочные работы по теме «Неравенства», которые помогут учителям математики успешно осуществлять уровневое изучения неравенств и их систем в курсе алгебры основной школы, используя 12 -балльную шкалу оценивания знаний учащихся. При разработке дидактических уровневых задач учебную тему принимали параграф действующего учебника.
К каждой теме, которая касается неровностей, подобрали значительное количество задач четырех уровней сложности. При подборе задач мы пользовались критериями оценки учебных достижений учащихся по математике, разработанными Министерством образования и науки Украины.
Введение к работе
Поиск путей совершенствования процесса изучения алгебры и начал
анализа ведется много лет. Исследования проводятся в разных
направлениях, среди которых можно выделить следующие:
- усиление прикладной направленности обучения и упрощение некоторых
логических моментов в курсе математического анализа базовой
школы;
- изменение методики изучения основных понятий математического
анализа на основе моделирования некоторых непрерывных
процессов;
- совершенствование системы упражнений путем дополнения ее
эвристическими задачами;
- решение проблем индивидуализации и дифференциации обучения;
- методические особенности применения пакета прикладных программ в
обучении математике;
- проблемы компьютеризации при обучении математике;
- формирование исследовательских навыков у старшеклассников и
другие.
Решению названных вопросов посвящены исследования В.В. Анисимова,
Е.Г. Глаголевой, Л.О. Денищевой, А.Н. Землякова, В. И. Казиева,
Н.Р. Колмаковой, С.А. Мор-кина, М.И. Немытовой, Л. С. Нураковой,
И.Ф. Соколовского, Г.В. Токмазова, Г.С. Шевченко и многих других
ученых.
Наличие многочисленных исследований по этим направлениям не
случайно, поскольку подготовить выпускников к жизни в динамичном
мире - значит вооружить их необходимыми знаниями, способами
овладения ими. Умение учиться не возникает само собой, как
следствие дополнительных педагогических требований, оно становиться
результатом серьезной работы не только педагогов, но и самих
учащихся.
Поиск решения проблемы - как создать условия для того, чтобы каждый
ученик в условиях дифференциации обучения, изучил курс математики в
том объеме, который ему необходим - привел нас к необходимости
нахождения одного из решений вопроса, связанного с использованием
компьютера в старших классах гуманитарного профиля.
Данное исследование дает возможность продолжить изучение тех
вопросов, которые возникают при использовании компьютера. А именно:
какой образ компьютера складывается в сознании ребенка по мере его
знакомства с этим обучающим средством; каковы преобладающие мотивы
обучения детей в 10-11 классах гуманитарного профиля в условиях
компьютеризации; какие факторы наиболее сильно воздействуют на
динамику поведения этих учащихся на уроках; при каких условиях
целесообразно использовать ЭВМ на уроках алгебры и начал анализа;
что меняется в деятельности учителя и в его поведении во время
компьютерных уроков. Но больше всего вызывают интерес такие
проблемы: получают ли учащиеся, общаясь с
компьютером, новые возможности для своего развития? Изменяется ли
роль учителя во время компьютерных уроков, наконец, какую роль в
процессе использования компьютера в обучении алгебры и начал
анализа играет программное обеспечение?
Наш интерес вызвали такие проблемы: какие психолого-педагогические
особенности учащихся гуманитарных классов важно учитывать при
использовании компьютера в процессе изучения алгебры и начал
анализа; как использование компьютера влияет на повышение
активности и самостоятельности старшеклассников гуманитарного
профиля; как использовать классно-урочную систему обучения для
применения компьютера; как подобрать учебный материал для
компьютерных уроков и, наконец, как организовать работу компьютера
на различных уроках и отдельных этапах урока?
Значение математического образования в гуманитарных классах
многостороннее. Здесь важно учитывать тот факт, что учащиеся
гуманитарных классов в основном завершают свое математическое
образование в средней школе.
Актуальность исследования определена необходимостью формировать у
школьников общие умения и навыки учебной деятельности и таким
образом сделать детей активными участниками учебного процесса,
заинтересованными в полноценных образовательных результатах .
Опыт работы в гуманитарных классах показывает, что использование
традиционных методов и средств обучения явно не достаточно
старшеклассникам для изучения алгебры и начал анализа. Многие
учащиеся полагаются на копирование с доски написанного учителем,
механическое запоминание, что ведет к перегрузке, стрессовым
состояниям, чувству собственной неполноценности. Такого положения,
когда школьники оказываются, как бы пленниками неадекватных
способов учебно-познавательной деятельности, можно было бы избежать
благодаря соответствующей целенаправленной работе. Чем сложнее и
насыщеннее становится учебная деятельность, тем выше требования к
ее эффективности.
В последние годы внедрение электронной вычислительной техники в
сферу образования повлияло как на деятельность ученика, так и на
деятельность преподавателя, что неизбежно привело к поиску
совершенствования процесса изучения алгебры и начал анализа.
Компьютер становится важнейшим средством стимулирования учебных
достижений учащихся. Опираясь на данные современных
психолого-педагогических исследований, необходимость разграничивать
индивидуальные особенности учащихся как таковые и индивидуальные
различия в их учебно-познавательной деятельности, отставания в
учебе вызваны не врожденным отсутствием способностей, а применением
непродуктивных способов учебной работы. При обращении к анализу
психологических процессов личности учеников гуманитарных классов
возникает необходимость исследовать деятельность учащихся при
использовании компьютера на уроках алгебры и начал анализа. И,
исходя из этого, организовывать работу старшеклассников и педагога
так, чтобы вооружить учащихся эффективными приемами учебной
деятельности, сформировать положительное отношение к ней,
выработать ответственное отношение к предмету.
Целью настоящего исследования является разработка обобщенных схем
организации работы компьютера на различных уроках и отдельных
этапах урока и на их основе создание компьютерных обучающих
программ (на примерах отдельных тем учебной программы) для
использования в процессе изучения курса алгебры и начал анализа в
старших классах гуманитарного профиля.
Объект исследования - процесс обучения алгебре и началам анализа в
гуманитарных классах.
Предметом исследования является использование компьютера в процессе
изучения курса алгебры и начал анализа в 10-11 классах
гуманитарного профиля.
При этом _ под использованием компьютера мы рассматриваем такую
организацию работы с учебным материалом, при которой обеспечиваются
необходимые условия для продуктивной познавательной деятельности
учащихся, учитываются интересы, наклонности и потребности учащихся,
выбравших гуманитарное направление в обучении, формируются
практически необходимые знания, умения, навыки, рациональные приемы
мышления и деятельности.
Гипотеза исследования основывалась на
предположении о том, что обучение алгебре и началам анализа
учащихся 10-11 классов гуманитарного профиля на основе
разработанной методики способствует повышению эффективности
учебного процесса.
На основе анализа научной, методической литературы и практики
обучения алгебре и началам анализа в гуманитарных классах средней
школы, а также с учетом отечественного и зарубежного опыта
использования компьютера в процессе обучения математике были
определены задачи исследования:
1. Выявить психолого-педагогические особенности использования
компьютера при изучении алгебры и начал анализа в гуманитарных
классах.
2. Разработать методику подбора учебного материала в курсе алгебры
и начал анализа, при изучении которого в 10-11 классах
гуманитарного профиля целесообразно эффективное использование
компьютера.
3. Разработать методику использования компьютера при изучении курса
алгебры и начал анализа в 10-11 классах гуманитарного профиля.
4. Разработать компьютерные обучающие программы на примерах
отдельных тем учебной программы.
5. Проверить эффективность предложенной методики и выработать
рекомендации по ее практическому применению.
Для решения поставленных задач применялись различные методы
исследования: изучение и анализ психолого-педагогической,
математической и методической
литературы, программ, учебников и учебных пособий по математике для
средней школы; наблюдения за учебным процессом; беседы с учителями
и учащимися, их анкетирование; проверка уровня математической
подготовки старшеклассников путем проведения диагностических
контрольных работ; изучение педагогического опыта; теоретическое
обобщение результатов исследования; моделирование отдельных уроков;
разработка сценариев программного обеспечения; педагогический
эксперимент.
Целями проведения эксперимента является анализ
психолого-педагогических особенностей учащихся гуманитарных
классов, причин низкого уровня усвоения знаний учащимися и поиск
возможностей совершенствования процесса изучения курса алгебры и
начал анализа с использованием компьютера. В результате был сделан
вывод о целесообразности использования компьютера и сформулирована
гипотеза исследования. Одновременно началась работа по созданию
соответствующего программного обеспечения. Необходимость его
создания была продиктована результатами поискового, а затем,
обучающего экспериментов в 1994-1998 гг. Для разработки обучающих
программ был выбран язык программирования BASIC как повсеместно
используемый в школах России.
Научная новизна исследования заключается в следующем :
- разработана методика использования компьютера при изучении курса
алгебры и начал анализа в 10-11 классах гуманитарного профиля;
- созданы компьютерные обучающие программы на основе обобщенных
схем организации работы компьютеры для использования в старших
классах гуманитарного профиля в процессе обучения алгебре и началам
анализа.
Практическая значимость исследования заключается в том, что
результаты исследования могут быть использованы в •процессе
обучения учащихся алгебре и началам анализа средних школ.
На защиту выносятся:
1) методика обучения алгебре и началам анализа в 10-11 классах
гуманитарного профиля на основе компьютерных технологий;
2) реализация разработанной методики с применением созданных
обучающих программ в целях повьшіения эффективности обучения
алгебре и началам анализа учащихся старших классов гуманитарного
профиля.
Апробация результатов исследования осуществлялась при обучении
учащихся 10-11 классов гуманитарного профиля по разработанной
методике в Лицее Дагестанского госуниверситета при факультете
международной и довузовской подготовки (г. Махачкала). Основные
результаты исследования были опубликованы в журнале "Вестник
Дагестанского госуниверситета (1998, 1999 гг.) и обсуждались на
научно-практической конференции в Ставропольском университете (1999
г.), на VII международной конференции "Циклы природы и общества" в
г.
Ставрополе (1999 г.), на заседаниях педагогических советов Лицея
факультета международной и довузовской подготовки и на ежегодных
научных конференциях преподавателей кафедры высшей алгебры и
геометрии Дагестанского госуниверситета. В целях нахождения
эффективных решений поставленных задач автор преподавал в 10-11
классах гуманитарного профиля в Лицее Дагестанского госуниверситета
при факультете международной и довузовской подготовки (г.
Махачкала) с 1994 по 1998 годы.
Структура и объем диссертации. Диссертация состоит из введения,
двух глав, заключения, списка литературы и 8 приложений. Общий
объем диссертации составляет 17 6 страниц (основной текст - 108
страниц, приложения - 53 страницы, библиография - 14 3
источника).
В первой главе "Теоретические основы использования компьютера при
изучении курса алгебры и начал анализа в 10-11 классах
гуманитарного профиля" рассматриваются психолого-педагогические
особенности использования компьютера в гуманитарных классах. На
основе наблюдения за уроками, проводимыми с использованием
компьютера и без него, в 10-11 классах гуманитарного профиля
делаются выводы о положительных сторонах использования компьютера
как средств обучения. Также отмечается ряд отрицательных моментов,
которые проявляются в процессе использования компьютера и не должны
оставаться без внимания, делается анализ появления негативных
факторов и их устранения. На основе изучения деятельности
старшеклассников гуманитарных классов при изучении алгебры и начал
анализа с использованием компьютера делается вывод о необходимости
использования компьютера в учебном процессе для повышения
активности и самостоятельности учащихся. Рассматривается
классно-урочная система обучения с использованием компьютера при
изучении алгебры и начал анализа в гуманитарных классах.
Во второй главе "Методика использования компьютера при изучении
курса алгебры и начал анализа в 10-11 классах гуманитарного
профиля" излагаются особенности организации учебного материала в
курсе алгебры и начал анализа в 10-11 классах гуманитарного профиля
при использовании компьютера, методы и приемы использования
компьютера. Раскрывается суть организационной и практической работы
на занятиях при проведении экспериментальных исследований, дается
анализ результатов в контрольных и экспериментальных классах Лицея
Дагестанского госуниверситета.
В заключении диссертации формулируются выводы по результатам
проведенного исследования, направленного на совершенствование
методики использования компьютера при изучении алгебры и начал
анализа в старших классах гуманитарного профиля.
Психолого-педагогические особенности использования компьютера при
изучении алгебры и начал анализа в гуманитарных классах
Анализ психолого-педагогической литературы по проблеме
дифференциации обучения математике в общеобразовательных
учреждениях, в том числе и профильной дифференциации [14, 41, 45,
69, 117 и др.], показывает, что значимость математического w
образования для гуманитарных классах должна быть не только меньше,
но в определенной степени даже и больше, чем для математических.
Ведь учащиеся гуманитарных классов завершают в средней школе свое
математическое образование. Они не смогут в будущем осознать
философию математики, увидеть ее историю, как это сделает другая
часть молодежи, изучая математику в вузах. В то же время для
гуманитариев особенно важно понимать исторический путь развития
математики, уметь различать глубокие философские концепции за
отдельными фактами науки. Поэтому в школе учащиеся гуманитарного
направления должны полу чить более широкое математическое
образование, чем они получают сейчас. В программах по математике
для гуманитарных классов больше места должны занять во просы
мировоззренческого характера, описания ее при- _ ложений в
различных областях человеческой деятельности .
При этом выделяются психолого-педагогические особенности учащихся
гуманитарных и математических классов, а именно:
1. У учащихся гуманитарных классов преобладает наглядно-образное,
мышление, а математических - абстрактно-логическое .
2. Восприятие красоты математики направлено у учащихся гуманитарных
классов на ее проявления в живой природе, в произведениях
искусства, в конкретных математических объектах. Учащиеся
математических классов красоту математики видят в необычных,
неожиданных решениях задач.
3. На уроке в гуманитарных классах внимание может быть устойчивым в
среднем не более 12 минут. В математических классах этот показатель
колеблется от 20 до 25 минут.
4. У гуманитариев наибольшим интересом пользуются вопросы истории
математики, прикладные аспекты, занимательный материал. Математики
предпочитают решение нестандартных задач, исследовательских
проблем.
5. Из форм работы на уроке гуманитарии предпочитают следующее:
объяснение учителем нового материала; лабораторные работы; деловые
игры; выполнение индивидуальных заданий с привлечением
научно-популярной литературы. Математики - решение нестандартных,
проблемных, исследовательских задач..
6. Из методов самостоятельной работы гуманитарии выбирают
коллективные. Например, при разборе задач в классе прибегают к
дискуссиям, в ходе которых ищут способ решения. Математики чаще
действуют совершенно индивидуально.
7. У гуманитариев богаче воображение, чем у математиков, сильнее
проявляются эмоции.
На психолого-педагогическом уровне трудность, возникающая при
использовании компьютера в процессе обучения, состоит в пересмотре
концептуального аппарата описания разных уровней отражения [26, 28,
31, 44, 49, 70, 137 и др.]. Так, существует мнение определенной
части специалистов, что обучение с помощью ЭВМ существенно меняет
смысл глагола "знать". Понятие "накапливать информацию в памяти"
трансформируется в "процесс получения доступа к информации".
Структура мышления у "докомпьютерного" ученика обусловлена
структурой печатного текста, которой свойственны линейность,
аналитичность, рациональность, а в имитационной среде, созданной
компьютером, стимулирует образность, гибкость, связность,
структурность мышления.
Использование компьютера в учебной деятельности старшеклассников
гуманитарных классов -одно из условий повышения их активности и
самостоятельности
Использование компьютера в учебной деятельности учащихся, в том
числе и в учебной деятельности учащихся старших классов
гуманитарного профиля, стало реальностью в современной системе
образования.
Философской и научной основой использования компьютера в учебном
процессе является "освоение информационной картины мира, сознание
единства законов функционирования информации в природе и обществе,
практическое применение этих законов при создании индустрии
производства и обработки информации" [4 9, с.18] .
Профильная дифференциация в школе оказала существенное влияние на
преподавание математики в гуманитарных классах. Программа, по
которой занимаются учащиеся в классах гуманитарного профиля,
отличается от общеобразовательной по количеству часов, отводимых на
математику (3 ч в неделю), по содержанию и глубине изучения
материала. Для детей, выбравших гуманитарное направление обучения,
вклад учебного предмета рассматривается преимущественно с позиций
общей культуры. В дальнейшем выпускник гуманитарного класса может
вообще не использовать математический материал непосредственно в
своей будущей профессии. Однако в качестве основной задачи, на
решение которой должен быть направлен процесс обучения в
гуманитарных классах, ставится задача целенаправленного
формирования рационального стиля мышления учащихся. Решение этой
задачи можно значительно облегчить с использованием
компьютеров.
Правильно организованная учебная деятельность на уроках алгебры и
начал анализа дает возможность непрерывного диалога между учителем
и учащимся, формирующего активное отношение к учению.
Психолого-педагогические особенности учащихся гуманитарных классов
проявляются и в специфическом отношении к предмету и в своеобразном
восприятии математики. Отношение к предмету у учащихся, выбравших
гуманитарное направление, можно отметить, в основном, как
пассивное. Они слабо проявляют интерес к алгебре и началам анализа,
а чаще рассматривают как второстепенный для них предмет.
Несосредоточенность на работе в классе, невключенность в нее,
по-видимому, связаны с пассивными и инертными способами учения.
Здесь во многом можно решить проблему за счет использования
компьютера в учебной деятельности старшеклассников гуманитарных
классов - на уроках алгебры и начал анализа. Комплексный подход к
использованию компьютера во время обучения на уроках становится
необходимым условием повышения их активности и самостоятельности,
благодаря чему заметно усиливается интерес к самому предмету,
повышается успеваемость.
В настоящее время право использования компьютера на уроках
становится не просто нравственным идеалом, а является неотъемлемой
частью эффективного средства обучения.
Поразительно большое число учащихся 10-11 классов гуманитарного
профиля, приходящие в выпускной класс, не владеют основными общими
умениями и навыками, которые необходимы для изучения алгебры и
начал анализа. Работа на уроке ограничивается списыванием с доски и
решением упражнений по шаблону. Как следствие, они вынуждены
всецело полагаться на заучивание, испытывая при этом чувство
столкновения с практически невыполнимой задачей. Учителя,
понимающие непосредственное влияние профильной дифференциации на
активность и самостоятельность учащихся, признают связь между
недостаточной сформулированностью общеучебных навыков и стрессами,
вызванными низкой успеваемостью. Многие учащиеся доходят до
отчаяния, испытывают состояние неполноценности только потому, что
попадают в полную зависимость от привычных, но совершенно
неподходящих способов учения. За формирование учебных умений и
навыков, связанных с конкретными способами осуществления
учебно-познавательной деятельности, отвечает исключительно
преподаватель математики. Поэтому используя компьютер при изучении
курса алгебры и начал анализа в 10-11 классах гуманитарного профиля
существенно меняется роль учителя.
Организация обучения курсу алгебры и начал анализа с-
использованием компьютера в 10-11 классах гуманитарного профиля
Для изучения алгебры и начал анализа в десятом классе выделяется 68
часов, такое же количество часов дается в одиннадцатом классе. За
основу нами было взято тематическое планирование учебного
материала, по которой работают в гуманитарных классах Лицея при
Дагестанском государственном университете (см. приложение 1) .
Отбор необходимого содержания учебного материала исходит из
требований программы по математике для учащихся гуманитарных
классов. Для реализации идеи использования компьютера как
эффективного средства обучения учебный материал разбивается по типу
характерных структурных элементов. Затем целенаправленно
конструируются различные по своей структуре и назначению уроки с
использованием компьютера, отличающиеся сочетанием их компонентов,
значимостью каждого из них, продолжительностью и
взаимодействием.
В этой связи весь учебный материал разбивается на теоретический,
практический, контроля и корректировки знаний. Необходимость такого
разбиения обуславливается поиском и выявлением такой совокупности
уроков, особенность строения которых позволила бы ориентироваться в
многообразии конструируемых обучающих уроков с использованием
компьютера, помогала бы в их творческой разработке.
Преимущества организации такой учебной работы в форме урока можно
обосновать следующим:
- постоянный состав учащихся примерно одного возраста и уровня
подготовленности;
- класс работает в соответствии со своим годовым планом профильной
ориентации;
- учебный процесс осуществляется в виде отдельных взаимосвязанных,
следующих один за другим уроков;
- каждый урок посвящается только одному предмету;
- постоянное чередование уроков (по расписанию);
- руководящая роль учителя;
- применяются различные виды и формы познавательной деятельности
учащихся.
Урок является законченным в смысловом, временном и организационном
отношении отрезком учебного процесса. От качества отдельных занятий
в конечном итоге зависит общее качество школьной подготовки.
Поэтому ведется постоянный поиск создания и внедрения таких
технологий урока, которые позволяют эффективно и в короткие сроки
решать задачи обучения данного состава учащихся. Это особенно важно
для учащихся гуманитарных классов, которые свое математическое
образование почти завершают в школе, а количество часов, отводимых
на изучение математики, весьма ограничено. Для этой категории
учащихся необходим особый подход в организации работы с учебным
материалом так, чтобы они смогли получить в определенном смысле
более широкое математическое образование, чем они получают
сейчас.
Структура урока с использованием компьютера строится исходя из
требований, которые определяются социальным заказом, личными
потребностями учащихся, це-лями и задачами обучения,
закономерностями и принципами учебного процесса для учащихся
гуманитарного профиля, выделенными в параграфе 1.3. Требования к
организации урока алгебры и начал анализа для гуманитариев, где
компьютер выступает как средство обучения, по нашему мнению, можно
выразить следующим.
1. Построение урока на основе передовой педагогической практики, с
учетом закономерностей учебно-воспитательного процесса.
2. Использование на уроке новейших достижений науки, современных
адаптивных диалоговых обучающих информационных программ.
3. Оптимальная реализация на уроке дидактических принципов и
правил, с обязательным их учетом при составлении сценариев для
обучающих программ.
4. Обеспечение необходимых условий для продуктивной познавательной
деятельности учащихся.
5. Обязательный акцент на учете интересов, наклонностей и
потребностей учащихся, выбравших гуманитарное направление в
обучении.
6. Установление осознаваемых учащимися межпредметных связей.
7. Связь с ранее изученными знаниями и умениями, опора на
достигнутый уровень развития учащихся.
Тема исследования охватывала материал, который изучался в 9 классах. Учителям было объяснено, в чем заключается суть эксперимента, какие особенности обучения по разработанной методике.
Ученики экспериментальной группы работали по школьной программе и учебникам, а ученики экспериментального класса работали по разработанной нами методике. В конце темы ученикам, как экспериментальной группы, так и контрольного класса было предложено тематические уровню проверочные работы по теме «Неравенства».
Для того, чтобы выяснить точно, как влияет применение данной методики в преподавании алгебры на формировании математических знаний, ученые применяли метод корреляции на примере данных классов.
Для этого определяли коэффициент корреляции, который является мерой целостности рассматриваемого связи. Чем ближе коэффициент к 1, тем ближе зависимость между применением разработанной методики и подтверждением соответствующих уровней знаний. Если связь между признаками отсутствует, то коэффициент корреляции будет равен или близок к 0.
В результате мы получили, что полученные коэффициенты корреляции близки к 1. Это свидетельствует о существовании тесной связи между примененной методикой изучения неравенств и их систем и достижением учениками соответствующих уровней знаний. Поэтому можно говорить о целесообразности внедрения такой методической системы в учебный процесс.
Итак, в результате исследовательской деятельности и обработки научной и методической литературы, мы разработали методику преподавания темы «Неравенства и их систем» в 9 классе. После такого изложения материала хотелось бы, чтобы ученики почерпнули для себя интересную информацию, усвоили основные понятия, поняли принципы их использования.
Практическое значение исследования заключается в том, что разработанная методика поможет учителям при преподавании темы «Неравенства», в подборе и составлении соответствующих задач к каждому из четырех уровней усвоения учащимися учебного материала.
Итак, современная школа ориентирована на дифференциальный подход, который продиктован образовательной реформой, является по нашему мнению, целесообразным и необходимым, а также требует создания новых методических разработок и написания современных учебников, которые бы в наибольшей степени соответствовали современным принципам организации учебно-воспитательного процесса в школе.
Общие вопросы изучения тригонометрических функций в школьном курсе
Во введении говорилось о необходимости изучения тригонометрических функций числового аргумента в школьном курсе алгебре и математического анализа. Что же обуславливает данную необходимость?
Итак, основными целями изучения тригонометрических функций числового аргумента являются:
-
ознакомление учащихся с новым видом трансцендентных функций;
-
развитие навыков вычислительной практики (работа с трансцендентными функциями зачастую требует громоздких вычислений);
-
наглядная иллюстрация всех основных свойств функций (в особенности периодичности);
-
установление межпредметных связей с практикой (изучение колебаний маятника, электрического тока, волновой теории света невозможны без знаний о тригонометрических функциях);
-
развитие логического мышления (обилие формул порождает необходимость преобразований не алгебраического характера, которые носят исследовательский характер).
В изучении тригонометрических функций можно выделить следующие этапы:
-
Первое знакомство с тригонометрическими функциями углового аргумента в геометрии. Значение аргумента рассматривается в промежутке (0о;90о). На этом этапе учащиеся узнают, что sin, сos, tg и ctg угла зависят от его градусной меры, знакомятся с табличными значениями, основным тригонометрическим тождеством и некоторыми формулами приведения.
-
Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0о;180о). На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений.
-
Введение понятий тригонометрических функций числового аргумента.
-
Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение графиков функций, проведение исследования, в том числе и с помощью производной.
Отметим, что существует несколько способов определения тригонометрических функций. Их можно подразделить на две группы: аналитические и геометрические. К аналитическим способам относят определение функции у = sin х как решения дифференциального уравнения f ''(х)=-c*f(х) или как сумму степенного ряда sin х = х - х3 /3!+ х5 /5! - …
К геометрическим способам относят определение тригонометрических функций на основе проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного треугольника и определения с помощью числовой окружности. В школьном курсе предпочтение отдается геометрическим способам в силу их простоты и наглядности.
Отметим, что изучение тригонометрических функций в школьном курсе имеет некоторые особенности. Во-первых, до изучения тригонометрических функций, рассматривались функции вида у=f(x), где х и у - некоторые действительные числа, здесь же - углу ставится в соответствие число, что является несколько непривычным для учащихся. Кроме того, раньше все функции задавались формулами, в которых явным образом был указан порядок действий над значениями аргумента для получения значений функции. Теперь же учащиеся сталкиваются с функциями, заданными таблично.
Таким образом, изучая тригонометрические функции, учащиеся лучше начинают разбираться в сущности самого понятия функции. Они начинают осознавать, что функцией может быть зависимость между любыми множествами объектов, даже если они имеют различную природу (лишь бы каждому значению аргумента соответствовало единственное значение функции).
§ 2. Анализ изложения темы «Тригонометрические функции» в различных школьных учебниках
В настоящее время вопросы тригонометрии изучаются в 10-11 классах в рамках 85 - часового курса "Алгебра и начала анализа". В разных вариантах тематических планов, опирающихся на учебники разных авторов, отводится от 15 до 28 часов; при этом в основном ставятся следующие цели:
-ввести понятие синуса, косинуса, тангенса и котангенса для произвольного угла;
-
систематизировать, обобщить и расширить уже имеющиеся у учащихся знания о тригонометрических функциях углового аргумента;
-
изучить свойства тригонометрических функций;
-
научить учащихся строить графики тригонометрических функций и выполнять некоторые преобразования этих графиков.
Проанализируем с точки зрения реализации вышеперечисленных целей те учебники, которые наиболее распространенны в общеобразовательных школах, а именно учебники [16], [2], [3], [11].
Прежде всего, отметим некоторые особенности этих учебников как методических пособий в целом, а не по данной теме. Вообще, данные учебники дают цельное и полное представление о школьном курсе алгебры и начала анализа, отвечают требованиям обязательного минимума содержания образования. Но каждый из них имеет свои особенности. Учебник [16], например, отличается более доступным для школьников, по сравнению с остальными учебниками, изложением теоретического материала, которое ведется очень подробно, обстоятельно и достаточно живым литературным языком, наличием большого числа примеров с подробными решениями. Построение всего курса осуществляется на основе приоритетности функционально-графической линии. Учебник [11] имеет прикладную направленность, содержание отличается большей научностью и близостью к математическому анализу, язык изложения в большей мере научен, чем доступен. Теоретический материал изложен достаточно кратко и лаконично. Учебник [3] также имеет прикладную направленность, но в отличие от [11] ориентирован на физические приложения математических знаний и умений. В конце учебника представлены несколько лабораторных работ, например, «Построение математической модели механического движения». В конце учебника весь изученный материал представлен в виде схем и таблиц, что удобно не только ученику при подготовке к какому-либо контрольному мероприятию, но и учителю при подготовке к уроку или к системе уроков. Также среди достоинств этого учебника стоит отметить и тот факт, что каждая глава открывается вводной беседой, подготавливающей появление новых основных понятий, и заключительной беседой, которая включает в себя сведения, полезные для учащихся, интересующихся математикой.
Ну, а учебник [2] по сравнению с другими изобилует большим количеством цитат и шуточных математических рисунков. Это, несомненно, развивает математический кругозор учащихся, но, что касается содержательной стороны этого учебника, то, по моему мнению, он больше подойдет для обучения математике в профильных (не математических) классах.
Перейдем канализу изложения конкретной темы «Тригонометрические функции» в данных учебниках. Напомним, что в школьном курсе математики в разные годы использовались разные варианты введения тригонометрических функций: при помощи тригонометрического круга, при помощи проекции и некоторые другие.
В современных учебных пособиях предпочтение отдается определению с помощью единичной окружности. При этом только в [16] уделено достаточное внимание работе с числовой окружностью как с самостоятельным объектом изучения, и это является одним из достоинств этого учебника.
Слишком поспешное введение понятий синуса и косинуса «по окружности» приводит к трудностям при дальнейшем обучении: многие учащиеся испытывают затруднения с геометрическим истолкованием «тригонометрического языка». Таким образом, не получается создать надежный фундамент для успешного изучения материала.
В учебнике [16] на работу с числовой окружностью отводится 5 часов, что составляет почти 20% от 28 запланированных часов на изучение всей темы «Тригонометрические функции». Вообще говоря, здесь рассматриваются две математические модели: «числовая окружность» и «числовая окружность на координатной плоскости». То есть учащиеся обучаются работать одновременно в двух системах координат: в прямоугольной декартовой и криволинейной. Это поможет им в дальнейшем, когда понятия синуса и косинуса угла будут вводиться через координаты.
Здесь не только четко выделяется алгоритм построения точки на числовой окружности, но и проводится аналогия с числовой прямой, с указанием основных сходств и различий в построении точки на окружности и на прямой. Неплохо в учебнике [16] мотивируется и само введение числовой окружности: «В реальной жизни двигаться приходится не только по прямой, но и по окружности. Будем считать беговую дорожку стадиона окружностью…». К тому же, уже на этапе изучения числовой окружности в неявном виде происходит подготовка к решению простейших тригонометрических уравнений и неравенств.
Например, рассматриваются задания типа: «Найти на числовой окружности точки с ординатой у = 1/2 и записать, каким числам t они соответствуют», «Найти на числовой окружности точки с абсциссой х < 1/2 и записать, каким числам t они соответствуют».
Итак, в учебнике [16], в отличие от остальных учебников, проводится достаточно хорошая пропедевтическая работа для введения тригонометрических функций.
В учебнике [3] также присутствуют элементы работы с числовой окружностью, но не в таком количестве как в [16]. Здесь выделяется отдельный параграф «Вращательное движение и его свойства», в котором рассматриваются такие вопросы как построение точки по заданной мере угла и свойства вращательного движения.
В учебнике [11] в качестве подготовительной работы для введения тригонометрических функций выступает лишь повторение следующих вопросов:
-
радианная мера угла (измерение углов в радианах, таблица значений тригонометрических функций (рассматривается исходя из геометрических соображений)),
-
основные формулы тригонометрии (основное тригонометрическое тождество, формулы суммы и разности двух аргументов, формулы приведения, формулы суммы и разности синусов и косинусов, формулы двойного и половинного аргументов).
Вообще вопросы тригонометрии в этом учебнике рассматриваются в следующем порядке: тригонометрические преобразования - тригонометрические функции - тригонометрические уравнения и неравенства, в отличие от учебника [16], по которому сначала изучаются функции, затем уравнения и неравенства, а только потом преобразования (как свойства функций).
Обучение же по учебникам [2] и [3] предполагает изучение тригонометрических функций не в начале 10 класса (как это представлено в учебниках [11] и [16]), а в конце него. Авторы учебника [2] предлагают приступить к изучениию тригонометрии после изучения показательной и логарифмической функций. Причем, сначала изучаются тригонометрические преобразования, затем - тригонометрические уравнения и только после этого - тригонометрические функции. Такое расположение темы имеет ряд особенностей:
-
изучение тригонометрических уравнений подразумевает изучение обратных тригонометрических функций. Таким образом, сначала учащиеся детально прорабатывают понятия арксинуса, арккосинуса и арктангенса, а затем только приступают к работе с синусом, косинусом и тангенсом, хотя с точки зрения логики, целесообразнее сделать наоборот;
-
изучение тригонометрических функций после тригонометрических уравнений выкидывает из рассмотрения один из немаловажных методов решения тригонометрических уравнений - а именно графический метод (к тому времени мы ещё не умеем строить графики тригонометрических функций).
В учебнике же [3] же вообще предлагается изучать тригонометрию уже после изучения производной. Это позволяет вычислять приближенные значения тригонометрических функций в точках, тем самым облегчая их исследование, помогая при построении графиков и решении тригонометрических уравнений.
Что касается введения самих тригонометрических функций, то и здесь каждый из учебников имеет свои особенности. Начнем с определения синуса и косинуса. В учебнике [2] дается следующее определение: «Сosх - это абсцисса точки единичной окружности, полученной поворотом точки Р (1;0) вокруг начала координат на угол х, а sinх - ее ордината». В [16]: «Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют косинусом числа t, а ординату точки М называют синусом числа t». Эти два определения, в общем-то, принципиально не различаются, за исключением только того, что в учебнике [2] тригонометрические функции определяются как функции углового аргумента, а в [16] как функции числового аргумента, да еще присутствуют различия в обозначении переменной (заметим, что при работе с числовой окружностью лучше употреблять символы sin t, cos t, tg t, ctg t, учитывая, что знак х в сознании детей ассоциируется с абсциссой в декартовой прямоугольной системе координат, а не с длиной пройденного по числовой окружности пути).
В учебнике же [11] как таковых определений синуса и косинуса нет, а вместо них присутствует фраза «… нетрудно понять, что ордината точки Р - это синус угла , а абсцисса этой точки - косинус угла », а затем приведено геометрическое подтверждение этого факта. Благодаря этому, у учащихся не возникает недоумения по поводу того, почему раньше синусом называли отношение длин катета и гипотенузы, а сейчас откуда-то выплыли какие-то абсциссы и ординаты. В учебнике [16] этот факт тоже довольно неплохо пояснен, но с опозданием в 3 параграфа, а в учебнике [3] пояснение отсутствует вовсе.
Тангенс же во всех учебниках, за исключением [11], определяется как отношение синуса к косинусу. В учебнике же [11] опять не дается четкого определения тангенса, а приводится лишь геометрическая интерпретация «ордината точки пересечения прямой ОР (Р- точка на единичной окружности) и касательной к окружности в точке (1;0) равна тангенсу угла ».
Определения котангенса авторы дают аналогично определениям тангенса за исключением учебника [2], в котором котангенс почему-то совсем игнорируется и не рассматривается как функция.
Остановимся подробнее на вопросах исследования и построения графиков тригонометрических функций.
В учебнике [16] процесс построения графика и исследования функции происходит следующим образом: уже известные ребятам факты обобщаются и формулируются как свойства функций. Сначала рассматриваются такие свойства функции y=sin(x), как область определения, множество значений, нечетность, возрастание на отрезке [0;/2] и убывание на отрезке [/2; 3/2], ограниченность сверху и снизу, наибольшее и наименьшее значение. Затем составляется таблица основных значений функции на отрезке [0;], строятся соответствующие точки и плавно соединяются.
Используя свойство нечетности синуса, полученный график отображается относительно начала координат на отрезок [-;0], используя свойство периодичности, график функции достраивается на остальных отрезках длиной 2. С опорой на построенный график, выделяется свойство непрерывности функции синус и область ее значений. Исследование функции cos х и построение ее графика как и во всех остальных учебниках основывается на том факте, что cos х = sin (х+/2).
В учебнике [3]построение синусоиды происходит при помощи единичной окружности переносом значения синуса к соответствующим точкам оси ОХ. А затем, после построения графика, еще раз происходит возвращение к свойствам и к тому, как они проявляются на графике. В учебнике [11] синусоида строится подобно тому, как она строится в [3], но все свойства функций за исключением области определения и множества значений рассматриваются в следующей теме «Основные свойства функций», а затем только переносятся на тригонометрические.
Отметим, что в учебниках [16] и [11] не обоснован тот факт, что областью определения функций sin и cos является множество всех действительных чисел. Конечно, этот факт достаточно очевиден, но тем не менее учебник пишется не для учителя, а для учеников, а «мера очевидности», как известно, у всех разная. Поэтому не стоит забывать об обосновании даже очевидных фактов, ведь это приучает ребят к столь необходимой при изучении математики логической четкости и аккуратности мысли.
Что касается области значений тригонометрический функций, то ни в одном из учебников нет четкого обоснования данного свойства. Все «попытки» обоснования этого свойства сводятся к рассмотрению двойных неравенств: -1 sin х 1 и -1 соs х 1, которые выполняются для всех значений х. Однако, отсюда совершенно не следует то, что в область значений данных функций входят все точки отрезка [-1;1].*
При обосновании свойств четности и нечетности тригонометрических функций доказательство тождества sin(-х) = -sin(х) сводится в основном к симметричности точек х и -х, которая также четко не обоснована ни в одном из учебников. *
Монотонность же тригонометрических функций во всех учебниках, за исключением [11], иллюстрируется с помощью числовой окружности. В учебнике [11] в силу того, что тригонометрические преобразования изучаются перед тригонометрическими функциями, монотонность функции у=sin(х) обоснована более доказательно, но все же некоторые недочеты имеются.*
При изучении свойства периодичности авторы учебников [16], [2] и [11] дают следующее определение периодичности: «Функция f(x) называется периодической, если существует такое число Т0, что для любого х из области определения данной функции выполняется равенство f(x-T)=f(x)=f(x+T). Число Т называется периодом функции f(x)». В учебнике [3] равенство f(x-T)=f(x)=f(x+T) заменяется менее сильным равенством f(x)=f(x+T), но зато снимаются ограничения на х. Здесь х может быть любым, а не только из области определения. Заметим, что для функций, областью определения которых является все множество R, эти два определения будут не только равносильными, но и одинаково корректными (см. [23] (стр. 108 №145)). Но если применять второе определение к функции у=sinх, то у учащихся может вызвать затруднения сравнение значений данной функции в точках, например, - и . Поэтому более целесообразным является использование первого определения.
Проанализируем теперь системы задач, направленные на отработку умений и навыков, которые предусмотрены программой по теме «Тригонометрические функции».
Система задач в учебнике [3] содержит в себе задания на перевод из градусной меры в радианную и наоборот, построение углов на единичной окружности, движение точки по окружности, определение тригонометрических функций, исследование и построение графиков комбинаций тригонометрических функций, нахождение значений тригонометрических функций в некоторых точках и их знаков на некоторых промежутках, нахождение производных комбинаций тригонометрических функций и вычисление приближенных значений тригонометрических функций.
В учебниках [2] и [11] работе со свойствами комбинаций тригонометрических функций уделяется уже гораздо большее внимание, чем в учебнике [3], присутствуют задачи теоретического плана, например, «Докажите, что если функция y=f(x) является периодической, то и y=k*f(x)+b тоже периодическая», не остаются без практической отработки и гармонические колебания. В учебнике [2] присутствует еще одна особенность: здесь подобрано большое количество задач с ограничением на переменную х, что помогает учащимся в осознании того факта, что «не всякие свойства функции, рассматриваемой на множестве всех действительных чисел, сохраняются при наложении ограничений на область определения этой функции».
Наиболее же полноценной из всех является система задач в учебнике [16]. Здесь, кроме всего уже вышеперечисленного, большое внимание уделено отработке навыков и умений работы с числовой окружностью, присутствуют задачи для работы с тригонометрическими функциями как числового, так и углового аргументов, используются функции, заданные кусочно, отрабатываются умения решать уравнения, содержащие тригонометрические функции, графическим методом.
Вообще, говоря о системе задач этих учебников, следует отметить некоторые недостатки учебника [3]. В идеале, решение каждой последующей задачи должно не только опираться на предыдущую, но и содержать какие-то дополнительные идеи. Здесь же не везде четко прослеживается система, да и по уровню сложности задачи не столь уж разнообразны.
Зато наличие отдельного задачника к учебнику [16] позволило дать в нем полноценную по объему систему упражнений, достаточную для работы в классе, для домашних заданий и повторения. Все задания дифференцированы по блокам, отдельно выделены даже устные и полуустные упражнения, что дает возможность более рационального использования учебного времени.
Таким образом, наиболее удачным учебным пособием в плане изучения темы «Тригонометрические функции» в курсе алгебры и начала анализа является учебно-методический комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит.
§ 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа
В изучении тригонометрических функций в школе можно выделить два основных этапа:
-
Первоначальное знакомство с тригонометрическими функциями углового аргумента в курсе геометрии (8-9 класс).
-
Систематизация и расширение знаний о тригонометрических функциях в курсе алгебры и начал анализа (10-11 класс ).
На первом этапе не доказывается и не уточняется, что изучаемые зависимости являются функциями. Изменение синуса и косинуса при изменении угла доказываются на основе свойств наклонной. Эти понятия достаточно абстрактны для курса геометрии, поэтому усваиваются довольно плохо. Но еще большие трудности вызывает переход к аргументу, большему 900. Ведь мы определяли тригонометрические функции через отношение сторон прямоугольного треугольника, а, как известно, в прямоугольном треугольнике не может быть угла с градусной мерой, большей 900. Для объяснения этого факта уже на этом этапе приходится рассматривать окружность, и это является своеобразной пропедевтической работой для введения тригонометрических функций числового аргумента с помощью окружности в курсе алгебры и начал анализа.
На втором этапе происходит переход от углового аргумента к числовому. С самого начала курса мы должны рассматривать тригонометрические функции углов любой величины - значит предварительно нужно познакомить учеников с углом как с величиной, способной изменятся от - до +. В курсе геометрии такое понятие не фигурировало, следовательно, это необходимо восполнить на втором этапе. Таким образом, возникает необходимость введения числовой окружности, работу с которой целесообразно провести также на втором этапе.
В качестве пропедевтической работы для изучения модели числовой окружности желательно рассмотреть геометрические задачи на нахождение длины дуг четверти окружности данного радиуса, ее трети и половины. Обобщая полученные результаты, необходимо подвести учащихся к тому факту, что для дальнейшей работы выгоднее выбирать окружности именно единичного, а не произвольного радиуса.
В процессе работы с числовой окружностью у учащихся должны быть сформированы следующие умения:
-
находить на числовой окружности точки, соответствующие заданным числам, выраженным в долях числа и выраженным не в долях числа ;
-
составлять аналитические записи для дуг числовой окружности;
-
определять принадлежность точки какой-либо координатной четверти;
-
работать одновременно в двух системах координат - в криволинейной и прямоугольно-декартовой и осуществлять переход от одной системы координат к другой;
-
находить координаты точек числовой окружности и отыскивать на числовой окружности точки по заданным координатам;
Для этого целесообразно рассматривать задания следующих типов:
-
Найти на числовой окружности точки /2, 9, 26/3, -5/4, -7/6…..
-
Найти на числовой окружности точки 1, 2, -7, 4.5, -31 ….
-
Определить, каким четвертям принадлежат точки 21/4, -37/6, 10, -95.
-
Отметить на числовой окружности точки t, удовлетворяющие неравенствам: а) /6+2к t 2/3+2к, к
б) -/3+2к t 3/4+2к, к
-
Найти декартовы координаты точек, соответствующих числам /4, -3/2, 23/6, -13/3…..
-
Найти положительные и отрицательные числа, которым соответствуют точки с координатами (1/2;3/2), (-2/2; 2/2); (3/2; -1/2), (-1,0)….
-
Найти на числовой окружности точки с ординатами (абсциссами) равными -3/2, 1/2, -2/2, 0, -1, абсциссы (ординаты) которых отрицательны, и записать, каким числам они соответствуют.
-
Найти на числовой окружности точки с ординатой (абсциссой) > -2/2 и записать, каким числам они соответствуют.
В процессе работы с числовой окружностью следует обратить внимание на следующие моменты.
В арсенале учителя должно находится как минимум два макета с числовыми окружностями. На первом из них отсчет ведется в положительном направлении с указанием расположения точек 0, /6, /4, /3, /2, 2/3…. , на втором - в отрицательном с указанием точек -0, -/6, -/4, -/3, -/2, -2/3…., причем второй макет желательно вывесить после того, как учащиеся ответят или попытаются ответить на вопрос: «Что будет, если точка будет двигаться не положительном, а в отрицательном направлении?».
Эта мотивационная задача позволяет еще раз провести связь между числовой окружностью и числовой прямой. Ведь на числовой прямой можно было откладывать не только положительные, но и отрицательные значения, причем сколь угодно большие. На числовой окружности можно делать то же самое, но следует учитывать тот факт, что на прямой соответствие между точками и числами взаимно-однозначное, а на окружности у каждой точки бесконечно много имен, отличающихся друг от друга на 2к, где к.
Это главное отличие учащиеся должны четко понимать и осознавать. Для этого числовую окружность можно сравнить с колесом, а числовую прямую с бесконечной нитью, на которой отмечены точки. Наматывая нитку на колесо, предварительно совместив соответствующие нулевые точки, можно заметить, что точки, отличающиеся на 2, попадут в одно и тоже место на колесе, благодаря тому, что длина числовой окружности единичного радиуса составляет именно 2.
Больше всего проблем, связанных с неоднозначностью соответствия между точками и числами на окружности возникает при решении задач вида: «Найти на числовой окружности точки с ординатой (абсциссой) большей 3/2 и записать, каким числам они соответствуют».
Такие неравенства, характеризующие дугу, рекомендуется на начальном этапе составлять в два шага. На первом шаге составить так называемое «ядро» аналитической записи /3 <t< 2/3, и только на втором составить общую запись /3+2k<t< 2/3+2k, где к Z.
По этому поводу осмелюсь не согласиться с статьей [10], в который автор пишет, что уточнение «где к Z» можно опускать, записывая его только в парадных случаях - на контрольных или экзаменационных работах. В большинстве случаев это действительно можно делать совершенно безболезненно, но как быть, если при отборе корней уравнения или неравенства, или при наложении определенных ограничений на функцию, параметр к сможет принимать не все а, например, только положительные или только четные значения?
Учащиеся, привыкшие писать +2k, не задумываясь над тем, какие значения может принимать параметр к, и в этом случае напишут +2k, что автоматически сделает их решение неверным.
Это приведет и к недопониманию того факта, что, например, множества «4k, где к Z» и «2k, где к 2Z» совпадают. Это, в свою очередь, может породить затруднения при рассмотрении функций с периодом, равным 4. А ведь таким функциям уделяется немало времени при изучении темы «Тригонометрические функции».
Таким образом, нельзя оставлять недоработанными никакие, даже самые маленькие детали, ведь незначительные с виду недоработки, возникающие при изучении числовой окружности, в процессе изучения самих тригонометрических функций могут стать причиной возникновения больших пробелов в знаниях.
Теперь, когда мы научились работать с числовой окружностью как самостоятельным объектом, можно приступать к введению самих тригонометрических функций.
Не стоит забывать, что определения тригонометрических функций с помощью числовой окружности плохо укладываются в сознании ребят по одной простой причине: на первом этапе определения были даны в геометрической трактовке - как отношения сторон прямоугольного треугольника.
Из психологии известно: «если какое-нибудь важное понятие вводится в первый раз, то ассоциации, сопутствующие ему, врезаются в сознание учащегося чрезвычайно прочно. Последующие впечатления бывают слабее и не могут стереть того обличия, в котором это понятие явилось впервые». [5]
Несмотря на то, что мы уже использовали окружность для введения «новых» определений синуса и косинуса на этапе расширения множества значений, принимаемых углом необходимо еще раз провести взаимосвязь между прямоугольным треугольником и числовой окружностью.
Напомним, что в школьных учебниках этому факту почему-то не уделяется должного внимания (см. главу «Анализ изложения темы «Тригонометрические функции» в различных школьных учебниках»), поэтому учителю стоит обратить внимание на то, чтобыпривведении тригонометрических функций на этом этапе были озвучены следующие моменты.
Рассмотрим числовую окружность единичного радиуса, расположенную в прямоугольно декартовых координатах. Рис.1
В положительном направлении от оси ОХ отложим угол такой, что 0 << 900. Обозначим полученную на окружности точку как Р. Опустим из точки Р перпендикуляр на ось ОХ, получим точку М. Рассмотрим получившийся прямоугольный треугольник ОМР. Sin по определению равен отношению МР/ОР, но радиус окружности ОР равен единице, следовательно, Sin = МР. Аналогичным образом, cos = ОМ. Заметим, что длина ОМ - это абсцисса точки Р в прямоугольно-декартовой системе координат, а длина МР- ее ордината. Таким образом, синус и косинус угла определяются через ординату и абсциссу точки Р, что является более удобным при работе в прямоугольно-декартовой системе координат.
Работая с числовой окружностью, мы уже усвоили тот факт, что так как длина дуги единичной окружности легко выражается через центральный угол, на нее опирающийся, то точку Р, можно построить и другим способом - откладывая дугу заданной длины. А так как длина дуги - всегда действительное число, значит, от тригонометрических функций углового аргумента легко можно перейти к тригонометрическим функциям числового аргумента.
Сейчас вернемся к наложенным на угол ограничениям. Угол принадлежит промежутку от 00 до 900, а значит и длина дуги лежит между нулем и /2. Используя все ту же геометрическую интерпретацию, легко показать, что эти определения можно распространить и на любые углы и числа.
Понятия тангенса и котангенса можно вводить двояко: как отношение синуса к косинусу (косинуса к синусу) и как ординату (абсциссу) точки пересечения касательной к окружности в точке (1;0) ((0;1)) и прямой ОР.
Рис.2 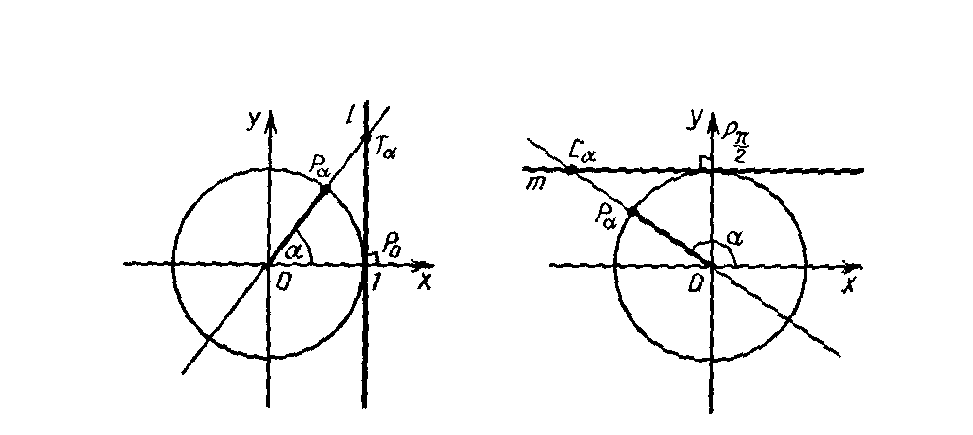
Вообще говоря, определив функции синус и косинус, мы уже не нуждаемся в числовой окружности как средстве для введения понятий тангенса и котангенса. Но раз уж мы взялись работать с этой моделью, то неплохо бы показать, как определить функции тангенс и котангенс, используя только их геометрическое определения (заметим, что выражения «тангенс угла - это отношение синуса к косинусу » и « котангенс угла - это отношение косинуса к синусу » не являются определениями - это уже свойства).
Использование второго подхода поможет нам не только на этапе изучения самих тригонометрических функций, но и на этапе решения тригонометрических уравнений и неравенств. Поэтому целесообразнее использовать именно второй подход, а определение тангенса как отношение синуса к косинусу рассматривать как свойство.
Итак, мы ввели понятия всех тригонометрических функций (которые предусмотрены программой). Но перед тем, как перейти к их исследованию и построению графиков, необходимо проследить, чтобы у учащихся были отработаны следующие навыки:
-
Нахождение значений всех тригонометрических функций в «главных» точках.
(Для лучшего запоминания значений тригонометрических функций можно использовать следующую вспомогательную таблицу:
/6
/4
/3
/2
sin
![]()
cos
![]()
Здесь значения синуса и косинуса представлены в наиболее удобной для восприятия и запоминания форме.)
-
Решение простейших тригонометрических уравнений и неравенств.
-
Определение знаков тригонометрических функций в заданных точках.
-
Упрощение выражений с использованием основного тригонометрического тождества и формул приведения.
-
Нахождение по заданному значению одной из тригонометрических функций значений всех остальных тригонометрических функций.
Приобретая вышеперечисленные навыки, учащиеся тем самым получают арсенал средств, достаточный для более основательного исследования и построения графиков тригонометрических функций.
Работа по построению графиков и исследованию функций может проводиться двумя способами:
-
Сначала по точкам строится график, а затем с помощью графической интерпретации исследуются все свойства функции
-
Построение графика происходит после исследования функции, а наглядные представления о свойствах учащиеся получают, анализируя поведение функций на числовой окружности.
Наиболее целесообразно применять второй подход, так как при этом подходе, во-первых, все свойства тригонометрических функций иллюстрируются на обеих моделях (на числовой окружности и на графике), а, во-вторых, это является хорошей подготовительной работой для дальнейшего обучения исследованию функций и построению графиков с помощью производной.
Несмотря на то, что анализируя поведение функции на числовой окружности, мы всего лишь иллюстрируем некоторое свойство, не стоит забывать, что иногда «доказательство» с помощью окружности является единственным доступным для школьников способом обоснования некоторых фактов. Хотя некоторые случаи все-таки требуют более четкого обоснования формулируемых утверждений.
Остановимся подробнее на исследовании тригонометрических функций.
-
Область определения.
«Областью определения функции действительного переменного называется множество действительных значений аргумента, при которых функция принимает действительные же значения».
Область определения функций у=sinx и у=соsx - множество всех действительных чисел. Этот факт достаточно легко обосновывается с помощью окружности: каждому действительному числу х соответствует точка на окружности Рх. Каждой точке Рх соответствуют ее абсцисса и ордината, каждая из них - это действительное число. Значит, значения функций у=sinx и у=соsx для любого действительного х будут действительными числами.
У функций у=tg х и у=сtg х область определения имеет некоторые ограничения. Обосновать это свойство можно исходя из того факта, что
tg х = sinx/ соsx. Тогда областью определения функции у=tg х будут все действительные числа, за исключением нулей функции у=соsx. Этот же самый факт можно обосновать и с помощью окружности:
рис.3
любому действительному числу х соответствует точка на окружности Рх. Если х /2+к, кZ, то эта точка имеет координаты, отличные от (0;1) и (0;-1), тогда через точки О и Рх. можно провести прямую, которая пересекает касательную к окружности, проходящую через точку (1;0), в некоторой точке Тх. Эта точка имеет ординату, которая является действительным числом. То есть в таких точках функция у=tg х будет принимать действительные значения. Если же х = /2+к, кZ, то прямая ОРх. будет совпадать с осью ОУ, а, следовательно, будет параллельна касательной к окружности. В этом случае мы не сможем найти точку Тх и ее ординату, а, значит, в этих точках функция у=tg х будет не определена. Таким образом, делаем вывод , что Дtgx =R/{/2+к }, кZ. Для функции у=сtg х рассуждения аналогичны, а, значит, учащиеся вполне могут провести их самостоятельно.
Область определения как свойство функций является ко времени изучения тригонометрии уже достаточно хорошо изученным, а процесс ее нахождения уже перешедшим из разряда умений в разряд навыков. Тем не менее при изучении тригонометрических функций стоит еще раз обратить внимание на отыскание области определения в особенности функций типа: у = сtg х * tg х; у=(sin х*соs х)/ сtg х, а также кусочно-заданных функций
сtg (х+/2), х<sin х, х<-/2
у = у =
1/(sin х +1), хtg х/(х-7) 2
2) Область значений функции.
«Областью значений функции f называется множество, состоящее из всех чисел f(х), таких, что х принадлежит области определения функции f». Четкого обоснования того факта, что областью значений функций у=sin х и у=соs х является отрезок [-1;1] ни в одном из действующих школьных учебников не приводится, а вместо этого рассматриваются неравенства -1 sin х 1 и -1 соs х 1, которые выполняются для всех значений х. Однако, отсюда совершенно не следует то, что в область значений данных функций входят все точки отрезка [-1;1]. На этот момент стоит обратить особое внимание, дабы разграничить в умах учащихся два совершенно различных свойства: ограниченность и область значений. Рассмотрим пример.
Рис.4
Функция f(x) в данном случае является ограниченной (выполняются неравенства -1 f(x) 1), но отрезок [-1;1] не является множеством значений данной функции. Поэтому необходимо все-таки показать тот факт, что любое число из отрезка [-1;1] является значением функции у=sin х (у=соs х) в некоторой точке. Показать это можно хотя бы следующим образом.
Возьмем произвольное действительное число х1 такое, что
-1 х1 1. Рассмотрим отрезок [-1;1] принадлежащий оси ОХ и возьмем точку этого отрезка соответствующую х1, восстановим из нее перпендикуляр к оси ОХ. Он пересечет единичную окружность в некоторой точке Рх1 Заметим, что х1 - это абсцисса точки Рх1, а, значит, число х1 является значением функции у=соs х для точки Рх1. (Аналогично для функции у=sin х.)
рис.5
После изучения области значений целесообразно рассмотреть свойство ограниченности функций у=соs х и у=sin х и провести взаимосвязь между этими свойствами не только для тригонометрических, но и для других классов функций.
3) Четность и нечетность.
При изучении свойств четности и нечетности тригонометрических функций необходимо четко обосновать тот факт, что sin(-х) = -sin(х), acos(-х) = cos(х) для любых действительных значений х. Чаще всего обоснование этого факта сводится к симметричности точек окружности, соответствующих числам или углам t и - t в зависимости от того, на каком этапе происходит обоснование. «Если числу t соответствует точка М числовой окружности, то числу -t соответствует точка Р, симметричная точке М относительно горизонтального диаметра окружности (то есть относительно оси абсцисс). У таких точек одна и та же абсцисса, а ординаты равны по модулю, но отличаются знаком. Следовательно, sin(-t) = -sin(t), a cos(-t) = cos(t)» (см. [16]).
Заметим, что факт симметричности точек t и - t не является очевидным, а значит, сам нуждается в обосновании, провести которое можно, например, рассмотрев треугольник МОР. Обозначим точку пересечения отрезка МР с осью ОХ за В. Тогда треугольник МОР равнобедренный (ОМ = ОР как радиусы одной окружности), луч ОВ является биссектрисой угла МОР, а, следовательно, и высотой и медианой треугольника МОР. Тогда точки М и Р действительно будут симметричными относительно оси ОХ по определению. Это и позволяет сделать вывод о значениях синуса и косинуса противоположных углов. После этого обоснование равенств tg (-t) =-tg (t) и ctg (-t) = -ctg (t) не составит никакой трудности.
Далее следует еще раз обратить внимание учащихся на следующий факт. В определениях четных и нечетных функций в явном виде не указано то, что такие функции имеют область определения, симметричную относительно начала координат, но этот факт часто оказывается полезным при решении задач типа «Докажите, что функция у= sinx, не является ни четной, ни нечетной». Используя вышеупомянутый факт и определив, что область определения данной функции не является симметричной относительно начала координат, сразу можно сделать вывод о том, что функция у=sinx, действительно, не является ни четной, ни нечетной, не рассматривая соответствующих уравнений.
Так же полезно определять четность функций, заданных кусочно. Например, определить являются ли следующие функции четными или нечетными:
Sin (x), если х 0 Соs(x/2), если х
f(x)= f(x)= 2 + х2, если - х
Соs(x), если х0 Соs(x/2), если х
4) Монотонность.
При рассмотрении свойства монотонности тригонометрических функций в большинстве действующих учебников (кроме [11]) не приводится четкого доказательства возрастания функций y=sinx и y=соsx на промежутках [-/2;/2] и [-;0] соответственно, а обоснование этих фактов проводится с опорой на числовую окружность: «При движении точки по четвертой и по первой четвертям окружности в положительном направлении ( от -/2 до /2 ) ее ордината постепенно увеличивается (от -1 до 1), значит функция y=sinx является возрастающей на этом промежутке» (см. [16]). Более строгое доказательство этого факта приводится с опорой на формулу разности синусов и применимо в случае, когда тригонометрические преобразования изучаются раньше тригонометрических функций, то есть когда формула разности синусов к моменту исследования тригонометрических функций является уже известной (см. [11]). «Пусть
-/2 х1 х2 /2,
применяя формулу разности синусов находим
sin х2 - sin х1 = 2 соs [(х1 +х2)/2]*sin [(х2 - х1)/2].
Из неравенства -/2 х1 х2 /2 следует, что
-/2 (х1 + х2)/2 /2 и 0 (х2 - х1)/2/2,
поэтому соs(х1+х2)/2 0 и sin(х2-х1)/2 0, а следовательно, sin х2 - sin х1 0 то есть sin х2 sin х1»(см. [11]). При этом учителю следует обратить внимание на пояснение того, как из неравенства -/2 х1 х2 /2 получаются неравенства -/2 (х1+х2)/2 /2 и 0 (х2-х1 )/2 /2.
Это целесообразно проиллюстрировать, изобразив отрезок [-/2;/2]. Заметим, что (х1+х2)/2 не что иное, как среднее арифметическое чисел х1 и х2, а, следовательно, принадлежит отрезку [х1;х2], который, в свою очередь, целиком лежит в отрезке [-/2;/2], то есть первое неравенство имеет место. Гораздо большую трудность вызывает обоснование второго неравенства. Заметим, что модуль разности х2-х1 - это расстояние между точками х1 и х2, а так как обе точки принадлежат одному отрезку [-/2;/2], то расстояние между ними не может превышать длины этого отрезка, то есть . С другой стороны модуль - функция неотрицательная, более того, в данном случае положительная, так как х1 и х2 различны. Имеем 0 х2-х1, но так как х1 х2, то х2-х1 = (х2-х1). Разделив все части неравенства на 2, получим доказываемое неравенство.
Доказательство возрастания функции y=tgx на интервале (-/2;/2), целесообразнее всего проводить аналогичным образом, используя формулу разности тангенсов (см [11]). В случае же, когда преподавание ведется по учебникам, в которых тригонометрические преобразования изучаются после функций, то есть формула разности тангенсов к моменту исследования функций еще не известна, доказательство лучше проводить, разбив интервал (-/2;/2) на два полуинтервала [0;/2) и (-/2;0]. Обоснование возрастания функции y=tgx на полуинтервале [0;/2) не сложно и приведено во всех учебниках, а доказательство монотонности на втором интервале авторы учебников [16] и [2] почему-то считают сложным и опускают вовсе. Поэтому учителю следует обратиться к учебнику [3], в котором дано довольно строгое, но вместе с тем несложное доказательство:
Пусть -/2 х1 х2 0, тогда 0 -х2 -х1 /2. Теперь числа -х1 и -х2 лежат в первой четверти, в которой тангенс возрастает, следовательно tg(-х2 )tg(-х1). Так как y=tgx нечетная функция, то
tg(-х2 ) tg(-х1) -tg (х2 ) - tg(х1),
а следовательно tg(х1) tg(х2). Что и означает, что функция y=tgx возрастает на промежутке (-/2;0], а значит и на интервале (-/2;/2). Доказательство монотонности функции y=сtgx целесообразно предложить в качестве задания для самостоятельного выполнения.
5) Нули функции и промежутки знакопостоянства.
Нахождение нулей функций и промежутков знакопостоянства сводится к решению простейших тригонометрических уравнений и неравенств, которые учащиеся рассматривали при изучении числовой окружности и не вызывает затруднений.
6) Периодичность.
Изучению этого свойства необходимо уделить особое внимание, так как учащиеся впервые сталкиваются с периодическими функциями. Для отработки понятия периодичности функции целесообразно использовать следующие упражнения.
1. На рисунке изображена часть графика периодической функции на отрезке [-2;2], длина которого равна периоду функции. Постройте график функции на отрезках [-6;-2], [2;3].
2. Постройте график периодической функции y=f(x), с периодом равным 2, если известно, что f(x)=х2/2 на отрезке [-1;1].
3. Является ли число 16 периодом функции y=sinx? А ее основным периодом?
4. Найти основные периоды функций y=sin(6x), y=соs(x/2), y=sin(кx).
5. Докажите, что если функция y=f(x) является периодической, то и y=k*f(x)+b тоже периодическая.
6. Пусть функция f периодическая, Т1 и Т2 - ее периоды. Докажите, что любое число вида nТ1 +mТ2, где n,mN, также является периодом функции f.
7. Докажите, что функции f(x) = sinx2 и cos (x)*cosx не являются периодическими.
8. Докажите, что возрастающая функция не может быть периодической. И т.п.
Следует обратить внимание учащихся на тот факт, что периодическая функция имеет бесконечное множество периодов, среди которых стараются выделить, если это возможно, наименьший положительный период, который называют основным.
После этого все свойства тригонометрических функций желательно проиллюстрировать на графике и свести в одну таблицу.
Рис.6 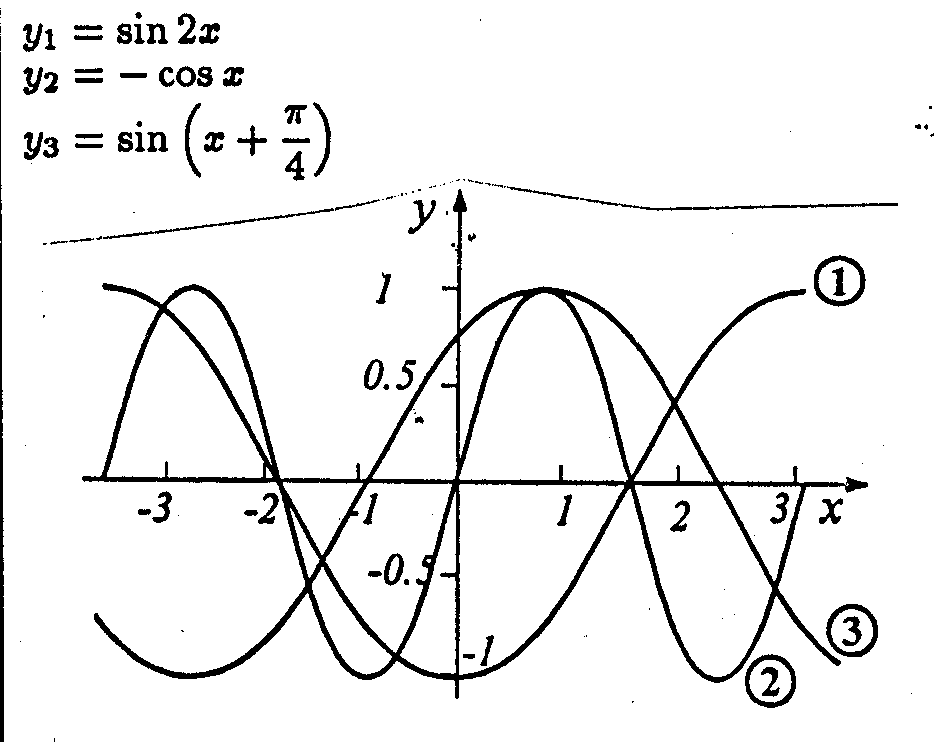
2. Какими свойствами обладают данные функции на отрезке [-/2; /2], а на отрезке [0; ]?
*</<sup>* более подробно эти вопросы изложены в параграфе 3