- Учителю
- Курс лекций по дисциплине «Математика» для студентов 2 курса на базе 9 классов и для студентов 1 курса на базе 11 классов
Курс лекций по дисциплине «Математика» для студентов 2 курса на базе 9 классов и для студентов 1 курса на базе 11 классов
Государственное бюджетное образовательное учреждение
среднего профессионального образования
«Краснодарский краевой базовый медицинский колледж»
Министерства здравоохранения краснодарского края
Курс лекций по дисциплине «Математика»
для студентов 2 курса на базе 9 классов и для студентов 1 курса на базе 11 классов
Краснодар, 2012
Введение
Математика - один из важнейших предметов в учебных заведениях. Она приобретает особое значение в связи с необычайным ростом науки, технического прогресса в нашей стране.
Без математики жизнь невозможна. В любой профессии, отрасли - какие ни возьми, везде нужна математика. Математика - это наука прошлого и будущего, она необходима всем как инструмент для познания мира, для создания новых открытий, создания современных технологий.
Математика развивает у человека логическое мышление, целеустремлённость, воображение, умение мыслить и находить выход из любых ситуаций. Она заставляет думать, помогает человечеству открывать и использовать законы природы и в наше время является могучим двигателем науки и техники. Не каждый может стать математиком, но математика в жизни нужна будет каждому.
Математика является образовательной учебной дисциплиной, которая обеспечивает общеобразовательный уровень подготовки студентов медицинского колледжа.
На II курсе на базе 9 классов и I курсе на базе 11 классов специальности «Сестринское дело» студенты ККБМК продолжают изучение учебной дисциплины «Математика». Данная дисциплина предполагает получение, как теоретических знаний, так и практических умений и навыков.
Теоретическая часть курса математики усваивается студентами в ходе лекционных занятий и во время самостоятельной внеаудиторной работе.
Необходимость разработки данного пособия обусловлена тем, что студенты I, II курсов не всегда успевают подробно записывать текст лекции со слов преподавателя, который ограничен аудиторным временем занятия. В пособии каждая тема изучаемого материала раскрыта более полно, с соответствующими разъяснениями и примерами.
В пособии удалось вместить весь курс по дисциплине «Математика» для студентов II курса на базе 9 классов и I курса на базе 11 классов специальности «Сестринское дело». Поэтому у студентов отпадает необходимость пользоваться большим количеством учебников, чтобы усвоить изучаемую тему. В конце каждой лекции имеются контрольные вопросы, позволяющие студенту выполнить самооценку степени успеваемости теоретического материала.
В пособие имеется список литературы.
Лекция №1
Тема: «Введение в математику как науку»
Цель: Познакомиться с математикой как с наукой и изучить символику математического анализа.
План лекции:
1. Математика как наука.
2. Математическая символика.
3. Понятие функции.
4. Способы задания функции.
5. Понятие графика функции.
6. Понятие сложной функции.
Математика - чрезвычайно своеобразная наука, философский анализ целого ряда положений которой весьма сложен. И хотя особенности математического знания были предметом пристального внимания выдающихся философов и математиков всех времен и народов, многие методологические проблемы математики остаются недостаточно разработанными, что в свою очередь тормозит развитие как «чистой» и прикладной математики, так и других отраслей науки, в том числе философии. Философия в сфере математики способствует выработке адекватного понимания математического знания, решению естественно возникающих вопросов о предмете и методах математики, специфике ее понятий.
Действительно философское понимание математики может предстать только как сумма выводов, сумма определений, полученных на основе анализа различных ее сторон. Правильное понимание математики не может быть получено умозрительно или путем простого сравнения случаев, которые подходят под известное интуитивное представление, и подыскания затем некоторых объединяющих их признаков. Такой метод необходим для предварительного понимания любого предмета, но сам по себе он недостаточен. Математики много раз меняли представление о своей науке и делали это каждой раз под давлением определенных фактов, которые заставляли их отказаться от устоявшихся привычных воззрений. Другими словами, современное понимание математики не может быть сформулировано как простое собрание имеющихся интуитивных представлений об этой науке, не может быть взято непосредственно из знакомства с теми или другими математическими теориями, то есть только на основе здравого смысла математика. Оно требует исследования истории математики, необходимо прибегнуть к исследованиям ее структуры, функции, отношения к другим наукам.
Условные обозначения, принятые в математическом анализе:
- любой
- существует
! - существует и единственный
- пустое множество
Определение: Если каждому числу х из множества чисел D поставлено в соответствие единственное число у, то говорят, что на множестве D задана функция f и пишут y=f(x), где х - называется независимой переменной или аргументом этой функции, а множество D - область определения этой функции.
Все значения, которые принимает функция f(x) (при х![]() D), образуют область значения (изменения) функции Е.
D), образуют область значения (изменения) функции Е.
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Существует три способа задания функции: табличный, аналитический, графический.
Табличный способ задания функции состоит в том, что для каждого значения аргумента х рядом выписывается соответствующее значение у, получается таблица.
Например:
x
y
3
-2
-1
4
С точки зрения математики здесь изучается зависимость между определенными переменными, другими словами изучается некоторая функция. При опыте ведутся записи, в простейшем случае отмечается время (аргумент функции) и записывается показание прибора (соответствующее значение функции), т.е. функция задается таблицей. А задача исследователя состоит в том, чтобы по полученной таблице изучить функцию.
Способ задания функции с помощью формулы у=f(х), где f(x) некоторое выражение с переменной х - называется аналитическим способом.
Пример. Функция у=f(х) задана аналитической формулой:
![]() Найти f(-х)?
Найти f(-х)?
Чтобы найти f(-х), надо в f(х) всюду вместо х подставить (-х). Получим:
![]()
Пример. Найти область определения функции ![]()
Выражение вида ![]() определено при тех х, для которых х-1
определено при тех х, для которых х-1![]() 0, т.е. при х
0, т.е. при х![]() 1. Значит, область определения функции это луч [1,+∞).
1. Значит, область определения функции это луч [1,+∞).
Пример. Найти области определения и значений функции
y=lg(4-3x-x2).
Решение: Логарифмическая функция определена, если 4-3x-x2>0. Корни квадратного трехчлена: x1=-4, x2=1. Записанное выше неравенство равносильно неравенству -(x+4)(x-1)>0 , что возможно при x>4 и x<1. Область определения данной функции есть интервал (-4;1). Так как в D 0<4-3x-x2![]() 25/4, то интервал (-∞ ;lg(25/4)) - область значения функции.
25/4, то интервал (-∞ ;lg(25/4)) - область значения функции.
Весьма распространённым, особенно в экспериментальных науках, является графический способ задания функции. Рассмотрим множество F точек координатной плоскости XOY, обладающее следующими свойствами: любая прямая, параллельная оси ординат, пересекает это множество не более чем в одной точке. Пусть множество абсцисс всех точек множества F представляет собой отрезок [a,b]. Возьмем произвольное число х из отрезка [a,b] и проведем через точку х прямую параллельную оси ординат. Эта прямая пересекает F в точке М.
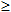
Спроецировав точку М на ось ординат, найдем число f(x), соответствующее числу х. Тем самым на отрезке задана функция у=f(x).
Определение: Графиком функции y=f(x) называется множество точек F(x,y) плоскости XOY, координаты которых удовлетворяют функциональной зависимости y=f(x).
Удобнее всего изучать функцию, заданную и аналитически и графически (по заданной формуле строится график). На практике для построения графика функции составляют таблицу значений функций при некоторых значениях аргумента, наносят на плоскость соответствующие точки и соединяют их плавной линией.
Определение: Если функция u=φ(x) определена на области D, G - область ее значений, функция y=f(u) определена на области G, то функция y=f(φ(x))=T(x) называется сложной функцией, составленной из функции f и φ, или функцией f от функции φ. Функцию y=f(φ(x)) называют композицией двух функций y=f(u) и u=φ(x).
Сложная функция может быть композицией большего числа функций: трех, четырех и т.д. Например, функция y=cos(x2+1) - композиция двух функций y=cosu и u=x2+1; функция y=lg(sin2x) - композиция трех функций.
К основным элементарным функциям относятся пять классов функций: степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические.
Вопросы к лекции №1:
-
Какова роль математики в мире?
-
Какие условные обозначения математического анализа вам знакомы?
-
Что такое функция?
-
Что такое область определения?
-
Что такое область значения?
-
Какие способы задания функции вам известны?
-
Какие классы элементарных функций вам знакомы?
Лекция №2
Тема: «Предел функции»
Цель: Изучить основные свойства и методы вычисления пределов функций.
План лекции:
-
Определение предела функции.
-
Определение односторонних пределов.
-
Предел функции при стремлении аргумента к бесконечности.
-
Основные теоремы о пределах.
-
Примеры вычисления пределов.
Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)
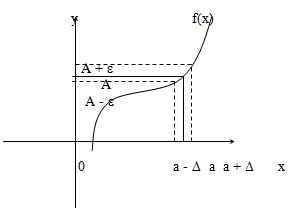
Определение. Число А называется пределом функции f(x) при ха, если для любого >0 существует такое число >0, что для всех х таких, что
0 < x - a <
верно неравенство f(x) - A< . То же определение может быть записано в другом виде:
Если а - < x < a + , x a, то верно неравенство А - < f(x) < A + .
Запись предела функции в точке: 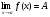
Определение. Если f(x) A1 при х а только при x < a, то 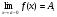 - называется пределом функции f(x) в точке х = а слева, а если f(x) A2 при х а только при x > a, то
- называется пределом функции f(x) в точке х = а слева, а если f(x) A2 при х а только при x > a, то 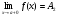 называется пределом функции f(x) в точке х = а справа.
называется пределом функции f(x) в точке х = а справа.
Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.
Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А - конечный предел функции f(x).
Предел функции при стремлении аргумента к бесконечности.
Определение. Число А называется пределом функции f(x) при х, если для любого числа >0 существует такое число М>0, что для всех х, х>M выполняется неравенство
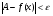
При этом предполагается, что функция f(x) определена в окрестности бесконечности.
Записывают: 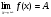
Аналогично можно определить пределы 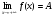 для любого х>M и
для любого х>M и
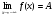 для любого х<M.
для любого х<M.
Основные теоремы о пределах.
Теорема 1. 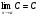 , где С = const.
, где С = const.
Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при ха.
Теорема 2. 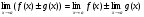
Доказательство этой теоремы будет приведено ниже.
Теорема 3. 
Следствие. 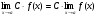
Теорема 4. 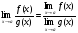 при
при 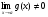
Теорема 5. Если f(x)>0 вблизи точки х = а и 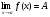 , то А>0.
, то А>0.
Аналогично определяется знак предела при f(x) < 0, f(x) 0, f(x) 0.
Теорема 6. Если g(x) f(x) u(x) вблизи точки х = а и  , то и
, то и  .
.
Определение. Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что f(x)<M вблизи точки х = а.
Теорема 7. Если функция f(x) имеет конечный предел при ха, то она ограничена вблизи точки х = а.
Пример 1. Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
![]()
Пример 2.
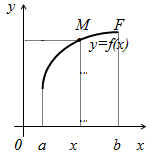
Пример 3.
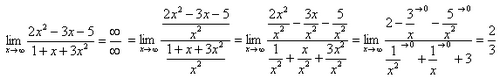
Вопросы к лекции №2:
-
Что такое предел функции?
-
Что такое предел функции слева?
-
Что такое предел функции справа?
-
Какие пределы называются односторонними?
-
Какой предел называют пределом на бесконечности?
-
Перечистите теоремы о пределах?
Лекция №3
Тема: «Дифференциальное исчисление»
Цель: Изучить основные свойства производных. Научить применять теоретические знания при решении задач.
План лекции:
-
Дифференциальное исчисление.
-
Производная функции, ее геометрический и физический смысл.
-
Односторонние производные функции в точке.
-
Основные правила дифференцирования.
-
Производные основных элементарных функций.
Важнейшим понятием математического анализа является производная, которая определяет скорость изменения функции.
Дифференциальное исчисление - раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление дифференциального исчисления в самостоятельную математическую дисциплину связано с именами И. а и Г. а (вторая половина 17 века). Они сформулировали основные положения раздела и чётко указали на взаимно обратный характер операций дифференцирования и интегрирования. Создание дифференциального исчисления открыло новую эпоху в развитии математики. Оно повлекло за собой появление ряда математических дисциплин: теории рядов, теории дифференциальных уравнений, дифференциальной геометрии и вариационного исчисления. Методы математического анализа нашли применение во всех разделах математики.
Производная функции, ее геометрический и физический смысл Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

у
f(x)
f(x0 +x) P
f
f(x0) M
x
x0 x0 + x x
Пусть f(x) определена на некотором промежутке (a, b). Тогда 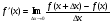 тангенс угла наклона секущей МР к графику функции.
тангенс угла наклона секущей МР к графику функции.
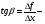 , где - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
, где - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой: 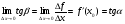
Уравнение нормали к кривой: 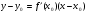 .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t) - закон движения (изменения координат) - мгновенная скорость движения.
Соответственно, вторая производная функции - скорость изменения скорости, т.е. ускорение.
Односторонние производные функции в точке.
Определение. Правой (левой) производной функции f(x) в точке х = х0 называется правое (левое) значение предела отношения 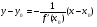 при условии, что это отношение существует.
при условии, что это отношение существует.
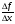
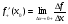
Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.
Например: f(x) = x - имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Понятно, что это условие не является достаточным.
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v - функции, дифференцируемые в точке х.
1) (u v) = u v
2) (uv) = uv + uv
3)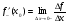 , если v 0
, если v 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)С = 0; 9) 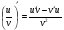
2)(xm) = mxm-1; 10) 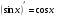
3) 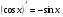 11)
11) 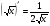
4) 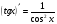 12)
12) 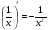
5) 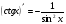 13)
13) 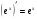
6) 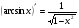 14)
14) 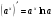
7)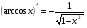 15)
15) 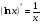
8) 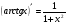 16)
16) 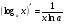
Вопросы к лекции №3:
-
Что такое производная функции?
-
В чем состоит геометрический смысл производной?
-
В чем состоит физический смысл производной?
-
Каковы основные правила дифференцирования?
-
Перечислите несколько производных элементарных функций?
Лекция №4
Тема: «Интегральное исчисление»
Цель: Изучить основные свойства и правила интегрирования.
План лекции:
-
Определение неопределенного интеграла.
-
Свойства неопределенного интеграла.
-
Таблица интегралов.
-
Определенный интеграл.
-
Свойства определенного интеграла.
-
Геометрический смысл определенного интеграла.
-
Примеры вычисления интегралов.
-
Методы интегрирования.
Определение неопределенного интеграла
В дифференциальном исчислении мы решали следующую основную задачу: по данной функции найти ее производную. Рассмотри обратную задачу: дана функция 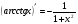 ; требуется найти такую функцию
; требуется найти такую функцию 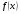 , производная которой равна
, производная которой равна 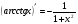 , т.е.:
, т.е.:
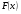 (1)
(1)
Определение. Функция 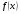 называется первообразной от функции
называется первообразной от функции 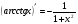 на отрезке
на отрезке 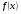 , если во всех точках этого отрезка выполняется равенство (1).
, если во всех точках этого отрезка выполняется равенство (1).
Пример. Найти первообразную от функции 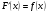 . Из определения первообразной следует, что
. Из определения первообразной следует, что 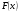 - первообразная функции
- первообразная функции 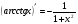 , поскольку:
, поскольку:
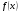 .
.
Задача отыскания по данной функции ее первообразной решается не однозначно. В рассмотренном примере первообразной для функции 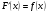 является не только функция
является не только функция 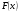 , но и , к примеру,
, но и , к примеру, 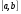 и
и 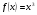 и вообще
и вообще 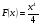 (где
(где 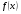 - некоторая константа), что можно проверить дифференцированием данных функций.
- некоторая константа), что можно проверить дифференцированием данных функций.
Теорема. Если функция 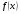 первообразная для функции
первообразная для функции 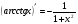 на отрезке
на отрезке 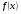 , то всякая другая первообразная для функции
, то всякая другая первообразная для функции 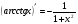 отличается от
отличается от 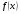 на постоянное слагаемое, т.е. может быть представлено в следующем виде:
на постоянное слагаемое, т.е. может быть представлено в следующем виде:
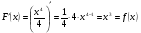
Введем теперь понятие неопределенного интеграла.
Определение. Если функция 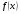 является первообразной для функции
является первообразной для функции 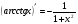 , выражение
, выражение 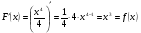 называется неопределенным интегралом и обозначается символом
называется неопределенным интегралом и обозначается символом 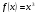 . Таким образом можно записать:
. Таким образом можно записать:
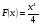
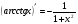 - подынтегральная функция;
- подынтегральная функция;
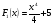 - подынтегральное выражение;
- подынтегральное выражение;
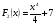 - знак неопределенного интеграла;
- знак неопределенного интеграла;
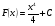 - переменная интегрирования.
- переменная интегрирования.
Свойства неопределенного интеграла
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
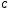
2. Производная от неопределенного интеграла равна подынтегральной функции.
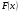
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.
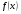
4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов от каждого слагаемого в отдельности, т.е.:
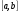
5. Постоянный множитель можно вынести за знак неопределенного интеграла, т.е.:
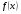
Таблица интегралов
1. 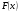
2. 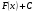
3. 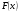
4. 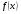
5. 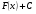
6. 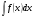
7. 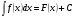
8. 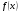
9. 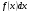
10. 
11. 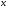
12. 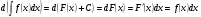
13. 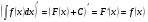
Определенный интеграл
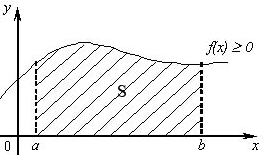
Пусть на отрезке 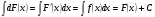 определена неотрицательная функция
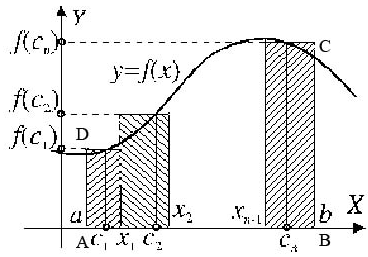
определена неотрицательная функция 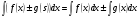 . Рассмотрим криволинейную трапециюADCB, ограниченную кривой f(х), двумя вертикальными прямыми х=a и х=b и отрезком
. Рассмотрим криволинейную трапециюADCB, ограниченную кривой f(х), двумя вертикальными прямыми х=a и х=b и отрезком 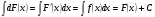 оси
оси 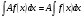 , т.е. криволинейную трапецию.
, т.е. криволинейную трапецию.
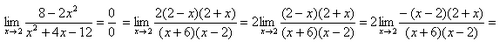
Разобьем отрезок 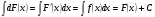 произвольными числами
произвольными числами 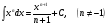 (a< x1,< x2<... xn-1,<b) на
(a< x1,< x2<... xn-1,<b) на 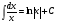 более мелких промежутков
более мелких промежутков 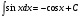 . На каждом из этих промежутков выберем произвольно по одной точке:
. На каждом из этих промежутков выберем произвольно по одной точке: 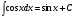 .
.
Составим сумму: 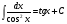 . Она называется интегральной суммой. Каждое слагаемое интегральной суммы представляет собой площадь прямоугольника, покрытого штриховкой на рис. 1. Итак, площадь самой криволинейной трапеции приближенно равна
. Она называется интегральной суммой. Каждое слагаемое интегральной суммы представляет собой площадь прямоугольника, покрытого штриховкой на рис. 1. Итак, площадь самой криволинейной трапеции приближенно равна 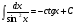 .
.
При безграничном убывании всех 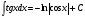 к нулю погрешность этого равенства также стремится к нулю и точное значение площади криволинейной трапеции получается как предел
к нулю погрешность этого равенства также стремится к нулю и точное значение площади криволинейной трапеции получается как предел 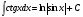 при стремлении всех
при стремлении всех 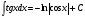 к нулю.
к нулю.
Введем обозначение: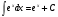 ,
, 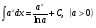 . Величину
. Величину 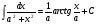 иногда называют параметром разбиения.
иногда называют параметром разбиения.
Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что величина 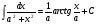 стремится к нулю. Если при этом существует предел
стремится к нулю. Если при этом существует предел
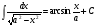 ,
,
то этот предел называется определенным интегралом от функции 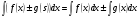 по отрезку
по отрезку 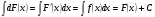 . Если такой предел существует, то он не зависит от первоначального разбиения промежутка
. Если такой предел существует, то он не зависит от первоначального разбиения промежутка 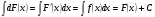 и выбора точек
и выбора точек 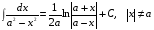 . Для обозначения предела был введен символ:
. Для обозначения предела был введен символ:
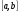
Число а называется нижним пределом интегрирования, а число b верхним пределом интегрирования.
Свойства определенного интеграла.
1. 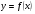
2. 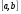
3. 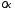
4. 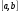
5. 
6. Если для всех
для всех 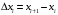 , то
, то 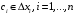
7. Если M - наибольшее значение функции f(x) на отрезке [a;b], а m - наименьшее значение функции f(x) на отрезке [a;b], то
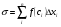
9. Для любых чисел a, b,c
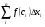
10. Интеграл от нечетной функции по симметричному отрезку равен нулю
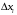
Геометрический смысл определенного интеграла.
Определенный интеграл равен площади криволинейной трапеции, ограниченной кривой 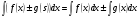 , осью
, осью 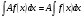 и прямыми
и прямыми 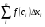 ,
, 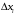 :
: 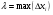
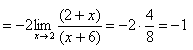
Примеры вычисления интегралов:
-
. Вычислить интеграл
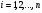 .
.
Решение.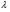 .
.
-
Вычислить интеграл
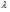 .
.
Решение. На основании свойств определенного интеграла и формулы Ньютона-Лейбница получаем
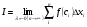
-
Вычислить интеграл
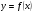 .
.
Решение. Представим дифференциал как 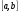 , тогда
, тогда
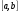
-
Найти неопределенный интеграл:
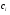 .
.
Решение: 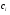 =
=
=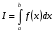
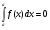
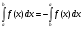
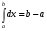
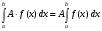 .
.
-
Найти неопределенный интеграл:
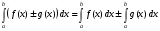 .
.
Решение: 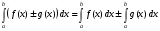 =
=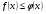
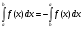
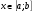 .
.
-
Найти неопределенный интеграл
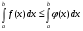
Решение: 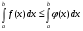 =
=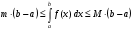
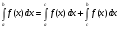
Методы интегрирования
Всякое обратное действие сложнее прямого. Это в полной мере относится к такому действию как интегрирование. Прежде чем воспользоваться таблицей интегралов необходимо заданный интеграл преобразовать к табличному.
Метод замены переменной интегрирования
Это наиболее часто используемый метод. Он применяется, когда подинтегральная функция является сложной функцией.
Пример: Вычислить интеграл: 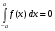
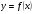
Метод интегрирования по частям
Этот метод применяется тогда, когда подинтегральная функция содержит:
1. Какую-либо обратную функцию: ln x, arcsinx, arccos x и т.д.
2. Произведение степенной функции на экспоненту или тригонометрическую функцию: xsinx, х2ехр х и т.д.
3. Произведение экспоненты на тригонометрическую функцию.
Пример: Вычислить интеграл 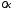
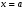 =1
=1
Вопросы к лекции №4:
-
Что такое неопределенный интеграл?
-
Что такое первообразная функции?
-
Перечислите свойства неопределенного интеграла?
-
Назовите некоторые интегралы элементарных функций?
-
Что такое определенный интеграл?
-
В чем отличие определенного и неопределенного интегралов?
-
В чем состоит геометрический смысл определенного интеграла?
-
В чем заключаются методы интегрирования?
Лекция №5
Тема: «Теория вероятности, математическая статистика, дискретная математика»
Цель: Изучить основные свойства теории вероятности и математической статистики.
План лекции:
-
О теории вероятности.
-
Основные понятия и формулы комбинаторики.
-
Перестановки.
-
Сочетания.
-
Размещения.
-
Примеры решения задач.
-
Случайное событие, его частота и вероятность.
-
Достоверные и невозможные события.
-
Аксиомы сложения и умножения вероятностей.
-
Формула Бернулли.
Теория вероятности занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним или невозможным. Согласно П.Лапласу, внесшему, пожалуй, наибольший вклад в развитие теории вероятностей, она "по существу представляет собой не что иное, как здравый смысл, сведенный к вычислениям". Слово "вероятно", его синонимы и производные от него могут употребляться в различных значениях. Примерами некоторых из них являются следующие утверждения: "Возможно, завтра будет дождь", "Вероятно, теория естественного отбора Дарвина верна" и "Если я брошу монету 100 раз, то, вероятно, что она выпадет вверх "орлом" от 40 до 60 раз". Математическая теория вероятностей имеет дело с утверждениями, аналогичными последнему.
Основные понятия и формулы комбинаторики
В обыденной жизни нам нередко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни одного из них, для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи, требующие такого решения, называются комбинаторными.
С теоретико-множественной точки зрения решение комбинаторных задач связано с выбором из некоторого множества подмножеств, обладающих определенными свойствами, и упорядочением множеств. Область математики, в которой изучают комбинаторные задачи, называется комбинаторикой.
Из истории развития теории вероятности - в средние века возникла теория азартных игр, послужившая прообразом будущего математического моделирования. Формулы комбинаторики используются в теории вероятности и математической статистике.
Перестановки
Пусть имеется множество, состоящее из п различных элементов. Упорядоченная последовательность всех элементов этого множества называется перестановкой без повторений (или просто перестановкой). Перестановка без повторений - это размещение без повторений из п элементов по п.
Число перестановок без повторений обозначают Р п.
Формула числа перестановок
Р п = п (п-1) (п-2)... 1 = п!
Обратить внимание. 0! = 1, 1! = 1.
Сочетания
Не всегда нас интересует порядок, в котором располагаются элементы. В тех случаях, когда нас интересует лишь состав группы, говорят о сочетаниях.
Пусть имеется множество, состоящее из п различных элементов. Подмножество из k элементов этого множества называется сочетанием без повторений (или просто сочетанием) из п элементов по т. Число сочетаний обозначают С mn.
Формула для числа сочетаний без повторений:
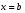
Размещения
В комбинаторике размещением называется расположение "предметов" на некоторых "местах" при условии, что каждое место занято в точности одним предметом и все предметы различны.
В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы < 2,1,3 > и < 3,2,1 > являются различными, хотя состоят из одних и тех же элементов {1,2,3} (то есть, совпадают как сочетания).
Примеры решения задач.
1. Для дежурства с понедельника по субботу назначено 6 студентов, Сколькими способами можно составить график дежурств?
Решение. Так как каждый человек будет дежурить один день, то графики отличаются только порядком дежурства. Таким образом, график - это упорядоченный список из 6 человек. Следовательно, число таких вариантов равно числу перестановок из 6 элементов:
Р6 = 6! = 720.
2. Из 10 терапевтов, 12 хирургов и 15 фельдшеров необходимо выбрать 5 терапевтов, 3 хирургов, 7 фельдшеров. Сколькими способами можно это сделать?
Решение. Записать соответствующие параметры в формулы числа сочетаний и вычислить.
3. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений.
Размещаются здесь десять цифр по 6. Значит, ответ на выше поставленную задачу будет:
![]()
Ответ:151200 способов
4. В группе ТД - 21 обучается 24 студентов. Сколькими способами можно составить график дежурства по техникуму, если группа дежурных состоит из трех студентов?
Решение: число способов равно числу размещений из 24 элементов по 3, т.е. равно А243. По формуле находим
![]()
Ответ: 12144 способа
Случайное событие, его частота и вероятность
Случайными событиями называются такие события, которые могут произойти или не произойти при осуществлении совокупности условий, связанных с возможностью появления данных событий.
Случайные события обозначают буквами А, В, С... Каждое осуществление рассматриваемой совокупности условий называется испытанием. Число испытаний может неограниченно возрастать. Отношение числа т наступлений данного случайного события А в данной серии испытаний к общему числу п испытаний этой серии называется частотой появлений события А в данной серии испытаний (или просто частотой события А). Частота случайного события всегда заключена между нулем и единицей.
Массовые случайные события обладают свойством устойчивости частоты: наблюдаемые в различных сериях однородных испытаний (с достаточно большим числом испытаний в каждой серии) значения частоты данного случайного события колеблются от серии к серии в довольно тесных пределах.
Именно это обстоятельство позволяет при изучении случайных событий применить математические методы, приписывая каждому массовому случайному событию его вероятность, за которую принимается то (вообще говоря, заранее неизвестное) число, около которого колеблется наблюдаемая частота события.
Вероятность, случайного события А обозначается через Р(А). Вероятность случайного события, как и его частота, заключена между нулем и единицей: 0<=Р(А)=> 1
Достоверные и невозможные события
Достоверному событию (т. е. событию, которое должно произойти при каждом испытании) приписывается вероятность Р(А) = 1,
Невозможному событию (т. е. событию, которое не может произойти ни при одном испытании) приписывается вероятность Р(А) = 0.
В некоторых простейших случаях вероятность случайного события может быть определена заранее. Это можно сделать, например тогда, когда возможные результаты каждого из однородных испытаний могут быть представлены в виде п единственно возможных, несовместных друг с другом и равновозможных исходов («случаев»), т. е. кроме этих п исходов не может быть никаких других, никакие два из них не могут произойти одновременно и есть основания считать, что любой из них не является более возможным, чем другие).
Если из этих п единственно возможных, несовместных и равновозможных случаев т случаев связаны с наступлением события А (или, как говорят в теории вероятностей, «благоприятствуют» А), то за вероятность события А принимается отношение m к n: Р (А) = m / n.
Аксиомы сложения и умножения вероятностей
-
Сумма событий
Объединением (или суммой) нескольких случайных событий называется событие, состоящее в осуществлении по крайней мере одного из данных событий.
Объединение событий А1, А2, А3,…Ап обозначается через А1 + А2 + А3 + …+ Ап.
Если объединяемые события несовместны (никакие два из них не могут произойти одновременно), то вероятность объединения нескольких событий равна сумме вероятностей объединяемых событий (аксиома сложения вероятностей):
Р(А1+А2+ …+ Ап) = P(A1)+ Р(А2) + ... + Р(Ап)
Событие, состоящее в не наступлении случайного события А, называется событием, противоположным событию А, и обозначается через 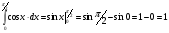 .
.
Объединение событий А и 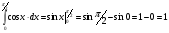 . дает событие достоверно, а так события А и
. дает событие достоверно, а так события А и 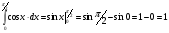 . несовместны, то Р (А) + Р (
. несовместны, то Р (А) + Р (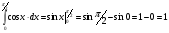 .) = 1 или Р (А) = 1 - Р (
.) = 1 или Р (А) = 1 - Р (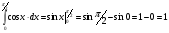 ).
).
Полная группа событий.
Если в результате данного испытания может наступить лишь одно из несовместных событий А1, А2, А3,…Ап, то . события А1, А2, А3,…Ап образуют так называемую полную группу событий. Так как объединение событий полной группы является событием достоверным, то для таких событий имеет место равенство: P(A1)+ Р(А2) + ... + Р(Ап) = 1.
-
Произведение событий.
Совмещением (или произведением) двух случайных событий А1 и А2 называется сложное событие, заключающееся в одновременном или последовательном осуществлении обоих событий. Совмещение событий А1 и А2 обозначается через А1А2.
Под условной вероятностью события А2 по отношению к событию А1 (обозначение Р (A2 / A1 ) понимается вероятность осуществления события А2, определенная в предположении, что событие A1имело место.
Вероятность совмещения двух событии А1 и А2 равна произведению вероятности одного из них на условную вероятность второго по отношению к первому (аксиома умножения вероятностей):
Р (А1•А2) = P(A1)• Р (A2 / A1 ) = Р (А2) • Р (А1/А2).
Два случайных события А1 и А2 называются независимыми, если условная вероятность одного из них по отношению к другому равна безусловной вероятности этого же события: Р (A2 / A1 )=Р(А2).
Для независимых событий вероятность их совмещения равна произведению их вероятностей: Р (А1•А2) = P(A1)• Р(А2)
Формула Бернулли
Если производится п независимых испытании, в каждом из которых вероятность появления события А одна и та же и равна р, то вероятность того, что событие А появится в этих п испытаниях m-раз. выражается формулой Бернулли:
![]()
Пример. В четырех попытках разыгрываются некоторые предметы. Вероятность выигрыша в каждой попытке известна и равна 0,5. Какова вероятность выигрыша ровно трех предметов?
Решение. По формуле Бернулли находим
![]()
Вопросы к лекции №5:
-
Какие задачи называются комбинаторными?
-
Что такое комбинаторика?
-
Что такое перестановки?
-
Что такое сочетания?
-
Что такое случайное событие?
-
Что такое испытание?
-
Что такое вероятность?
-
Какие события называются достоверными и невозможными?
-
Назовите аксиомы сложения и умножения вероятностей?
Список использованной литературы
Основная:
1. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования / Григорьев В. П., Дубинский Ю.А. - 4-е издание - М.: Издательский центр «Академия», 2008 г.
2. "Теория вероятностей и математическая статистика". Гмурман В.Е. М., "Высшая школа", 2008.
3. "Высшая математика в упражнениях и задачах". Учебное пособие в 2-х частях. Данко П.Е., Попов А.Г., Кожевникова Т.Я. М., "Высшая школа", 2008.
4. Фихтенгольц Г. М. «Курс дифференциального и интегрального исчисления».М., «Физматгиз», 2008.
Дополнительная:
1. Колде Я.К. "Практикум по теории вероятностей и математической статистике". М., "Высшая школа", 1991.
2. Матвеева Н.М. "Курс математики для техникумов", ч. 1 и 2. М., "Наука", 1987.
3. Яковлев Г.Н. "Алгебра и начала анализа", ч. 1 и 2. М., "Наука", 1988.