Урок Касательная к окружности

Урок геометрии в 8-м классе

Тема: "Касательная к окружности"

Цели:

• Ввести понятия касательной, точки касания, отрезков касательных, проведенных из одной точки.

• Рассмотреть свойство касательной и ее признак и показать применение при решении задач.

• Рассмотреть свойство отрезков касательных, проведенных из одной точки и развивать его применение в процессе решения задач.

• Рассмотреть свойство касательной и её признак и показать их применение, расширяя кругозор учащихся, в природе и технике.

Задачи урока:

Образовательные:

Обеспечить овладение основными алгоритмическими приёмами построения касательной к окружности,

Сформировать умения применять теоретические знания к решению задач.

Воспитательные:

Развивать мышление и речь учащихся, кругозор.

Работать над формированием умений наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии.

Привитие интереса к математике.

Практические: сформировать умение строить касательную к окружности, рассмотреть примеры в природе и технике.

Оборудование:

Циркуль, треугольник, линейка

Мультимедийный проектор, слайды,

Ход урока

I. Организационный момент.

II. Проверка домашнего задания

1. Повторить элементы окружности

2. От чего зависит взаимное расположение прямой и окружности? (рассказ по слайдам)

3. Три случая расположения прямой и окружности

4. Решение задачи №633 (слайд)

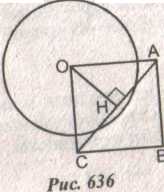
Рисунок 1

III. Актуализация знаний.

Тест с целью проверки теории

Среди следующих утверждений укажите истинные:

Окружность и прямая имеют две общие точки, если:

а) расстояние от центра окружности до прямой не превосхо­дит радиуса окружности;

б) расстояние от центра окружности до прямой меньше ра­диуса окружности;

в) расстояние от окружности до прямой меньше радиуса окружности.

Закончите фразу, чтобы получилось верное высказывание.

Окружность и прямая имеют одну общую точку, если...

Установите истинность или ложность следующих утвержде­ний:

а) Прямая, а является секущей по отношению к окружности,

если она имеет с окружностью общие точки.

б) Прямая, а является секущей по отношению к окружности,

если она пересекает окружность в двух точках.

в) Прямая, а является секущей по отношению к окружности,

если расстояние от центра окружности до данной прямой

не больше радиуса.

IV. Объяснение нового материала.

1. Цели урока:

Сегодня мы более подробно рассмотрим касательную к окружности.

Что мы знаем о касательной к окружности? (определение, расстояние от точки до прямой)

Можете ли вы на чертеже отличить касательную от других прямых?

В тетради начертить окружность произвольного радиуса с центром в точке О, провести касательную в точке А.

Сколько касательных можно провести через точку А

Один ученик выполняет задание у доски.

На этом уроке мы рассмотрим свойства окружности и прямой c.

2. Какими же свойствами обладает эта прямая? Чтобы ответить на этот вопрос - проведите отрезок соединяющий центр окружности и точку касания, измерьте получившийся угол. (90)

- Что можно сказать о касательной и радиусе? - Они перпендикулярны.

3. Прочтите теорему.

Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

Доказательство разбирается в ходе беседы.

Учащиеся делают новый чертёж.

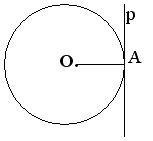
Допустим, что прямая р не перпендикулярна к радиусу ОА(На рисунке сделать построение другим цветом). Сравните расстояние от центра окружности до прямой р с радиусом окружности.

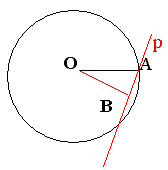
Назовите перпендикуляр к прямой р ОВ

Наклонную ОА

-Расстояние от точки О до прямой р , это ОВ, меньше радиуса окружности ОА, который в данном случае будет являться наклонной по отношению к прямой р, а расстояние от точки О до прямой р - перпендикуляр, а, как известно, любая наклонная больше перпендикуляра, проведённого из той же точки к той же прямой, т. е. ОВ<ОА.

- Сколько тогда общих точек у прямой р и окружности? (2)

- Может ли прямая р быть касательной к окружности? Почему?

Т. к. прямая р имеет две общие точки с окружностью, то она не может бать касательной по определению.

- Верно ли предположение, что прямая р не перпендикулярна радиусу окружности? О чём это говорит?

Предположение не верно, следовательно прямая р перпендикулярна радиусу ОА.

3. Теперь запишем это доказательство в тетради.

Слайд с доказательством.

A к окружности, А-точка касания.

Доказать: рОА.

Доказательство:

Предположим, что рОА, тогда ОА наклонная к прямой р, а ОВр, т. к. ОВ<ОА, то расстояние от центра окружности О до прямой р меньше радиуса, следовательно прямая р и окружность имеют две общие точки, что противоречит условию: прямая р - касательная, т. о. р ОА.

V. Закрепление.

1. Построение касательной.

Вернемся к нашему рисунку.

Проверьте, правильно ли вы построили касательную?

Что для этого нужно сделать?

Построение: Ученик, подготовленный заранее, объясняет построение касательной к окружности в заданной точке. Учащиеся выполняют построение в тетради.

Дано: окружность, О - центр, А - лежит на окружности.

Построить касательную к окружности в точке А.

ОА - прямая.

От точки А отложим ОА=ОА.

Из точек О и О проведём окружности, радиусом большим ОА.

Через точки пересечения окружностей проведём прямую а.

Прямая, а будет касательной по определению.

Еще один способ практический способ построения касательной с помощью зеркала. Как вы думаете, как с помощью зеркала проверить правильно ли вы построили касательную

2. Решите задачи по готовым чертежам

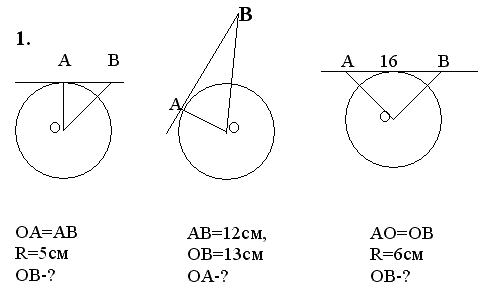
VI. Применение касательной для науки и техники

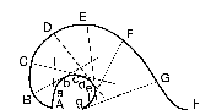
1.Построение эвольвенты.

Эвольвентой круга называется траектория точки, лежащей на прямой, которая перекатывается без скольжения по окружности радиуса r_в, называемой основной.

2. У Лукоморья дуб зелёный
   
   Златая цепь на дубе том.
   
   И днём и ночью кот учёный
   
   Всё ходит по цепи кругом.

Нам эти строки знакомы с детства, мы никогда не задумывались над тем, какую линию вычерчивает кот.

Как вы думаете, что это за линия? (Чаще всего ученики отвечают - окружность)

Два ученика, выходят к столу, на котором расположен ватман, макет дуба и небольшой котёнок (мягкая игрушка), к которому прикреплен маркер, привязанный к "дубу".

Один ученик придерживает "дуб", а второй передвигает игрушку "по цепи кругом". На ватмане вычерчивается кривая.

Учитель показывает слайды построения эвольвенты.

Таким образом для построения этой кривой надо хорошо уметь строить касательную в заданной точке.

С этой же кривой связана и биология .

3. Ученик рассказывает о берёзовом долгоносике, демонстрируя разрез листа , и сворачивает его.

Слайд с циклоидой

4. Слайд о космической скорости

5 Искры на точильном камне, брызги от буксующего колеса летят по касательной

VII. Закрепление изученного материала (обучающая самостоятельная работа)

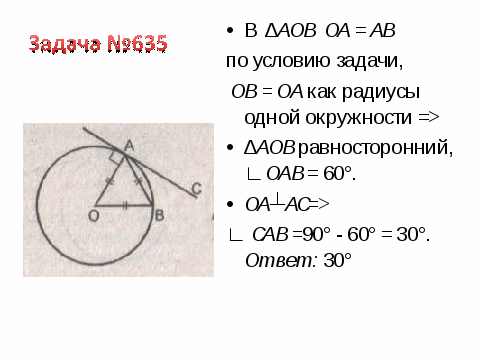
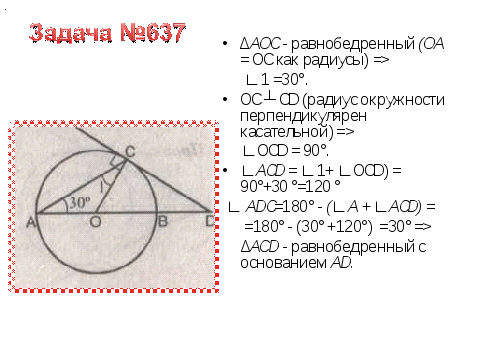
VIII. Подведение итогов.

Что нового мы узнали сегодня на уроке?

Выставление оценок

IX. Домашнее задание.

П. 69, страница 159 вопросы 1-4,

страница 178,

решить задачи №634,636